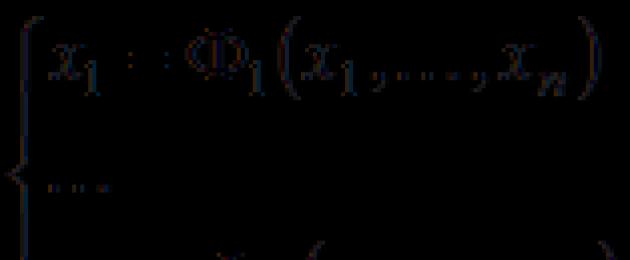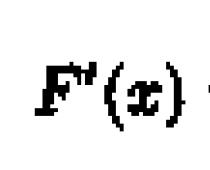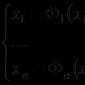Usando il metodo delle iterazioni semplici, risolvi un sistema di equazioni non lineari. Risolvere sistemi di equazioni non lineari

Il sistema di equazioni non lineari ha la forma:

Qui ci sono variabili sconosciute e il sistema (7) è chiamato sistema di ordine normale se almeno una delle funzioni è non lineare.

Risolvere sistemi di equazioni non lineari è uno dei problemi più difficili della matematica computazionale. La difficoltà è determinare se il sistema ha una soluzione e, in caso affermativo, quante. Il perfezionamento delle soluzioni in una determinata area è un compito più semplice.

Lascia che le funzioni siano definite in aree. Quindi la regione sarà la regione in cui è possibile trovare la soluzione. I metodi più comuni per perfezionare la soluzione sono il metodo delle iterazioni semplici e il metodo di Newton.

Metodo di iterazioni semplici per la risoluzione di sistemi di equazioni non lineari

Dal sistema originario (7), mediante trasformazioni equivalenti, si passa ad un sistema della forma:

Processo iterativo definito da formule

puoi iniziare dando una prima approssimazione. Una condizione sufficiente per la convergenza del processo iterativo è una delle due condizioni:

Scriviamo la prima condizione:

Scriviamo la seconda condizione:

Consideriamo uno dei modi per portare il sistema (7) alla forma (8) che ammette iterazioni convergenti.

Sia dato un sistema del secondo ordine della forma:

È necessario portarlo nel modulo:

Moltiplichiamo la prima equazione del sistema per una costante sconosciuta, la seconda per, quindi le aggiungiamo e le aggiungiamo a entrambi i lati dell'equazione. Otteniamo la prima equazione del sistema trasformato

Determiniamo le costanti incognite dalle condizioni di convergenza sufficienti

Scriviamo queste condizioni in modo più dettagliato:

Assumendo che le espressioni sotto il segno del modulo siano uguali a zero, otteniamo un sistema di quattro equazioni con quattro incognite per la determinazione delle costanti:

Con tale scelta di parametri, le condizioni di convergenza saranno soddisfatte se le derivate parziali delle funzioni e cambieranno non molto rapidamente in prossimità del punto.

Per risolvere il sistema, è necessario impostare l'approssimazione iniziale e calcolare i valori delle derivate e, a questo punto. Il calcolo viene eseguito ad ogni passaggio delle iterazioni, mentre,.

Il metodo delle iterazioni semplici è autocorrettivo, universale e facile da implementare su un computer. Se il sistema ha un ordine grande, l'uso di questo metodo, che ha un tasso di convergenza lento, non è raccomandato. In questo caso viene utilizzato il metodo di Newton, che ha una convergenza più rapida.

Metodo di Newton per la risoluzione di sistemi di equazioni non lineari

Sia richiesto di risolvere un sistema di equazioni non lineari della forma (7). Supponiamo che la soluzione esista in un dominio in cui tutte le funzioni sono continue e hanno almeno la derivata prima. Il metodo di Newton è un processo iterativo, che viene eseguito secondo una determinata formula della seguente forma:

Difficoltà nell'utilizzo del metodo di Newton:

esiste una matrice inversa?

va fuori zona?

Il metodo modificato di Newton semplifica il primo compito. La modifica consiste nel fatto che la matrice viene calcolata non in ogni punto, ma solo in quello iniziale. Pertanto, il metodo di Newton modificato ha la seguente formula:

Ma il metodo di Newton modificato non dà una risposta alla seconda domanda.

Il processo iterativo secondo le formule (8) o (10) termina se è soddisfatta la seguente condizione

Il vantaggio del metodo di Newton è la sua rapida convergenza rispetto al metodo delle iterazioni semplici.

Formula di calcolo Il metodo di Newton sembra:

dove n=0,1,2,..

Geometricamente Il metodo di Newton significa che l'approssimazione successiva alla radice è il punto di intersezione con l'asse x. tangente tracciata al grafico della funzione y=f(x) al punto.

Teorema sulla convergenza del metodo di Newton.

Sia una semplice radice dell'equazione, in un intorno di cui la funzione è due volte continuamente differenziabile.

Allora c'è un intorno così piccolo della radice che, per una scelta arbitraria dell'approssimazione iniziale da questo intorno, la successione iterativa del metodo di Newton non va oltre l'intorno ed è valida la seguente stima

Il metodo di Newton(1) sensibile alla scelta dell'approssimazione iniziale X 0 .

In pratica, per la convergenza monotona del metodo, è necessario:

1a derivata f(x)

2a derivata f(x) deve essere di segno costante sull'intervallo di localizzazione [ a , b ] di una radice isolata;

per la prima approssimazione X 0 viene scelto quel limite dell'intervallo di localizzazione su cui il prodotto della funzione e la sua derivata 2a è maggiore di zero (f(c)f '' (c) > 0 , dove c è uno dei limiti dell'intervallo) .

. Per una certa precisione >

Come affermato nel teorema, il metodo di Newton ha convergenza locale, cioè la sua area di convergenza è un piccolo intorno della radice .

Una scelta sbagliata può dare una sequenza iterativa divergente.

Il metodo dell'iterazione semplice (il metodo delle ripetizioni successive).

Per applicare il metodo di iterazione semplice, segue l'equazione originale convertire in un modulo conveniente per l'iterazione .

Questa trasformazione può essere eseguita in vari modi.

La funzione è chiamata funzione iterativa.

La formula di calcolo del metodo di iterazione semplice è:

dove n=0,1,2,..

Teorema sulla convergenza del metodo dell'iterazione semplice.

Sia in qualche intorno della radice che la funzione sia continuamente differenziabile e soddisfi la disuguaglianza

dove 0 < q < 1 - costante.

Quindi, indipendentemente dalla scelta dell'approssimazione iniziale dall'intorno specificato, la sequenza iterativa non lascia questo intorno, il metodo converge

con la velocità della sequenza geometrica e la stima dell'errore :

Criterio di cessazione del processo iterativo .

Per una data accuratezza >0, i calcoli dovrebbero essere eseguiti fino alla disuguaglianza

Se il valore è , è possibile utilizzare un criterio più semplice per la fine delle iterazioni:

Se nella disuguaglianza (5) q > 1, allora il metodo iterativo (4) diverge.

Se nella disuguaglianza (5) q= 1 , allora il metodo iterativo (4) può convergere o divergere.

Nel caso se q > = 1 , allora il metodo iterativo (4) diverge e

applicato metodo di iterazione semplice con parametro di iterazione.

Il punto chiave nell'applicazione è la trasformazione equivalente dell'equazione:

af(x) = 0

x = x+af(x), (9)

dove α – parametro iterativo (costante reale).

Formula di calcolo metodo di iterazione semplice con parametro di iterazione sembra:

X (n+1) = x (n) + af(x (n) ) , (10)

dove n=0,1,2,..

Il processo iterativo costruito secondo la forma (10) converge, Se:

1a derivata di una funzione f(x)è di segno costante e delimitata sull'intervallo di localizzazione di una radice isolata;

segno di parametro iterativo α opposto al segno della derivata 1a della funzione f(x) sull'intervallo di localizzazione di una radice isolata;

modulo valore parametro iterativo α è stimato dalla disuguaglianza

| α | < 2/M , (11)

dove M è il modulo massimo della 1a derivata della funzione f(x)

Quindi, con tale scelta del parametro iterativo , il metodo (10) converge per qualsiasi valore dell'approssimazione iniziale appartenente all'intervallo , al ritmo di una progressione geometrica con denominatore q uguale a

dove m è il modulo minimo della 1a derivata della funzione f(x) sull'intervallo di localizzazione di una radice isolata.

MINISTERO DELL'ISTRUZIONE E DELLA SCIENZA DELL'UCRAINA

SUMY STATE UNIVERSITÀ

Dipartimento di Informatica

CORSO DI LAVORO

A CORSO:

Metodi numerici

"Metodi iterativi per la risoluzione di sistemi di equazioni non lineari"

1. Metodi per risolvere sistemi di equazioni non lineari. Informazione Generale

2.1 Metodo delle iterazioni semplici

2.2 Trasformazione di Aitken

2.3 Il metodo di Newton

2.3.1 Modifiche al metodo di Newton

2.3.2 Metodi quasi newtoniani

2.4 Altri metodi iterativi per la risoluzione di sistemi di equazioni non lineari

2.4.1 Metodo Picard

2.4.2 Metodo di discesa del gradiente

2.4.3 Metodo di rilassamento

3. Implementazione di metodi iterativi in ​​modo programmatico e utilizzando il pacchetto matematico Maple

3.1 Metodo di iterazione semplice

3.2 Metodo di discesa del gradiente

3.3 Il metodo di Newton

3.4 Metodo di Newton modificato

Elenco della letteratura usata

1. Metodi per la risoluzione di equazioni non lineari. Informazione Generale.

Diamo un sistema di equazioni, dove

- alcuni operatori non lineari: (1.1)

Può anche essere rappresentato in forma matriciale:

(1.1)

La sua soluzione è chiamata tale valore

, per cui

Un problema molto comune è il problema computazionale di trovare alcune o tutte le soluzioni del sistema (1.1) da n equazioni algebriche o trascendentali non lineari con n sconosciuto.

Indica con X vettore colonna ( X 1 , X 2 ,..., x n)T e scrivi il sistema di equazioni sotto forma di formula (1.2): F(X) = 0, dove F=(f 1 , f 2 ,...,fn)T.

Tali sistemi di equazioni possono sorgere direttamente, ad esempio, durante la progettazione di sistemi fisici, o indirettamente. Quindi, ad esempio, quando si risolve il problema di ridurre al minimo una determinata funzione G(X) è spesso necessario determinare quei punti in cui il gradiente di questa funzione è uguale a zero. Supponendo F= grad g, otteniamo un sistema non lineare.

In contrasto con i sistemi di equazioni algebriche lineari, che possono essere risolti utilizzando entrambi dritto(o preciso) e iterativo(o approssimativo) metodi, la soluzione di sistemi di equazioni non lineari può essere ottenuta solo con metodi approssimati, iterativi. Consentono di ottenere una sequenza di approssimazioni

. Se il processo iterativo converge, allora il valore limite è la soluzione del dato sistema di equazioni.

Per una completa comprensione dei metodi per trovare una soluzione al sistema, è necessario spiegare un concetto come il "tasso di convergenza". Se per la sequenza x n, convergendo al limite X *, la formula è corretta

(Kè un numero reale positivo), allora Kè detto tasso di convergenza della successione data.

2. Metodi iterativi per la risoluzione di sistemi di equazioni non lineari

2.1 Metodo delle iterazioni semplici

Il metodo delle iterazioni semplici (approssimazioni successive) è uno dei principali in matematica computazionale e viene utilizzato per risolvere un'ampia classe di equazioni. Descriviamo e giustifichiamo questo metodo per sistemi di equazioni non lineari della forma

f io (x 1 ,x 2 ,...x n) = 0, io=1,2,..n;

Portiamo il sistema di equazioni in una forma speciale:

(2.1)

O in forma vettoriale

. (2.2)

Inoltre, il passaggio a questo sistema dovrebbe avvenire solo a condizione che

è una mappatura di contrazione.

Usando qualche approssimazione iniziale X(0) = (x 1 (0) ,x 2 (0) ,...x n (0))

costruire un processo iterativo X (k+1) =  (X (k)). I calcoli continuano fino a quando la condizione non viene soddisfatta

. Allora la soluzione del sistema di equazioni è il punto fisso della mappatura.

Giustifichiamo il metodo in una certa norma

spazi.

Presentiamo un teorema sulla convergenza, il cui soddisfacimento delle condizioni porta a trovare una soluzione al sistema.

Teorema (sulla convergenza). Permettere

uno). La funzione vettoriale Ф(х) è definita nel dominio

; la condizione

3). equa disuguaglianza

Quindi in un processo iterativo:

, – soluzione del sistema di equazioni; ,

Commento. La disuguaglianza della condizione 2) è la condizione di Lipschitz per la funzione vettoriale Ф(х) nel dominio S con una costante

(condizione di compressione). Lo mostra Fè l'operatore di contrazione nel dominio S, cioè l'equazione (2.2) è soggetta al principio della mappatura delle contrazioni. Le affermazioni del teorema indicano che l'equazione (2.2) ha una soluzione nella regione S, e approssimazioni successive convergono a questa soluzione al ritmo di una successione geometrica con denominatore q.

Prova. Perché il

, quindi per l'approssimazione, dovuta all'ipotesi 3), abbiamo . Significa che . Mostriamo che , k=2,3,… e per approssimazioni vicine la disuguaglianza (2.3) è soddisfatta

Discuteremo per induzione. In

l'affermazione è vera, perché e . Assumiamo che le approssimazioni appartengano a S e che la disuguaglianza (2.3) valga per . Poiché , quindi per tenere conto della condizione 2) del teorema abbiamo .

Per ipotesi induttiva

LAVORO DI LABORATORIO №3-4.

Opzione numero 5.

Obbiettivo: imparare a risolvere sistemi di equazioni non lineari (SNU) con il metodo delle iterazioni semplici (MPI) e il metodo di Newton utilizzando un computer.

1. Studiare MPI e metodo di Newton per la risoluzione di sistemi di equazioni non lineari.

2. Utilizzando un esempio specifico, apprendere la procedura per risolvere i sistemi di equazioni non lineari di MPI e il metodo di Newton utilizzando un computer.

3. Scrivete un programma e usatelo per risolvere un sistema di equazioni con una precisione di .

ESEMPIO DI LAVORO

Esercizio.

1. Risolvi analiticamente il SLE:

2. Costruire le formule di lavoro del metodo MPI e di Newton per la soluzione numerica del sistema all'approssimazione iniziale: .

3. Scrivere un programma in qualsiasi linguaggio di programmazione che implementi il ​​processo iterativo costruito.

Soluzione.

Metodo analitico.

La soluzione analitica della LSE sono i punti e .

Metodo delle iterazioni semplici (MPI).

Per costruire le formule di lavoro dell'MPI per la soluzione numerica del sistema, è necessario prima portarlo nella forma:

Per fare ciò, moltiplichiamo la prima equazione del sistema per una costante sconosciuta, la seconda per, quindi le aggiungiamo e le aggiungiamo a entrambe le parti dell'equazione. Otteniamo la prima equazione del sistema trasformato:

Determiniamo le costanti incognite dalle condizioni sufficienti per la convergenza del processo iterativo:

Scriviamo queste condizioni in modo più dettagliato:

Assumendo che le espressioni sotto il segno del modulo siano uguali a zero, otteniamo un sistema di equazioni algebriche lineari (SLAE) di ordine 4 con 4 incognite:

Per risolvere il sistema è necessario calcolare le derivate parziali:

Quindi lo SLAE sarà scritto come segue:

Si noti che se le derivate parziali cambiano poco in prossimità dell'approssimazione iniziale, allora:

Quindi lo SLAE sarà scritto come segue:

La soluzione di questo sistema sono i punti , , , . Quindi le formule di lavoro dell'MPI per la risoluzione della LSE assumeranno la forma:

Per l'implementazione su computer, le formule di lavoro possono essere riscritte come segue:

Il processo iterativo può essere avviato impostando l'approssimazione iniziale x 0 =-2, y 0 =-4. Il processo termina quando due condizioni sono soddisfatte contemporaneamente: e . In questo caso, i valori e sono un valore approssimativo di una delle soluzioni LSE.

Il metodo di Newton.

Costruire formule di lavoro del metodo di Newton nella forma

dove , è necessario:

1. Trova la matrice delle derivate parziali:

2. Trova il determinante di questa matrice:

3. Definisci la matrice inversa:

Dopo aver effettuato le trasformazioni:

Otteniamo la formula di lavoro del metodo di Newton per l'implementazione su un computer:

diagramma a blocchi Il metodo di MPI e Newton per la risoluzione di LSE è mostrato nella Figura 1.

Fig.1 Schemi di MPI e metodo di Newton.

Testi del programma:

Programma P3_4; (Iterazioni)

utilizza Crt;

var: intero;

clrscr;

xn:=x-(x-y+2)+(1/2)*(x*y-3);

yn:=y+(2/3)*(x-y+2)+(1/6)*(x*y-3);

writeln (n:3, x:9:5, xn:9:5, (xn-x):9:5, y:9:5, yn:9:5, (yn-y):9:5) ;

n:=n+1;

fino a (abs(x-zx)<=eps) and (abs(y-zy)<=eps);

leggilo;

2) Metodo di Newton:

Programma P3_4; (Newton)

utilizza Crt;

var: intero;

x0,x,xn,y0,y,yn,eps,zx,zy:real;

clrscr;

n:=0; x0:=-2; x:=x0; y0:=-4; y:=y0; eps:=0,001;

writeln (" n x(i) x(i+1) x(i+1)-x(i) y(i) y(i+1) y(i+1)-y(i)");

xn:=x-(1/(x+y))*(x*x-x*y+2*x+x-y+2);

yn:=y-(1/(x+y))*(x*y*(-y)-3*(-y)+x*y-3);

writeln (n:3, x:9:5, xn:9:5, abs(xn-x):9:5, y:9:5, yn:9:5, abs(yn-y):9: 5);

n:=n+1;

fino a (abs(x-zx)<=eps) and (abs(y-zy)<=eps);

Risultati dello sviluppo del programma:

· Fig. 2 – un programma che funziona secondo il metodo delle iterazioni semplici;

· Fig.3 - programma, funzionante secondo il metodo di Newton.

Fig.2 Risposta: x(16)≈-3.00023, y(16)≈-1.00001

Fig.3 Risposta: x(8)≈-3.00000, y(8)≈-1.00000

Il metodo dell'iterazione semplice, chiamato anche metodo di approssimazione successiva, è un algoritmo matematico per trovare il valore di una quantità incognita raffinandola gradualmente. L'essenza di questo metodo è che, come suggerisce il nome, esprimendo via via quelli successivi dall'approssimazione iniziale, si ottengono risultati sempre più raffinati. Questo metodo viene utilizzato per trovare il valore di una variabile in una data funzione, nonché per risolvere sistemi di equazioni, sia lineari che non lineari.

Consideriamo come questo metodo viene implementato durante la risoluzione di SLAE. Il metodo di iterazione semplice ha il seguente algoritmo:

1. Verifica della condizione di convergenza nella matrice originaria. Teorema di convergenza: se la matrice originaria del sistema ha dominanza diagonale (cioè, in ogni riga, gli elementi della diagonale principale devono essere maggiori in modulo della somma degli elementi delle diagonali secondarie in modulo), allora il metodo del semplice iterazioni è convergente.

2. La matrice del sistema originario non ha sempre una dominanza diagonale. In questi casi, il sistema può essere modificato. Le equazioni che soddisfano la condizione di convergenza non vengono toccate e con quelle che non lo soddisfano formano combinazioni lineari, cioè moltiplicare, sottrarre, sommare equazioni tra loro fino ad ottenere il risultato desiderato.

Se nel sistema risultante ci sono coefficienti scomodi sulla diagonale principale, i termini della forma c i *x i vengono aggiunti a entrambe le parti di tale equazione, i cui segni devono coincidere con i segni degli elementi diagonali.

3. Trasformazione del sistema risultante nella forma normale:

x - =β - +α*x -

Questo può essere fatto in molti modi, ad esempio, come segue: dalla prima equazione, esprimi x 1 in termini di altre incognite, dalla seconda - x 2, dalla terza - x 3, ecc. Qui usiamo le formule:

α ij = -(a ij / a ii)

io = b io /a ii
Dovresti nuovamente assicurarti che il sistema risultante di forma normale soddisfi la condizione di convergenza:

∑ (j=1) |α ij |≤ 1, mentre i= 1,2,...n

4. Iniziamo ad applicare, infatti, lo stesso metodo delle approssimazioni successive.

x (0) - approssimazione iniziale, esprimiamo tramite esso x (1) , quindi tramite x (1) esprimiamo x (2) . La formula generale in forma matriciale si presenta così:

x (n) = β - +α*x (n-1)

Calcoliamo fino a raggiungere la precisione richiesta:

max |x io (k)-x io (k+1) ≤ ε

Quindi, diamo un'occhiata al metodo di iterazione semplice in pratica. Esempio:
Risolvi SLAE:

4,5x1-1,7x2+3,5x3=2
3,1x1+2,3x2-1,1x3=1
1.8x1+2.5x2+4.7x3=4 con accuratezza ε=10 -3

Vediamo se predominano gli elementi diagonali modulo.

Vediamo che solo la terza equazione soddisfa la condizione di convergenza. Trasformiamo la prima e la seconda equazione, aggiungiamo la seconda alla prima equazione:

7,6x1+0,6x2+2,4x3=3

Sottrarre il primo dal terzo:

2,7x1+4,2x2+1,2x3=2

Abbiamo convertito il sistema originale in uno equivalente:

7,6x1+0,6x2+2,4x3=3
-2,7x1+4,2x2+1,2x3=2
1,8x1+2,5x2+4,7x3=4

Ora riportiamo il sistema alla normalità:

x1=0,3947-0,0789x2-0,3158x3
x2=0,4762+0,6429x1-0,2857x3
x3= 0,8511-0,383x1-0,5319x2

Verifichiamo la convergenza del processo iterativo:

0.0789+0.3158=0,3947 ≤ 1
0.6429+0.2857=0.9286 ≤ 1
0,383+ 0,5319= 0,9149 ≤ 1 , cioè la condizione è soddisfatta.

0,3947
Ipotesi iniziale x(0) = 0,4762
0,8511

Sostituendo questi valori nell'equazione di forma normale, otteniamo i seguenti valori:

0,08835
x(1) = 0,486793
0,446639

Sostituendo nuovi valori, otteniamo:

0,215243
x(2) = 0,405396
0,558336

Continuiamo i calcoli finché non ci avviciniamo ai valori che soddisfano la condizione data.

x(7) = 0,441091

Verifichiamo la correttezza dei risultati ottenuti:

4,5*0,1880 -1.7*0,441+3.5*0,544=2,0003
3.1*0.1880+2.3*0.441-1.1x*0.544=0.9987
1.8*0,1880+2.5*0,441+4.7*0,544=3,9977

I risultati ottenuti sostituendo i valori trovati nelle equazioni originali soddisfano pienamente le condizioni dell'equazione.

Come possiamo vedere, il semplice metodo di iterazione fornisce risultati abbastanza accurati, tuttavia, per risolvere questa equazione, abbiamo dovuto dedicare molto tempo ed eseguire calcoli ingombranti.