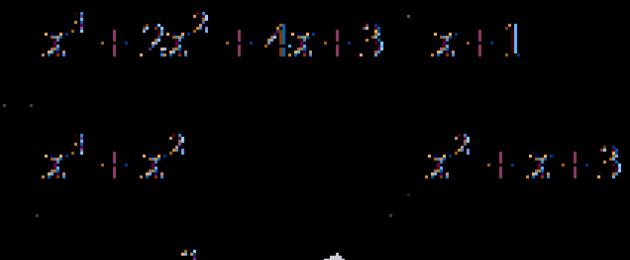Soluzione dell'equazione di 5° grado in radicali. Soluzione di equazioni di grado superiore

Al canale youtube del nostro sito sito per essere a conoscenza di tutte le nuove video lezioni.

Per prima cosa, ricordiamo le formule di base dei gradi e le loro proprietà.

Prodotto di un numero un accade su se stesso n volte, possiamo scrivere questa espressione come a a … a=a n

1. a 0 = 1 (a ≠ 0)

3. un n un m = un n + m

4. (un n) m = un nm

5. a n b n = (ab) n

7. a n / a m \u003d a n - m

Potenza o equazioni esponenziali - sono equazioni in cui le variabili sono in potenze (o esponenti) e la base è un numero.

Esempi di equazioni esponenziali:

In questo esempio, il numero 6 è la base, è sempre in basso, e la variabile X grado o misura.

Diamo altri esempi di equazioni esponenziali.
2 x *5=10
16x-4x-6=0

Ora diamo un'occhiata a come vengono risolte le equazioni esponenziali?

Prendiamo una semplice equazione:

2x = 2 3

Un tale esempio può essere risolto anche nella mente. Si può notare che x=3. Dopotutto, in modo che la sinistra e parte destra erano uguali, devi mettere il numero 3 invece di x.
Ora vediamo come dovrebbe essere presa questa decisione:

2x = 2 3
x = 3

Per risolvere questa equazione, abbiamo rimosso stessi motivi(cioè, due) e annota ciò che è rimasto, questi sono gradi. Abbiamo ottenuto la risposta che stavamo cercando.

Ora riassumiamo la nostra soluzione.

Algoritmo per risolvere l'equazione esponenziale:
1. Necessità di controllare lo stesso se le basi dell'equazione a destra ea sinistra. Se i motivi non sono gli stessi, stiamo cercando opzioni per risolvere questo esempio.
2. Dopo che le basi sono le stesse, equiparare grado e risolvere la nuova equazione risultante.

Ora risolviamo alcuni esempi:

Iniziamo in modo semplice.

Le basi sui lati sinistro e destro sono uguali al numero 2, il che significa che possiamo scartare la base e uguagliare i loro gradi.

x+2=4 L'equazione più semplice è risultata.
x=4 - 2
x=2
Risposta: x=2

Nell'esempio seguente, puoi vedere che le basi sono diverse, queste sono 3 e 9.

3 3x - 9x + 8 = 0

Per cominciare, trasferiamo i nove sul lato destro, otteniamo:

Ora devi fare le stesse basi. Sappiamo che 9=3 2 . Usiamo la formula della potenza (a n) m = a nm .

3 3x \u003d (3 2) x + 8

Otteniamo 9 x + 8 \u003d (3 2) x + 8 \u003d 3 2 x + 16

3 3x \u003d 3 2x + 16 ora è chiaro che le basi sui lati sinistro e destro sono le stesse e uguali a tre, il che significa che possiamo scartarle ed eguagliare i gradi.

3x=2x+16 ha ottenuto l'equazione più semplice
3x-2x=16
x=16
Risposta: x=16.

Diamo un'occhiata al seguente esempio:

2 2x + 4 - 10 4x \u003d 2 4

Prima di tutto, guardiamo le basi, le basi sono due e quattro diverse. E dobbiamo essere gli stessi. Trasformiamo la quadrupla secondo la formula (a n) m = a nm .

4x = (2 2)x = 2 2x

E usiamo anche una formula a n a m = a n + m:

2 2x+4 = 2 2x 2 4

Aggiungi all'equazione:

2 2x 2 4 - 10 2 2x = 24

Abbiamo fatto un esempio per le stesse ragioni. Ma altri numeri 10 e 24 interferiscono con noi: cosa farne? Se guardi da vicino, puoi vedere che sul lato sinistro ripetiamo 2 2x, ecco la risposta: possiamo mettere 2 2x tra parentesi:

2 2x (2 4 - 10) = 24

Calcoliamo l'espressione tra parentesi:

2 4 — 10 = 16 — 10 = 6

Dividiamo l'intera equazione per 6:

Immagina 4=2 2:

2 2x \u003d 2 2 basi sono le stesse, scartale e identifica i gradi.
2x \u003d 2 si è rivelata l'equazione più semplice. Lo dividiamo per 2, otteniamo
x = 1
Risposta: x = 1.

Risolviamo l'equazione:

9 x - 12*3 x +27= 0

Trasformiamo:
9 x = (3 2) x = 3 2x

Otteniamo l'equazione:
3 2x - 12 3x +27 = 0

Le nostre basi sono le stesse, pari a 3. In questo esempio è chiaro che la prima tripla ha un grado doppio (2x) rispetto alla seconda (solo x). In questo caso, puoi decidere metodo di sostituzione. Il numero con il grado più piccolo è sostituito da:

Quindi 3 2x \u003d (3 x) 2 \u003d t 2

Sostituiamo tutti i gradi con x nell'equazione con t:

t 2 - 12t + 27 \u003d 0
Otteniamo un'equazione quadratica. Risolviamo attraverso il discriminante, otteniamo:
D=144-108=36
t1 = 9
t2 = 3

Torna a Variabile X.

Prendiamo t 1:
t 1 \u003d 9 \u003d 3 x

Questo è,

3x = 9
3 x = 3 2
x 1 = 2

È stata trovata una radice. Cerchiamo il secondo, da t 2:
t 2 \u003d 3 \u003d 3 x
3 x = 3 1
x 2 = 1
Risposta: x 1 \u003d 2; x 2 = 1.

Sul sito puoi nella sezione AIUTARE A DECIDERE di porre domande di tuo interesse, ti risponderemo sicuramente.

Unisciti a un gruppo

In generale, un'equazione che ha un grado maggiore di 4 non può essere risolta in radicali. Ma a volte possiamo ancora trovare le radici del polinomio a sinistra nell'equazione di grado più alto, se lo rappresentiamo come prodotto di polinomi in un grado non superiore a 4. La soluzione di tali equazioni si basa sulla scomposizione del polinomio in fattori, quindi ti consigliamo di rivedere questo argomento prima di studiare questo articolo.

Molto spesso, si ha a che fare con equazioni di grado superiore con coefficienti interi. In questi casi, possiamo provare a trovare radici razionali, e quindi fattorizzare il polinomio per poi convertirlo in un'equazione di grado inferiore, che sarà facile da risolvere. Nell'ambito di questo materiale, considereremo proprio questi esempi.

Equazioni di grado superiore a coefficienti interi

Tutte le equazioni della forma a n x n + a n - 1 x n - 1 + . . . + a 1 x + a 0 = 0 , possiamo ridurre a un'equazione dello stesso grado moltiplicando entrambi i membri per a n n - 1 e cambiando la variabile della forma y = a n x:

un n x n + un n - 1 x n - 1 + . . . + a 1 x + a 0 = 0 ann xn + an - 1 ann - 1 xn - 1 + … + a 1 (an) n - 1 x + a 0 (an) n - 1 = 0 y = anx ⇒ yn + bn - 1 yn - 1 + … + b 1 y + b 0 = 0

Anche i coefficienti risultanti saranno interi. Quindi, dovremo risolvere l'equazione ridotta dell'ennesimo grado con coefficienti interi, che ha la forma x n + a n x n - 1 + ... + a 1 x + a 0 = 0.

Calcoliamo le radici intere dell'equazione. Se l'equazione ha radici intere, devi cercarle tra i divisori del termine libero a 0. Scriviamoli e li sostituiamo nell'uguaglianza originale uno per uno, controllando il risultato. Una volta ottenuta un'identità e trovata una delle radici dell'equazione, possiamo scriverla nella forma x - x 1 · P n - 1 (x) = 0 . Qui x 1 è la radice dell'equazione e P n - 1 (x) è il quoziente di x n + a n x n - 1 + ... + a 1 x + a 0 diviso per x - x 1 .

Sostituisci i restanti divisori in P n - 1 (x) = 0 , iniziando con x 1 , poiché le radici possono essere ripetute. Dopo aver ottenuto l'identità, si considera trovata la radice x 2 e l'equazione può essere scritta come (x - x 1) (x - x 2) P n - 2 (x) \u003d 0. Qui P n - 2 (x ) sarà quoziente dalla divisione di P n - 1 (x) per x - x 2 .

Continuiamo a selezionare i divisori. Trova tutte le radici intere e denota il loro numero come m. Dopodiché, l'equazione originale può essere rappresentata come x - x 1 x - x 2 · … · x - x m · P n - m (x) = 0 . Qui P n - m (x) è un polinomio di n - m -esimo grado. Per il calcolo è conveniente utilizzare lo schema di Horner.

Se la nostra equazione originale ha coefficienti interi, non possiamo finire con radici frazionarie.

Di conseguenza, abbiamo ottenuto l'equazione P n - m (x) = 0, le cui radici possono essere trovate in qualsiasi modo conveniente. Possono essere irrazionali o complessi.

Facciamo vedere esempio specifico come viene applicato un tale schema di soluzione.

Esempio 1

Condizione: trova la soluzione dell'equazione x 4 + x 3 + 2 x 2 - x - 3 = 0 .

Soluzione

Iniziamo con la ricerca di radici intere.

Abbiamo un'intercettazione pari a meno tre. Ha divisori pari a 1 , - 1 , 3 e - 3 . Sostituiamoli nell'equazione originale e vediamo quale di essi darà identità come risultato.

Per x uguale a uno, otteniamo 1 4 + 1 3 + 2 1 2 - 1 - 3 \u003d 0, il che significa che uno sarà la radice di questa equazione.

Ora dividiamo il polinomio x 4 + x 3 + 2 x 2 - x - 3 per (x - 1) in una colonna:

Quindi x 4 + x 3 + 2 x 2 - x - 3 = x - 1 x 3 + 2 x 2 + 4 x + 3.

1 3 + 2 1 2 + 4 1 + 3 = 10 ≠ 0 (- 1) 3 + 2 (- 1) 2 + 4 - 1 + 3 = 0

Abbiamo un'identità, il che significa che abbiamo trovato un'altra radice dell'equazione, uguale a - 1.

Dividiamo il polinomio x 3 + 2 x 2 + 4 x + 3 per (x + 1) in una colonna:

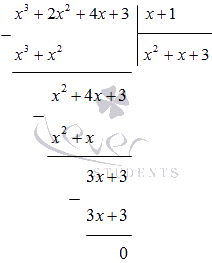
Lo capiamo

x 4 + x 3 + 2 x 2 - x - 3 = (x - 1) (x 3 + 2 x 2 + 4 x + 3) = = (x - 1) (x + 1) (x 2 + x + 3)

Sostituiamo il prossimo divisore nell'equazione x 2 + x + 3 = 0, partendo da - 1:

1 2 + (- 1) + 3 = 3 ≠ 0 3 2 + 3 + 3 = 15 ≠ 0 (- 3) 2 + (- 3) + 3 = 9 ≠ 0

Le uguaglianze risultanti non saranno corrette, il che significa che l'equazione non ha più radici intere.

Le radici rimanenti saranno le radici dell'espressione x 2 + x + 3 .

D \u003d 1 2 - 4 1 3 \u003d - 11< 0

Ne consegue che questo trinomio quadrato non ha radici reali, ma ve ne sono di coniugate complesse: x = - 1 2 ± i 11 2 .

Chiariamo che invece di dividere in una colonna, si può usare lo schema di Horner. Questo viene fatto in questo modo: dopo aver determinato la prima radice dell'equazione, riempiamo la tabella.

Nella tabella dei coefficienti, possiamo vedere immediatamente i coefficienti del quoziente dalla divisione dei polinomi, che significa x 4 + x 3 + 2 x 2 - x - 3 = x - 1 x 3 + 2 x 2 + 4 x + 3.

Dopo aver trovato la radice successiva, uguale a - 1 , otteniamo quanto segue:

Risposta: x \u003d - 1, x \u003d 1, x \u003d - 1 2 ± io 11 2.

Esempio 2

Condizione: risolvi l'equazione x 4 - x 3 - 5 x 2 + 12 = 0.

Soluzione

Il membro libero ha divisori 1 , - 1 , 2 , - 2 , 3 , - 3 , 4 , - 4 , 6 , - 6 , 12 , - 12 .

Controlliamoli in ordine:

1 4 - 1 3 - 5 1 2 + 12 = 7 ≠ 0 (- 1) 4 - (- 1) 3 - 5 (- 1) 2 + 12 = 9 ≠ 0 2 4 2 3 - 5 2 2 + 12 = 0

Quindi x = 2 sarà la radice dell'equazione. Dividi x 4 - x 3 - 5 x 2 + 12 per x - 2 usando lo schema di Horner:

Di conseguenza, otteniamo x - 2 (x 3 + x 2 - 3 x - 6) = 0 .

2 3 + 2 2 - 3 2 - 6 = 0

Quindi 2 sarà di nuovo una radice. Dividi x 3 + x 2 - 3 x - 6 = 0 per x - 2:

Di conseguenza, otteniamo (x - 2) 2 (x 2 + 3 x + 3) = 0 .

Controllare i restanti divisori non ha senso, poiché l'uguaglianza x 2 + 3 x + 3 = 0 è più veloce e conveniente da risolvere usando il discriminante.

Risolviamo l'equazione quadratica:

x 2 + 3 x + 3 = 0 D = 3 2 - 4 1 3 = - 3< 0

Otteniamo una complessa coppia coniugata di radici: x = - 3 2 ± i 3 2 .

Risposta: x = - 3 2 ± io 3 2 .

Esempio 3

Condizione: trova le radici reali per l'equazione x 4 + 1 2 x 3 - 5 2 x - 3 = 0.

Soluzione

x 4 + 1 2 x 3 - 5 2 x - 3 = 0 2 x 4 + x 3 - 5 x - 6 = 0

Eseguiamo la moltiplicazione 2 3 di entrambe le parti dell'equazione:

2 x 4 + x 3 - 5 x - 6 = 0 2 4 x 4 + 2 3 x 3 - 20 2 x - 48 = 0

Sostituiamo le variabili y = 2 x:

2 4 x 4 + 2 3 x 3 - 20 2 x - 48 = 0 y 4 + y 3 - 20 y - 48 = 0

Di conseguenza, abbiamo ottenuto un'equazione standard di 4° grado, che può essere risolta secondo lo schema standard. Controlliamo i divisori, dividiamo e alla fine otteniamo che ha 2 radici reali y \u003d - 2, y \u003d 3 e due complesse. Non presenteremo l'intera soluzione qui. In virtù della sostituzione, le radici reali di questa equazione saranno x = y 2 = - 2 2 = - 1 e x = y 2 = 3 2 .

Risposta: x 1 \u003d - 1, x 2 \u003d 3 2

Se noti un errore nel testo, evidenzialo e premi Ctrl+Invio

Nel XVI secolo, i matematici si imbattono in numeri complessi quasi per caso (vedi capitolo 11). A XVIII secolo i numeri complessi erano considerati un'estensione del dominio dei numeri reali, ma lavorare con essi portava comunque a un errore di parità, poiché Leonard E, nel suo grande lavoro sulla teoria dei numeri Arithmetical Investigations (1801), evitava l'uso del cosiddetto "immaginario numeri". Mi sembra che la parte più importante di questo lavoro sia la prima dimostrazione del teorema fondamentale dell'algebra. Gauss si rese conto dell'importanza di questo teorema, creando diverse dimostrazioni aggiuntive negli anni successivi. Nel 1849 ha rivisto la prima versione, questa volta utilizzando numeri complessi. Usando termini moderni, possiamo dire che per qualsiasi equazione polinomiale finita con coefficienti reali o complessi, tutte le sue radici saranno numeri reali o complessi. Quindi, otteniamo una risposta negativa all'annosa domanda se la soluzione delle equazioni polinomiali richieda ordine elevato creare numeri di ordine superiore a quelli complessi.

Uno dei problemi più spinosi dell'algebra di quel tempo era la questione se sia possibile risolvere con metodi algebrici, cioè usando un numero finito di passi algebrici, un polinomio di quinto ordine - un quintico. Ora la scuola insegna la formula per risolvere le equazioni quadratiche e dal XVI secolo sono noti metodi simili per risolvere le equazioni di terzo e quarto grado (Capitolo 11). Ma nessun metodo è stato trovato per i quinti. Può sembrare che il teorema fondamentale dell'algebra contenga la promessa di una risposta positiva, ma in realtà garantisce semplicemente che esistono soluzioni, non dice nulla sull'esistenza di formule che danno soluzioni esatte (metodi numerici e grafici approssimativi esistevano già da quella volta). E poi c'erano due geni della matematica con un destino tragico.

Niels Henrik Abel (1802–1829) nacque in una grande famiglia povera che viveva in un piccolo villaggio della Norvegia, un paese devastato da lunghi anni di guerra con l'Inghilterra e la Svezia. Il maestro, che era amico del ragazzo, gli diede lezioni private, ma dopo la morte del padre, all'età di diciotto anni, nonostante giovane età e salute fragile, Abele fu costretto a mantenere la sua famiglia. Nel 1824 pubblicò un articolo scientifico in cui affermava che il quintico non è risolvibile algebricamente, come, infatti, qualsiasi polinomio di ordine superiore. Abel credeva che questo articolo sarebbe servito come suo passaggio per il mondo scientifico e lo inviò a Gauss presso l'Università di Gottinga. Sfortunatamente, Gauss non è mai riuscito a tagliare le pagine con un coltello (qualsiasi lettore doveva farlo a quei tempi) e non ha letto l'articolo. Nel 1826, il governo norvegese ha finalmente fornito fondi per Abel per viaggiare in giro per l'Europa. Temendo che il contatto personale con Gauss non gli avrebbe portato grande gioia, il matematico decise di non visitare Göttingen e andò invece a Berlino. Lì fece amicizia con August Leopold Crelle (1780–1855), un matematico, architetto e ingegnere che consigliò il Ministero dell'Istruzione prussiano in materia di matematica. Krell stava per fondare il Journal of Clean and matematica applicata". Così Abel ebbe l'opportunità di distribuire il suo lavoro e pubblicò molto, soprattutto nei primi numeri della Rivista, che iniziò subito a essere considerata una pubblicazione scientifica molto prestigiosa e autorevole. Il norvegese vi pubblicò una versione estesa della sua dimostrazione che il quintico è irrisolvibile con metodi algebrici. E poi è andato a Parigi. Questo viaggio ha sconvolto molto Abel, perché praticamente non ha ricevuto il sostegno dei matematici francesi di cui aveva così tanto bisogno. Si avvicinò ad Augustin Louis Cauchy (1789-1857), che a quel tempo era il principale luminare analisi matematica ma era molto complesso. Come disse lo stesso Abel, "Cauchy è pazzo e non si può farci nulla, anche se al momento è l'unico capace di qualcosa in matematica". Se si cerca di giustificare la mancanza di rispetto e il disprezzo emanati da Gauss e Cauchy, si può dire che il Quintic raggiunse una certa fama e attirò l'attenzione sia di rispettati matematici che di originali. Abele tornò in Norvegia, dove soffriva sempre più di tubercolosi. Continuò a inviare la sua opera a Crelle, ma morì nel 1829, ignaro della misura in cui la sua reputazione in mondo scientifico. Due giorni dopo la sua morte, Abel ricevette un'offerta per assumere una posizione scientifica a Berlino.

Abel ha mostrato che qualsiasi polinomio al di sopra del quarto ordine non può essere risolto usando radicali, come radici quadrate, radici cubiche o ordine superiore. Tuttavia, le condizioni esplicite in cui, in casi speciali, questi polinomi potrebbero essere risolti, e il metodo per risolverli, sono stati formulati da Galois. Évariste Galois (1811–1832) visse una vita breve e movimentata. Era un matematico incredibilmente dotato. Galois era implacabile nei confronti di coloro che considerava meno talentuosi di lui e allo stesso tempo non sopportava l'ingiustizia sociale. Non mostrò alcuna attitudine per la matematica finché non lesse Elements of Geometry di Legendre (pubblicato nel 1794, questo libro fu il principale libro di testo per i successivi cento anni). Poi ha letteralmente ingoiato il resto delle opere di Legendre e, in seguito, di Abele. Il suo entusiasmo, la fiducia in se stessi e l'intolleranza hanno portato a conseguenze davvero disastrose nei suoi rapporti con insegnanti ed esaminatori. Galois ha partecipato al concorso per l'ammissione al Politecnico, la culla della matematica francese, ma per impreparazione non ha superato l'esame. Per qualche tempo dopo aver incontrato un nuovo insegnante che ne ha riconosciuto il talento, è riuscito a mantenere la calma. Nel marzo 1829 Galois pubblicò il suo primo articolo sulle frazioni continue, che considerava il suo lavoro più significativo. Ha inviato un messaggio sulle sue scoperte all'Accademia delle scienze e Cauchy ha promesso di presentarle, ma ha dimenticato. Inoltre, ha semplicemente perso il manoscritto.

Il secondo fallimento di Galois nell'entrare nella Scuola Politecnica è entrato nel folklore matematico. Era così abituato ad avere costantemente idee matematiche complesse nella sua testa che era infuriato per la meschina pignoleria degli esaminatori. Poiché gli esaminatori avevano difficoltà a capire le sue spiegazioni, gettò un panno cancellabile in faccia a uno di loro. Poco dopo, suo padre morì, suicidandosi a causa di intrighi della chiesa. Al suo funerale è quasi scoppiata una rivolta. Nel febbraio 1830 Galois scrisse i seguenti tre articoli, inviandoli all'Accademia delle scienze per il Gran Premio di matematica. Joseph Fourier, allora segretario dell'Accademia, morì senza averli letti e dopo la sua morte gli articoli non furono trovati tra le sue carte. Un tale flusso di delusioni farebbe crollare chiunque. Galois si ribellò contro coloro che erano al potere perché sentiva che non riconoscevano i suoi meriti e uccisero suo padre. Si tuffò a capofitto nella politica, diventando un ardente repubblicano - non la decisione più saggia in Francia nel 1830. In un ultimo disperato tentativo, inviò un articolo scientifico al famoso fisico e matematico francese Siméon Denis Poisson (1781–1840), che in risposta chiese ulteriori prove.

Questa era l'ultima cannuccia. Nel 1831 Galois fu arrestato due volte - prima con l'accusa di chiedere l'assassinio del re Luigi Filippo, e poi per proteggerlo - le autorità temevano una rivolta repubblicana! Questa volta, è stato condannato a sei mesi di reclusione con l'accusa inventata di aver indossato illegalmente l'uniforme del battaglione di artiglieria sciolto a cui si era unito. Rilasciato sulla parola, ha intrapreso un'attività che lo disgustava tanto quanto qualsiasi altra cosa nella vita. Nelle lettere al suo devoto amico Chevalier si sente la sua delusione. Il 29 maggio 1832 accettò una sfida a duello, le cui ragioni non sono del tutto chiare. “Sono caduto vittima di una civettuola disonorevole. La mia vita sta svanendo in una miserabile lite", scrive in una lettera a tutti i repubblicani. Più lavoro notevole Galois è stato abbozzato la notte prima del duello fatale. Le denunce sono sparse ai margini: "Non ho più tempo, non ho più tempo". Doveva lasciare ad altri i dettagli dei passaggi intermedi che non erano essenziali per comprendere l'idea principale. Aveva bisogno di buttare su carta le basi delle sue scoperte: le origini di quello che oggi è chiamato il teorema di Galois. Concluse il suo testamento chiedendo a Chevalier di "richiedere a Jacobi e Gauss di esprimere pubblicamente la loro opinione, non sulla correttezza, ma sull'importanza di questi teoremi". Al mattino presto, Galois andò a incontrare il suo rivale. Hanno dovuto sparare da una distanza di 25 passi. Galois è stato ferito ed è morto in ospedale la mattina successiva. Aveva solo vent'anni.

Galois ha fatto affidamento sul lavoro di Lagrange e Cauchy, ma ha sviluppato un metodo più generale. Era estremamente traguardo importante nel campo della risoluzione dei quinti. Lo scienziato ha prestato meno attenzione alle equazioni originali o all'interpretazione grafica e ha pensato di più alla natura delle radici stesse. Per semplificare, Galois considerava solo i cosiddetti quintici irriducibili, cioè quelli che non potevano essere fattorizzati sotto forma di polinomi di ordine inferiore (come dicevamo, per eventuali equazioni di polinomi fino al quarto ordine esistono formule per trovarne le radici ). In generale, un polinomio irriducibile con coefficienti razionali è un polinomio che non può essere scomposto in polinomi più semplici che hanno coefficienti razionali. Ad esempio, (x 5 - 1) può essere fattorizzato (x-1)(x 4 + x 3 + x 2 + x + 1), invece (x 5 - 2) irriducibile. L'obiettivo di Galois era determinare le condizioni in cui tutte le soluzioni di un'equazione polinomiale irriducibile generale possono essere trovate in termini di radicali.

La chiave della soluzione è che le radici di qualsiasi equazione algebrica irriducibile non sono indipendenti, possono essere espresse l'una nei termini dell'altra. Queste relazioni sono state formalizzate nel gruppo di tutte le possibili permutazioni, il cosiddetto gruppo di simmetria radice - per un quintico questo gruppo contiene 5! = 5 x 4 x 3 x 2 x 1 = 120 elementi. Gli algoritmi matematici della teoria di Galois sono molto complessi e, molto probabilmente, anche per questo, furono inizialmente compresi con grande difficoltà. Ma dopo che il livello di astrazione ha permesso di passare dalle soluzioni algebriche delle equazioni alla struttura algebrica dei gruppi ad esse associati, Galois è stato in grado di prevedere la solvibilità dell'equazione in base alle proprietà di tali gruppi. Inoltre, la sua teoria forniva anche un metodo con cui si potevano trovare queste stesse radici. Per quanto riguarda i quinti, il matematico Joseph Liouville (1809–1882), che nel 1846 pubblicò più opere di Galois nel suo Journal of Pure and Applied Mathematics, notò che il giovane scienziato si dimostrò un "bellissimo teorema", e affinché "un'equazione irriducibile del grado originario sia risolvibile in termini di radicali, è necessario e sufficiente che tutte le sue radici sono funzioni razionali, due di esse». Poiché questo è impossibile per un quintico, non può essere risolto con i radicali.

In tre anni, il mondo matematico ha perso due delle sue nuove stelle più luminose. Seguirono accuse reciproche e ricerche dell'anima, e Abel e Galois ottennero il meritato riconoscimento, ma solo postumo. Nel 1829 Carl Jacobi, tramite Legendre, venne a conoscenza del manoscritto "perduto" di Abele e nel 1830 scoppiò uno scandalo diplomatico quando il console norvegese a Parigi chiese che l'articolo del suo connazionale fosse trovato. Alla fine, Cauchy ha trovato l'articolo, solo per averlo perso di nuovo negli editori dell'accademia! Nello stesso anno, Abel ricevette il Gran Premio di Matematica (insieme a Jacobi) - ma era già morto. Nel 1841 fu pubblicata la sua biografia. Nel 1846, Liouville curò alcuni dei manoscritti di Galois per la pubblicazione e nella sua introduzione espresse rammarico per il fatto che l'accademia avesse inizialmente rifiutato il lavoro di Galois a causa della sua complessità - "in effetti, la chiarezza della presentazione è necessaria quando l'autore conduce il lettore fuori dai sentieri battuti in territori selvaggi inesplorati". Continua: “Galois non c'è più! Non cadiamo in inutili critiche. Scartiamo i difetti e guardiamo alle virtù! Frutta breve vita Galois è contenuto in sole sessanta pagine. Il direttore della rivista matematica per i candidati all'École Normale e all'Ecole Polytechnique ha commentato così il caso Galois: “Un candidato con un'intelligenza elevata è stato eliminato da un esaminatore con un livello di pensiero inferiore. Barbarus hic ego sum, quia non intelligor illis."

Innanzitutto, la seconda pagina di quest'opera non è gravata di nomi, cognomi, descrizioni della posizione nella società, titoli ed elegie in onore di qualche principe avaro, la cui borsa si aprirà con questi incensi - con la minaccia di chiuderla quando le lodi saranno finite. Non vedrai qui lodi rispettose, scritte in lettere tre volte più grandi del testo stesso, rivolte a chi ha una posizione elevata nella scienza, a qualche saggio mecenate - cosa obbligatoria (direi inevitabile) per qualcuno dell'età di venti che vuole scrivere qualcosa. Non sto dicendo a nessuno qui che sono in debito con i loro consigli e il loro supporto per tutte le cose buone del mio lavoro. Non lo dico perché sarebbe una bugia. Se dovessi citare uno dei grandi della società o della scienza (attualmente la differenza tra queste due classi di persone è quasi impercettibile), giuro non sarebbe un segno di gratitudine. Lo devo a loro di aver pubblicato il primo di questi due articoli così tardi, e di aver scritto tutto questo in carcere - in un luogo che difficilmente può essere considerato adatto alla riflessione scientifica, e mi stupisco spesso della mia moderazione e capacità di mantengo la bocca chiusa in relazione agli stupidi e viziosi Zoil. Mi sembra di poter usare la parola "Zoils" senza temere di essere accusato di indecenza, poiché è così che mi riferisco ai miei avversari. Non scriverò qui come e perché fui mandato in prigione, ma devo dire che i miei manoscritti il ​​più delle volte si perdevano semplicemente nelle cartelle dei signori dell'accademia, anche se, a dire il vero, non riesco a immaginare una tale indiscrezione da parte di persone sulla cui coscienza la morte di Abele. Secondo me, chiunque vorrebbe essere paragonato a questo geniale matematico. Basti pensare che il mio articolo sulla teoria delle equazioni è stato inviato all'Accademia delle scienze nel febbraio 1830, che gli estratti sono stati inviati nel febbraio 1829, eppure nessuno di essi è stato stampato, e anche il manoscritto si è rivelato essere impossibile tornare.

Galois, prefazione inedita, 1832

Classe: 9

Obiettivi di base:

1. Consolidare il concetto di equazione razionale intera di th grado.
2. Formulare i principali metodi per risolvere equazioni di grado superiore (n > 3).
3. Insegnare i metodi di base per risolvere equazioni di grado superiore.
4. Insegnare con la forma dell'equazione per determinare di più metodo efficace le sue decisioni.

Forme, metodi e tecniche pedagogiche utilizzati dall'insegnante nella lezione:

• Sistema di formazione a lezione-seminario (lezioni frontali - spiegazione di nuovo materiale, seminari - risoluzione dei problemi).
• Tecnologie dell'informazione e della comunicazione (rilevamento frontale, lavoro orale con la classe).
• Formazioni differenziate, di gruppo e individuali.
• L'uso del metodo della ricerca nella formazione finalizzata allo sviluppo apparato matematico e capacità mentali di ogni singolo studente.
• Materiale stampato: un riepilogo individuale della lezione (concetti di base, formule, dichiarazioni, materiale della lezione viene compresso sotto forma di diagrammi o tabelle).

Piano di lezione:

1. Organizzare il tempo.
   Lo scopo dello stage: coinvolgere gli studenti attività didattiche definire il contenuto della lezione.
2. Aggiornare le conoscenze degli studenti.
   Lo scopo dello stage: aggiornare le conoscenze degli studenti su argomenti correlati precedentemente studiati
3. Imparare un nuovo argomento (lezione). Scopo dello stage: formulare i principali metodi per la risoluzione di equazioni di grado superiore (n > 3)
4. Riassumendo.
   Lo scopo dello stage: evidenziare ancora una volta i punti chiave del materiale studiato a lezione.
5. Compiti a casa.
   Scopo della fase: formulare compiti a casa per studenti.

Riepilogo della lezione

1. Momento organizzativo.

La formulazione dell'argomento della lezione: “Equazioni di gradi superiori. Metodi per la loro soluzione”.

2. Attualizzazione delle conoscenze degli studenti.

Indagine teorica - conversazione. Ripetizione di alcune informazioni precedentemente studiate dalla teoria. Gli studenti formulano definizioni di base e forniscono affermazioni di teoremi necessari. Vengono forniti esempi che dimostrano il livello di conoscenza precedentemente acquisito.

• Il concetto di equazione con una variabile.
• Il concetto della radice dell'equazione, la soluzione dell'equazione.
• concetto equazione lineare con una variabile, il concetto di equazione quadratica con una variabile.
• Il concetto di equivalenza delle equazioni, equazione-conseguenze (il concetto di radici estranee), transizione non di conseguenza (il caso della perdita delle radici).
• Il concetto del tutto espressione razionale con una variabile.
• Il concetto di un'intera equazione razionale n esimo grado. La forma standard di un'intera equazione razionale. intero ridotto equazione razionale.
• Transizione a un insieme di equazioni di gradi inferiori calcolando l'equazione originale.
• Il concetto di polinomio n esimo grado da X. Il teorema di Bezout. Conseguenze dal teorema di Bezout. Teoremi della radice ( Z-radici e Q-radici) di un'intera equazione razionale a coefficienti interi (rispettivamente ridotti e non ridotti).
• Lo schema di Horner.

3. Imparare un nuovo argomento.

Considereremo l'intera equazione razionale n esima potenza della forma standard con una variabile sconosciuta x:Pn(x)= 0 , dove P n (x) = un n x n + un n-1 x n-1 + un 1 x + un 0– polinomio n esimo grado da X, un n ≠ 0 . Se un n = 1 allora tale equazione è chiamata equazione razionale intera ridotta n esimo grado. Consideriamo tali equazioni per valori diversi n ed elencare i metodi principali della loro soluzione.

n= 1 è un'equazione lineare.

n= 2 è un'equazione quadratica. Formula discriminante. Formula per il calcolo delle radici. Il teorema di Vieta. Selezione di un quadrato intero.

n= 3 è un'equazione cubica.

metodo di raggruppamento.

Esempio: x 3 – 4 x 2 – x+ 4 = 0 (x - 4) (x 2– 1) = 0 X 1 = 4 , x2 = 1,X 3 = -1.

Equazione cubica reciproca della forma ascia 3 + bx 2 + bx + un= 0. Risolviamo combinando termini con gli stessi coefficienti.

Esempio: X 3 – 5X 2 – 5X + 1 = 0 (X + 1)(X 2 – 6X + 1) = 0 X 1 = -1, X 2 = 3 + 2, X 3 = 3 – 2.

Selezione delle radici Z in base al teorema. Lo schema di Horner. Quando si applica questo metodo, è necessario sottolineare che l'enumerazione in questo caso è finita e selezioniamo le radici secondo un certo algoritmo secondo il teorema su Z-radici dell'equazione razionale intera ridotta a coefficienti interi.

Esempio: X 3 – 9X 2 + 23X– 15 = 0. L'equazione viene ridotta. Scriviamo i divisori del termine libero ( + 1; + 3; + 5; + 15). Applichiamo lo schema di Horner:

	X 3	X 2	X 1	X 0	produzione
	1	-9	23	-15
1	1	1 x 1 - 9 = -8	1 x (-8) + 23 = 15	1 x 15 - 15 = 0	1 - radice
	X 2	X 1	X 0

Noi abbiamo ( X – 1)(X 2 – 8X + 15) = 0 X 1 = 1, X 2 = 3, X 3 = 5.

Equazione a coefficienti interi. Selezione di radici Q in base al teorema. Lo schema di Horner. Quando si applica questo metodo, è necessario sottolineare che l'enumerazione in questo caso è finita e selezioniamo le radici secondo un certo algoritmo secondo il teorema di Q-radici di un'equazione razionale intera non ridotta a coefficienti interi.

Esempio: 9 X 3 + 27X 2 – X– 3 = 0. L'equazione non viene ridotta. Scriviamo i divisori del termine libero ( + 1; + 3). Scriviamo i divisori del coefficiente alla massima potenza dell'incognita. ( + 1; + 3; + 9) Pertanto, cercheremo delle radici tra i valori ( + 1; + ; + ; + 3). Applichiamo lo schema di Horner:

	X 3	X 2	X 1	X 0	produzione
	9	27	-1	-3
1	9	1 x 9 + 27 = 36	1 x 36 - 1 = 35	1 x 35 - 3 = 32 ≠ 0	1 non è una radice
-1	9	-1 x 9 + 27 = 18	-1 x 18 - 1 = -19	-1 x (-19) - 3 = 16 ≠ 0	-1 non è una radice
	9	x9 + 27 = 30	x 30 - 1 = 9	x 9 - 3 = 0	radice
	X 2	X 1	X 0

Noi abbiamo ( X – )(9X 2 + 30X + 9) = 0 X 1 = , X 2 = - , X 3 = -3.

Per comodità di calcolo quando si sceglie Q -radici può essere conveniente apportare un cambio di variabile, andare all'equazione sopra e regolare Z -radici.

• Se l'intercetta è 1

.

• Se è possibile utilizzare la sostituzione del modulo y=kx

.

Formula Cardano. Esiste un metodo universale per risolvere le equazioni cubiche: questa è la formula di Cardano. Questa formula è associata ai nomi dei matematici italiani Gerolamo Cardano (1501–1576), Nicolò Tartaglia (1500–1557), Scipione del Ferro (1465–1526). Questa formula non rientra nell'ambito del nostro corso.

n= 4 è un'equazione di quarto grado.

metodo di raggruppamento.

Esempio: X 4 + 2X 3 + 5X 2 + 4X – 12 = 0 (X 4 + 2X 3) + (5X 2 + 10X) – (6X + 12) = 0 (X + 2)(X 3 + 5X- 6) = 0 (X + 2)(X– 1)(X 2 + X + 6) = 0 X 1 = -2, X 2 = 1.

Metodo di sostituzione variabile.

• Equazione biquadratica della forma ascia 4 + bx 2+s = 0 .

Esempio: X 4 + 5X 2 - 36 = 0. Sostituzione y = X 2. Da qui y 1 = 4, y 2 = -9. Ecco perché X 1,2 = + 2 .

• Equazione reciproca del quarto grado della forma ascia 4 + bx 3+c X 2 + bx + un = 0.

Risolviamo combinando termini con gli stessi coefficienti sostituendo la forma

• ascia 4 + bx 3 + cx 2 – bx + un = 0.

• Equazione generalizzata all'indietro del quarto grado della forma ascia 4 + bx 3 + cx 2 + kbx + k2 a = 0.

• Sostituzione generale. Alcune sostituzioni standard.

Esempio 3 . Sostituzione vista generale(segue dalla forma di una particolare equazione).

n = 3.

Equazione a coefficienti interi. Selezione delle radici Q n = 3.

Formula generale. Esiste un metodo universale per risolvere le equazioni di quarto grado. Questa formula è associata al nome di Ludovico Ferrari (1522-1565). Questa formula non rientra nell'ambito del nostro corso.

n > 5 - equazioni di quinto grado e superiori.

Equazione a coefficienti interi. Selezione delle radici Z in base al teorema. Lo schema di Horner. L'algoritmo è simile a quello discusso sopra per n = 3.

Equazione a coefficienti interi. Selezione delle radici Q in base al teorema. Lo schema di Horner. L'algoritmo è simile a quello discusso sopra per n = 3.

Equazioni simmetriche. Ogni equazione reciproca di grado dispari ha una radice X= -1 e dopo averlo scomposto in fattori, otteniamo che un fattore ha la forma ( X+ 1) e il secondo fattore è un'equazione reciproca di grado pari (il suo grado è uno in meno rispetto al grado dell'equazione originale). Qualsiasi equazione reciproca di grado pari insieme a una radice della forma x = φ contiene anche la radice del modulo. Utilizzando queste affermazioni, risolviamo il problema abbassando il grado dell'equazione in studio.

Metodo di sostituzione variabile. Uso dell'omogeneità.

Non esiste una formula generale per risolvere intere equazioni di quinto grado (lo hanno dimostrato il matematico italiano Paolo Ruffini (1765–1822) e il matematico norvegese Nils Henrik Abel (1802–1829)) e potenze superiori (lo hanno dimostrato i francesi matematico Evariste Galois (1811–1832) )).

• Ricordiamo ancora che in pratica è possibile utilizzare combinazioni i metodi sopra elencati. È conveniente passare a un insieme di equazioni di gradi inferiori di fattorizzazione dell'equazione originale.
• Al di fuori dell'ambito della nostra discussione odierna, sono ampiamente utilizzati nella pratica metodi grafici risolvere equazioni e metodi di soluzione approssimati equazioni di grado superiore.
• Ci sono situazioni in cui l'equazione non ha radici R.
Quindi la soluzione si riduce a mostrare che l'equazione non ha radici. Per dimostrarlo, analizziamo il comportamento delle funzioni considerate su intervalli di monotonia. Esempio: Equazione X 8 – X 3 + 1 = 0 non ha radici.
• Utilizzo della proprietà di monotonia delle funzioni
. Ci sono situazioni in cui l'uso di varie proprietà delle funzioni ci consente di semplificare il compito.
Esempio 1: Equazione X 5 + 3X– 4 = 0 ha una radice X= 1. Per la proprietà di monotonia delle funzioni analizzate, non ci sono altre radici.
Esempio 2: Equazione X 4 + (X– 1) 4 = 97 ha radici X 1 = -2 e X 2 = 3. Dopo aver analizzato il comportamento delle corrispondenti funzioni sugli intervalli di monotonia, concludiamo che non ci sono altre radici.

4. Riassumendo.

Riepilogo: Ora abbiamo imparato i metodi di base per risolvere varie equazioni di grado superiore (per n > 3). Il nostro compito è imparare come utilizzare efficacemente gli algoritmi di cui sopra. A seconda del tipo di equazione, dovremo imparare a determinare quale metodo di soluzione è il più efficace in questo caso, oltre ad applicare correttamente il metodo scelto.

5. Compiti a casa.

: voce 7, pp. 164–174, nn. 33–36, 39–44, 46,47.

: №№ 9.1–9.4, 9.6–9.8, 9.12, 9.14–9.16, 9.24–9.27.

Possibili argomenti di relazioni o abstract su questo argomento:

• Formula Cardano
• Metodo grafico per la risoluzione di equazioni. Esempi di soluzioni.
• Metodi per la soluzione approssimata di equazioni.

Analisi dell'assimilazione del materiale e dell'interesse degli studenti per l'argomento:

L'esperienza dimostra che l'interesse degli studenti in primo luogo è la possibilità di selezionare Z-radici e Q-radici di equazioni utilizzando un algoritmo abbastanza semplice che utilizza lo schema di Horner. Gli studenti sono anche interessati a vari tipi standard di sostituzione delle variabili, che possono semplificare notevolmente il tipo di problema. I metodi grafici di soluzione sono generalmente di particolare interesse. In questo caso, puoi anche analizzare le attività in un metodo grafico per risolvere le equazioni; discutere la vista generale del grafico per un polinomio di 3, 4, 5 gradi; analizzare come il numero di radici di equazioni di 3, 4, 5 gradi è correlato al tipo del grafico corrispondente. Di seguito è riportato un elenco di libri in cui è possibile trovare ulteriori informazioni su questo argomento.

Bibliografia:

1. Vilenkin N.Ya. ecc. “Algebra. Un libro di testo per studenti delle classi 9 con uno studio approfondito della matematica ”- M., Education, 2007 - 367 p.
2. Vilenkin N.Ya., Shibasov LP, Shibasova Z.F.“Dietro le pagine di un libro di matematica. Aritmetica. Algebra. Classi 10-11” – M., Illuminismo, 2008 – 192 p.
3. Vygodsky M.Ya."Manuale di matematica" - M., AST, 2010 - 1055 p.
4. Galitsky M.L.“Raccolta di problemi in algebra. Esercitazione per le classi 8-9 con approfondimento di matematica ”- M., Education, 2008 - 301 p.
5. Zvavich LI et al., “L'algebra e gli inizi dell'analisi. 8-11 celle Un manuale per scuole e classi con approfondimento della matematica ”- M., Drofa, 1999 - 352 p.
6. Zvavich LI, Averyanov DI, Pigarev BP, Trushanina TN“Incarichi in matematica per preparare un esame scritto in classe 9” - M., Education, 2007 - 112 p.
7. Ivanov AA, Ivanov AP"Prove tematiche per la sistematizzazione della conoscenza in matematica" parte 1 - M., Fizmatkniga, 2006 - 176 p.
8. Ivanov AA, Ivanov AP"Prove tematiche per la sistematizzazione della conoscenza in matematica" parte 2 - M., Fizmatkniga, 2006 - 176 p.
9. Ivanov A.P.“Prove e fogli di prova matematica. Esercitazione". - M., Fizmatkniga, 2008 - 304 pag.
10. Leibson K.L.“Raccolta di compiti pratici in matematica. Classe parte 2–9” – M., MTsNMO, 2009 – 184 p.
11. Makarychev Yu.N., Mindyuk NG."Algebra. Capitoli aggiuntivi per libro di testo scolastico Grado 9 Libro di testo per studenti di scuole e classi con approfondimento della matematica”. - M., Istruzione, 2006 - 224 p.
12. Mordkovich AG"Algebra. Studio approfondito. 8 ° grado. Libro di testo” – M., Mnemosyne, 2006 – 296 p.
13. Savin A.P. “dizionario enciclopedico giovane matematico” – M., Pedagogia, 1985 – 352 p.
14. Survillo GS, Simonov AS “Materiali didattici in Algebra per Grade 9 con approfondimento di matematica” – M., Enlightenment, 2006 – 95 p.
15. Chulkov PV“Equazioni e disuguaglianze nel corso scolastico di matematica. Lezioni 1–4” – M., Primo settembre 2006 – 88 p.
16. Chulkov PV“Equazioni e disuguaglianze nel corso scolastico di matematica. Lezioni 5–8” – M., Primo settembre 2009 – 84 p.

Ritenere risolvere equazioni con una variabile di grado maggiore della seconda.

Il grado dell'equazione P(x) = 0 è il grado del polinomio P(x), cioè la più grande delle potenze dei suoi termini con coefficiente diverso da zero.

Quindi, ad esempio, l'equazione (x 3 - 1) 2 + x 5 \u003d x 6 - 2 ha un quinto grado, perché dopo le operazioni di apertura di parentesi e portando quelle simili, otteniamo un'equazione equivalente x 5 - 2x 3 + 3 \u003d 0 di quinto grado.

Richiama le regole che serviranno per risolvere equazioni di grado superiori alla seconda.

Affermazioni sulle radici di un polinomio e sui suoi divisori:

1. Polinomio ennesimo grado ha un numero di radici non superiore al numero n, e le radici della molteplicità m ricorrono esattamente m volte.

2. Un polinomio di grado dispari ha almeno una radice reale.

3. Se α è la radice di Р(х), allora Р n (х) = (х – α) · Q n – 1 (x), dove Q n – 1 (x) è un polinomio di grado (n – 1) .

4.

5. Un polinomio ridotto con coefficienti interi non può avere radici razionali frazionarie.

6. Per un polinomio di terzo grado

P 3 (x) \u003d ax 3 + bx 2 + cx + d una delle due cose è possibile: o si decompone in un prodotto di tre binomi

P 3 (x) \u003d a (x - α) (x - β) (x - γ), o si decompone nel prodotto di un binomio e un trinomio quadrato P 3 (x) \u003d a (x - α) ( x 2 + βx + γ).

7. Qualsiasi polinomio di quarto grado si espande nel prodotto di due trinomi quadrati.

8. Un polinomio f(x) è divisibile per un polinomio g(x) senza resto se esiste un polinomio q(x) tale che f(x) = g(x) q(x). Per dividere i polinomi si applica la regola della "divisione per angolo".

9. Perché il polinomio P(x) sia divisibile per il binomio (x – c), è necessario e sufficiente che il numero c sia la radice di P(x) (Corollario del teorema di Bezout).

10. Teorema di Vieta: Se x 1, x 2, ..., x n sono le radici reali del polinomio

P (x) = a 0 x n + a 1 x n - 1 + ... + a n, allora valgono le seguenti uguaglianze:

x 1 + x 2 + ... + x n \u003d -a 1 / a 0,

x 1 x 2 + x 1 x 3 + ... + x n - 1 x n \u003d a 2 / a 0,

x 1 x 2 x 3 + ... + x n - 2 x n - 1 x n \u003d -a 3 / a 0,

x 1 x 2 x 3 x n \u003d (-1) n a n / a 0.

Soluzione di esempi

Esempio 1

Trova il resto dopo aver diviso P (x) \u003d x 3 + 2/3 x 2 - 1/9 per (x - 1/3).

Soluzione.

Secondo il corollario del teorema di Bezout: "Il resto della divisione di un polinomio per un binomio (x - c) è uguale al valore del polinomio in c." Troviamo P(1/3) = 0. Pertanto, il resto è 0 e il numero 1/3 è la radice del polinomio.

Risposta: R = 0.

Esempio 2

Dividi l '"angolo" 2x 3 + 3x 2 - 2x + 3 per (x + 2). Trova il resto e il quoziente incompleto.

Soluzione:

2x 3 + 3x 2 – 2x + 3| x + 2

2x 3 + 4x 2 2x 2 – x

X 2 – 2 X

Risposta: R = 3; quoziente: 2x 2 - x.

Metodi di base per la risoluzione di equazioni di grado superiore

1. Introduzione di una nuova variabile

Il metodo per introdurre una nuova variabile è già familiare dall'esempio equazioni biquadratiche. Consiste nel fatto che per risolvere l'equazione f (x) \u003d 0, viene introdotta una nuova variabile (sostituzione) t \u003d xn o t \u003d g (x) e f (x) viene espressa tramite t, ottenendo un nuova equazione r (t). Quindi risolvendo l'equazione r(t), trova le radici:

(t 1 , t 2 , …, t n). Successivamente, si ottiene un insieme di n equazioni q(x) = t 1 , q(x) = t 2 , ... , q(x) = t n, da cui si trovano le radici dell'equazione originale.

Esempio 1

(x 2 + x + 1) 2 - 3x 2 - 3x - 1 = 0.

Soluzione:

(x 2 + x + 1) 2 - 3 (x 2 + x) - 1 = 0.

(x 2 + x + 1) 2 - 3 (x 2 + x + 1) + 3 - 1 = 0.

Sostituzione (x 2 + x + 1) = t.

t2 - 3t + 2 = 0.

t 1 \u003d 2, t 2 \u003d 1. Sostituzione inversa:

x 2 + x + 1 = 2 o x 2 + x + 1 = 1;

x 2 + x - 1 = 0 oppure x 2 + x = 0;

Risposta: Dalla prima equazione: x 1, 2 = (-1 ± √5) / 2, dalla seconda: 0 e -1.

2. Fattorizzazione con il metodo del raggruppamento e delle formule di moltiplicazione abbreviate

Anche la base di questo metodo non è nuova e consiste nel raggruppare i termini in modo tale che ogni gruppo contenga un fattore comune. Per fare questo, a volte devi usare alcuni trucchi artificiali.

Esempio 1

x 4 - 3x 2 + 4x - 3 = 0.

Soluzione.

Immagina - 3x 2 = -2x 2 - x 2 e gruppo:

(x 4 - 2x 2) - (x 2 - 4x + 3) = 0.

(x 4 - 2x 2 +1 - 1) - (x 2 - 4x + 3 + 1 - 1) = 0.

(x 2 - 1) 2 - 1 - (x - 2) 2 + 1 = 0.

(x 2 - 1) 2 - (x - 2) 2 \u003d 0.

(x 2 - 1 - x + 2) (x 2 - 1 + x - 2) = 0.

(x 2 - x + 1) (x 2 + x - 3) = 0.

x 2 - x + 1 \u003d 0 o x 2 + x - 3 \u003d 0.

Risposta: non ci sono radici nella prima equazione, dalla seconda: x 1, 2 \u003d (-1 ± √13) / 2.

3. Fattorizzazione con il metodo dei coefficienti indefiniti

L'essenza del metodo è che il polinomio originale viene scomposto in fattori con coefficienti sconosciuti. Usando la proprietà che i polinomi sono uguali se i loro coefficienti sono uguali alle stesse potenze, si trovano i coefficienti di espansione sconosciuti.

Esempio 1

x 3 + 4x 2 + 5x + 2 = 0.

Soluzione.

Un polinomio di 3° grado può essere scomposto in un prodotto di fattori lineari e quadrati.

x 3 + 4x 2 + 5x + 2 \u003d (x - a) (x 2 + bx + c),

x 3 + 4x 2 + 5x + 2 = x 3 + bx 2 + cx - ax 2 - abx - ac,

x 3 + 4x 2 + 5x + 2 \u003d x 3 + (b - a) x 2 + (cx - ab) x - ac.

Risolvere il sistema:

(b – a = 4,
(c – ab = 5,
(-ac=2,

(a = -1,
(b=3,
(c = 2, cioè

x 3 + 4x 2 + 5x + 2 \u003d (x + 1) (x 2 + 3x + 2).

Le radici dell'equazione (x + 1) (x 2 + 3x + 2) = 0 sono facili da trovare.

Risposta 1; -2.

4. Il metodo per selezionare la radice in base al coefficiente più alto e libero

Il metodo si basa sull'applicazione di teoremi:

1) Qualsiasi radice intera di un polinomio con coefficienti interi è un divisore del termine libero.

2) Affinché la frazione irriducibile p / q (p è un intero, q è un naturale) sia la radice di un'equazione a coefficienti interi, è necessario che il numero p sia un divisore intero del termine libero a 0, e q è un divisore naturale del coefficiente più alto.

Esempio 1

6x 3 + 7x 2 - 9x + 2 = 0.

Soluzione:

6: q = 1, 2, 3, 6.

Quindi p/q = ±1, ±2, ±1/2, ±1/3, ±2/3, ±1/6.

Avendo trovato una radice, ad esempio - 2, troveremo altre radici usando la divisione per un angolo, il metodo dei coefficienti indefiniti o lo schema di Horner.

Risposta: -2; 1/2; 1/3.

Avete domande? Non sai come risolvere le equazioni?
Per ottenere l'aiuto di un tutor - registrati.
La prima lezione è gratuita!

sito, con copia integrale o parziale del materiale, è richiesto un link alla fonte.