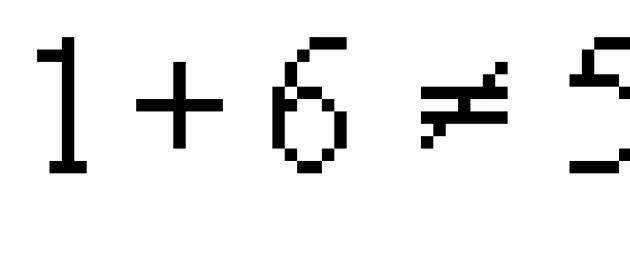Lösa ekvationer med hjälp av Vieta-satsexemplen. Vietsats, invers vietformel och exempel med lösning för dummies

François Vieta (1540-1603) - matematiker, skapare av de berömda Vieta-formlerna

Vietas sats behövs för att snabbt lösa andragradsekvationer (i enkla termer).

Närmare bestämt t Vietas teorem - detta är summan av rötterna till denna andragradsekvation är lika med den andra koefficienten, som tas med motsatt tecken, och produkten är lika med den fria termen. Denna egenskap har en given andragradsekvation som har rötter.

Med hjälp av Vieta-satsen kan du enkelt lösa andragradsekvationer genom urval, så låt oss säga "tack" till den här matematikern med ett svärd i händerna för vår glada 7:e klass.

Bevis för Vietas sats

För att bevisa satsen kan du använda de välkända rotformlerna, tack vare vilka vi kommer att komponera summan och produkten av rötterna till andragradsekvationen. Först efter det kan vi se till att de är likvärdiga och följaktligen .

Låt oss säga att vi har en ekvation: . Denna ekvation har följande rötter: och . Låt oss bevisa att .

Enligt formlerna för rötterna till andragradsekvationen:

1. Hitta summan av rötterna:

Låt oss analysera denna ekvation, eftersom vi fick den exakt så här:

= .

Steg 1. Vi reducerar bråken till en gemensam nämnare, visar det sig:

= = .

Steg 2. Vi har en bråkdel där du behöver öppna fästena:

Vi minskar bråkdelen med 2 och får:

Vi har bevisat sambandet för summan av rötterna i en andragradsekvation med hjälp av Vietas sats.

2. Hitta produkten av rötterna:

= = = = = .

Låt oss bevisa denna ekvation:

Steg 1. Det finns en regel för att multiplicera bråk, enligt vilken vi multiplicerar denna ekvation:

Nu minns vi definitionen av kvadratroten och överväger:

= .

Steg 3. Vi minns diskriminanten i andragradsekvationen: . Därför, istället för D (diskriminant), ersätter vi i den sista bråkdelen, då får vi:

= .

Steg 4. Öppna parenteserna och lägg till liknande termer till bråk:

Steg 5. Vi minskar "4a" och får.

Så vi har bevisat sambandet för produkten av rötter enligt Vietas sats.

VIKTIG!Om diskriminanten är noll, har andragradsekvationen bara en rot.

Sats invers mot Vietas sats

Enligt satsen, inversen av Vietas sats, kan vi kontrollera om vår ekvation är rätt löst. För att förstå själva satsen måste vi överväga det mer i detalj.

Om siffrorna är:

Och då är de rötterna till andragradsekvationen.

Bevis på Vietas omvända sats

Steg 1.Låt oss ersätta uttryck för dess koefficienter i ekvationen:

Steg 2Låt oss transformera vänster sida av ekvationen:

Steg 3. Låt oss hitta rötterna till ekvationen, och för detta använder vi egenskapen att produkten är lika med noll:

Eller . Var kommer det ifrån: eller.

Exempel med lösningar av Vietas sats

Exempel 1

Träning

Hitta summan, produkten och kvadratsumman av rötterna i en andragradsekvation utan att hitta rötterna till ekvationen.

Lösning

Steg 1. Kom ihåg den diskriminerande formeln. Vi byter ut våra siffror mot bokstäverna. Det vill säga , är ett substitut för , och . Detta medför:

Det visar sig:

Title="(!LANG:Renderd av QuickLaTeX.com" height="13" width="170" style="vertical-align: -1px;">. Если дискриминант больше нуля, тогда у уравнения есть корни. По теореме Виета их сумма , а произведение . !}

Vi uttrycker summan av rötternas kvadrater genom deras summa och produkt:

Svar

7; 12; 25.

Exempel 2

Träning

Lös ekvationen. I det här fallet ska du inte använda formlerna i andragradsekvationen.

Lösning

Denna ekvation har rötter som är större än noll i termer av diskriminanten (D). Följaktligen, enligt Vieta-satsen, är summan av rötterna till denna ekvation 4, och produkten är 5. Först bestämmer vi talets divisorer, vars summa är 4. Dessa är talen "5" och "-1". Deras produkt är lika med - 5, och summan - 4. Därför, enligt satsen, motsatsen till Vietas sats, är de rötterna till denna ekvation.

Svar

OCH Exempel 4

Träning

Skriv en ekvation där varje rot är två gånger motsvarande rot i ekvationen:

Lösning

Enligt Vietas teorem är summan av rötterna i denna ekvation 12, och produkten = 7. Därför är de två rötterna positiva.

Summan av rötterna till den nya ekvationen kommer att vara lika med:

Och arbetet.

Genom ett teorem omvänt till Vietas sats har den nya ekvationen formen:

Svar

Resultatet blev en ekvation där varje rot är dubbelt så stor:

Så vi tittade på hur man löser en ekvation med hjälp av Vietas teorem. Det är mycket praktiskt att använda denna sats om uppgifter löses som är förknippade med tecknen på rötterna i andragradsekvationer. Det vill säga, om den fria termen i formeln är ett positivt tal, och om det finns reella rötter i andragradsekvationen, kan båda vara antingen negativa eller positiva.

Och om den fria termen är ett negativt tal, och om det finns reella rötter i andragradsekvationen, kommer båda tecknen att vara olika. Det vill säga, om en rot är positiv, så kommer den andra roten bara att vara negativ.

Användbara källor:

1. Dorofeev G. V., Suvorova S. B., Bunimovich E. A. Algebra Grad 8: Moskva "Enlightenment", 2016 – 318 s.
2. Rubin A. G., Chulkov P. V. - lärobok Algebra Grad 8: Moskva "Balass", 2015 - 237 s.
3. Nikolsky S. M., Potopav M. K., Reshetnikov N. N., Shevkin A. V. – Algebra Grade 8: Moscow “Enlightenment”, 2014 – 300

Vietas sats, invers Vieta-formel och exempel med lösning för dummies uppdaterad: 22 november 2019 av: Vetenskapliga artiklar.Ru

Formulering och bevis för Vietas sats för andragradsekvationer. Omvänd Vieta-sats. Vietas sats för kubiska ekvationer och ekvationer av godtycklig ordning.

Innehåll

Se även: Rötterna till en andragradsekvation

Kvadratisk ekvation

Vietas sats

Låt och beteckna rötterna till den reducerade andragradsekvationen
(1) .
Då är summan av rötterna lika med koefficienten vid taget med motsatt tecken. Produkten av rötterna är lika med den fria termen:
;
.

En anteckning om flera rötter

Om diskriminanten för ekvation (1) är noll, har denna ekvation en rot. Men för att undvika besvärliga formuleringar är det allmänt accepterat att i detta fall har ekvation (1) två multipla eller lika stora rötter:
.

Bevis ett

Låt oss hitta rötterna till ekvation (1). För att göra detta, tillämpa formeln för rötterna till andragradsekvationen:
;
;
.

Hitta summan av rötterna:
.

För att hitta produkten använder vi formeln:
.
Sedan

.

Teoremet har bevisats.

Bevis två

Om talen och är rötterna till andragradsekvationen (1), då
.
Vi öppnar fästena.

.
Således kommer ekvation (1) att ha formen:
.
Jämför vi med (1) finner vi:
;
.

Teoremet har bevisats.

Omvänd Vieta-sats

Låt det finnas godtyckliga siffror. Då och är rötterna till andragradsekvationen
,
var
(2) ;
(3) .

Bevis på Vietas omvända sats

Tänk på andragradsekvationen
(1) .
Vi måste bevisa att om och , då och är rötterna till ekvation (1).

Ersätt (2) och (3) i (1):
.
Vi grupperar termerna på vänster sida av ekvationen:
;
;
(4) .

Ersättare i (4):
;
.

Ersättare i (4):
;
.
Ekvationen är uppfylld. Det vill säga talet är roten till ekvation (1).

Teoremet har bevisats.

Vietas sats för den fullständiga andragradsekvationen

Betrakta nu hela andragradsekvationen
(5) ,
var , och är några siffror. Och .

Vi dividerar ekvation (5) med:
.
Det vill säga, vi har fått ovanstående ekvation
,
var ; .

Då har Vieta-satsen för den fullständiga andragradsekvationen följande form.

Låt och beteckna rötterna till den fullständiga andragradsekvationen
.
Sedan bestäms summan och produkten av rötterna av formlerna:
;
.

Vietas sats för en kubikekvation

På liknande sätt kan vi upprätta samband mellan rötterna till en kubikekvation. Tänk på kubikekvationen
(6) ,
där , , , finns några siffror. Och .
Låt oss dividera denna ekvation med:
(7) ,
var , , .
Låt , , vara rötterna till ekvation (7) (och ekvation (6)). Sedan

.

Jämför vi med ekvation (7) finner vi:
;
;
.

Vietas sats för en n:te gradsekvation

På samma sätt kan man hitta samband mellan rötterna , , ... , , för ekvationen för n:e graden
.

Vietas sats för en n:te gradensekvation har följande form:
;
;
;

.

För att få dessa formler skriver vi ekvationen i följande form:
.
Sedan likställer vi koefficienterna vid , , , ... , och jämför den fria termen.

Referenser:
I. Bronstein, K.A. Semendyaev, Handbok i matematik för ingenjörer och studenter vid högre utbildningsinstitutioner, Lan, 2009.
CENTIMETER. Nikolsky, M.K. Potapov et al., Algebra: en lärobok för 8:e klass av utbildningsinstitutioner, Moskva, utbildning, 2006.

Se även:

I åttan får eleverna lära sig andragradsekvationer och hur man löser dem. Samtidigt, som erfarenheten visar, använder de flesta elever bara en metod när de löser fullständiga andragradsekvationer – formeln för rötterna till en andragradsekvation. För elever med god muntlig räkneförmåga är denna metod uppenbart irrationell. Elever får ofta lösa andragradsekvationer på gymnasiet och där är det helt enkelt synd att lägga tid på att räkna ut diskriminanten. Enligt min åsikt, när man studerar andragradsekvationer, bör mer tid och uppmärksamhet ägnas åt tillämpningen av Vieta-satsen (enligt programmet för AG Mordkovich Algebra-8 är bara två timmar planerade för att studera ämnet "Vieta-satsen. Nedbrytning av ett kvadratiskt trinomium till linjära faktorer").

I de flesta algebraläroböcker är denna sats formulerad för en reducerad andragradsekvation och säger att om ekvationen har rötter och , då uppfyller de likheterna , . Sedan formuleras ett uttalande i motsats till Vietas teorem, och ett antal exempel erbjuds för att arbeta med detta ämne.

Låt oss ta specifika exempel och spåra lösningens logik på dem med hjälp av Vietas teorem.

Exempel 1. Lös ekvationen.

Anta att denna ekvation har rötter, nämligen och . Sedan, enligt Vietas teorem, jämlikheterna

Observera att produkten av rötterna är ett positivt tal. Så, rötterna till ekvationen har samma tecken. Och eftersom summan av rötterna också är ett positivt tal, drar vi slutsatsen att båda rötterna i ekvationen är positiva. Låt oss gå tillbaka till produkten av rötter. Antag att rötterna till ekvationen är positiva heltal. Då kan den korrekta första likheten erhållas på endast två sätt (upp till faktorordningen): eller . Låt oss kontrollera för de föreslagna sifferparen genomförbarheten av det andra påståendet i Vieta-satsen: . Således uppfyller siffrorna 2 och 3 båda likheterna, och är därför rötterna till den givna ekvationen.

Svar: 2; 3.

Vi pekar ut huvudstadierna av resonemang när vi löser den givna andragradsekvationen med hjälp av Vieta-satsen:

skriv ner påståendet om Vietas sats

(*)

• bestäm tecknen för ekvationens rötter (Om produkten och summan av rötterna är positiva är båda rötterna positiva tal. Om produkten av rötterna är ett positivt tal och summan av rötterna är negativ, då båda rötterna är negativa tal. Om produkten av rötterna är ett negativt tal, har rötterna olika tecken. Dessutom, om summan av rötterna är positiv, är roten med en större modul ett positivt tal, och om summan av rötterna är mindre än noll, då är roten med en större modul ett negativt tal);
• välj par av heltal vars produkt ger den korrekta första likheten i notationen (*);
• från de hittade nummerparen, välj det par som, när det sätts in i den andra likheten i notationen (*), ger den korrekta likheten;
• ange i svaret ekvationens hittade rötter.

Låt oss ge några fler exempel.

Exempel 2: Lös ekvationen .

Lösning.

Låt och vara rötterna till den givna ekvationen. Sedan genom Vietas sats Observera att produkten är positiv och summan är negativ. Så båda rötterna är negativa tal. Vi väljer par av faktorer som ger produkten 10 (-1 och -10; -2 och -5). Det andra paret siffror summerar till -7. Så talen -2 och -5 är rötterna till denna ekvation.

Svar: -2; -5.

Exempel 3. Lös ekvationen .

Lösning.

Låt och vara rötterna till den givna ekvationen. Sedan genom Vietas teorem Observera att produkten är negativ. Så rötterna är av olika tecken. Summan av rötterna är också ett negativt tal. Därför är roten med den största modulen negativ. Vi väljer ut par av faktorer som ger produkten -10 (1 och -10; 2 och -5). Det andra paret siffror summerar till -3. Så talen 2 och -5 är rötterna till denna ekvation.

Svar: 2; -5.

Observera att Vieta-satsen i princip kan formuleras för den fullständiga andragradsekvationen: om andragradsekvationen har rötter och , då tillfredsställer de jämlikheterna , . Tillämpningen av denna sats är dock ganska problematisk, eftersom åtminstone en av rötterna (om någon, naturligtvis) i den fullständiga andragradsekvationen är ett bråktal. Och arbetet med valet av bråk är långt och svårt. Men det finns fortfarande en väg ut.

Betrakta den fullständiga andragradsekvationen . Multiplicera båda sidor av ekvationen med den första koefficienten a och skriv ekvationen i formuläret . Vi introducerar en ny variabel och får en reducerad andragradsekvation , vars rötter och (om några) kan hittas med hjälp av Vieta-satsen. Då blir rötterna till den ursprungliga ekvationen . Observera att det är mycket lätt att skriva den reducerade hjälpekvationen: den andra koefficienten bevaras och den tredje koefficienten är lika med produkten ess. Med en viss färdighet komponerar eleverna omedelbart en hjälpekvation, hittar dess rötter med hjälp av Vieta-satsen och anger rötterna till den givna fullständiga ekvationen. Låt oss ge exempel.

Exempel 4. Lös ekvationen .

Låt oss göra en hjälpekvation och genom Vietas sats finner vi dess rötter. Alltså rötterna till den ursprungliga ekvationen .

Svar: .

Exempel 5. Lös ekvationen .

Hjälpekvationen har formen . Enligt Vietas teorem är dess rötter . Vi hittar rötterna till den ursprungliga ekvationen .

Svar: .

Och ett fall till när tillämpningen av Vietas teorem låter dig verbalt hitta rötterna till en komplett andragradsekvation. Det är lätt att bevisa det talet 1 är roten till ekvationen , om och endast om. Den andra roten av ekvationen hittas av Vieta-satsen och är lika med . Ytterligare ett uttalande: så att talet -1 är roten till ekvationen nödvändigt och tillräckligt för att. Då är den andra roten av ekvationen enligt Vietas sats lika med . Liknande påståenden kan formuleras för den reducerade andragradsekvationen.

Exempel 6. Lös ekvationen.

Observera att summan av ekvationens koefficienter är noll. Alltså rötterna till ekvationen .

Svar: .

Exempel 7. Lös ekvationen.

Koefficienterna för denna ekvation uppfyller egenskapen (verkligen 1-(-999)+(-1000)=0). Alltså rötterna till ekvationen .

Svar: ..

Exempel för tillämpning av Vietas sats

Uppgift 1. Lös den givna andragradsekvationen med hjälp av Vietas sats.

1.	6.	11.	16.
2.	7.	12.	17.
3.	8.	13.	18.
4.	9.	14.	19.
5.	10.	15.	20.

Uppgift 2. Lös den fullständiga andragradsekvationen genom att använda övergången till den reducerade hjälpekvationen.

1.	6.	11.	16.
2.	7.	12.	17.
3.	8.	13.	18.
4.	9.	14.	19.
5.	10.	15.	20.

Uppgift 3. Lös en andragradsekvation med hjälp av egenskapen.

Mellan andragradsekvationens rötter och koefficienter finns det förutom rotformlerna andra användbara samband som ges av Vietas sats. I den här artikeln kommer vi att ge en formulering och bevis på Vietas sats för en andragradsekvation. Därefter betraktar vi en sats omvänd till Vietas sats. Efter det kommer vi att analysera lösningarna för de mest karakteristiska exemplen. Slutligen skriver vi ner Vieta-formlerna som definierar sambandet mellan de verkliga rötterna algebraisk ekvation grad n och dess koefficienter.

Sidnavigering.

Vietas sats, formulering, bevis

Från formlerna för rötterna i andragradsekvationen a x 2 +b x+c=0 av formen , där D=b 2 −4 a c , relationerna x 1 +x 2 = −b/a, x 1 x 2 = c/a . Dessa resultat bekräftas Vietas sats:

Sats.

Om x 1 och x 2 är rötterna till andragradsekvationen ax 2 +b x+c=0, då är summan av rötterna lika med förhållandet mellan koefficienterna b och a, taget med motsatt tecken, och produkten av rötterna är lika med förhållandet mellan koefficienterna c och a, det vill säga .

Bevis.

Vi kommer att bevisa Vieta-satsen enligt följande schema: vi sammanställer summan och produkten av rötterna i andragradsekvationen med hjälp av de kända rotformlerna, efter det transformerar vi de resulterande uttrycken och ser till att de är lika med −b /a respektive c/a.

Låt oss börja med summan av rötterna, komponera den. Nu tar vi bråken till en gemensam nämnare, det har vi. I täljaren för det resulterande bråket , varefter : . Slutligen, efter 2, får vi . Detta bevisar den första relationen i Vietas sats för summan av rötterna i en andragradsekvation. Låt oss gå vidare till den andra.

Vi komponerar produkten av rötterna till andragradsekvationen:. Enligt regeln för multiplikation av bråk kan den sista produkten skrivas som. Nu multiplicerar vi parentesen med parentesen i täljaren, men det går snabbare att kollapsa denna produkt med formel för skillnad på kvadrater, Så . Sedan, kom ihåg, utför vi nästa övergång. Och eftersom formeln D=b 2 −4 a·c motsvarar diskriminanten i andragradsekvationen, då b 2 −4·a·c kan ersättas med den sista bråkdelen istället för D, får vi . Efter att ha öppnat parenteserna och reducerat liknande termer kommer vi fram till bråket , och dess minskning med 4·a ger . Detta bevisar det andra förhållandet i Vietas sats för produkten av rötter.

Om vi ​​utelämnar förklaringarna kommer beviset för Vieta-satsen att ta en kortfattad form:
,
.

Det återstår bara att notera att när diskriminanten är lika med noll, har andragradsekvationen en rot. Men om vi antar att ekvationen i detta fall har två identiska rötter, så gäller också likheterna från Vieta-satsen. För D=0 är roten av andragradsekvationen , då och , och eftersom D=0 , det vill säga b 2 −4·a·c=0 , varav b 2 =4·a·c , alltså .

I praktiken används Vietas sats oftast i relation till den reducerade andragradsekvationen (med högsta koefficient a lika med 1 ) av formen x 2 +p·x+q=0 . Ibland formuleras den för andragradsekvationer av just denna typ, vilket inte begränsar generaliteten, eftersom vilken andragradsekvation som helst kan ersättas med en ekvivalent ekvation genom att dividera båda dess delar med ett icke-nolltal a. Här är motsvarande formulering av Vietas teorem:

Sats.

Summan av rötterna till den reducerade andragradsekvationen x 2 + px + q \u003d 0 är lika med koefficienten vid x, taget med motsatt tecken, och produkten av rötterna är en fri term, det vill säga x 1 + x 2 \u003d −p, x 1 x 2 \u003d q .

Sats invers mot Vietas sats

Den andra formuleringen av Vieta-satsen, som ges i föregående stycke, indikerar att om x 1 och x 2 är rötterna till den reducerade andragradsekvationen x 2 +p x+q=0, då är relationerna x 1 +x 2 = − p, x 1 x 2=q. Å andra sidan, av de skrivna relationerna x 1 +x 2 =−p, x 1 x 2 =q, följer att x 1 och x 2 är rötterna till andragradsekvationen x 2 +p x+q=0. Med andra ord, påståendet mot Vietas teorem är sant. Vi formulerar det i form av ett teorem och bevisar det.

Sats.

Om talen x 1 och x 2 är sådana att x 1 +x 2 =−p och x 1 x 2 =q, då är x 1 och x 2 rötterna till den reducerade andragradsekvationen x 2 +p x+q=0 .

Bevis.

Efter att ha ersatt koefficienterna p och q i ekvationen x 2 +p x+q=0 för deras uttryck genom x 1 och x 2, omvandlas den till en ekvivalent ekvation.

Vi ersätter talet x 1 istället för x i den resulterande ekvationen, vi har likheten x 1 2 −(x 1 + x 2) x 1 + x 1 x 2 =0, som för alla x 1 och x 2 är den korrekta numeriska likheten 0=0, eftersom x 1 2 −(x 1 + x 2) x 1 + x 1 x 2 = x 1 2 −x 1 2 −x 2 x 1 + x 1 x 2 =0. Därför är x 1 roten till ekvationen x 2 −(x 1 + x 2) x + x 1 x 2 \u003d 0, vilket betyder att x 1 är roten till ekvivalentekvationen x 2 +p x+q=0 .

Om i ekvationen x 2 −(x 1 + x 2) x + x 1 x 2 \u003d 0 ersätt talet x 2 istället för x, då får vi likheten x 2 2 −(x 1 + x 2) x 2 + x 1 x 2 =0. Detta är den korrekta ekvationen eftersom x 2 2 −(x 1 + x 2) x 2 + x 1 x 2 = x 2 2 −x 1 x 2 −x 2 2 +x 1 x 2 =0. Därför är x 2 också roten till ekvationen x 2 −(x 1 + x 2) x + x 1 x 2 \u003d 0, och därav ekvationerna x 2 +p x+q=0 .

Detta fullbordar beviset för satsen i motsats till Vietas sats.

Exempel på användning av Vietas sats

Det är dags att prata om den praktiska tillämpningen av Vietas teorem och dess inversa teorem. I det här underavsnittet kommer vi att analysera lösningarna för flera av de mest typiska exemplen.

Vi börjar med att tillämpa en sats omvänd på Vietas sats. Det är bekvämt att använda det för att kontrollera om de givna två talen är rötterna till en given andragradsekvation. I det här fallet beräknas deras summa och skillnad, varefter giltigheten av relationerna kontrolleras. Om båda dessa relationer är uppfyllda, dras slutsatsen att dessa tal är rötterna till ekvationen, i kraft av satsen omvänd till Vietas sats. Om åtminstone en av relationerna inte är uppfylld, är dessa tal inte rötterna till andragradsekvationen. Detta tillvägagångssätt kan användas när man löser andragradsekvationer för att kontrollera de hittade rötterna.

Exempel.

Vilket av talparen 1) x 1 =−5, x 2 =3, eller 2), eller 3) är ett par rötter i andragradsekvationen 4 x 2 −16 x+9=0?

Lösning.

Koefficienterna för den givna andragradsekvationen 4 x 2 −16 x+9=0 är a=4 , b=−16 , c=9 . Enligt Vietas sats måste summan av andragradsekvationens rötter vara lika med −b/a, det vill säga 16/4=4, och produkten av rötterna måste vara lika med c/a, det vill säga 9 /4.

Låt oss nu beräkna summan och produkten av siffrorna i vart och ett av de tre givna paren och jämföra dem med de just erhållna värdena.

I det första fallet har vi x 1 +x 2 =−5+3=−2 . Det resulterande värdet skiljer sig från 4, därför kan ytterligare verifiering inte utföras, men med satsen, inversen av Vietas sats, kan vi omedelbart dra slutsatsen att det första paret av tal inte är ett par rötter i en given andragradsekvation .

Låt oss gå vidare till det andra fallet. Här är det första villkoret uppfyllt. Vi kontrollerar det andra villkoret: , det resulterande värdet skiljer sig från 9/4 . Därför är det andra talparet inte ett par rötter i en andragradsekvation.

Det sista fallet återstår. Här och . Båda villkoren är uppfyllda, så dessa tal x 1 och x 2 är rötterna till den givna andragradsekvationen.

Svar:

Satsen, motsatsen till Vietas sats, kan användas i praktiken för att välja rötterna till en andragradsekvation. Vanligtvis väljs heltalsrötter för de givna andragradsekvationerna med heltalskoefficienter, eftersom detta i andra fall är ganska svårt att göra. Samtidigt använder de det faktum att om summan av två tal är lika med den andra koefficienten i andragradsekvationen, taget med ett minustecken, och produkten av dessa tal är lika med den fria termen, så är dessa tal rötterna till denna andragradsekvation. Låt oss ta itu med detta med ett exempel.

Låt oss ta andragradsekvationen x 2 −5 x+6=0 . För att talen x 1 och x 2 ska vara rötterna till denna ekvation måste två likheter x 1 +x 2 \u003d 5 och x 1 x 2 \u003d 6 vara uppfyllda. Det återstår att välja sådana siffror. I det här fallet är detta ganska enkelt att göra: sådana siffror är 2 och 3, eftersom 2+3=5 och 2 3=6. Således är 2 och 3 rötterna till denna andragradsekvation.

Theorem converse to Vieta's theorem är särskilt praktiskt för att hitta den andra roten av den reducerade andragradsekvationen när en av rötterna redan är känd eller uppenbar. I det här fallet hittas den andra roten från någon av relationerna.

Låt oss till exempel ta andragradsekvationen 512 x 2 −509 x−3=0 . Här är det lätt att se att enheten är roten till ekvationen, eftersom summan av koefficienterna för denna andragradsekvation är noll. Alltså x 1 = 1 . Den andra roten x 2 kan hittas till exempel från relationen x 1 x 2 =c/a. Vi har 1 x 2 =−3/512 , varav x 2 =−3/512 . Så vi har definierat båda rötterna till andragradsekvationen: 1 och −3/512.

Det är tydligt att valet av rötter endast är ändamålsenligt i de enklaste fallen. I andra fall, för att hitta rötterna, kan du använda formlerna för andragradsekvationens rötter genom diskriminanten.

En annan praktisk tillämpning av satsen, inversen av Vietas sats, är sammanställningen av andragradsekvationer för givna rötter x 1 och x 2. För att göra detta räcker det med att beräkna summan av rötterna, vilket ger koefficienten x med motsatt tecken på den givna andragradsekvationen, och produkten av rötterna, som ger den fria termen.

Exempel.

Skriv en andragradsekvation vars rötter är talen −11 och 23.

Lösning.

Beteckna x 1 =−11 och x 2 =23 . Vi beräknar summan och produkten av dessa tal: x 1 + x 2 \u003d 12 och x 1 x 2 \u003d −253. Därför är dessa tal rötterna till den givna andragradsekvationen med den andra koefficienten -12 och den fria termen -253. Det vill säga, x 2 −12·x−253=0 är den önskade ekvationen.

Svar:

x 2 −12 x−253=0 .

Vietas sats används mycket ofta för att lösa uppgifter relaterade till tecken på rötterna i andragradsekvationer. Hur hänger Vietas sats ihop med tecknen för rötterna i den reducerade andragradsekvationen x 2 +p x+q=0? Här är två relevanta uttalanden:

• Om den fria termen q är ett positivt tal och om andragradsekvationen har reella rötter, så är de båda positiva eller båda negativa.
• Om den fria termen q är ett negativt tal och om andragradsekvationen har reella rötter, så är deras tecken olika, med andra ord, en rot är positiv och den andra är negativ.

Dessa påståenden följer av formeln x 1 x 2 =q, samt reglerna för att multiplicera positiva, negativa tal och tal med olika tecken. Tänk på exempel på deras tillämpning.

Exempel.

R är positivt. Enligt diskriminantformeln hittar vi D=(r+2) 2 −4 1 (r−1)= r 2 +4 r+4−4 r+4=r 2 +8 , värdet av uttrycket r 2 +8 är positivt för vilket reellt r som helst, alltså D>0 för vilket reellt r som helst. Därför har den ursprungliga andragradsekvationen två rötter för alla reella värden på parametern r.

Låt oss nu ta reda på när rötterna har olika tecken. Om tecknen på rötterna är olika, är deras produkt negativ, och enligt Vieta-satsen är produkten av rötterna i den givna andragradsekvationen lika med den fria termen. Därför är vi intresserade av de värden på r för vilka den fria termen r−1 är negativ. För att hitta värdena för r som är av intresse för oss måste vi alltså lösa en linjär ojämlikhet r−1<0 , откуда находим r<1 .

Svar:

vid r<1 .

Vieta formler

Ovan talade vi om Vietas teorem för en andragradsekvation och analyserade de samband den hävdar. Men det finns formler som förbinder de verkliga rötterna och koefficienterna inte bara för andragradsekvationer, utan också för kubiska ekvationer, fyrdubbla ekvationer och i allmänhet, algebraiska ekvationer grad n. De kallas Vieta formler.

Vi skriver Vieta-formlerna för en algebraisk ekvation av grad n av formen, medan vi antar att den har n reella rötter x 1, x 2, ..., x n (bland dem kan det finnas samma):

Få Vieta formler tillåter polynomfaktoriseringssats, samt definitionen av lika polynom genom likheten av alla deras motsvarande koefficienter. Så polynomet och dess expansion till linjära faktorer av formen är lika. Genom att öppna parenteserna i den sista produkten och likställa motsvarande koefficienter får vi Vieta-formlerna.

Speciellt för n=2 har vi redan bekanta Vieta-formler för andragradsekvationen.

För en kubikekvation har Vieta-formlerna formen

Det återstår bara att notera att på vänster sida av Vieta-formlerna finns de så kallade elementära symmetriska polynom.

Bibliografi.

• Algebra: lärobok för 8 celler. Allmän utbildning institutioner / [Yu. N. Makarychev, N.G. Mindyuk, K.I. Neshkov, S.B. Suvorova]; ed. S. A. Teljakovskij. - 16:e upplagan. - M. : Utbildning, 2008. - 271 sid. : sjuk. - ISBN 978-5-09-019243-9.
• Mordkovich A.G. Algebra. 8: e klass. Kl 14.00 Del 1. En lärobok för studenter vid utbildningsinstitutioner / A. G. Mordkovich. - 11:e uppl., raderad. - M.: Mnemozina, 2009. - 215 s.: ill. ISBN 978-5-346-01155-2.
• Algebra och början av matematisk analys. Årskurs 10: lärobok. för allmänbildning institutioner: grundläggande och profil. nivåer / [Yu. M. Kolyagin, M.V. Tkacheva, N.E. Fedorova, M.I. Shabunin]; ed. A. B. Zhizhchenko. - 3:e uppl. - M.: Upplysning, 2010.- 368 sid. : sjuk. - ISBN 978-5-09-022771-1.

Vietas teorem används ofta för att testa redan hittade rötter. Om du har hittat rötterna kan du använda formlerna \(\begin(cases)x_1+x_2=-p \\x_1 \cdot x_2=q\end(cases)\) för att beräkna värdena \(p\ ) och \(q\ ). Och om de visar sig vara desamma som i den ursprungliga ekvationen, så hittas rötterna korrekt.

Låt oss till exempel använda , lösa ekvationen \(x^2+x-56=0\) och få rötterna: \(x_1=7\), \(x_2=-8\). Låt oss kontrollera om vi gjorde ett misstag i processen att lösa. I vårt fall \(p=1\) och \(q=-56\). Enligt Vietas sats har vi:

\(\begin(cases)x_1+x_2=-p \\x_1 \cdot x_2=q\end(cases)\) \(\Leftrightarrow\) \(\begin(cases)7+(-8)=-1 \\7\cdot(-8)=-56\end(cases)\) \(\Leftrightarrow\) \(\begin(cases)-1=-1\\-56=-56\end(cases)\ )

Båda påståendena konvergerade, vilket betyder att vi löste ekvationen korrekt.

Detta test kan göras oralt. Det tar 5 sekunder och räddar dig från dumma misstag.

Omvänd Vieta-sats

Om \(\begin(cases)x_1+x_2=-p \\x_1 \cdot x_2=q\end(cases)\), då är \(x_1\) och \(x_2\) rötterna till andragradsekvationen \ (x^ 2+px+q=0\).

Eller på ett enkelt sätt: om du har en ekvation av formen \(x^2+px+q=0\), då genom att lösa systemet \(\begin(cases)x_1+x_2=-p \\x_1 \ cdot x_2=q\ end(cases)\) hittar du dess rötter.

Tack vare detta teorem kan du snabbt hitta rötterna till en andragradsekvation, speciellt om dessa rötter är . Denna färdighet är viktig eftersom den sparar mycket tid.

Exempel . Lös ekvationen \(x^2-5x+6=0\).

Lösning : Med den inversa Vieta-satsen får vi att rötterna uppfyller villkoren: \(\begin(cases)x_1+x_2=5 \\x_1 \cdot x_2=6\end(cases)\).
Titta på den andra ekvationen för \(x_1 \cdot x_2=6\) systemet. Till vilka två kan talet \(6\) delas upp? På \(2\) och \(3\), \(6\) och \(1\) eller \(-2\) och \(-3\), och \(-6\) och \(- ett\). Och vilket par att välja, kommer den första ekvationen i systemet att berätta: \(x_1+x_2=5\). \(2\) och \(3\) är lika, eftersom \(2+3=5\).
Svar : \(x_1=2\), \(x_2=3\).

Exempel . Använd inversen av Vietas teorem och hitta rötterna till andragradsekvationen:
a) \(x^2-15x+14=0\); b) \(x^2+3x-4=0\); c) \(x^2+9x+20=0\); d) \(x^2-88x+780=0\).

Lösning :
a) \(x^2-15x+14=0\) - vilka faktorer sönderfaller \(14\) till? \(2\) och \(7\), \(-2\) och \(-7\), \(-1\) och \(-14\), \(1\) och \(14\ ). Vilka par av tal summerar till \(15\)? Svar: \(1\) och \(14\).

b) \(x^2+3x-4=0\) - i vilka faktorer bryts \(-4\) ned? \(-2\) och \(2\), \(4\) och \(-1\), \(1\) och \(-4\). Vilka par av tal summerar till \(-3\)? Svar: \(1\) och \(-4\).

c) \(x^2+9x+20=0\) – till vilka faktorer bryts \(20\) ned? \(4\) och \(5\), \(-4\) och \(-5\), \(2\) och \(10\), \(-2\) och \(-10\ ), \(-20\) och \(-1\), \(20\) och \(1\). Vilka par av tal summerar till \(-9\)? Svar: \(-4\) och \(-5\).

d) \(x^2-88x+780=0\) - i vilka faktorer bryts \(780\) ned? \(390\) och \(2\). Lägger de ihop till \(88\)? Nej. Vilka andra multiplikatorer har \(780\)? \(78\) och \(10\). Lägger de ihop till \(88\)? Ja. Svar: \(78\) och \(10\).

Det är inte nödvändigt att dekomponera den sista termen i alla möjliga faktorer (som i det sista exemplet). Du kan direkt kontrollera om deras summa ger \(-p\).

Viktig! Vietas sats och omvända satsen fungerar bara med , det vill säga en vars koefficient framför \(x^2\) är lika med en. Om vi ​​initialt har en icke-reducerad ekvation, kan vi göra den reducerad genom att helt enkelt dividera med koefficienten framför \ (x ^ 2 \).

till exempel, låt ekvationen \(2x^2-4x-6=0\) ges och vi vill använda en av Vietas satser. Men vi kan inte, eftersom koefficienten före \(x^2\) är lika med \(2\). Låt oss bli av med det genom att dividera hela ekvationen med \(2\).

\(2x^2-4x-6=0\) \(|:2\)
\(x^2-2x-3=0\)

Redo. Nu kan vi använda båda satserna.

Svar på ofta ställda frågor

Fråga: Med Vietas teorem kan du lösa alla ?
Svar: Tyvärr inte. Om det inte finns heltal i ekvationen eller om ekvationen inte har några rötter alls, så hjälper inte Vietas sats. I det här fallet måste du använda diskriminerande . Som tur är har 80 % av ekvationerna i skolmattekursen heltalslösningar.