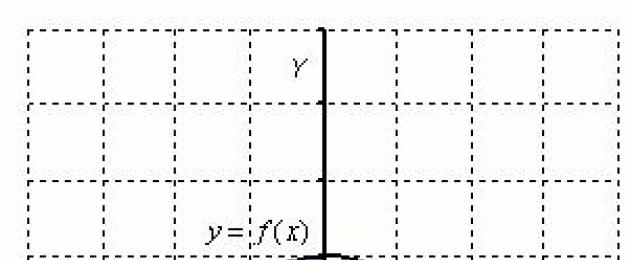Vi börjar överväga den faktiska processen för att beräkna dubbelintegralen och bekanta oss med dess geometriska betydelse.

Dubbelintegralen är numeriskt lika med arean av en platt figur (integrationsregion). Detta är den enklaste formen av dubbelintegralen, när funktionen av två variabler är lika med en: .

Låt oss först överväga problemet i allmänna termer. Nu kommer du att bli förvånad över hur enkelt det verkligen är! Låt oss beräkna arean av en platt figur avgränsad av linjer. För visshetens skull antar vi att på intervallet . Arean av denna figur är numeriskt lika med:

Låt oss avbilda området på ritningen:

Låt oss välja det första sättet att kringgå området:

På det här sättet:

Och omedelbart ett viktigt tekniskt knep: itererade integraler kan betraktas separat. Först den inre integralen, sedan den yttre integralen. Denna metod rekommenderas starkt för nybörjare i ämnet tekannor.

1) Beräkna den interna integralen, medan integrationen utförs över variabeln "y":

Den obestämda integralen här är den enklaste, och då används den banala Newton-Leibniz-formeln, med den enda skillnaden att gränserna för integration är inte siffror, utan funktioner. Först bytte vi ut den övre gränsen med "y" (antiderivativ funktion), sedan den nedre gränsen

2) Resultatet som erhålls i första stycket måste ersättas med den externa integralen:

En mer kompakt notation för hela lösningen ser ut så här:

Den resulterande formeln är exakt arbetsformeln för att beräkna arean av en platt figur med den "vanliga" bestämda integralen! Se lektion Beräknar arean med hjälp av en bestämd integral, där är hon vid varje tur!

Det är, problemet med att beräkna arean med hjälp av en dubbelintegral lite annorlunda från problemet med att hitta området med hjälp av en bestämd integral! Faktum är att de är en och samma!

Följaktligen bör inga svårigheter uppstå! Jag kommer inte att överväga särskilt många exempel, eftersom du faktiskt har stött på detta problem upprepade gånger.

Exempel 9

Lösning: Låt oss avbilda området på ritningen:

Låt oss välja följande ordning för korsning av regionen:

Här och nedan kommer jag inte gå in på hur man korsar ett område eftersom det första stycket var mycket detaljerat.

På det här sättet:

Som jag redan har noterat är det bättre för nybörjare att beräkna itererade integraler separat, jag kommer att följa samma metod:

1) Först, med hjälp av Newton-Leibniz-formeln, behandlar vi den interna integralen:

2) Resultatet som erhålls i det första steget ersätts med den yttre integralen:

Punkt 2 är faktiskt att hitta arean av en platt figur med hjälp av en bestämd integral.

Svar:

Här finns en så dum och naiv uppgift.

Ett nyfiket exempel på en oberoende lösning:

Exempel 10

Med hjälp av den dubbla integralen, beräkna arean av en plan figur avgränsad av linjerna , ,

Ett exempel på en slutlig lösning i slutet av lektionen.

I exempel 9-10 är det mycket mer lönsamt att använda det första sättet att kringgå området, nyfikna läsare kan förresten ändra ordningen på förbifarten och beräkna ytorna på det andra sättet. Om du inte gör ett misstag kan du naturligtvis få samma områdesvärden.

Men i vissa fall är det andra sättet att kringgå området mer effektivt, och som avslutning på den unga nördens kurs, låt oss titta på ytterligare ett par exempel på detta ämne:

Exempel 11

Med hjälp av den dubbla integralen, beräkna arean av en plan figur avgränsad av linjer.

Lösning: vi ser fram emot två paraboler med en bris som ligger på sidan. Du behöver inte le, liknande saker i flera integraler stöter ofta på.

Vad är det enklaste sättet att göra en ritning?

Låt oss representera parabeln som två funktioner:
- övre gren och - nedre gren.

På liknande sätt representerar vi parabeln som de övre och nedre grenarna.

Arean av figuren beräknas med hjälp av dubbelintegralen enligt formeln:

Vad händer om vi väljer det första sättet att kringgå området? Först måste detta område delas upp i två delar. Och för det andra kommer vi att observera denna sorgliga bild: . Integraler är naturligtvis inte av en superkomplex nivå, men ... det finns ett gammalt matematiskt talesätt: den som är vän med rötterna behöver ingen kvittning.

Därför, från det missförstånd som ges i villkoret, uttrycker vi de omvända funktionerna:

De omvända funktionerna i detta exempel har fördelen att de omedelbart sätter hela parabeln utan några löv, ekollon, grenar och rötter.

Enligt den andra metoden kommer områdesövergången att vara som följer:

På det här sättet:

Som de säger, känn skillnaden.

1) Vi behandlar den interna integralen:

Vi ersätter resultatet med den yttre integralen:

Integration över variabeln "y" borde inte vara pinsamt, om det fanns en bokstav "zyu" - det skulle vara bra att integrera över den. Fast vem läste andra stycket i lektionen Hur man beräknar volymen av en rotationskropp, han upplever inte längre det minsta pinsamt med integration över "y".

Var också uppmärksam på det första steget: integranden är jämn och integrationssegmentet är symmetriskt omkring noll. Därför kan segmentet halveras, och resultatet kan fördubblas. Denna teknik kommenteras i detalj i lektionen. Effektiva metoder för att beräkna den definitiva integralen.

Vad ska man lägga till…. Allt!

Svar:

För att testa din integrationsteknik kan du försöka beräkna . Svaret borde vara exakt detsamma.

Exempel 12

Med hjälp av den dubbla integralen, beräkna arean av en plan figur avgränsad av linjer

Det här är ett gör-det-själv-exempel. Det är intressant att notera att om du försöker använda det första sättet att kringgå området, kommer figuren inte längre att delas upp i två, utan i tre delar! Och följaktligen får vi tre par itererade integraler. Det händer ibland.

Mästarklassen har kommit till sitt slut, och det är dags att gå vidare till stormästarnivån - Hur beräknar man dubbelintegralen? Lösningsexempel. Jag ska försöka att inte vara så manisk i den andra artikeln =)

Önskar dig framgång!

Lösningar och svar:

Exempel 2:Lösning: Rita ett område på ritningen:

Låt oss välja följande ordning för korsning av regionen:

På det här sättet:
Låt oss gå vidare till omvända funktioner:


På det här sättet:
Svar:

Exempel 4:Lösning: Låt oss gå vidare till direkta funktioner:


Låt oss utföra ritningen:

Låt oss ändra ordningen för att korsa området:

Svar:

Områdesövergångsordning:

På det här sättet:

1)
2)

Svar:

Definitiv integral. Hur man beräknar arean av en figur

Vi övergår nu till övervägandet av tillämpningar av integralkalkylen. I den här lektionen kommer vi att analysera en typisk och vanligaste uppgift. Hur man använder en bestämd integral för att beräkna arean av en plan figur. Slutligen, de som söker mening i högre matematik - må de finna den. Du vet aldrig. I det verkliga livet måste du approximera en sommarstuga med elementära funktioner och hitta dess område med hjälp av en viss integral.

För att framgångsrikt bemästra materialet måste du:

1) Förstå den obestämda integralen åtminstone på en mellannivå. Därför bör dummies först läsa lektionen Inte.

2) Kunna tillämpa Newton-Leibniz formel och beräkna den bestämda integralen. Du kan etablera varma vänskapliga relationer med vissa integraler på sidan Definitiv integral. Lösningsexempel.

I själva verket, för att hitta området för en figur, behöver du inte så mycket kunskap om den obestämda och bestämda integralen. Uppgiften "beräkna arean med hjälp av en bestämd integral" innebär alltid konstruktion av en ritning, så dina kunskaper och ritfärdigheter kommer att vara en mycket mer relevant fråga. I detta avseende är det användbart att uppdatera graferna för de viktigaste elementära funktionerna i minnet, och åtminstone att kunna bygga en rak linje, en parabel och en hyperbel. Detta kan göras (många behöver det) med hjälp av metodmaterial och en artikel om geometriska transformationer av grafer.

Egentligen är alla bekanta med problemet med att hitta området med hjälp av en bestämd integral sedan skolan, och vi kommer att gå lite före skolans läroplan. Den här artikeln kanske inte existerar alls, men faktum är att problemet uppstår i 99 fall av 100, när en student plågas av ett hatat torn med entusiasm för att bemästra en kurs i högre matematik.

Materialet i denna workshop presenteras enkelt, i detalj och med ett minimum av teori.

Låt oss börja med en kurvlinjär trapets.

Krökt trapets kallas en platt figur som avgränsas av axeln , raka linjer och grafen för en funktion kontinuerlig på ett segment som inte ändrar tecken på detta intervall. Låt denna figur lokaliseras inte mindre abskissa:

Sedan arean av en kurvlinjär trapets är numeriskt lika med en viss integral. Varje bestämd integral (som finns) har en mycket bra geometrisk betydelse. På lektionen Definitiv integral. Lösningsexempel Jag sa att en bestämd integral är ett tal. Och nu är det dags att konstatera ytterligare ett användbart faktum. Ur geometrins synvinkel är den bestämda integralen AREA.

Det är, den bestämda integralen (om den finns) motsvarar geometriskt arean av någon figur. Tänk till exempel på den bestämda integralen . Integranden definierar en kurva på planet som är belägen ovanför axeln (de som vill kan slutföra ritningen), och den bestämda integralen i sig är numeriskt lika med arean av motsvarande kurvlinjära trapets.

Exempel 1

Detta är en typisk uppgiftsbeskrivning. Det första och viktigaste ögonblicket i beslutet är konstruktionen av en ritning. Dessutom måste ritningen byggas HÖGER.

När du bygger en ritning rekommenderar jag följande ordning: först det är bättre att konstruera alla linjer (om några) och endast Sedan- paraboler, hyperbler, grafer för andra funktioner. Funktionsdiagram är mer lönsamma att bygga punkt till punkt, med tekniken för punktvis konstruktion finns i referensmaterialet Grafer och egenskaper hos elementära funktioner. Där kan du också hitta material som är mycket användbart i relation till vår lektion – hur man snabbt bygger en parabel.

I det här problemet kan lösningen se ut så här.
Låt oss rita (observera att ekvationen definierar axeln):

Jag kommer inte att kläcka en kurvlinjär trapets, det är uppenbart vilket område vi pratar om här. Lösningen fortsätter så här:

På segmentet finns grafen för funktionen över axeln, Det är därför:

Svar:

Som har svårt att beräkna den bestämda integralen och tillämpa Newton-Leibniz formel , se föreläsningen Definitiv integral. Lösningsexempel.

När uppgiften är klar är det alltid bra att titta på ritningen och ta reda på om svaret är sant. I det här fallet, "med ögat" räknar vi antalet celler i ritningen - ja, cirka 9 kommer att skrivas, det verkar vara sant. Det är helt klart att om vi hade, säg, svaret: 20 kvadratenheter, så gjordes uppenbarligen ett misstag någonstans - 20 celler passar uppenbarligen inte in i figuren i fråga, högst ett dussin. Om svaret visade sig vara negativt löstes också uppgiften felaktigt.

Exempel 2

Beräkna arean av figuren avgränsad av linjerna , , och axeln

Det här är ett gör-det-själv-exempel. Fullständig lösning och svar i slutet av lektionen.

Vad ska man göra om den kurvlinjära trapetsen är lokaliserad under axeln?

Exempel 3

Beräkna arean av figuren avgränsad av linjer och koordinataxlar.

Lösning: Låt oss rita:

Om den kurvlinjära trapetsen är belägen under axeln(eller åtminstone inte högre given axel), kan dess area hittas med formeln:
I detta fall:

Uppmärksamhet! Blanda inte ihop de två typerna av uppgifter:

1) Om du blir ombedd att lösa bara en bestämd integral utan någon geometrisk betydelse, så kan den vara negativ.

2) Om du blir ombedd att hitta arean av en figur med hjälp av en bestämd integral, är arean alltid positiv! Det är därför minuset visas i den nyss betraktade formeln.

I praktiken är figuren oftast placerad i både det övre och nedre halvplanet, och därför går vi vidare från de enklaste skolproblemen till mer meningsfulla exempel.

Exempel 4

Hitta arean av en platt figur avgränsad av linjer, .

Lösning: Först måste du slutföra ritningen. Generellt sett är vi mest intresserade av linjers skärningspunkter när vi konstruerar en ritning i områdesproblem. Låt oss hitta skärningspunkterna för parabeln och linjen. Detta kan göras på två sätt. Det första sättet är analytiskt. Vi löser ekvationen:

Därför den nedre gränsen för integration, den övre gränsen för integration.
Det är bäst att inte använda denna metod om möjligt..

Det är mycket mer lönsamt och snabbare att bygga linjerna punkt för punkt, samtidigt som gränserna för integrationen upptäcks som "av sig själva". Den punkt för punkt konstruktionstekniken för olika diagram diskuteras i detalj i hjälpen Grafer och egenskaper hos elementära funktioner. Ändå måste den analytiska metoden för att hitta gränserna ibland användas om till exempel grafen är tillräckligt stor, eller om den gängade konstruktionen inte avslöjade gränserna för integration (de kan vara bråkdelar eller irrationella). Och vi kommer också att överväga ett sådant exempel.

Vi återgår till vår uppgift: det är mer rationellt att först konstruera en rät linje och först sedan en parabel. Låt oss göra en ritning:

Jag upprepar att med punktvis konstruktion upptäcks gränserna för integrationen oftast "automatiskt".

Och nu arbetsformeln: Om det finns någon kontinuerlig funktion på intervallet större än eller lika med någon kontinuerlig funktion, då området av figuren som begränsas av graferna för dessa funktioner och räta linjer, kan hittas av formeln:

Här är det inte längre nödvändigt att tänka på var figuren är placerad - ovanför axeln eller under axeln, och grovt sett, det spelar roll vilket diagram som är OVAN(i förhållande till en annan graf), och vilken är UNDER.

I exemplet under övervägande är det uppenbart att på segmentet är parabeln belägen ovanför den räta linjen, och därför är det nödvändigt att subtrahera från

Slutförandet av lösningen kan se ut så här:

Den önskade figuren begränsas av en parabel ovanifrån och en rak linje underifrån.
På segmentet enligt motsvarande formel:

Svar:

Faktum är att skolformeln för arean av en kurvlinjär trapets i det nedre halvplanet (se enkelt exempel nr 3) är ett specialfall av formeln . Eftersom axeln ges av ekvationen , och grafen för funktionen är lokaliserad inte högre yxor alltså

Och nu ett par exempel för en oberoende lösning

Exempel 5

Exempel 6

Hitta arean av figuren som omges av linjerna, .

När man löser problem för att beräkna arean med hjälp av en viss integral inträffar ibland en rolig incident. Ritningen gjordes korrekt, beräkningarna var korrekta, men på grund av ouppmärksamhet ... hittade området för fel figur, det var så din lydiga tjänare skruvade ihop flera gånger. Här är ett fall från verkligheten:

Exempel 7

Beräkna arean av figuren avgränsad av linjerna , , , .

Lösning: Låt oss göra en ritning först:

…Eh, ritningen blev skit, men allt verkar vara läsligt.

Figuren vars område vi behöver hitta är skuggad i blått.(titta noga på skicket - hur siffran är begränsad!). Men i praktiken, på grund av ouppmärksamhet, uppstår ofta ett "glitch", att du måste hitta området för figuren som är skuggad i grönt!

Det här exemplet är också användbart i det att figurens area beräknas med två bestämda integraler. Verkligen:

1) På segmentet ovanför axeln finns en rak linjegraf;

2) På segmentet ovanför axeln finns en hyperbelgraf.

Det är ganska uppenbart att områdena kan (och bör) läggas till, därför:

Svar:

Låt oss gå vidare till ytterligare en meningsfull uppgift.

Exempel 8

Beräkna arean av en figur avgränsad av linjer,
Låt oss presentera ekvationerna i en "skola"-form och utföra en punkt-för-punkt-ritning:

Det framgår av ritningen att vår övre gräns är "bra": .
Men vad är den nedre gränsen? Det är tydligt att detta inte är ett heltal, men vad? Kanske ? Men var finns garantin att ritningen är gjord med perfekt noggrannhet, det kan det mycket väl visa sig. Eller rot. Tänk om vi inte fick grafen rätt alls?

I sådana fall måste man lägga ytterligare tid och förfina gränserna för integration analytiskt.

Låt oss hitta skärningspunkterna för linjen och parabeln.
För att göra detta löser vi ekvationen:


,

Verkligen,.

Den ytterligare lösningen är trivial, det viktigaste är att inte bli förvirrad i substitutioner och tecken, beräkningarna här är inte de lättaste.

På segmentet , enligt motsvarande formel:

Svar:

Tja, som avslutning på lektionen kommer vi att överväga två uppgifter som är svårare.

Exempel 9

Beräkna arean av figuren avgränsad av linjer, ,

Lösning: Rita denna figur på ritningen.

Fan, jag glömde skriva under schemat och gjorde om bilden, förlåt, inte hotz. Inte en teckning, kort sagt, idag är en dag =)

För punkt-för-punkt-konstruktion är det nödvändigt att känna till utseendet på sinusoiden (och i allmänhet är det användbart att veta grafer över alla elementära funktioner), samt vissa sinusvärden, de finns i trigonometrisk tabell. I vissa fall (som i detta fall) är det tillåtet att konstruera en schematisk ritning, på vilken grafer och integrationsgränser måste visas i princip korrekt.

Det är inga problem med integrationsgränserna här, de följer direkt av villkoret: - "x" ändras från noll till "pi". Vi fattar ett ytterligare beslut:

På segmentet är grafen för funktionen placerad ovanför axeln, därför:

I den här lektionen lär vi oss hur man räknar områden av platta figurer, som kallas kurvlinjära trapetser .

Exempel på sådana figurer finns i figuren nedan.

Å ena sidan är det extremt enkelt att hitta arean för en platt figur med hjälp av en bestämd integral. Vi pratar om området för figuren, som begränsas ovanifrån av en viss kurva, underifrån - av abskissaxeln ( Oxe), och till vänster och höger finns några raka linjer. Enkelheten är den den bestämda integralen av funktionen till vilken kurvan ges, och det finns arean för en sådan figur(krökt trapets).

För att beräkna arean av en figur behöver vi:

1. Definitiv integral av funktionen som definierar kurvan , vilket begränsar den kurvlinjära trapetsen uppifrån. Och här kommer den första betydande nyansen: en krökt trapets kan begränsas av en kurva inte bara ovanifrån, utan också underifrån . Hur ska man agera i detta fall? Enkelt men viktigt att komma ihåg: integralen i detta fall tas med ett minustecken .
2. Gränser för integration a och b, som vi finner från linjeekvationerna som binder figuren till vänster och höger: x = a , x = b, var a och b- tal.

Separat, några fler nyanser.

Kurvan som begränsar den kurvlinjära trapetsen uppifrån (eller underifrån) måste vara graf över en kontinuerlig och icke-negativ funktion y = f(x) .

X-värden måste tillhöra segmentet [a, b] . Det vill säga, till exempel, linjer som en sektion av en svamp beaktas inte, där benet passar perfekt in i detta segment och locket är mycket bredare.

Sidosegment kan degenerera till punkter . Om du såg en sådan figur på ritningen bör detta inte förvirra dig, eftersom denna punkt alltid har sitt eget värde på x-axeln. Så allt är i sin ordning med integrationens gränser.

Nu kan du gå vidare till formler och beräkningar. Alltså området s kurvlinjär trapets kan beräknas med formeln

Om f(x) ≤ 0 (grafen för funktionen är placerad under axeln Oxe), då område av en krökt trapets kan beräknas med formeln

Det finns också fall då både de övre och nedre gränserna för figuren är funktioner, respektive y = f(x) och y = φ (x) , då beräknas arean för en sådan figur med formeln

. (3)

Vi löser problem tillsammans

Låt oss börja med fall där arean av en figur kan beräknas med formeln (1).

Exempel 1Oxe) och direkt x = 1 , x = 3 .

Lösning. Eftersom y = 1/x> 0 på segmentet, då hittas arean av den krökta trapetsen av formeln (1):

.

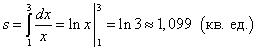Exempel 2 Hitta arean av figuren som avgränsas av grafen för funktionen, rät linje x= 1 och x-axeln ( Oxe ).

Lösning. Resultatet av att tillämpa formel (1):

Om då s= 1/2; om då s= 1/3 osv.

Exempel 3 Hitta arean av figuren som begränsas av grafen för funktionen, x-axeln ( Oxe) och direkt x = 4 .

Lösning. Figuren som motsvarar problemets tillstånd är en kurvlinjär trapets, där det vänstra segmentet har degenererats till en punkt. Integrationsgränserna är 0 och 4. Eftersom vi enligt formel (1) finner arean för den krökta trapetsen:

.

Exempel 4 Hitta området för figuren som avgränsas av linjerna , , och som ligger i 1:a kvartalet.

Lösning. För att använda formel (1), representerar vi arean av figuren som ges av villkoren i exemplet som summan av ytorna i en triangel OAB och kurvlinjär trapets ABC. När du beräknar arean av en triangel OAB integrationens gränser är punkternas absciss O och A, och för figuren ABC- Absciss av poäng A och C (Aär skärningspunkten för linjen OA och paraboler, och C- skärningspunkten mellan parabeln och axeln Oxe). Genom att gemensamt lösa (som ett system) ekvationerna för en rät linje och en parabel får vi (punktens abskiss A) och (abskissan för en annan skärningspunkt mellan linjen och parabeln, som inte behövs för lösningen). På samma sätt får vi , (abskiss av poäng C och D). Nu har vi allt för att hitta arean av figuren. Vi hittar:

Exempel 5 Hitta arean för en kurvlinjär trapets ACDB, om ekvationen för kurvan CD och abskiss A och B 1 respektive 2.

Lösning. Vi uttrycker denna ekvation av kurvan genom Y: Arean av den kurvlinjära trapetsen hittas av formeln (1):

.

Låt oss gå vidare till fall där arean av en figur kan beräknas med formeln (2).

Exempel 6 Hitta arean av figuren som begränsas av parabeln och x-axeln ( Oxe ).

Lösning. Denna figur ligger under x-axeln. Därför använder vi formel (2) för att beräkna dess area. Integrationens gränser är abskissorna och skärningspunkterna mellan parabeln och axeln Oxe. Därmed,

Exempel 7 Hitta arean mellan x-axeln ( Oxe) och två närliggande sinusvågor.

Lösning. Arean av denna figur kan hittas med formeln (2):

.

Låt oss hitta varje term separat:

.

.

Äntligen hittar vi området:

.

Exempel 8 Hitta arean av figuren som är innesluten mellan parabeln och kurvan.

Lösning. Låt oss uttrycka linjernas ekvationer i termer av Y:

Arean enligt formel (2) kommer att erhållas som

,

var a och b- Absciss av poäng A och B. Vi hittar dem genom att lösa ekvationerna tillsammans:

Äntligen hittar vi området:

Och slutligen finns det fall då arean av en figur kan beräknas med formeln (3).

Exempel 9 Hitta arean av figuren som är innesluten mellan parabolerna och .

Vi kom på hur man hittar området för en kurvlinjär trapets G. Här är de resulterande formlerna:
för en kontinuerlig och icke-negativ funktion y=f(x) på segmentet,
för en kontinuerlig och icke-positiv funktion y=f(x) på segmentet .

Men när man löser problem med att hitta området måste man ofta hantera mer komplexa figurer.

I den här artikeln kommer vi att prata om att beräkna arean av figurer vars gränser är explicit specificerade av funktioner, det vill säga som y=f(x) eller x=g(y), och analysera i detalj lösningen av typiska exempel .

Sidnavigering.

Formel för att beräkna arean av en figur som begränsas av linjerna y=f(x) eller x=g(y) .

Sats.

Låt funktionerna och vara definierade och kontinuerliga på segmentet och för valfritt värde x från . Sedan område av figur G, avgränsat av linjer x=a , x=b , och beräknas med formeln .

En liknande formel är giltig för området för figuren som avgränsas av linjerna y \u003d c, y \u003d d och: .

Bevis.

Låt oss visa formelns giltighet för tre fall:

I det första fallet, när båda funktionerna är icke-negativa, på grund av områdets additivitetsegenskap, är summan av arean av den ursprungliga figuren G och den kurvlinjära trapetsen lika med figurens area. Därmed,

Så, . Den sista övergången är möjlig på grund av den definitiva integralens tredje egenskap.

På samma sätt, i det andra fallet, är jämlikheten sann. Här är en grafisk illustration:

I det tredje fallet, när båda funktionerna är icke-positiva, har vi . Låt oss illustrera detta:

Nu kan vi gå vidare till det allmänna fallet när funktionerna och korsar Ox-axeln.

Låt oss beteckna skärningspunkterna. Dessa punkter delar upp segmentet i n delar, där . Figuren G kan representeras av siffrornas förening . Det är uppenbart att på dess intervall faller under ett av de tre fall som behandlats tidigare, därför hittas deras områden som

Därmed,

Den sista övergången är giltig på grund av den femte egenskapen hos den bestämda integralen.

Grafisk illustration av det allmänna fallet.

Formeln alltså bevisad.

Det är dags att gå vidare till att lösa exempel för att hitta arean av figurer som avgränsas av linjerna y=f(x) och x=g(y) .

Exempel på beräkning av arean av en figur avgränsad av linjerna y=f(x) eller x=g(y) .

Vi kommer att börja lösningen av varje problem genom att konstruera en figur på ett plan. Detta kommer att tillåta oss att representera en komplex figur som en förening av enklare figurer. Vid svårigheter med konstruktionen, se artiklarna:; och .

Exempel.

Beräkna arean av en figur som avgränsas av en parabel och räta linjer, x=1, x=4.

Lösning.

Låt oss bygga dessa linjer på planet.

Överallt på segmentet, grafen för en parabel ovan rakt. Därför tillämpar vi den tidigare erhållna formeln för arean och beräknar den bestämda integralen med hjälp av Newton-Leibniz formel:

Låt oss komplicera exemplet lite.

Exempel.

Beräkna arean av figuren avgränsad av linjer.

Lösning.

Hur skiljer sig detta från tidigare exempel? Tidigare hade vi alltid två räta linjer parallella med x-axeln, och nu bara en x=7 . Frågan uppstår omedelbart: var ska man ta den andra gränsen för integration? Låt oss ta en titt på ritningen för detta.

Det blev tydligt att den nedre gränsen för integration när man hittar området för figuren är abskissan för skärningspunkten för grafen för den räta linjen y \u003d x och semiparabeln. Vi finner denna abskissa från jämlikheten:

Därför är skärningspunktens abskiss x=2 .

Notera.

I vårt exempel och på ritningen kan man se att linjerna och y=x skär varandra i punkten (2;2) och de tidigare beräkningarna verkar överflödiga. Men i andra fall är det kanske inte så självklart. Därför rekommenderar vi att du alltid analytiskt beräknar abskissorna och ordinaterna för linjers skärningspunkter.

Uppenbarligen är grafen för funktionen y=x placerad ovanför grafen för funktionen på intervallet . Vi använder formeln för att beräkna arean:

Låt oss komplicera uppgiften ännu mer.

Exempel.

Beräkna arean av figuren avgränsad av graferna för funktioner och .

Lösning.

Låt oss bygga en graf med omvänd proportionalitet och en parabel .

Innan vi tillämpar formeln för att hitta arean av en figur måste vi bestämma gränserna för integration. För att göra detta hittar vi abskissorna för linjernas skärningspunkter genom att likställa uttrycken och .

För värden på x andra än noll, är likheten motsvarar tredje gradens ekvation med heltalskoefficienter. Du kan hänvisa till avsnittet för att återkalla algoritmen för att lösa det.

Det är lätt att kontrollera att x=1 är roten till denna ekvation: .

Dela upp uttrycket till binomialen x-1 har vi:

Således hittas de återstående rötterna från ekvationen :

Nu från ritningen blev det klart att figuren G är omsluten ovanför den blåa och under den röda linjen i intervallet . Således kommer det erforderliga området att vara lika med

Låt oss titta på ett annat typiskt exempel.

Exempel.

Beräkna arean av en figur avgränsad av kurvor och abskissaxeln.

Lösning.

Låt oss göra en ritning.

Detta är en vanlig potensfunktion med en exponent på en tredjedel, funktionens plot kan erhållas från grafen genom att visa den symmetriskt kring x-axeln och lyfta den med ett.

Hitta skärningspunkterna för alla linjer.

X-axeln har ekvationen y=0 .

Graferna för funktionerna och y=0 skär varandra i punkten (0;0) eftersom x=0 är den enda reella roten av ekvationen.

Funktionsgrafer och y=0 skär vid (2;0), eftersom x=2 är den enda roten av ekvationen .

Funktionsgrafer och skär i punkten (1;1) eftersom x=1 är den enda roten i ekvationen . Detta uttalande är inte helt självklart, men är en strikt ökande funktion, och - strikt minskande, därför ekvationen har högst en rot.

Den enda anmärkningen: i det här fallet, för att hitta området, måste du använda en formel för formuläret . Det vill säga att begränsningslinjerna måste representeras som funktioner av argumentet y, men med en svart linje.

Låt oss definiera skärningspunkterna för linjerna.

Låt oss börja med grafer över funktioner och:

Låt oss hitta skärningspunkten för grafer för funktioner och:

Det återstår att hitta skärningspunkten för linjerna och:

Som du kan se matchar värdena.

Sammanfatta.

Vi har analyserat alla de vanligaste fallen av att hitta arean av en figur som avgränsas av uttryckligen givna linjer. För att göra detta måste du kunna bygga linjer på ett plan, hitta linjernas skärningspunkter och tillämpa formeln för att hitta arean, vilket innebär förmågan att beräkna vissa integraler.

Exempel1 . Beräkna arean av figuren avgränsad av linjer: x + 2y - 4 = 0, y = 0, x = -3 och x = 2

Låt oss bygga en figur (se fig.) Vi bygger en rak linje x + 2y - 4 \u003d 0 längs två punkter A (4; 0) och B (0; 2). Om vi ​​uttrycker y i termer av x får vi y \u003d -0,5x + 2. Enligt formel (1), där f (x) \u003d -0,5x + 2, a \u003d -3, b \u003d 2, vi hitta

S \u003d \u003d [-0,25 \u003d 11,25 kvm. enheter

Exempel 2 Beräkna arean av figuren avgränsad av linjer: x - 2y + 4 \u003d 0, x + y - 5 \u003d 0 och y \u003d 0.

Lösning. Låt oss bygga en figur.

Låt oss bygga en rät linje x - 2y + 4 = 0: y = 0, x = - 4, A (-4; 0); x = 0, y = 2, B(0; 2).

Låt oss konstruera en rät linje x + y - 5 = 0: y = 0, x = 5, С(5; 0), x = 0, y = 5, D(0; 5).

Hitta linjernas skärningspunkt genom att lösa ekvationssystemet:

x = 2, y = 3; M(2; 3).

För att beräkna den erforderliga arean delar vi AMC-triangeln i två trianglar AMN och NMC, eftersom när x ändras från A till N begränsas arean av en rät linje, och när x ändras från N till C är det en rät linje

För triangel AMN har vi: ; y \u003d 0,5x + 2, d.v.s. f (x) \u003d 0,5x + 2, a \u003d - 4, b \u003d 2.

För NMC-triangeln har vi: y = - x + 5, dvs f(x) = - x + 5, a = 2, b = 5.

Genom att beräkna arean av var och en av trianglarna och lägga till resultaten finner vi:

kvm enheter

kvm enheter

9 + 4, 5 = 13,5 kvm. enheter Kontrollera: = 0,5 AC = 0,5 kvm. enheter

Exempel 3 Beräkna arean av en figur avgränsad av linjer: y = x 2 , y = 0, x = 2, x = 3.

I det här fallet är det nödvändigt att beräkna arean av en krökt trapets som begränsas av en parabel y = x 2 , raka linjer x \u003d 2 och x \u003d 3 och Ox-axeln (se fig.) Enligt formel (1) hittar vi arean av en kurvlinjär trapetsoid

= = 6kv. enheter

Exempel 4 Beräkna arean av en figur avgränsad av linjer: y \u003d - x 2 + 4 och y = 0

Låt oss bygga en figur. Det önskade området är inneslutet mellan parabeln y \u003d - x 2 + 4 och axel Oh.

Hitta skärningspunkterna för parabeln med x-axeln. Om vi ​​antar y \u003d 0, hittar vi x \u003d Eftersom denna siffra är symmetrisk kring Oy-axeln, beräknar vi arean av figuren till höger om Oy-axeln och dubblar resultatet: \u003d + 4x] kvadrat. enheter 2 = 2 kvm. enheter

Exempel 5 Beräkna arean av en figur avgränsad av linjer: y 2 = x, yx = 1, x = 4

Här är det nödvändigt att beräkna arean av den krökta trapetsen som begränsas av den övre grenen av parabeln y 2 \u003d x, Ox-axeln och räta linjer x \u003d 1x \u003d 4 (se fig.)

Enligt formel (1), där f(x) = a = 1 och b = 4, har vi = (= kvadratenheter

Exempel 6 . Beräkna arean av figuren avgränsad av linjer: y = sinx, y = 0, x = 0, x= .

Det önskade området begränsas av en halvvågssinusform och Ox-axeln (se fig.).

Vi har - cosx \u003d - cos \u003d 1 + 1 \u003d 2 kvadratmeter. enheter

Exempel 7 Beräkna arean av figuren avgränsad av linjer: y \u003d - 6x, y \u003d 0 och x \u003d 4.

Figuren är placerad under Ox-axeln (se fig.).

Därför hittas dess area av formeln (3)

= =

Exempel 8 Beräkna arean av figuren avgränsad av linjerna: y \u003d och x \u003d 2. Vi kommer att bygga kurvan y \u003d av punkter (se figur). Således hittas figurens yta av formeln (4)

Exempel 9 .

X 2 + y 2 = r 2 .

Här måste du beräkna arean som begränsas av cirkeln x 2 + y 2 = r 2 , dvs arean av en cirkel med radie r centrerad vid origo. Låt oss hitta den fjärde delen av detta område, och ta gränserna för integration från 0

dor; vi har: 1 = = [

Därmed, 1 =

Exempel 10 Beräkna arean av figuren avgränsad av linjer: y \u003d x 2 och y = 2x

Denna siffra begränsas av parabeln y \u003d x 2 och rät linje y \u003d 2x (se fig.) För att bestämma skärningspunkterna för de givna linjerna löser vi ekvationssystemet: x 2 – 2x = 0 x = 0 och x = 2

Genom att använda formel (5) för att hitta arean får vi

= }