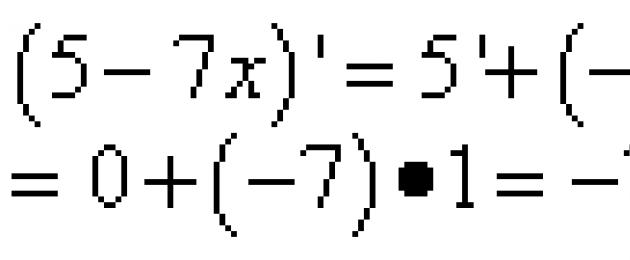The operation of finding a derivative is called differentiation.
As a result of solving the problems of finding derivatives for the simplest (and not very simple) functions by defining the derivative as the limit of the ratio of the increment to the increment of the argument, a table of derivatives and precisely defined rules of differentiation appeared. The first in the field of finding derivatives were Isaac Newton (1643-1727) and Gottfried Wilhelm Leibniz (1646-1716).
Therefore, in our time, in order to find the derivative of any function, it is not necessary to calculate the above-mentioned limit of the ratio of the increment of the function to the increment of the argument, but you just need to use the table of derivatives and the rules of differentiation. The following algorithm is suitable for finding the derivative.
To find the derivative, you need an expression under the stroke sign disassemble simple functions and determine what actions (product, sum, quotient) these functions are linked. Further, the derivatives of elementary functions are found in the table of derivatives, and the formulas for derivatives of the product, sum and quotient are found in the rules of differentiation. Derivative table and rules of differentiation are given after the first two examples.
Example 1. Find the derivative of a function
Solution. From the rules of differentiation, we find out that the derivative of the sum of functions is the sum of the derivatives of functions, i.e.
From the table of derivatives we find out that the derivative of the "x" is equal to one, and the derivative of the sine is equal to the cosine. We substitute these values into the sum of derivatives and find the derivative required by the condition of the problem:
Example 2. Find the derivative of a function
Solution. We differentiate as the derivative of the sum, in which the second term with a constant factor, it can be taken outside the sign of the derivative:
![]()
If there are still questions about where what comes from, they, as a rule, become clearer after familiarization with the table of derivatives and the simplest rules of differentiation. We are going to them right now.
Derivative table of simple functions
| 1. Derivative of a constant (number). Any number (1, 2, 5, 200 ...) that is in the function expression. Always zero. This is very important to remember, as it is required very often. | |
| 2. Derivative of the independent variable. Most often "x". Always equal to one. This is also important to remember for a long time. | |
| 3. Derivative degree. When solving problems, you need to transform non-square roots into a degree. | |
| 4. Derivative of a variable to the power of -1 | |
| 5. Derivative of the square root | |
| 6. Derivative of sine | |
| 7. Derivative of the cosine | |
| 8. Derivative of the tangent | |
| 9. Derivative of the cotangent | |
| 10. Derivative of the arcsine | |
| 11. Derivative of the arccosine | |
| 12. Derivative of the arctangent | |
| 13. Derivative of the arc cotangent | |
| 14. Derivative of the natural logarithm | |
| 15. Derivative of the logarithmic function | |
| 16. Derivative of the exponent | |
| 17. Derivative of the exponential function |
Differentiation rules
| 1. Derivative of the sum or difference | |
| 2. Derivative of the work | |
| 2a. Derivative of an expression multiplied by a constant factor | |
| 3. Derivative of the quotient | |
| 4. Derivative of a complex function |  |
Rule 1.If functions
differentiable at some point, then at the same point the functions
moreover
![]()
those. the derivative of the algebraic sum of functions is equal to the algebraic sum of the derivatives of these functions.
Consequence. If two differentiable functions differ by a constant term, then their derivatives are equal, i.e.
Rule 2.If functions
differentiable at some point, then at the same point their product is also differentiable
moreover
![]()
those. the derivative of the product of two functions is equal to the sum of the products of each of these functions by the derivative of the other.
Corollary 1. The constant factor can be moved outside the sign of the derivative:
Corollary 2. The derivative of the product of several differentiable functions is equal to the sum of the products of the derivative of each of the factors by all the others.
For example, for three factors:
Rule 3.If functions
differentiable at some point and , then at this point it is differentiable and their quotientu / v, and
![]()
those. the derivative of the quotient of two functions is equal to the fraction, the numerator of which is the difference between the products of the denominator and the derivative of the numerator and the numerator and the derivative of the denominator, and the denominator is the square of the previous numerator.
Where what to look for on other pages
When finding the derivative of the product and the quotient in real problems, it is always necessary to apply several differentiation rules at once, so there are more examples of these derivatives in the article"Derivative of a work and a particular function".
Comment. Do not confuse a constant (that is, a number) as a summand and as a constant factor! In the case of a term, its derivative is equal to zero, and in the case of a constant factor, it is taken out of the sign of the derivatives. This is a typical mistake that occurs at the initial stage of studying derivatives, but after solving several one- or two-component examples, the average student no longer makes this mistake.
And if, when differentiating a work or a particular, you have a term u"v, in which u- a number, for example, 2 or 5, that is, a constant, then the derivative of this number will be equal to zero and, therefore, the entire term will be equal to zero (this case is analyzed in Example 10).
Another common mistake is the mechanical solution of a derivative of a complex function as a derivative of a simple function. So derivative of a complex function a separate article is devoted. But first, we will learn to find the derivatives of simple functions.
Along the way, you can not do without expression transformations. To do this, you may need to open the tutorials in new windows Actions with powers and roots and Actions with fractions .
If you are looking for solutions to derivatives of fractions with powers and roots, that is, when a function looks like ![]() , then follow the lesson Derivative of the Sum of Fractions with Powers and Roots.
, then follow the lesson Derivative of the Sum of Fractions with Powers and Roots.
If you have a task like ![]() , then your lesson "Derivatives of simple trigonometric functions".
, then your lesson "Derivatives of simple trigonometric functions".
Step by step examples - how to find the derivative
Example 3. Find the derivative of a function
Solution. We determine the parts of the function expression: the whole expression represents the product, and its factors are sums, in the second of which one of the terms contains a constant factor. We apply the rule of product differentiation: the derivative of the product of two functions is equal to the sum of the products of each of these functions by the derivative of the other:
![]()
Next, we apply the rule for differentiating the sum: the derivative of the algebraic sum of functions is equal to the algebraic sum of the derivatives of these functions. In our case, in each sum, the second term with a minus sign. In each sum we see both an independent variable, the derivative of which is equal to one, and a constant (number), the derivative of which is equal to zero. So, "x" for us turns into one, and minus 5 - into zero. In the second expression, "x" is multiplied by 2, so we multiply two by the same unit as the derivative of "x". We get the following values of the derivatives:
We substitute the found derivatives into the sum of the products and obtain the derivative of the entire function required by the condition of the problem:
![]()
And you can check the solution of the problem for the derivative on.
Example 4. Find the derivative of a function
Solution. We are required to find the derivative of the quotient. We apply the formula for differentiating the quotient: the derivative of the quotient of two functions is equal to a fraction, the numerator of which is the difference between the products of the denominator and the derivative of the numerator and the numerator and the derivative of the denominator, and the denominator is the square of the previous numerator. We get:

We have already found the derivative of the factors in the numerator in Example 2. Let's not forget that the product that is the second factor in the numerator in the current example is taken with a minus sign:

If you are looking for solutions to problems in which you need to find the derivative of a function, where there is a continuous heap of roots and powers, such as, for example, ![]() then welcome to class "Derivative of the sum of fractions with powers and roots" .
then welcome to class "Derivative of the sum of fractions with powers and roots" .
If you need to learn more about the derivatives of sines, cosines, tangents and other trigonometric functions, that is, when the function looks like ![]() , then your lesson "Derivatives of simple trigonometric functions" .
, then your lesson "Derivatives of simple trigonometric functions" .
Example 5. Find the derivative of a function
Solution. In this function, we see a product, one of the factors of which is the square root of the independent variable, the derivative of which we familiarized ourselves with in the table of derivatives. According to the rule of differentiation of the product and the tabular value of the derivative of the square root, we obtain:

You can check the solution of the problem for the derivative on derivatives calculator online .
Example 6. Find the derivative of a function
Solution. In this function, we see the quotient, the dividend of which is the square root of the independent variable. According to the rule of differentiation of the quotient, which we repeated and applied in example 4, and the table value of the derivative of the square root, we get:

To get rid of the fraction in the numerator, multiply the numerator and denominator by.
- The general case of a formula for the derivative of a root of arbitrary degree- a fraction, in the numerator of which is one, and in the denominator, a number equal to the power of the root, for which the derivative was calculated, multiplied by the root of the same power, the radical expression of which is the variable in the power of the root, for which the derivative was calculated, reduced by one
- Derivative of the square root- is a special case of the previous formula. Derivative of the square root of x is a fraction, the numerator of which is one, and the denominator is two, multiplied by the square root of x
- Derivative of the cube root, also a special case of the general formula. The cube root derivative is the unit divided by three cube roots of x square.
Below are the transformations that explain why the formulas for finding the derivative of the square and cube root are exactly as shown in the figure.
Of course, these formulas do not need to be memorized at all, if we take into account that extracting a root of a derived degree is the same as raising to a power of a fraction, the denominator of which is equal to the same degree. Then finding the derivative of the root is reduced to applying the formula for finding the derivative of the degree of the corresponding fraction.
Derivative of a variable under the square root
(√x) "= 1 / (2√x) or 1/2 x -1/2
Explanation:
(√x) "= (x 1/2)"
Square root is exactly the same as raising to the 1/2 power,therefore, to find the derivative of the root, you can apply the formula from the rule for finding the derivative of a variable to an arbitrary power:
(x 1/2) "= 1/2 x -1/2 = 1 / (2√x)
Derivative of the cube root (derivative of the root of the third degree)
The derivative of the cube root is found in exactly the same way as the square root.Imagine the cube root as a power of 1/3 and find the derivative according to the general rules of differentiation. A short formula can be seen in the picture above, and below is an explanation of why this is so.

The -2/3 power is obtained by subtracting one from 1/3
Complex functions do not always fit the definition of a complex function. If there is a function of the form y = sin x - (2 - 3) a r c t g x x 5 7 x 10 - 17 x 3 + x - 11, then it cannot be considered complex, unlike y = sin 2 x.
This article will show the concept of a complex function and its identification. Let's work with formulas for finding the derivative with examples of solutions in the conclusion. The use of the table of derivatives and the rule of differentiation significantly reduces the time to find the derivative.
Basic definitions
Definition 1A complex function is a function whose argument is also a function.
It is denoted in this way: f (g (x)). We have that the function g (x) is considered an argument to f (g (x)).
Definition 2
If there is a function f and is a cotangent function, then g (x) = ln x is a natural logarithm function. We get that the complex function f (g (x)) will be written as arctan (lnx). Or a function f, which is a function raised to the 4th power, where g (x) = x 2 + 2 x - 3 is considered an entire rational function, we get that f (g (x)) = (x 2 + 2 x - 3) 4 ...
Obviously g (x) can be tricky. From the example y = sin 2 x + 1 x 3 - 5, you can see that the value of g has a cube root with a fraction. This expression is allowed to be denoted as y = f (f 1 (f 2 (x))). Whence we have that f is the sine function, and f 1 is the function located under the square root, f 2 (x) = 2 x + 1 x 3 - 5 is a fractional rational function.
Definition 3
The nesting degree is determined by any natural number and is written as y = f (f 1 (f 2 (f 3 (... (F n (x)))))).
Definition 4
The concept of function composition refers to the number of nested functions by the condition of the problem. For the solution, the formula for finding the derivative of a complex function of the form
(f (g (x))) "= f" (g (x)) g "(x)
Examples of
Example 1Find the derivative of a complex function of the form y = (2 x + 1) 2.
Solution
By the condition, you can see that f is a squaring function, and g (x) = 2 x + 1 is considered a linear function.
Let's apply the derivative formula for a complex function and write:
f "(g (x)) = ((g (x)) 2)" = 2 · (g (x)) 2 - 1 = 2 · g (x) = 2 · (2 x + 1); g "(x) = (2 x + 1)" = (2 x) "+ 1" = 2 x "+ 0 = 2 1 x 1 - 1 = 2 ⇒ (f (g (x))) "= f" (g (x)) g "(x) = 2 (2 x + 1) 2 = 8 x + 4
It is necessary to find a derivative with a simplified original form of the function. We get:
y = (2 x + 1) 2 = 4 x 2 + 4 x + 1
Hence we have that
y "= (4 x 2 + 4 x + 1)" = (4 x 2) "+ (4 x)" + 1 "= 4 · (x 2)" + 4 · (x) "+ 0 = = 4 2 x 2 - 1 + 4 1 x 1 - 1 = 8 x + 4
The results matched.
When solving problems of this kind, it is important to understand where the function of the form f and g (x) will be located.
Example 2
You should find the derivatives of complex functions of the form y = sin 2 x and y = sin x 2.
Solution
The first notation of the function says that f is a squaring function and g (x) is a sine function. Then we get that
y "= (sin 2 x)" = 2 sin 2 - 1 x (sin x) "= 2 sin x cos x
The second entry shows that f is a sine function, and g (x) = x 2 we denote a power function. It follows that the product of a complex function can be written as
y "= (sin x 2)" = cos (x 2) (x 2) "= cos (x 2) 2 x 2 - 1 = 2 x cos (x 2)
The formula for the derivative y = f (f 1 (f 2 (f 3 (... (Fn (x)))))) will be written as y "= f" (f 1 (f 2 (f 3 (... ( fn (x)))))) f 1 "(f 2 (f 3 (... (fn (x))))) f 2" (f 3 (.. (fn (x)) )) ·. ... ... · F n "(x)
Example 3
Find the derivative of the function y = sin (ln 3 a r c t g (2 x)).
Solution
This example shows the complexity of writing and locating functions. Then y = f (f 1 (f 2 (f 3 (f 4 (x))))) denote, where f, f 1, f 2, f 3, f 4 (x) is a sine function, a function of raising in 3 degree, function with logarithm and base e, arctangent function and linear.
From the formula for the definition of a complex function, we have that
y "= f" (f 1 (f 2 (f 3 (f 4 (x))))) f 1 "(f 2 (f 3 (f 4 (x)))) f 2" (f 3 (f 4 (x))) f 3 "(f 4 (x)) f 4" (x)
We get what to find
- f "(f 1 (f 2 (f 3 (f 4 (x))))) as the sine derivative according to the table of derivatives, then f" (f 1 (f 2 (f 3 (f 4 (x)))) ) = cos (ln 3 arctan (2 x)).
- f 1 "(f 2 (f 3 (f 4 (x)))) as the derivative of the power function, then f 1" (f 2 (f 3 (f 4 (x)))) = 3 ln 3 - 1 arctan (2 x) = 3 ln 2 arctan (2 x).
- f 2 "(f 3 (f 4 (x))) as the derivative of the logarithmic, then f 2" (f 3 (f 4 (x))) = 1 a r c t g (2 x).
- f 3 "(f 4 (x)) as the derivative of the arctangent, then f 3" (f 4 (x)) = 1 1 + (2 x) 2 = 1 1 + 4 x 2.
- When finding the derivative f 4 (x) = 2 x, subtract 2 outside the sign of the derivative using the formula for the derivative of a power function with an exponent equal to 1, then f 4 "(x) = (2 x)" = 2 x "= 2 1 x 1 - 1 = 2.
We combine the intermediate results and get that
y "= f" (f 1 (f 2 (f 3 (f 4 (x))))) f 1 "(f 2 (f 3 (f 4 (x)))) f 2" (f 3 (f 4 (x))) f 3 "(f 4 (x)) f 4" (x) = = cos (ln 3 arctan (2 x)) 3 ln 2 arctan (2 x) 1 arctan (2 x) 1 1 + 4 x 2 2 = = 6 cos (ln 3 arctan (2 x)) ln 2 arctan (2 x) arctan (2 x) (1 + 4 x 2)
The analysis of such functions is reminiscent of nesting dolls. Differentiation rules cannot always be applied explicitly using a table of derivatives. It is often necessary to apply a formula for finding derivatives of complex functions.
There are some differences between a complex view and a complex function. With an obvious ability to distinguish this, finding derivatives will be especially easy.
Example 4
It is necessary to consider giving a similar example. If there is a function of the form y = t g 2 x + 3 t g x + 1, then it can be considered as a complex form g (x) = t g x, f (g) = g 2 + 3 g + 1. Obviously, it is necessary to apply a formula for a complex derivative:
f "(g (x)) = (g 2 (x) + 3 g (x) + 1)" = (g 2 (x)) "+ (3 g (x))" + 1 "= = 2 · g 2 - 1 (x) + 3 · g "(x) + 0 = 2 g (x) + 3 · 1 · g 1 - 1 (x) = = 2 g (x) + 3 = 2 tgx + 3; g "(x) = (tgx)" = 1 cos 2 x ⇒ y "= (f (g (x)))" = f "(g (x)) g" (x) = (2 tgx + 3 ) 1 cos 2 x = 2 tgx + 3 cos 2 x
A function of the form y = t g x 2 + 3 t g x + 1 is not considered difficult, since it has the sum of t g x 2, 3 t g x and 1. However, t g x 2 is considered a complex function, then we obtain a power function of the form g (x) = x 2 and f, which is a function of the tangent. To do this, it is necessary to differentiate by the amount. We get that
y "= (tgx 2 + 3 tgx + 1)" = (tgx 2) "+ (3 tgx)" + 1 "= = (tgx 2)" + 3 · (tgx) "+ 0 = (tgx 2)" + 3 cos 2 x
We proceed to finding the derivative of a complex function (t g x 2) ":
f "(g (x)) = (tan (g (x)))" = 1 cos 2 g (x) = 1 cos 2 (x 2) g "(x) = (x 2)" = 2 x 2 - 1 = 2 x ⇒ (tgx 2) "= f" (g (x)) g "(x) = 2 x cos 2 (x 2)
We get that y "= (t g x 2 + 3 t g x + 1)" = (t g x 2) "+ 3 cos 2 x = 2 x cos 2 (x 2) + 3 cos 2 x
Complex functions can be included in complex functions, and complex functions themselves can be complex functions.
Example 5
For example, consider a complex function of the form y = log 3 x 2 + 3 cos 3 (2 x + 1) + 7 e x 2 + 3 3 + ln 2 x (x 2 + 1)
This function can be represented in the form y = f (g (x)), where the value of f is a function of the logarithm to base 3, and g (x) is considered the sum of two functions of the form h (x) = x 2 + 3 cos 3 (2 x + 1) + 7 ex 2 + 3 3 and k (x) = ln 2 x (x 2 + 1). Obviously, y = f (h (x) + k (x)).
Consider the function h (x). This is the ratio l (x) = x 2 + 3 cos 3 (2 x + 1) + 7 to m (x) = e x 2 + 3 3
We have that l (x) = x 2 + 3 cos 2 (2 x + 1) + 7 = n (x) + p (x) is the sum of two functions n (x) = x 2 + 7 and p (x) = 3 cos 3 (2 x + 1), where p (x) = 3 p 1 (p 2 (p 3 (x))) is a complex function with a numerical coefficient 3, and p 1 is a cubing function, p 2 as a cosine function, p 3 (x) = 2 x + 1 - a linear function.
We got that m (x) = ex 2 + 3 3 = q (x) + r (x) is the sum of two functions q (x) = ex 2 and r (x) = 3 3, where q (x) = q 1 (q 2 (x)) is a complex function, q 1 is a function with exponential function, q 2 (x) = x 2 is a power function.
This shows that h (x) = l (x) m (x) = n (x) + p (x) q (x) + r (x) = n (x) + 3 p 1 (p 2 ( p 3 (x))) q 1 (q 2 (x)) + r (x)
Passing to an expression of the form k (x) = ln 2 x s 2 (x)) with rational integer t (x) = x 2 + 1, where s 1 is the squaring function, and s 2 (x) = ln x is logarithmic with base e.
It follows that the expression takes the form k (x) = s (x) t (x) = s 1 (s 2 (x)) t (x).
Then we get that
y = log 3 x 2 + 3 cos 3 (2 x + 1) + 7 ex 2 + 3 3 + ln 2 x (x 2 + 1) = = fn (x) + 3 p 1 (p 2 (p 3 (x))) q 1 (q 2 (x)) = r (x) + s 1 (s 2 (x)) t (x)
By function structures, it became clear how and what formulas should be used to simplify an expression when differentiating it. To familiarize yourself with such problems and for the concept of their solution, it is necessary to turn to the point of differentiation of the function, that is, finding its derivative.
If you notice an error in the text, please select it and press Ctrl + Enter
Derivation of the formula for the derivative of a power function (x to the power of a). Derivatives of roots of x are considered. Formula for the derivative of a higher-order power function. Examples of calculating derivatives.
ContentSee also: Power function and roots, formulas and graph
Power function plots
Basic formulas
The derivative of x to the power of a is equal to a times x to the power of a minus one:
(1)
.
The derivative of the nth root of x to the mth power is:
(2)
.
Derivation of the formula for the derivative of a power function
Case x> 0
Consider a power function of a variable x with exponent a:
(3)
.
Here a is an arbitrary real number. Consider the case first.
To find the derivative of function (3), we use the properties of the power function and transform it to the following form:
.
Now we find the derivative by applying:
;
.
Here .
Formula (1) is proved.
Derivation of the formula for the derivative of a root of degree n from x to degree m
Now consider a function that is a root of the following form:
(4)
.
To find the derivative, we transform the root to a power function:
.
Comparing with formula (3), we see that
.
Then
.
Using formula (1), we find the derivative:
(1)
;
;
(2)
.
In practice, there is no need to memorize formula (2). It is much more convenient to first transform the roots to power functions, and then find their derivatives using formula (1) (see examples at the end of the page).
Case x = 0
If, then the power function is also defined for the value of the variable x = 0
... Let us find the derivative of function (3) at x = 0
... To do this, we will use the definition of the derivative:
.
Substitute x = 0
:
.
In this case, by the derivative we mean the right-hand limit for which.
So we found:
.
Hence it is seen that at,.
At , .
At , .
This result is obtained by the formula (1):
(1)
.
Therefore, formula (1) is also valid for x = 0
.
Case x< 0
Consider function (3) again:
(3)
.
For some values of the constant a, it is also defined for negative values of the variable x. Namely, let a be a rational number. Then it can be represented as an irreducible fraction:
,
where m and n are integers with no common divisor.
If n is odd, then the power function is also defined for negative values of the variable x. For example, for n = 3
and m = 1
we have a cube root of x:
.
It is also defined for negative values of the variable x.
Let us find the derivative of the power function (3) for and for rational values of the constant a, for which it is defined. To do this, we represent x in the following form:
.
Then ,
.
We find the derivative by moving the constant outside the sign of the derivative and applying the rule for differentiating a complex function:
.
Here . But
.
Since, then
.
Then
.
That is, formula (1) is also valid for:
(1)
.
Higher order derivatives
Now we find the derivatives of higher orders of the power function
(3)
.
We have already found the first-order derivative:
.
Taking the constant a outside the sign of the derivative, we find the second-order derivative:
.
Similarly, we find the derivatives of the third and fourth orders:
;
.
From this it is clear that derivative of arbitrary nth order looks like this:
.
notice, that if a is a natural number,, then the n -th derivative is constant:
.
Then all subsequent derivatives are equal to zero:
,
at .
Derivative calculation examples
Example
Find the derivative of the function:
.
We transform the roots to powers:
;
.
Then the original function takes the form:
.
We find the derivatives of the powers:
;
.
The derivative of the constant is zero:
.
Instructions
Before finding the derivative of the root, pay attention to the rest of the functions present in the example being solved. If the problem has many radical expressions, then use the following rule for finding the derivative of the square root:
(√x) "= 1 / 2√x.
And to find the derivative of the cube root, use the formula:
(³√x) "= 1/3 (³√x) ²,
where ³√x denotes the cubic root of x.
If, intended for differentiation, there is a variable in fractional, then translate the root into a power function with the corresponding exponent. For a square root, this will be the degree of ½, and for a cubic root, it will be ⅓:
√x = x ^ 1,
³√x = x ^ ⅓,
where ^ denotes exponentiation.
To find the derivative of a power function in general and x ^ 1, x ^ ⅓, in particular, use the following rule:
(x ^ n) "= n * x ^ (n-1).
For the derivative of the root, this relation implies:
(x ^ 1) "= 1 x ^ (-1) and
(x ^ ⅓) "= ⅓ x ^ (-⅔).
After differentiating everything, take a close look at the rest of the example. If your answer is a very cumbersome expression, then you can probably simplify it. Most of the school examples are designed in such a way that they end up with a small number or a compact expression.
In many derivative problems, roots (square and cubic) are found together with other functions. To find the derivative of the root in this case, apply the following rules:
the derivative of a constant (constant number, C) equals zero: C "= 0;
the constant factor is taken out of the sign of the derivative: (k * f) "= k * (f)" (f is an arbitrary function);
the derivative of the sum of several functions is equal to the sum of the derivatives: (f + g) "= (f)" + (g) ";
the derivative of the product of two functions equals ... no, not the product of derivatives, but the following expression: (fg) "= (f)" g + f (g) ";
the derivative of the quotient is also not equal to the partial derivative, but is found according to the following rule: (f / g) "= ((f)" g - f (g) ") / g².
note
On this page, you can calculate the derivative of a function online to obtain a detailed solution to the problem. The solution of the derivatives of a function is made using the rules of differentiation that students study in the course of mathematical analysis at the institute. In order to find the derivative of a function, you need to enter a function for differentiation in the "Function" field according to the data entry rules.
Useful advice
The derivative of a function is the limit of the ratio of the increment of a function to the increment of the argument when the increment of the argument tends to zero: The mathematical meaning of this definition is not very easy to understand, since in the school algebra course the concept of the limit of a function is either not studied at all, or is studied very superficially. But in order to learn how to find the derivatives of various functions, this is not necessary.
Sources:
- derivative root of x
- In contact with 0
- Google+ 0
- OK 0
- Facebook 0