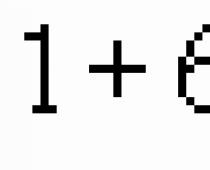Balance in mechanics. Stable and unstable equilibrium

DEFINITION

sustainable balance- this is an equilibrium in which the body, taken out of equilibrium and left to itself, returns to its previous position.

This occurs if, with a slight displacement of the body in any direction from the initial position, the resultant of the forces acting on the body becomes non-zero and is directed towards the equilibrium position. For example, a ball lying at the bottom of a spherical cavity (Fig. 1a).

DEFINITION

Unstable equilibrium- this is an equilibrium in which the body, taken out of the equilibrium position and left to itself, will deviate even more from the equilibrium position.

In this case, with a small displacement of the body from the equilibrium position, the resultant of the forces applied to it is nonzero and is directed from the equilibrium position. An example is a ball located at the top of a convex spherical surface (Fig. 1 b).

DEFINITION

Indifferent balance- this is an equilibrium in which the body, taken out of equilibrium and left to itself, does not change its position (state).

In this case, with small displacements of the body from its original position, the resultant of the forces applied to the body remains equal to zero. For example, a ball lying on a flat surface (Fig. 1, c).

Fig.1. Different types of body balance on a support: a) stable balance; b) unstable equilibrium; c) indifferent equilibrium.

Static and dynamic balance of bodies

If, as a result of the action of forces, the body does not receive acceleration, it can be at rest or move uniformly in a straight line. Therefore, we can talk about static and dynamic equilibrium.

DEFINITION

Static balance- this is such an equilibrium when, under the action of applied forces, the body is at rest.

dynamic balance- this is such an equilibrium when, under the action of forces, the body does not change its motion.

In a state of static equilibrium is a lantern suspended on cables, any building structure. As an example of dynamic equilibrium, we can consider a wheel that rolls on a flat surface in the absence of friction forces.

It follows that if the geometric sum of all external forces applied to the body is equal to zero, then the body is at rest or performs uniform rectilinear motion. In this case, it is customary to say that the forces applied to the body balance each other. When calculating the resultant, all forces acting on the body can be applied to the center of mass.

For a non-rotating body to be in equilibrium, it is necessary that the resultant of all forces applied to the body be equal to zero.

$(\overrightarrow(F))=(\overrightarrow(F_1))+(\overrightarrow(F_2))+...= 0$

If a body can rotate about some axis, then for its equilibrium it is not enough that the resultant of all forces be equal to zero.

The rotating action of a force depends not only on its magnitude, but also on the distance between the line of action of the force and the axis of rotation.

The length of the perpendicular drawn from the axis of rotation to the line of action of the force is called the arm of the force.

The product of the modulus of force $F$ and the arm d is called the moment of force M. The moments of those forces that tend to rotate the body counterclockwise are considered positive.

The rule of moments: a body with a fixed axis of rotation is in equilibrium if the algebraic sum of the moments of all forces applied to the body about this axis is zero:

In the general case, when a body can move translationally and rotate, both conditions must be met for equilibrium: the resultant force must be equal to zero and the sum of all moments of forces must be equal to zero. Both of these conditions are not sufficient for rest.

Figure 1. Indifferent equilibrium. Wheel rolling on a horizontal surface. The resultant force and the moment of forces are equal to zero

A wheel rolling on a horizontal surface is an example of indifferent equilibrium (Fig. 1). If the wheel is stopped at any point, it will be in equilibrium. Along with indifferent equilibrium in mechanics, states of stable and unstable equilibrium are distinguished.

A state of equilibrium is called stable if, with small deviations of the body from this state, forces or moments of forces arise that tend to return the body to an equilibrium state.

With a small deviation of the body from the state of unstable equilibrium, forces or moments of forces arise that tend to remove the body from the equilibrium position. A ball lying on a flat horizontal surface is in a state of indifferent equilibrium.

Figure 2. Different types of balance of a ball on a support. (1) -- indifferent equilibrium, (2) -- unstable equilibrium, (3) -- stable equilibrium

A ball located at the top of a spherical ledge is an example of an unstable equilibrium. Finally, the ball at the bottom of the spherical cavity is in a state of stable equilibrium (Fig. 2).

For a body with a fixed axis of rotation, all three types of equilibrium are possible. Indifferent equilibrium occurs when the axis of rotation passes through the center of mass. In stable and unstable equilibrium, the center of mass is on a vertical line passing through the axis of rotation. In this case, if the center of mass is below the axis of rotation, the state of equilibrium is stable. If the center of mass is located above the axis, the equilibrium state is unstable (Fig. 3).

Figure 3. Stable (1) and unstable (2) equilibrium of a homogeneous circular disk fixed on the O axis; point C is the center of mass of the disk; $(\overrightarrow(F))_t\ $-- gravity; $(\overrightarrow(F))_(y\ )$-- axis elastic force; d -- shoulder

A special case is the equilibrium of a body on a support. In this case, the elastic force of the support is not applied to one point, but is distributed over the base of the body. The body is in equilibrium if a vertical line drawn through the center of mass of the body passes through the support area, i.e., inside the contour formed by lines connecting the support points. If this line does not cross the area of support, then the body overturns.

Task 1

The inclined plane is inclined at an angle of 30o to the horizon (Fig. 4). There is a body P on it, the mass of which is m=2 kg. Friction can be neglected. The thread thrown over the block makes an angle of 45o with the inclined plane. At what weight of the load Q will the body P be in equilibrium?

Figure 4

The body is under the action of three forces: the force of gravity P, the tension of the thread with the load Q and the elastic force F from the side of the plane pressing on it in the direction perpendicular to the plane. Let us decompose the force Р into components: $\overrightarrow(Р)=(\overrightarrow(Р))_1+(\overrightarrow(Р))_2$. Condition $(\overrightarrow(P))_2=$ For equilibrium, taking into account the doubling of effort by the moving block, it is necessary that $\overrightarrow(Q)=-(2\overrightarrow(P))_1$. Hence the equilibrium condition: $m_Q=2m(sin \widehat((\overrightarrow(P))_1(\overrightarrow(P))_2)\ )$. Substituting the values, we get: $m_Q=2\cdot 2(sin \left(90()^\circ -30()^\circ -45()^\circ \right)\ )=1.035\ kg$.

In the wind, the tethered balloon hangs over a different point on the Earth, to which the cable is attached (Fig. 5). The cable tension is 200 kg, the angle with the vertical is a=30$()^\circ$. What is the force of wind pressure?

This lecture covers the following questions:

1. Conditions for the equilibrium of mechanical systems.

2. Stability of equilibrium.

3. An example of determining equilibrium positions and studying their stability.

The study of these issues is necessary to study the oscillatory movements of a mechanical system relative to the equilibrium position in the discipline "Machine Parts", to solve problems in the disciplines "Theory of Machines and Mechanisms" and "Strength of Materials".

An important case of motion of mechanical systems is their oscillatory motion. Oscillations are repeated movements of a mechanical system with respect to some of its positions, occurring more or less regularly in time. The course work considers the oscillatory motion of a mechanical system relative to the equilibrium position (relative or absolute).

A mechanical system can oscillate for a sufficiently long period of time only near a position of stable equilibrium. Therefore, before compiling the equations of oscillatory motion, it is necessary to find the equilibrium positions and investigate their stability.

Equilibrium conditions for mechanical systems.

According to the principle possible movements(the basic equation of statics), in order for a mechanical system, on which ideal, stationary, confining and holonomic constraints are imposed, to be in equilibrium, it is necessary and sufficient that all generalized forces in this system be equal to zero:

where is the generalized force corresponding to j- oh generalized coordinate;

s- the number of generalized coordinates in the mechanical system.

If differential equations of motion were compiled for the system under study in the form of Lagrange equations of the second kind, then to determine the possible equilibrium positions, it is sufficient to equate the generalized forces to zero and solve the resulting equations with respect to the generalized coordinates.

If the mechanical system is in equilibrium in a potential force field, then from equations (1) we obtain the following equilibrium conditions:

Therefore, in the equilibrium position, the potential energy has an extreme value. Not every equilibrium defined by the above formulas can be realized in practice. Depending on the behavior of the system when deviating from the equilibrium position, one speaks of the stability or instability of this position.

Balance stability

The definition of the concept of stability of an equilibrium position was given at the end of the 19th century in the works of the Russian scientist A. M. Lyapunov. Let's look at this definition.

To simplify the calculations, we will further agree on the generalized coordinates q 1 , q 2 ,...,q s count from the equilibrium position of the system:

where

An equilibrium position is called stable if for any arbitrarily small numberyou can find another number , that in the case when the initial values of the generalized coordinates and velocities will not exceed:

values of generalized coordinates and velocities during further motion of the system will not exceed .

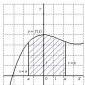
In other words, the equilibrium position of the system q 1 = q 2 = ...= q s= 0 is called sustainable, if it is always possible to find such sufficiently small initial values, at which the motion of the systemwill not leave any given arbitrarily small neighborhood of the equilibrium position. For a system with one degree of freedom, the stable motion of the system can be visualized in the phase plane (Fig. 1).For a stable equilibrium position, the movement of the representative point, starting in the region [ ] , will not go beyond the area in the future.

Fig.1

The equilibrium position is called asymptotically stable , if over time the system will approach the equilibrium position, that is

Determining the conditions for the stability of an equilibrium position is a rather difficult task, so we restrict ourselves to the simplest case: the study of the stability of the equilibrium of conservative systems.

Sufficient conditions for the stability of equilibrium positions for such systems are defined by Lagrange - Dirichlet theorem : the equilibrium position of a conservative mechanical system is stable if, in the equilibrium position, the potential energy of the system has an isolated minimum .

The potential energy of a mechanical system is determined up to a constant. We choose this constant so that in the equilibrium position potential energy was equal to zero:

P(0)=0.

Then, for a system with one degree of freedom, a sufficient condition for the existence of an isolated minimum, along with the necessary condition (2), is the condition

Since in the equilibrium position the potential energy has an isolated minimum and P(0)=0 , then in some finite neighborhood of this position

П(q)=0.

Functions that have a constant sign and are equal to zero only when all their arguments are zero are called sign-definite. Therefore, in order for the equilibrium position of a mechanical system to be stable, it is necessary and sufficient that, in the vicinity of this position, the potential energy be a positively defined function of generalized coordinates.

For linear systems and for systems that can be reduced to linear for small deviations from the equilibrium position (linearized), the potential energy can be represented as a quadratic form of generalized coordinates

where - generalized stiffness coefficients.

Generalized coefficientsare constant numbers that can be determined directly from the expansion of the potential energy into a series or from the values of the second derivatives of the potential energy with respect to the generalized coordinates in the equilibrium position:

It follows from formula (4) that the generalized stiffness coefficients are symmetric with respect to the indices

For , in order to satisfy sufficient conditions for the stability of the equilibrium position, the potential energy must be a positive definite quadratic form of its generalized coordinates.

In mathematics there is Sylvester's criterion , which gives necessary and sufficient conditions for the positive definiteness of quadratic forms: the quadratic form (3) will be positive definite if the determinant composed of its coefficients and all its principal diagonal minors are positive, i.e. if the coefficients will satisfy the conditions

.....

In particular, for linear system with two degrees of freedom, the potential energy and the conditions of the Sylvester criterion will have the form

In a similar way, one can study the positions of relative equilibrium if, instead of potential energy, one introduces into consideration the potential energy of the reduced system.

P An example of determining equilibrium positions and studying their stability

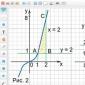
Fig.2

Consider mechanical system consisting of a tube AB, which is the pivot OO 1 connected to the horizontal axis of rotation, and a ball that moves through the tube without friction and is connected to a point A tubes with a spring (Fig. 2). Let us determine the equilibrium positions of the system and evaluate their stability for the following parameters: tube length l 2 = 1 m , rod length l 1 = 0,5 m . undeformed spring length l 0 = 0.6 m, spring rate c= 100 N/m. Tube weight m 2 = 2 kg, rod - m 1 = 1 kg and ball - m 3 = 0.5 kg. Distance OA equals l 3 = 0.4 m.

Let us write an expression for the potential energy of the system under consideration. It consists of the potential energy of three bodies in a uniform gravity field and the potential energy of a deformed spring.

The potential energy of a body in the field of gravity is equal to the product of the weight of the body and the height of its center of gravity above the plane in which the potential energy is considered to be zero. Let the potential energy be zero in the plane passing through the axis of rotation of the rod OO 1 , then for gravity

For the elastic force, the potential energy is determined by the amount of deformation

Let us find the possible equilibrium positions of the system. The coordinate values in the equilibrium positions are the roots of the following system of equations.

A similar system of equations can be compiled for any mechanical system with two degrees of freedom. In some cases, it is possible to obtain an exact solution of the system. For system (5), such a solution does not exist, so the roots must be sought using numerical methods.

Solving the system of transcendental equations (5), we obtain two possible equilibrium positions:

To assess the stability of the obtained equilibrium positions, we find all the second derivatives of the potential energy with respect to the generalized coordinates and determine the generalized stiffness coefficients from them.

A body is at rest (or moves uniformly and in a straight line) if the vector sum of all forces acting on it is zero. The forces are said to balance each other. When we are dealing with a body of a certain geometric shape, when calculating the resultant force, all forces can be applied to the center of mass of the body.

The condition for the equilibrium of bodies

In order for a body that does not rotate to be in equilibrium, it is necessary that the resultant of all forces acting on it be equal to zero.

F → = F 1 → + F 2 → + . . + F n → = 0 .

The figure above shows the balance solid body. The block is in a state of equilibrium under the action of three forces acting on it. The lines of action of the forces F 1 → and F 2 → intersect at the point O. The point of application of gravity is the center of mass of the body C. These points lie on one straight line, and when calculating the resultant force F 1 → , F 2 → and m g → are reduced to point C .

The condition that the resultant of all forces be equal to zero is not enough if the body can rotate around some axis.

The shoulder of the force d is the length of the perpendicular drawn from the line of action of the force to the point of its application. The moment of force M is the product of the arm of the force and its modulus.

The moment of force tends to rotate the body around its axis. Those moments that rotate the body counterclockwise are considered positive. The unit of measure of the moment of force in international system C - 1 N m e t r.

Definition. moment rule

If the algebraic sum of all the moments applied to the body relative to the fixed axis of rotation is equal to zero, then the body is in equilibrium.

M1 + M2 + . . + M n = 0

Important!

In the general case, for the equilibrium of bodies, two conditions must be met: the resultant force is equal to zero and the rule of moments is observed.

There are different types of equilibrium in mechanics. Thus, a distinction is made between stable and unstable, as well as indifferent equilibrium.

A typical example of an indifferent equilibrium is a rolling wheel (or ball), which, if stopped at any point, will be in a state of equilibrium.

Stable equilibrium is such an equilibrium of a body when, with its small deviations, forces or moments of forces arise that tend to return the body to an equilibrium state.

Unstable equilibrium - a state of equilibrium, with a small deviation from which the forces and moments of forces tend to bring the body out of balance even more.

In the figure above, the position of the ball is (1) - indifferent equilibrium, (2) - unstable equilibrium, (3) - stable equilibrium.

body with fixed axle rotation can be in any of the described equilibrium positions. If the axis of rotation passes through the center of mass, there is an indifferent equilibrium. In stable and unstable equilibrium, the center of mass is located on a vertical line that passes through the axis of rotation. When the center of mass is below the axis of rotation, the equilibrium is stable. Otherwise, vice versa.

A special case of equilibrium is the equilibrium of a body on a support. In this case, the elastic force is distributed over the entire base of the body, and does not pass through one point. A body is at rest in equilibrium when a vertical line drawn through the center of mass intersects the area of support. Otherwise, if the line from the center of mass does not fall into the contour formed by the lines connecting the support points, the body overturns.

An example of the balance of a body on a support is the famous Leaning Tower of Pisa. According to legend, Galileo Galilei dropped balls from it when he conducted his experiments on studying free fall tel.

A line drawn from the center of mass of the tower intersects the base approximately 2.3 m from its center.

If you notice a mistake in the text, please highlight it and press Ctrl+Enter

Class: 10

Presentation for the lesson

Back forward

Attention! The slide preview is for informational purposes only and may not represent the full extent of the presentation. If you are interested in this work, please download the full version.

Lesson Objectives: To study the state of equilibrium of bodies, to get acquainted with various types of equilibrium; find out the conditions under which the body is in equilibrium.

Lesson objectives:

Training: To study two conditions of equilibrium, types of equilibrium (stable, unstable, indifferent). Find out under what conditions bodies are more stable.
Developing: To promote the development of cognitive interest in physics. Development of skills to compare, generalize, highlight the main thing, draw conclusions.
Educational: To cultivate attention, the ability to express one's point of view and defend it, to develop the communication skills of students.

Lesson type: lesson learning new material with computer support.

Equipment:

Disk "Work and power" from "Electronic lessons and tests.
Table "Equilibrium conditions".
Prism inclined with a plumb line.
Geometric bodies: cylinder, cube, cone, etc.
Computer, multimedia projector, interactive whiteboard or screen.
Presentation.

During the classes

Today in the lesson we will learn why the crane does not fall, why the Roly-Vstanka toy always returns to its original state, why the Leaning Tower of Pisa does not fall?

I. Repetition and updating of knowledge.

Formulate Newton's first law. What is the status of the law?
What question does Newton's second law answer? Formula and wording.
What question does Newton's third law answer? Formula and wording.
What is the resultant force? How is she?
From the disk "Movement and interaction of bodies" complete task No. 9 "The resultant of forces with different directions" (the rule of vector addition (2, 3 exercises)).

II. Learning new material.

1. What is called equilibrium?

Equilibrium is a state of rest.

2. Equilibrium conditions.(slide 2)

a) When is the body at rest? What law does this come from?

The first equilibrium condition: A body is in equilibrium if the geometric sum of the external forces applied to the body is zero. ∑ F = 0

b) Let two equal forces act on the board, as shown in the figure.

Will she be in balance? (No, she will turn)

At rest is only central point and the rest are moving. This means that for the body to be in equilibrium, it is necessary that the sum of all forces acting on each element be equal to 0.

The second equilibrium condition: The sum of the moments of forces acting clockwise must be equal to the sum of the moments of forces acting counterclockwise.

∑ M clockwise = ∑ M counterclockwise

Moment of force: M = F L

L - shoulder of force - the shortest distance from the fulcrum to the line of action of the force.

3. The center of gravity of the body and its location.(slide 4)

Center of gravity of the body- this is the point through which the resultant of all parallel gravity forces acting on individual elements of the body passes (at any position of the body in space).

Find the center of gravity of the following figures:

4. Types of balance.

a) (slides 5-8)

Conclusion: Equilibrium is stable if, with a small deviation from the equilibrium position, there is a force tending to return it to this position.

The position in which its potential energy is minimal is stable. (slide 9)

b) The stability of bodies located on the fulcrum or on the fulcrum.(slides 10-17)

Conclusion: For the stability of a body located on one point or line of support, it is necessary that the center of gravity be below the point (line) of support.

c) The stability of bodies on a flat surface.

(slide 18)

1) Support surface- this is not always a surface that is in contact with the body (but one that is limited by lines connecting the legs of the table, tripod)

2) Analysis of a slide from "Electronic lessons and tests", disk "Work and power", lesson "Types of balance".

Picture 1.

How are the stools different? (Square footing)
Which one is more stable? (with larger area)
How are the stools different? (Location of the center of gravity)
Which one is the most stable? (which center of gravity is lower)
Why? (Because it can be deflected to a larger angle without tipping over)

3) Experience with a deviating prism

Let's put a prism with a plumb line on the board and begin to gradually lift it over one edge. What do we see?
As long as the plumb line crosses the surface bounded by the support, the balance is maintained. But as soon as the vertical passing through the center of gravity begins to go beyond the boundaries of the support surface, the bookcase overturns.

Parsing slides 19–22.

Conclusions:

The body with the largest area of support is stable.
Of two bodies of the same area, the body whose center of gravity is lower is stable, because it can be deflected without overturning at a large angle.

Parsing slides 23–25.

Which ships are the most stable? Why? (For which the cargo is located in the holds, and not on the deck)

What cars are the most stable? Why? (To increase the stability of cars on turns, the roadbed is tilted in the direction of the turn.)

Conclusions: Equilibrium can be stable, unstable, indifferent. The stability of the bodies is greater, the larger the area of support and the lower the center of gravity.

III. Application of knowledge about the stability of bodies.

What specialties most need knowledge about the balance of bodies?
Designers and designers of various structures ( high-rise buildings, bridges, TV towers, etc.)
Circus artists.
Drivers and other professionals.

(slides 28–30)

Why does Roly-Vstanka return to the equilibrium position at any inclination of the toy?
Why is the Leaning Tower of Pisa tilted and not falling?
How do cyclists and motorcyclists keep their balance?

Lesson takeaways:

There are three types of equilibrium: stable, unstable, indifferent.
The position of the body is stable, in which its potential energy is minimal.
The stability of bodies on a flat surface is greater, the larger the area of support and the lower the center of gravity.

Homework: § 54 – 56 (G.Ya. Myakishev, B.B. Bukhovtsev, N.N. Sotsky)

Used sources and literature:

G.Ya. Myakishev, B.B. Bukhovtsev, N.N. Sotsky. Physics. Grade 10.
Filmstrip "Stability" 1976 (scanned by me on a film scanner).
Disk "Movement and interaction of bodies" from "Electronic lessons and tests".
Disk "Work and power" from "Electronic lessons and tests".

total:0
In contact with 0
Google+ 0
OK 0
Facebook 0