The area of ​​a parallelogram is sine. Parallelogram area

The derivation of the formula for the area of ​​a parallelogram is reduced to constructing a rectangle equal to a given parallelogram in area. We take one side of the parallelogram as the base, and the perpendicular drawn from any point of the opposite side to the straight line containing the base will be called the height of the parallelogram. Then the area of ​​the parallelogram will be equal to the product of its base and height.

Theorem.The area of ​​a parallelogram is equal to the product of its base times its height.

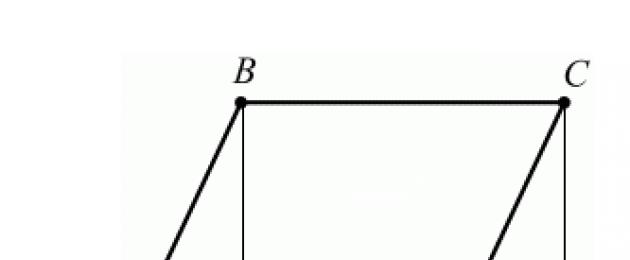
Proof. Consider a parallelogram with area. Let's take the side for the base and draw the heights (Figure 2.3.1). It is required to prove that.

Figure 2.3.1

Let us first prove that the area of ​​the rectangle is also equal. A trapezoid is made up of a parallelogram and a triangle. On the other hand, it is made up of a rectangle NVSK and a triangle. But right triangles are equal in hypotenuse and acute angle (their hypotenuses are equal as opposite sides of a parallelogram, and angles 1 and 2 are equal as corresponding angles at the intersection of parallel secant lines), so their areas are equal. Therefore, the areas of the parallelogram and the rectangle are also equal, that is, the area of ​​the rectangle is equal. According to the rectangle area theorem, but since, then.

The theorem has been proven.

Example 2.3.1.

A circle is inscribed in a rhombus with a side and an acute angle. Determine the area of ​​a quadrilateral whose vertices are the tangent points of the circle with the sides of the rhombus.

Decision:

The radius of a circle inscribed in a rhombus (Figure 2.3.2), since the Quadrilateral is a rectangle, since its corners are based on the diameter of the circle. Its area, where (the leg lying against the corner),.

Figure 2.3.2

So,

Answer:

Example 2.3.2.

Given a rhombus whose diagonals are 3 cm and 4 cm. Heights and are drawn from the vertex of an obtuse angle Calculate the area of ​​the quadrangle

Decision:

Rhombus area (Figure 2.3.3).

So,

Answer:

Example 2.3.3.

The area of ​​a quadrilateral is Find the area of ​​a parallelogram whose sides are equal and parallel to the diagonals of the quadrilateral.

Decision:

Since and (Figure 2.3.4), then is a parallelogram and, therefore,.

Figure 2.3.4

Similarly, we obtain whence it follows that.

Answer:.

2.4 Area of ​​a triangle

There are several formulas for calculating the area of ​​a triangle. Consider those that are studied in school.

The first formula follows from the formula for the area of ​​a parallelogram and is offered to students in the form of a theorem.

Theorem.The area of ​​a triangle is half the product of its base times its height..

Proof. Let be the area of ​​the triangle. Take the side of the base of the triangle and draw the height. Let's prove that:

Figure 2.4.1

We will complete the triangle to a parallelogram as shown in the figure. Triangles are equal in three sides (- their common side, and as opposite sides of a parallelogram), so their areas are equal. Therefore, the area S of the triangle ABC is equal to half the area of ​​the parallelogram, i.e.

The theorem has been proven.

It is important to draw students' attention to two consequences of this theorem. Namely:

The area of ​​a right triangle is half the product of its legs.

If the heights of two triangles are equal, then their areas are related as bases.

These two corollaries play an important role in solving various kinds of problems. Based on this one, we prove another theorem that is widely used in solving problems.

Theorem. If the angle of one triangle is equal to the angle of another triangle, then their areas are related as the products of the sides containing equal angles.

Proof. Let and be the areas of triangles u whose angles and are equal.

Figure 2.4.2

Let's prove that: .

Let's make a triangle. on the triangle so that the vertex is aligned with the vertex, and the sides overlap, respectively, on the rays.

Figure 2.4.3

Triangles and have a common height, therefore,. Triangles also have a common height - therefore,. Multiplying the resulting equalities, we obtain .

The theorem has been proven.

Second formula.The area of ​​a triangle is equal to half the product of its two sides and the sine of the angle between them. There are several ways to prove this formula, and I will use one of them.

Proof. From geometry, a theorem is known that the area of ​​\u200b\u200ba triangle is equal to half the product of the base and the height lowered to this base:

In the case of an acute triangle . In the case of an obtuse angle. Ho, and therefore . So, in both cases. Substituting instead in the geometric formula for the area of ​​a triangle, we obtain the trigonometric formula for the area of ​​a triangle:

The theorem has been proven.

Third formula for the area of ​​\u200b\u200ba triangle - Heron's formula, named after the ancient Greek scientist Heron of Alexandria, who lived in the first century AD. This formula allows you to find the area of ​​a triangle, knowing its sides. It is convenient in that it allows you not to make any additional constructions and not measure angles. Its conclusion is based on the second of the triangle area formulas we have considered and the cosine theorem: and.

Before proceeding to the implementation of this plan, we note that

Similarly, we have:

Now we express the cosine through and:

Since any angle in a triangle is greater or lesser, then. Means, .

Now we separately transform each of the factors in the radical expression. We have:

Substituting this expression into the area formula, we get:

The topic "Area of ​​a triangle" is of great importance in the school mathematics course. The triangle is the simplest of geometric shapes. It is a "structural element" of school geometry. The vast majority of geometric problems come down to solving triangles. The problem of finding the area of ​​a regular and arbitrary n-gon is no exception.

Example 2.4.1.

What is the area of ​​an isosceles triangle if its base and side are?

Decision:

-isosceles,

Figure 2.4.4

Let's draw on the property of an isosceles triangle - median and height. Then

In according to the Pythagorean theorem:

Finding the area of ​​a triangle:

Answer:

Example 2.4.2.

In a right triangle, the bisector of an acute angle divides the opposite leg into segments 4 and 5 cm long. Determine the area of ​​the triangle.

Decision:

Let (Figure 2.4.5). Then (because BD is a bisector). Hence we have , i.e. Means,

Figure 2.4.5

Answer:

Example 2.4.3.

Find the area of ​​an isosceles triangle if its base is equal to , and the length of the height drawn to the base is equal to the length of the segment connecting the midpoints of the base and side.

Decision:

By condition, - the middle line (Figure 2.4.6). Since wemeem:

or , whence Hence,

What is a parallelogram? A parallelogram is a quadrilateral whose opposite sides are pairwise parallel.

1. The area of ​​a parallelogram is calculated by the formula:

\[ \LARGE S = a \cdot h_(a)\]

where:
a is the side of the parallelogram,
h a is the height drawn to this side.

2. If the lengths of two adjacent sides of the parallelogram and the angle between them are known, then the area of ​​the parallelogram is calculated by the formula:

\[ \LARGE S = a \cdot b \cdot sin(\alpha) \]

3. If the diagonals of the parallelogram are given and the angle between them is known, then the area of ​​the parallelogram is calculated by the formula:

\[ \LARGE S = \frac(1)(2) \cdot d_(1) \cdot d_(2) \cdot sin(\alpha) \]

Parallelogram Properties

In a parallelogram, opposite sides are equal: \(AB = CD \) , \(BC = AD \)

In a parallelogram, opposite angles are: \(\angle A = \angle C \) , \(\angle B = \angle D \)

The diagonals of the parallelogram at the point of intersection are bisected \(AO = OC \) , \(BO = OD \)

The diagonal of a parallelogram divides it into two equal triangles.

The sum of the angles of a parallelogram adjacent to one side is 180 o:

\(\angle A + \angle B = 180^(o) \), \(\angle B + \angle C = 180^(o)\)

\(\angle C + \angle D = 180^(o) \), \(\angle D + \angle A = 180^(o)\)

The diagonals and sides of a parallelogram are related by the following relationship:

\(d_(1)^(2) + d_(2)^2 = 2a^(2) + 2b^(2) \)

In a parallelogram, the angle between the heights is equal to its acute angle: \(\angle K B H =\angle A \) .

Bisectors of angles adjacent to one side of a parallelogram are mutually perpendicular.

Bisectors of two opposite angles of a parallelogram are parallel.

Parallelogram features

A quadrilateral is a parallelogram if:

\(AB = CD \) and \(AB || CD \)

\(AB = CD \) and \(BC = AD \)

\(AO = OC \) and \(BO = OD \)

\(\angle A = \angle C \) and \(\angle B = \angle D \)

When solving problems on this topic, in addition to basic properties parallelogram and the corresponding formulas, you can remember and apply the following:

1. The bisector of the interior angle of a parallelogram cuts off an isosceles triangle from it
2. Bisectors of internal angles adjacent to one of the sides of a parallelogram are mutually perpendicular
3. Bisectors coming from opposite internal angles of a parallelogram, parallel to each other or lie on one straight line
4. The sum of the squares of the diagonals of a parallelogram is equal to the sum of the squares of its sides
5. The area of ​​a parallelogram is half the product of the diagonals times the sine of the angle between them.

Let's consider the tasks in the solution of which these properties are used.

Task 1.

The bisector of angle C of parallelogram ABCD intersects side AD at point M and the continuation of side AB beyond point A at point E. Find the perimeter of the parallelogram if AE \u003d 4, DM \u003d 3.

Decision.

1. Triangle CMD isosceles. (Property 1). Therefore, CD = MD = 3 cm.

2. Triangle EAM is isosceles.
Therefore, AE = AM = 4 cm.

3. AD = AM + MD = 7 cm.

4. Perimeter ABCD = 20 cm.

Answer. 20 cm

Task 2.

Diagonals are drawn in a convex quadrilateral ABCD. It is known that the areas of triangles ABD, ACD, BCD are equal. Prove that the given quadrilateral is a parallelogram.

Decision.

1. Let BE be the height of triangle ABD, CF be the height of triangle ACD. Since, according to the condition of the problem, the areas of the triangles are equal and they have a common base AD, then the heights of these triangles are equal. BE = CF.

2. BE, CF are perpendicular to AD. Points B and C are located on the same side of the line AD. BE = CF. Therefore, the line BC || AD. (*)

3. Let AL be the altitude of triangle ACD, BK the altitude of triangle BCD. Since, according to the condition of the problem, the areas of the triangles are equal and they have a common base CD, then the heights of these triangles are equal. AL = BK.

4. AL and BK are perpendicular to CD. Points B and A are located on the same side of the straight line CD. AL = BK. Therefore, the line AB || CD (**)

5. Conditions (*), (**) imply that ABCD is a parallelogram.

Answer. Proven. ABCD is a parallelogram.

Task 3.

On the sides BC and CD of the parallelogram ABCD, the points M and H are marked, respectively, so that the segments BM and HD intersect at the point O;<ВМD = 95 о,