En la última lección, dominamos (o repetimos, según quién) con éxito los conceptos clave de toda la trigonometría. Este círculo trigonométrico , ángulo en un círculo , seno y coseno de este ángulo , y también dominado señales funciones trigonométricas por trimestres . Lo dominamos en detalle. En los dedos, se podría decir.
Pero esto todavía no es suficiente. Para tener éxito aplicación práctica Con todos estos conceptos simples, necesitamos una habilidad útil más. Es decir, correcto trabajando con esquinas en trigonometría. Sin esta habilidad en trigonometría, no hay manera. Incluso en los ejemplos más primitivos. ¿Por qué? Sí, ¡porque el ángulo es la cifra operativa clave en toda trigonometría! No, no funciones trigonométricas, ni seno y coseno, ni tangente y cotangente, es decir la esquina misma. Sin ángulo significa que no hay funciones trigonométricas, sí...
¿Cómo trabajar con ángulos en un círculo? Para ello, debemos comprender firmemente dos puntos.
1) Cómo¿Se miden los ángulos en un círculo?
2) Qué¿Se cuentan (miden)?
La respuesta a la primera pregunta es el tema de la lección de hoy. Abordaremos la primera pregunta en detalle aquí y ahora. No daré aquí la respuesta a la segunda pregunta. Porque está bastante desarrollado. Al igual que la segunda pregunta en sí misma es muy resbaladiza, sí). No entraré en detalles todavía. Este es el tema de la siguiente lección aparte.
¿Empezamos?
¿Cómo se miden los ángulos en un círculo? Ángulos positivos y negativos.
Quienes lean el título del párrafo quizá ya tengan los pelos de punta. ¡¿Cómo es eso?! ¿Ángulos negativos? ¿Es esto siquiera posible?
a negativo números Ya nos hemos acostumbrado. Podemos representarlos en el eje numérico: a la derecha del cero están los positivos, a la izquierda del cero están los negativos. Sí, y periódicamente miramos el termómetro por la ventana. Especialmente en invierno, cuando hace frío). Y el dinero del teléfono está en negativo (es decir, deber) a veces se van. Todo esto me resulta familiar.
¿Qué pasa con las esquinas? Resulta que los ángulos negativos en matemáticas. ¡ahí hay también! Todo depende de cómo medir este ángulo... no, no en la recta numérica, ¡sino en el círculo numérico! Es decir, en círculo. El círculo: ¡aquí está, un análogo de la recta numérica en trigonometría!
Entonces, ¿Cómo se miden los ángulos en un círculo? No hay nada que podamos hacer, primero tendremos que dibujar este mismo círculo.
Haré este hermoso dibujo:
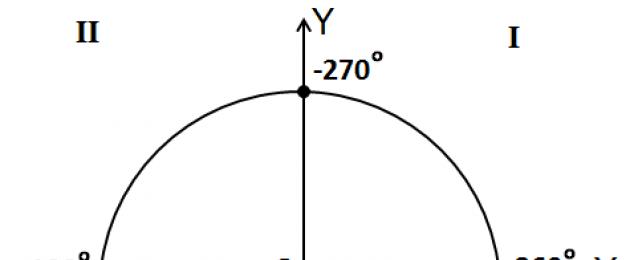
Es muy similar a las imágenes de la última lección. Hay ejes, hay un círculo, hay un ángulo. Pero también hay nueva información.
También agregué números de 0°, 90°, 180°, 270° y 360° en los ejes. Ahora esto es más interesante.) ¿Qué clase de números son estos? ¡Bien! Estos son los valores de los ángulos medidos desde nuestro lado fijo que caen a los ejes de coordenadas. Recordamos que el lado fijo del ángulo siempre está estrechamente ligado al semieje positivo OX. Y cualquier ángulo en trigonometría se mide precisamente desde este semieje. Este punto de partida básico para los ángulos debe tenerse firmemente en cuenta. Y los ejes se cruzan en ángulos rectos, ¿verdad? Entonces sumamos 90° en cada cuarto.
Y más añadido flecha roja. Con un plus. El rojo está pensado para llamar la atención. Y está bien grabado en mi memoria. Porque esto debe recordarse de forma fiable.) ¿Qué significa esta flecha?
Entonces resulta que si torcemos nuestra esquina a lo largo de la flecha con un signo más(contra agujas del reloj, según la numeración de cuartos), luego el ángulo se considerará positivo! Como ejemplo, la figura muestra un ángulo de +45°. Por cierto, tenga en cuenta que los ángulos axiales 0°, 90°, 180°, 270° y 360° también se rebobinan en dirección positiva. Sigue la flecha roja.
Ahora veamos otra imagen:

Aquí casi todo es igual. Sólo los ángulos de los ejes están numerados. invertido. Agujas del reloj. Y tienen un signo menos.) Todavía dibujado flecha azul. También con un menos. Esta flecha es la dirección de los ángulos negativos del círculo. Ella nos muestra que si posponemos nuestro rincón agujas del reloj, Eso el ángulo se considerará negativo. Por ejemplo, mostré un ángulo de -45°.
Por cierto, tenga en cuenta que la numeración de los trimestres nunca cambia. No importa si movemos los ángulos hacia más o hacia menos. Siempre estrictamente en el sentido contrario a las agujas del reloj).
Recordar:
1. El punto de partida para los ángulos es desde el semieje positivo OX. Por el reloj – “menos”, contra el reloj – “más”.
2. La numeración de los cuartos es siempre en sentido antihorario, independientemente del sentido en el que se calculen los ángulos.
Por cierto, no es obligatorio marcar los ángulos en los ejes 0°, 90°, 180°, 270°, 360° cada vez que se dibuja un círculo. Esto se hace simplemente para entender el punto. Pero estos números deben estar presentes. en tu cabeza al resolver cualquier problema de trigonometría. ¿Por qué? Sí, ¡porque este conocimiento básico proporciona respuestas a muchas otras preguntas en toda la trigonometría! La pregunta más importante es ¿En qué cuarto cae el ángulo que nos interesa? Lo creas o no, responder correctamente a esta pregunta resuelve la mayor parte de todos los demás problemas de trigonometría. Nos ocuparemos de esta importante tarea (distribuir ángulos en cuartos) en la misma lección, pero un poco más tarde.
¡Debemos recordar los valores de los ángulos que se encuentran en los ejes de coordenadas (0°, 90°, 180°, 270° y 360°)! Recuérdalo firmemente, hasta que se vuelva automático. Y tanto un más como un menos.
Pero a partir de este momento comienzan las primeras sorpresas. Y junto con ellas, preguntas capciosas que me dirigen, sí...) ¿Qué pasa si en una circunferencia hay un ángulo negativo? coincide con lo positivo? Resulta que el mismo punto en un círculo se puede denotar tanto por un ángulo positivo como por un ángulo negativo???
¡Absolutamente correcto! Esto es cierto.) Por ejemplo, un ángulo positivo de +270° ocupa un círculo misma situacion , lo mismo que un ángulo negativo de -90°. O, por ejemplo, un ángulo positivo de +45° en un círculo tomará misma situacion , lo mismo que el ángulo negativo -315°.
Miramos el siguiente dibujo y vemos todo:

De la misma manera, un ángulo positivo de +150° caerá en el mismo lugar que un ángulo negativo de -210°, un ángulo positivo de +230° caerá en el mismo lugar que un ángulo negativo de -130°. Etcétera…
¿Y ahora qué puedo hacer? ¿Cómo contar exactamente los ángulos, si puedes hacerlo de esta manera? ¿Cual es correcta?
Respuesta: en todos los sentidos correcto! Las matemáticas no prohíben ninguna de las dos direcciones para contar ángulos. Y la elección de una dirección específica depende únicamente de la tarea. Si la tarea no dice nada en texto plano sobre el signo del ángulo (como "definir el más grande negativo esquina" etc.), luego trabajamos con los ángulos que nos sean más convenientes.
Por supuesto, por ejemplo, en temas tan interesantes como ecuaciones trigonométricas y desigualdades, la dirección en la que se calculan los ángulos puede tener un gran impacto en la respuesta. Y en los temas relevantes consideraremos estos escollos.
Recordar:
Cualquier punto de una circunferencia puede designarse mediante un ángulo positivo o negativo. ¡Alguien! Lo que queramos.
Ahora pensemos en esto. ¿Descubrimos que un ángulo de 45° es exactamente igual que un ángulo de -315°? ¿Cómo me enteré de estos mismos 315?° ? ¿No puedes adivinarlo? ¡Sí! A través de una rotación completa.) En 360°. Tenemos un ángulo de 45°. ¿Cuánto tiempo se tarda en completar una rotación completa? restar 45° desde 360° - entonces obtenemos 315° . Vamos a lado negativo– y obtenemos un ángulo de -315°. ¿Aún no lo tienes claro? Luego mira la imagen de arriba nuevamente.
Y esto siempre debe hacerse al convertir ángulos positivos en negativos (y viceversa): dibuje un círculo, marque aproximadamente un ángulo dado, calculamos cuántos grados faltan para completar una revolución completa y movemos la diferencia resultante en la dirección opuesta. Eso es todo.)
¿Qué más crees que tienen de interesante los ángulos que ocupan la misma posición en un círculo? Y el hecho de que en esos rincones exactamente lo mismo ¡Seno, coseno, tangente y cotangente! ¡Siempre!
Por ejemplo:
Sen45° = sen(-315°)
Cos120° = cos(-240°)
Tg249° = tg(-111°)
Ctg333° = ctg(-27°)
¡Pero esto es extremadamente importante! ¿Para qué? ¡Sí, todo por lo mismo!) Para simplificar expresiones. Porque simplificar expresiones es un procedimiento clave para una solución exitosa cualquier tareas de matemáticas. Y también en trigonometría.
Entonces, con regla general Descubrimos cómo contar los ángulos de un círculo. Bueno, si comenzamos a hablar de vueltas completas, de cuartos de vuelta, entonces es hora de torcer y dibujar estas mismas esquinas. ¿Dibujamos?)
Empecemos con positivo esquinas Serán más fáciles de dibujar.
Dibujamos ángulos dentro de una revolución (entre 0° y 360°).
Dibujemos, por ejemplo, un ángulo de 60°. Aquí todo es sencillo, sin complicaciones. Dibujamos ejes de coordenadas y un círculo. Puedes hacerlo directamente a mano, sin ningún compás ni regla. Dibujemos esquemáticamente: No vamos a dibujar contigo. No es necesario que cumpla con ningún GOST, no será castigado).
Puedes (por ti mismo) marcar los valores de los ángulos en los ejes y apuntar la flecha en la dirección contrareloj. Después de todo, ¿vamos a ahorrar como una ventaja?) No es necesario que hagas esto, pero debes tener todo en mente.
Y ahora dibujamos el segundo lado (en movimiento) de la esquina. ¿En qué trimestre? ¡En el primero, por supuesto! Porque 60 grados está estrictamente entre 0° y 90°. Así que empatamos en el primer cuarto. En un angulo aproximadamente 60 grados hacia el lado fijo. Como contar aproximadamente¿60 grados sin transportador? ¡Fácilmente! 60° es dos terceras partes de ángulo recto! Mentalmente dividimos el primer diablo del círculo en tres partes, tomando dos tercios para nosotros. Y dibujamos... ¡Cuánto llegamos allí (si colocamos un transportador y medimos) - 55 grados o 64 - no importa! Es importante que todavía esté en algún lugar. alrededor de 60°.
Obtenemos la imagen:

Eso es todo. Y no se necesitaron herramientas. ¡Desarrollemos nuestro ojo! Te resultará útil en problemas de geometría.) Este dibujo antiestético es indispensable cuando necesitas garabatear rápidamente un círculo y un ángulo, sin pensar realmente en la belleza. Pero al mismo tiempo garabatea Bien, sin errores, con toda la información necesaria. Por ejemplo, como ayuda para resolver ecuaciones y desigualdades trigonométricas.
Dibujemos ahora un ángulo, por ejemplo, 265°. ¿Averigüemos dónde podría estar ubicado? Bueno, está claro que ni en el primer cuarto ni en el segundo: terminan en 90 y 180 grados. Puedes calcular que 265° son 180° más otros 85°. Es decir, al semieje negativo OX (donde 180°) hay que sumarle aproximadamente 85°. O, aún más simple, supongamos que 265° no alcanza el semieje negativo OY (donde está 270°), unos desafortunados 5°. En definitiva, en el tercer cuarto habrá este ángulo. Muy cerca del semieje negativo OY, a 270 grados, ¡pero todavía en el tercero!
Dibujemos:

Una vez más, aquí no se requiere una precisión absoluta. En realidad, este ángulo resulta ser, digamos, 263 grados. Pero a la pregunta más importante. (¿qué trimestre?) Respondimos correctamente. ¿Por qué es esta la pregunta más importante? Sí, porque cualquier trabajo con un ángulo en trigonometría (no importa si dibujamos este ángulo o no) comienza con la respuesta exactamente a esta pregunta. Siempre. Si ignoras esta pregunta o intentas responderla mentalmente, entonces los errores son casi inevitables, sí... ¿Lo necesitas?
Recordar:
Cualquier trabajo con un ángulo (incluido el dibujo de este mismo ángulo en un círculo) siempre comienza determinando el cuarto en el que cae este ángulo.
Ahora espero que puedas representar con precisión ángulos, por ejemplo, 182°, 88°, 280°. EN correcto cuarteles. En el tercero, primero y cuarto, si eso...)
El cuarto cuarto termina con un ángulo de 360°. Esta es una revolución completa. Está claro que este ángulo ocupa la misma posición en el círculo que 0° (es decir, el origen). Pero los ángulos no terminan ahí, sí...
¿Qué hacer con ángulos mayores a 360°?
"¿Existen realmente tales cosas?"- usted pregunta. ¡Suceden! Existe, por ejemplo, un ángulo de 444°. Y a veces, digamos, un ángulo de 1000°. Hay todo tipo de ángulos.) Es solo que visualmente esos ángulos exóticos se perciben un poco más difíciles que los ángulos a los que estamos acostumbrados dentro de una revolución. Pero también necesitas poder dibujar y calcular esos ángulos, sí.
Para dibujar correctamente esos ángulos en un círculo, debes hacer lo mismo: descubre ¿En qué cuarto cae el ángulo que nos interesa? ¡Aquí la capacidad de determinar con precisión el cuarto es mucho más importante que en el caso de ángulos de 0° a 360°! El procedimiento para determinar el trimestre en sí se complica con un solo paso. Verás lo que es pronto.
Entonces, por ejemplo, necesitamos determinar en qué cuadrante cae el ángulo de 444°. Empecemos a girar. ¿Dónde? ¡Un plus, por supuesto! ¡Nos dieron un ángulo positivo! +444°. Giramos, giramos... Le dimos una vuelta y llegamos a 360°.
¿Cuánto tiempo queda hasta 444°?Contamos la cola restante:
444°-360° = 84°.
Entonces, 444° es una rotación completa (360°) más otros 84°. Obviamente este es el primer trimestre. Entonces, el ángulo de 444° cae en el primer trimestre. La mitad de la batalla está hecha.
Ahora solo queda representar este ángulo. ¿Cómo? ¡Muy simple! Damos una vuelta completa a lo largo de la flecha roja (más) y agregamos otros 84°.
Como esto:

Aquí no me molesté en abarrotar el dibujo: etiquetar los cuartos, dibujar ángulos en los ejes. Todas estas cosas buenas deberían haber estado en mi cabeza durante mucho tiempo).
Pero usé un “caracol” o una espiral para mostrar exactamente cómo se forma un ángulo de 444° a partir de ángulos de 360° y 84°. La línea roja punteada es una revolución completa. A la que se atornillan adicionalmente 84° (línea continua). Por cierto, tenga en cuenta que si descarta esta revolución completa, ¡esto no afectará la posición de nuestro ángulo de ninguna manera!
¡Pero esto es importante! Posición del ángulo 444° coincide completamente con una posición de ángulo de 84°. No hay milagros, así es como resulta).
¿Es posible descartar no una revolución completa, sino dos o más?
¿Por qué no? Si el ángulo es grande, entonces no sólo es posible, ¡sino incluso necesario! ¡El ángulo no cambiará! Más precisamente, el ángulo mismo, por supuesto, cambiará de magnitud. ¡Pero su posición en el círculo no lo es en absoluto!) Por eso lleno revoluciones, que no importa cuántas copias agregues, no importa cuántas restes, igual terminarás en el mismo punto. Bonito, ¿no?
Recordar:
Si sumas (restas) cualquier ángulo a un ángulo entero el número de revoluciones completas, ¡la posición del ángulo original en el círculo NO cambiará!
Por ejemplo:
¿En qué cuarto cae el ángulo de 1000°?
¡Ningún problema! Contamos cuántas revoluciones completas hay en mil grados. Una revolución es de 360°, otra ya es de 720°, la tercera es de 1080°... ¡Para! ¡Demasiado! Esto significa que se asienta en un ángulo de 1000°. dos vueltas completas. Los sacamos de 1000° y calculamos el resto:
1000°- 2 360° = 280°
Entonces, la posición del ángulo es de 1000° en el círculo. lo mismo, como en un ángulo de 280°. ¿Con cuál es mucho más agradable trabajar?) ¿Y dónde queda este rincón? Cae en el cuarto cuarto: 270° (semieje negativo OY) más otros diez.
Dibujemos:

Aquí ya no dibujé dos vueltas completas con una espiral punteada: resulta demasiado larga. Acabo de dibujar la cola restante. desde cero, descartando Todo vueltas extra. Es como si no existieran en absoluto).
Una vez más. En el buen sentido, los ángulos de 444° y 84°, así como los de 1000° y 280°, son diferentes. Pero para el seno, el coseno, la tangente y la cotangente, estos ángulos son: ¡lo mismo!
Como puedes ver, para trabajar con ángulos mayores a 360° es necesario determinar ¿Cuántas revoluciones completas se encuentran en un ángulo grande dado? Este es el paso adicional que se debe realizar primero cuando se trabaja con tales ángulos. Nada complicado, ¿verdad?
Rechazar revoluciones completas es, por supuesto, una experiencia agradable). Pero en la práctica, cuando se trabaja con ángulos absolutamente terribles, surgen dificultades.
Por ejemplo:
¿En qué cuarto cae el ángulo 31240°?
Entonces, ¿vamos a sumar 360 grados muchas, muchas veces? Es posible, si no se quema demasiado. Pero no sólo podemos sumar.) ¡También podemos dividir!
¡Así que dividamos nuestro enorme ángulo en 360 grados!
Con esta acción descubriremos exactamente cuántas revoluciones completas se esconden en nuestros 31240 grados. Puedes dividirlo en una esquina, puedes (susurrarle al oído :)) en una calculadora.)
Obtenemos 31240:360 = 86,777777….
El hecho de que el número resulte ser fraccionario no da miedo. Solo nosotros entero¡Me interesan las revoluciones! Por lo tanto, no es necesario dividir completamente).
Entonces, en nuestro carbón peludo se encuentran hasta 86 revoluciones completas. Horror…
sera en grados86·360° = 30960°
Como esto. Esta es exactamente la cantidad de grados que se pueden sacar sin dolor de un ángulo determinado de 31240°. Restos:
31240° - 30960° = 280°
¡Todo! ¡La posición del ángulo 31240° está completamente identificada! Mismo lugar que 280°. Aquellos. cuarto trimestre.) ¿Creo que ya hemos representado este ángulo antes? ¿Cuándo se dibujó el ángulo de 1000°?) Allí también hicimos 280 grados. Coincidencia.)
Entonces, la moraleja de esta historia es:
Si nos dan un ángulo aterrador y considerable, entonces:
1. Determine cuántas revoluciones completas hay en esta esquina. Para hacer esto, divide el ángulo original por 360 y descarta la parte fraccionaria.
2. Contamos cuántos grados hay en el número de revoluciones resultante. Para ello, multiplica el número de revoluciones por 360.
3. Restamos estas revoluciones al ángulo original y trabajamos con el ángulo habitual que va de 0° a 360°.
¿Cómo trabajar con ángulos negativos?
¡Ningún problema! Exactamente igual que con los positivos, sólo que con una única diferencia. ¿Cuál? ¡Sí! Necesitas doblar las esquinas reverso, menos! En el sentido de las agujas del reloj.)
Dibujemos, por ejemplo, un ángulo de -200°. En primer lugar, todo es como de costumbre para los ángulos positivos: ejes, círculo. Dibujemos también una flecha azul con un signo menos y señalemos los ángulos en los ejes de manera diferente. Naturalmente, también habrá que contarlos en sentido negativo. Estos serán los mismos ángulos, pasando de 90°, pero contados en la dirección opuesta, hasta el menos: 0°, -90°, -180°, -270°, -360°.
La imagen se verá así:

Cuando se trabaja con ángulos negativos, a menudo surge una sensación de ligero desconcierto. ¡¿Cómo es eso?! ¿Resulta que el mismo eje es, digamos, +90° y -270° al mismo tiempo? No, algo huele mal aquí...
¡Sí, todo está limpio y transparente! ¡Ya sabemos que cualquier punto de un círculo se puede llamar ángulo positivo o negativo! Absolutamente cualquiera. Incluso en algunos de los ejes de coordenadas. En nuestro caso necesitamos negativo cálculo de ángulos. Entonces ajustamos todas las esquinas a menos).
Ahora dibujar correctamente el ángulo -200° no es nada difícil. Esto es -180° y menos otros 20°. Empezamos a oscilar de cero a menos: volamos por el cuarto trimestre, también perdemos el tercero, alcanzamos -180°. ¿Dónde debería gastar los veinte restantes? ¡Sí, todo está ahí! Por horas.) El ángulo total -200° cae dentro segundo cuarto.

¿Entiendes ahora lo importante que es recordar firmemente los ángulos en los ejes de coordenadas?
¡Los ángulos en los ejes de coordenadas (0°, 90°, 180°, 270°, 360°) deben recordarse con precisión para determinar exactamente el cuarto donde cae el ángulo!
¿Qué pasa si el ángulo es grande, con varias vueltas completas? ¡Está bien! ¿Qué diferencia hay si estas revoluciones completas se vuelven positivas o negativas? ¡Un punto en un círculo no cambiará su posición!
Por ejemplo:
¿En qué cuarto cae el ángulo de -2000°?
¡Todos iguales! Primero, contamos cuántas revoluciones completas hay en este malvado rincón. Para no estropear los signos, dejemos el signo menos por ahora y simplemente dividamos 2000 entre 360. Obtendremos 5 con cola. No nos importa la cola por ahora, la contaremos un poco más tarde cuando dibujemos la esquina. Nosotros contamos cinco revoluciones completas en grados:
5 360° = 1800°
Guau. Esta es exactamente la cantidad de grados adicionales que podemos desechar con seguridad y sin dañar nuestra salud.
Contamos la cola restante:
2000° – 1800° = 200°
Pero ahora podemos recordar lo negativo.) ¿Dónde enrollaremos la cola de 200°? ¡Menos, por supuesto! Se nos da un ángulo negativo.)
2000° = -1800° - 200°
Entonces dibujamos un ángulo de -200°, solo que sin revoluciones adicionales. Lo acabo de dibujar, pero que así sea, lo dibujaré una vez más. Manualmente.

Está claro que el ángulo dado -2000°, así como -200°, cae dentro de segundo cuarto.
Entonces, volvamos locos... perdón... de cabeza:
Si se da un ángulo negativo muy grande, entonces la primera parte de trabajar con él (encontrar el número de revoluciones completas y descartarlas) es la misma que cuando se trabaja con un ángulo positivo. Iniciar sesión menos En este punto la decisión no juega ningún papel. El signo se tiene en cuenta solo al final, cuando se trabaja con el ángulo que queda después de quitar las revoluciones completas.
Como puede ver, dibujar ángulos negativos en un círculo no es más difícil que los positivos.
¡Todo es igual, sólo que en la otra dirección! ¡Por la hora!
¡Ahora viene la parte más interesante! Observamos ángulos positivos, ángulos negativos, ángulos grandes, ángulos pequeños: todo el rango. También descubrimos que cualquier punto de un círculo se puede llamar ángulo positivo y negativo, descartamos revoluciones completas... ¿Alguna idea? Hay que posponerlo...
¡Sí! Cualquiera que sea el punto del círculo que tomes, corresponderá a ¡Número infinito de ángulos! Grandes y no tan grandes, positivos y negativos, ¡de todo tipo! Y la diferencia entre estos ángulos será entero número de revoluciones completas. ¡Siempre! Así funciona el círculo trigonométrico, sí...) Por eso contrarrestar la tarea es encontrar el ángulo usando el seno/coseno/tangente/cotangente conocido - solucionable ambiguo. Y mucho más difícil. A diferencia del problema directo, dado un ángulo, encuentre el conjunto completo de sus funciones trigonométricas. Y en temas más serios de trigonometría ( arcos, trigonométrico ecuaciones Y desigualdades ) nos encontraremos con este truco todo el tiempo. Nos estamos acostumbrando).
1. ¿En qué cuarto cae el ángulo de -345°?
2. ¿En qué cuarto cae el ángulo de 666°?
3. ¿En qué cuarto cae el ángulo 5555°?
4. ¿En qué cuarto cae el ángulo de -3700°?
5. ¿Qué signo significaporque999°?
6. ¿Qué signo significactg999°?
¿Y funcionó? ¡Maravilloso! ¿Hay un problema? Entonces tú.
Respuestas:
1. 1
2. 4
3. 2
4. 3
5. "+"
6. "-"
Esta vez las respuestas se dan en orden, rompiendo con la tradición. Porque sólo hay cuatro cuartos y sólo dos signos. Realmente no huirás...)
En la próxima lección hablaremos de radianes, del misterioso número "pi", aprenderemos cómo convertir radianes a grados de forma fácil y sencilla y viceversa. ¡Y nos sorprenderá descubrir que incluso estos simples conocimientos y habilidades serán suficientes para resolver con éxito muchos problemas de trigonometría no triviales!
círculo trigonométrico- uno de los elementos básicos de la geometría para resolver ecuaciones con seno, coseno, tangente y cotangente.
¿Cuál es la definición de este término, cómo construir este círculo, cómo determinar un cuarto en trigonometría, cómo averiguar los ángulos en un círculo trigonométrico construido? Hablaremos de esto y mucho más más adelante.
círculo trigonométrico
La forma trigonométrica de un círculo numérico en matemáticas es un círculo que tiene un solo radio con un centro al principio. Plano coordinado. Como regla general, está formado por un espacio de fórmulas de seno con coseno, tangente y cotangente en un sistema de coordenadas.

El objetivo de una esfera de este tipo con un espacio de n dimensiones es que gracias a ella se pueden describir funciones trigonométricas. Parece simple: un círculo, dentro del cual hay un sistema de coordenadas y múltiples triángulos rectángulos formados a partir de este círculo usando funciones trigonométricas.
¿Qué es el seno, el coseno, la tangente y la cotangente en un triángulo rectángulo?
Un triángulo rectángulo es aquel en el que uno de los ángulos mide 90°. Está formado por los catetos y la hipotenusa con todos los significados de la trigonometría. Los catetos son dos lados del triángulo que son adyacentes al ángulo de 90°, y el tercero es la hipotenusa, siempre es más larga que los catetos.

El seno es la razón entre uno de los catetos y la hipotenusa, el coseno es la razón entre el otro cateto y la tangente es la razón entre dos catetos. La relación simboliza la división. Tangente es también división de un ángulo agudo por seno y coseno. Una cotangente es la razón opuesta de una tangente.
Las fórmulas para las dos últimas razones son las siguientes: tg(a) = sin(a) / cos(a) y ctg(a) = cos(a) / sin(a).
Construyendo un círculo unitario
La construcción de un círculo unitario se reduce a dibujarlo con un radio unitario en el centro del sistema de coordenadas. Luego, para construir, es necesario contar los ángulos y, moviéndose en el sentido contrario a las agujas del reloj, recorrer todo el círculo, colocando las líneas de coordenadas correspondientes a ellos.

La construcción comienza luego de dibujar un círculo y fijar un punto en su centro colocando el sistema de coordenadas OX. El punto O encima del eje de coordenadas es el seno y X es el coseno. En consecuencia, son la abscisa y la ordenada. Entonces necesitas tomar medidas ∠. Se realizan en grados y radianes.
Es fácil traducir estos indicadores: un círculo completo equivale a dos pi radianes. El ángulo desde cero en sentido antihorario tiene un signo +, y ∠ desde 0 en sentido horario tiene un signo -. Los valores positivos y negativos del seno y el coseno se repiten en cada revolución del círculo.
Ángulos en un círculo trigonométrico
Para dominar la teoría del círculo trigonométrico, es necesario comprender cómo se cuentan ∠ y de qué manera se miden. Se calculan de forma muy sencilla.

El círculo está dividido por el sistema de coordenadas en cuatro partes. Cada parte forma ∠ 90°. La mitad de estos ángulos miden 45 grados. En consecuencia, dos partes de un círculo miden 180° y tres partes miden 360°. ¿Cómo usar esta información?
Si es necesario resolver el problema de encontrar ∠, recurren a teoremas sobre triángulos y las leyes básicas de Pitágoras asociadas con ellos.
Los ángulos se miden en radianes:
- de 0 a 90° — valores de ángulo de 0 a ∏/2;
- de 90 a 180° — valores de ángulo de ∏/2 a ∏;
- de 180 a 270° - de ∏ a 3*∏/2;
- último trimestre de 270 0 a 360 0 - valores de 3*∏/2 a 2*∏.

Para conocer una medida específica, convertir radianes a grados o viceversa, debes recurrir a una hoja de trucos.
Convertir ángulos de grados a radianes
Los ángulos se pueden medir en grados o radianes. Se requiere ser consciente de la conexión entre ambos significados. Esta relación se expresa en trigonometría mediante una fórmula especial. Al comprender la relación, puede aprender cómo controlar rápidamente los ángulos y pasar de grados a radianes.
Para saber exactamente a qué equivale un radian, puedes utilizar la siguiente fórmula:
1 rad. = 180 / ∏ = 180 / 3,1416 = 57,2956
En definitiva, 1 radian es igual a 57° y hay 0,0175 radianes en 1 grado:
1 grado = (∏ /180) rad. = 3,1416/180 rad. = 0,0175 rad.

Coseno, seno, tangente, cotangente en un círculo trigonométrico
Coseno con seno, tangente y cotangente en un círculo trigonométrico: funciones de ángulos alfa de 0 a 360 grados. Cada función tiene un valor positivo o negativo dependiendo de la magnitud del ángulo. Simbolizan la relación. triangulos rectángulos, formado en un círculo.
Contar ángulos en un círculo trigonométrico.
¡Atención!
Hay adicionales
materiales en la Sección Especial 555.
Para los que son muy "no muy..."
Y para los que “mucho…”)
Es casi lo mismo que en la lección anterior. Hay ejes, un círculo, un ángulo, todo está en orden. Se agregaron números de cuartos (en las esquinas del cuadrado grande), del primero al cuarto. ¿Qué pasa si alguien no lo sabe? Como puede ver, cuartos (también se llaman una hermosa palabra"cuadrantes") están numerados en sentido antihorario. Se agregaron valores de ángulos en los ejes. Todo está claro, no hay problemas.
Y se agrega una flecha verde. Con un plus. ¿Qué significa? Déjame recordarte que el lado fijo del ángulo. Siempre clavado al semieje positivo OX. Entonces, si rotamos el lado móvil del ángulo a lo largo de la flecha con un signo más, es decir. en orden ascendente de números de trimestre, el ángulo se considerará positivo. Como ejemplo, la imagen muestra un ángulo positivo de +60°.
Si dejamos de lado las esquinas en sentido contrario, en el sentido de las agujas del reloj, el ángulo se considerará negativo. Pase el cursor sobre la imagen (o toque la imagen en su tableta), verá una flecha azul con un signo menos. Esta es la dirección de lectura del ángulo negativo. Por ejemplo, se muestra un ángulo negativo (- 60°). Y también verás cómo han cambiado los números de los ejes... También los convertí a ángulos negativos. La numeración de los cuadrantes no cambia.
Aquí es donde suelen empezar los primeros malentendidos. ¿¡Cómo es eso!? ¿Qué pasa si un ángulo negativo en un círculo coincide con uno positivo? Y, en general, ¿resulta que la misma posición del lado en movimiento (o punto en el círculo numérico) se puede llamar ángulo negativo y positivo?
Sí. Exactamente. Digamos que un ángulo positivo de 90 grados forma un círculo. exactamente lo mismo posición como un ángulo negativo de menos 270 grados. Un ángulo positivo, por ejemplo +110° grados, toma exactamente lo mismo posición como ángulo negativo -250°.
Ningún problema. Todo es correcto). La elección del cálculo del ángulo positivo o negativo depende de las condiciones de la tarea. Si la condición no dice nada en texto claro sobre el signo del ángulo, (como "determinar el más pequeño positivoángulo", etc.), luego trabajamos con los valores que nos convienen.
Una excepción (¡¿y cómo podríamos vivir sin ellos?!) son desigualdades trigonométricas, pero ahí dominaremos este truco.
Y ahora una pregunta para ti. ¿Cómo supe que la posición del ángulo de 110° es la misma que la posición del ángulo de -250°?
Permítanme insinuar que esto está relacionado con una revolución completa. En 360°... ¿No está claro? Luego dibujamos un círculo. Lo dibujamos nosotros mismos, en papel. marcando la esquina aproximadamente 110°. Y Nosotros pensamos, cuánto tiempo queda hasta una revolución completa. Sólo quedarán 250°...
¿Entiendo? Y ahora, ¡atención! Si los ángulos de 110° y -250° ocupan un círculo mismo
situación, ¿y luego qué? Sí, los ángulos son 110° y -250° exactamente lo mismo
¡Seno, coseno, tangente y cotangente!
Aquellos. sin110° = sin(-250°), ctg110° = ctg(-250°) y así sucesivamente. ¡Esto es realmente importante! Y en sí mismo, hay muchas tareas en las que es necesario simplificar expresiones y, como base para el posterior dominio de fórmulas de reducción y otras complejidades de la trigonometría.
Por supuesto, tomé 110° y -250° al azar, únicamente como ejemplo. Todas estas igualdades funcionan para cualquier ángulo que ocupe la misma posición en el círculo. 60° y -300°, -75° y 285°, etc. Permítanme señalar de inmediato que los ángulos en estos pares son diferente. Pero tienen funciones trigonométricas. lo mismo.
Creo que entiendes qué son los ángulos negativos. Es bastante simple. En sentido antihorario: conteo positivo. En el camino - negativo. Considere el ángulo positivo o negativo. depende de nosotros. De nuestro deseo. Bueno, y también de la tarea, por supuesto... Espero que entiendas cómo pasar en funciones trigonométricas de ángulos negativos a positivos y viceversa. Dibuja un círculo, un ángulo aproximado y observa cuánto falta para completar una revolución completa, es decir hasta 360°.
Ángulos mayores a 360°.
Tratemos con ángulos mayores a 360°. ¿Existen tales cosas? Los hay, por supuesto. ¿Cómo dibujarlos en un círculo? ¡Ningún problema! Digamos que necesitamos entender en qué cuarto caerá un ángulo de 1000°. ¡Fácilmente! Damos una vuelta completa en sentido antihorario (¡el ángulo que nos dieron es positivo!). Rebobinamos 360°. Bueno, ¡sigamos adelante! Una vuelta más: ya son 720°. ¿Cuanto queda? 280°. No es suficiente para dar una vuelta completa... Pero el ángulo es de más de 270°, y este es el límite entre el tercer y el cuarto cuarto. Por lo tanto, nuestro ángulo de 1000° cae en el cuarto cuarto. Todo.
Como puedes ver, es bastante simple. Permítanme recordarles una vez más que el ángulo de 1000° y el ángulo de 280°, que obtuvimos descartando las revoluciones completas “extra”, son, estrictamente hablando, diferente esquinas. Pero las funciones trigonométricas de estos ángulos. exactamente lo mismo! Aquellos. sen1000° = sen280°, cos1000° = cos280°, etc. Si fuera un seno, no notaría la diferencia entre estos dos ángulos...
¿Por qué es necesario todo esto? ¿Por qué necesitamos convertir ángulos de uno a otro? Sí, todo por lo mismo.) Para simplificar expresiones. La simplificación de expresiones es, de hecho, la principal tarea de las matemáticas escolares. Bueno, y en el camino se entrena la cabeza.)
Bueno, ¿practiquemos?)
Respondemos preguntas. Los simples primero.
1. ¿En qué cuarto cae el ángulo de -325°?
2. ¿En qué cuarto cae el ángulo de 3000°?
3. ¿En qué cuarto cae el ángulo -3000°?
¿Hay un problema? ¿O incertidumbre? Vaya a la Sección 555, Práctica del círculo trigonométrico. Allí, en la primera lección de este mismo " Trabajo practico..." todo en detalle... En semejante preguntas de incertidumbre por ser ¡no debería!
4. ¿Qué signo tiene sen555°?
5. ¿Qué signo tiene tg555°?
¿Has determinado? ¡Excelente! ¿Tienes alguna duda? Necesitas ir a la Sección 555... Por cierto, allí aprenderás a dibujar tangente y cotangente en un círculo trigonométrico. Algo muy útil.
Y ahora las preguntas son más sofisticadas.
6. Reducir la expresión sen777° al seno del ángulo positivo más pequeño.
7. Reduce la expresión cos777° al coseno del ángulo negativo más grande.
8. Reduce la expresión cos(-777°) al coseno del ángulo positivo más pequeño.
9. Reduce la expresión sen777° al seno del ángulo negativo más grande.
¿Qué, las preguntas 6 a 9 te desconcertaron? Acostúmbrate, en el Examen Estatal Unificado no encuentras tales formulaciones... Que así sea, lo traduciré. ¡Solo para ti!
Las palabras "traer una expresión a..." significan transformar la expresión para que su significado no ha cambiado A apariencia modificado según la asignación. Entonces, en las tareas 6 y 9 debemos obtener un seno, dentro del cual hay ángulo positivo más pequeño. Todo lo demás no importa.
Daré las respuestas en orden (en violación de nuestras reglas). Pero qué hacer, sólo hay dos señales y sólo cuatro cuartos... No tendrá muchas opciones para elegir.
6. pecado57°.
7. cos(-57°).
8. cos57°.
9. -pecado(-57°)
Supongo que las respuestas a las preguntas 6 a 9 confundieron a algunas personas. Especialmente -pecado(-57°), ¿en serio?) De hecho, en las reglas elementales para calcular ángulos hay lugar para errores... Por eso tuve que hacer una lección: "¿Cómo determinar los signos de funciones y dar ángulos en un círculo trigonométrico?" En la Sección 555. Las tareas 4 a 9 están cubiertas allí. Bien ordenado, con todos los inconvenientes. Y están aquí.)
En la próxima lección nos ocuparemos de los misteriosos radianes y el número "Pi". Aprendamos a convertir fácil y correctamente grados a radianes y viceversa. Y nos sorprenderá descubrir que esta información básica en el sitio basta ya para resolver algunos problemas de trigonometría personalizados!
Si te gusta este sitio...
Por cierto, tengo un par de sitios más interesantes para ti).
Podrás practicar la resolución de ejemplos y descubrir tu nivel. Pruebas con verificación instantánea. Aprendamos, ¡con interés!)
Puede familiarizarse con funciones y derivadas.
Tipo de lección: sistematización del conocimiento y control intermedio.
Equipo: círculo trigonométrico, pruebas, tarjetas de tareas.
Objetivos de la lección: sistematizar lo aprendido material teórico según las definiciones de seno, coseno, tangente de un ángulo; comprobar el grado de adquisición de conocimientos sobre este tema y su aplicación en la práctica.
Tareas:
- Generalizar y consolidar los conceptos de seno, coseno y tangente de un ángulo.
- Formar una comprensión integral de las funciones trigonométricas.
- Promover el deseo y la necesidad de los estudiantes de estudiar material trigonométrico; cultivar una cultura de la comunicación, la capacidad de trabajar en grupo y la necesidad de autoeducación.
“Quien hace y piensa por sí mismo desde pequeño,
Entonces se vuelve más fiable, más fuerte y más inteligente.
(V. Shukshin)
DURANTE LAS CLASES
I. Momento organizacional
La clase está representada por tres grupos. Cada grupo tiene un consultor.
El profesor anuncia el tema, las metas y los objetivos de la lección.
II. Actualización de conocimientos (trabajo frontal con la clase)
1) Trabajar en grupos en tareas:
1. Formule la definición de ángulo sin.
– ¿Qué signos tiene el sen α en cada cuadrante de coordenadas?
– ¿A qué valores tiene sentido la expresión sen α y qué valores puede tomar?
2. El segundo grupo son las mismas preguntas para cos α.
3. El tercer grupo prepara respuestas a las mismas preguntas tg α y ctg α.
En este momento, tres estudiantes trabajan de forma independiente en la pizarra utilizando tarjetas (representantes de diferentes grupos).
Tarjeta número 1.
Trabajo practico.
Usando el círculo unitario, calcula los valores de sen α, cos α y tan α para ángulos de 50, 210 y – 210.
Tarjeta número 2.
Determine el signo de la expresión: tg 275; porque 370; pecado 790; tg 4.1 y pecado 2.
Tarjeta número 3.
1) Calcular:
2) Comparar: cos 60 y cos 2 30 – sen 2 30
2) Oralmente:
a) Se propone una serie de números: 1; 1.2; 3; , 0, , – 1. Entre ellos hay redundantes. ¿Qué propiedad del sen α o cos α pueden expresar estos números? (¿Pueden el sen α o el cos α tomar estos valores)?
b) ¿Tiene sentido la expresión: cos (–); pecado 2; tg 3: ctg (– 5); ; ctg0;
cotg(–π). ¿Por qué?
c) ¿Existe un valor mínimo y máximo de sen o cos, tg, ctg?
d) ¿Es cierto?
1) α = 1000 es el ángulo del segundo cuarto;
2) α = – 330 es el ángulo del cuarto IV.
e) Los números corresponden al mismo punto del círculo unitario.
3) Trabajar en el tablero
No. 567 (2; 4) – Encuentra el valor de la expresión
No. 583 (1-3) Determinar el signo de la expresión.
Tarea: mesa en cuaderno. N° 567(1, 3) N° 578
III. Adquirir conocimientos adicionales. Trigonometría en la palma de tu mano
Maestro: Resulta que los valores de los senos y cosenos de los ángulos están “ubicados” en la palma de tu mano. Extienda la mano (cualquiera de ellas) y separe los dedos lo más posible (como en el cartel). Se invita a un estudiante. Medimos los ángulos entre nuestros dedos.
Toma un triángulo donde hay un ángulo de 30, 45 y 60 90 y aplica el vértice del ángulo al montículo de la Luna en la palma de tu mano. El Monte de la Luna se encuentra en la intersección de las extensiones del dedo meñique y el pulgar. Combinamos un lado con el dedo meñique y el otro lado con uno de los otros dedos.
Resulta que hay un ángulo de 90º entre el meñique y el pulgar, de 30º entre el meñique y el anular, de 45º entre el meñique y el medio y de 60º entre el meñique y el índice, y esto es válido para todas las personas. sin excepción.

dedo meñique No. 0 – corresponde a 0,
número 1 sin nombre – corresponde a 30,
promedio No. 2 – corresponde a 45,
número de índice 3 – corresponde a 60,
grande No. 4 – corresponde a 90.
Así, tenemos 4 dedos en nuestra mano y recordamos la fórmula:

Dedo no. |
Esquina |
Significado |
|
||
|
||
|
Esto es sólo una regla mnemotécnica. En general, el valor de sen α o cos α debe saberse de memoria, pero a veces esta regla ayudará en tiempos difíciles.
Elabora una regla para cos (los ángulos no cambian, pero se cuentan desde el pulgar). Una pausa física asociada con los signos sin α o cos α.
IV. Comprobación de sus conocimientos de conocimientos y habilidades.
Trabajo independiente con retroalimentación.
Cada alumno recibe un test (4 opciones) y la hoja de respuestas es la misma para todos.
Prueba
Opción 1
1) ¿En qué ángulo de rotación el radio tomará la misma posición que cuando gira en un ángulo de 50?
2) Encuentra el valor de la expresión: 4cos 60 – 3sen 90.
3) Qué número es menor que cero: sen 140, cos 140, sen 50, tg 50.
opcion 2
1) ¿En qué ángulo de rotación el radio tomará la misma posición que cuando gira en un ángulo de 10?
2) Encuentra el valor de la expresión: 4cos 90 – 6sen 30.
3) Qué número es mayor que cero: sen 340, cos 340, sen 240, tg (– 240).
Opción 3
1) Encuentra el valor de la expresión: 2ctg 45 – 3cos 90.
2) Qué número es menor que cero: sen 40, cos (– 10), tan 210, sen 140.
3) ¿Qué cuarto de ángulo es el ángulo α, si sen α > 0, cos α?< 0.
Opción 4
1) Encuentra el valor de la expresión: tg 60 – 6ctg 90.
2) Qué número es menor que cero: sin(– 10), cos 140, tg 250, cos 250.
3) ¿Qué ángulo del cuadrante es el ángulo α, si ctg α?< 0, cos α> 0.
A |
B |
EN |
GRAMO |
D |
mi |
Y |
z |
Y |
l |
METRO |
|
norte |
ACERCA DE |
PAG |
R |
CON |
t |
Ud. |
F |
X |
sh |
YU |
I |
(la palabra clave es trigonometría)
V. Información de la historia de la trigonometría
Maestro: La trigonometría es una rama de las matemáticas bastante importante para la vida humana. La forma moderna de trigonometría la dio el mayor matemático del siglo XVIII, Leonhard Euler, suizo de nacimiento. largos años Trabajó en Rusia y fue miembro de la Academia de Ciencias de San Petersburgo. Introdujo definiciones conocidas de funciones trigonométricas, formuló y demostró fórmulas conocidas, las aprenderemos más adelante. La vida de Euler es muy interesante y le aconsejo que la conozca a través del libro de Yakovlev "Leonard Euler".
(Mensaje de los chicos sobre este tema)
VI. Resumiendo la lección
Juego "Tic Tac Toe"
Participan los dos estudiantes más activos. Están apoyados por grupos. Las soluciones a las tareas se anotan en un cuaderno.
Tareas
1) Encuentra el error
a) sen 225 = – 1,1 c) sen 115< О
b) cos 1000 = 2 d) cos (– 115) > 0
2) Expresa el ángulo en grados.
3) Expresa el ángulo 300 en radianes.
4) ¿Cuál es el valor mayor y menor que puede tener la expresión: 1+ sin α;
5) Determinar el signo de la expresión: sen 260, cos 300.
6) ¿En qué cuarto del círculo numérico se encuentra el punto?
7) Determinar los signos de la expresión: cos 0,3π, sin 195, ctg 1, tg 390
8) Calcular:
9) Comparar: pecado 2 y pecado 350
VII. reflexión de la lección
Maestro:¿Dónde podemos encontrarnos con la trigonometría?
¿En qué lecciones de noveno grado, e incluso ahora, utiliza los conceptos de pecado α, cos α; tgα; ctg α y ¿con qué propósito?
En pocas palabras, se trata de verduras cocidas en agua según una receta especial. Consideraré dos componentes iniciales (ensalada de verduras y agua) y el resultado final: borscht. Geométricamente, se puede considerar como un rectángulo, en el que un lado representa la lechuga y el otro representa el agua. La suma de estos dos lados indicará borscht. La diagonal y el área de dicho rectángulo de "borscht" son conceptos puramente matemáticos y nunca se utilizan en recetas de borscht.
¿Cómo se convierte la lechuga y el agua en borscht desde un punto de vista matemático? ¿Cómo puede la suma de dos segmentos de recta convertirse en trigonometría? Para entender esto, necesitamos funciones angulares lineales.
No encontrará nada sobre funciones angulares lineales en los libros de texto de matemáticas. Pero sin ellos no puede haber matemáticas. Las leyes de las matemáticas, al igual que las leyes de la naturaleza, funcionan independientemente de si conocemos o no su existencia.
Las funciones angulares lineales son leyes de la suma. Vea cómo el álgebra se convierte en geometría y la geometría en trigonometría.
¿Es posible prescindir de funciones angulares lineales? Es posible, porque los matemáticos todavía se las arreglan sin ellos. El truco de los matemáticos es que siempre nos hablan sólo de aquellos problemas que ellos mismos saben resolver y nunca de aquellos que no pueden resolver. Mirar. Si conocemos el resultado de la suma y un término, usamos la resta para encontrar el otro término. Todo. No conocemos otros problemas y no sabemos cómo solucionarlos. ¿Qué debemos hacer si solo conocemos el resultado de la suma y no conocemos ambos términos? En este caso, el resultado de la suma debe descomponerse en dos términos utilizando funciones angulares lineales. A continuación, nosotros mismos elegimos cuál puede ser un término, y las funciones angulares lineales muestran cuál debería ser el segundo término para que el resultado de la suma sea exactamente el que necesitamos. Puede haber un número infinito de tales pares de términos. EN La vida cotidiana Podemos hacerlo bien sin descomponer la suma; la resta es suficiente para nosotros. Pero cuando investigación científica leyes de la naturaleza, descomponer una suma en sus componentes puede resultar muy útil.
Otra ley de la suma de la que a los matemáticos no les gusta hablar (otro de sus trucos) requiere que los términos tengan las mismas unidades de medida. Para ensalada, agua y borscht, pueden ser unidades de peso, volumen, valor o unidad de medida.
La figura muestra dos niveles de diferencia para matemáticas. El primer nivel son las diferencias en el campo de los números, que se indican a, b, C. Esto es lo que hacen los matemáticos. El segundo nivel son las diferencias en el campo de las unidades de medida, que se muestran entre corchetes y se indican con la letra Ud.. Esto es lo que hacen los físicos. Podemos comprender el tercer nivel: las diferencias en el área de los objetos que se describen. Diferentes objetos pueden tener el mismo número de unidades de medida idénticas. Lo importante que es esto lo podemos ver en el ejemplo de la trigonometría del borscht. Si agregamos subíndices a la misma designación de unidad para diferentes objetos, podemos decir exactamente qué cantidad matemática describe un objeto en particular y cómo cambia con el tiempo o debido a nuestras acciones. Carta W. Designaré el agua con una letra. S Designaré la ensalada con una letra. B- borscht. Así se verán las funciones angulares lineales para borscht.
Si tomamos una parte del agua y una parte de la ensalada, juntas se convertirán en una porción de borscht. Aquí te sugiero que te tomes un pequeño descanso del borscht y recuerdes tu infancia lejana. ¿Recuerdas cómo nos enseñaron a juntar conejitos y patos? Era necesario encontrar cuántos animales habría. ¿Qué nos enseñaron a hacer entonces? Nos enseñaron a separar unidades de medida de números y a sumar números. Sí, cualquier número se puede sumar a cualquier otro número. Este es un camino directo al autismo de las matemáticas modernas: hacemos incomprensiblemente qué, incomprensiblemente por qué, y entendemos muy mal cómo se relaciona esto con la realidad, debido a los tres niveles de diferencia, los matemáticos operan con solo uno. Sería más correcto aprender a pasar de una unidad de medida a otra.
Se pueden contar en trozos conejitos, patos y animalitos. Una unidad de medida común para diferentes objetos nos permite sumarlos. Esta es una versión infantil del problema. Veamos un problema similar para los adultos. ¿Qué obtienes cuando agregas conejitos y dinero? Hay dos posibles soluciones aquí.
Primera opción. Determinamos el valor de mercado de los conejitos y lo sumamos a la cantidad de dinero disponible. Obtuvimos el valor total de nuestra riqueza en términos monetarios.
Segunda opción. Puedes sumar el número de conejitos al número de billetes que tenemos. Recibiremos la cantidad bienes muebles en pedazos.
Como puedes ver, la misma ley de la suma te permite obtener resultados diferentes. Todo depende de qué queremos saber exactamente.
Pero volvamos a nuestro borscht. Ahora podemos ver qué sucederá con diferentes valores de ángulos de funciones angulares lineales.
El ángulo es cero. Tenemos ensalada, pero no agua. No podemos cocinar borscht. La cantidad de borscht también es cero. Esto no significa en absoluto que cero borscht sea igual a cero agua. Puede haber cero borscht con cero ensalada (ángulo recto).
Para mí personalmente, esta es la principal prueba matemática de que . El cero no cambia el número cuando se suma. Esto sucede porque la suma en sí es imposible si solo hay un término y falta el segundo término. Puede sentir esto como quiera, pero recuerde: todas las operaciones matemáticas con cero fueron inventadas por los propios matemáticos, así que deseche su lógica y abarrote estúpidamente las definiciones inventadas por los matemáticos: "la división por cero es imposible", "cualquier número multiplicado por cero es igual a cero”, “más allá del punto de punción cero” y otras tonterías. Es suficiente recordar una vez que el cero no es un número, y nunca más tendrá la pregunta de si el cero es un número natural o no, porque esa pregunta pierde todo significado: ¿cómo puede algo que no es un número considerarse un número? ? Es como preguntar de qué color se debe clasificar un color invisible. Agregar un cero a un número es lo mismo que pintar con pintura que no está. Agitamos un pincel seco y les dijimos a todos que “pintamos”. Pero me desvío un poco.
El ángulo es mayor que cero pero menor que cuarenta y cinco grados. Tenemos mucha lechuga, pero poca agua. Como resultado, obtendremos un borscht espeso.
El ángulo es de cuarenta y cinco grados. Disponemos de cantidades iguales de agua y ensalada. Este es el borscht perfecto (perdónenme, chefs, son solo matemáticas).
El ángulo es mayor que cuarenta y cinco grados, pero menor que noventa grados. Disponemos mucha agua y poca ensalada. Obtendrás borscht líquido.
Ángulo recto. Tenemos agua. De la ensalada lo único que queda son recuerdos, mientras seguimos midiendo el ángulo de la línea que una vez marcó la ensalada. No podemos cocinar borscht. La cantidad de borscht es cero. En este caso aguanta y bebe agua mientras la tengas)))
Aquí. Algo como esto. Puedo contar otras historias aquí que serían más que apropiadas aquí.
Dos amigos tenían acciones en un negocio común. Después de matar a uno de ellos, todo pasó al otro.
El surgimiento de las matemáticas en nuestro planeta.
Todas estas historias se cuentan en el lenguaje de las matemáticas utilizando funciones angulares lineales. En otra ocasión les mostraré el lugar real de estas funciones en la estructura de las matemáticas. Mientras tanto, volvamos a la trigonometría del borscht y consideremos las proyecciones.
sábado, 26 de octubre de 2019
Vi un video interesante sobre serie gruesa Uno menos uno más uno menos uno - Numberphile. Los matemáticos mienten. No realizaron una verificación de igualdad durante su razonamiento.
Esto hace eco de mis pensamientos sobre .
Echemos un vistazo más de cerca a las señales de que los matemáticos nos están engañando. Al comienzo del argumento, los matemáticos dicen que la suma de una secuencia DEPENDE de si tiene un número par de elementos o no. Este es un HECHO OBJETIVAMENTE ESTABLECIDO. ¿Qué pasa después?
Luego, los matemáticos restan la secuencia de la unidad. ¿A qué conduce esto? Esto conduce a un cambio en el número de elementos de la secuencia: un número par se convierte en impar, un número impar se convierte en par. Después de todo, agregamos un elemento igual a uno a la secuencia. A pesar de toda la similitud externa, la secuencia antes de la transformación no es igual a la secuencia después de la transformación. Incluso si hablamos de una secuencia infinita, debemos recordar que una secuencia infinita con un número impar de elementos no es igual a una secuencia infinita con un número par de elementos.
Al poner un signo igual entre dos secuencias con diferente número de elementos, los matemáticos afirman que la suma de la secuencia NO DEPENDE del número de elementos de la secuencia, lo que contradice un HECHO OBJETIVAMENTE ESTABLECIDO. Un razonamiento adicional sobre la suma de una secuencia infinita es falso, ya que se basa en una igualdad falsa.
Si ves que los matemáticos, durante las pruebas, colocan paréntesis, reordenan elementos de una expresión matemática, añaden o quitan algo, ten mucho cuidado, lo más probable es que estén intentando engañarte. Al igual que los magos de las cartas, los matemáticos utilizan diversas manipulaciones de expresión para distraer su atención y, en última instancia, darle un resultado falso. Si no puedes repetir un truco con cartas sin conocer el secreto del engaño, entonces en matemáticas todo es mucho más simple: ni siquiera sospechas nada sobre el engaño, pero repetir todas las manipulaciones con una expresión matemática te permite convencer a otros de la exactitud de el resultado obtenido, igual que cuando te convencieron.
Pregunta de la audiencia: ¿El infinito (como el número de elementos de la secuencia S) es par o impar? ¿Cómo se puede cambiar la paridad de algo que no tiene paridad?
El infinito es para los matemáticos, como el Reino de los Cielos es para los sacerdotes: nadie ha estado allí nunca, pero todos saben exactamente cómo funciona todo allí))) Estoy de acuerdo, después de la muerte serás absolutamente indiferente si viviste un número par o impar de días, pero... Agregando solo un día al comienzo de su vida, obtendremos una persona completamente diferente: su apellido, nombre y patronímico son exactamente iguales, solo la fecha de nacimiento es completamente diferente: era nacido un día antes que tú.
Ahora vayamos al punto))) Digamos que una secuencia finita que tiene paridad pierde esta paridad cuando va al infinito. Entonces cualquier segmento finito de una secuencia infinita debe perder la paridad. No vemos esto. El hecho de que no podamos decir con seguridad si una secuencia infinita tiene un número par o impar de elementos no significa que la paridad haya desaparecido. La paridad, si existe, no puede desaparecer sin dejar rastro hacia el infinito, como en la manga de un rotulador. Existe una muy buena analogía para este caso.
¿Alguna vez le has preguntado al cuco sentado en el reloj en qué dirección gira la manecilla del reloj? Para ella, la flecha gira hacia adentro. direccion contraria lo que llamamos "en el sentido de las agujas del reloj". Por paradójico que parezca, la dirección de rotación depende únicamente de desde qué lado observamos la rotación. Y entonces tenemos una rueda que gira. No podemos decir en qué dirección se produce la rotación, ya que podemos observarla tanto desde un lado del plano de rotación como desde el otro. Sólo podemos dar testimonio de que hay rotación. Completa analogía con la paridad de una secuencia infinita. S.
Ahora agreguemos una segunda rueda giratoria, cuyo plano de rotación es paralelo al plano de rotación de la primera rueda giratoria. Todavía no podemos decir con seguridad en qué dirección giran estas ruedas, pero podemos decir con certeza si ambas ruedas giran en la misma dirección o en la dirección opuesta. Comparando dos secuencias infinitas S Y 1-S, demostré con ayuda de las matemáticas que estas secuencias tienen diferentes paridades y poner un signo igual entre ellas es un error. Personalmente, confío en las matemáticas, no confío en los matemáticos))) Por cierto, para comprender completamente la geometría de las transformaciones de secuencias infinitas, es necesario introducir el concepto "simultaneidad". Esto será necesario dibujarlo.
miércoles, 7 de agosto de 2019
Para concluir la conversación, debemos considerar un conjunto infinito. La cuestión es que el concepto de “infinito” afecta a los matemáticos como una boa constrictor afecta a un conejo. El horror tembloroso del infinito priva a los matemáticos sentido común. He aquí un ejemplo:
Se localiza la fuente original. Alfa significa número real. El signo igual en las expresiones anteriores indica que si sumas un número o infinito al infinito, nada cambiará, el resultado será el mismo infinito. Si tomamos el conjunto infinito como ejemplo números naturales, entonces los ejemplos considerados se pueden presentar de la siguiente manera:
Para demostrar claramente que tenían razón, los matemáticos idearon muchos métodos diferentes. Personalmente, considero todos estos métodos como chamanes bailando con panderetas. Básicamente, todo se reduce al hecho de que algunas de las habitaciones están desocupadas y entran nuevos invitados, o que algunos de los visitantes son arrojados al pasillo para dejar espacio a los invitados (de manera muy humana). He expresado mis opiniones sobre tales decisiones en la forma historia fantástica sobre la Rubia. ¿En qué se basa mi razonamiento? Reubicar a un número infinito de visitantes requiere una cantidad de tiempo infinita. Después de que hayamos dejado libre la primera habitación para un huésped, uno de los visitantes siempre caminará por el pasillo desde su habitación a la siguiente hasta el fin de los tiempos. Por supuesto, el factor tiempo puede ignorarse estúpidamente, pero esto entrará en la categoría de "ninguna ley está escrita para tontos". Todo depende de lo que estemos haciendo: ajustar la realidad a las teorías matemáticas o viceversa.
¿Qué es un “hotel sin fin”? Un hotel infinito es un hotel que siempre tiene cualquier número de camas vacías, independientemente de cuántas habitaciones estén ocupadas. Si todas las habitaciones del interminable corredor de "visitantes" están ocupadas, hay otro corredor interminable con habitaciones de "invitados". Habrá un número infinito de tales corredores. Además, el “hotel infinito” tiene un número infinito de pisos en un número infinito de edificios en un número infinito de planetas en un número infinito de universos creados por un número infinito de Dioses. Los matemáticos no consiguen distanciarse de lo banal problemas cotidianos: Dios-Alá-Buda es siempre uno solo, hay un solo hotel, hay un solo corredor. Por eso los matemáticos están tratando de hacer malabarismos con los números de serie de las habitaciones de hotel, convenciéndonos de que es posible "meter lo imposible".
Les demostraré la lógica de mi razonamiento usando el ejemplo de un conjunto infinito de números naturales. Primero debes responder una pregunta muy simple: ¿cuántos conjuntos de números naturales hay, uno o muchos? No hay una respuesta correcta a esta pregunta, ya que nosotros mismos inventamos los números; los números no existen en la naturaleza. Sí, la naturaleza es excelente para contar, pero para ello utiliza otras herramientas matemáticas que no nos son familiares. En otra ocasión os contaré lo que piensa la Naturaleza. Como inventamos los números, nosotros mismos decidiremos cuántos conjuntos de números naturales hay. Consideremos ambas opciones, como corresponde a verdaderos científicos.
Opcion uno. “Se nos dará” un único conjunto de números naturales, que yace serenamente en el estante. Sacamos este juego del estante. Eso es todo, no quedan otros números naturales en el estante ni ningún lugar donde llevarlos. No podemos agregar uno a este conjunto porque ya lo tenemos. ¿Qué pasa si realmente quieres? Ningún problema. Podemos coger uno del juego que ya hemos cogido y devolverlo a la estantería. Después de eso, podemos coger uno del estante y añadirlo a lo que nos queda. Como resultado, obtendremos nuevamente un conjunto infinito de números naturales. Puedes anotar todas nuestras manipulaciones así:
Anoté las acciones en notación algebraica y en notación de teoría de conjuntos, con un listado detallado de los elementos del conjunto. El subíndice indica que tenemos un único conjunto de números naturales. Resulta que el conjunto de números naturales permanecerá sin cambios solo si se le resta uno y se le suma la misma unidad.
Opción dos. Tenemos muchos conjuntos infinitos diferentes de números naturales en nuestro estante. Destaco - DIFERENTES, a pesar de que son prácticamente indistinguibles. Tomemos uno de estos conjuntos. Luego tomamos uno de otro conjunto de números naturales y lo sumamos al conjunto que ya hemos tomado. Incluso podemos sumar dos conjuntos de números naturales. Esto es lo que obtenemos:
Los subíndices "uno" y "dos" indican que estos elementos pertenecían a conjuntos diferentes. Sí, si sumas uno a un conjunto infinito, el resultado también será un conjunto infinito, pero no será el mismo que el conjunto original. Si agrega otro conjunto infinito a un conjunto infinito, el resultado es un nuevo conjunto infinito que consta de los elementos de los dos primeros conjuntos.
El conjunto de los números naturales se utiliza para contar de la misma manera que una regla para medir. Ahora imagina que agregaste un centímetro a la regla. Esta será una línea diferente, no igual a la original.
Puede aceptar o no mi razonamiento: es asunto suyo. Pero si alguna vez te encuentras con problemas matemáticos, piensa si estás siguiendo el camino del razonamiento falso recorrido por generaciones de matemáticos. Después de todo, estudiar matemáticas, en primer lugar, forma en nosotros un estereotipo estable de pensamiento, y sólo entonces aumenta nuestras capacidades mentales (o, por el contrario, nos priva del libre pensamiento).
pozg.ru
domingo, 4 de agosto de 2019
Estaba terminando una posdata de un artículo sobre y vi este maravilloso texto en Wikipedia:
Leemos: "... rico bases teóricas Las matemáticas de Babilonia no tenían un carácter holístico y estaban reducidas a un conjunto de técnicas dispares, desprovistas de un sistema común y de una base de evidencia".
¡Guau! Qué inteligentes somos y qué tan bien podemos ver los defectos de los demás. ¿Es difícil para nosotros mirar las matemáticas modernas en el mismo contexto? Parafraseando ligeramente el texto anterior, personalmente obtuve lo siguiente:
La rica base teórica de las matemáticas modernas no es de naturaleza holística y se reduce a un conjunto de secciones dispares, desprovistas de un sistema común y una base de evidencia.
No iré muy lejos para confirmar mis palabras: tiene un lenguaje y convenciones que son diferentes del lenguaje y las convenciones de muchas otras ramas de las matemáticas. Los mismos nombres en diferentes ramas de las matemáticas pueden tener significados diferentes. Quiero dedicar toda una serie de publicaciones a los errores más evidentes de las matemáticas modernas. Nos vemos pronto.
Sábado, 3 de agosto de 2019.
¿Cómo dividir un conjunto en subconjuntos? Para hacer esto, debe ingresar una nueva unidad de medida que esté presente en algunos de los elementos del conjunto seleccionado. Veamos un ejemplo.
Que tengamos mucho A compuesto por cuatro personas. Este conjunto se forma a partir de “personas”. Designemos los elementos de este conjunto con la letra A, el subíndice con un número indicará el número de serie de cada persona en este conjunto. Introduzcamos una nueva unidad de medida "género" y designémosla con la letra b. Dado que las características sexuales son inherentes a todas las personas, multiplicamos cada elemento del conjunto. A basado en el género b. Observe que nuestro conjunto de "personas" ahora se ha convertido en un conjunto de "personas con características de género". Después de esto podemos dividir las características sexuales en masculinas. bm y de mujeres peso corporal características sexuales. Ahora podemos aplicar un filtro matemático: seleccionamos una de estas características sexuales, sin importar cuál sea masculina o femenina. Si una persona lo tiene, lo multiplicamos por uno, si no existe tal signo, lo multiplicamos por cero. Y luego utilizamos las matemáticas escolares habituales. Mira lo que paso.
Después de la multiplicación, reducción y reordenamiento, terminamos con dos subconjuntos: el subconjunto de hombres bm y un subconjunto de mujeres bw. Los matemáticos razonan aproximadamente de la misma manera cuando aplican la teoría de conjuntos en la práctica. Pero no nos cuentan los detalles, sino que nos dan el resultado final: "muchas personas están formadas por un subconjunto de hombres y un subconjunto de mujeres". Naturalmente, es posible que tengas una pregunta: ¿con qué precisión se han aplicado las matemáticas en las transformaciones descritas anteriormente? Me atrevo a asegurarles que esencialmente todo se hizo correctamente, basta con conocer las bases matemáticas de la aritmética, el álgebra de Boole y otras ramas de las matemáticas. ¿Lo que es? En otra ocasión os hablaré de esto.
En cuanto a los superconjuntos, puedes combinar dos conjuntos en un superconjunto seleccionando la unidad de medida presente en los elementos de estos dos conjuntos.
Como puede ver, las unidades de medida y las matemáticas ordinarias hacen de la teoría de conjuntos una reliquia del pasado. Una señal de que no todo va bien en la teoría de conjuntos es que los matemáticos han creado su propio lenguaje y notación para la teoría de conjuntos. Los matemáticos actuaron como alguna vez lo hicieron los chamanes. Sólo los chamanes saben cómo aplicar "correctamente" su "conocimiento". Nos enseñan este “conocimiento”.
En conclusión, quiero mostrarles cómo manipulan los matemáticos.
Digamos que Aquiles corre diez veces más rápido que la tortuga y está mil pasos detrás de ella. Durante el tiempo que le toma a Aquiles correr esta distancia, la tortuga se arrastrará cien pasos en la misma dirección. Cuando Aquiles corre cien pasos, la tortuga gatea otros diez pasos, y así sucesivamente. El proceso continuará hasta el infinito, Aquiles nunca alcanzará a la tortuga.
Este razonamiento se convirtió en un shock lógico para todas las generaciones posteriores. Aristóteles, Diógenes, Kant, Hegel, Hilbert... Todos ellos consideraron de una forma u otra la aporía de Zenón. El shock fue tan fuerte que " ...las discusiones continúan hasta el día de hoy; la comunidad científica aún no ha podido llegar a una opinión común sobre la esencia de las paradojas...estuvieron involucrados en el estudio del tema Análisis matemático, teoría de conjuntos, nuevos enfoques físicos y filosóficos; Ninguno de ellos se convirtió en una solución generalmente aceptada al problema..."[Wikipedia, "La aporía de Zenón". Todos entienden que están siendo engañados, pero nadie entiende en qué consiste el engaño.
Desde un punto de vista matemático, Zenón en su aporía demostró claramente la transición de la cantidad a. Esta transición implica aplicaciones en lugar de permanentes. Hasta donde yo entiendo, aparato matemático El uso de unidades de medida variables aún no se ha desarrollado o no se ha aplicado a la aporía de Zenón. Aplicar nuestra lógica habitual nos lleva a una trampa. Nosotros, por inercia del pensamiento, aplicamos unidades de tiempo constantes al valor recíproco. Desde un punto de vista físico, esto parece como si el tiempo se desacelerara hasta detenerse por completo en el momento en que Aquiles alcanza a la tortuga. Si el tiempo se detiene, Aquiles ya no podrá escapar de la tortuga.
Si damos la vuelta a nuestra lógica habitual, todo encaja. Aquiles corre a velocidad constante. Cada segmento posterior de su camino es diez veces más corto que el anterior. En consecuencia, el tiempo dedicado a superarlo es diez veces menor que el anterior. Si aplicamos el concepto de "infinito" en esta situación, entonces sería correcto decir "Aquiles alcanzará a la tortuga infinitamente rápido".
¿Cómo evitar esta trampa lógica? Permanezca en unidades de tiempo constantes y no cambie a unidades recíprocas. En el lenguaje de Zenón se ve así:
En el tiempo que le toma a Aquiles correr mil pasos, la tortuga gateará cien pasos en la misma dirección. Durante el siguiente intervalo de tiempo igual al primero, Aquiles correrá otros mil pasos y la tortuga se arrastrará cien pasos. Ahora Aquiles está ochocientos pasos por delante de la tortuga.
Este enfoque describe adecuadamente la realidad sin paradojas lógicas. Pero esta no es una solución completa al problema. La afirmación de Einstein sobre la irresistibilidad de la velocidad de la luz es muy similar a la aporía de Zenón “Aquiles y la tortuga”. Todavía tenemos que estudiar, repensar y resolver este problema. Y la solución no debe buscarse sin cesar números grandes, pero en unidades de medida.
Otra aporía interesante de Zenón habla de una flecha voladora:
Una flecha voladora está inmóvil, ya que en cada momento está en reposo, y como está en reposo en cada momento, siempre está en reposo.
En esta aporía, la paradoja lógica se supera de manera muy simple: basta con aclarar que en cada momento una flecha voladora está en reposo en diferentes puntos del espacio, lo que, de hecho, es movimiento. Es necesario señalar aquí otro punto. A partir de una fotografía de un automóvil en la carretera es imposible determinar ni el hecho de su movimiento ni la distancia hasta él. Para determinar si un automóvil se está moviendo, necesita dos fotografías tomadas desde el mismo punto en diferentes momentos del tiempo, pero no puede determinar la distancia desde ellas. Para determinar la distancia a un automóvil, necesita dos fotografías tomadas desde diferentes puntos del espacio en un momento dado, pero a partir de ellas no puede determinar el hecho del movimiento (por supuesto, aún necesita datos adicionales para los cálculos, la trigonometría lo ayudará ). Lo que quiero llamar la atención especialmente es que dos puntos en el tiempo y dos puntos en el espacio son cosas diferentes que no deben confundirse, porque brindan diferentes oportunidades para la investigación.
Te mostraré el proceso con un ejemplo. Seleccionamos el "sólido rojo en un grano": este es nuestro "todo". Al mismo tiempo, vemos que estas cosas tienen arco y las hay sin arco. Después de eso, seleccionamos parte del “todo” y formamos un conjunto “con un lazo”. Así es como los chamanes obtienen su alimento vinculando su teoría de conjuntos a la realidad.
Ahora hagamos un pequeño truco. Tomemos "sólido con un grano con un lazo" y combinemos estos "enteros" según el color, seleccionando los elementos rojos. Tenemos mucho "rojo". Ahora la última pregunta: ¿los conjuntos resultantes “con lazo” y “rojo” son el mismo conjunto o son dos conjuntos diferentes? Sólo los chamanes saben la respuesta. Más precisamente, ellos mismos no saben nada, pero como dicen, así será.
Este sencillo ejemplo muestra que la teoría de conjuntos es completamente inútil cuando se trata de la realidad. ¿Cuál es el secreto? Formamos un conjunto de "sólidos rojos con un grano y un lazo". La formación se realizó en cuatro unidades de medida diferentes: color (rojo), fuerza (sólido), rugosidad (con granos), decoración (con lazo). Sólo un conjunto de unidades de medida nos permite describir adecuadamente objetos reales en el lenguaje de las matemáticas.. Esto es lo que parece.
La letra "a" con diferentes índices denota diferentes unidades de medida. Entre paréntesis se destacan las unidades de medida por las que se distingue el "todo" en la etapa preliminar. Entre paréntesis se saca la unidad de medida por la que se forma el conjunto. La última línea muestra el resultado final: un elemento del conjunto. Como puedes ver, si usamos unidades de medida para formar un conjunto, entonces el resultado no depende del orden de nuestras acciones. Y esto son matemáticas, y no danzas de chamanes con panderetas. Los chamanes pueden llegar “intuitivamente” al mismo resultado, argumentando que es “obvio”, porque las unidades de medida no forman parte de su arsenal “científico”.
Usando unidades de medida, es muy fácil dividir un conjunto o combinar varios conjuntos en un superconjunto. Echemos un vistazo más de cerca al álgebra de este proceso.
- En contacto con 0
- Google+ 0
- DE ACUERDO 0
- Facebook 0