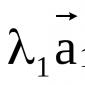Clasificación de sistemas heterogéneos. §6

La resolución de sistemas de ecuaciones algebraicas lineales (SLAE) es sin duda el tema más importante en un curso de álgebra lineal. Una gran cantidad de problemas de todas las ramas de las matemáticas se reducen a la resolución de sistemas. ecuaciones lineales. Estos factores explican el motivo de este artículo. El material del artículo está seleccionado y estructurado para que con su ayuda puedas

• elija el método óptimo para resolver su sistema de ecuaciones algebraicas lineales,
• estudiar la teoría del método elegido,
• resuelva su sistema de ecuaciones lineales considerando soluciones detalladas a ejemplos y problemas típicos.

Breve descripción del material del artículo.

Primero, damos todas las definiciones y conceptos necesarios e introducimos notaciones.

A continuación, consideraremos métodos para resolver sistemas de ecuaciones algebraicas lineales en los que el número de ecuaciones es igual al número de variables desconocidas y que tienen una solución única. En primer lugar, nos centraremos en el método de Cramer, en segundo lugar, mostraremos el método matricial para resolver dichos sistemas de ecuaciones y, en tercer lugar, analizaremos el método de Gauss (el método de eliminación secuencial de variables desconocidas). Para consolidar la teoría, definitivamente resolveremos varios SLAE de diferentes formas.

Posteriormente pasaremos a la resolución de sistemas de ecuaciones algebraicas lineales de forma general, en los que el número de ecuaciones no coincide con el número de variables desconocidas o la matriz principal del sistema es singular. Formulemos el teorema de Kronecker-Capelli, que nos permite establecer la compatibilidad de los SLAE. Analicemos la solución de sistemas (si son compatibles) utilizando el concepto de base menor de una matriz. También consideraremos el método de Gauss y describiremos en detalle las soluciones de los ejemplos.

Definitivamente nos detendremos en la estructura de la solución general de sistemas homogéneos y no homogéneos de ecuaciones algebraicas lineales. Demos el concepto de sistema fundamental de soluciones y mostremos cómo se escribe la solución general de un SLAE utilizando los vectores del sistema fundamental de soluciones. Para una mejor comprensión, veamos algunos ejemplos.

En conclusión, consideraremos sistemas de ecuaciones que pueden reducirse a lineales, así como varios problemas en cuya solución surgen SLAE.

Navegación de páginas.

Definiciones, conceptos, designaciones.

Consideraremos sistemas de p ecuaciones algebraicas lineales con n variables desconocidas (p puede ser igual a n) de la forma

Variables desconocidas, - coeficientes (algunos números reales o complejos), - términos libres (también números reales o complejos).

Esta forma de grabación SLAE se llama coordinar.

EN forma matricial escribir este sistema de ecuaciones tiene la forma,
Dónde - la matriz principal del sistema, - una matriz de columnas de variables desconocidas, - una matriz de columnas de términos libres.

Si agregamos una columna de matriz de términos libres a la matriz A como la (n+1)ésima columna, obtenemos la llamada matriz extendida sistemas de ecuaciones lineales. Normalmente, una matriz extendida se denota con la letra T y la columna de términos libres está separada por una línea vertical de las columnas restantes, es decir,

Resolver un sistema de ecuaciones algebraicas lineales. Se llama conjunto de valores de variables desconocidas que convierte todas las ecuaciones del sistema en identidades. La ecuación matricial para valores dados de las variables desconocidas también se convierte en una identidad.

Si un sistema de ecuaciones tiene al menos una solución, entonces se llama articulación.

Si un sistema de ecuaciones no tiene soluciones, entonces se llama no conjunto.

Si un SLAE tiene una solución única, entonces se llama cierto; Si hay más de una solución, entonces... incierto.

Si los términos libres de todas las ecuaciones del sistema son iguales a cero , entonces el sistema se llama homogéneo, de lo contrario - heterogéneo.

Resolución de sistemas elementales de ecuaciones algebraicas lineales.

Si el número de ecuaciones de un sistema es igual al número de variables desconocidas y el determinante de su matriz principal no es igual a cero, entonces dichos SLAE se denominarán elemental. Tales sistemas de ecuaciones tienen una solución única, y en el caso sistema homogéneo todas las variables desconocidas son cero.

Comenzamos a estudiar tales SLAE en escuela secundaria. Al resolverlas, tomamos una ecuación, expresamos una variable desconocida en términos de otras y la sustituimos en las ecuaciones restantes, luego tomamos la siguiente ecuación, expresamos la siguiente variable desconocida y la sustituimos en otras ecuaciones, y así sucesivamente. O utilizaron el método de la suma, es decir, sumaron dos o más ecuaciones para eliminar algunas variables desconocidas. No nos detendremos en estos métodos en detalle, ya que son esencialmente modificaciones del método de Gauss.

Los principales métodos para resolver sistemas elementales de ecuaciones lineales son el método de Cramer, el método matricial y el método de Gauss. Vamos a solucionarlos.

Resolución de sistemas de ecuaciones lineales mediante el método de Cramer.

Supongamos que necesitamos resolver un sistema de ecuaciones algebraicas lineales.

en el que el número de ecuaciones es igual al número de variables desconocidas y el determinante de la matriz principal del sistema es distinto de cero, es decir, .

Sea el determinante de la matriz principal del sistema, y - determinantes de matrices que se obtienen de A por sustitución 1º, 2º,…, enésimo columna respectivamente a la columna de miembros gratuitos:

Con esta notación, las variables desconocidas se calculan utilizando las fórmulas del método de Cramer como . Así se encuentra la solución de un sistema de ecuaciones algebraicas lineales mediante el método de Cramer.

Ejemplo.

método de cramer .

Solución.

La matriz principal del sistema tiene la forma . Calculemos su determinante (si es necesario, consulte el artículo):

Dado que el determinante de la matriz principal del sistema es distinto de cero, el sistema tiene una solución única que se puede encontrar mediante el método de Cramer.

Compongamos y calculemos los determinantes necesarios. (obtenemos el determinante reemplazando la primera columna de la matriz A con una columna de términos libres, el determinante reemplazando la segunda columna con una columna de términos libres y reemplazando la tercera columna de la matriz A con una columna de términos libres) :

Encontrar variables desconocidas usando fórmulas :

Respuesta:

La principal desventaja del método de Cramer (si se le puede llamar desventaja) es la complejidad de calcular los determinantes cuando el número de ecuaciones en el sistema es más de tres.

Resolución de sistemas de ecuaciones algebraicas lineales mediante el método matricial (utilizando una matriz inversa).

Sea un sistema de ecuaciones algebraicas lineales en forma matricial, donde la matriz A tiene dimensión n por n y su determinante es distinto de cero.

Dado que , entonces la matriz A es invertible, es decir, existe matriz inversa. Si multiplicamos ambos lados de la igualdad por la izquierda, obtenemos una fórmula para encontrar una matriz-columna de variables desconocidas. Así obtuvimos una solución a un sistema de ecuaciones algebraicas lineales mediante el método matricial.

Ejemplo.

Resolver sistema de ecuaciones lineales. método matricial.

Solución.

Reescribamos el sistema de ecuaciones en forma matricial:

Porque

entonces el SLAE se puede resolver utilizando el método matricial. Usando la matriz inversa, la solución de este sistema se puede encontrar como .

Construyamos una matriz inversa usando una matriz a partir de sumas algebraicas de elementos de la matriz A (si es necesario, consulte el artículo):

Queda por calcular la matriz de variables desconocidas multiplicando la matriz inversa. a una columna de matriz de miembros gratuitos (si es necesario, consulte el artículo):

Respuesta:

o en otra notación x 1 = 4, x 2 = 0, x 3 = -1.

El principal problema a la hora de encontrar soluciones a sistemas de ecuaciones algebraicas lineales utilizando el método matricial es la complejidad de encontrar la matriz inversa, especialmente para matrices cuadradas de orden superior a tercero.

Resolución de sistemas de ecuaciones lineales mediante el método de Gauss.

Supongamos que necesitamos encontrar una solución a un sistema de n ecuaciones lineales con n variables desconocidas.
cuyo determinante de la matriz principal es distinto de cero.

La esencia del método Gauss. Consiste en eliminar secuencialmente las variables desconocidas: primero se excluye x 1 de todas las ecuaciones del sistema, a partir de la segunda, luego se excluye x 2 de todas las ecuaciones, a partir de la tercera, y así sucesivamente, hasta que solo quede la variable desconocida x n en la última ecuación. Este proceso de transformar ecuaciones del sistema para eliminar secuencialmente variables desconocidas se llama método gaussiano directo. Después de completar el avance del método gaussiano, se encuentra x n a partir de la última ecuación, usando este valor de la penúltima ecuación, se calcula x n-1, y así sucesivamente, se encuentra x 1 a partir de la primera ecuación. El proceso de calcular variables desconocidas al pasar de la última ecuación del sistema a la primera se llama inverso del método gaussiano.

Describamos brevemente el algoritmo para eliminar variables desconocidas.

Supondremos que , ya que siempre podemos lograrlo reordenando las ecuaciones del sistema. Eliminemos la variable desconocida x 1 de todas las ecuaciones del sistema, comenzando por la segunda. Para ello, a la segunda ecuación del sistema le sumamos la primera, multiplicada por , a la tercera ecuación le sumamos la primera, multiplicada por , y así sucesivamente, a la enésima ecuación le sumamos la primera, multiplicada por . El sistema de ecuaciones después de tales transformaciones tomará la forma

dónde y .

Habríamos llegado al mismo resultado si hubiéramos expresado x 1 en términos de otras variables desconocidas en la primera ecuación del sistema y hubiéramos sustituido la expresión resultante en todas las demás ecuaciones. Por tanto, la variable x 1 queda excluida de todas las ecuaciones, a partir de la segunda.

A continuación se procede de forma similar, pero sólo con parte del sistema resultante, que está marcado en la figura.

Para ello, a la tercera ecuación del sistema le sumamos la segunda, multiplicada por , a la cuarta ecuación le sumamos la segunda, multiplicada por , y así sucesivamente, a la enésima ecuación le sumamos la segunda, multiplicada por . El sistema de ecuaciones después de tales transformaciones tomará la forma

dónde y . Por tanto, la variable x 2 queda excluida de todas las ecuaciones, comenzando por la tercera.

A continuación procedemos a eliminar la incógnita x 3, mientras actuamos de manera similar con la parte del sistema marcada en la figura.

Entonces continuamos la progresión directa del método gaussiano hasta que el sistema toma la forma

A partir de este momento comenzamos lo contrario del método gaussiano: calculamos x n de la última ecuación como , usando el valor obtenido de x n encontramos x n-1 de la penúltima ecuación, y así sucesivamente, encontramos x 1 de la primera ecuación. .

Ejemplo.

Resolver sistema de ecuaciones lineales. Método de Gauss.

Solución.

Excluyamos la variable desconocida x 1 de la segunda y tercera ecuaciones del sistema. Para ello, a ambos lados de la segunda y tercera ecuaciones sumamos las partes correspondientes de la primera ecuación, multiplicadas por y por, respectivamente:

Ahora eliminamos x 2 de la tercera ecuación sumando a su izquierda y lado derecho los lados izquierdo y derecho de la segunda ecuación, multiplicados por:

Esto completa el movimiento hacia adelante del método de Gauss; comenzamos el movimiento hacia atrás.

De la última ecuación del sistema de ecuaciones resultante encontramos x 3:

De la segunda ecuación obtenemos .

De la primera ecuación encontramos la variable desconocida restante y así completamos el método inverso de Gauss.

Respuesta:

X1 = 4, X2 = 0, X3 = -1.

Resolución de sistemas de ecuaciones algebraicas lineales de forma general.

En general, el número de ecuaciones del sistema p no coincide con el número de variables desconocidas n:

Estos SLAE pueden no tener soluciones, tener una única solución o tener infinitas soluciones. Esta afirmación también se aplica a los sistemas de ecuaciones cuya matriz principal es cuadrada y singular.

Teorema de Kronecker-Capelli.

Antes de encontrar una solución a un sistema de ecuaciones lineales, es necesario establecer su compatibilidad. La respuesta a la pregunta de cuándo SLAE es compatible y cuándo es inconsistente viene dada por Teorema de Kronecker-Capelli:
Para que un sistema de p ecuaciones con n incógnitas (p puede ser igual a n) sea consistente, es necesario y suficiente que el rango de la matriz principal del sistema sea igual al rango de la matriz extendida, es decir , Rango(A)=Rango(T).

Consideremos, como ejemplo, la aplicación del teorema de Kronecker-Capelli para determinar la compatibilidad de un sistema de ecuaciones lineales.

Ejemplo.

Descubra si el sistema de ecuaciones lineales tiene soluciones.

Solución.

. Utilicemos el método de bordear a menores. Menor de segundo orden diferente de cero. Veamos los menores de tercer orden que lo bordean:

Dado que todos los menores limítrofes de tercer orden son iguales a cero, el rango de la matriz principal es igual a dos.

A su vez, el rango de la matriz extendida es igual a tres, ya que el menor es de tercer orden

diferente de cero.

De este modo, Rang(A), por tanto, utilizando el teorema de Kronecker-Capelli, podemos concluir que el sistema original de ecuaciones lineales es inconsistente.

Respuesta:

El sistema no tiene soluciones.

Entonces, hemos aprendido a establecer la inconsistencia de un sistema usando el teorema de Kronecker-Capelli.

Pero ¿cómo encontrar solución a un SLAE si se establece su compatibilidad?

Para hacer esto, necesitamos el concepto de base menor de una matriz y un teorema sobre el rango de una matriz.

Menor orden más alto La matriz A, distinta de cero, se llama básico.

De la definición de base menor se deduce que su orden es igual al rango de la matriz. Para una matriz A distinta de cero puede haber varias bases menores; siempre hay una base menor.

Por ejemplo, considere la matriz .

Todos los menores de tercer orden de esta matriz son iguales a cero, ya que los elementos de la tercera fila de esta matriz son la suma de los elementos correspondientes de la primera y segunda fila.

Los siguientes menores de segundo orden son básicos, ya que son distintos de cero

Menores no son básicos, ya que son iguales a cero.

Teorema de rango matricial.

Si el rango de una matriz de orden p por n es igual a r, entonces todos los elementos de fila (y columna) de la matriz que no forman la base menor elegida se expresan linealmente en términos de los elementos de fila (y columna) correspondientes que forman la base menor.

¿Qué nos dice el teorema del rango matricial?

Si, de acuerdo con el teorema de Kronecker-Capelli, hemos establecido la compatibilidad del sistema, entonces elegimos cualquier base menor de la matriz principal del sistema (su orden es igual a r) y excluimos del sistema todas las ecuaciones que lo hacen. no forma la base menor seleccionada. El SLAE obtenido de esta forma será equivalente al original, ya que las ecuaciones descartadas aún son redundantes (según el teorema de rango matricial, son una combinación lineal de las ecuaciones restantes).

Como resultado, después de descartar ecuaciones innecesarias del sistema, son posibles dos casos.

Si el número de ecuaciones r en el sistema resultante es igual al número de variables desconocidas, entonces será definido y la única solución se podrá encontrar mediante el método de Cramer, el método matricial o el método de Gauss.

Ejemplo.

.

Solución.

Rango de la matriz principal del sistema. es igual a dos, ya que el menor es de segundo orden diferente de cero. Rango de matriz extendido también es igual a dos, ya que el único menor de tercer orden es cero

y el menor de segundo orden considerado anteriormente es diferente de cero. Con base en el teorema de Kronecker-Capelli, podemos afirmar la compatibilidad del sistema original de ecuaciones lineales, ya que Rango(A)=Rango(T)=2.

Como base menor tomamos . Está formado por los coeficientes de la primera y segunda ecuaciones:


La tercera ecuación del sistema no participa en la formación de la base menor, por lo que la excluimos del sistema basándonos en el teorema del rango de la matriz:


Así obtuvimos un sistema elemental de ecuaciones algebraicas lineales. Resolvámoslo usando el método de Cramer:


Respuesta:

x1 = 1, x2 = 2.

Si el número de ecuaciones r en el SLAE resultante es menor que el número de variables desconocidas n, entonces en los lados izquierdos de las ecuaciones dejamos los términos que forman la base menor y transferimos los términos restantes a los lados derechos de la ecuaciones del sistema con signo opuesto.

Las variables desconocidas (r de ellas) que quedan en el lado izquierdo de las ecuaciones se llaman principal.

Las variables desconocidas (hay n - r piezas) que están en el lado derecho se llaman gratis.

Ahora creemos que las variables desconocidas libres pueden tomar valores arbitrarios, mientras que las r variables desconocidas principales se expresarán mediante variables desconocidas libres de una manera única. Su expresión se puede encontrar resolviendo el SLAE resultante utilizando el método de Cramer, el método matricial o el método de Gauss.

Veámoslo con un ejemplo.

Ejemplo.

Resolver un sistema de ecuaciones algebraicas lineales. .

Solución.

Encontremos el rango de la matriz principal del sistema. por el método de frontera con menores. Tomemos un 1 1 = 1 como menor distinto de cero de primer orden. Comencemos a buscar un menor distinto de cero de segundo orden que bordee este menor:


Así es como encontramos un menor distinto de cero de segundo orden. Comencemos a buscar un menor de tercer orden distinto de cero:


Por tanto, el rango de la matriz principal es tres. El rango de la matriz extendida también es igual a tres, es decir, el sistema es consistente.

Tomamos como base el menor de tercer orden distinto de cero encontrado.

Para mayor claridad, mostramos los elementos que forman la base menor:


Dejamos los términos involucrados en la base menor en el lado izquierdo de las ecuaciones del sistema y transferimos el resto con signos opuestos a los lados derechos:


Demos a las variables desconocidas libres x 2 y x 5 valores arbitrarios, es decir, aceptamos , donde están los números arbitrarios. En este caso, la SLAE tomará la forma


Resolvamos el sistema elemental resultante de ecuaciones algebraicas lineales utilizando el método de Cramer:


Por eso, .

En tu respuesta, no olvides indicar variables desconocidas libres.

Respuesta:

¿Dónde están los números arbitrarios?

Resumir.

Para resolver un sistema de ecuaciones algebraicas lineales generales, primero determinamos su compatibilidad utilizando el teorema de Kronecker-Capelli. Si el rango de la matriz principal no es igual al rango de la matriz extendida, concluimos que el sistema es incompatible.

Si el rango de la matriz principal es igual al rango de la matriz extendida, entonces seleccionamos una base menor y descartamos las ecuaciones del sistema que no participan en la formación de la base menor seleccionada.

Si el orden de la base menor es igual al número de variables desconocidas, entonces el SLAE tiene una solución única, que se puede encontrar mediante cualquier método que conozcamos.

Si el orden de la base menor es menor que el número de variables desconocidas, entonces en el lado izquierdo de las ecuaciones del sistema dejamos los términos con las principales variables desconocidas, transferimos los términos restantes a los lados derechos y damos valores arbitrarios a las variables desconocidas libres. Del sistema resultante de ecuaciones lineales encontramos las principales incógnitas. variables por método Cramer, método matricial o método gaussiano.

Método de Gauss para la resolución de sistemas de ecuaciones algebraicas lineales de forma general.

El método de Gauss se puede utilizar para resolver sistemas de ecuaciones algebraicas lineales de cualquier tipo sin probar primero su coherencia. El proceso de eliminación secuencial de variables desconocidas permite sacar una conclusión tanto sobre la compatibilidad como sobre la incompatibilidad del SLAE, y si existe una solución, permite encontrarla.

Desde un punto de vista computacional, es preferible el método gaussiano.

Míralo Descripción detallada y analizó ejemplos en el artículo del método de Gauss para la resolución de sistemas de ecuaciones algebraicas lineales de forma general.

Escribir una solución general a sistemas algebraicos lineales homogéneos y no homogéneos utilizando vectores del sistema fundamental de soluciones.

En esta sección hablaremos de sistemas simultáneos homogéneos y no homogéneos de ecuaciones algebraicas lineales que tienen un número infinito de soluciones.

Tratemos primero con sistemas homogéneos.

Sistema fundamental de soluciones. Un sistema homogéneo de p ecuaciones algebraicas lineales con n variables desconocidas es una colección de (n – r) soluciones linealmente independientes de este sistema, donde r es el orden de la base menor de la matriz principal del sistema.

Si denotamos soluciones linealmente independientes de un SLAE homogéneo como X (1) , X (2) , …, X (n-r) (X (1) , X (2) , …, X (n-r) son matrices columnares de dimensión n por 1), entonces la solución general de este sistema homogéneo se representa como una combinación lineal de vectores del sistema fundamental de soluciones con arbitrario coeficientes constantes C 1, C 2, ..., C (n-r), es decir, .

¿Qué significa el término solución general de un sistema homogéneo de ecuaciones algebraicas lineales (oroslau)?

El significado es simple: la fórmula lo establece todo. soluciones posibles el SLAE original, es decir, tomando cualquier conjunto de valores de constantes arbitrarias C 1, C 2, ..., C (n-r), según la fórmula obtendremos una de las soluciones del SLAE homogéneo original.

Por lo tanto, si encontramos un sistema fundamental de soluciones, entonces podemos definir todas las soluciones de este SLAE homogéneo como.

Mostremos el proceso de construcción de un sistema fundamental de soluciones para un SLAE homogéneo.

Seleccionamos la base menor del sistema original de ecuaciones lineales, excluimos todas las demás ecuaciones del sistema y transferimos todos los términos que contienen variables desconocidas libres a los lados derechos de las ecuaciones del sistema con signos opuestos. Démosle a las variables desconocidas libres los valores 1,0,0,...,0 y calculemos las principales incógnitas resolviendo el sistema elemental de ecuaciones lineales resultante de cualquier forma, por ejemplo, usando el método de Cramer. Esto dará como resultado X (1), la primera solución del sistema fundamental. Si a las incógnitas libres les damos los valores 0,1,0,0,…,0 y calculamos las incógnitas principales, obtenemos X (2). Etcétera. Si asignamos los valores 0.0,…,0.1 a las variables desconocidas libres y calculamos las incógnitas principales obtenemos X(n-r). De esta forma se construirá un sistema fundamental de soluciones para un SLAE homogéneo y su solución general podrá escribirse en la forma .

Para sistemas no homogéneos de ecuaciones algebraicas lineales, la solución general se representa en la forma , donde es la solución general del sistema homogéneo correspondiente, y es la solución particular del SLAE no homogéneo original, que obtenemos dando los valores a las incógnitas libres. ​0,0,...,0 y calculando los valores de las principales incógnitas.

Veamos ejemplos.

Ejemplo.

Encuentre el sistema fundamental de soluciones y la solución general de un sistema homogéneo de ecuaciones algebraicas lineales. .

Solución.

El rango de la matriz principal de sistemas homogéneos de ecuaciones lineales es siempre igual al rango de la matriz extendida. Encontremos el rango de la matriz principal utilizando el método de menores limítrofes. Como menor distinto de cero de primer orden, tomamos el elemento a 1 1 = 9 de la matriz principal del sistema. Encontremos el menor limítrofe distinto de cero de segundo orden:

Se ha encontrado un menor de segundo orden, distinto de cero. Repasemos los menores de tercer orden que lo bordean en busca de uno distinto de cero:

Todos los menores limítrofes de tercer orden son iguales a cero, por lo tanto, el rango de la matriz principal y extendida es igual a dos. Echemos . Para mayor claridad, observemos los elementos del sistema que lo forman:

La tercera ecuación de la SLAE original no participa en la formación de la base menor, por tanto, se puede excluir:

Dejamos los términos que contienen las principales incógnitas en los lados derechos de las ecuaciones y transferimos los términos con incógnitas libres a los lados derechos:

Construyamos un sistema fundamental de soluciones al sistema homogéneo original de ecuaciones lineales. El sistema fundamental de soluciones de este SLAE consta de dos soluciones, ya que el SLAE original contiene cuatro variables desconocidas y el orden de su base menor es igual a dos. Para encontrar X (1), le damos a las variables desconocidas libres los valores x 2 = 1, x 4 = 0, luego encontramos las principales incógnitas del sistema de ecuaciones.
.

El término "sistema" se utiliza en diversas ciencias. Respectivamente, Diferentes situaciones Se utilizan varias definiciones del sistema: desde filosóficas hasta formales. Para los propósitos del curso, la siguiente definición es la más adecuada: un sistema es un conjunto de elementos unidos por conexiones y que funcionan juntos para lograr un objetivo.

Los sistemas se caracterizan por una serie de propiedades, las principales de las cuales se dividen en tres grupos: estáticas, dinámicas y sintéticas.

1.1 Propiedades estáticas de los sistemas.

Estático Las propiedades son las características de un determinado estado del sistema. Esto es lo que tiene el sistema en un momento dado.

Integridad. Todo sistema aparece como algo unificado, completo, separado, diferente de todo lo demás. Esta propiedad se llama integridad del sistema. Te permite dividir el mundo entero en dos partes: el sistema y el medio ambiente.

Franqueza. El sistema aislado, a diferencia de todo lo demás, no está aislado del medio ambiente. Por el contrario, están conectados e intercambian diversos tipos de recursos (materia, energía, información, etc.). Esta característica se designa con el término "apertura".

Las conexiones entre el sistema y el medio ambiente son direccionales: de alguna manera, el medio ambiente influye en el sistema (entradas del sistema), en otras, el sistema influye en el medio ambiente, hace algo en el medio ambiente y genera algo en el medio ambiente (salidas del sistema). . La descripción de las entradas y salidas de un sistema se denomina modelo de caja negra. Este modelo carece de información sobre características internas sistemas. A pesar de su aparente simplicidad, un modelo de este tipo suele ser suficiente para trabajar con el sistema.

En muchos casos, al gestionar equipos o personas, la información únicamente sobre las entradas y salidas del sistema permite alcanzar con éxito el objetivo. Sin embargo, para ello el modelo debe cumplir ciertos requisitos. Por ejemplo, el usuario puede tener dificultades si no sabe que en algunos modelos de televisor es necesario sacar el botón de encendido en lugar de presionarlo. Por tanto, para una gestión exitosa, el modelo debe contener toda la información necesaria para lograr el objetivo. Al intentar satisfacer este requisito pueden ocurrir cuatro tipos de errores, los cuales se derivan de que el modelo siempre contiene un número finito de conexiones, mientras que en un sistema real el número de conexiones es ilimitado.

Un error del primer tipo ocurre cuando un sujeto considera erróneamente una relación como significativa y decide incluirla en el modelo. Esto conduce a la aparición de elementos adicionales e innecesarios en el modelo. Un error del segundo tipo, por el contrario, se comete cuando se decide excluir del modelo una conexión supuestamente insignificante, sin la cual, de hecho, lograr el objetivo es difícil o incluso imposible.

La respuesta a la pregunta de qué error es peor depende del contexto en el que se plantea. Está claro que el uso de un modelo que contiene un error conduce inevitablemente a pérdidas. Las pérdidas pueden ser pequeñas, aceptables, intolerables o inaceptables. El daño que produce un error tipo 1 se debe a que la información que contiene es superflua. Cuando trabaje con un modelo de este tipo, tendrá que gastar recursos en registrar y procesar información innecesaria, por ejemplo, desperdiciar memoria de la computadora y tiempo de procesamiento en ella. Es posible que esto no afecte la calidad de la solución, pero ciertamente afectará el costo y la puntualidad. Las pérdidas por un error del segundo tipo son daños por el hecho de que no hay suficiente información para lograr el objetivo por completo; el objetivo no se puede lograr por completo.

Ahora está claro que el peor error es aquel en el que las pérdidas son mayores, y esto depende de circunstancias concretas. Por ejemplo, si el tiempo es un factor crítico, entonces un error del primer tipo se vuelve mucho más peligroso que un error del segundo tipo: una decisión tomada a tiempo, aunque no sea la mejor, es preferible a una óptima, pero tardía. .

Se considera que un error del tercer tipo es consecuencia de la ignorancia. Para evaluar la importancia de una determinada conexión, es necesario saber si existe. Si no se sabe esto, entonces la cuestión de incluir la conexión en el modelo no merece la pena. Si tal conexión es insignificante, entonces en la práctica su presencia en la realidad y su ausencia en el modelo pasarán desapercibidas. Si la conexión es significativa, surgirán dificultades similares a las del error tipo II. La diferencia es que un error tipo 3 es más difícil de corregir: para ello es necesario adquirir nuevos conocimientos.

Un error del cuarto tipo ocurre cuando una conexión esencial conocida se atribuye erróneamente al número de entradas o salidas del sistema. Por ejemplo, está bien establecido que en la Inglaterra del siglo XIX la salud de los hombres que llevaban sombrero de copa era significativamente superior a la de los hombres que llevaban gorra. De esto no se desprende que el tipo de tocado pueda considerarse como un insumo para un sistema de predicción del estado de salud.

Heterogeneidad interna de sistemas, distinción de partes. Si miras dentro de la “caja negra”, resulta que el sistema es heterogéneo, no monolítico. Se puede encontrar que diferentes cualidades difieren en diferentes partes del sistema. La descripción de la heterogeneidad interna del sistema se reduce a aislar áreas relativamente homogéneas y trazar límites entre ellas. Así aparece el concepto de partes del sistema. Tras un examen más detenido, resulta que las piezas grandes identificadas también son heterogéneas, lo que requiere identificar piezas aún más pequeñas. El resultado es una descripción jerárquica de las partes del sistema, lo que se denomina modelo de composición.

La información sobre la composición del sistema se puede utilizar para trabajar con el sistema. Los objetivos de interacción con el sistema pueden ser diferentes y, por tanto, los modelos de composición de un mismo sistema también pueden diferir. A primera vista, no es difícil distinguir las partes del sistema; “llaman la atención”. En algunos sistemas, las partes surgen arbitrariamente, en el proceso de crecimiento y desarrollo natural (organismos, sociedades, etc.). Los sistemas artificiales se ensamblan deliberadamente a partir de piezas previamente conocidas (mecanismos, edificios, etc.). También existen tipos mixtos de sistemas, como reservas naturales y sistemas agrícolas. Por otro lado, desde el punto de vista del rector, estudiante, contador y directivo de empresas, la universidad consta de distintas partes. Un avión consta de diferentes partes desde el punto de vista del piloto, la azafata y el pasajero. Las dificultades de crear un modelo de composición se pueden representar de tres maneras.

En primer lugar, el todo se puede dividir en partes de diferentes maneras. En este caso, el método de división está determinado por el objetivo. Por ejemplo, la composición de un automóvil se presenta de manera diferente a los automovilistas novatos, a los futuros conductores profesionales, a los mecánicos que se preparan para trabajar en un centro de servicio de automóviles y a los vendedores en los concesionarios de automóviles. ¿Es natural preguntarse si algunas partes del sistema existen “realmente”? La respuesta está contenida en la formulación de la propiedad en cuestión: estamos hablando de distinguibilidad y no de separabilidad de partes. Puedes distinguir entre las partes del sistema necesarias para lograr el objetivo, pero no puedes separarlas.

En segundo lugar, el número de partes del modelo de composición también depende del nivel en el que se detiene la fragmentación del sistema. Las partes de las ramas terminales del árbol jerárquico resultante se denominan elementos. En diferentes circunstancias, la descomposición finaliza en diferentes niveles. Por ejemplo, al describir el próximo trabajo, es necesario dar a un trabajador experimentado y a un novato instrucciones con distintos grados de detalle. Así, el modelo de composición depende de lo que se considera elemental. Hay casos en que un elemento tiene un carácter natural y absoluto (célula, individuo, fonema, electrón).

En tercer lugar, cualquier sistema es parte sistema más grande y, a veces, varios sistemas a la vez. Un metasistema de este tipo también puede dividirse en subsistemas de diferentes maneras. Esto significa que el límite externo del sistema es relativo, condicional. Los límites del sistema se determinan teniendo en cuenta los objetivos del sujeto que utilizará el modelo del sistema.

Estructura. La propiedad de la estructuración es que las partes del sistema no están aisladas ni son independientes entre sí; están interconectados e interactúan entre sí. Además, las propiedades del sistema dependen significativamente de cómo interactúan exactamente sus partes. Por eso es tan importante la información sobre las conexiones de los elementos del sistema. La lista de conexiones esenciales entre los elementos del sistema se denomina modelo de estructura del sistema. La dotación de cualquier sistema de una determinada estructura se denomina estructuración.

El concepto de estructuración profundiza aún más la idea de la integridad del sistema: las conexiones, por así decirlo, mantienen unidas las partes y las mantienen unidas como un todo. La integridad, señalada anteriormente como una propiedad externa, recibe una explicación de apoyo desde dentro del sistema: a través de la estructura.

Al construir un modelo, también ocurren estructuras. ciertas dificultades. El primero de ellos se debe a que el modelo de estructura se determina después de seleccionar el modelo de composición, y depende de cuál sea exactamente la composición del sistema. Pero incluso con una composición fija, el modelo de estructura es variable. Esto se debe a la posibilidad de definir el significado de las conexiones de diferentes maneras. Por ejemplo, un gerente moderno recomienda, junto con la estructura formal de su organización, tener en cuenta la existencia de relaciones informales entre los empleados, que también afectan el funcionamiento de la organización. La segunda dificultad surge del hecho de que cada elemento del sistema, a su vez, es una “pequeña caja negra”. Por tanto, los cuatro tipos de errores son posibles al definir las entradas y salidas de cada elemento incluido en el modelo de estructura.

1.2 PROPIEDADES DINÁMICAS DE LOS SISTEMAS

Si consideramos el estado del sistema en un nuevo momento, podemos detectar nuevamente las cuatro propiedades estáticas. Pero si superpones “fotografías” del sistema en diferentes momentos del tiempo, verás que difieren en detalles: durante el tiempo entre los dos momentos de observación, se produjeron algunos cambios en el sistema y su entorno. Dichos cambios pueden ser importantes al trabajar con el sistema y, por lo tanto, deben reflejarse en las descripciones del sistema y tenerse en cuenta al trabajar con él. Las características de los cambios a lo largo del tiempo dentro y fuera del sistema se denominan propiedades dinámicas del sistema. Generalmente hay cuatro diferentes. propiedades dinámicas sistemas.

Funcionalidad. Procesos Y(t) que ocurren en las salidas del sistema se consideran sus funciones. Las funciones de un sistema son su comportamiento en el entorno externo, los resultados de sus actividades y los productos producidos por el sistema.

De la multiplicidad de resultados se deriva una multiplicidad de funciones, cada una de las cuales puede ser utilizada por alguien y para algo. Por tanto, un mismo sistema puede servir para diferentes propósitos. Un sujeto que utiliza un sistema para sus propios fines evaluará naturalmente sus funciones y las organizará en relación con sus necesidades. Así aparecen los conceptos de función principal, secundaria, neutra, indeseable, superflua, etc.

Estimulación. Ciertos procesos también ocurren en las entradas del sistema. X(t), afectando al sistema y convirtiéndose después de una serie de transformaciones en el sistema en Y(t). Impactos X(t) se llaman estímulos, y la susceptibilidad misma de cualquier sistema a influencias externas y el cambio en su comportamiento bajo estas influencias se llama estimulabilidad.

Variabilidad del sistema en el tiempo. En cualquier sistema se producen cambios que hay que tener en cuenta. En términos del modelo del sistema, podemos decir que los valores de las variables internas (parámetros) pueden cambiar z(t), composición y estructura del sistema y cualquier combinación de los mismos. La naturaleza de estos cambios también puede ser diferente. Por lo tanto, se pueden considerar otras clasificaciones de cambios.

La clasificación más obvia es por la velocidad del cambio (lento, rápido). La velocidad del cambio se mide en relación con cualquier velocidad tomada como estándar. Es posible introducir una gran cantidad de gradaciones de velocidad. También es posible clasificar tendencias. en cambios en el sistema en cuanto a su estructura y composición.

Podemos hablar de cambios que no afectan a la estructura del sistema: unos elementos se sustituyen por otros equivalentes; opciones z(t) puede cambiar sin cambiar la estructura. Este tipo de dinámica del sistema se llama funcionamiento. Los cambios pueden ser de naturaleza cuantitativa: la composición del sistema aumenta, y aunque su estructura cambia automáticamente, esto no afecta las propiedades del sistema hasta cierto punto (por ejemplo, la expansión de un vertedero). Estos cambios se denominan crecimiento del sistema. Con cambios cualitativos en el sistema, sus propiedades esenciales cambian. Si esos cambios van en una dirección positiva, se les llama desarrollo. Con los mismos recursos, un sistema desarrollado logra mejores resultados y pueden aparecer nuevas cualidades (funciones) positivas. Esto se debe a un aumento en el nivel de coherencia y organización del sistema.

El crecimiento se produce principalmente debido al consumo de recursos materiales, el desarrollo, debido a la asimilación y uso de información. El crecimiento y el desarrollo pueden ocurrir simultáneamente, pero no necesariamente están relacionados. El crecimiento es siempre limitado (debido a los recursos materiales limitados) y el desarrollo desde el exterior no es limitado, ya que la información sobre el entorno externo es inagotable. El desarrollo es el resultado de la formación, pero la formación no puede realizarse en lugar del alumno. Por tanto, existe una limitación interna al desarrollo. Si el sistema “no quiere” aprender, no puede desarrollarse y no lo hará.

Además de los procesos de crecimiento y desarrollo, en el sistema también pueden ocurrir procesos inversos. Los cambios opuestos al crecimiento se llaman declive, contracción, disminución. Un cambio opuesto al desarrollo se llama degradación, pérdida o debilitamiento de propiedades beneficiosas.

Los cambios considerados son monótonos, es decir, se dirigen “en una dirección”. Evidentemente, los cambios monótonos no pueden durar para siempre. En la historia de cualquier sistema, se pueden distinguir períodos de declive y ascenso, estabilidad e inestabilidad, cuya secuencia forma un individuo. ciclo vital sistemas.

Se pueden utilizar otras clasificaciones de procesos que ocurren en el sistema: según la previsibilidad, los procesos se dividen en aleatorios y deterministas; Según el tipo de dependencia del tiempo, los procesos se dividen en monótonos, periódicos, armónicos, pulsados, etc.

Existencia en un entorno cambiante. No sólo este sistema está cambiando, sino también todos los demás. Para el sistema considerado, esto parece un cambio continuo en el entorno. Esta circunstancia tiene muchas consecuencias para el propio sistema, que debe adaptarse a las nuevas condiciones para no perecer. Al considerar un sistema específico, generalmente se presta atención a las características de una reacción particular del sistema, por ejemplo, la velocidad de reacción. Si consideramos los sistemas que almacenan información (libros, medios magnéticos), entonces la velocidad de respuesta a los cambios en el entorno externo debe ser mínima para garantizar la preservación de la información. Por otro lado, la velocidad de respuesta del sistema de control debe ser muchas veces mayor que la tasa de cambio en el medio ambiente, ya que el sistema debe seleccionar una acción de control incluso antes de que el estado del medio ambiente cambie irreversiblemente.

1.3 PROPIEDADES SINTÉTICAS DE LOS SISTEMAS

Las propiedades sintéticas incluyen propiedades colectivas, integrales y generalizadas que describen la interacción del sistema con el medio ambiente y tienen en cuenta la integridad en el sentido más general.

Aparición. La combinación de elementos en un sistema conduce al surgimiento de propiedades cualitativamente nuevas que no se derivan de las propiedades de las partes, inherentes sólo al sistema mismo y que existen sólo mientras el sistema sea un todo. Estas cualidades del sistema se denominan
emergente (del inglés “to rise”).

Se pueden encontrar ejemplos de propiedades emergentes en varios campos. Por ejemplo, ninguna de las partes del avión puede volar, pero el avión, sin embargo, vuela. Las propiedades del agua, muchas de las cuales no se comprenden completamente, no se derivan de las propiedades del hidrógeno y el oxígeno.

Sean dos cajas negras, cada una de las cuales tiene una entrada, una salida y realiza una operación: sumar uno al número en la entrada. Al conectar dichos elementos según el diagrama que se muestra en la figura, obtenemos un sistema sin entradas, pero con dos salidas. En cada ciclo de operación el sistema emitirá numero mayor, en este caso sólo aparecerán números pares en una entrada y sólo números impares en la otra.

A	b
Fig.1.1. Conexión de elementos del sistema: a) sistema con dos salidas; b) conexión paralela de elementos

Las propiedades emergentes de un sistema están determinadas por su estructura. Esto significa que con diferentes combinaciones de elementos surgirán diferentes propiedades emergentes. Por ejemplo, si conecta elementos en paralelo, entonces funcionalmente nuevo sistema no diferirá de un elemento. La aparición se manifestará en un aumento de la confiabilidad del sistema debido a la conexión en paralelo de dos elementos idénticos, es decir, debido a la redundancia.

Vale la pena señalar un caso importante cuando los elementos del sistema poseen todas sus propiedades. Esta situación es típica de la construcción fractal de un sistema. Al mismo tiempo, los principios de estructuración de las partes son los mismos que los del sistema en su conjunto. Un ejemplo de sistema fractal es una organización en la que la gestión está estructurada de manera idéntica en todos los niveles de la jerarquía.

Inseparabilidad en partes. Esta propiedad es, de hecho, una consecuencia de la emergencia. Se enfatiza especialmente porque su importancia práctica es grande y la subestimación es muy común.

Cuando se retira una pieza del sistema, suceden dos cosas: eventos importantes. En primer lugar, esto cambia la composición del sistema y, por tanto, su estructura. Este será un sistema diferente con diferentes propiedades. En segundo lugar, un elemento eliminado del sistema se comportará de manera diferente debido a que su entorno cambiará. Todo esto quiere decir que se debe tener precaución al considerar un elemento de forma aislada del resto del sistema.

Inherencia. Cuanto más integral sea el sistema (del inglés inherente - “ser parte de algo”), mejor estará coordinado y adaptado a ambiente, es compatible con él. El grado de inherencia varía y puede cambiar. La conveniencia de considerar la inherencia como una de las propiedades del sistema se debe a que de ello depende el grado y la calidad de la implementación de la función elegida por parte del sistema. En los sistemas naturales, la herencia aumenta mediante la selección natural. En los sistemas artificiales, la inherencia debería ser una preocupación especial del diseñador.

En algunos casos, la herencia se garantiza con la ayuda de sistemas intermediarios intermedios. Los ejemplos incluyen adaptadores para usar aparatos eléctricos extranjeros junto con enchufes de estilo soviético; middleware (como el servicio COM en Windows) que permite que dos programas de diferentes fabricantes se comuniquen entre sí.

Conveniencia. En los sistemas creados por el hombre, la subordinación tanto de la estructura como de la composición al logro del objetivo planteado es tan obvia que se puede reconocer propiedad fundamental cualquier sistema artificial. Esta propiedad se llama conveniencia. El objetivo para el cual se crea el sistema determina qué propiedad emergente garantizará el logro del objetivo y esto, a su vez, dicta la elección de la estructura y composición del sistema. Para extender el concepto de conveniencia a los sistemas naturales, es necesario aclarar el concepto de finalidad. La clarificación se realiza tomando como ejemplo un sistema artificial.

La historia de cualquier sistema artificial comienza en algún momento 0, cuando el valor existente del vector de estado Y 0 resulta insatisfactorio, es decir, surge una situación problemática. El sujeto no está satisfecho con esta condición y le gustaría cambiarla. Quede satisfecho con los valores del vector de estado Y*. Esta es la primera definición del objetivo. Además, se descubre que Y* no existe ahora y, por diversas razones, no se puede lograr en un futuro próximo. El segundo paso para definir una meta es reconocerla como un estado futuro deseado. Inmediatamente queda claro que el futuro no tiene límites. El tercer paso para aclarar el concepto de meta es estimar el tiempo T* en el que se puede alcanzar el estado deseado Y* en determinadas condiciones. Ahora el objetivo se vuelve bidimensional, es un punto (T*, Y*) en el gráfico. La tarea consiste en pasar del punto (0, Y 0) al punto (T*, Y*). Pero resulta que este camino se puede tomar por diferentes trayectorias, y sólo una de ellas puede realizarse. Deje que la elección recaiga en la trayectoria Y*( t). Por lo tanto, la meta ahora significa no sólo el estado final (T*, Y*), sino también toda la trayectoria Y*( t) (“metas intermedias”, “plan”). Entonces, el objetivo son los estados futuros deseados Y*( t).

Después del tiempo T*, el estado Y* se vuelve real. Por tanto, es posible definir el objetivo como un inmueble futuro. Esto permite decir que los sistemas naturales también tienen la propiedad de conveniencia, lo que nos permite abordar la descripción de sistemas de cualquier naturaleza desde una posición unificada. La principal diferencia entre los sistemas naturales y artificiales es que los sistemas naturales, al obedecer las leyes de la naturaleza, logran metas objetivas y sistemas artificiales se crean para lograr objetivos subjetivos.

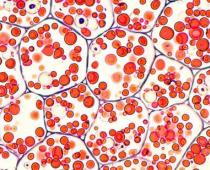
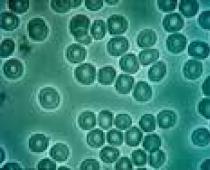
Mayoría característica común de cualquier sistema heterogéneo: la presencia de dos ( o más) fases que están separadas entre sí por una interfaz pronunciada. Esta característica distingue a los sistemas heterogéneos de las soluciones, que también constan de varios componentes que forman una mezcla homogénea. A una de las fases la llamaremos continua dispersiva y a la otra finamente dividida y distribuida en la primera fase dispersa. Dependiendo del tipo de medio de dispersión se distinguen mezclas heterogéneas, líquidas y gaseosas. En mesa 5.1 muestra la clasificación de sistemas no homogéneos según el tipo de fases dispersas y dispersas.

Tabla 5.1

Clasificación de sistemas heterogéneos.

Clasificación y características de sistemas heterogéneos.

Sistema heterogéneo Se considera sistema a aquel que consta de dos o más fases. Cada fase tiene su propia interfaz y puede separarse mecánicamente de la otra.

Un sistema heterogéneo consta de una fase interna (dispersa) y una fase externa (medio de dispersión), en la que se ubican las partículas de la fase dispersa. Los sistemas en los que la fase externa es líquida se denominan sistemas líquidos no homogéneos, y si los gases se denominan sistemas gaseosos no homogéneos. . Sistemas heterogéneos se llaman heterogéneos y homogéneos - homogéneos. Se entiende por sistema líquido homogéneo un líquido puro o una solución de cualquier sustancia que contenga. Un sistema líquido heterogéneo o heterogéneo es un líquido en el que hay sustancias no disueltas en forma de partículas diminutas. Los sistemas heterogéneos a menudo se denominan dispersos.

Se distinguen los siguientes tipos de sistemas no homogéneos: suspensiones, emulsiones, espumas, polvos, vapores, nieblas.

Suspensión Es un sistema formado por una fase líquida continua en la que se encuentran suspendidas partículas sólidas. Por ejemplo, salsas con harina, leche con almidón, melaza con cristales de azúcar.

Dependiendo del tamaño de las partículas, las suspensiones se dividen en gruesas (tamaño de partícula superior a 100 micrones), finas (0,1-100 micrones) y soluciones coloidales, que contenga partículas sólidas de 0,1 micras de tamaño o menos.

Emulsión Es un sistema formado por un líquido y gotas de otro líquido distribuidas en él que no se han disuelto en el primero. Se trata, por ejemplo, de leche, una mezcla de aceite vegetal y agua. Existen emulsiones gaseosas en las que el medio de dispersión es líquido y la fase dispersa es gaseosa.

Espuma Es un sistema formado por un líquido y burbujas de gas distribuidas en él. Por ejemplo, cremas y otros productos batidos. Las espumas tienen propiedades similares a las emulsiones.

Las emulsiones y espumas se caracterizan por la posibilidad de transición de la fase dispersa a un medio de dispersión y viceversa. Esta transición, posible con una determinada relación de masa de fases, se denomina inversión de fase o simplemente inversión.

Aerosoles Se denomina sistema disperso con un medio de dispersión gaseoso y una fase dispersa sólida o líquida, que está formado por partículas desde tamaños cuasi moleculares hasta microscópicos que tienen la propiedad de permanecer suspendidos por un tiempo más o menos largo. Este concepto combina polvo, humo y niebla. Por ejemplo, el polvo de harina se forma durante la molienda, el tamizado y el transporte de la harina; polvo de azúcar que se forma durante el secado del azúcar, etc. Se forma humo cuando se quema combustible sólido y niebla cuando se condensa el vapor.

En los aerosoles, el medio de dispersión es gas o aire, y la fase dispersa en polvo y humo es sólida y en nieblas es líquida.

Polvo y humo- sistemas compuestos por partículas gaseosas y sólidas distribuidas en ellos con tamaños de 5 a 50 micrones y de 0,3 a 5 micrones, respectivamente. La niebla es un sistema formado por gotas de gas y líquido de 0,3-3 micrones distribuidas en él, formadas como resultado de la condensación.

Un indicador cualitativo que caracteriza la uniformidad de tamaño de las partículas de aerosol es el grado de dispersión. Un aerosol se denomina monodisperso cuando las partículas que lo constituyen son del mismo tamaño, y polidisperso cuando contiene partículas de diferente tamaño. Los aerosoles monodispersos prácticamente no existen en la naturaleza. Sólo existen unos pocos aerosoles cuyo tamaño de partículas sólo se aproxima a los sistemas monodispersos (hifas de hongos, nieblas producidas especialmente, etc.).

Dispersos o heterogéneos Dependiendo del número de fases dispersas, los sistemas pueden ser de uno o varios componentes. Por ejemplo, la leche es un sistema multicomponente (tiene dos fases dispersas: grasa y proteína); salsas (las fases dispersas son harina, grasa, etc.).

Métodos de separación Los sistemas heterogéneos se clasifican según el tamaño de las partículas suspendidas de la fase dispersa, la diferencia de densidades de las fases dispersa y continua, así como la viscosidad de la fase continua. Se utilizan los siguientes métodos principales de separación: sedimentación, filtración, centrifugación, separación húmeda, electropurificación.

Precipitación Es un proceso de separación en el que las partículas sólidas o líquidas de una fase dispersa suspendidas en un líquido o gas se separan de la fase continua bajo la influencia de fuerzas de gravedad, centrífugas o electrostáticas. La sedimentación por gravedad se llama sedimentación.

Filtración - proceso Separación mediante un tabique poroso capaz de dejar pasar líquido o gas y retener partículas sólidas suspendidas en el medio. La filtración se realiza bajo la influencia de fuerzas de presión y sirve para una separación más fina de suspensiones y polvos que durante la sedimentación.

Centrifugación- el proceso de separación de suspensiones y emulsiones bajo la influencia de la fuerza centrífuga.

Separación húmeda- el proceso de atrapar partículas suspendidas en un gas utilizando un líquido.

Electrolimpieza- purificación de gases bajo la influencia de fuerzas eléctricas.

Los métodos para separar sistemas líquidos y gaseosos no homogéneos se basan en los mismos principios, pero el equipo utilizado tiene varias características.

2.4.1. Definición. Se nos dará un sistema no homogéneo de ecuaciones lineales.

Considere un sistema homogéneo

cuya matriz de coeficientes coincide con la matriz de coeficientes del sistema (2.4.1). Entonces el sistema (2.4.2) se llama sistema homogéneo reducido (2.4.1).

2.4.2. Teorema. La solución general de un sistema no homogéneo es igual a la suma de alguna solución particular del sistema no homogéneo y la solución general del sistema homogéneo reducido..

Así, para encontrar una solución general al sistema no homogéneo (2.4.1) es suficiente:

1) Investigue la compatibilidad. En caso de compatibilidad:

2) Encuentre la solución general del sistema homogéneo reducido.

3) Encuentre cualquier solución particular a la original (no homogénea).

4) Sumando la solución particular encontrada y la solución general del sistema dado, encuentre la solución general del sistema original.

2.4.3. Ejercicio. Investigue la compatibilidad del sistema y, en el caso de compatibilidad, encuentre su solución general en la forma de la suma de lo particular y lo general.

Solución. a) Para resolver el problema aplicamos el esquema anterior:

1) Examinamos la compatibilidad del sistema. (por el método de menores limítrofes): El rango de la matriz principal es 3 (ver la solución al Ejercicio 2.2.5, a), y el menor distinto de cero de orden máximo está compuesto por elementos del 1er, 2.ª, 4.ª filas y 1.ª, 3.ª y 4.ª columnas. Para encontrar el rango de la matriz extendida, la bordeamos con la tercera fila y la sexta columna de la matriz extendida: =0. Medio, rg A =rg=3, y el sistema es consistente. En particular, es equivalente al sistema

2) Encontremos una solución general X 0 sistema homogéneo reducido

X 0 ={(-2a - b ; a ; b ; b ; b ) | a , b Î R}

(ver solución al Ejercicio 2.2.5, a)).

3) Encontremos cualquier solución particular x h del sistema original. . Para ello, en el sistema (2.4.3), equivalente al original, las incógnitas libres X 2 y X Suponemos que 5 es igual a, por ejemplo, cero (este es el dato más conveniente):

y resuelve el sistema resultante: X 1 =- , X 3 =- , X 4=-5. Por tanto, (- ; 0; - ; -5; 0) ¾ es una solución particular del sistema.

4) Encuentre la solución general X n del sistema original. :

Xn={x h }+X 0 ={(- ; 0; - ; -5; 0)} + {(-2a - b ; a ; b ; b ; b )}=

={(- -2a - b ; a ; - + b ; -5+b ; b )}.

Comentario. Compare la respuesta que recibió con la segunda respuesta del ejemplo 1.2.1 c). Para obtener la respuesta en la primera forma para 1.2.1 c) se toman las incógnitas básicas X 1 , X 3 , X 5 (cuyo menor tampoco es igual a cero), y como libre ¾ X 2 y X 4 .

§3. Algunas aplicaciones.

3.1. Sobre el tema de las ecuaciones matriciales. Te recordamos que ecuación matricial sobre el campo F es una ecuación en la que la incógnita es una matriz sobre el campo F .

Las ecuaciones matriciales más simples son ecuaciones de la forma

HACHA=B , xa =B (2.5.1)

Dónde A , B ¾ matriz dada (conocida) sobre un campo F , A X ¾ tales matrices, tras la sustitución de las cuales las ecuaciones (2.5.1) se convierten en verdaderas igualdades matriciales. En particular, el método matricial de ciertos sistemas se reduce a resolver una ecuación matricial.

En el caso de que las matrices A en las ecuaciones (2.5.1) no son degeneradas, tienen soluciones, respectivamente X =A B Y X =LICENCIADO EN LETRAS. .

En el caso de que al menos una de las matrices del lado izquierdo de las ecuaciones (2.5.1) sea singular, este método ya no es adecuado, ya que la matriz inversa correspondiente A no existe. En este caso, encontrar soluciones a las ecuaciones (2.5.1) se reduce a resolver sistemas.

Pero primero, introduzcamos algunos conceptos.

Llamemos al conjunto de todas las soluciones del sistema. decisión general . Llamemos a una solución tomada por separado de un sistema indefinido solución privada .

3.1.1. Ejemplo. Resolver ecuación matricial sobre campo. R.

A) X = ; b) X = ; V) X = .

Solución. a) Como =0, entonces la fórmula X =A B no es adecuado para resolver esta ecuación. si en el trabajo xa =B matriz A tiene 2 filas, entonces la matriz X tiene 2 columnas. Número de líneas X debe coincidir con el número de líneas B . Es por eso X tiene 2 líneas. De este modo, X ¾ alguna matriz cuadrada de segundo orden: X = . sustituyamos X en la ecuación original:

Multiplicando las matrices del lado izquierdo de (2.5.2), llegamos a la igualdad

Dos matrices son iguales si y sólo si tienen las mismas dimensiones y sus elementos correspondientes son iguales. Por tanto (2.5.3) es equivalente al sistema

Este sistema es equivalente al sistema

Resolviéndolo, por ejemplo, utilizando el método gaussiano, llegamos a un conjunto de soluciones (5-2 b , b , -2d , d ), Dónde b , d funcionan independientemente unos de otros R. De este modo, X = .

b) Similar a a) tenemos X = y.

Este sistema es inconsistente (¡compruébalo!). Por lo tanto, esta ecuación matricial no tiene soluciones.

c) Denotemos esta ecuación por HACHA =B . Porque A tiene 3 columnas y B tiene 2 columnas, entonces X ¾ alguna matriz de dimensión 3´2: X = . Por tanto tenemos la siguiente cadena de equivalencias:

Resolvemos el último sistema usando el método gaussiano (omitimos comentarios)

Llegamos así al sistema

cuya solución es (11+8 z , 14+10z , z , -49+8w , -58+10w ,w ) Dónde z , w funcionan independientemente unos de otros R.

Respuesta: a) X = , b , d Î R.

b) No hay soluciones.

V) X = z , w Î R.

3.2. Sobre la cuestión de la permutabilidad de matrices. En general, el producto de matrices no es conmutable, es decir, si A Y B tal que AB Y LICENCIADO EN LETRAS. se definen, entonces, en términos generales, AB ¹ LICENCIADO EN LETRAS. . pero un ejemplo matriz de identidad mi muestra que la conmutabilidad también es posible A.E. =E.A. para cualquier matriz A , si solo A.E. Y E.A. fueron determinados.

En esta sección consideraremos problemas para encontrar el conjunto de todas las matrices que conmutan con una determinada. De este modo,

Desconocido X 1 , y 2 y z 3 puede tomar cualquier valor: X 1 =a , y 2 =b , z 3 =gramo . Entonces

De este modo, X = .

Respuesta. A) X d ¾ cualquier número.

b) X ¾ conjunto de matrices de la forma , donde a , b Y gramo ¾ cualquier número.