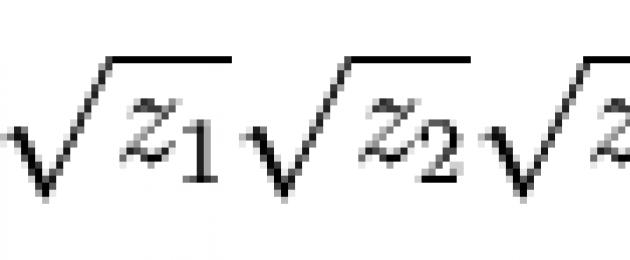Entra al canal de youtube de nuestra web para estar al día de todas las nuevas lecciones en vídeo.
Primero, recordemos las fórmulas básicas de las potencias y sus propiedades.
producto de un numero a ocurre sobre sí mismo n veces, podemos escribir esta expresión como a a … a=a n
1. un 0 = 1 (un ≠ 0)
3. una norte una metro = una norte + metro
4. (un n) m = un nm
5. a n b n = (ab) n
7. un norte / un metro = un norte - metro
Poder o ecuaciones exponenciales – son ecuaciones en las que las variables están en potencias (o exponentes) y la base es un número.
Ejemplos de ecuaciones exponenciales:
En este ejemplo, el número 6 es la base, siempre está abajo y la variable X grado o indicador.
Demos más ejemplos de ecuaciones exponenciales.
2×5=10
16x - 4x - 6=0
Ahora veamos cómo se resuelven las ecuaciones exponenciales.
Tomemos una ecuación simple:
2 x = 2 3
Este ejemplo se puede resolver incluso en tu cabeza. Se puede ver que x=3. Después de todo, para que la izquierda y parte derecha eran iguales, necesitas reemplazar x con el número 3.
Ahora veamos cómo formalizar esta decisión:
2 x = 2 3
x = 3
Para resolver dicha ecuación, eliminamos motivos idénticos(es decir, dos) y anotó lo que quedaba, estos son grados. Obtuvimos la respuesta que estábamos buscando.
Ahora resumamos nuestra decisión.
Algoritmo para resolver la ecuación exponencial:
1. Necesidad de comprobar lo mismo si la ecuación tiene bases a la derecha y a la izquierda. Si los motivos no son los mismos, buscamos opciones para solucionar este ejemplo.
2. Después de que las bases sean iguales, equiparar grados y resuelve la nueva ecuación resultante.
Ahora veamos algunos ejemplos:
Comencemos con algo simple.
Las bases de los lados izquierdo y derecho son iguales al número 2, lo que significa que podemos descartar la base e igualar sus grados.
x+2=4 Se obtiene la ecuación más simple.
x=4 – 2
x=2
Respuesta:x=2
En el siguiente ejemplo puedes ver que las bases son diferentes: 3 y 9.
3 3x - 9x+8 = 0
Primero, movemos el nueve hacia el lado derecho y obtenemos:
Ahora necesitas hacer las mismas bases. Sabemos que 9=3 2. Usemos la fórmula de potencia (an) m = a nm.
3 3x = (3 2)x+8
Obtenemos 9 x+8 =(3 2) x+8 =3 2x+16
3 3x = 3 2x+16 Ahora está claro que en los lados izquierdo y derecho las bases son iguales e iguales a tres, lo que significa que podemos descartarlas e igualar los grados.
3x=2x+16 obtenemos la ecuación más simple
3x - 2x=16
x=16
Respuesta:x=16.
Veamos el siguiente ejemplo:
2 2x+4 - 10 4 x = 2 4
En primer lugar, nos fijamos en las bases, bases dos y cuatro. Y necesitamos que sean iguales. Transformamos los cuatro usando la fórmula (an) m = a nm.
4 x = (2 2) x = 2 2 x
Y también usamos una fórmula a n a m = a n + m:
2 2x+4 = 2 2x 2 4
Suma a la ecuación:
2 2x 2 4 - 10 2 2x = 24
Dimos un ejemplo por las mismas razones. Pero nos molestan otros números 10 y 24. ¿Qué hacer con ellos? Si miras de cerca puedes ver que en el lado izquierdo tenemos 2 2x repetido, aquí está la respuesta: podemos poner 2 2x entre paréntesis:
2 2x (2 4 - 10) = 24
Calculemos la expresión entre paréntesis:
2 4 — 10 = 16 — 10 = 6
Dividimos toda la ecuación por 6:
Imaginemos 4=2 2:
2 2x = 2 2 bases son iguales, las descartamos e igualamos los grados.
2x = 2 es la ecuación más simple. lo dividimos por 2 y obtenemos
x = 1
Respuesta: x = 1.
Resolvamos la ecuación:
9x – 12*3x +27= 0
Convirtamos:
9x = (3 2)x = 3 2x
Obtenemos la ecuación:
3 2x - 12 3x +27 = 0
Nuestras bases son iguales, iguales a tres, en este ejemplo puedes ver que las tres primeras tienen el doble de grado (2x) que la segunda (solo x). En este caso puedes resolver método de reemplazo. Reemplazamos el número con el grado más pequeño:
Entonces 3 2x = (3 x) 2 = t 2
Reemplazamos todas las potencias x en la ecuación con t:
t 2 - 12t+27 = 0
Obtenemos ecuación cuadrática. Resolviendo por el discriminante obtenemos:
D=144-108=36
t 1 = 9
t2 = 3
Volviendo a la variable X.
Tome t 1:
t 1 = 9 = 3x
Eso es,
3 x = 9
3 x = 3 2
x1 = 2
Se encontró una raíz. Buscamos el segundo del t 2:
t 2 = 3 = 3x
3 x = 3 1
x2 = 1
Respuesta: x 1 = 2; x2 = 1.
En la web podrás consultar cualquier duda que tengas en el apartado AYUDA A DECIDIR, seguro que te responderemos.
Únete al grupo
Solución de Descartes-Euler
Habiendo realizado la sustitución, obtenemos una ecuación de la siguiente forma (se llama “incompleta”):
y 4 + pagy 2 + qy + r = 0 .Raíces y 1 , y 2 , y 3 , y 4 de dicha ecuación son iguales a una de las siguientes expresiones:
en el que se seleccionan combinaciones de caracteres de tal forma que se cumpla la siguiente relación:
,
y z 1 , z 2 y z 3 son las raíces de la ecuación cúbica.
La solución de Ferrari
articulo principal: método ferrari
Representemos la ecuación de cuarto grado en la forma:
AX 4 + BX 3 + CX 2 + DX + mi = 0,Su solución se puede encontrar a partir de las siguientes expresiones:
si β = 0, resolviendo tu 4 + α tu 2 + γ = 0 y, haciendo la sustitución 
, busquemos las raíces: . 
, (cualquier signo raíz cuadrada servirá), (tres raíces complejas, una de las cuales servirá) 
Dos ± s deben tener el mismo signo, ± t - son independientes. Para encontrar todas las raíces, necesitas encontrar x para combinaciones con signo ± s ,± t = +,+ para +,− para −,+ para −,−. Las raíces dobles aparecerán dos veces, las triples tres veces y las cuaternarias cuatro veces. El orden de las raíces depende de qué raíz cúbica Ud. seleccionado. ver también
- Tipos de ecuaciones de 4to grado fáciles de resolver: Ecuación bicuadrática, ecuación recíproca de cuarto grado
Literatura
- Korn G., Korn T. (1974) Manual de matemáticas.
Enlaces
- La decisión de Ferrari
Fundación Wikimedia. 2010.
Vea qué es una “ecuación de cuarto grado” en otros diccionarios:
ecuación de cuarto grado- - [L.G. Sumenko. Diccionario inglés-ruso sobre tecnologías de la información. M.: Empresa estatal TsNIIS, 2003.] Temas tecnologías de la información en general EN ecuación de cuarto grado... Guía del traductor técnico
Gráfica de un polinomio de 4º grado con cuatro raíces y tres puntos críticos. Una ecuación de cuarto grado en matemáticas es una ecuación algebraica de la forma: Cuarto grado para ecuaciones algebraicas es el punto más alto al que... ... Wikipedia
Una ecuación de la forma: anxn + an − 1xn − 1 + ... + a1x + a0 = 0 se llama recíproca si sus coeficientes en posiciones simétricas son iguales, es decir, si an − k = ak, para k = 0, 1, ..., n. Contenido 1 Ecuación de cuarto grado ... Wikipedia
En el que el término desconocido está elevado a la cuarta potencia. diccionario completo palabras extranjeras, que han entrado en uso en el idioma ruso. Popov M., 1907. ECUACIÓN BICUÁDRICA de lat. bis, dos veces y quadratum, cuadrado. La ecuación en la que el mayor grado... ... Diccionario de palabras extranjeras de la lengua rusa.
Junto a la aritmética existe la ciencia de los números y, a través de los números, de las cantidades en general. Sin estudiar las propiedades de cantidades concretas y definidas, ambas ciencias investigan las propiedades de cantidades abstractas como tales, independientemente de... ... diccionario enciclopédico F. Brockhaus y I.A. Efrón
Un conjunto de conocimientos aplicados que permite a los ingenieros aeronáuticos estudiar en el campo de la aerodinámica, los problemas de resistencia, la construcción de motores y la dinámica de vuelo de las aeronaves (es decir, la teoría) para crear una nueva aeronave o mejorarla... ... Enciclopedia de Collier
La actividad matemática más antigua fue contar. Era necesaria una cuenta para realizar un seguimiento del ganado y realizar el comercio. Algunas tribus primitivas contaban el número de objetos relacionándolos con varias partes del cuerpo, principalmente... ... Enciclopedia de Collier
Historia de la tecnología por período y región: revolución neolítica Tecnologías del antiguo Egipto Ciencia y tecnología india antigua Ciencia y Tecnología China antigua Tecnologías Antigua Grecia Tecnologías Antigua Roma Tecnologías del mundo islámico... ... Wikipedia
Una ecuación es una relación matemática que expresa la igualdad de dos expresiones algebraicas. Si la igualdad es cierta para cualquier valores aceptables incógnitas incluidas en él, entonces se llama identidad; por ejemplo, una proporción de la forma... ... Enciclopedia de Collier
El teorema de Abel Ruffini establece que la ecuación general de potencia en no tiene solución en radicales. Contenido 1 Detalles... Wikipedia
En el caso general, la solución de una ecuación de cuarto grado se lleva a cabo utilizando métodos para resolver ecuaciones para grados superiores, por ejemplo, mediante el método Ferrari o utilizando el esquema de Horner. Pero algunas ecuaciones de cuarto grado tienen una solución más simple.
Existen varios tipos especiales de ecuaciones de cuarto grado, cuyos métodos de resolución aprenderá a continuación:
- Ecuación bicuadrática $ax^4+bx^2+c=0$;
- Ecuaciones recíprocas de la forma $ax^4+bx^3+cx^2 +bx+ a=0$;
- Ecuaciones de la forma $ax^4+b=0$.
Resolver ecuaciones bicuadráticas de cuarto grado.
Las ecuaciones bicuadráticas $ax^4+bx^2+c=0$ se reducen a ecuaciones cuadráticas reemplazando la variable $x^2$ por una nueva, por ejemplo, $y$. Después del reemplazo, se resuelve la nueva ecuación resultante y luego el valor de la variable encontrada se sustituye en la ecuación $x^2=y$. El resultado de la solución serán las raíces de la ecuación $x^2=y$.
Ejemplo 1
Resuelve la ecuación $x(x-1)(x-2)(x-3)=24$:
Ampliemos los paréntesis en el polinomio:
$(x^2-3x)(x^2-3x+2)=24$
De esta forma, resulta obvio que podemos elegir la expresión $y=x^2-3x$ como nueva variable; sustituyémosla:
$y\cdot (y+2)=24$
Ahora resolvamos dos ecuaciones cuadráticas $x^2-3x=-4$ y $x^2-3x=-6$.
Las raíces de la primera ecuación son $x_1(1,2)=4;-1$, la segunda no tiene soluciones.
Resolver ecuaciones recíprocas de grado 4.
Estas ecuaciones de la forma $ax^4+bx^3+cx^2 +bx+ a=0$ repiten con sus coeficientes para términos de orden inferior los coeficientes para polinomios de grados superiores. Para resolver dicha ecuación, primero divídala por $x^2$:
$ax^4+bx^3+cx^2 +bx+ a=0|:x^2$
$ax^2+bx+c+\frac(b)(x) + \frac(a)(x^2)=0$
$a(x^2+\frac(1)(x^2))+b(x+\frac(1)(x)) + c=0$
Luego reemplace $(x+\frac(1)(x))$ con una nueva variable, luego $(x^2+\frac(1)(x^2))=y^2-2$, después de la sustitución obtenemos el siguiente eleva al cuadrado la ecuación:
$a(y^2-2)+por+c=0$
Después de esto, buscamos las raíces de las ecuaciones $x+\frac(1)(x)=y_1$ y $x+\frac(1)(x)=y_2$.
Se utiliza un método similar para resolver ecuaciones recíprocas de la forma $ax^4+bx^3+cx^2 +kbx+ k^2a=0$.
Ejemplo 2
Resuelve la ecuación:
$3x^4-2x^3-9x^2-4x+12=0$
Esta ecuación es una ecuación recíproca de la forma $ax^4+bx^3+cx^2 +kbx+ k^2a=0$. Por lo tanto, dividimos toda la ecuación por $x^2$:
$3x^2-2x-9 \cdot \frac(2 \cdot 2)(x)+3 \cdot (\frac(2)(x))^2=0$
$3(x^2+\frac(4)(x^2))-2(x+\frac(2)(x)-9=0$
Reemplacemos la expresión $x+\frac(2)(x)$: $3(y^2-4)-2y-9=0$
Calculemos las raíces de esta ecuación, son iguales a $y_1=3$ y $y_2=-\frac(7)(3)$.
En consecuencia, ahora es necesario resolver dos ecuaciones $x+\frac(2)(x)=3$ y $x+\frac(2)(x)=-\frac(7)(3)$. La solución de la primera ecuación es $x_1=1, x_2=2$, la segunda ecuación no tiene raíces.
Por lo tanto, las raíces de la ecuación original son $x_1=1, x_2=2$.
Ecuaciones de la forma $ax^4+b=0$
Las raíces de una ecuación de este tipo se encuentran mediante fórmulas de multiplicación abreviadas.
Poco después de que Cardano publicara un método para resolver ecuaciones cúbicas, sus estudiantes y seguidores encontraron formas de reducir la ecuación general de cuarto grado a una ecuación cúbica. Presentamos el método más sencillo, que pertenece a L. Ferrari.
Al presentar el método, necesitará utilizar el siguiente lema elemental.
Lema. Con el fin de trinomio cuadrático era el cuadrado de un binomio lineal, es necesario y suficiente que su discriminante sea igual a cero.
Prueba. Necesidad. Dejar . Luego Suficiencia. deja entonces
La idea del método presentado es presentar el lado izquierdo de la ecuación como la diferencia de dos cuadrados. Luego se puede descomponer en dos factores de segundo grado y resolver la ecuación conducirá a resolver dos ecuaciones cuadráticas. Para lograr el objetivo, representemos el lado izquierdo en la forma:
Aquí y es una incógnita auxiliar, que debe seleccionarse de modo que la expresión entre corchetes resulte ser el cuadrado de un binomio lineal. En virtud del lema, para ello es necesario y suficiente satisfacer la condición
Esta condición es una ecuación de tercer grado con respecto a y. Después de abrir el paréntesis, se convierte al formulario.
Sea una de las raíces de esta ecuación. Entonces la condición se cumplirá, por lo que se cumple
para algunos k e I. La ecuación original toma la forma
Igualando cada uno de los factores a cero, encontraremos las cuatro raíces de la ecuación original.
Hagamos una observación más. Sean las raíces del primer factor y sean las raíces del segundo. Luego sumando estas igualdades obtenemos que
Así, hemos obtenido una expresión para la raíz de la ecuación cúbica auxiliar en términos de las raíces de la ecuación original de cuarto grado.
Ejemplo. Resuelve la ecuación. Según el método descrito anteriormente, transformamos el lado izquierdo:
Ahora pongamos. Después de las formaciones obtenemos la ecuación.
Es fácil ver que una de las raíces de esta ecuación es el número. Sustituyéndolo en el lado izquierdo transformado de la ecuación original, obtenemos:
Igualando los factores a cero, obtenemos
En cuanto a las ecuaciones superiores al cuarto grado, se conocían algunas clases de ecuaciones de forma relativamente particular, admitiendo soluciones algebraicas en radicales, es decir, en forma de resultados. operaciones aritmeticas y acciones de extracción de raíces. Sin embargo, los intentos de proporcionar soluciones a ecuaciones generales de grado cinco y superiores fracasaron hasta, finalmente, principios del siglo XIX. Ruffini y Abel no demostraron que una solución de este tipo para ecuaciones generales por encima del cuarto grado sea imposible. Finalmente, en 1830, el brillante matemático francés E. Galois logró encontrar lo necesario y condiciones suficientes(que son bastante difíciles de verificar) para la solubilidad de una ecuación específica en radicales. Al mismo tiempo, Galois creó y utilizó la teoría de los grupos de permutación, que era nueva para su época.
2x 4 + 5x 3 - 11x 2 - 20x + 12 = 0
Primero necesitas encontrar una raíz usando el método de selección. Suele ser un divisor del término libre. En este caso, los divisores del número. 12 son ±1, ±2, ±3, ±4, ±6, ±12. Empecemos a sustituirlos uno por uno:
1: 2 + 5 - 11 - 20 + 12 = -12 ⇒ número 1
-1: 2 - 5 - 11 + 20 + 12 = 18 ⇒ número -1 no es raíz de un polinomio
2: 2 ∙ 16 + 5 ∙ 8 - 11 ∙ 4 - 20 ∙ 2 + 12 = 0 ⇒ número 2 es la raíz del polinomio
Hemos encontrado 1 de las raíces del polinomio. La raíz del polinomio es 2, lo que significa que el polinomio original debe ser divisible por x - 2. Para realizar la división de polinomios utilizamos el esquema de Horner:
| 2 | 5 | -11 | -20 | 12 | |
| 2 |
Los coeficientes del polinomio original se muestran en la línea superior. La raíz que encontramos se coloca en la primera celda de la segunda fila. 2. La segunda línea contiene los coeficientes del polinomio que resulta de la división. Se cuentan así:
| En la segunda celda de la segunda fila escribimos el número. 2, simplemente moviéndolo desde la celda correspondiente de la primera fila. | ||||||||||||
| 2 ∙ 2 + 5 = 9 | ||||||||||||
| 2 ∙ 9 - 11 = 7 | ||||||||||||
| 2 ∙ 7 - 20 = -6 | ||||||||||||
| 2 ∙ (-6) + 12 = 0 |
El último número es el resto de la división. Si es igual a 0, entonces hemos calculado todo correctamente.
2x 4 + 5x 3 - 11x 2 - 20x + 12 = (x - 2)(2x 3 + 9x 2 + 7x - 6)
Pero, este no es el final. Puedes intentar expandir el polinomio de la misma manera. 2x 3 + 9x 2 + 7x - 6.
Nuevamente buscamos una raíz entre los divisores del término libre. Divisores de números -6 son ±1, ±2, ±3, ±6.
1: 2 + 9 + 7 - 6 = 12 ⇒ número 1 no es raíz de un polinomio
-1: -2 + 9 - 7 - 6 = -6 ⇒ número -1 no es raíz de un polinomio
2: 2 ∙ 8 + 9 ∙ 4 + 7 ∙ 2 - 6 = 60 ⇒ número 2 no es raíz de un polinomio
-2: 2 ∙ (-8) + 9 ∙ 4 + 7 ∙ (-2) - 6 = 0 ⇒ número -2 es la raíz del polinomio
Escribamos la raíz encontrada en nuestro esquema de Horner y comencemos a completar las celdas vacías:
| En la segunda celda de la tercera fila escribimos el número. 2, simplemente moviéndolo desde la celda correspondiente de la segunda fila. | ||||||||||||||||||
| -2 ∙ 2 + 9 = 5 | ||||||||||||||||||
| -2 ∙ 5 + 7 = -3 | ||||||||||||||||||
| -2 ∙ (-3) - 6 = 0 |
Así, factorizamos el polinomio original:
2x 4 + 5x 3 - 11x 2 - 20x + 12 = (x - 2)(x + 2)(2x 2 + 5x - 3)
Polinomio 2x 2 + 5x - 3 También se puede factorizar. Para ello, puedes resolver la ecuación cuadrática mediante el discriminante, o puedes buscar la raíz entre los divisores del número. -3. De una forma u otra llegaremos a la conclusión de que la raíz de este polinomio es el número -3
| En la segunda celda de la cuarta fila escribimos el número. 2, simplemente moviéndolo desde la celda correspondiente de la tercera fila. | ||||||||||||||||||||||||
| -3 ∙ 2 + 5 = -1 | ||||||||||||||||||||||||
| -3 ∙ (-1) - 3 = 0 |
Por tanto, descompusimos el polinomio original en factores lineales.
- En contacto con 0
- Google+ 0
- DE ACUERDO 0
- Facebook 0
