Il ragionamento basato esclusivamente su fatti esatti e conclusioni precise basate su questi fatti sono chiamati considerazioni rigorose. Nei casi in cui devono essere utilizzati fatti incerti per prendere decisioni, il ragionamento rigoroso diventa inadatto. Pertanto, uno dei punti di forza di qualsiasi sistema esperto è la sua capacità di formare ragionamenti in condizioni di incertezza così come fanno gli esperti umani. Tale ragionamento non è rigoroso. Puoi tranquillamente parlare della presenza logica sfocata.
Incertezza e, di conseguenza, la logica fuzzy può essere considerata come la mancanza di informazioni adeguate per prendere una decisione. L'incertezza diventa un problema perché può impedire la creazione della soluzione migliore e persino causare la ricerca di una soluzione di scarsa qualità. Va notato che una soluzione di alta qualità trovata in tempo reale è spesso considerata più accettabile della soluzione migliore, che richiede molto tempo per essere calcolata. Ad esempio, un ritardo nel fornire il trattamento per condurre ulteriori test può comportare la morte del paziente senza aiuto.
Il motivo dell'incertezza è la presenza di vari errori nelle informazioni. Classificazione semplificata Questi errori possono essere rappresentati nella loro suddivisione nelle seguenti tipologie:
- ambiguità delle informazioni, il cui verificarsi è dovuto al fatto che alcune informazioni possono essere interpretate in modi diversi;
- incompletezza delle informazioni relativa alla mancanza di alcuni dati;
- l'inadeguatezza delle informazioni dovuta all'uso dei dati non corrisponde alla situazione reale (le possibili cause sono errori soggettivi: bugie, disinformazione, malfunzionamento dell'apparecchiatura);
- errori di misurazione che derivano dal mancato rispetto dei requisiti di correttezza e accuratezza dei criteri di presentazione dei dati quantitativi;
- errori casuali, la cui manifestazione sono fluttuazioni casuali dei dati rispetto al loro valore medio (il motivo potrebbe essere: inaffidabilità dell'attrezzatura, moto browniano, effetti termici, ecc.).
Ad oggi, è stato sviluppato un numero significativo di teorie dell'incertezza che tentano di eliminare alcuni o addirittura tutti gli errori e di fornire un'inferenza affidabile in condizioni di incertezza. Le più utilizzate nella pratica sono le teorie basate sulla definizione classica di probabilità e sulla probabilità a posteriori.
La probabilità è uno degli strumenti più antichi e importanti per risolvere i problemi di intelligenza artificiale. Probabilitàè un modo quantitativo per tenere conto dell'incertezza. La probabilità classica ha origine da una teoria proposta per la prima volta da Pascal e Fermat nel 1654. Da allora, molto lavoro è stato svolto nel campo della probabilità e nell'implementazione di numerose applicazioni della probabilità nella scienza, nella tecnologia, negli affari, nell'economia e in altri campi.
probabilità classica
probabilità classica detta anche probabilità a priori, poiché la sua definizione si riferisce a sistemi ideali. Il termine "a priori" indica una probabilità che è determinata "a eventi", senza tener conto di molti fattori che si verificano nel mondo reale. Il concetto di probabilità a priori si estende agli eventi che si verificano in sistemi ideali che sono soggetti all'usura o all'influenza di altri sistemi. In un sistema ideale, il verificarsi di uno qualsiasi degli eventi si verifica allo stesso modo, il che rende la loro analisi molto più semplice.
La formula fondamentale per la probabilità classica (P) è definita come segue:
In questa formula wè il numero di eventi attesi, e Nè il numero totale di eventi con uguale probabilità che sono possibili risultati di un esperimento o di un test. Ad esempio, la probabilità di ottenere qualsiasi faccia di un dado a sei facce è 1/6 e pescare qualsiasi carta da un mazzo contenente 52 carte diverse è 1/52.
Assiomi della teoria della probabilità
Una teoria formale della probabilità può essere creata sulla base di tre assiomi:

Gli assiomi di cui sopra hanno permesso di porre le basi per la teoria della probabilità, ma non considerano la probabilità di eventi che si verificano in sistemi reali - non ideali. In contrasto con l'approccio a priori, nei sistemi reali, per determinare la probabilità di qualche evento P(E), si applica il metodo di determinazione della probabilità sperimentale come limite di distribuzione di frequenza:

Probabilità posteriore
In questa formula f(E) denota la frequenza di occorrenza di un evento tra N esimo numero di osservazioni dei risultati complessivi. Questo tipo di probabilità è anche chiamato probabilità a posteriori, cioè. probabilità determinata "dopo gli eventi". La definizione della probabilità a posteriori si basa sulla misurazione della frequenza con cui un evento si verifica durante un gran numero di test. Ad esempio, determinare il tipo sociale di un cliente bancario meritevole di credito in base all'esperienza empirica.
Eventi che non si escludono a vicenda possono influenzarsi a vicenda. Tali eventi appartengono alla classe di quelli complessi. La probabilità di eventi complessi può essere calcolata analizzando i rispettivi spazi campionari. Questi spazi campionari possono essere rappresentati utilizzando i diagrammi di Venn, come mostrato in Fig. uno

Fig.1 Spazio campione per due eventi non mutuamente esclusivi
La probabilità del verificarsi dell'evento A, determinata tenendo conto del fatto che l'evento B si è verificato, è chiamata probabilità condizionata ed è indicata P(A|B). La probabilità condizionata è definita come segue:

Probabilità a priori
In questa formula, la probabilità P(B) non dovrebbe essere zero ed è una probabilità a priori, che viene determinata prima che siano note altre informazioni aggiuntive. probabilità a priori, che viene applicato in connessione con l'uso della probabilità condizionale, è talvolta chiamato probabilità assoluta.
C'è un problema che è essenzialmente l'opposto del problema del calcolo della probabilità condizionale. Consiste nel determinare la probabilità inversa, che mostra la probabilità dell'evento precedente, tenendo conto di quegli eventi che si sono verificati in futuro. In pratica, questo tipo di probabilità si verifica abbastanza spesso, ad esempio, quando si esegue la diagnostica medica o la diagnostica delle apparecchiature, in cui vengono rilevati determinati sintomi e il compito è trovare una possibile causa.
Per risolvere questo problema, viene utilizzato Teorema di Bayes, dal nome del matematico britannico del XVIII secolo Thomas Bayes. La teoria bayesiana è ora ampiamente utilizzata per analizzare gli alberi decisionali in economia e scienze sociali. Il metodo di ricerca della soluzione bayesiana viene utilizzato anche nel sistema esperto PROSPECTOR per identificare siti promettenti per l'esplorazione mineraria. Il sistema PROSPECTOR ha guadagnato ampia popolarità come il primo sistema esperto, con l'aiuto del quale è stato scoperto un prezioso deposito di molibdeno, che è costato 100 milioni di dollari.
Un evento casuale è valutato da un numero che determina l'intensità della manifestazione di questo evento. Questo numero è chiamato probabilità sviluppi P()
. La probabilità di un evento elementare è  . La probabilità di un evento è una misura numerica del grado di obiettività, la possibilità di questo evento. Maggiore è la probabilità, più probabile sarà l'evento.
. La probabilità di un evento è una misura numerica del grado di obiettività, la possibilità di questo evento. Maggiore è la probabilità, più probabile sarà l'evento.
Qualsiasi evento che corrisponde all'intero spazio dei risultati S, è chiamato certo evento, cioè. un evento che deve necessariamente verificarsi a seguito dell'esperimento (ad esempio, la perdita di un numero qualsiasi di punti da 1 a 6 su un dado). Se l'evento non appartiene al set S, quindi viene considerato impossibile(ad esempio, lasciando cadere un numero di punti maggiore di 6 su un dado). La probabilità di un evento impossibile è 0, la probabilità di un certo evento è 1. Tutti gli altri eventi hanno una probabilità da 0 a 1.
Sviluppi e e  chiamato di fronte, Se e arriva quando non lo fa
chiamato di fronte, Se e arriva quando non lo fa  . Ad esempio, evento e– “perdita di un numero pari di punti”, quindi l'evento
. Ad esempio, evento e– “perdita di un numero pari di punti”, quindi l'evento  - Numero dispari di punti. Due eventi e 1
e e 2
chiamato incompatibile se non esiste un esito comune a entrambi gli eventi.
- Numero dispari di punti. Due eventi e 1
e e 2
chiamato incompatibile se non esiste un esito comune a entrambi gli eventi.
Per determinare le probabilità di eventi casuali, vengono utilizzati metodi diretti o indiretti. Quando si calcola direttamente la probabilità, si distinguono schemi di calcolo a priori e a posteriori, quando condurre osservazioni (esperimenti) o contare a priori il numero di esperimenti m, in cui l'evento si è manifestato, e il numero totale di esperimenti eseguiti n. I metodi indiretti si basano sulla teoria assiomatica. Poiché gli eventi sono definiti come insiemi, tutte le operazioni di teoria degli insiemi possono essere eseguite su di essi. Teoria degli insiemi, analisi funzionale sono state proposte dall'accademico A.N. Kolmogorov e costituì la base della teoria assiomatica della probabilità. Presentiamo gli assiomi delle probabilità.
Assiomaio. Campo dell'eventoF(S) è un'algebra di insiemi.
Questo assioma indica l'analogia tra teoria degli insiemi e teoria della probabilità.
AssiomaII.
Ad ogni set daF(S) è associato a un numero reale P(
daF(S) è associato a un numero reale P( ), chiamata probabilità di un evento
), chiamata probabilità di un evento :
:
a condizione S 1 S 2 = (per eventi incompatibili S 1 e S 2 ), o per una serie di eventi incompatibili
dove N– numero di eventi elementari (possibili esiti).
Probabilità di un evento casuale
|
|
dove  sono le probabilità di eventi elementari
sono le probabilità di eventi elementari  , incluso nel sottoinsieme
, incluso nel sottoinsieme  .
.
Esempio 1.1. Determina la probabilità di ottenere ogni numero quando si lancia un dado, ottenendo un numero pari, numero 4 .
Soluzione. La probabilità che ogni numero esca dall'insieme
S = (1, 2, 3, 4, 5, 6)
 1/6.
1/6.
La probabilità di ottenere un numero pari, ad es.  ={2,
4, 6},
in base a (1.6) sarà P(
={2,
4, 6},
in base a (1.6) sarà P(  )
= 1/6 + 1/6 + 1/6 = 3/6 = 1/2
.
)
= 1/6 + 1/6 + 1/6 = 3/6 = 1/2
.
Probabilità di ottenere un numero 4
, cioè.  =
{4, 5, 6 }
,
=
{4, 5, 6 }
,
P(  )
= 1/6 + 1/6 + 1/6 = 3/6 = 1/2.
)
= 1/6 + 1/6 + 1/6 = 3/6 = 1/2.
Compiti per lavoro autonomo
1. Ci sono 20 palline bianche, 30 nere e 50 rosse in un canestro. Determina la probabilità che la prima pallina estratta dal canestro sia bianca. Nero; rosso.
2. Ci sono 12 ragazzi e 10 ragazze nel gruppo studentesco. Qual è la probabilità che il seminario sulla teoria della probabilità sia assente: 1) un giovane; 2) una ragazza; 3) due giovani?
3. Nel corso dell'anno, 51 giorni sono stati distinti dal fatto che in questi giorni ha piovuto (o nevicato). Qual è la probabilità che rischi di rimanere sorpreso dalla pioggia (o dalla neve): 1) andare al lavoro; 2) andare in campeggio per 5 giorni?
4. Crea un problema sull'argomento di questo compito e risolvilo.
1.1.3. Definizione di probabilità a posteriori (probabilità statistica o frequenza
evento casuale)
Nella determinazione a priori della probabilità, si è assunto che  equiprobabile. Questo è tutt'altro che sempre vero, più spesso succede così
equiprobabile. Questo è tutt'altro che sempre vero, più spesso succede così  a
a  . Assunzione
. Assunzione  porta ad un errore nella definizione a priori P(
porta ad un errore nella definizione a priori P(  )
secondo lo schema stabilito. Per determinare
)
secondo lo schema stabilito. Per determinare  , ma in generale P(
, ma in generale P(  )
condurre test mirati. Nel corso di tali test (ad esempio, il test risulta negli esempi 1.2, 1.3) in uno stato diverso di varie condizioni, influenze, fattori causali, ad es. in diverso casi, potrebbero essercene vari risultati(varie manifestazioni dell'informazione dell'oggetto in studio) Ciascun risultato del test corrisponde a un elemento
)
condurre test mirati. Nel corso di tali test (ad esempio, il test risulta negli esempi 1.2, 1.3) in uno stato diverso di varie condizioni, influenze, fattori causali, ad es. in diverso casi, potrebbero essercene vari risultati(varie manifestazioni dell'informazione dell'oggetto in studio) Ciascun risultato del test corrisponde a un elemento  o un sottoinsieme
o un sottoinsieme
 imposta S.Se si definisce m come numero di eventi favorevoli MA risultati derivanti da n test, quindi la probabilità a posteriori (probabilità statistica o frequenza di un evento casuale MA)
imposta S.Se si definisce m come numero di eventi favorevoli MA risultati derivanti da n test, quindi la probabilità a posteriori (probabilità statistica o frequenza di un evento casuale MA)
Basato sulla legge dei grandi numeri per
 UN
UN
|
|
quelli. con un aumento del numero di prove, la frequenza di un evento casuale (a posteriori, o statistica, probabilità) tende alla probabilità di tale evento.
Esempio 1.2. La probabilità di ottenere croce quando viene lanciata una moneta, determinata dallo schema dei casi, è 0,5. È necessario lanciare una moneta 10, 20, 30 ... volte e determinare la frequenza di croce di un evento casuale dopo ogni serie di prove.
Soluzione. K. Poisson ha lanciato una moneta 24.000 volte, mentre croce è caduta 11.998 volte. Quindi, secondo la formula (1.7), la probabilità di ottenere croce
 .
.
Compiti per lavoro autonomo
Basato su un ampio materiale statistico ( n ) sono stati ottenuti i valori delle probabilità di occorrenza delle singole lettere dell'alfabeto russo e uno spazio () nei testi, riportati nella tabella 1.1.
Tabella 1.1. La probabilità che si verifichino lettere dell'alfabeto nel testo
|
| ||||||||
|
| ||||||||
|
| ||||||||
|
|
Prendi una pagina di qualsiasi testo e determina la frequenza delle varie lettere su quella pagina. Aumentare l'ambito dei test a due pagine. Confronta i risultati ottenuti con i dati della tabella. Trai una conclusione.
Quando si spara ai bersagli, è stato ottenuto il seguente risultato (vedi Tabella 1.2).
Tabella 1.2. Risultato del tiro al bersaglio
Qual è la probabilità che il bersaglio sarebbe stato colpito dal primo colpo se fosse stato di dimensioni inferiori a "dieci", "nove", ecc.?
3. Pianificare ed eseguire test simili per altri eventi. Presenta i loro risultati.
I. Probabilità condizionali. Probabilità a priori ea posteriori. 3
II.Eventi indipendenti. 5
III.Verifica di ipotesi statistiche. Validità statistica. 7
IV. Utilizzo del test del chi quadrato 19
1. Determinazione dell'affidabilità della differenza tra un insieme di frequenze e un insieme di probabilità. 19
2. Determinazione dell'affidabilità della differenza tra diversi insiemi di frequenze. 26
COMPITO INDIVIDUALE 33
Lezione 2
Probabilità condizionali. Probabilità a priori ea posteriori.
Una variabile casuale è data da tre oggetti: un insieme di eventi elementari, un insieme di eventi e una probabilità di eventi. Vengono chiamati i valori che una variabile casuale può assumere eventi elementari. Vengono chiamati insiemi di eventi elementari eventi. Per variabili casuali numeriche e altre non molto complesse, qualsiasi insieme di eventi elementari concretamente dato è un evento.
Facciamo un esempio: lanciare un dado.
In totale ci sono 6 eventi elementari: "punto", "2 punti", "3 punti" ... "6 punti". Evento - qualsiasi insieme di eventi elementari, ad esempio "pari" - la somma degli eventi elementari "2 punti", "4 punti" e "6 punti".
La probabilità di qualsiasi evento elementare P(A) è 1/6:
la probabilità di un evento è il numero di eventi elementari in esso inclusi, diviso per 6.
Abbastanza spesso, oltre alla probabilità nota di un evento, ci sono alcune informazioni aggiuntive che modificano questa probabilità. Ad esempio, la letalità dei pazienti. ricoverato in ospedale con ulcera gastrica emorragica acuta, è di circa il 10%. Tuttavia, se il paziente ha più di 80 anni, questo tasso di mortalità è del 30%.
Per descrivere tali situazioni, il cosiddetto probabilità condizionali. Sono indicati come P(A/B) e si leggono "probabilità dell'evento A dato l'evento B". Per calcolare la probabilità condizionata si usa la formula:
Torniamo all'esempio precedente:
Lasciare tra i pazienti ricoverati in ospedale con ulcera gastrica emorragica acuta 20% - pazienti di età superiore a 80 anni. Inoltre, tra tutti i pazienti, la percentuale di pazienti deceduti di età superiore agli 80 anni è del 6% (ricordiamo che la percentuale di tutti i decessi è del 10%). In questo caso
Quando si definiscono le probabilità condizionali, vengono spesso utilizzati i termini a priori(letteralmente - sperimentare) e a posteriori(letteralmente - dopo l'esperienza) probabilità.
Usando le probabilità condizionali, è possibile calcolarne altre da una probabilità, ad esempio scambiando un evento e una condizione.
Consideriamo questa tecnica utilizzando l'esempio dell'analisi della relazione tra il rischio di febbre reumatica (febbre reumatica) e uno degli antigeni che ne sono un fattore di rischio.
L'incidenza della febbre reumatica è di circa l'1%. Indichiamo la presenza di reumatismi come R + , mentre P(R +)=0.01.
La presenza di un antigene sarà indicata come A+. Si trova nel 95% dei pazienti con reumatismi e nel 6% delle persone che non soffrono di reumatismi. Nella nostra notazione, queste sono: probabilità condizionali P (A + / R +) \u003d 0,95 e P (A + / R -) \u003d 0,06.
Sulla base di queste tre probabilità, determineremo successivamente altre probabilità.
Innanzitutto, se l'incidenza dei reumatismi è P(R+)=0,01, allora la probabilità di non ammalarsi è P(R-)=1-P(R+)=0,99.
Dalla formula per la probabilità condizionata, troviamo che
P (A + e R +) \u003d P (A + / R +) * P (R +) \u003d 0,95 * 0,01 \u003d 0,0095, o lo 0,95% della popolazione soffre contemporaneamente di reumatismi e ha un antigene.
Allo stesso modo
P (A + e R -) \u003d P (A + / R -) * P (R -) \u003d 0,06 * 0,99 \u003d 0,0594, o il 5,94% della popolazione porta l'antigene, ma non soffre di reumatismi.
Poiché tutti coloro che hanno un antigene hanno i reumatismi o non si ammalano (ma non entrambi contemporaneamente), la somma delle ultime due probabilità fornisce la frequenza di trasporto dell'antigene nella popolazione nel suo insieme:
P (LA +) \u003d P (LA + e R +) + P (LA + e R -) \u003d 0,0095 + 0,0594 \u003d 0,0689
Di conseguenza, la percentuale di persone che non hanno l'antigene lo è
P (LA -) \u003d 1- P (LA +) \u003d 0,9311
Poiché l'incidenza dei reumatismi è dell'1% e la proporzione di persone con antigene e reumatismi è dello 0,95%, la proporzione di persone con reumatismi e che non hanno l'antigene è:
P (A - e R +) \u003d P (R +) - P (A + e R +) \u003d 0,01 - 0,0095 \u003d 0,0005
Ora ci sposteremo nella direzione opposta, passando dalle probabilità degli eventi e delle loro combinazioni alle probabilità condizionate. Secondo la formula di probabilità condizionata originale P (A + / R +) \u003d P (R + e A +) / P (A +) \u003d 0,0095 / 0,0689 0,1379, ovvero circa il 13,8% delle persone che indossano l'antigene diventa reumatico febbre. Poiché l'incidenza della popolazione nel suo insieme è solo dell'1%, il fatto di rilevare l'antigene aumenta la probabilità di reumatismi di 14 volte.
Allo stesso modo, P (R + /A -) \u003d P (R + e A -) / P (A -) \u003d 0,0005 / 0,9311 0,000054, ovvero il fatto che nessun antigene sia stato rilevato durante il test si riduce di 19 volte più probabilità di avere la febbre reumatica.
Formattiamo questa attività in un foglio di calcolo Excel:
|
Presenza di reumatismi R+ | ||
|
Presenza di antigene in pazienti con A+ | ||
|
Presenza di antigene in A+ non malato | ||
|
Probabilità di non ammalarsi |
P(R-)=1- P(R+) | |
|
Allo stesso tempo, soffrono di reumatismi e hanno un antigene |
P (LA + e R +) \u003d P (LA + / R +) * P (R +) | |
|
Portano l'antigene, ma non contraggono i reumatismi |
P (LA + e R -) \u003d P (LA + / R -) * P (R -) | |
|
Frequenza portante dell'antigene nella popolazione nel suo insieme |
P (LA +) \u003d P (LA + e R +) + P (LA + e R -) | |
|
Percentuale di persone che non hanno l'antigene |
P (LA -) \u003d 1- P (LA +) | |
|
Percentuale di persone con febbre reumatica che non hanno l'antigene |
P (A - e R +) \u003d P (R +) - P (A + e R +) | |
|
Le persone che portano l'antigene svilupperanno la febbre reumatica |
P (LA + / R +) \u003d P (R + e A +) / P (LA +) | |
|
Le persone che non portano l'antigene non svilupperanno reumatismi |
P (R + / A -) \u003d P (R + e A -) / P (A -) |
Puoi vedere il processo di creazione di una tabella picture2\p2-1.gif
Domanda numero 38. Gruppo completo di eventi. Formula di probabilità totale. formule di Bayes.
Due eventi. Indipendenza collettiva. La formulazione del teorema della moltiplicazione in questo caso.
Domanda numero 37. Probabilità condizionata. Teorema della moltiplicazione. Definizione di indipendenza
La probabilità condizionata è la probabilità di un evento dato che un altro evento è già accaduto.
P (LA │ B) \u003d p (AB) / p (B)
La probabilità condizionata riflette l'impatto di un evento sulla probabilità di un altro.
Teorema della moltiplicazione.
La probabilità di produrre eventi è determinata dalla formula P (A 1, A 2, .... A n) \u003d P (A 1) P (A 2 / A 1) ... P (A n / A 1 A 2 ... A n -1)
Per il prodotto di due eventi, ne consegue che
P(AB)=P(A/B)P(B)=P(B/A)P(A)
Se un evento non dipende dall'altro, se il verificarsi di uno di essi non influisce sulla probabilità del verificarsi dell'altro, anche quest'ultimo è indipendente dal primo. Questo dà piena ragione per chiamare tali eventi indipendenti. Matematicamente, indipendenza significa che la probabilità condizionata di un evento è uguale alla sua probabilità (probabilità incondizionata).
1. Dicono che l'evento A non dipende dall'evento B se
P(A│B)=P(A)
Se l'evento A non dipende dall'evento B, l'evento B non dipende dall'evento A.
2. Se gli eventi A e B sono indipendenti, allora P(AB)=P(A)P(B) - questa uguaglianza viene utilizzata per determinare eventi indipendenti.
Si dovrebbe distinguere tra indipendenza a coppie degli eventi e indipendenza nell'aggregato.
Gli eventi А1,А2,….An sono chiamati collettivamente indipendenti se sono indipendenti a coppie e ciascuno di essi non dipende dal prodotto di nessun insieme di altri eventi.
Se gli eventi А1,А2,….An sono complessivamente indipendenti, allora
P (LA 1, LA 2, .... UN n) \u003d P (LA 1) P (LA 2) ... P (LA n).
In ogni gruppo, si verificherà sicuramente qualche evento come risultato del test e il verificarsi di uno di essi esclude il verificarsi di tutti gli altri. Tali eventi sono chiamati un gruppo di eventi completo.
Definizione: se un gruppo di eventi è tale che almeno uno di essi deve verificarsi come risultato del test e due di essi sono incompatibili, allora questo gruppo di eventi è chiamato gruppo completo.
Ogni evento di un gruppo completo è chiamato evento elementare. Ogni evento elementare è ugualmente probabile, poiché non c'è motivo di credere che qualcuno di loro sia più possibile di qualsiasi altro evento dell'intero gruppo.
Due eventi opposti formano un gruppo completo.
La frequenza relativa dell'evento A è il rapporto tra il numero di esperienze che hanno portato all'evento A e il numero totale di esperienze.
La differenza tra la frequenza relativa e la probabilità sta nel fatto che la probabilità viene calcolata senza il prodotto diretto degli esperimenti e la frequenza relativa - dopo l'esperienza.
Formula di probabilità totale
(dove A è un evento, H1, H2 ... Hi sono incompatibili a coppie, formando un gruppo completo e A può verificarsi insieme a H1, H2 Hi)
P(A)=P(A|H 1) P(H 1)+P(A|H 2)P(H 2)+P(A|H 3)P(H 3)+…+P(A| Hn)P(Hn)
Formula di Bayes
Commento. Gli eventi Нi sono chiamati ipotesi di probabilità, р(Нi) – probabilità a priori delle ipotesi Нi e probabilità Р(Нi/А) – probabilità a posteriori delle ipotesi Нi.
Si sappia il risultato dell'esperimento, cioè che si è verificato l'evento A. Questo fatto può cambiare le probabilità a priori (cioè conosciute prima dell'esperimento) delle ipotesi. Per rivalutare le probabilità di ipotesi con un risultato noto dell'esperimento, viene utilizzata la formula di Bayes:
Esempio. Dopo due colpi di due tiratori, le cui probabilità di successo sono 0,6 e 0,7, c'era un buco nel bersaglio. Trova la probabilità che il primo tiratore abbia colpito.
Soluzione. Lascia che l'evento A sia un successo con due colpi,
e ipotesi: H1 - il primo colpo e il secondo mancato,
H2 - il primo mancato e il secondo colpo,
H3 - entrambi colpiti,
H4 - entrambi persi.
Probabilità di ipotesi:
p(H1) = 0,6 0,3 = 0,18,
p(H2) = 0,4 0,7 = 0,28,
p(H3) = 0,6 0,7 = 0,42,
p(H4) = 0,4 0,3 = 0,12.
Allora p(A/H1) = p(A/H2) = 1,
p(A/H3) = p(A/H4) = 0.
Pertanto, la probabilità totale p(A) = 0,18 1 + 0,28 1 + 0,42 0 + 0,12 0 = 0,46.
La formula della probabilità totale consente di calcolare la probabilità di un evento di interesse attraverso le probabilità condizionate di tale evento, assumendo determinate ipotesi, nonché le probabilità di queste ipotesi.
Definizione 3.1. Lascia che l'evento A possa verificarsi solo insieme ad uno degli eventi H1, H2, ..., Hp, formando un gruppo completo di eventi incompatibili. Allora gli eventi H1, H2,…, Hp sono chiamati ipotesi.
Teorema 3.1. La probabilità dell'evento A, che si verifica insieme alle ipotesi H1, H2, ..., Hp, è pari a:
dove p(Hi) è la probabilità dell'i-esima ipotesi e p(A/Hi) è la probabilità dell'evento A a condizione che questa ipotesi sia realizzata. La formula (P(A)= ) è chiamata formula di probabilità totale
Domanda numero 39. Schema Bernoulli. Probabilità di m successi in una serie di n prove
- In contatto con 0
- Google+ 0
- OK 0
- Facebook 0

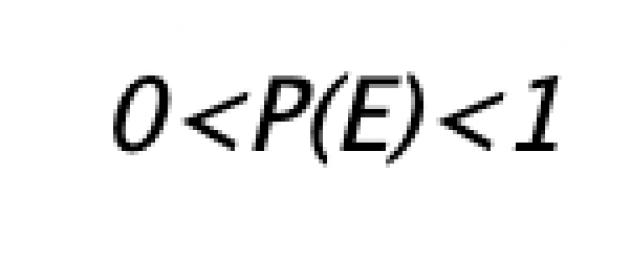
 ,
, ,
n
,
,
n
,