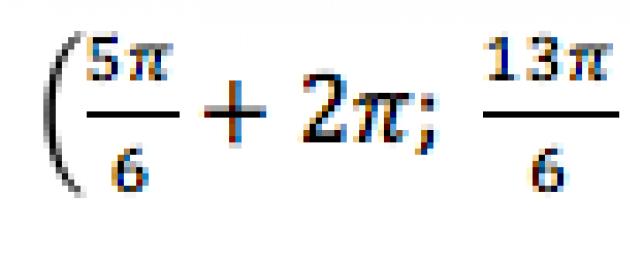Progetto di algebra “Risoluzione delle disuguaglianze trigonometriche” Completato dallo studente della classe 10 “B” Kazachkova Yulia Supervisore: insegnante di matematica Kochakova N.N.
Obiettivo Consolidare il materiale sull'argomento "Risoluzione delle disuguaglianze trigonometriche" e creare un promemoria per gli studenti per prepararsi per il prossimo esame.
Obiettivi: riassumere il materiale su questo argomento. Sistematizzare le informazioni ricevute. Considera questo argomento nell'esame di stato unificato.
Rilevanza La rilevanza dell'argomento che ho scelto risiede nel fatto che i compiti sull'argomento "Risolvere le disuguaglianze trigonometriche" sono inclusi nei compiti dell'Esame di Stato Unificato.
Disuguaglianze trigonometriche Una disuguaglianza è una relazione che collega due numeri o espressioni attraverso uno dei segni: (maggiore di); ≥ (maggiore o uguale a). Una disuguaglianza trigonometrica è una disuguaglianza contenente funzioni trigonometriche.
Disuguaglianze trigonometriche La soluzione delle disuguaglianze contenenti funzioni trigonometriche si riduce, di regola, alla soluzione delle disuguaglianze più semplici della forma: sin x>a, sin x a, cosx a, tgx a,ctg x
Algoritmo per risolvere le disuguaglianze trigonometriche Sull'asse corrispondente a una data funzione trigonometrica, segna il valore numerico dato di questa funzione. Traccia una linea attraverso il punto segnato che interseca la circonferenza unitaria. Seleziona i punti di intersezione di una linea e di un cerchio, tenendo conto del segno di disuguaglianza stretto o non stretto. Seleziona l'arco di cerchio su cui si trovano le soluzioni della disuguaglianza. Determina i valori degli angoli nell'iniziale e punti finali archi di cerchio. Scrivi la soluzione della disuguaglianza tenendo conto della periodicità della funzione trigonometrica data.
Formule per risolvere le disuguaglianze trigonometriche sinx >a; x (arcoseno a + 2πn; π- arcoseno a + 2πn). sinx UN; x (- arccos a + 2πn; arccos a + 2πn). cosxUN; x (arcog a + πn ; + πn). tgx UN; x (πn; arcotan + πn). ctgx
Soluzione grafica delle disuguaglianze trigonometriche fondamentali sinx >a
Soluzione grafica delle disuguaglianze trigonometriche fondamentali sinx Soluzione grafica delle disuguaglianze trigonometriche fondamentali cosx >a Soluzione grafica delle disuguaglianze trigonometriche fondamentali cosx Soluzione grafica delle disuguaglianze trigonometriche fondamentali tgx >a Soluzione grafica delle disuguaglianze trigonometriche fondamentali tgx Soluzione grafica delle disuguaglianze trigonometriche fondamentali ctgx >a
Le disuguaglianze sono relazioni della forma a › b, dove a e b sono espressioni contenenti almeno una variabile. Le disuguaglianze possono essere strette - ‹, › e non strette - ≥, ≤.
Le disuguaglianze trigonometriche sono espressioni della forma: F(x) › a, F(x) ‹ a, F(x) ≤ a, F(x) ≥ a, in cui F(x) è rappresentata da una o più funzioni trigonometriche .
Un esempio della disuguaglianza trigonometrica più semplice è: sin x ‹ 1/2. È consuetudine risolvere graficamente tali problemi; a questo scopo sono stati sviluppati due metodi.
Metodo 1 - Risolvere le disuguaglianze rappresentando graficamente una funzione
Per trovare un intervallo che soddisfi le condizioni di disuguaglianza sin x ‹ 1/2, è necessario eseguire i seguenti passaggi:
- SU asse delle coordinate costruire una sinusoide y = sin x.
- Sullo stesso asse tracciamo il grafico dell'argomento numerico della disuguaglianza, ovvero una retta passante per il punto ½ dell'ordinata OY.
- Segna i punti di intersezione dei due grafici.
- Ombreggia il segmento che rappresenta la soluzione dell'esempio.
Quando in un'espressione sono presenti segni rigidi, i punti di intersezione non sono soluzioni. Poiché il periodo positivo più piccolo di una sinusoide è 2π, scriviamo la risposta come segue:
Se i segni dell'espressione non sono rigidi, l'intervallo della soluzione deve essere racchiuso tra parentesi quadre - . La risposta al problema può anche essere scritta come la seguente disuguaglianza: 
Metodo 2 - Risolvere le disuguaglianze trigonometriche utilizzando il cerchio unitario
Tali problemi possono essere facilmente risolti utilizzando cerchio trigonometrico. L'algoritmo per trovare le risposte è molto semplice:
- Per prima cosa devi disegnare un cerchio unitario.
- Quindi è necessario annotare il valore della funzione arco dell'argomento del lato destro della disuguaglianza sull'arco del cerchio.
- È necessario tracciare una retta passante per il valore della funzione arco parallela all'asse delle ascisse (OX).
- Dopodiché non resta che selezionare l'arco di cerchio, che è l'insieme delle soluzioni della disuguaglianza trigonometrica.
- Scrivi la risposta nel modulo richiesto.
Analizziamo le fasi della soluzione utilizzando l'esempio della disuguaglianza sin x › 1/2. I punti α e β sono contrassegnati sul cerchio - valori
I punti dell'arco situati sopra α e β sono l'intervallo per risolvere la disuguaglianza data.
Se devi risolvere un esempio per cos, l'arco della risposta sarà posizionato simmetricamente all'asse OX, non OY. Puoi considerare la differenza tra gli intervalli di soluzione per sin e cos nei diagrammi sottostanti nel testo.
Le soluzioni grafiche per le disuguaglianze tangenti e cotangenti differiranno sia dal seno che dal coseno. Ciò è dovuto alle proprietà delle funzioni.
Arcotangente e arcotangente sono tangenti a un cerchio trigonometrico e il periodo positivo minimo per entrambe le funzioni è π. Per utilizzare rapidamente e correttamente il secondo metodo, è necessario ricordare su quale asse sono tracciati i valori di sin, cos, tg e ctg.
La tangente tangente corre parallela all'asse OY. Se tracciamo il valore dell'arcotan a sulla circonferenza unitaria, il secondo punto richiesto si troverà nel quarto diagonale. Angoli
Sono punti di interruzione per la funzione, poiché il grafico tende a raggiungerli, ma non li raggiunge mai.
Nel caso della cotangente, la tangente corre parallela all'asse OX e la funzione viene interrotta nei punti π e 2π.
Disuguaglianze trigonometriche complesse
Se l'argomento della funzione di disuguaglianza è rappresentato non solo da una variabile, ma da un'intera espressione contenente un'incognita, allora stiamo già parlando di disuguaglianza complessa. Il processo e la procedura per risolverlo sono leggermente diversi dai metodi sopra descritti. Supponiamo di dover trovare una soluzione alla seguente disuguaglianza:
La soluzione grafica prevede la costruzione di una sinusoide ordinaria y = sin x utilizzando valori di x selezionati arbitrariamente. Calcoliamo una tabella con le coordinate per i punti di controllo del grafico:
Il risultato dovrebbe essere una bella curva.
Per facilitare la ricerca di una soluzione, sostituiamo l’argomento della funzione complessa
L'intersezione di due grafici ci consente di determinare l'area dei valori desiderati in cui è soddisfatta la condizione di disuguaglianza.
Il segmento trovato è una soluzione per la variabile t:
Tuttavia, l'obiettivo dell'attività è trovare tutte le possibili varianti dell'incognita x:
Risolvere la doppia disuguaglianza è abbastanza semplice; è necessario spostare π/3 nelle parti estreme dell'equazione ed eseguire i calcoli richiesti:
Rispondi al compito assomiglierà all'intervallo per la disuguaglianza rigorosa:
Tali problemi richiederanno esperienza e destrezza da parte degli studenti nella gestione delle funzioni trigonometriche. Più compiti formativi vengono risolti durante il processo di preparazione, più facile e veloce lo studente troverà la risposta alla domanda. Domanda esame di Stato Unificato test.
Risoluzione di semplici equazioni trigonometriche
Innanzitutto, ricordiamo le formule per risolvere le equazioni trigonometriche più semplici.
- $sinx=a$
- $cosx=a$
- $tgx=a$
- $ctgx=a$
Risoluzione di semplici disuguaglianze trigonometriche.
Per risolvere le disuguaglianze trigonometriche più semplici, dobbiamo prima risolvere l'equazione corrispondente e quindi, utilizzando un cerchio trigonometrico, trovare una soluzione alla disuguaglianza. Consideriamo le soluzioni alle più semplici disuguaglianze trigonometriche utilizzando esempi.
Esempio 1
$sinx\ge\frac(1)(2)$
Troviamo una soluzione disuguaglianza trigonometrica $sinx=\frac(1)(2)$
\ \
Figura 1. Soluzione della disuguaglianza $sinx\ge \frac(1)(2)$.
Poiché la disuguaglianza ha segno “maggiore o uguale a”, la soluzione si trova sull’arco superiore del cerchio (relativo alla soluzione dell’equazione).
Risposta: $\left[\frac(\pi )(6)+2\pi n,\frac(5\pi )(6)+2\pi n\right]$.
Esempio 2
Troviamo la soluzione della disuguaglianza trigonometrica $cosx=\frac(\sqrt(3))(2)$
\ \
Segniamo la soluzione sul cerchio trigonometrico
Poiché la disuguaglianza ha il segno “minore di”, la soluzione si trova sull'arco di cerchio situato a sinistra (rispetto alla soluzione dell'equazione).
Risposta: $\left(\frac(\pi )(6)+2\pi n,\frac(11\pi )(6)+2\pi n\right)$.
Esempio 3
$tgx\le \frac(\sqrt(3))(3)$
Troviamo la soluzione della disuguaglianza trigonometrica $tgx=\frac(\sqrt(3))(3)$
\ \
Anche qui abbiamo bisogno di un dominio di definizione. Come ricordiamo, la funzione tangente $x\ne \frac(\pi )(2)+\pi n,n\in Z$
Segniamo la soluzione sul cerchio trigonometrico
Figura 3. Soluzione della disuguaglianza $tgx\le \frac(\sqrt(3))(3)$.
Poiché la disuguaglianza ha un segno “minore o uguale”, la soluzione si trova sugli archi circolari contrassegnati in blu nella Figura 3.
Risposta:$\ \left(-\frac(\pi )(2)+2\pi n\right.,\left.\frac(\pi )(6)+2\pi n\right]\cup \left (\frac(\pi )(2)+2\pi n,\destra.\sinistra.\frac(7\pi )(6)+2\pi n\destra]$
Esempio 4
Troviamo la soluzione della disuguaglianza trigonometrica $ctgx=\sqrt(3)$
\ \
Anche qui abbiamo bisogno di un dominio di definizione. Come ricordiamo, la funzione tangente $x\ne \pi n,n\in Z$
Segniamo la soluzione sul cerchio trigonometrico
Figura 4. Soluzione della disuguaglianza $ctgx\le \sqrt(3)$.
Poiché la disuguaglianza ha segno “maggiore di”, la soluzione si trova sugli archi circolari contrassegnati in blu nella Figura 4.
Risposta:$\ \left(2\pi n,\frac(\pi )(6)+2\pi n\right)\cup \left(\pi +2\pi n,\frac(7\pi )( 6)+2\pi n\destra)$
Ministero dell'Istruzione della Repubblica di Bielorussia
Istituzione educativa
"Università statale di Gomel
intitolato a Francysk Skaryna"
Facoltà di Matematica
Dipartimento di Algebra e Geometria
Accettato per la difesa
Testa Dipartimento Shemetkov L.A.
Equazioni trigonometriche e disuguaglianze
Corsi
Esecutore:
studente del gruppo M-51
CM. Gorskij
Supervisore scientifico Ph.D.-M.Sc.,
docente senior
V.G. Safonov
Gomel 2008
INTRODUZIONE
METODI FONDAMENTALI PER LA RISOLUZIONE DI EQUAZIONI TRIGONOMETRICHE
Fattorizzazione
Risolvere equazioni convertendo il prodotto di funzioni trigonometriche in una somma
Risolvere equazioni utilizzando formule a triplo argomento
Moltiplicazione per una funzione trigonometrica
EQUAZIONI TRIGONOMETRICHE NON STANDARD
DISUGUAGLIANZE TRIGONOMETRICHE
SELEZIONE DELLE RADICI
COMPITI PER UNA SOLUZIONE INDIPENDENTE
CONCLUSIONE
ELENCO DELLE FONTI UTILIZZATE
Nell'antichità la trigonometria nacque in connessione con le esigenze dell'astronomia, della topografia e dell'edilizia, cioè era di natura puramente geometrica e rappresentava principalmente<<исчисление хорд>>. Nel corso del tempo, alcuni momenti analitici hanno cominciato a intervallarsi in esso. Nella prima metà del XVIII secolo si verificò un brusco cambiamento, dopo il quale la trigonometria prese una nuova direzione e si spostò verso analisi matematica. Fu in questo periodo che le relazioni trigonometriche iniziarono ad essere considerate funzioni.
Le equazioni trigonometriche sono uno degli argomenti più difficili in un corso di matematica scolastica. Le equazioni trigonometriche sorgono quando si risolvono problemi di planimetria, stereometria, astronomia, fisica e altri campi. Equazioni e disuguaglianze trigonometriche si trovano anno dopo anno tra le attività di test centralizzate.
La differenza più importante tra le equazioni trigonometriche e le equazioni algebriche è che le equazioni algebriche hanno un numero finito di radici, mentre le equazioni trigonometriche --- infinito, il che complica notevolmente la selezione delle radici. Un'altra caratteristica specifica delle equazioni trigonometriche è la forma non univoca di scrittura della risposta.
Questa tesi è dedicata ai metodi per risolvere equazioni e disequazioni trigonometriche.
La tesi è composta da 6 sezioni.
La prima sezione fornisce le informazioni teoriche di base: definizione e proprietà delle funzioni trigonometriche e trigonometriche inverse; tabella dei valori delle funzioni trigonometriche per alcuni argomenti; esprimere funzioni trigonometriche in termini di altre funzioni trigonometriche, che è molto importante per trasformare le espressioni trigonometriche, specialmente quelle contenenti funzioni trigonometriche inverse; oltre alle formule trigonometriche di base, ben note da corso scolastico, vengono fornite formule che semplificano le espressioni contenenti funzioni trigonometriche inverse.
La seconda sezione descrive i metodi di base per risolvere le equazioni trigonometriche. Vengono considerati la soluzione delle equazioni trigonometriche elementari, il metodo della fattorizzazione e i metodi per ridurre le equazioni trigonometriche a quelle algebriche. Poiché le soluzioni delle equazioni trigonometriche possono essere scritte in diversi modi, e la forma di queste soluzioni non consente di stabilire immediatamente se queste soluzioni sono uguali o diverse, il che può<<сбить с толку>> durante la risoluzione dei test, viene considerato lo schema generale per la risoluzione delle equazioni trigonometriche e viene considerata in dettaglio la trasformazione di gruppi di soluzioni generali di equazioni trigonometriche.
La terza sezione esamina le equazioni trigonometriche non standard, le cui soluzioni si basano sull'approccio funzionale.
La quarta sezione discute le disuguaglianze trigonometriche. Vengono discussi in dettaglio i metodi per risolvere le disuguaglianze trigonometriche elementari, sia sulla circonferenza unitaria che con il metodo grafico. Viene descritto il processo di risoluzione delle disuguaglianze trigonometriche non elementari attraverso disuguaglianze elementari e il metodo degli intervalli, già ben noto agli scolari.
La quinta sezione presenta di più compiti difficili: quando è necessario non solo risolvere un'equazione trigonometrica, ma anche selezionare radici dalle radici trovate che soddisfano alcune condizioni. Questa sezione fornisce soluzioni alle tipiche attività di selezione della radice. Vengono fornite le informazioni teoriche necessarie per selezionare le radici: partizionare un insieme di interi in sottoinsiemi disgiunti, risolvere equazioni in interi (diafante).
La sesta sezione presenta compiti per una soluzione indipendente, presentati sotto forma di test. Le 20 attività di test contengono le attività più difficili che possono essere incontrate durante i test centralizzati.
Equazioni trigonometriche elementari
Le equazioni trigonometriche elementari sono equazioni della forma , dove --- una delle funzioni trigonometriche: , , , .
Le equazioni trigonometriche elementari hanno un numero infinito di radici. Ad esempio, i seguenti valori soddisfano l'equazione: , , , ecc. Formula generale lungo il quale si trovano tutte le radici dell'equazione, dove , è:
Qui può assumere qualsiasi valore intero, ognuno di essi corrisponde a una radice specifica dell'equazione; in questa formula (così come in altre formule con cui vengono risolte le equazioni trigonometriche elementari) vengono chiamati parametro. Di solito scrivono , sottolineando così che il parametro può accettare qualsiasi valore intero.
Le soluzioni dell'equazione , dove , si trovano dalla formula
L'equazione viene risolta utilizzando la formula
e l'equazione è la formula
Notiamo in particolare alcuni casi speciali di equazioni trigonometriche elementari, quando la soluzione può essere scritta senza utilizzare formule generali:
Quando si risolvono equazioni trigonometriche ruolo importante interpreta il periodo delle funzioni trigonometriche. Pertanto presentiamo due utili teoremi:
Teorema Se --- il periodo principale della funzione, allora il numero è il periodo principale della funzione.
I periodi delle funzioni e si dicono commensurabili se esistono numeri naturali E allora .
Teorema Se le funzioni periodiche e , hanno commisurato e , allora hanno un periodo comune, che è il periodo delle funzioni , , .
Il teorema afferma che il periodo della funzione , , , è e non è necessariamente il periodo principale. Ad esempio, il periodo principale delle funzioni e --- e il periodo principale del loro prodotto --- .
Introdurre un argomento ausiliario
Con il modo standard di trasformare le espressioni della forma 
è la seguente tecnica: let --- angolo, dato dalle uguaglianze 
, 
. Per chiunque esiste un tale angolo. Così . Se , o , , , negli altri casi.
Schema per la risoluzione di equazioni trigonometriche
Lo schema di base che utilizzeremo per risolvere le equazioni trigonometriche è il seguente:
risolvere una data equazione si riduce alla risoluzione di equazioni elementari. Soluzioni --- conversioni, fattorizzazione, sostituzione delle incognite. Il principio guida è non perdere le proprie radici. Ciò significa che quando passiamo alle equazioni successive, non abbiamo paura della comparsa di radici extra (estranee), ma ci preoccupiamo solo che ogni equazione successiva della nostra “catena” (o un insieme di equazioni nel caso di ramificazione ) è una conseguenza del precedente. Uno di metodi possibili la selezione della radice è un controllo. Notiamo subito che nel caso delle equazioni trigonometriche, le difficoltà legate alla selezione delle radici e al controllo, di regola, aumentano notevolmente rispetto alle equazioni algebriche. Dopotutto, dobbiamo controllare serie costituite da un numero infinito di termini.
Una menzione speciale dovrebbe essere fatta alla sostituzione delle incognite durante la risoluzione di equazioni trigonometriche. Nella maggior parte dei casi, dopo la necessaria sostituzione, risulta equazione algebrica. Inoltre, le equazioni non sono così rare che, sebbene siano trigonometriche aspetto, sostanzialmente non lo sono, poiché dopo il primo passaggio ---sostituzioni variabili --- si trasformano in algebriche e il ritorno alla trigonometria avviene solo nella fase di risoluzione delle equazioni trigonometriche elementari.
Ricordiamolo ancora una volta: la sostituzione dell'incognita dovrebbe essere effettuata alla prima occasione, l'equazione risultante dopo la sostituzione deve essere risolta fino alla fine, compresa la fase di selezione delle radici, e solo successivamente restituita all'incognita originale;
Una delle caratteristiche delle equazioni trigonometriche è che in molti casi la risposta può essere scritta in vari modi. Anche per risolvere l'equazione 
la risposta può essere scritta così:
1) sotto forma di due serie: 
, , ;
2) in forma standard, che è una combinazione delle serie precedenti: , ;
3) perché 
, allora la risposta può essere scritta nella forma 
, . (Di seguito, la presenza del parametro , , o nel record di risposta significa automaticamente che questo parametro accetta tutti i possibili valori interi. Le eccezioni verranno specificate.)
Ovviamente i tre casi elencati non esauriscono tutte le possibilità per scrivere la risposta all'equazione in esame (ce ne sono infinite).
Ad esempio, quando l'uguaglianza è vera 
. Pertanto nei primi due casi, se , possiamo sostituire con .
Di solito la risposta viene scritta sulla base del punto 2. È utile ricordare la seguente raccomandazione: se il lavoro non termina con la risoluzione dell'equazione, è comunque necessario condurre ricerche e selezionare le radici, quindi la forma di registrazione più conveniente è indicato al punto 1. (Una raccomandazione simile dovrebbe essere data per l'equazione.)
Consideriamo un esempio che illustri quanto detto.
Esempio Risolvi l'equazione.
Soluzione. Il modo più ovvio è il seguente. Questa equazione si divide in due: e . Risolvendo ciascuno di essi e combinando le risposte ottenute, troviamo .
Un altro modo. Dal , quindi, sostituzione e utilizzo delle formule per la riduzione della laurea. Dopo piccole trasformazioni otteniamo , da dove 
.
A prima vista, la seconda formula non presenta particolari vantaggi rispetto alla prima. Tuttavia, se prendiamo, ad esempio, risulta che, ad es. l'equazione ha una soluzione, mentre il primo metodo ci porta alla risposta 
. "Vedere" e dimostrare l'uguaglianza 
non così semplice.
Risposta. .
Conversione e combinazione di gruppi di soluzioni generali di equazioni trigonometriche
Considereremo progressione aritmetica, estendendosi all'infinito in entrambe le direzioni. I membri di questa progressione possono essere divisi in due gruppi di membri, situati a destra e a sinistra di un certo membro chiamato membro centrale o membro zero della progressione.
Fissando uno dei termini di una progressione infinita con un numero pari a zero, dovremo effettuare una doppia numerazione per tutti i restanti termini: positiva per i termini posti a destra, e negativa per i termini posti a sinistra dello zero.
In generale, se la differenza della progressione è il termine zero, la formula per qualsiasi (esimo) termine di una progressione aritmetica infinita è:
Trasformazioni di formule per qualsiasi membro di una progressione aritmetica infinita
1. Se aggiungi o sottrai la differenza della progressione rispetto al termine zero, la progressione non cambierà, ma si sposterà solo il termine zero, ad es. La numerazione dei membri cambierà.
2. Se il coefficiente a variabile moltiplicato per , ciò comporterà solo una riorganizzazione dei gruppi di membri di destra e di sinistra.
3. Se termini successivi di una progressione infinita
ad esempio , , ..., , rendono i termini centrali delle progressioni con la stessa differenza pari a:
quindi una progressione e una serie di progressioni esprimono gli stessi numeri.
Esempio La riga può essere sostituita dalle tre righe seguenti: , , .
4. Se infinite progressioni con la stessa differenza hanno come termini centrali numeri che formano una progressione aritmetica con differenza , allora queste serie possono essere sostituite da una progressione con differenza , e con un termine centrale uguale a uno qualsiasi dei termini centrali di queste progressioni, cioè. Se
quindi queste progressioni vengono combinate in una:
Esempio
. entrambi sono combinati in un unico gruppo, poiché 
.
Per trasformare i gruppi che hanno soluzioni comuni in gruppi che non hanno soluzioni comuni, questi gruppi vengono scomposti in gruppi con un punto comune, e poi si cerca di unire i gruppi risultanti, escludendo quelli ripetitivi.
Fattorizzazione
Il metodo di fattorizzazione è il seguente: se
quindi ogni soluzione dell'equazione
è la soluzione di un insieme di equazioni
L’affermazione opposta è, in generale, falsa: non tutte le soluzioni alla popolazione sono una soluzione all’equazione. Ciò si spiega con il fatto che le soluzioni delle singole equazioni potrebbero non essere incluse nel dominio di definizione della funzione.
Esempio Risolvi l'equazione.
Soluzione. Utilizzando l'identità trigonometrica di base, rappresentiamo l'equazione nella forma
Risposta.
; 
.
Convertire la somma delle funzioni trigonometriche in un prodotto
Esempio
Risolvi l'equazione 
.
Soluzione. Applicando la formula, otteniamo l'equazione equivalente
Risposta. .
Esempio Risolvi l'equazione.
Soluzione. In questo caso, prima di applicare le formule per la somma delle funzioni trigonometriche, dovresti utilizzare la formula di riduzione 
. Di conseguenza, otteniamo l'equazione equivalente
Risposta.
, 
.
Risolvere equazioni convertendo il prodotto di funzioni trigonometriche in una somma
Quando si risolvono una serie di equazioni, vengono utilizzate le formule.
Esempio Risolvi l'equazione
Soluzione.
Risposta. , .
Esempio Risolvi l'equazione.
Soluzione. Applicando la formula, otteniamo un'equazione equivalente:
Risposta. .
Risoluzione di equazioni mediante formule di riduzione
Per risolvere una vasta gamma di equazioni trigonometriche ruolo chiave giocano le formule.
Esempio Risolvi l'equazione.
Soluzione. Applicando la formula, otteniamo un'equazione equivalente.
Risposta. ; .
Risolvere equazioni utilizzando formule a triplo argomento
Esempio Risolvi l'equazione.
Soluzione. Applicando la formula, otteniamo l'equazione
Risposta. ; .
Esempio
Risolvi l'equazione 
.
Soluzione. Applicando le formule per ridurre il grado otteniamo: 
. Applicando otteniamo:
Risposta. ; .
Uguaglianza delle funzioni trigonometriche con lo stesso nome
Esempio Risolvi l'equazione.
Soluzione.
Risposta. , .
Esempio
Risolvi l'equazione 
.
Soluzione. Trasformiamo l'equazione.
Risposta. .
Esempio È noto che e soddisfare l'equazione
Trova l'importo.
Soluzione. Dall'equazione ne consegue che
Risposta. .
Consideriamo le somme della forma
Questi importi possono essere convertiti in un prodotto moltiplicandoli e dividendoli per, quindi otteniamo
Questa tecnica può essere utilizzata per risolvere alcune equazioni trigonometriche, ma va tenuto presente che di conseguenza potrebbero apparire radici estranee. Riassumiamo queste formule:
Esempio Risolvi l'equazione.
Soluzione. Si può vedere che l'insieme è una soluzione dell'equazione originale. Pertanto, moltiplicare i lati sinistro e destro dell'equazione per non porterà alla comparsa di radici aggiuntive.
Abbiamo 
.
Risposta. ; .
Esempio Risolvi l'equazione.
Soluzione. Moltiplichiamo i lati sinistro e destro dell'equazione per e applichiamo le formule per convertire il prodotto delle funzioni trigonometriche in una somma, otteniamo
Questa equazione è equivalente alla combinazione di due equazioni e , da cui e .
Poiché le radici dell'equazione non sono le radici dell'equazione, dovremmo escludere . Ciò significa che nell'insieme è necessario escludere .
Risposta. E , .
Esempio
Risolvi l'equazione 
.
Soluzione. Trasformiamo l'espressione:
L'equazione verrà scritta come:
Risposta. .
Ridurre le equazioni trigonometriche a quelle algebriche
Riducibile a quadrato
Se l'equazione è della forma
quindi la sostituzione lo porta al quadrato, poiché 
() E.
Se al posto del termine è presente , la sostituzione richiesta sarà .
Equazione
arriva a equazione quadratica
presentazione come 
. È facile verificare ciò per cui , non sono radici dell'equazione, ed effettuando la sostituzione , l'equazione si riduce ad un'equazione quadratica.
Esempio Risolvi l'equazione.
Soluzione. Spostiamolo sul lato sinistro, sostituiamolo con ed esprimiamolo tramite e .
Dopo le semplificazioni otteniamo: . Dividi termine per termine ed effettua la sostituzione:
Tornando a , troviamo 
.
Equazioni omogenee rispetto a ,
Consideriamo un'equazione della forma
Dove , , , ..., , --- valido numeri. In ogni termine sul lato sinistro dell'equazione, i gradi dei monomi sono uguali, cioè la somma dei gradi di seno e coseno è la stessa e uguale. Questa equazione si chiama omogeneo rispetto a e , e il numero viene chiamato indicatore di omogeneità .
È chiaro che se , allora l'equazione assumerà la forma:
le cui soluzioni sono i valori a cui , cioè i numeri , . Anche la seconda equazione scritta tra parentesi è omogenea, ma i gradi sono inferiori di 1.
Se , allora questi numeri non sono le radici dell'equazione.
Quando otteniamo: , e il lato sinistro dell'equazione (1) assume il valore .
Quindi, per , e , quindi possiamo dividere entrambi i membri dell'equazione per . Di conseguenza, otteniamo l'equazione:
che, per sostituzione, può essere facilmente ridotto ad algebrico:
Equazioni omogenee con indice di omogeneità 1. Quando abbiamo l'equazione .
Se , allora questa equazione è equivalente all'equazione , , da cui , .
Esempio Risolvi l'equazione.
Soluzione. Questa equazione è omogenea di primo grado. Dividendo entrambe le parti per otteniamo: , , , .
Risposta. .
Esempio Quando arriviamo equazione omogenea Tipo
Soluzione.
Se , quindi dividiamo entrambi i membri dell'equazione per , otteniamo l'equazione 
, che può essere facilmente ridotto al quadrato per sostituzione: 
. Se 
, allora l'equazione ha radici reali , . L'equazione originale avrà due gruppi di soluzioni: , , .
Se 
, allora l'equazione non ha soluzioni.
Esempio Risolvi l'equazione.
Soluzione. Questa equazione secondo omogeneo gradi. Dividendo entrambi i membri dell'equazione per , otteniamo: . Lasciamo , allora , , . , , ; .
Risposta.
.
L'equazione si riduce ad un'equazione della forma
Per fare ciò è sufficiente utilizzare l'identità 
In particolare, l'equazione si riduce a omogenea se la sostituiamo con 
, allora otteniamo un'equazione equivalente:
Esempio Risolvi l'equazione.
Soluzione. Trasformiamo l'equazione in una omogenea:
Dividiamo entrambi i lati dell'equazione per 
, otteniamo l'equazione:
Sia , arriviamo quindi all'equazione quadratica: 
, , 
, 
, .
Risposta.
.
Esempio Risolvi l'equazione.
Soluzione. Facciamo il quadrato di entrambi i lati dell'equazione, tenendo conto che hanno valori positivi: , ,
Lascia stare e poi otteniamo 
, , .
Risposta. .
Equazioni risolte utilizzando le identità 
È utile conoscere le seguenti formule:
Esempio Risolvi l'equazione.
Soluzione. Usando, otteniamo
Risposta.
Non offriamo le formule stesse, ma un metodo per ricavarle:
quindi,
Allo stesso modo, .
Esempio
Risolvi l'equazione 
.
Soluzione. Trasformiamo l'espressione:
L'equazione verrà scritta come:
Accettando, riceviamo. , . Quindi
Risposta. .
Sostituzione trigonometrica universale
Equazione trigonometrica della forma
Dove --- razionale una funzione con l'aiuto delle formule - , così come con l'aiuto delle formule - può essere ridotta a equazione razionale rispetto agli argomenti , , , , dopo i quali l'equazione può essere ridotta ad un'equazione algebrica razionale rispetto all'utilizzo delle formule di sostituzione trigonometrica universale
È da notare che l'uso delle formule può portare ad un restringimento della DO dell'equazione originale, poiché non è definita nei punti, quindi in tali casi è necessario verificare se gli angoli sono le radici dell'equazione originale .
Esempio Risolvi l'equazione.
Soluzione. Secondo le condizioni del compito. Applicando le formule ed effettuando la sostituzione, otteniamo
da dove e quindi .
Equazioni della forma
Equazioni della forma , dove --- polinomio, vengono risolti utilizzando la sostituzione delle incognite
Esempio Risolvi l'equazione.
Soluzione. Effettuando la sostituzione e tenendo conto di ciò, otteniamo
Dove , . --- estraneo radice, perché . Radici dell'equazione 
Sono .
Utilizzo delle limitazioni delle funzionalità
Nella pratica del testing centralizzato, non è così raro imbattersi in equazioni la cui soluzione si basa sulle funzioni limitate e . Per esempio:
Esempio Risolvi l'equazione.
Soluzione. Poiché , , allora il lato sinistro non supera ed è uguale a , se
Per trovare valori che soddisfino entrambe le equazioni, procediamo come segue. Risolviamone uno, poi tra i valori trovati selezioneremo quelli che soddisfano l'altro.
Cominciamo dal secondo: , . Poi , 
.
È chiaro che solo per i numeri pari ci saranno .
Risposta. .
Un'altra idea si realizza risolvendo la seguente equazione:
Esempio
Risolvi l'equazione 
.
Soluzione. Usiamo la proprietà funzione esponenziale: , 
.
Sommando queste disuguaglianze termine per termine abbiamo:
Pertanto, il lato sinistro di questa equazione è uguale se e solo se sono soddisfatte due uguaglianze:
cioè può assumere i valori , , , oppure può assumere i valori , .
Risposta. , .
Esempio
Risolvi l'equazione 
.
Soluzione., . Quindi, 
.
Risposta. .
Esempio Risolvi l'equazione
Soluzione. Indichiamo quindi dalla definizione della funzione trigonometrica inversa che abbiamo 
E 
.
Poiché, allora la disuguaglianza segue dall'equazione, cioè . Da e , quindi e . Tuttavia, ecco perché.
Se e, allora. Poiché era stato precedentemente stabilito che , allora .
Risposta. , .
Esempio Risolvi l'equazione
Soluzione. Regione valori accettabili le equazioni sono .
Per prima cosa mostriamo che la funzione
Per qualsiasi, può assumere solo valori positivi.
Immaginiamo la funzione come segue: .
Dal , allora avviene, cioè 
.
Pertanto, per dimostrare la disuguaglianza, è necessario dimostrarlo 
. A questo scopo, cubiamo quindi entrambi i lati di questa disuguaglianza
La disuguaglianza numerica risultante indica che . Se teniamo conto anche di questo, allora il lato sinistro dell'equazione non è negativo.
Consideriamo ora il lato destro dell'equazione.
Perché 
, Quello
Questo però è noto 
. Ne consegue che, cioè lato destro l'equazione non supera . È stato precedentemente dimostrato che il lato sinistro dell'equazione è non negativo, quindi l'uguaglianza può verificarsi solo se entrambi i lati sono uguali, e questo è possibile solo se .
Risposta. .
Esempio Risolvi l'equazione
Soluzione. Indichiamo e 
. Applicando la disuguaglianza di Cauchy-Bunyakovsky, otteniamo . Ne consegue che 
. D'altra parte, c'è 
. Pertanto, l’equazione non ha radici.
Risposta. .
Esempio Risolvi l'equazione:
Soluzione. Riscriviamo l'equazione come:
Risposta. .
Metodi funzionali per la risoluzione di equazioni trigonometriche e combinate
Non tutte le equazioni risultanti dalle trasformazioni possono essere ridotte a un'equazione dell'una o dell'altra forma standard, per la quale esiste un metodo di soluzione specifico. In questi casi, risulta utile utilizzare proprietà delle funzioni e come monotonia, limitatezza, parità, periodicità, ecc. Quindi, se una delle funzioni diminuisce e la seconda aumenta nell'intervallo, allora se l'equazione ha un radice su questo intervallo, questa radice è unica e quindi, ad esempio, può essere trovata mediante selezione. Se la funzione è limitata sopra, e , e la funzione è limitata sotto, e , allora l'equazione è equivalente al sistema di equazioni
Esempio Risolvi l'equazione
Soluzione. Trasformiamo l'equazione originale nella forma
e risolverlo come quadratico relativo a . Quindi otteniamo,
Risolviamo la prima equazione della popolazione. Tenendo conto della natura limitata della funzione, arriviamo alla conclusione che l'equazione può avere radice solo sul segmento. In questo intervallo la funzione aumenta, e la funzione 
diminuisce. Pertanto, se questa equazione ha una radice, allora è unica. Troviamo per selezione.
Risposta. .
Esempio Risolvi l'equazione
Soluzione. Lascia e 
, allora l'equazione originale può essere scritta come equazione funzionale. Poiché la funzione è dispari, allora . In questo caso, otteniamo l'equazione.
Poiché , ed è monotona su , l'equazione è equivalente all'equazione, cioè 
, che ha una sola radice.
Risposta. .
Esempio
Risolvi l'equazione 
.
Soluzione. Basandosi sul teorema sulla derivata di una funzione complessa, è chiaro che la funzione 
decrescente (funzione decrescente, crescente, decrescente). Da ciò è chiaro che la funzione 
definito su , decrescente. Ecco perché data equazione ha al massimo una radice. Perché 
, Quello
Risposta. .
Esempio Risolvi l'equazione.
Soluzione. Consideriamo l'equazione su tre intervalli.
a) Lascia . Quindi su questo insieme l'equazione originale è equivalente all'equazione . Che non ha soluzioni nell'intervallo, perché 
, , UN . Nell'intervallo, anche l'equazione originale non ha radici, perché 
, UN .
b) Sia . Quindi su questo insieme l'equazione originale è equivalente all'equazione
le cui radici nell'intervallo sono i numeri , , , .
c) Sia . Quindi su questo insieme l'equazione originale è equivalente all'equazione
Che non ha soluzioni nell'intervallo, perché , e . Nell'intervallo, anche l'equazione non ha soluzioni, perché , , UN .
Risposta. , , , .
Metodo della simmetria
Il metodo della simmetria è conveniente da usare quando la formulazione del compito richiede la soluzione unica di un'equazione, disuguaglianza, sistema, ecc. o un'indicazione esatta del numero di soluzioni. In questo caso, dovrebbe essere rilevata qualsiasi simmetria delle espressioni fornite.
È inoltre necessario tenere conto della varietà dei diversi tipi di simmetria possibili.
Altrettanto importante è il rigoroso rispetto delle fasi logiche nel ragionamento con simmetria.
In genere, la simmetria consente solo di stabilire condizioni necessarie, e quindi è necessario verificarne la sufficienza.
Esempio Trova tutti i valori del parametro per cui l'equazione ha una soluzione unica.
Soluzione. Notare che --- Anche funzioni, quindi il lato sinistro dell'equazione è una funzione pari.
Quindi se --- soluzione equazioni, cioè anche la soluzione dell'equazione. Se --- l'unica cosa soluzione dell'equazione, quindi necessario , .
Selezioneremo possibile valori, richiedendo che sia la radice dell'equazione.
Notiamo subito che altri valori non possono soddisfare le condizioni del problema.
Ma non è ancora noto se tutti quelli selezionati soddisfino effettivamente le condizioni del problema.
Adeguatezza.
1), l'equazione assumerà la forma 
.
2), l’equazione assumerà la forma:
È ovvio che, per tutti e 
. Pertanto l’ultima equazione è equivalente al sistema:
Abbiamo quindi dimostrato che per , l’equazione ha un’unica soluzione.
Risposta. .
Soluzione con esplorazione delle funzioni
Esempio Dimostrare che tutte le soluzioni dell'equazione
Numeri interi.
Soluzione. Il periodo principale dell'equazione originale è . Pertanto, esaminiamo prima questa equazione sull'intervallo.
Trasformiamo l'equazione nella forma:
Usando un microcalcolatore otteniamo:
Se , allora dalle uguaglianze precedenti otteniamo:
Avendo risolto l'equazione risultante, otteniamo: .
I calcoli eseguiti consentono di assumere che le radici dell'equazione appartenente al segmento siano , e .
I test diretti confermano questa ipotesi. Pertanto, è stato dimostrato che le radici dell'equazione sono solo numeri interi , .
Esempio
Risolvi l'equazione 
.
Soluzione. Troviamo il periodo principale dell'equazione. La funzione ha un periodo base pari a . Il periodo principale della funzione è . Il minimo comune multiplo di e è uguale a . Pertanto, il periodo principale dell'equazione è . Permettere .
Ovviamente, è una soluzione all’equazione. All'intervallo. La funzione è negativa. Pertanto, altre radici dell'equazione dovrebbero essere cercate solo sugli intervalli x e .
Utilizzando un microcalcolatore, troviamo innanzitutto i valori approssimativi delle radici dell'equazione. Per fare ciò, componiamo una tabella di valori di funzione 
sugli intervalli e ; cioè sugli intervalli e .
| 0 | 0 | 202,5 | 0,85355342 |
| 3 | -0,00080306 | 207 | 0,6893642 |
| 6 | -0,00119426 | 210 | 0,57635189 |
| 9 | -0,00261932 | 213 | 0,4614465 |
| 12 | -0,00448897 | 216 | 0,34549155 |
| 15 | -0,00667995 | 219 | 0,22934931 |
| 18 | -0,00903692 | 222 | 0,1138931 |
| 21 | -0,01137519 | 225 | 0,00000002 |
| 24 | -0,01312438 | 228 | -0,11145712 |
| 27 | -0,01512438 | 231 | -0,21961736 |
| 30 | -0,01604446 | 234 | -0,32363903 |
| 33 | -0,01597149 | 237 | -0,42270819 |
| 36 | -0,01462203 | 240 | -0,5160445 |
| 39 | -0,01170562 | 243 | -0,60290965 |
| 42 | -0,00692866 | 246 | -0,65261345 |
| 45 | 0,00000002 | 249 | -0,75452006 |
| 48 | 0,00936458 | 252 | -0,81805397 |
| 51 | 0,02143757 | 255 | -0,87270535 |
| 54 | 0,03647455 | 258 | -0,91803444 |
| 57 | 0,0547098 | 261 | -0,95367586 |
| 60 | 0,07635185 | 264 | -0,97934187 |
| 63 | 0,10157893 | 267 | -0,99482505 |
| 66 | 0,1305352 | 270 | -1 |
| 67,5 | 0,14644661 |
Dalla tabella sono facilmente distinguibili le seguenti ipotesi: le radici dell'equazione appartenente al segmento sono i numeri: ; ; . I test diretti confermano questa ipotesi.
Risposta.
; 
; .
Risolvere le disuguaglianze trigonometriche utilizzando la circonferenza unitaria
Quando si risolvono le disuguaglianze trigonometriche della forma , dov'è una delle funzioni trigonometriche, è conveniente utilizzare cerchio trigonometrico per presentare nel modo più chiaro le soluzioni alla disuguaglianza e scrivere la risposta. Il metodo principale per risolvere le disuguaglianze trigonometriche è ridurle alle più semplici disuguaglianze di tipo. Diamo un'occhiata a un esempio di come risolvere tali disuguaglianze.
Esempio Risolvi la disuguaglianza.
Soluzione. Disegniamo un cerchio trigonometrico e segniamo su di esso i punti per i quali l'ordinata supera .
La soluzione a questa disuguaglianza sarà . È anche chiaro che se un certo numero differisce da qualsiasi numero dell'intervallo specificato di , anche questo non sarà inferiore a . Pertanto, devi solo aggiungere alle estremità del segmento della soluzione trovata. Infine, troviamo che le soluzioni alla disuguaglianza originaria saranno tutte 
.
Risposta.
.
Per risolvere le disuguaglianze con tangente e cotangente, è utile il concetto di linea di tangenti e cotangenti. Queste sono le rette e, rispettivamente (in Figura (1) e (2)), tangenti al cerchio trigonometrico.
È facile vedere che se costruiamo un raggio con origine nell'origine delle coordinate, formando un angolo con la direzione positiva dell'asse delle ascisse, allora la lunghezza del segmento dal punto al punto di intersezione di questo raggio con la retta tangente è esattamente uguale alla tangente dell'angolo che questo raggio forma con l'asse delle ascisse. Un'osservazione simile avviene per la cotangente.
Esempio Risolvi la disuguaglianza.
Soluzione. Indichiamo , quindi la disuguaglianza assumerà la forma più semplice: . Consideriamo un intervallo di lunghezza pari al più piccolo periodo positivo (LPP) della tangente. Su questo segmento, utilizzando la retta delle tangenti, stabiliamo che . Ricordiamo ora cosa è necessario aggiungere poiché NPP funziona. COSÌ, 
. Tornando alla variabile, otteniamo che.
Risposta.
.
È conveniente risolvere le disuguaglianze con funzioni trigonometriche inverse utilizzando grafici di funzioni trigonometriche inverse. Mostriamo come si fa con un esempio.
Risolvere graficamente le disuguaglianze trigonometriche
Tieni presente che se --- periodico funzione, allora per risolvere la disuguaglianza è necessario trovare la sua soluzione su un segmento la cui lunghezza è uguale al periodo della funzione. Tutte le soluzioni alla disuguaglianza originale saranno costituite dai valori trovati, così come da tutti quelli che differiscono da quelli trovati per un numero intero qualsiasi di periodi della funzione.
Consideriamo la soluzione alla disuguaglianza ().
Poiché , allora la disuguaglianza non ha soluzioni. Se , allora l'insieme delle soluzioni della disuguaglianza --- impostato tutti i numeri reali.
Permettere . La funzione seno ha il periodo positivo più piccolo, quindi la disuguaglianza può essere risolta prima su un segmento di lunghezza, ad esempio sul segmento. Costruiamo grafici di funzioni e (). sono dati da disuguaglianze della forma: e, da dove,
In questo lavoro sono stati considerati metodi per risolvere equazioni e disuguaglianze trigonometriche, sia a livello semplice che olimpico. Sono stati considerati i principali metodi per risolvere equazioni e disuguaglianze trigonometriche e, inoltre, specifici --- caratteristico solo per equazioni e disequazioni trigonometriche e metodi funzionali generali per risolvere equazioni e disequazioni applicati alle equazioni trigonometriche.
La tesi fornisce informazioni teoriche di base: definizione e proprietà delle funzioni trigonometriche e trigonometriche inverse; esprimere funzioni trigonometriche in termini di altre funzioni trigonometriche, che è molto importante per trasformare le espressioni trigonometriche, specialmente quelle contenenti funzioni trigonometriche inverse; Oltre alle formule trigonometriche di base, ben conosciute dal corso scolastico, vengono fornite formule che semplificano le espressioni contenenti funzioni trigonometriche inverse. Vengono considerati la soluzione delle equazioni trigonometriche elementari, il metodo della fattorizzazione e i metodi per ridurre le equazioni trigonometriche a quelle algebriche. Dato che le soluzioni delle equazioni trigonometriche possono essere scritte in diversi modi e la forma di queste soluzioni non consente di determinare immediatamente se queste soluzioni sono uguali o diverse, viene considerato uno schema generale per la risoluzione delle equazioni trigonometriche e la trasformazione vengono considerati in dettaglio i gruppi di soluzioni generali delle equazioni trigonometriche. Vengono discussi in dettaglio i metodi per risolvere le disuguaglianze trigonometriche elementari, sia sulla circonferenza unitaria che con il metodo grafico. Viene descritto il processo di risoluzione delle disuguaglianze trigonometriche non elementari attraverso disuguaglianze elementari e il metodo degli intervalli, già ben noto agli scolari. Vengono fornite le soluzioni ai compiti tipici per la selezione delle radici. Vengono fornite le informazioni teoriche necessarie per selezionare le radici: partizionare un insieme di interi in sottoinsiemi disgiunti, risolvere equazioni in interi (diafante).
I risultati di questa tesi possono essere utilizzati come materiale didattico durante la preparazione dei corsi e tesi, quando si compilano i corsi facoltativi per gli scolari, il lavoro può essere utilizzato anche per preparare gli studenti agli esami di ammissione e ai test centralizzati.
Vygodsky Ya.Ya., Manuale di matematica elementare. /Vygodsky Ya.Ya. --- M.: Nauka, 1970.
Igudisman O., La matematica nella prova orale / Igudisman O. --- M.: Iris Press, Rolf, 2001.
Azarov A.I., equazioni/Azarov A.I., Gladun O.M., Fedosenko V.S. --- Mn.: Trivio, 1994.
Litvinenko V.N., Laboratorio sulla matematica elementare / Litvinenko V.N. --- M.: Educazione, 1991.
Sharygin I.F., Corso facoltativo di matematica: risoluzione di problemi / Sharygin I.F., Golubev V.I. --- M.: Educazione, 1991.
Bardushkin V., Equazioni trigonometriche. Selezione radice/B. Bardushkin, A. Prokofiev.// Matematica, n. 12, 2005 p. 23--27.
Vasilevsky A.B., Compiti per attività extrascolastiche in matematica/Vasilevskij A.B. --- Mn.: Asveta popolare. 1988. --- 176 pag.
Sapunov P. I., Trasformazione e unione di gruppi di soluzioni generali di equazioni trigonometriche / Sapunov P. I. // Educazione matematica, numero 3, 1935.
Borodin P., Trigonometria. Materiali esami di ammissione all'Università statale di Mosca [testo]/P. Borodin, V. Galkin, V. Panferov, I. Sergeev, V. Tarasov // Matematica n. 1, 2005 p. 36--48.
Samusenko A.V., Matematica: Errori comuni candidati: Manuale di riferimento/Samusenko A.V., Kazachenok V.V. --- Mn.: Scuola superiore, 1991.
Azarov A.I., Metodi funzionali e grafici per risolvere problemi di esame / Azarov A.I., Barvenov S.A., --- Mn.: Aversev, 2004.
- VKontakte 0
- Google+ 0
- OK 0
- Facebook 0
