Att lösa problem i matematik är ofta åtföljt av många svårigheter för eleverna. Att hjälpa studenten att hantera dessa svårigheter, samt lära dem att tillämpa sina befintliga teoretiska kunskaper när de löser specifika problem i alla delar av kursen i ämnet "Matematik" är huvudsyftet med vår webbplats.
När eleverna börjar lösa problem om ämnet ska eleverna kunna konstruera en punkt på ett plan med hjälp av dess koordinater, samt hitta koordinaterna för en given punkt.
Beräkning av avståndet mellan två punkter A(x A; y A) och B(x B; y B) tagna på ett plan utförs med hjälp av formeln d = √((x A – x B) 2 + (y A – y B) 2), där d är längden på segmentet som förbinder dessa punkter på planet.
Om en av ändarna på segmentet sammanfaller med koordinaternas ursprung och den andra har koordinaterna M(x M; y M), kommer formeln för beräkning av d att ha formen OM = √(x M 2 + y M 2 ).
1. Beräkning av avståndet mellan två punkter baserat på de givna koordinaterna för dessa punkter
Exempel 1.
Hitta längden på segmentet som förbinder koordinatplan punkterna A(2; -5) och B(-4; 3) (fig. 1).
Lösning.
Problemformuleringen säger: x A = 2; xB = -4; y A = -5 och y B = 3. Hitta d.
Genom att tillämpa formeln d = √((x A – x B) 2 + (y A – y B) 2), får vi:
d = AB = √((2 – (-4)) 2 + (-5 – 3) 2) = 10.
2. Beräkning av koordinaterna för en punkt som är lika långt från tre givna punkter
Exempel 2.
Hitta koordinaterna för punkt O 1, som är lika långt från tre punkter A(7; -1) och B(-2; 2) och C(-1; -5).
Lösning.
Av formuleringen av problemvillkoren följer att O 1 A = O 1 B = O 1 C. Låt önskad punkt O 1 ha koordinater (a; b). Med formeln d = √((x A – x B) 2 + (y A – y B) 2) finner vi:
OiA = √((a – 7) 2 + (b + 1) 2);
OiB = √((a + 2) 2 + (b – 2) 2);
OiC = √((a + 1) 2 + (b + 5) 2).
Låt oss skapa ett system med två ekvationer:
(√((a – 7) 2 + (b + 1) 2) = √((a + 2) 2 + (b – 2) 2),
(√((a – 7) 2 + (b + 1) 2) = √((a + 1) 2 + (b + 5) 2).
Efter att ha kvadrerat vänster och rätt delar vi skriver ekvationerna:
((a – 7) 2 + (b + 1) 2 = (a + 2) 2 + (b – 2) 2,
((a – 7) 2 + (b + 1) 2 = (a + 1) 2 + (b + 5) 2.
Förenkla, låt oss skriva
(-3a + b + 7 = 0,
(-2a – b + 3 = 0.
Efter att ha löst systemet får vi: a = 2; b = -1.
Punkt O 1 (2; -1) är lika långt från de tre punkter som anges i villkoret som inte ligger på samma räta linje. Denna punkt är mitten av en cirkel som går genom tre givna poäng (Fig. 2).
3. Beräkning av abskissan (ordinatan) för en punkt som ligger på abskissan (ordinatan) och ligger på ett givet avstånd från en given punkt
Exempel 3.
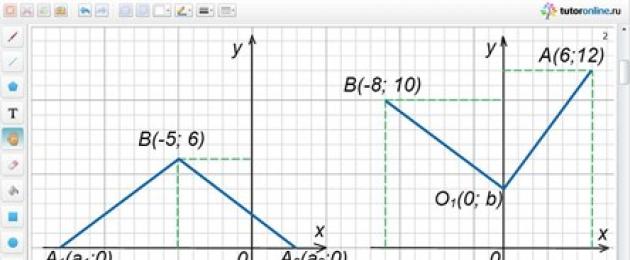
Avståndet från punkt B(-5; 6) till punkt A som ligger på Ox-axeln är 10. Hitta punkt A.
Lösning.
Av formuleringen av problemvillkoren följer att ordinatan för punkt A är lika med noll och AB = 10.
När vi betecknar abskissan för punkt A med a, skriver vi A(a; 0).
AB = √((a + 5) 2 + (0 – 6) 2) = √((a + 5) 2 + 36).
Vi får ekvationen √((a + 5) 2 + 36) = 10. Förenklat har vi
a 2 + 10a – 39 = 0.
Rötterna till denna ekvation är a 1 = -13; och 2 = 3.
Vi får två poäng A 1 (-13; 0) och A 2 (3; 0).
Undersökning:
A 1 B = √((-13 + 5) 2 + (0 – 6) 2) = 10.
A 2 B = √((3 + 5) 2 + (0 – 6) 2) = 10.
Båda erhållna poängen är lämpliga beroende på förhållandena för problemet (Fig. 3).
4. Beräkning av abskissan (ordinatan) för en punkt som ligger på abskissan (ordinatan) och är på samma avstånd från två givna punkter
Exempel 4.
Hitta en punkt på Oy-axeln som är på samma avstånd från punkterna A (6, 12) och B (-8, 10).
Lösning.
Låt koordinaterna för den punkt som krävs av villkoren för problemet, som ligger på Oy-axeln, vara O 1 (0; b) (vid den punkt som ligger på Oy-axeln är abskissan noll). Det följer av villkoret att O 1 A = O 1 B.
Med formeln d = √((x A – x B) 2 + (y A – y B) 2) finner vi:
OiA = √((0 – 6) 2 + (b – 12) 2) = √(36 + (b – 12) 2);
O 1 B = √((a + 8) 2 + (b – 10) 2) = √(64 + (b – 10) 2).
Vi har ekvationen √(36 + (b – 12) 2) = √(64 + (b – 10) 2) eller 36 + (b – 12) 2 = 64 + (b – 10) 2.
Efter förenkling får vi: b – 4 = 0, b = 4.
Punkt O 1 (0; 4) krävs av villkoren för problemet (Fig. 4).
5. Beräkning av koordinaterna för en punkt som ligger på samma avstånd från koordinataxlarna och någon given punkt
Exempel 5.
Hitta punkt M som ligger på koordinatplanet på samma avstånd från koordinataxlarna och från punkt A(-2; 1).
Lösning.
Den erforderliga punkten M, liksom punkt A(-2; 1), ligger i den andra koordinatvinkeln, eftersom den är lika långt från punkterna A, P 1 och P 2 (Fig. 5). Avstånden för punkt M från koordinataxlarna är desamma, därför kommer dess koordinater att vara (-a; a), där a > 0.
Av villkoren för problemet följer att MA = MR 1 = MR 2, MR 1 = a; MP 2 = |-a|,
de där. |-a| = a.
Med formeln d = √((x A – x B) 2 + (y A – y B) 2) finner vi:
MA = √((-a + 2) 2 + (a – 1) 2).
Låt oss göra en ekvation:
√((-а + 2) 2 + (а – 1) 2) = а.
Efter kvadrering och förenkling har vi: a 2 – 6a + 5 = 0. Lös ekvationen, hitta a 1 = 1; och 2 = 5.
Vi får två punkter M 1 (-1; 1) och M 2 (-5; 5) som uppfyller villkoren för problemet. 
6. Beräkning av koordinaterna för en punkt som är belägen på samma specificerade avstånd från abskissan (ordinataxeln) och från den givna punkten
Exempel 6.
Hitta en punkt M så att dess avstånd från ordinataaxeln och från punkt A(8; 6) är lika med 5.
Lösning.
Av villkoren för problemet följer att MA = 5 och abskissan för punkt M är lika med 5. Låt ordinatan för punkt M vara lika med b, sedan M(5; b) (Fig. 6).
Enligt formeln d = √((x A – x B) 2 + (y A – y B) 2) har vi:
MA = √((5 – 8) 2 + (b – 6) 2).
Låt oss göra en ekvation:
√((5 – 8) 2 + (b – 6) 2) = 5. Förenklat får vi: b 2 – 12b + 20 = 0. Rötterna till denna ekvation är b 1 = 2; b 2 = 10. Följaktligen finns det två punkter som uppfyller villkoren för problemet: M 1 (5; 2) och M 2 (5; 10).
Det är känt att många studenter, när de löser problem självständigt, behöver ständiga konsultationer om tekniker och metoder för att lösa dem. Ofta kan en elev inte hitta ett sätt att lösa ett problem utan hjälp av en lärare. Eleven kan få nödvändiga råd om problemlösning på vår hemsida.
Har du fortfarande frågor? Vet du inte hur man hittar avståndet mellan två punkter på ett plan?
För att få hjälp av en handledare, registrera dig.
Första lektionen är gratis!
webbplats, vid kopiering av material helt eller delvis krävs en länk till källan.
Låt , (Figur 2.3). Krävs för att hitta.
Figur 2.3. Avståndet mellan två punkter.
Från det rektangulära enligt Pythagoras sats har vi
Det är ,
Denna formel är giltig för vilken plats som helst av punkter och .
II. Indelning av ett segment i detta avseende:
Låt , . Det krävs att hitta , liggande på segmentet och dividera det i ett givet förhållande (Figur 2.4.).
Figur 2.4. Uppdelning av ett segment i detta avseende.
Från likheten ~, det vill säga varifrån. Likaså.
Således,
– formel för att dividera ett segment i förhållande till .
Om då
– koordinater för mitten av segmentet.
Kommentar. De härledda formlerna kan generaliseras till fallet med ett rumsligt rektangulärt kartesiskt koordinatsystem. Låt poängen , . Sedan
- formel för att hitta avståndet mellan punkter och .
Formel för att dividera ett segment i relation.
Förutom kartesiska på planet och i rymden kan du konstruera stort antal andra koordinatsystem, det vill säga sätt att karakterisera en punkts position på ett plan eller i rymden med hjälp av två eller tre numeriska parametrar (koordinater). Låt oss titta på några av de befintliga system koordinater
På ett plan är det möjligt att bestämma polärt koordinatsystem , som särskilt används vid studiet av rotationsrörelser.
Figur 2.5. Polärt koordinatsystem.
Låt oss fixa en punkt på planet och en halvlinje som kommer ut från det, och även välja en skalenhet (Figur 2.5). Punkten kallas Pol , halvlinje – polära axeln . Låt oss tilldela två siffror till en godtycklig punkt:
– polär radie , lika med avståndet från punkt M till pol O;
– polär vinkel , lika med vinkel mellan polaxeln och halvlinjen.
Mätt i radianer räknas värdenas positiva riktning från moturs, vanligtvis antaget.
Den polära radien motsvarar polen, den polära vinkeln är inte definierad för den.
Låt oss hitta sambandet mellan rektangulära och polära koordinater (Figur 2.6).
Figur 2.6. Samband mellan rektangulära och polära koordinatsystem.
Vi kommer att betrakta ursprunget för det rektangulära koordinatsystemet som en pol och att strålen är polaxeln. Låta - in ett rektangulärt kartesiskt koordinatsystem och - i ett polärt koordinatsystem. Låt oss hitta sambandet mellan rektangulära och polära koordinater.
Från rektangulär och från rektangulär. Alltså formlerna
uttrycka de rektangulära koordinaterna för en punkt i termer av dess polära koordinater.
Det omvända förhållandet uttrycks av formlerna
Kommentar. Den polära vinkeln kan också bestämmas från formeln, som tidigare har bestämts från rektangulära koordinater i vilken kvadrant punkten ligger.
Exempel 1. Hitta de polära koordinaterna för en punkt.
Lösning. Vi beräknar ; Den polära vinkeln hittas från förhållandena:
Därför, därför.
Exempel 2. Hitta de rektangulära koordinaterna för punkten.
Lösning. Vi räknar
Vi får.
I det tredimensionella rummet används, förutom det rektangulära kartesiska koordinatsystemet, ofta cylindriska och sfäriska koordinatsystem.
Cylindriskt koordinatsystemär ett polärt koordinatsystem i planet, till vilket läggs en rumsaxel vinkelrät mot detta plan (Figur 2.7). Positionen för vilken punkt som helst kännetecknas av tre siffror - dess cylindriska koordinater: , där och är de polära koordinaterna (polär radie och polär vinkel) för projektionen av punkten på det plan i vilket det polära koordinatsystemet är valt - applikationen, som är lika med avståndet från punkten till det angivna planet.
Figur 2.7. Cylindriskt koordinatsystem
För att fastställa förhållandet mellan det rektangulära kartesiska koordinatsystemet och det cylindriska, placerar vi dem i förhållande till varandra som i figur 2.8 (vi placerar planet i planet, och polaxeln sammanfaller med den positiva riktningen för axeln, axeln är vanligt i båda koordinatsystemen).
Låt vara de rektangulära koordinaterna för punkten, vara de cylindriska koordinaterna för denna punkt, och vara projektionen av punkten på planet. Sedan
formler som förbinder rektangulära och cylindriska koordinater för en punkt.
Figur 2.8. Förhållandet mellan den rektangulära kartesiska
och cylindriska koordinatsystem
Kommentar. Cylindriska koordinater används ofta när man överväger rotationskroppar, med axeln placerad längs rotationsaxeln.
Sfäriskt koordinatsystem kan konstrueras enligt följande. Låt oss välja polaxeln i planet. Genom punkten drar vi en rät linje vinkelrätt mot planet (normal). Då kan vilken punkt som helst i rymden associeras med tre reella tal, där är avståndet från punkten till, är vinkeln mellan axeln och projektionen av segmentet på planet, och är vinkeln mellan normalen och segmentet. Lägg märke till att , , .
Om vi placerar planet i planet och väljer att polaxeln ska sammanfalla med axelns positiva riktning och väljer axeln som normal (Figur 2.9), får vi formler som förbinder dessa två koordinatsystem
Figur 2.9. Förhållandet mellan sfärisk och rektangulär kartesisk
koordinatsystem
Skalära mängder, eller skalärer kännetecknas helt av sitt numeriska värde i det valda enhetssystemet. Vector kvantiteter eller vektorer, förutom deras numeriska värde, också har en riktning. Till exempel, om vi säger att vinden blåser med en hastighet av 10 m/sek, så kommer vi att införa ett skalärt värde på vindhastighet, men om vi säger att sydvästvinden blåser med en hastighet av 10 m/sek, då i detta fall kommer vindhastigheten redan att vara en vektor.
Vektor kallas ett riktat segment med en viss längd, dvs. ett segment av en viss längd, där en av begränsningspunkterna tas som början och den andra - som slutet. Vi kommer att beteckna vektorn antingen eller (Figur 2.10).
Längden på en vektor betecknas med symbolen eller och kallas vektorns modul. En vektor vars längd är 1 kallas enda . Vektorn kallas noll , om dess början och slut sammanfaller, och betecknas med θ eller . Nollvektorn har ingen specifik riktning och har en längd lika med noll. Vektorer som ligger på samma linje eller på parallella linjer kallas kolinjär . De två vektorerna kallas likvärdig , om de är kolinjära, har samma längd och samma riktning. Alla nollvektorer anses lika.
Två kolinjär vektor, skiljer sig från noll, med lika moduler, men i motsatt riktning, kallas motsatt . Vektorn motsatt betecknas med , för den motsatta vektorn.
Till numret linjära operationer övervektorer inkluderar operationerna addition, subtraktion av vektorer och multiplikation av en vektor med ett tal, dvs. operationer vars resultat är en vektor.
Låt oss definiera de angivna operationerna på vektorer. Låt två vektorer och ges. Låt oss ta en godtycklig punkt O och konstruera en vektor och plotta vektorn från punkt A. Sedan anropas vektorn som förbinder början av den första termen i vektorn med slutet av den andra belopp dessa vektorer betecknas med . Den övervägda regeln för att hitta summan av vektorer kallas triangelregler (Figur 2.11).
Samma summa av vektorer kan erhållas på annat sätt (Figur 2.12). Låt oss plotta vektorn och vektorn från punkten. Låt oss konstruera ett parallellogram på dessa vektorer som på sidorna. Vektorn, som är diagonalen för parallellogrammet som dras från vertexet, blir summan. Denna regel för att hitta summan kallas parallellogramregler .
Summan av valfritt ändligt antal vektorer kan erhållas med hjälp av streckade linjeregeln (Figur 2.13). Från en godtycklig punkt plottar vi en vektor, sedan plottar vi en vektor osv. Vektorn som förbinder början av den första till slutet av den sista är summan
| |
Genom skillnad två vektorer och kallas en sådan vektor, vars summa med den subtraherade vektorn ger vektorn. Härifrån regel för att konstruera en skillnadsvektor(Figur 2.14). Från punkten plottar vi vektorn och vektorn. Vektorn som förbinder ändarna av minuendvektorn och subtrahendvektorn och riktad från subtrahenden till minuendvektorn är skillnaden.
Produkt av en vektor för ett reellt tal λ är en vektor som är kolinjär med vektorn och har längden och samma riktning som vektorn if , och riktningen motsatt vektorn if .
Gick in i linjära operationer över vektorer har egenskaper :
10 . Kommutativitet för addition: .
20 . Tilläggsassociativitet: .
trettio . Förekomst av ett neutralt element genom addition: .
4 0 . Existensen av det motsatta elementet genom addition:
50 . Fördelning av multiplikation med ett tal i förhållande till addition av vektorer: .
6 0 . Fördelning av att multiplicera en vektor med summan av två tal:
7 0 . Associativitetsegenskapen för multiplikation av en vektor med en produkt av tal: .
Låt ett system av vektorer ges:
Uttrycket där λ i (i = 1,2,…, n) är några tal kallas Linjär kombination system av vektorer (2.1). Systemet av vektorer (2.1) kallas linjärt beroende , om deras linjära kombination är lika med noll, förutsatt att inte alla tal λ 1, λ 2, ..., λ n är lika med noll. Systemet av vektorer (2.1) kallas linjärt oberoende , om deras linjära kombination är lika med noll endast om alla tal λ i = 0 (). En annan definition kan ges linjärt beroende vektorer. Systemet av vektorer (2.1) kallas linjärt beroende , om någon vektor i detta system uttrycks linjärt i termer av de andra, annars vektorsystemet (2.1) linjärt oberoende .
För vektorer som ligger i planet är följande påståenden sanna.
10 . Alla tre vektorer på ett plan är linjärt beroende.
20 . Om antalet av dessa vektorer på planet är fler än tre, så är de också linjärt beroende.
trettio . För att två vektorer på ett plan ska vara linjärt oberoende är det nödvändigt och tillräckligt att de är icke-kollinjära.
Således är det maximala antalet linjärt oberoende vektorer på planet två.
Vektorerna kallas i samma plan , om de ligger i samma plan eller är parallella med samma plan. Följande påståenden är sanna för rymdvektorer.
10 . Var fjärde vektor av rymden är linjärt beroende.
20 . Om antalet av dessa vektorer i rymden är fler än fyra, så är de också linjärt beroende.
trettio . För att tre vektorer ska vara linjärt oberoende är det nödvändigt och tillräckligt att de är icke-samplanära.
Således är det maximala antalet linjärt oberoende vektorer i rymden tre.
Varje maximalt delsystem av linjärt oberoende vektorer genom vilket vilken vektor som helst av detta system uttrycks kallas grund den som övervägs vektorsystem . Det är lätt att dra slutsatsen att basen på planet består av två icke-kolineära vektorer, och basen i rymden består av tre icke-koplanära vektorer. Antalet basvektorer kallas rang vektorsystem. Utvidgningskoefficienterna för en vektor till basvektorer kallas vektorkoordinater på denna grund.
Låt vektorerna bilda en bas och låt , då är talen λ 1, λ 2, λ 3 koordinaterna för vektorn i basen Skriv i detta fall Det kan visas att nedbrytningen av vektorn i basen är unik . Den huvudsakliga innebörden av grunden är att linjära operationer på vektorer blir vanliga linjära operationer på tal - koordinaterna för dessa vektorer. Med hjälp av egenskaperna för linjära operationer på vektorer kan vi bevisa följande sats.
Sats. När två vektorer läggs till läggs deras motsvarande koordinater till. När en vektor multipliceras med ett tal, multipliceras alla dess koordinater med det talet.
Således, om och , då , där , och där , λ är ett visst tal.
Vanligtvis betecknas mängden av alla vektorer i planet, reducerade till ett gemensamt ursprung, med införda linjära operationer, med V 2, och mängden av alla vektorer i rymden, reducerade till ett gemensamt ursprung, betecknas med V 3. Uppsättningarna V 2 och V 3 kallas utrymmen av geometriska vektorer.
Vinkel mellan vektorer och kallas den minsta vinkeln () med vilken en av vektorerna måste roteras tills den sammanfaller med den andra efter att ha fört dessa vektorer till ett gemensamt ursprung.
Punkt produkt två vektorer är ett tal lika med produkten av modulerna för dessa vektorer och cosinus för vinkeln mellan dem. Den skalära produkten av vektorer och betecknas med , eller
Om vinkeln mellan vektorerna och är lika med , då
Ur geometrisk synvinkel skalär produkt av vektorer är lika med produkten av modulen för en vektor och projektionen på den av en annan vektor. Av jämlikhet (2.2) följer att
Härifrån villkor för ortogonalitet för två vektorer: två vektorer Och är ortogonala om och endast om deras skalära produkt är lika med noll, dvs. .
Punktprodukten av vektorer är inte en linjär operation eftersom dess resultat är ett tal, inte en vektor.
Egenskaper hos den skalära produkten.
1º. – kommutativitet.
2º. – distribution.
3º. – associativitet med avseende på en numerisk faktor.
4º. - egenskapen hos en skalär kvadrat.
Från fastighet 4º följer definitionen vektor längd :
Låt en grund ges i utrymmet V 3, där vektorerna är enhetsvektorer (de kallas enhetsvektorer), riktningen för var och en av dem sammanfaller med den positiva riktningen för koordinataxlarna Ox, Oy, Oz för den rektangulära kartesiska koordinaten systemet.
Låt oss expandera rymdvektorn V 3 enligt denna bas (Figur 2.15):
Vektorer kallas vektorkomponenter längs koordinataxlarna, eller komponenter, tal a x, a y, a z– rektangulära kartesiska koordinater för vektorn A. Vektorns riktning bestäms av vinklarna α, β, γ som bildas av den med koordinatlinjerna. Cosinus för dessa vinklar kallas riktningsvektorn. Sedan bestäms riktningscosinuserna av formlerna:
Det är lätt att visa det
Låt oss uttrycka den skalära produkten i koordinatform.
Låt det vara. Multiplicera dessa vektorer som polynom och ta hänsyn till att vi får ett uttryck för att hitta prickprodukt i koordinatform:
de där. skalärprodukten av två vektorer är lika med summan av parade produkter av koordinater med samma namn.
Från (2.6) och (2.4) följer formeln för att hitta vektor längd :
Från (2.6) och (2.7) får vi en formel för bestämning vinkel mellan vektorer:
En trippel av vektorer kallas ordnad om det anges vilken av dem som anses vara den första, vilken som anses vara den andra och vilken som anses vara den tredje.
Beordrade tre vektorer kallad höger , om efter att ha fört dem till ett gemensamt ursprung från slutet av den tredje vektorn, görs den kortaste svängen från den första till den andra vektorn moturs. Annars kallas trippeln av vektorer vänster . Till exempel, i figur 2.15, bildar vektorerna , , den högra trippeln av vektorer, och vektorerna , , bildar den vänstra trippeln av vektorer.
På liknande sätt introduceras begreppet höger och vänster koordinatsystem i tredimensionellt rum.
Vektor konstverk vektor för vektor är en vektor (en annan notation) som:
1) har längd , där är vinkeln mellan vektorerna och ;
2) vinkelrätt mot vektorerna och (), dvs. är vinkelrät mot det plan där vektorerna och ;
Per definition hittar vi vektorprodukten av koordinatenhetsvektorerna , , :
Om , , bestäms koordinaterna för vektorprodukten av en vektor och en vektor av formeln:
Av definitionen följer geometrisk betydelse vektor produkt : vektormodul lika med arean parallellogram byggt på vektorer och .
Egenskaper för en vektorprodukt:
4 0 . , om vektorerna och är kolinjära, eller en av dessa vektorer är noll.
Exempel 3. Parallellogrammet är byggt på vektorerna och , där , , . Beräkna längden på diagonalerna för detta parallellogram, vinkeln mellan diagonalerna och parallellogrammets area.
Lösning. Konstruktionen av vektorer och visas i figur 2.16, konstruktionen av ett parallellogram på dessa vektorer visas i figur 2.17.
Låt oss göra en analytisk lösning på detta problem. Låt oss uttrycka de vektorer som definierar diagonalerna för det konstruerade parallellogrammet genom vektorerna och , och sedan genom och . Vi hittar , . Därefter hittar vi längderna på parallellogrammets diagonaler som längden på de konstruerade vektorerna
Vinkeln mellan parallellogrammets diagonaler betecknas med . Sedan har vi från formeln för skalärprodukten av vektorer:
Därav, .
Med hjälp av egenskaperna hos vektorprodukten beräknar vi parallellogrammets area:
Låt tre vektorer , och , ges. Låt oss föreställa oss att vektorn multipliceras vektoriellt med och vektorn och den resulterande vektorn multipliceras skalärt med vektorn, och därigenom bestämmer talet. Det kallas vektor-skalär eller blandat arbete tre vektorer och . Betecknas med eller.
Låt oss ta reda på geometrisk betydelse av blandad produkt (Figur 2.18). Låt , , inte vara i samma plan. Låt oss bygga en parallellepiped på dessa vektorer som på kanter. Korsprodukten är en vektor vars modul är lika med arean av parallellogrammet (basen av parallellepipeden), byggd på vektorerna och och är riktad vinkelrätt mot parallellogrammets plan.
Punktprodukt (lika med produkten av vektorns modul och projektionen på ). Höjden på den konstruerade parallellepipeden är det absoluta värdet av denna projektion. Följaktligen är det absoluta värdet av den blandade produkten av tre vektorer lika med volymen av parallellepipeden byggd på vektorerna , och , d.v.s. .
Därav volymen triangulär pyramid, byggd på vektorerna , och , beräknas med formeln .
Låt oss notera några fler egenskaper hos en blandad produkt vektorer.
1 o. Produktens tecken är positivt om vektorerna , , och bildar ett system med samma namn som huvudet, och negativt annars.
Verkligen, den skalära produkten är positiv om vinkeln mellan och är spetsig och negativ om vinkeln är trubbig. Med en spetsig vinkel mellan och är vektorerna och placerade på ena sidan i förhållande till basen av parallellepipeden, och därför, från slutet av vektorn, kommer rotationen från till att vara synlig på samma sätt som från slutet av vektorn. vektor, dvs. i positiv riktning (moturs).
I en trubbig vinkel är både vektorerna och vektorerna placerade på olika sidor i förhållande till parallellogrammets plan som ligger vid basen av parallellepipeden, och därför, från slutet av vektorn, är rotationen från till synlig i negativ riktning ( medurs).
2 o En blandad produkt förändras inte när dess faktorer omarrangeras cirkulärt: .
3 o När två valfria vektorer omarrangeras ändrar den blandade produkten endast tecknet. Till exempel, , . , . - okända system.
Systemet(3.1) kallas homogen , om alla medlemmar är lediga. Systemet (3.1) kallas heterogen , om minst en av de fria medlemmarna .
Systemlösning kallas en uppsättning tal, när man substituerar dem i systemets ekvationer istället för motsvarande okända, förvandlas varje ekvation i systemet till en identitet. Ett system som inte har någon lösning kallas oförenlig, eller kontroversiell . Ett system som har minst en lösning kallas gemensam .
Ledsystemet kallas vissa , om den har en unik lösning. Om ett konsekvent system har mer än en lösning kallas det osäker . Homogent systemär alltid gemensam, då den har enl minst, noll lösning. Ett uttryck för de okända från vilka någon specifik lösning av systemet kan erhållas kallas allmänt beslut , och varje specifik lösning av systemet är dess privat lösning . Två system med samma okända likvärdig (likvärdig ), om varje lösning av en av dem är en lösning av den andra eller båda systemen är inkonsekventa.
Låt oss överväga metoder för att lösa system linjära ekvationer.
En av de viktigaste metoderna för att lösa linjära ekvationssystem är Gauss metod, eller sekventiell metod uteslutning av okända. Kärnan i denna metod är att reducera ett system av linjära ekvationer till en stegvis form. I detta fall måste följande ekvationer utföras: elementära transformationer :
1. Ordna om systemets ekvationer.
2. Lägga till ytterligare en ekvation till en ekvation.
3. Multiplicera båda sidor av ekvationen med ett annat tal än noll.
Som ett resultat kommer systemet att ta formen:
Om vi fortsätter denna process ytterligare, eliminerar vi det okända från alla ekvationer, med början med den tredje. För att göra detta, multiplicera den andra ekvationen med siffror och lägg till den 3:e, ..., till -e ekvationen i systemet. Följande steg i Gauss-metoden utförs på liknande sätt. Om vi som ett resultat av transformationerna får en identisk ekvation, tar vi bort den från systemet. Om i något steg av den Gaussiska metoden en ekvation av formen erhålls:
då är det aktuella systemet inkonsekvent och dess vidare lösning upphör. Om en ekvation av formen (3.2) inte påträffas vid uppfyllelse elementära transformationer, då i högst - steg kommer systemet (3.1) att omvandlas till en stegvis form:
För att få en viss lösning av systemet kommer det att vara nödvändigt att tilldela specifika värden till de fria variablerna i (3.4).
Observera att eftersom i Gauss-metoden alla transformationer utförs på koefficienterna vid okända ekvationer och fria termer, i praktiken tillämpas denna metod vanligtvis på en matris som består av koefficienter för okända och en kolumn med fria termer. Denna matris kallas utökad. Med hjälp av elementära transformationer reduceras denna matris till en stegvis form. Sedan, med hjälp av den resulterande matrisen, rekonstrueras systemet och alla tidigare resonemang appliceras på det.
Exempel 1. Lös systemet:
Lösning. Vi skapar en utökad matris och reducerar den till en stegvis form:
~ *) ~ **) ~ ***)
*) - den andra raden multiplicerades med och den tredje raden ströks över.
I §§ 5, 6 och 10 i detta kapitel kommer vi att överväga några av de enklaste problemen inom analytisk geometri, till vilka många mer komplexa problem ofta reduceras. Ett sådant problem är problemet med avståndet mellan två punkter.
Låt två punkter ges i ett rektangulärt koordinatsystem valt på ett plan Låt oss uttrycka avståndet d mellan dessa två punkter genom deras koordinater.
Låt oss hitta projektionerna av punkterna A och B på koordinataxlarna (fig. 8). Kommer att ha:

Genom en av dessa punkter, till exempel A, drar vi en rät linje parallell med abskissaxeln tills den skär den räta linjen i punkt C
Från den högra triangeln ACB får vi:
![]()
(här är AC och CB längderna på sidorna av triangel ACB). Men eftersom
(1 kap. 3 §), då
Det är klart att här måste vi ta aritmetiskt värde rot
Således är avståndet mellan två givna punkter lika med kvadratroten av summan av kvadraterna av skillnaderna mellan samma koordinater för dessa punkter.
Kommentar. Om de givna punkterna A till B ligger på en rät linje parallell koordinataxel, då får vi inte triangel ABC, utan formel (3) kommer att vara giltig i detta fall också. Ja, om till exempel punkterna A till B ligger på en rät linje parallell med Ox-axeln, så är det uppenbarligen (kapitel I, § 3). Detsamma kan erhållas från formel (3), eftersom i detta fall
Att beräkna avstånd mellan punkter baserat på deras koordinater på ett plan är elementärt; på jordens yta är det lite mer komplicerat: vi kommer att överväga att mäta avståndet och initial azimut mellan punkter utan projektionstransformationer. Låt oss först förstå terminologin.
Introduktion
Stor cirkelbågelängd– det kortaste avståndet mellan två punkter på ytan av en sfär, mätt längs linjen som förbinder dessa två punkter (en sådan linje kallas ortodromi) och som passerar längs sfärens yta eller annan rotationsyta. Sfärisk geometri skiljer sig från normal euklidisk geometri och avståndsekvationerna har också en annan form. I euklidisk geometri är det kortaste avståndet mellan två punkter en rak linje. På en sfär finns det inga raka linjer. Dessa linjer på sfären är en del av stora cirklar - cirklar vars centrum sammanfaller med sfärens centrum. Initial azimut- azimut, med vilken när man börjar röra sig från punkt A, efter storcirkeln för det kortaste avståndet till punkt B, kommer slutpunkten att vara punkt B. När man förflyttar sig från punkt A till punkt B längs storcirkellinjen, är azimuten från den nuvarande positionen är slutpunkt B förändras hela tiden. Den initiala azimuten skiljer sig från en konstant, varefter azimuten från den aktuella punkten till den sista punkten inte ändras, men rutten som följs är inte det kortaste avståndet mellan två punkter.Genom två valfria punkter på ytan av en sfär, om de inte är direkt motsatta varandra (det vill säga de är inte antipoder), kan en unik storcirkel ritas. Två punkter delar en stor cirkel i två bågar. Längden på en kort båge är det kortaste avståndet mellan två punkter. Ett oändligt antal stora cirklar kan ritas mellan två antipodalpunkter, men avståndet mellan dem kommer att vara detsamma på vilken cirkel som helst och lika med halva cirkelns omkrets, eller π*R, där R är sfärens radie.

På ett plan (i ett rektangulärt koordinatsystem) representerar stora cirklar och deras fragment, som nämnts ovan, bågar i alla projektioner utom den gnomoniska, där stora cirklar är raka linjer. I praktiken betyder det att flygplan och annan flygtransport alltid använder sträckan för det minsta avståndet mellan punkter för att spara bränsle, det vill säga flygningen genomförs längs ett stort cirkelavstånd, på ett plan ser det ut som en båge.

Jordens form kan beskrivas som en sfär, så storcirkelavståndsekvationer är viktiga för att beräkna det kortaste avståndet mellan punkter på jordens yta och används ofta i navigering. Att beräkna avstånd med denna metod är mer effektivt och i många fall mer exakt än att beräkna det för projicerade koordinater (i rektangulära koordinatsystem), eftersom det för det första inte kräver översättning geografiska koordinater in i ett rektangulärt koordinatsystem (utför projektionstransformationer) och för det andra kan många projektioner, om de är felaktigt valda, leda till betydande längdförvrängningar på grund av egenskaperna hos projektionsförvrängningar. Det är känt att det inte är en sfär, utan en ellipsoid som beskriver jordens form mer exakt, men den här artikeln diskuterar beräkningen av avstånd specifikt på en sfär; för beräkningar används en sfär med en radie på 6 372 795 meter , vilket kan leda till ett fel vid beräkning av avstånd i storleksordningen 0,5 %.
Formler
Det finns tre sätt att beräkna storcirkelns sfäriska avstånd. 1. Sfärisk cosinussats Vid små avstånd och litet beräkningsdjup (antal decimaler) kan användningen av formeln leda till betydande avrundningsfel. φ1, λ1; φ2, λ2 - latitud och longitud för två punkter i radianer Δλ - skillnad i koordinater i longitud Δδ - vinkelskillnad Δδ = arccos (sin φ1 sin φ2 + cos φ1 cos φ2 cos Δλ) För att omvandla vinkelavståndet multiplicera vinkelskillnaden med jordens radie (6372795 meter), kommer enheterna för det slutliga avståndet att vara lika med enheterna i vilka radien uttrycks (i det här fallet meter). 2. Haversine formel Används för att undvika problem med korta avstånd. 3. Modifiering för antipoderna Den tidigare formeln är också föremål för problemet med antipodalpunkter; för att lösa det används följande modifiering.Min implementering på PHP
// Earth radius define("EARTH_RADIUS", 6372795); /* * Avstånd mellan två punkter * $φA, $λA - latitud, 1:a punktens longitud, * $φB, $λB - latitud, 2:a punktens longitud * Skrivet baserat på http://gis-lab.info/ qa/great-circles.html * Mikhail Kobzarev< >* */ funktion calculateTheDistance ($φA, $λA, $φB, $λB) ( // omvandla koordinater till radianer $lat1 = $φA * M_PI / 180; $lat2 = $φB * M_PI / 180; $long1 = $λA * M_PI / 180; $long2 = $λB * M_PI / 180; // cosinus och sinus för latituder och longitudskillnader $cl1 = cos($lat1); $cl2 = cos($lat2); $sl1 = sin($lat1 ); $sl2 = sin($lat2); $delta = $long2 - $long1; $cdelta = cos($delta); $sdelta = sin($delta); // storcirkellängdsberäkningar $y = sqrt(pow ( $cl2 * $sdelta, 2) + pow($cl1 * $sl2 - $sl1 * $cl2 * $cdelta, 2)); $x = $sl1 * $sl2 + $cl1 * $cl2 * $cdelta; / / $ad = atan2($y, $x); $dist = $ad * EARTH_RADIUS; return $dist; ) Exempel på ett funktionsanrop: $lat1 = 77.1539; $lång1 = -139,398; $lat2 = -77,1804; $lång2 = -139,55; echo calculateTheDistance($lat1, $long1, $lat2, $long2) . "meter"; // Returnera "17166029 meter"Artikel hämtad från sajten
Sats 1. För två punkter och ett plan uttrycks avståndet mellan dem med formeln:
Till exempel, om poäng och ges, är avståndet mellan dem:
2. Arean av en triangel.
Sats 2.
För alla poäng
inte ligger på samma räta linje, arean av en triangel uttrycks med formeln:
Låt oss till exempel hitta arean av triangeln som bildas av punkterna , och.
Kommentar. Om arean av en triangel är noll betyder det att punkterna ligger på samma linje.
3. Uppdelning av ett segment i ett givet förhållande.
Låt ett godtyckligt segment ges på planet och låt
– någon annan punkt i detta segment än slutpunkterna. Antalet som definieras av likhet kallas attityd, där punkten delar segmentet.
Problemet med att dela ett segment i en given relation är att: för en given relation och givna punktkoordinater
och hitta punktens koordinater.
Sats 3.
Om en punkt delar ett segment
i ett förhållande
,
då bestäms koordinaterna för denna punkt av formlerna: ![]() (1.3), var är punktens koordinater, och är punktens koordinater.
(1.3), var är punktens koordinater, och är punktens koordinater.
Följd: If är mittpunkten av segmentet
, var och, sedan (1.4) (sedan).
Till exempel. Poäng och ges. Hitta koordinaterna för en punkt som är två gånger närmare än till
Lösning: Den önskade punkten delar segmentet
i förhållande till sedan ![]() , Då
, Då ![]() ,
,![]() , fick
, fick
Polära koordinater
Det viktigaste efter det rektangulära koordinatsystemet är det polära koordinatsystemet. Den består av en viss punkt som kallas Pol, och strålen som utgår från den - polära axeln. Dessutom är skalenheten för att mäta längderna på segment inställd. 
Låt ett polärt koordinatsystem ges och låt vara en godtycklig punkt på planet. Låt vara avståndet från punkten
till punkten, – den vinkel med vilken polaxeln måste roteras för att passa in i strålen.
Polära koordinater för en punkt kallas nummer. I det här fallet anses numret vara den första koordinaten och anropas polär radie, numret är den andra koordinaten och kallas polär vinkel.
Betecknas med . Den polära radien kan ha vilket icke-negativt värde som helst:. Man brukar tro att den polära vinkeln varierar inom följande gränser:. Men i vissa fall är det nödvändigt att bestämma vinklar mätt från polaxeln medurs.
Förhållandet mellan en punkts polära koordinater och dess rektangulära koordinater.
Vi kommer att anta att ursprunget för det rektangulära koordinatsystemet är vid polen, och att abskissans positiva halvaxel sammanfaller med polaxeln. 
Låta – i ett rektangulärt koordinatsystem och – i ett polärt koordinatsystem. Definierad- rät triangel Med. Sedan (1,5). Dessa formler uttrycker rektangulära koordinater i termer av polära.
Å andra sidan, enligt Pythagoras sats och
![]() (1.6) – dessa formler uttrycker polära koordinater genom rektangulära.
(1.6) – dessa formler uttrycker polära koordinater genom rektangulära.
Observera att formeln definierar två värden för den polära vinkeln, eftersom. Från dessa två vinkelvärden väljer du den där likheterna är uppfyllda.
Till exempel, låt oss hitta de polära koordinaterna för punkten ..eller, eftersom jag fjärdedelar.
Exempel 1: Hitta en punkt som är symmetrisk till en punkt 
I förhållande till bisektrisen för den första koordinatvinkeln.
Lösning:
Låt oss dra igenom poängen A direkt l 1, vinkelrät mot bisektrisen l första koordinatvinkeln. Låt . På en rak linje l 1 lägg åt sidan segmentet SA 1 , lika med segmentet AC. Rätt trianglar ASO Och A 1 CO lika med varandra (på två sidor). Härav följer att | OA| = |O.A. 1 |. Trianglar VÄSEN Och OEA 1 är också lika med varandra (med hypotenusa och spetsig vinkel). Det drar vi slutsatsen |AD| = |OE| = 4,|OD| = |EA 1 | = 2, dvs. punkten har koordinater x = 4, y = -2, de där. A 1 (4;-2).
Observera att det finns ett allmänt uttalande: punkt A 1, symmetrisk till punkten i förhållande till halveringslinjen för den första och tredje koordinatvinkeln, har koordinater, dvs .
Exempel 2: Hitta den punkt där en linje går genom punkterna och , kommer att skära axeln Åh.
Lösning:
Koordinater för önskad punkt MED Det finns ( x; 0). Och eftersom poängen A,I Och MED ligga på samma räta linje, då måste villkoret vara uppfyllt (x 2 -x 1 )(y 3 -y 1 )-(x 3 -x 1 )(y 2 -y 1 ) = 0 (formel (1.2), area av triangeln ABC lika med noll!), där är punktens koordinater A, – poäng I, – poäng MED. Vi får, dvs. , . Därför poängen MED har koordinater, dvs.
Exempel 3: I det polära koordinatsystemet ges poäng. Hitta: A) avstånd mellan punkter och ; b) arean av triangeln OM 1 M 2 (HANDLA OM- Pol).
Lösning:
a) Låt oss använda formlerna (1.1) och (1.5):
det är, .
b) använda formeln för arean av en triangel med sidor A Och b och vinkeln mellan dem (), vi hittar arean av triangeln OM 1 M 2 . .
- I kontakt med 0
- Google+ 0
- OK 0
- Facebook 0