Funktionsderivata. Den geometriska betydelsen av derivatan

Derivatan av en funktion är ett av de knepiga ämnena i Läroplanen. Inte alla akademiker kommer att svara på frågan om vad ett derivat är.

Den här artikeln förklarar enkelt och tydligt vad ett derivat är och varför det behövs.. Vi kommer nu inte att sträva efter matematisk noggrannhet i presentationen. Det viktigaste är att förstå innebörden.

Låt oss komma ihåg definitionen:

Derivatan är funktionens förändringshastighet.

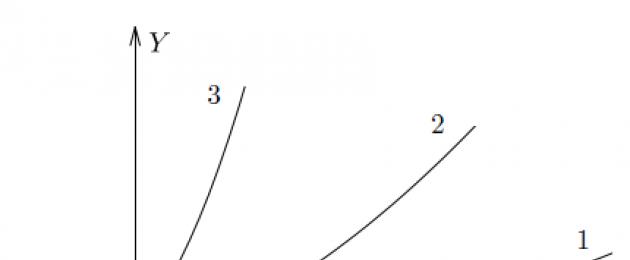
Figuren visar grafer över tre funktioner. Vilken tror du växer snabbast?

Svaret är uppenbart - det tredje. Den har den högsta förändringshastigheten, det vill säga den största derivatan.

Här är ett annat exempel.

Kostya, Grisha och Matvey fick jobb samtidigt. Låt oss se hur deras inkomster förändrades under året:

Du kan se allt på diagrammet direkt, eller hur? Kostyas inkomst har mer än fördubblats på sex månader. Och Grishas inkomst ökade också, men bara lite. Och Matthews inkomst minskade till noll. Startvillkoren är desamma, men funktionens förändringshastighet, d.v.s. derivat, - annorlunda. När det gäller Matvey är derivatet av hans inkomst generellt negativt.

Intuitivt kan vi enkelt uppskatta förändringshastigheten för en funktion. Men hur gör vi det?

Det vi egentligen tittar på är hur brant grafen för funktionen går upp (eller ner). Med andra ord, hur snabbt y ändras med x. Uppenbarligen kan samma funktion vid olika punkter ha ett annat värde på derivatan - det vill säga den kan ändras snabbare eller långsammare.

Derivatan av en funktion betecknas med .

Låt oss visa hur du hittar med hjälp av grafen.

En graf över någon funktion ritas. Ta en punkt på det med en abskissa. Rita en tangent till grafen för funktionen vid denna punkt. Vi vill utvärdera hur brant grafen för funktionen går uppåt. Ett praktiskt värde för detta är tangent för lutningen på tangenten.

Derivatan av en funktion i en punkt är lika med tangenten för lutningen av tangenten som ritas till grafen för funktionen vid den punkten.

Observera - som tangentens lutningsvinkel tar vi vinkeln mellan tangenten och axelns positiva riktning.

Ibland frågar eleverna vad som är tangenten till grafen för en funktion. Detta är en rät linje som har den enda gemensamma punkten med grafen i detta avsnitt, dessutom, som visas i vår figur. Det ser ut som en tangent till en cirkel.

Låt oss hitta . Vi kommer ihåg att tangenten för en spetsig vinkel i rät triangel lika med förhållandet mellan det motsatta benet och det intilliggande. Från triangeln:

Vi hittade derivatan med hjälp av grafen utan att ens veta formeln för funktionen. Sådana uppgifter finns ofta på provet i matematik under numret.

Det finns en annan viktig korrelation. Kom ihåg att den räta linjen ges av ekvationen

Kvantiteten i denna ekvation kallas lutning av en rak linje. Det är lika med tangenten för lutningsvinkeln för den räta linjen till axeln.

.

Det förstår vi

Låt oss komma ihåg denna formel. Det uttrycker den geometriska betydelsen av derivatan.

Derivatan av en funktion i en punkt är lika med lutningen på tangenten som ritas till grafen för funktionen vid den punkten.

Med andra ord är derivatan lika med tangenten för tangentens lutning.

Vi har redan sagt att samma funktion vid olika punkter kan ha en annan derivata. Låt oss se hur derivatan är relaterad till funktionens beteende.

Låt oss rita en graf över någon funktion. Låt denna funktion öka på vissa områden och minska på andra och i olika takt. Och låt denna funktion ha max- och minimumpoäng.

Vid ett tillfälle ökar funktionen. Tangenten till grafen, ritad vid punkten, bildar en spetsig vinkel med axelns positiva riktning. Så derivatan är positiv vid punkten.

Just nu minskar vår funktion. Tangenten vid denna punkt bildar en trubbig vinkel med axelns positiva riktning. Eftersom tangenten för en trubbig vinkel är negativ, är derivatan vid punkten negativ.

Så här händer:

Om en funktion ökar är dess derivata positiv.

Om den minskar är dess derivata negativ.

Och vad kommer att hända vid högsta och lägsta poäng? Vi ser att vid (maximipunkt) och (minimipunkt) är tangenten horisontell. Därför är tangenten för tangentens lutning vid dessa punkter noll, och derivatan är också noll.

Punkten är maxpoängen. Vid denna tidpunkt ersätts ökningen av funktionen av en minskning. Följaktligen ändras derivatans tecken vid punkten från "plus" till "minus".

Vid punkten - minimipunkten - är derivatan också lika med noll, men dess tecken ändras från "minus" till "plus".

Slutsats: med hjälp av derivatan kan du ta reda på allt som intresserar oss om funktionens beteende.

Om derivatan är positiv ökar funktionen.

Om derivatan är negativ, så minskar funktionen.

Vid maxpunkten är derivatan noll och ändrar tecken från plus till minus.

Vid minimipunkten är även derivatan noll och ändrar tecken från minus till plus.

Vi skriver dessa resultat i form av en tabell:

	ökar	högsta poäng	minskar	minimipunkt	ökar
+	0	-	0	+

Låt oss göra två små förtydliganden. Du kommer att behöva en av dem när du ska lösa provproblem. En annan - under det första året, med en mer seriös studie av funktioner och derivator.

Ett fall är möjligt när derivatan av en funktion vid något tillfälle är lika med noll, men funktionen har varken ett maximum eller ett minimum vid denna punkt. Detta sk :

Vid en punkt är tangenten till grafen horisontell och derivatan är noll. Men före punkten ökade funktionen - och efter punkten fortsätter den att öka. Tecknet för derivatan ändras inte - det har förblivit positivt som det var.

Det händer också att derivatan inte existerar vid punkten för maximum eller minimum. På grafen motsvarar detta ett skarpt brott, när det är omöjligt att rita en tangent vid en given punkt.

Men hur hittar man derivatan om funktionen inte ges av en graf, utan av en formel? I det här fallet gäller det

Försök först hitta omfattningen av funktionen:

Klarade du dig? Låt oss jämföra svaren:

Okej? Bra gjort!

Låt oss nu försöka hitta intervallet för funktionen:

Hittades? Jämföra:

Stämde det? Bra gjort!

Låt oss jobba med graferna igen, bara nu är det lite svårare – att hitta både funktionens domän och funktionens räckvidd.

Hur man hittar både domänen och intervallet för en funktion (avancerat)

Här är vad som hände:

Med grafiken tror jag att du kom på det. Låt oss nu försöka hitta funktionens domän i enlighet med formlerna (om du inte vet hur man gör detta, läs avsnittet om):

Klarade du dig? Kontroll svarar:

1. , eftersom rotuttrycket måste vara större än eller lika med noll.
2. , eftersom det är omöjligt att dividera med noll och det radikala uttrycket inte kan vara negativt.
3. , eftersom, respektive, för alla.
4. eftersom du inte kan dividera med noll.

Men vi har fortfarande ett ögonblick till som inte har lösts ...

Låt mig upprepa definitionen och fokusera på den:

Lagt märke till? Ordet "bara" är en mycket, mycket viktig del av vår definition. Jag ska försöka förklara för dig på fingrarna.

Låt oss säga att vi har en funktion som ges av en rät linje. . När ersätter vi detta värde i vår "regel" och får det. Ett värde motsvarar ett värde. Vi kan till och med göra en tabell med olika värden och plotta en given funktion för att verifiera detta.

"Se! - du säger, - "" träffas två gånger!" Så kanske parabeln inte är en funktion? Nej det är!

Att "" förekommer två gånger är långt ifrån en anledning att anklaga parabeln för tvetydighet!

Faktum är att vi, när vi räknade för, fick en match. Och när vi räknade med fick vi ett spel. Så det stämmer, parabeln är en funktion. Titta på diagrammet:

Jag förstår? Om inte, här är ett verkligt exempel för dig, långt ifrån matematik!

Låt oss säga att vi har en grupp sökande som träffades när de lämnade in dokument, som var och en berättade i ett samtal där han bor:

Håller med, det är ganska verkligt att flera killar bor i samma stad, men det är omöjligt för en person att bo i flera städer samtidigt. Detta är så att säga en logisk representation av vår "parabel" - Flera olika x motsvarar samma y.

Låt oss nu komma med ett exempel där beroendet inte är en funktion. Låt oss säga att samma killar berättade vilka specialiteter de sökte:

Här har vi en helt annan situation: en person kan enkelt ansöka om en eller flera vägbeskrivningar. Det är ett element set läggs i korrespondens flera element set. Respektive, det är inte en funktion.

Låt oss testa dina kunskaper i praktiken.

Bestäm utifrån bilderna vad som är en funktion och vad som inte är det:

Jag förstår? Och här är svarar:

• Funktionen är - B,E.
• Inte en funktion - A, B, D, D.

Du frågar varför? Ja, här är varför:

I alla siffror utom V) och E) det finns flera för en!

Jag är säker på att du nu enkelt kan skilja en funktion från en icke-funktion, säga vad ett argument är och vad en beroende variabel är, och även bestämma omfattningen av argumentet och omfattningen av funktionen. Låt oss gå vidare till nästa avsnitt - hur definierar man en funktion?

Sätt att ställa in en funktion

Vad tror du att orden betyder "ställ in funktion"? Just det, det innebär att förklara för alla vilken funktion vi pratar om i det här fallet. Förklara dessutom på ett sådant sätt att alla förstår dig rätt och att graferna över funktioner som ritats av människor enligt din förklaring var desamma.

Hur kan jag göra det? Hur ställer man in en funktion? Det enklaste sättet, som redan har använts mer än en gång i den här artikeln - med hjälp av en formel. Vi skriver en formel och genom att ersätta ett värde i den, beräknar vi värdet. Och som ni minns är en formel en lag, en regel enligt vilken det blir tydligt för oss och för en annan person hur ett X förvandlas till ett Y.

Vanligtvis är det precis vad de gör - i uppgifter ser vi färdiga funktioner definierade av formler, men det finns andra sätt att ställa in en funktion som alla glömmer bort, och därför frågan "hur kan du annars ställa in en funktion?" förvirrar. Låt oss ta en titt på allt i ordning och börja med den analytiska metoden.

Analytiskt sätt att definiera en funktion

Den analytiska metoden är uppgiften för en funktion som använder en formel. Detta är det mest universella och heltäckande och entydiga sättet. Om du har en formel, då vet du absolut allt om funktionen - du kan göra en värdetabell på den, du kan bygga en graf, bestämma var funktionen ökar och var den minskar, i allmänhet utforska den till fullo.

Låt oss överväga en funktion. Vad spelar det för roll?

"Vad betyder det?" - du frågar. Jag ska förklara nu.

Låt mig påminna dig om att uttrycket inom parentes i notationen kallas argumentet. Och detta argument kan vara vilket uttryck som helst, inte nödvändigtvis enkelt. Följaktligen, oavsett argument (uttryck inom parentes), kommer vi att skriva det istället i uttrycket.

I vårt exempel kommer det att se ut så här:

Överväg en annan uppgift relaterad till den analytiska metoden att specificera en funktion som du kommer att ha på tentamen.

Hitta värdet på uttrycket, vid.

Jag är säker på att du först blev rädd när du såg ett sådant uttryck, men det finns absolut inget läskigt i det!

Allt är detsamma som i föregående exempel: oavsett argument (uttryck inom parentes), kommer vi att skriva det istället i uttrycket. Till exempel för en funktion.

Vad bör göras i vårt exempel? Istället måste du skriva, och istället för -:

förkorta det resulterande uttrycket:

Det är allt!

Självständigt arbete

Försök nu själv hitta innebörden av följande uttryck:

1. , om
2. , om

Klarade du dig? Låt oss jämföra våra svar: Vi är vana vid att funktionen har formen

Även i våra exempel definierar vi funktionen på detta sätt, men analytiskt går det till exempel att definiera funktionen implicit.

Testa att bygga den här funktionen själv.

Klarade du dig?

Så här byggde jag den.

Vilken ekvation fick vi?

Höger! Linjär, vilket betyder att grafen blir en rak linje. Låt oss göra en tabell för att avgöra vilka punkter som hör till vår linje:

Det var precis vad vi pratade om ... En motsvarar flera.

Låt oss försöka rita vad som hände:

Är det vi har en funktion?

Det stämmer, nej! Varför? Försök att svara på denna fråga med en bild. Vad fick du?

"Eftersom ett värde motsvarar flera värden!"

Vilken slutsats kan vi dra av detta?

Det stämmer, en funktion kan inte alltid uttryckas explicit, och det som är "förklädd" som en funktion är inte alltid en funktion!

Tabellform för att definiera en funktion

Som namnet antyder är denna metod en enkel tallrik. Jaja. Som den vi redan gjort. Till exempel:

Här märkte du omedelbart ett mönster - Y är tre gånger större än X. Och nu "tänk mycket bra"-uppgiften: tror du att en funktion som ges i form av en tabell är likvärdig med en funktion?

Låt oss inte prata på länge, men låt oss rita!

Så. Vi ritar en funktion som ges på båda sätt:

Ser du skillnaden? Det handlar inte om de markerade punkterna! Ta en närmare titt:

Har du sett den nu? När vi ställer in funktionen i tabellform reflekterar vi på grafen endast de punkter som vi har i tabellen och linjen (som i vårt fall) passerar endast genom dem. När vi definierar en funktion på ett analytiskt sätt kan vi ta vilka punkter som helst, och vår funktion är inte begränsad till dem. Här är en sådan funktion. Kom ihåg!

Grafiskt sätt att bygga en funktion

Det grafiska sättet att konstruera en funktion är inte mindre bekvämt. Vi ritar vår funktion, och en annan intresserad kan hitta vad y är lika med vid ett visst x, och så vidare. Grafiska och analytiska metoder är bland de vanligaste.

Men här måste du komma ihåg vad vi pratade om i början - inte varje "squiggle" som ritas i koordinatsystemet är en funktion! Minns du? För säkerhets skull kopierar jag här definitionen av vad en funktion är:

Som regel brukar folk nämna exakt de tre sätten att specificera en funktion som vi har analyserat - analytisk (med hjälp av en formel), tabellform och grafisk, och glömmer helt bort att en funktion kan beskrivas verbalt. Så här? Ja, väldigt lätt!

Verbal beskrivning av funktionen

Hur ska man beskriva funktionen verbalt? Låt oss ta vårt senaste exempel - . Denna funktion kan beskrivas som "varje verkligt värde på x motsvarar dess trippelvärde". Det är allt. Inget komplicerat. Naturligtvis kommer du att invända - "det finns så komplexa funktioner att det helt enkelt är omöjligt att ställa in verbalt!" Ja, det finns några, men det finns funktioner som är lättare att beskriva verbalt än att ställa in med en formel. Till exempel: "varje naturvärde av x motsvarar skillnaden mellan siffrorna som det består av, medan den största siffran som finns i nummerinmatningen tas som minuend." Tänk nu på hur vår verbal beskrivning funktioner implementeras i praktiken:

Den största siffran i givet nummer- , respektive, - reduceras, sedan:

Huvudtyper av funktioner

Låt oss nu gå vidare till det mest intressanta - vi kommer att överväga de huvudsakliga typerna av funktioner som du arbetade / arbetar med och kommer att arbeta under skolan och institutet matematik, det vill säga vi kommer att lära känna dem, så att säga, och ge dem kort beskrivning. Läs mer om varje funktion i motsvarande avsnitt.

Linjär funktion

En funktion av formen, där, är reella tal.

Grafen för denna funktion är en rät linje, så konstruktionen av en linjär funktion reduceras till att hitta koordinaterna för två punkter.

Direkt position på koordinatplan beror på lutningsfaktorn.

Funktionsomfång (alias argumentomfång) - .

Värdeintervallet är .

kvadratisk funktion

Formens funktion, var

Funktionens graf är en parabel, när parabelns grenar är riktade nedåt, när - uppåt.

Många egenskaper hos en kvadratisk funktion beror på värdet på diskriminanten. Diskriminanten beräknas med formeln

Parabolens position på koordinatplanet i förhållande till värdet och koefficienten visas i figuren:

Domän

Värdeintervallet beror på extremumet för den givna funktionen (punkten på parabeln) och koefficienten (riktningen för parabelns grenar)

Omvänd proportionalitet

Funktionen som ges av formeln, där

Talet kallas den omvända proportionalitetsfaktorn. Beroende på vilket värde är hyperbelns grenar i olika rutor:

Domän - .

Värdeintervallet är .

SAMMANFATTNING OCH GRUNDFORMEL

1. En funktion är en regel enligt vilken varje element i en mängd tilldelas ett unikt element i mängden.

• - detta är en formel som anger en funktion, det vill säga beroendet av en variabel av en annan;
• - variabel eller argument;
• - beroende värde - ändras när argumentet ändras, det vill säga enligt någon specifik formel som speglar ett värdes beroende av ett annat.

2. Giltiga argumentvärden, eller omfattningen av en funktion, är vad som är relaterat till det möjliga under vilket funktionen är vettig.

3. Område av funktionsvärden- det här är vilka värden som krävs, med giltiga värden.

4. Det finns fyra sätt att ställa in funktionen:

• analytisk (med formler);
• tabellform;
• grafisk
• verbal beskrivning.

5. Huvudtyper av funktioner:

• : , där, är reella tal;
• : , var;
• : , var.

Derivatan av en funktion $y = f(x)$ vid en given punkt $х_0$ är gränsen för förhållandet mellan funktionens ökning och motsvarande ökning av dess argument, förutsatt att det senare tenderar mot noll:

$f"(x_0)=(lim)↙(△x→0)(△f(x_0))/(△x)$

Differentiering är operationen att hitta en derivata.

Tabell över derivator av några elementära funktioner

Fungera	Derivat
$c$	$0$
$x$	$1$
$x^n$	$nx^(n-1)$
$(1)/(x)$	$-(1)/(x^2)$
$√x$	$(1)/(2√x)$
$e^x$	$e^x$
$lnx$	$(1)/(x)$
$sinx$	$cosx$
$cosx$	$-sinx$
$tgx$	$(1)/(cos^2x)$
$ctgx$	$-(1)/(sin^2x)$

Grundläggande regler för differentiering

1. Derivatan av summan (skillnaden) är lika med summan (skillnaden) av derivator

$(f(x) ± g(x))"= f"(x)±g"(x)$

Hitta derivatan av funktionen $f(x)=3x^5-cosx+(1)/(x)$

Derivatan av summan (skillnaden) är lika med summan (skillnaden) av derivatorna.

$f"(x) = (3x^5)"-(cos x)" + ((1)/(x))" = 15x^4 + sinx - (1)/(x^2)$

2. Derivat av en produkt

$(f(x) g(x))"= f"(x) g(x)+ f(x) g(x)"$

Hitta derivatan $f(x)=4x cosx$

$f"(x)=(4x)" cosx+4x (cosx)"=4 cosx-4x sinx$

3. Derivat av kvoten

$((f(x))/(g(x)))"=(f"(x) g(x)-f(x) g(x)")/(g^2(x)) $

Hitta derivatan $f(x)=(5x^5)/(e^x)$

$f"(x)=((5x^5)" e^x-5x^5 (e^x)")/((e^x)^2)=(25x^4 e^x- 5x^5 e^x)/((e^x)^2)$

4. Derivatan av en komplex funktion är lika med produkten av derivatan av den externa funktionen och derivatan av den interna funktionen

$f(g(x))"=f"(g(x)) g"(x)$

$f"(x)=cos"(5x) (5x)"=-sin(5x) 5= -5sin(5x)$

Den fysiska betydelsen av derivatan

Om materiell punkt rör sig rätlinjigt och dess koordinater ändras beroende på tid enligt lagen $x(t)$, då är den momentana hastigheten för denna punkt lika med funktionens derivata.

Punkten rör sig längs koordinatlinjen enligt lagen $x(t)= 1,5t^2-3t + 7$, där $x(t)$ är koordinaten vid tiden $t$. Vid vilken tidpunkt kommer punktens hastighet att vara lika med $12$?

1. Hastighet är en derivata av $x(t)$, så låt oss hitta derivatan av den givna funktionen

$v(t) = x"(t) = 1,5 2t -3 = 3t -3$

2. För att hitta vid vilken tidpunkt $t$ hastigheten var lika med $12$, komponerar vi och löser ekvationen:

Den geometriska betydelsen av derivatan

Kom ihåg att ekvationen för en rät linje som inte är parallell med koordinataxlarna kan skrivas som $y = kx + b$, där $k$ är den räta linjens lutning. Koefficienten $k$ är lika med tangenten för lutningen mellan den räta linjen och den positiva riktningen för $Ox$-axeln.

Derivatan av funktionen $f(x)$ i punkten $x_0$ är lika med lutningen $k$ för tangenten till grafen vid den givna punkten:

Därför kan vi göra en generell jämlikhet:

$f"(x_0) = k = tgα$

I figuren ökar tangenten till funktionen $f(x)$, därav koefficienten $k > 0$. Eftersom $k > 0$, då $f"(x_0) = tgα > 0$. Vinkeln $α$ mellan tangenten och den positiva riktningen $Ox$ är skarp.

I figuren minskar tangenten till funktionen $f(x)$, därav koefficienten $k< 0$, следовательно, $f"(x_0) = tgα < 0$. Угол $α$ между касательной и положительным направлением оси $Ох$ тупой.

I figuren är tangenten till funktionen $f(x)$ parallell med $Ох$-axeln, därav koefficienten $k = 0$, därav $f"(x_0) = tg α = 0$. Punkten $ x_0$ där $f "(x_0) = 0$, anropad extremum.

Figuren visar grafen för funktionen $y=f(x)$ och tangenten till denna graf ritad vid punkten med abskissan $x_0$. Hitta värdet på derivatan av funktionen $f(x)$ vid punkten $x_0$.

Tangenten till grafen ökar, därför $f"(x_0) = tg α > 0$

För att hitta $f"(x_0)$, hittar vi tangenten för lutningen mellan tangenten och den positiva riktningen för $Ox$-axeln. För att göra detta slutför vi tangenten till triangeln $ABC$.

Hitta tangenten för vinkeln $BAC$. (Tangensen för en spetsig vinkel i en rätvinklig triangel är förhållandet mellan det motsatta benet och det intilliggande benet.)

$tg BAC = (BC)/(AC) = (3)/(12)= (1)/(4)=0,25$

$f"(x_0) = tg DU = $0,25

Svar: $0,25

Derivatan används också för att hitta intervallen för ökande och minskande funktioner:

Om $f"(x) > 0$ på ett intervall, så ökar funktionen $f(x)$ på detta intervall.

Om $f"(x)< 0$ на промежутке, то функция $f(x)$ убывает на этом промежутке.

Figuren visar grafen för funktionen $y = f(x)$. Hitta bland punkterna $х_1,х_2,х_3…х_7$ de punkter där derivatan av funktionen är negativ.

Skriv ner antalet datapunkter som svar.

Kommunal läroanstalt

"Saltykovskaya gymnasieskola

Rtishchevsky-distriktet i Saratov-regionen

Mästarklass i matematik

i 11:e klass

om detta ämne

"DERIVATIV FUNKTION

I ANVÄNDNINGENS UPPGIFTER"

Ledde mattelärare

Beloglazova L.S.

2012-2013 akademiskt år

Syftet med mästarklassen : att utveckla elevernas färdigheter i att tillämpa teoretiska kunskaper om ämnet "Derivat av en funktion" för att lösa problem av en enda statlig examen.

Uppgifter

Pedagogisk: generalisera och systematisera elevernas kunskaper om ämnet

"The derivative of the function", för att överväga prototyperna av USE-problemen i detta ämne, för att ge eleverna möjlighet att testa sina kunskaper samtidigt som de löser problem på egen hand.

Utvecklande: främja utvecklingen av minne, uppmärksamhet, självkänsla och självkontroll; grundläggande kärnkompetenser(jämförelse, jämförelse, klassificering av objekt, bestämning av adekvata metoder för att lösa lärande uppgift på grundval av givna algoritmer, förmågan att agera självständigt i en situation av osäkerhet, att kontrollera och utvärdera sin verksamhet, att hitta och eliminera orsakerna till svårigheter).

Pedagogisk: främja:

bildandet av elevernas ansvarsfulla inställning till lärande;

utveckling av ett hållbart intresse för matematik;

skapa positiv inre motivation att studera matematik.

Teknologier: individuellt differentierat lärande, IKT.

Lär ut metoder: verbala, visuella, praktiska, problematiska.

Arbetsformer: individuell, frontal, i par.

Utrustning och material för lektionen: projektor, duk, PC för varje elev, simulator (Bilaga nr 1), presentation för lektionen (Bilaga nr 2), individuellt - differentierade kort för självständigt arbete i par (Bilaga nr 3), lista över webbplatser, individuellt differentierade läxa (Bilaga nr 4).

Förklaring till mästarklassen. Denna mästarklass hålls i årskurs 11 för att förbereda sig för tentamen. Syftar till att tillämpa teoretiskt material på ämnet "Derivat av en funktion" vid lösning av examinationsuppgifter.

Mästarklassens varaktighet- 30 minuter.

Strukturen för mästarklassen

I. Organisationsmoment -1 min.

II Kommunikation av ämnet, mål för mästarklassen, motivation för utbildningsaktiviteter - 1 min.

III. Framarbete. Utbildning "Uppdrag B8 ANVÄNDNING". Analys av arbetet med simulatorn - 6 min.

IV.Individuellt - differentierat arbete i par. Oberoende problemlösning B14. Ömsesidig kontroll - 7 min.

V. Kontrollera individuella läxor. Uppgift med parameter C5 ANVÄND

3 min.

VI .On-line testning. Analys av testresultat - 9 min.

VII. Individuellt differentierade läxor -1 min.

VIII. Betyg på lektionen - 1 min.

IX. Lektionssammanfattning. Reflektion -1 min.

Master class framsteg

jag .Arrangera tid.

II .Kommunikation av ämnet, mästarklassens mål, motivering av utbildningsaktiviteter.

(Bild 1-2, Bilaga nr 2)

Ämnet för vår lektion är "Derivatan av en funktion i tentamens uppgifter." Alla känner till talesättet "Spolen är liten och dyr." En av dessa "spolar" i matematik är derivatan. Derivatet används för att lösa många praktiska uppgifter matematik, fysik, kemi, ekonomi och andra discipliner. Det låter dig lösa problem enkelt, vackert, intressant.

Ämnet "Derivat" presenteras i uppgifterna i del B (B8, B14) i det enhetliga provet. Vissa C5-uppgifter kan också lösas med hjälp av en derivata. Men för att lösa dessa problem krävs goda matematiska förberedelser och icke-standardiserat tänkande.

Du har arbetat med de dokument som reglerar strukturen och innehållet i kontrollmätmaterialen för Unified State Examination in Mathematics 2013. Dra slutsatsen attvilka kunskaper och färdigheter behöver du för att framgångsrikt lösa problemen med examen på ämnet "Derivat".

(Bild 3-4, Bilaga nr 2)

Vi studerat"Kodifierare innehållselement i MATHEMATICS för sammanställning av kontrollmätmaterial för att genomföra en enhetlig examen",

"Kodifierare av krav på utbildningsnivån för utexaminerade","Specifikation kontrollera mätmaterial","Demoversion"kontrollmätmaterial från Unified State examen 2013 "ochkommit på vilka kunskaper och färdigheter om en funktion och dess derivata behövs för att framgångsrikt lösa problem i ämnet "Derivat".

Nödvändig

• KÄNNA TILL

P regler för beräkning av derivat;

derivator av grundläggande elementära funktioner;

geometrisk och fysisk betydelse av derivatan;
ekvationen för tangenten till grafen för funktionen;
undersökning av en funktion med hjälp av en derivata.

KUNNA

utföra åtgärder med funktioner (beskriv beteendet och egenskaperna för en funktion enligt grafen, hitta dess max- och minivärden).

ANVÄNDA SIG AV

förvärvade kunskaper och färdigheter i praktisk verksamhet och vardag.

Du har teoretiska kunskaper inom ämnet "Derivat". Idag ska viLÄR ATT ANVÄNDA KUNSKAP OM DERIVATFUNKTIONEN FÖR LÖSNING AV ANVÄNDNINGSPROBLEM. ( Bild 4, ansökan nummer 2)

Trots allt inte utan anledning Aristoteles sa det "INTELLIGENS BESTÅR INTE BARA I KUNSKAP, UTAN OCKSÅ I Förmågan att tillämpa kunskap i praktiken"( Bild 5, ansökan nummer 2)

I slutet av lektionen kommer vi att återgå till målet för vår lektion och ta reda på om vi har uppnått det?

III . Framarbete. Utbildning "Uppdrag B8 ANVÄNDNING" (Bilaga nr 1) . Analys av arbetet med simulatorn.

Välj rätt svar bland de fyra givna.

Vad tycker du är svårigheten att klara uppgift B8?

Vad tror du är de typiska misstagen som akademiker gör på provet när de löser det här problemet?

När du svarar på frågorna i uppgift B8 ska du kunna beskriva beteendet och egenskaperna för en funktion på grafen för derivatan, och på grafen för funktionen, beteendet och egenskaperna för funktionens derivata. Och detta kräver goda teoretiska kunskaper om följande ämnen: "Geometrisk och mekanisk betydelse av derivatan. Tangent till grafen för en funktion. Tillämpning av derivatan för studier av funktioner.

Analysera vilka uppgifter som orsakade dig svårigheter?

Vilka teoretiska frågor behöver du veta?

IV. Individuellt - differentierat arbete i par. Oberoende problemlösning B14. Ömsesidig verifiering. (Bilaga nr 3)

Kom ihåg algoritmen för att lösa problem (B14 USE) för att hitta extrema punkter, funktionsextrema, de största och minsta värdena för funktionen på intervallet med hjälp av derivatan.

Lös problem med hjälp av derivatan.

Eleverna fick följande problem:

"Tänk på det, kan vissa B14-problem lösas på ett annat sätt, utan att använda ett derivat?"

1 par(Lukyanova D., Gavryushina D.)

1)B14. Hitta minimipunkten för funktionen y \u003d 10x-ln (x + 9) + 6

2) B14.Hitta det största värdet på en funktiony =

– Försök att lösa det andra problemet på två sätt.

2 par(Saninskaya T., Sazanov A.)

1)B14.Hitta det minsta värdet på funktionen y=(x-10) på segmentet

2) B14. Hitta maxpunkten för funktionen y \u003d -

(Eleverna försvarar sin lösning genom att skriva ner huvudstegen för att lösa problem på tavlan. Elever om 1 par (Lukyanova D., Gavryushina D.) tillhandahålla två sätt att lösa problem #2).

Lösning av ett problem. Slutsats som eleverna ska dra:

"Vissa B14 USE-problem med att hitta de minsta och största värdena på en funktion kan lösas utan att använda en derivata, baserat på funktioners egenskaper."

Analysera vilket misstag du gjorde i uppgiften?

Vilka teoretiska frågor behöver du upprepa?

V. Kontrollera individuella läxor. Uppgift med parameter C5(USE) ( Bild 7-8, Bilaga #2)

Lukyanova K. fick en individuell hemuppgift: välj ett problem med parametern (C5) från manualerna för att förbereda provet och lös det med hjälp av derivatan.

(Eleven ger en lösning på problemet, utifrån den funktionell-grafiska metoden, som en av metoderna för att lösa problem C5 ANVÄNDNING och ger kort förklaring den här metoden).

Vilken kunskap om funktionen och dess derivata är nödvändig för att lösa problem C5 ANVÄNDNING?

V I. Onlinetestning för uppgifter B8, B14. Analys av testresultat.

Webbplats för att testa i lektionen:

Vem gjorde inte misstag?

Vem upplevde svårigheter med att testa? Varför?

Vilka uppgifter är fel?

Avsluta vilka teoretiska frågor du behöver veta?

VI jag. Individuellt differentierade läxor

(Bild 9, ansökan nummer 2), (Bilaga nr 4).

Jag har förberett en lista över webbplatser för att förbereda mig inför provet. Du kan också surfa på dessa webbplatsern – linjetestning. För nästa lektion måste du: 1) upprepa teoretiskt material på ämnet "Derivat av en funktion";

2) på sajten "Öppen bank med uppdrag i matematik" ( ) hitta prototyper av uppgifter B8 och B14 och lösa minst 10 uppgifter;

3) Lukyanova K., Gavryushina D. lösa problem med parametrar. Resten av eleverna löser problem 1-8 (alternativ 1).

VIII. Lektionsbetyg.

Vilket betyg skulle du ge dig själv på lektionen?

Tror du att du skulle kunna göra det bättre i klassen?

IX. Sammanfattning av lektionen. Reflexion

Låt oss sammanfatta vårt arbete. Vad var syftet med lektionen? Tror du att det har uppnåtts?

Titta på tavlan och i en mening, välj början av frasen, fortsätt den mening som passar dig bäst.

Jag kände…

Jag lärde…

Jag lyckades …

Jag lyckades...

Jag ska försöka …

Jag blev förvånad över det …

Jag ville…

Kan du säga att det skedde en berikning av din kunskapsstock under lektionen?

Så du upprepade de teoretiska frågorna om derivatan av en funktion, tillämpade sina kunskaper i att lösa prototyper av USE-uppgifter (B8, B14), och Lukyanova K. genomförde uppgift C5 med en parameter, vilket är en uppgift av ökad grad av komplexitet.

Jag trivdes med att jobba med dig och Jag hoppas att du framgångsrikt kommer att kunna tillämpa de kunskaper du fått i matematiklektionerna inte bara i klara provet men också i vidare studier.

Jag skulle vilja avsluta lektionen med en italiensk filosofs ord Thomas av Aquino"Kunskap är en så dyrbar sak att det inte är skamligt att få den från någon källa" (Bild 10, Bilaga nr 2).

Jag önskar dig framgång med att förbereda dig inför provet!

PRAKTISKT ARBETE EXTRA-LÄRPLAN 2

Transformation av grafer över funktioner.

Mål

Rita funktionsgrafer med hjälp av olika transformationer, svara på frågan om problemet.

Slutförande av arbetet

Riktlinjer

Verket är utformat för 10 alternativ, alternativnumret matchar den sista siffran i serienumret i listan. Till exempel, 1, 11, 21, 31 ... utför 1 alternativ, 2,12, 22 ... - 2 alternativ, etc.

Arbetet består av två delar: den första delen av uppgifterna 1 - 5, dessa är uppgifter som måste utföras för att få tillgodoräknande, om dessa uppgifter är slutförda med ett fel behöver du korrigera dem och lämna in arbetet igen för verifiering . Den andra delen innehåller uppgifter, genom att slutföra vilka du kan tjäna ett extra betyg: huvuddelen +2 uppgifter - "4", huvuddelen +3 uppgifter - "5".

Uppgift 1. Grafen för en linjär funktion är en rät linje, två punkter räcker för att konstruera den. (vi tar värdena för argumentet x godtyckligt och överväger att ersätta värdet för funktionen y i formeln).

För att kontrollera om grafen för funktionen går genom den angivna punkten måste du ersätta punktens koordinater istället för x och y, om du får rätt likhet så går linjen genom den angivna punkten, annars passerar den inte .

Uppgift 2, 3, 4. Graferna för de angivna funktionerna hämtas från funktionernas grafer , med en förskjutning längs x- eller y-axeln.

, plotta först funktionen eller , sedan flyttar vi det med "a" enheter till höger eller vänster (+ a - till vänster, - a till höger), sedan flyttar vi det med "b" enheter upp eller ner (+ in - upp, - in - ner)

På samma sätt med andra funktioner:

Uppgift 5 Så här ritar du en funktionsgraf: , måste du: 1) bygga en graf över funktionen , 2) den del av grafen som är ovanför x-axeln lämnas oförändrad, 3) den del av grafen som är under x-axeln speglas.

Uppgifter för självständig lösning.

Obligatorisk del

Uppgift 1. Rita en graf för en linjär funktion, avgör om grafen för funktionen går genom den angivna punkten:

Uppgift 2. Rita en graf av en kvadratisk funktion, ange uppsättningen värden för denna funktion.

Uppgift 3. Bygg en graf över en funktion, avgör om den angivna funktionen ökar eller minskar.

Uppgift 4. Bygg en graf över funktionen, svara på uppgiftens fråga.

Uppgift 5. Bygg en graf över en funktion som innehåller tecknet för modulen.

Uppgifter för ytterligare bedömning.

Uppgift 6. Rita en graf av en funktion given bitvis, avgör om denna funktion har en brytpunkt:

Uppgift 7. Bestäm hur många lösningar ekvationssystemet har, motivera svaret. Dra slutsatser genom att svara på frågorna.

Vilka funktionsdiagram har du byggt i det här arbetet?

Vad heter grafen för en linjär funktion?

Vad heter grafen för en kvadratisk funktion?

Vilka diagramtransformationer känner du till?

Hur ligger grafen för en jämn funktion i koordinatsystemet? Graf över en udda funktion?