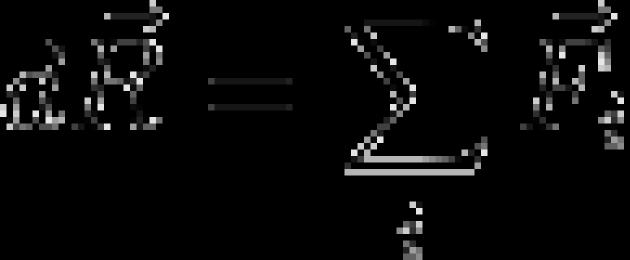Se: denna artikel har lästs 14066 gånger
Pdf Välj språk ... Ryska Ukrainska engelska
Kort recension
Hela materialet laddas ner ovan, efter att ha valt språk tidigare
Rörelsebelopp
Mängden rörelse för en materialpunkt är en vektorkvantitet lika med produkten av massan av en punkt med vektorn av dess hastighet.
Enheten för att mäta momentum är (kg m/s).
Rörelsebelopp mekaniskt system - en vektorkvantitet lika med den geometriska summan (huvudvektorn) av ett mekaniskt systems rörelsemängd är lika med produkten av hela systemets massa med hastigheten för dess masscentrum.
När en kropp (eller ett system) rör sig så att dess masscentrum är stationär, är kroppens rörelsemängd noll (till exempel kroppens rotation runt en fast axel som går genom kroppens masscentrum ).
Vid komplex rörelse kommer systemets rörelsemängd inte att karakterisera den roterande delen av rörelsen när den roterar runt massans centrum. Det vill säga momentumet karakteriserar endast systemets translationella rörelse (tillsammans med masscentrum).
Kraftimpuls
Kraftimpulsen kännetecknar kraftens verkan under en viss tidsperiod.
Kraftimpuls under en begränsad tidsperiod definieras som integralsumman av motsvarande elementära impulser.
Satsen om förändringen i mängden rörelse för en materialpunkt
(i differentiell form e ):
Tidsderivatan av en materialpunkts rörelsemängd är lika med den geometriska summan av krafterna som verkar på punkterna.
(v integrerad form ):
Förändringen i mängden rörelse hos en materialpunkt under en viss tidsperiod är lika med den geometriska summan av impulserna av krafter som appliceras på punkten under denna tidsperiod.
Satsen om förändringen i ett mekaniskt systems rörelsemängd
(i differentiell form ):
Tidsderivatan av systemets rörelsemängd är lika med den geometriska summan av alla yttre krafter som verkar på systemet.
(i integrerad form ):
Förändringen i systemets rörelsemängd under en viss tidsperiod är lika med den geometriska summan av impulserna av yttre krafter som verkar på systemet under denna tidsperiod.
Satsen gör det möjligt att från beaktande utesluta uppenbart okända inre krafter.
Satsen om förändringen i ett mekaniskt systems rörelsemängd och satsen om masscentrums rörelse är två olika former av samma sats.
Lagen om bevarande av systemets rörelsemängd
- Om summan av alla yttre krafter som verkar på systemet är lika med noll, kommer vektorn för systemets rörelsemängd att vara konstant i riktning och modul.
- Om summan av projektionerna av alla yttre krafter som verkar på någon godtycklig axel är noll, så är projektionen av rörelsemängden på denna axel konstant.
Slutsatser:
- Bevarandelagar indikerar att inre krafter inte kan ändra systemets totala rörelsemängd.
- Satsen om förändringen i ett mekaniskt systems rörelsemängd karakteriserar inte rotationsrörelsen hos ett mekaniskt system, utan endast translationell.
Ett exempel ges: Bestäm rörelsemängden för en skiva med en viss massa, om dess vinkelhastighet och storlek är kända.
Ett exempel på beräkning av en cylindrisk växel
Ett exempel på beräkning av en cylindrisk växel. Materialval, beräkning av tillåtna spänningar, beräkning av kontakt och böjhållfasthet utfördes.
Ett exempel på att lösa problemet med att böja en balk
I exemplet är diagram byggda sidokrafter och böjmoment, en farlig sektion hittades och en I-balk valdes. Uppgiften analyserade konstruktionen av diagram med hjälp av differentiella beroenden, genomfördes jämförande analys olika tvärsnitt av balken.
Ett exempel på att lösa problemet med axelvridning
Uppgiften är att kontrollera hållfastheten hos en stålaxel för en given diameter, material och tillåtna spänningar. Under lösningen ritas diagram över vridmoment, skjuvspänningar och torsionsvinklar. Skaftets egenvikt tas inte med i beräkningen.
Ett exempel på att lösa problemet med spänningskompression av en stång
Uppgiften är att kontrollera hållfastheten hos en stålstång vid en given tillåten spänning. Under lösningens gång ritas diagram över längsgående krafter, normalspänningar och förskjutningar. Stångens egenvikt tas inte med i beräkningen.
Tillämpning av satsen för bevarande av kinetisk energi
Ett exempel på att lösa problemet med tillämpningen av bevarandeteoremet rörelseenergi mekaniskt system
Bestämning av en punkts hastighet och acceleration enligt de givna rörelseekvationerna
Ett exempel på att lösa ett problem för att bestämma hastigheten och accelerationen för en punkt enligt de givna rörelseekvationerna
Bestämning av hastigheter och accelerationer för punkter i en stel kropp under planparallell rörelse
Ett exempel på att lösa problemet med att bestämma hastigheter och accelerationer för punkter fast med planparallell rörelse
Bestämning av krafter i stängerna på ett plant fackverk
Ett exempel på att lösa problemet med att bestämma krafterna i stängerna i en platt fackverk med Ritter-metoden och genom metoden att skära noder
Tillämpning av satsen om förändringen i rörelsemängd
Ett exempel på att lösa problemet med tillämpningen av satsen om förändringen i rörelsemängd för att bestämma vinkelhastighet en kropp som roterar runt en fast axel.
Alla mekaniska system som består av vilka kroppar som helst kan fungera som ett system, vilket diskuteras i satsen.
Uttalande av satsen
Mängden rörelse (impuls) för ett mekaniskt system kallas en kvantitet som är lika med summan av rörelsemängderna (impulser) för alla kroppar som ingår i systemet. Impulsen av yttre krafter som verkar på systemets kroppar är summan av impulserna av alla yttre krafter som verkar på systemets kroppar.
( kg m/s)
Satsen om förändringen i mängden rörelse hos systemet anger
Förändringen i systemets rörelsemängd under en viss tidsperiod är lika med impulsen av yttre krafter som verkar på systemet under samma tidsperiod.
Lagen om bevarande av systemets rörelsemängd
Om summan av alla yttre krafter som verkar på systemet är noll, så är systemets rörelsemängd (momentum) ett konstant värde.
,
får vi uttrycket för satsen om förändringen i systemets rörelsemängd i differentialform:
Att integrera båda sidor av den resulterande jämlikheten över ett godtyckligt tidsintervall mellan några och, vi får uttrycket för satsen om förändringen i systemets rörelsemängd i integralform:
Impulsvårdslag (Lagen om bevarande av momentum) hävdar att vektorsumman av momentan för alla kroppar i systemet är ett konstant värde om vektorsumman av de yttre krafterna som verkar på systemet är lika med noll.
(rörelsemoment m 2 kg s −1)
Sats om förändringen i rörelsemängden relativt centrum
tidsderivatan av rörelsemängden (momentet) för en materialpunkt i förhållande till något fast centrum är lika med momentet för kraften som verkar på punkten i förhållande till samma centrum.
dk 0 /dt = M 0 (F ) .
Satsen om förändringen av rörelsemängden kring axeln
tidsderivatan av rörelsemängden (vinkelmomentet) för en materialpunkt i förhållande till någon fast axel är lika med momentet för kraften som verkar på denna punkt i förhållande till samma axel.
dk x /dt = M x (F ); dk y /dt = M y (F ); dk z /dt = M z (F ) .
Överväga materiell punkt M massa m rör sig med våld F (Figur 3.1). Låt oss skriva ner och konstruera vektorn för rörelsemängd (momentum) M 0 materialpunkt i förhållande till mitten O :
Vi differentierar uttrycket för rörelsemängd (momentum k 0) efter tid:
Eftersom dr /dt = V , sedan korsprodukten V ⊗ m ⋅ V (kolinjära vektorer V och m ⋅ V ) är lika med noll. På samma gång d (m ⋅ V) /dt = F enligt satsen om en materiell punkts rörelsemängd. Därför får vi det
dk 0 /dt = r ⊗F , (3.3)
var r ⊗F = M 0 (F ) - vektor-kraftmoment F relativt fast centrum O ... Vektor k 0 ⊥ plan ( r , m ⊗V ), och vektorn M 0 (F ) ⊥ plan ( r ,F ), har vi äntligen
dk 0 /dt = M 0 (F ) . (3.4)
Ekvation (3.4) uttrycker satsen om förändringen av rörelsemängden (momentet) för en materialpunkt i förhållande till centrum: tidsderivatan av rörelsemängden (momentet) för en materialpunkt i förhållande till något fast centrum är lika med momentet för kraften som verkar på punkten i förhållande till samma centrum.
Att projicera likhet (3.4) på axeln för kartesiska koordinater får vi
dk x /dt = M x (F ); dk y /dt = M y (F ); dk z /dt = M z (F ) . (3.5)
Likheter (3.5) uttrycker satsen om förändringen i rörelsemängden (momentet) för en materialpunkt i förhållande till axeln: tidsderivatan av rörelsemängden (vinkelmomentet) för en materialpunkt i förhållande till någon fast axel är lika med momentet för kraften som verkar på denna punkt i förhållande till samma axel.
Betrakta konsekvenserna som följer av satser (3.4) och (3.5).
Följd 1. Tänk på fallet där kraften F under hela rörelsen av punkten passerar genom det fasta mitten O (fallet med en central kraft), dvs. när M 0 (F ) = 0. Sedan följer det av sats (3.4) att k 0 = konst ,
de där. i fallet med en central kraft förblir rörelsemängden (vinkelmomentet) för en materialpunkt i förhållande till centrum för denna kraft konstant i storlek och riktning (Figur 3.2).
Figur 3.2
Från tillståndet k 0 = konst det följer att banan för en rörlig punkt är en plan kurva, vars plan passerar genom centrum för denna kraft.
Följd 2. Låta M z (F ) = 0, dvs. kraft korsar axeln z eller är parallell med den. I det här fallet, som kan ses från den tredje av ekvationerna (3.5), k z = konst ,
de där. om momentet för kraften som verkar på en punkt i förhållande till någon fast axel alltid är noll, så förblir rörelsemängden (vinkelmomentet) för punkten i förhållande till denna axel konstant.
Bevis för satsen om förändringen i momentum
Låt systemet bestå av materialpunkter med massor och accelerationer. Alla krafter som verkar på systemets kroppar kan delas in i två typer:
Yttre krafter är krafter som verkar från kroppar som inte är en del av det aktuella systemet. De resulterande yttre krafterna som verkar på materialet pekar med numret i beteckna.
Inre krafter är de krafter med vilka själva systemets kroppar interagerar med varandra. Kraften med vilken till punkten med siffran i punkt med nummer är i kraft k, kommer vi att beteckna, och slagkraften i-th punkt på k punkten -. Uppenbarligen, för alltså
Med hjälp av de införda beteckningarna skriver vi ner Newtons andra lag för var och en av de materiella punkterna som behandlas i formuläret
Med tanke på att 
och summerar alla ekvationerna i Newtons andra lag får vi:
Uttrycket är summan av alla inre krafter som verkar i systemet. Enligt Newtons tredje lag, i denna summa, motsvarar varje kraft en kraft så att den därför uppfylls 
Eftersom hela summan består av sådana par, så är summan i sig lika med noll. Således kan man skriva
Genom att använda notationen för systemets rörelsemängd får vi
Att ta hänsyn till förändringen i impulsen från yttre krafter 
, får vi uttrycket för satsen om förändringen i systemets rörelsemängd i differentialform:
Således tillåter var och en av de senast erhållna ekvationerna oss att hävda: förändringen i systemets rörelsemängd inträffar endast som ett resultat av verkan av yttre krafter, och inre krafter kan inte utöva något inflytande på detta värde.
Genom att integrera båda sidor av den erhållna jämlikheten över ett godtyckligt taget tidsintervall mellan några och vi får uttrycket för satsen om förändringen i systemets rörelsemängd i integral form:
var och är värdena för systemets rörelsemängd vid tidpunkter och respektive och är impulsen av yttre krafter över en tidsperiod. I enlighet med vad som tidigare sagts och de införda beteckningarna,
Låt den materiella punkten röra sig under inverkan av kraft F... Det är nödvändigt att bestämma rörelsen av denna punkt i förhållande till det rörliga systemet Oxyz(se den komplexa rörelsen av en materialpunkt), som rör sig på ett känt sätt med avseende på ett stationärt system O 1 x 1 y 1 z 1 .
Grundekvationen för dynamik i ett stationärt system
Vi skriver ner den absoluta accelerationen av en punkt enligt Coriolis-satsen
var a magmuskler- absolut acceleration;
a rel- relativ acceleration;
a körfält- Bärbar acceleration;
a kor- Coriolisacceleration.
Vi skriver om (25) med hänsyn till (26)
Låt oss presentera notationen 
- bärbar tröghetskraft, 
- Coriolis tröghetskraft. Sedan tar ekvation (27) formen
Grundläggande ekvation av dynamik att studera relativ rörelse(28) skrivs på samma sätt som för absolut rörelse, endast translations- och Coriolis-tröghetskrafterna måste adderas till krafterna som verkar på punkten.
Allmänna satser om en materiell punkts dynamik
När du löser många problem kan du använda färdiga ämnen som erhållits på grundval av Newtons andra lag. Sådana problemlösningsmetoder kombineras i detta avsnitt.
Satsen om förändringen i mängden rörelse för en materialpunkt
Låt oss presentera följande dynamiska egenskaper:
1. Mängden rörelse för en materialpunktÄr en vektorkvantitet lika med produkten av massan av en punkt med vektorn av dess hastighet
.
(29)
2. Kraftimpuls
Elementär kraftimpulsÄr en vektorkvantitet lika med produkten av kraftvektorn med ett elementärt tidsintervall
(30).
Sedan full impuls
.
(31)
På F= const vi får S=Med.
Den totala impulsen för en begränsad tidsperiod kan endast beräknas i två fall när kraften som verkar på punkten är konstant eller beror på den tiden. I andra fall är det nödvändigt att uttrycka kraft som en funktion av tiden.
Likheten mellan dimensionerna impuls (29) och momentum (30) gör det möjligt att etablera ett kvantitativt samband mellan dem.
Betrakta rörelsen av en materiell punkt M under åtgärden godtycklig kraft F längs en godtycklig bana.
O 
UD: 
.
(32)
Vi separerar variablerna i (32) och integrerar
.
(33)
Som ett resultat, med hänsyn till (31), får vi
.
(34)
Ekvation (34) uttrycker följande sats.
Sats: Förändringen av rörelsemängden för en materiell punkt under en viss tidsperiod är lika med impulsen av kraften som verkar på punkten, över samma tidsintervall.
Vid problemlösning måste ekvation (34) projiceras på koordinataxeln
Det är bekvämt att använda detta teorem när det bland de givna och okända storheterna finns massan av en punkt, dess initiala och slutliga hastighet, krafter och rörelsetid.
Satsen om förändringen i rörelsemängden för en materiell punkt
M 
momentum för en materiell punkt i förhållande till centrum är lika med produkten av modulen för punktens rörelsemängd av axeln, dvs. kortaste avståndet (vinkelrätt) från centrum till den linje som sammanfaller med hastighetsvektorn
,
(36)
.
(37)
Sambandet mellan kraftmomentet (orsak) och momentet av momentet (konsekvens) fastställs av följande sats.
Låt en punkt M av en given massa m rör sig med våld F.
,
,
,
(38)
.
(39)
Låt oss beräkna derivatan av (39)
.
(40)
Genom att kombinera (40) och (38) får vi äntligen
.
(41)
Ekvation (41) uttrycker följande sats.
Sats: Tidsderivatan av vektorn för rörelsemängdsrörelsen för en materialpunkt i förhållande till ett visst centrum är lika med momentet för kraften som verkar på punkten i förhållande till samma centrum.
Vid problemlösning måste ekvation (41) projiceras på koordinataxeln
I ekvation (42) beräknas momenten för kvantiteterna av rörelse och kraft i förhållande till koordinataxlarna.
Av (41) följer bevarandelag för rörelsemängd (Keplers lag).
Om kraftmomentet som verkar på en materiell punkt i förhållande till något centrum är lika med noll, så behåller momentet för punkten i förhållande till detta centrum sin storlek och riktning.
Om 
, då 
.
Bevarandesatsen och lagen används i problem med krökt rörelse, speciellt när centrala krafter verkar.
Betrakta ett system som består av materialpunkter. Låt oss komponera för detta system differentialekvationer motion (13) och lägg till dem term för term. Då får vi
Den sista summan är lika med noll med egenskapen för inre krafter. Dessutom,
Vi hittar äntligen
Ekvation (20) uttrycker satsen om förändringen i systemets rörelsemängd i differentialform: tidsderivatan av systemets rörelsemängd är lika med den geometriska summan av alla yttre krafter som verkar på systemet. I projektioner till koordinataxlarna kommer att vara:
Låt oss hitta ett annat uttryck för satsen. Låt vid tidpunkten mängden rörelse i systemet är lika med och i ögonblicket blir det lika. När vi sedan multiplicerar båda sidor av likhet (20) med och integrerar, får vi
eftersom integralerna till höger ger impulser av yttre krafter.
Ekvation (21) uttrycker satsen om förändringen i systemets rörelsemängd i integralform: ändringen i systemets rörelsemängd under en viss tidsperiod är lika med summan av impulser som verkar på systemet av yttre krafter för samma tidsperiod.
I projektioner till koordinataxlarna kommer att vara:
Låt oss peka på sambandet mellan den bevisade satsen och satsen om masscentrums rörelse. Sedan ersätter vi detta värde med likhet (20) och tar hänsyn till att vi får, dvs ekvation (16).
Följaktligen är satsen om masscentrums rörelse och satsen om förändringen i systemets rörelsemängd i huvudsak två olika former samma teorem. I de fall då rörelsen hos en stel kropp (eller ett system av kroppar) studeras, kan vilken som helst av dessa former användas på samma sätt, och ekvation (16) är vanligtvis mer bekväm att använda. För ett kontinuerligt medium (vätska, gas), när man löser problem, används vanligtvis satsen om förändringen i systemets rörelsemängd. Detta teorem har också viktiga tillämpningar i teorin om nedslag (se kapitel XXXI) och i studiet av jetframdrivning (se § 114).
Differentialekvation för rörelse av en materiell punkt under inverkan av kraft F kan representeras i följande vektorform:
Sedan massan av punkten m accepterad konstant, då kan den anges under derivatans tecken. Sedan
Formel (1) uttrycker satsen om förändringen i en punkts rörelsemängd i differentialform: den första tidsderivatan av punktens rörelsemängd är lika med kraften som verkar på punkten.
I projektioner på koordinataxlarna kan (1) representeras som
Om båda sidorna av (1) multipliceras med dt, då får vi en annan form av samma sats - impulssatsen i differentialform:
de där. differentialen för punktens rörelsemängd är lika med elementarimpulsen för kraften som verkar på punkten.
Vi får fram båda sidor av (2) på koordinataxlarna
Genom att integrera båda sidor av (2) inom området från noll till t (fig. 1), har vi
var är punktens hastighet för tillfället t; - hastighet vid t = 0;
S- kraftimpuls över tid t.
Uttryck i formen (3) kallas ofta momentumsatsen i den slutliga (eller integral) formen: förändringen i en punkts rörelsemängd under vilken tidsperiod som helst är lika med kraftimpulsen under samma tidsperiod.
I projektioner på koordinataxlarna kan denna sats representeras enligt följande:
För en materiell punkt skiljer sig inte satsen om förändringen i rörelsemängden i någon av formerna i huvudsak från differentialekvationerna för rörelse för en punkt.
Satsen om förändringen i systemets rörelsemängd
Systemets rörelsemängd är vektorkvantiteten F lika med den geometriska summan (huvudvektorn) av rörelsemängderna för alla punkter i systemet.
Betrakta ett system som består av n materiella poäng. Låt oss sammanställa differentialekvationer för rörelse för detta system och lägga till dem term för term. Då får vi:
Den sista summan är lika med noll med egenskapen för inre krafter. Dessutom,
Vi hittar äntligen:
Ekvation (4) uttrycker satsen om förändringen i systemets rörelsemängd i differentialform: tidsderivatan av systemets rörelsemängd är lika med den geometriska summan av alla yttre krafter som verkar på systemet.
Låt oss hitta ett annat uttryck för satsen. Låt för tillfället t= 0 mängden rörelse i systemet är Q 0, och i tidens ögonblick t 1 blir lika Q 1. Multiplicera sedan båda sidor av likhet (4) med dt och genom att integrera får vi:
Eller var:
(S-kraftimpuls)
eftersom integralerna till höger ger impulser av yttre krafter,
Ekvation (5) uttrycker satsen om förändringen i systemets rörelsemängd i integralform: förändringen i systemets rörelsemängd under en viss tidsperiod är lika med summan av impulser av yttre krafter som verkar på systemet under samma tidsperiod.
I projektioner på koordinataxlarna kommer vi att ha:
Lagen om bevarande av momentum
Från satsen om förändringen i systemets rörelsemängd kan följande viktiga konsekvenser erhållas:
1. Låt summan av alla yttre krafter som verkar på systemet vara lika med noll:
Sedan följer av ekv. (4) att i detta fall Q = konst.
På det här sättet, om summan av alla yttre krafter som verkar på systemet är lika med noll, kommer vektorn för systemets rörelsemängd att vara konstant i 10 modul och riktning.
2.01 Låt de yttre krafterna som verkar på systemet vara sådana att summan av deras projektioner på någon axel (till exempel Ox) är lika med noll:
Sedan följer av ekvation (4 ') att i detta fall Q = konst.
På det här sättet, om summan av projektionerna av alla yttre krafter som verkar på någon axel är noll, då är projektionen av systemets rörelsemängd på denna axel ett konstant värde.
Dessa resultat uttrycker lagen om bevarande av systemets rörelsemängd. Av dem följer att interna krafter inte kan förändra systemets totala momentum.
Låt oss titta på några exempel:
· Jag känner för det. Om vi betraktar geväret och kulan som ett system, kommer trycket från pulvergaserna när de avfyras att vara en intern kraft. Denna kraft kan inte ändra systemets totala rörelsemängd. Men eftersom drivgaserna, som verkar på kulan, ger den en viss rörelse framåt, måste de samtidigt ge geväret samma rörelse. omvänd riktning... Detta gör att geväret rör sig bakåt, dvs. den så kallade rekylen. Ett liknande fenomen uppstår när man avfyrar en pistol (rollback).
· Arbeta om t och grebn om in och n och (propeller). Skruven ger rörelse till en viss mängd luft (eller vatten) längs skruvens axel och kastar denna massa tillbaka. Om vi betraktar den kasserade massan och flygplanet (eller fartyget) som ett system, så kan inte krafterna i samverkan mellan propellern och mediet som interna förändra det totala momentumet för detta system. Därför, när man kastar en massa luft (vatten) bakåt, erhåller flygplanet (eller fartyget) motsvarande hastighet framåt, så att den totala rörelsemängden för det aktuella systemet förblir lika med noll, eftersom det var noll innan rörelsen började.
En liknande effekt uppnås genom verkan av åror eller skovelhjul.
· Reagerar I en raket (raket) sprutas gasformiga produkter från bränsleförbränning ut med hög hastighet från hålet i raketens bakdel (från jetmotorns munstycke). Tryckkrafterna som verkar i detta fall kommer att vara interna krafter och de kan inte ändra det totala momentumet för raketdrivgassystemet. Men eftersom de utströmmande gaserna har en viss rörelse bakåt, får raketen en motsvarande hastighet framåt.
Axelmomentsatsen.
Betrakta en materialpunkt med massa m rör sig med våld F... Låt oss för det hitta sambandet mellan vektorernas rörelsemängd mV och F i förhållande till någon fast Z-axel.
m z (F) = xF - уF (7)
Likadant för kvantiteten m (mV) om du tar ut m parentesen blir
m z (mV) = m (xV - yV)(7`)
Om vi tar tidsderivatorna från båda sidor av denna jämlikhet, finner vi
På höger sida av det resulterande uttrycket är den första parentesen 0, eftersom dx / dt = V och dу / dt = V, den andra parentesen enligt formel (7) är lika med
m z (F), eftersom enligt dynamikens grundläggande lag:
Äntligen kommer vi att ha (8)
Den resulterande ekvationen uttrycker momentsatsen kring axeln: tidsderivatan av rörelsemängden för en punkt kring någon axel är lika med momentet verkande kraft ungefär samma axel. Ett liknande teorem gäller också för momenten i förhållande till något centrum O.
- I kontakt med 0
- Google+ 0
- OK 0
- Facebook 0
