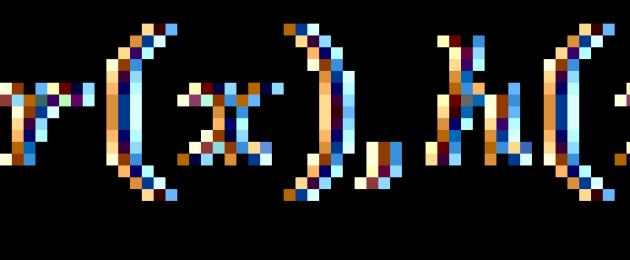Rationella ekvationer är exempel på träning. Videohandledning "Rationella ekvationer

Rationella ekvationer är ekvationer som innehåller rationella uttryck.

Definition 1

Rationella uttryck i detta fall är uttryck som kan skrivas som en vanlig bråkdel av formen $ \ frac (m) (n) $, medan $ m $ och $ n $ är heltal och $ n $ inte kan vara noll. Rationella uttryck inkluderar inte bara uttryck som innehåller bråk som $ \ frac (2) (3) $, utan också uttryck som bara innehåller heltal, eftersom vilket heltal som helst kan representeras som ett oegentligt bråk.

Låt oss nu överväga mer i detalj vad rationella ekvationer är.

Som vi nämnde ovan är rationella ekvationer ekvationer som innehåller rationella uttryck och variabler.

Beroende på var exakt variabeln finns i en rationell ekvation, kan den vara antingen en rationell bråkekvation eller en hel rationell ekvation.

Bråkekvationer kan innehålla ett bråk med en variabel i endast en del av ekvationen, medan en hel ekvation inte innehåller ett bråktal med en variabel.

Exempel på hela rationella ekvationer: $ 5x + 2 = 12 $; $ 3y = -7 (-4y + 5) $; $7a-14 = $256.

Exempel på rationella bråkekvationer: $ \ frac (3x-2) (x + 3) + \ frac (1) (2) = \ frac (5) (x) $; $ \ frac (7) (2y-3) = 5 $;

Det är värt att notera att endast ekvationer som innehåller ett bråk i nämnaren kallas rationella bråkekvationer, eftersom ekvationer som innehåller bråkuttryck utan variabler lätt kan reduceras till linjära integralekvationer.

Hur löser man rationella ekvationer?

Beroende på om du har att göra med en hel rationell ekvation eller en bråkdel, används lite olika algoritmer för att lösa.

Algoritm för att lösa hela rationella ekvationer

1. Först måste du bestämma den minsta gemensamma nämnaren för all jämlikhet.
2. Sedan måste du bestämma de faktorer med vilka du behöver multiplicera varje term i likheten.
3. Nästa steg är att få all jämställdhet till en gemensam nämnare.
4. Slutligen, genomförandet av sökandet efter rötterna till den resulterande hela rationella jämlikhet.

Exempel 1

Lös ekvationen: $ \ frac (5x + 9) (2) = \ frac (x) (4) $

Först hittar vi den gemensamma faktorn - i det här fallet är det antalet $ 4 $. För att bli av med nämnaren, multiplicera vänster sida med $ \ frac (2) (2) $, vi får:

$ 10x + 18 = x $ - den resulterande ekvationen är linjär, dess rot är $ x = -2 $.

Hur löser man rationella bråkekvationer?

I fallet med rationella bråkekvationer liknar lösningens ordning algoritmen för att lösa rationella heltalsekvationer, det vill säga objekt 1-4 bevaras, men efter att ha hittat de antagna rötterna vid användning av ojämna transformationer, rötterna måste kontrolleras genom att ersätta dem i ekvationen.

Exempel 2

Lös den rationella bråkekvationen: $ \ frac (x-3) (x-5) + \ frac (1) (x) = \ frac (x + 5) (x \ cdot (x-5)) $

För att få ett bråk till en gemensam nämnare, här är det $ x \ cdot (x-5) $, vi multiplicerar varje bråk med ett, presenterat i form av en faktor som krävs för att få en gemensam nämnare:

$ \ frac ((x-3) \ cdot x) ((x-5) \ cdot x) + \ frac (1 \ cdot (x-5)) (x \ cdot (x-5)) = \ frac ( x + 5) (x \ cdot (x-5)) $

Nu när hela bråket har en gemensam nämnare kan du bli av med den:

$ (x-3) \ cdot x + (x-5) = x + 5 $

$ x ^ 2 - 3x + x-5 = x + 5 $

Låt oss använda Vietas teorem för att lösa den resulterande andragradsekvationen:

$ \ begin (case) x_1 + x_2 = 3 \\ x_1 \ cdot x_2 = -10 \\ \ slut (case) $

$ \ begin (case) x_1 = 5 \\ x_2 = -2 \\ \ slut (case) $

Eftersom transformationen som används för att förenkla ekvationen inte är likvärdig, måste de resulterande rötterna kontrolleras i den ursprungliga ekvationen, för detta ersätter vi dem:

$ \ frac (-2-3) (- 2-5) + \ frac (1) (- 2) = \ frac (-2 + 5) ((- 2) \ cdot (-2-5)) $

$ \ frac (5) (7) - \ frac (1) (2) = \ frac (3) (14) $

$ \ frac (3) (14) = \ frac (3) (14) $ - därför är roten $ x_2 = -2 $ korrekt.

$ \ frac (5-3) (5-5) + \ frac (1) (5) = \ frac (5 + 5) ((- 2) \ cdot (5-5)) $

Här kan du direkt se att noll bildas i nämnaren, därför är roten $ x_1 = 5 $ en främmande.

Man måste komma ihåg att om en ekvation som innehåller ett uttryck av formen $ \ frac (m) (n) $ på vänster eller höger sida är lika med noll, kan bara bråkdelens täljare vara lika med noll. Detta beror på att om det bildas en nolla någonstans i nämnaren så är inte roten som testas roten till ekvationen, eftersom all likhet i detta fall förlorar sin betydelse. Rötterna som bringar nämnaren till noll kallas outsiders.

Om en bråkrationell ekvation har en ganska komplex form, för dess ytterligare förenkling och lösning är det möjligt att ersätta en del av ekvationen med en ny variabel, du har förmodligen redan sett exempel på sådana bråkrationella ekvationer:

Exempel 3

Lös ekvationen:

$ \ frac (1) (x ^ 2 + 3x-3) + \ frac (2) (x ^ 2 + 3x + 1) = \ frac (7) (5) $

För att förenkla lösningen introducerar vi variabeln $ t = x ^ 2 + 3x $:

$ \ frac (1) (t-3) + \ frac (2) (t + 1) = \ frac (7) (5) $

Den gemensamma nämnaren här är $ 5 \ cdot (t-3) (t + 1) $, vi multiplicerar alla delar av ekvationen med de nödvändiga faktorerna för att bli av med den:

$ \ frac (5 (t + 1)) (5 ​​​​(t-3) (t + 1)) + \ frac (2 \ cdot 5 (t-3)) (5 ​​​​(t + 1) ( t-3) ) = \ frac (7 (t + 1) (t-3)) (5 ​​​​(t-3) (t + 1)) $

5 $ (t + 1) +10 (t-3) = 7 (t + 1) (t-3) $

$ 5t + 5 + 10t-30 = 7 (t ^ 2-3t + t-3) $

$ 15t-25 = 7t ^ 2-14t-21 $

Vi beräknar rötterna genom diskriminanten:

$ t_1 = 4; t_2 = \ frac (1) (7) $

Eftersom vi använde icke-ekvivalenta transformationer är det nödvändigt att kontrollera de resulterande rötterna i nämnaren, de måste uppfylla villkoret $ 5 (t-3) (t + 1) ≠ 0 $. Båda rötterna uppfyller detta villkor.

Nu ersätter vi de erhållna rötterna istället för $ t $ och får två ekvationer:

$ x ^ 2 + 3x = 4 $ och $ x ^ 2 + 3x = \ frac (1) (7) $.

Enligt Vietas sats är rötterna till den första ekvationen $ x_1 = -4; x_2 = 1 $, rötterna till den andra beräknas genom diskriminanten och vi har $ x_ (1,2) = \ frac (-3 ± \ sqrt (\ frac (67) (7))) (2) $.

Alla rötter till ekvationen är: $ x_1 = -4; x_2 = 1, x_ (3,4) = \ frac (-3 ± \ sqrt (\ frac (67) (7))) (2) $.

Transformers till förenklad ekvationsform

Som du kan se ovan används olika transformationer för att lösa rationella ekvationer.

Det finns två typer av transformationer av ekvationer: ekvivalenta (identiska) och ojämlika.

Transformationer kallas ekvivalenta om de leder till en ekvation av ett nytt slag, vars rötter är desamma som originalets.

Identiska transformationer som kan användas för att ändra formen på den ursprungliga ekvationen utan ytterligare kontroller är följande:

• Multiplicera eller dividera hela ekvationen med något annat tal än noll;
• Flytta delar av en ekvation från vänster till höger och vice versa.

Ojämlika transformationer är transformationer under vilka främmande rötter kan uppstå. Ojämlika transformationer inkluderar:

• Kvadrera båda sidor av ekvationen;
• Att bli av med nämnare som innehåller en variabel;

Rötterna till rationella ekvationer lösta med ojämna transformationer måste kontrolleras genom substitution i den ursprungliga ekvationen, eftersom främmande rötter kan uppstå under ojämna transformationer. Inte alltid ojämlika transformationer leder till uppkomsten av främmande rötter, men det är fortfarande nödvändigt att ta hänsyn till detta.

Lösa rationella ekvationer med potenser större än två

De vanligaste metoderna för att lösa ekvationer med potenser på mer än två är variabeländringsmetoden, som vi övervägde ovan för exemplet med en rationell bråkekvation, samt faktoriseringsmetoden.

Låt oss ta en närmare titt på faktoriseringsmetoden.

Låt en ekvation av formen $ P (x) = 0 $ ges, och $ P (x) $ är ett polynom av grad större än två. Om denna ekvation kan faktoriseras så att den har formen $ P_1 (x) P_2 (x) P_3 (x) .. \ cdot P_n (x) = 0 $, så kommer lösningen av denna ekvation att vara uppsättningen av lösningar av ekvationerna $ P_1 (x ) = 0, P_2 (x) = 0, P_3 (x) = 0 ... P_n (x) = 0 $.

För den som inte kommer ihåg: en fri term av en ekvation är en term av ekvationer som inte innehåller en variabel som faktor. Samtidigt, efter att ha hittat en av rötterna till en sådan ekvation, kan den användas för ytterligare faktorisering av ekvationen.

Exempel 5

Lös ekvationen:

Divisorerna för den fria termen kommer att vara talen $ ± 1, ± 2, ± 3, ± 4, ± 6, ± 8, ± 12 $ och $ ± 24 $. När du kontrollerade dem visade sig den lämpliga roten vara $ x = 2 $. Detta betyder att det givna polynomet kan expanderas med denna rot: $ (x-2) (x ^ 2 + 6 + 12) = 0 $.

Polynomet i det andra paret av rotparenteser har inga rötter, vilket betyder att den enda roten i denna ekvation blir $ x = 2 $.

En annan typ av ekvation med en grad större än två är biquadratiska ekvationer av formen $ ax ^ 4 + bx ^ 2 + c = 0 $. Sådana ekvationer löses genom att ersätta $ x ^ 2 $ med $ y $, tillämpa den, vi får en ekvation av formen $ ay ^ 2 + y + c = 0 $, och sedan används det resulterande värdet av den nya variabeln för att beräkna den ursprungliga variabeln.

Det finns också en annan typ av ekvation som kallas retur-... Sådana ekvationer ser ut så här: $ ax ^ 4 + bx ^ 3 + cx ^ 2 + bx + a = 0 $. De har detta namn på grund av upprepningen av koefficienterna för högre grader och lägre grader.

Ett heltalsuttryck är ett matematiskt uttryck som består av tal och bokstavliga variabler med hjälp av addition, subtraktion och multiplikation. Heltal inkluderar också uttryck som inkluderar division med valfritt tal än noll.

Begreppet fraktionerat rationellt uttryck

Ett bråktalsuttryck är ett matematiskt uttryck som förutom operationerna addition, subtraktion och multiplikation som utförs på tal och alfabetiska variabler, samt division med ett tal som inte är lika med noll, även innehåller division med uttryck med alfabetiska variabler.

Rationella uttryck är alla hela och bråkdelar. Rationella ekvationer är ekvationer där vänster och höger sida är rationella uttryck. Om i en rationell ekvation vänster och höger sida är hela uttryck, så kallas en sådan rationell ekvation hel.

Om vänster eller höger sida i en rationell ekvation är bråkuttryck, så kallas en sådan rationell ekvation bråkdel.

Exempel på fraktionella rationella uttryck

1.x-3 / x = -6 * x + 19

2. (x-4) / (2 * x + 5) = (x + 7) / (x-2)

3. (x-3) / (x-5) + 1 / x = (x + 5) / (x * (x-5))

Ett schema för att lösa en rationell bråkekvation

1. Hitta den gemensamma nämnaren för alla bråk i ekvationen.

2. Multiplicera båda sidor av ekvationen med en gemensam nämnare.

3. Lös den resulterande hela ekvationen.

4. Kontrollera rötterna och uteslut de från dem som försvinner den gemensamma nämnaren.

Eftersom vi löser rationella bråkekvationer kommer det att finnas variabler i bråkens nämnare. Det betyder att de kommer att vara i den gemensamma nämnaren. Och i den andra punkten i algoritmen multiplicerar vi med en gemensam nämnare, då kan främmande rötter dyka upp. Vid vilken den gemensamma nämnaren blir lika med noll, vilket betyder att multiplicera med den blir meningslöst. Se därför till att kontrollera de erhållna rötterna i slutet.

Låt oss överväga ett exempel:

Lös den rationella bråkekvationen: (x-3) / (x-5) + 1 / x = (x + 5) / (x * (x-5)).

Vi kommer att följa det allmänna schemat: vi kommer först att hitta den gemensamma nämnaren för alla bråk. Vi får x * (x-5).

Multiplicera varje bråkdel med en gemensam nämnare och skriv den resulterande hela ekvationen.

(x-3) / (x-5) * (x * (x-5)) = x * (x + 3);
1/x* (x* (x-5)) = (x-5);
(x + 5) / (x * (x-5)) * (x * (x-5)) = (x + 5);
x * (x + 3) + (x-5) = (x + 5);

Låt oss förenkla den resulterande ekvationen. Vi får:

x ^ 2 + 3 * x + x-5 - x - 5 = 0;
x ^ 2 + 3 * x-10 = 0;

Vi har en enkel reducerad andragradsekvation. Vi löser det på något av de kända sätten, vi får rötterna x = -2 och x = 5.

Nu kontrollerar vi de erhållna lösningarna:

Ersätt siffrorna -2 och 5 i den gemensamma nämnaren. När x = -2 försvinner inte den gemensamma nämnaren x * (x-5), -2 * (- 2-5) = 14. Därför kommer talet -2 att vara roten till den ursprungliga rationella bråkekvationen.

När x = 5 blir den gemensamma nämnaren x * (x-5) noll. Därför är detta tal inte roten till den ursprungliga rationella bråkekvationen, eftersom det blir division med noll.

Vi har redan lärt oss hur man löser andragradsekvationer. Låt oss nu utvidga de studerade metoderna till rationella ekvationer.

Vad är rationellt uttryck? Vi har redan stött på detta koncept. Rationella uttryck uttryck kallas, sammansatta av tal, variabler, deras grader och tecken på matematiska operationer.

Följaktligen är rationella ekvationer ekvationer av formen:, där - rationella uttryck.

Tidigare betraktade vi endast de rationella ekvationerna som reduceras till linjära. Låt oss nu betrakta de rationella ekvationerna som också kan reduceras till kvadratiska.

Exempel 1

Lös ekvationen:.

Lösning:

Ett bråk är 0 om och endast om dess täljare är 0 och nämnaren inte är 0.

Vi får följande system:

Den första ekvationen i systemet är en andragradsekvation. Innan vi löser det, låt oss dividera alla dess koefficienter med 3. Vi får:

Vi får två rötter:; ...

Eftersom 2 aldrig är lika med 0 måste två villkor vara uppfyllda: ... Eftersom ingen av ovanstående rötter till ekvationen sammanfaller med de ogiltiga värdena för variabeln som erhölls genom att lösa den andra olikheten, är de båda lösningarna till denna ekvation.

Svar:.

Så låt oss formulera en algoritm för att lösa rationella ekvationer:

1. Flytta alla termer till vänster för att få 0 på höger sida.

2. Förvandla och förenkla den vänstra sidan, få alla bråk till en gemensam nämnare.

3. Den resulterande fraktionen är lika med 0, enligt följande algoritm: .

4. Skriv ner rötterna som erhålls i den första ekvationen och tillfredsställ den andra olikheten i svaret.

Låt oss ta ett annat exempel.

Exempel 2

Lös ekvationen: .

Lösning

Allra i början överför vi alla termer till vänster sida så att 0 blir kvar till höger. Vi får:

Nu tar vi den vänstra sidan av ekvationen till en gemensam nämnare:

Denna ekvation är ekvivalent med systemet:

Den första ekvationen i systemet är en andragradsekvation.

Koefficienter för denna ekvation:. Vi beräknar diskriminanten:

Vi får två rötter:; ...

Låt oss nu lösa den andra olikheten: produkten av faktorer är inte lika med 0 om och endast om ingen av faktorerna är lika med 0.

Två villkor måste vara uppfyllda: ... Vi får att av de två rötterna i den första ekvationen, bara en är lämplig - 3.

Svar:.

I den här lektionen kom vi ihåg vad ett rationellt uttryck är, och lärde oss också hur man löser rationella ekvationer som reducerar till andragradsekvationer.

I nästa lektion kommer vi att titta på rationella ekvationer som modeller av verkliga situationer, och även överväga rörelseproblem.

Bibliografi

1. Bashmakov M.I. Algebra, årskurs 8. - M .: Utbildning, 2004.
2. Dorofeev G.V., Suvorova S.B., Bunimovich E.A. et al., Algebra, 8. 5:e uppl. - M .: Utbildning, 2010.
3. Nikolsky S.M., Potapov M.A., Reshetnikov N.N., Shevkin A.V. Algebra, årskurs 8. Lärobok för läroanstalter. - M .: Utbildning, 2006.

1. Festival av pedagogiska idéer "Öppen lektion" ().
2. School.xvatit.com ().
3. Rudocs.exdat.com ().

Läxa

Den minsta gemensamma nämnaren används för att förenkla denna ekvation. Denna metod är användbar när du inte kan skriva en given ekvation med ett rationellt uttryck på varje sida av ekvationen (och använda kors och tvärs-metoden). Denna metod används när en rationell ekvation med tre eller fler fraktioner ges (vid två fraktioner är det bättre att använda korsmultiplikation).

Hitta den lägsta gemensamma nämnaren av bråken (eller minsta gemensamma multipel). NOZ är det minsta tal som är jämnt delbart med varje nämnare.

• Ibland är NOZ ett självklart nummer. Till exempel, om ekvationen ges: x / 3 + 1/2 = (3x +1) / 6, så är det uppenbart att den minsta gemensamma multipeln för talen 3, 2 och 6 kommer att vara 6.
• Om NOZ inte är uppenbart, skriv ner multiplerna av den största nämnaren och hitta en som kommer att vara en multipel av de andra nämnarna. Ofta kan NOZ hittas genom att helt enkelt multiplicera de två nämnarna. Till exempel, om ekvationen är x / 8 + 2/6 = (x - 3) / 9, då NOZ = 8 * 9 = 72.
• Om en eller flera nämnare innehåller en variabel, så blir processen något mer komplicerad (men inte omöjlig). I detta fall är NOZ ett uttryck (som innehåller en variabel) som divideras med varje nämnare. Till exempel, i ekvationen 5 / (x-1) = 1 / x + 2 / (3x) NOZ = 3x (x-1), eftersom detta uttryck är delbart med varje nämnare: 3x (x-1) / (x -1) = 3x; 3x (x-1) / 3x = (x-1); 3x (x-1) / x = 3 (x-1).

Multiplicera både täljaren och nämnaren för varje bråkdel med talet lika med resultatet av att dividera LCD-skärmen med motsvarande nämnare för varje bråkdel. Eftersom du multiplicerar både täljaren och nämnaren med samma tal, multiplicerar du faktiskt bråket med 1 (till exempel 2/2 = 1 eller 3/3 = 1).

• Så i vårt exempel, multiplicera x / 3 med 2/2 för att få 2x / 6, och multiplicera 1/2 med 3/3 för att få 3/6 (du behöver inte multiplicera 3x +1/6 eftersom det är nämnaren är 6).
• Fortsätt på samma sätt när variabeln finns i nämnaren. I vårt andra exempel, NOZ = 3x (x-1), så multiplicera 5 / (x-1) med (3x) / (3x) för att få 5 (3x) / (3x) (x-1); 1 / x multiplicera med 3 (x-1) / 3 (x-1) och få 3 (x-1) / 3x (x-1); 2 / (3x) multiplicera med (x-1) / (x-1) för att få 2 (x-1) / 3x (x-1).

Hitta "x". Nu när du har fört bråken till en gemensam nämnare kan du bli av med nämnaren. För att göra detta, multiplicera varje sida av ekvationen med en gemensam nämnare. Lös sedan den resulterande ekvationen, det vill säga hitta "x". För att göra detta, isolera variabeln på ena sidan av ekvationen.

• I vårt exempel: 2x / 6 + 3/6 = (3x +1) / 6. Du kan lägga till två bråk med samma nämnare, så skriv ekvationen som: (2x + 3) / 6 = (3x + 1) / 6. Multiplicera båda sidor av ekvationen med 6 och eliminera nämnarna: 2x + 3 = 3x +1. Lös och få x = 2.
• I vårt andra exempel (med en variabel i nämnaren) ser ekvationen ut (efter reduktion till en gemensam nämnare): 5 (3x) / (3x) (x-1) = 3 (x-1) / 3x (x) -1) + 2 (x-1) / 3x (x-1). Genom att multiplicera båda sidor av ekvationen med NOZ blir du av med nämnaren och får: 5 (3x) = 3 (x-1) + 2 (x-1), eller 15x = 3x - 3 + 2x -2, eller 15x = x - 5 Lös och få: x = -5/14.

Din integritet är viktig för oss. Av denna anledning har vi tagit fram en integritetspolicy som beskriver hur vi använder och lagrar din information. Läs vår integritetspolicy och låt oss veta om du har några frågor.

Insamling och användning av personlig information

Med personuppgifter avses uppgifter som kan användas för att identifiera en specifik person eller kontakta denne.

Du kan bli ombedd att lämna din personliga information när som helst när du kontaktar oss.

Nedan finns några exempel på de typer av personlig information vi kan samla in och hur vi kan använda sådan information.

Vilken personlig information vi samlar in:

• När du lämnar en förfrågan på webbplatsen kan vi samla in olika uppgifter, inklusive ditt namn, telefonnummer, e-postadress, etc.

Hur vi använder din personliga information:

• De personuppgifter vi samlar in gör att vi kan kontakta dig och rapportera unika erbjudanden, kampanjer och andra evenemang och kommande evenemang.
• Då och då kan vi använda din personliga information för att skicka viktiga meddelanden och meddelanden.
• Vi kan också komma att använda personuppgifter för interna ändamål, såsom att genomföra revisioner, dataanalyser och olika undersökningar för att förbättra de tjänster vi tillhandahåller och ge dig rekommendationer angående våra tjänster.
• Om du deltar i en prisdragning, tävling eller liknande reklamevenemang kan vi använda informationen du tillhandahåller för att administrera dessa program.

Utlämnande av information till tredje part

Vi lämnar inte ut information från dig till tredje part.

Undantag:

• Om det är nödvändigt - i enlighet med lagen, domstolsbeslut, i domstolsförfaranden och/eller på grundval av offentliga förfrågningar eller förfrågningar från statliga myndigheter på Ryska federationens territorium - att avslöja din personliga information. Vi kan också avslöja information om dig om vi fastställer att ett sådant avslöjande är nödvändigt eller lämpligt av säkerhetsskäl, brottsbekämpning eller andra socialt viktiga skäl.
• I händelse av en omorganisation, sammanslagning eller försäljning kan vi komma att överföra de personuppgifter vi samlar in till lämplig tredje part - den juridiska efterträdaren.

Skydd av personlig information

Vi vidtar försiktighetsåtgärder - inklusive administrativa, tekniska och fysiska - för att skydda din personliga information från förlust, stöld och missbruk, såväl som från obehörig åtkomst, avslöjande, ändring och förstörelse.

Respekt för din integritet på företagsnivå

För att säkerställa att din personliga information är säker, ger vi reglerna för sekretess och säkerhet till våra anställda, och övervakar strikt genomförandet av sekretessåtgärder.