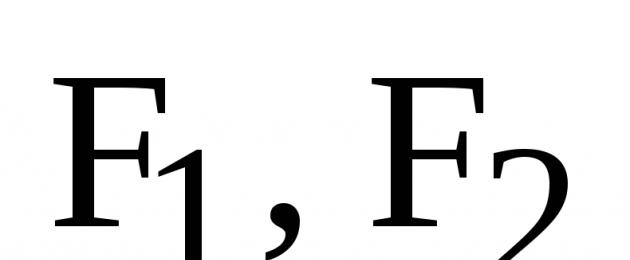Föreläsningar om algebra och geometri. Termin 1.

Föreläsning 15. Ellips.

Kapitel 15. Ellips.

klausul 1. Grundläggande definitioner.

Definition. En ellips är GMT för ett plan, summan av avstånden till två fasta punkter i planet, som kallas foci, är ett konstant värde.

Definition. Avståndet från en godtycklig punkt M i planet till ellipsens fokus kallas brännradien för punkten M.

Beteckningar:
– fokus på ellipsen,
– brännradier för punkt M.

Enligt definitionen av en ellips är en punkt M en punkt i en ellips om och endast om
- konstant värde. Denna konstant betecknas vanligtvis som 2a:

. (1)

Lägg märke till att
.

Per definition av en ellips är dess fokus fasta punkter, så avståndet mellan dem är också ett konstant värde för en given ellips.

Definition. Avståndet mellan ellipsens brännpunkter kallas brännvidden.

Beteckning:
.

Från en triangel
följer det
, dvs.

.

Låt oss beteckna med b talet lika med
, dvs.

. (2)

Definition. Attityd

(3)

kallas ellipsens excentricitet.

Låt oss introducera ett koordinatsystem på detta plan, som vi kommer att kalla kanoniskt för ellipsen.

Definition. Axeln som ellipsens brännpunkter ligger på kallas fokalaxeln.

Låt oss konstruera en kanonisk PDSC för ellipsen, se fig. 2.

Vi väljer fokalaxeln som abskissaxel och ritar ordinataaxeln genom mitten av segmentet
vinkelrätt mot fokalaxeln.

Då har fokus koordinater
,
.

klausul 2. Kanonisk ekvation för en ellips.

Sats. I det kanoniska koordinatsystemet för en ellips har ellipsekvationen formen:

. (4)

Bevis. Vi genomför bevisningen i två steg. I det första steget kommer vi att bevisa att koordinaterna för varje punkt som ligger på ellipsen uppfyller ekvation (4). I det andra steget kommer vi att bevisa att varje lösning av ekvation (4) ger koordinaterna för en punkt som ligger på ellipsen. Härifrån följer att ekvation (4) är uppfylld av de och endast de punkter i koordinatplanet som ligger på ellipsen. Av detta och av definitionen av ekvationen för en kurva kommer det att följa att ekvation (4) är en ekvation för en ellips.

1) Låt punkten M(x, y) vara en punkt på ellipsen, dvs. summan av dess fokala radier är 2a:

.

Låt oss använda formeln för avståndet mellan två punkter på koordinatplan och använd den här formeln för att hitta fokalradier för en given punkt M:

,
, varifrån vi får:

Låt oss flytta en rot till höger sida jämlikhet och kvadrera det:

Minska får vi:

Vi presenterar liknande, minska med 4 och ta bort radikalen:

.

Kvadrering

Öppna fästena och förkorta dem
:

var får vi:

Genom att använda jämlikhet (2) får vi:

.

Dela den sista jämställdheten med
, vi får jämställdhet (4) osv.

2) Låt nu ett par tal (x, y) uppfylla ekvation (4) och låt M(x, y) vara motsvarande punkt på koordinatplanet Oxy.

Sedan från (4) följer:

.

Vi ersätter denna likhet med uttrycket för fokalradier för punkt M:

.

Här använde vi jämlikhet (2) och (3).

Således,
. Likaså,
.

Notera nu att av jämlikhet (4) följer det

eller
etc.
, då följer ojämlikheten:

.

Härifrån följer i sin tur att

eller
Och

,
. (5)

Av jämställdhet (5) följer att
, dvs. punkten M(x, y) är en punkt på ellipsen osv.

Teoremet är bevisat.

Definition. Ekvation (4) kallas ellipsens kanoniska ekvation.

Definition. De kanoniska koordinataxlarna för en ellips kallas ellipsens huvudaxlar.

Definition. Ursprunget till det kanoniska koordinatsystemet för en ellips kallas ellipsens centrum.

klausul 3. Egenskaper av ellipsen.

Sats. (Egenskaper hos en ellips.)

1. I det kanoniska koordinatsystemet för en ellips, allt

ellipsens punkter är i rektangeln

,
.

2. Punkterna ligger på

3. En ellips är en kurva som är symmetrisk med avseende på

deras huvudyxor.

4. Ellipsens centrum är dess symmetricentrum.

Bevis. 1, 2) Följer omedelbart av ellipsens kanoniska ekvation.

3, 4) Låt M(x, y) vara en godtycklig punkt på ellipsen. Då uppfyller dess koordinater ekvation (4). Men då uppfyller punkternas koordinater också ekvation (4), och är därför punkter på ellipsen, varifrån satsens utsagor följer.

Teoremet är bevisat.

Definition. Storheten 2a kallas ellipsens huvudaxel, kvantiteten a kallas ellipsens halvstoraxel.

Definition. Storheten 2b kallas ellipsens mindre axel, kvantiteten b kallas ellipsens semiminoraxel.

Definition. Skärningspunkterna för en ellips med dess huvudaxlar kallas ellipsens hörn.

Kommentar. En ellips kan konstrueras enligt följande. På planet "hamrar vi en spik i brännpunkterna" och fäster en trådlängd på dem
. Sedan tar vi en penna och använder den för att sträcka tråden. Sedan flyttar vi blyertspennan längs planet och ser till att tråden är spänd.

Av definitionen av excentricitet följer det

Låt oss fixa talet a och rikta talet c till noll. Sedan kl
,
Och
. I den gräns vi får

eller
– en cirkels ekvation.

Låt oss nu styra
. Sedan
,
och vi ser att i gränsen urartar ellipsen till ett rakt linjesegment
i beteckningen i figur 3.

klausul 4. Parametriska ekvationer för ellipsen.

Sats. Låta
– godtyckliga reella tal. Sedan ekvationssystemet

,
(6)

är parametriska ekvationer för en ellips i det kanoniska koordinatsystemet för ellipsen.

Bevis. Det räcker för att bevisa att ekvationssystemet (6) är ekvivalent med ekvation (4), d.v.s. de har samma uppsättning lösningar.

1) Låt (x, y) vara en godtycklig lösning på system (6). Dividera den första ekvationen med a, den andra med b, kvadrera båda ekvationerna och lägg till:

.

De där. vilken lösning (x, y) som helst av system (6) uppfyller ekvation (4).

2) Omvänt, låt paret (x, y) vara en lösning till ekvation (4), d.v.s.

.

Av denna jämlikhet följer att punkten med koordinater
ligger på en cirkel med enhetsradie med centrum i origo, dvs. är en punkt på en trigonometrisk cirkel som en viss vinkel motsvarar
:

Av definitionen av sinus och cosinus följer det omedelbart

,
, Var
, varav det följer att paret (x, y) är en lösning till system (6), etc.

Teoremet är bevisat.

Kommentar. En ellips kan erhållas som ett resultat av enhetlig "komprimering" av en cirkel med radie a mot abskissaxeln.

Låta
– ekvation för en cirkel med centrum i origo. "Kompression" av en cirkel till abskissaxeln är inget annat än en transformation av koordinatplanet, utförd enligt följande regel. För varje punkt M(x, y) associerar vi en punkt på samma plan
, Var
,
- kompressionsförhållande.

Med denna transformation "övergår" varje punkt på cirkeln till en annan punkt på planet, som har samma abskissa, men en mindre ordinata. Låt oss uttrycka den gamla ordinatan för en punkt genom den nya:

och ersätt cirklar i ekvationen:

.

Härifrån får vi:

. (7)

Det följer av detta att om punkten M(x, y) låg på cirkeln före "kompressions"-transformationen, dvs. dess koordinater uppfyllde cirkelns ekvation, sedan efter "kompression" transformationen "transformerades" denna punkt till punkten
, vars koordinater uppfyller ellipsekvationen (7). Om vi ​​vill erhålla ekvationen för en ellips med semiminoraxel b, måste vi ta kompressionsfaktorn

.

klausul 5. Tangent till en ellips.

Sats. Låta
– godtycklig punkt på ellipsen

.

Sedan ekvationen för tangenten till denna ellips vid punkten
har formen:

. (8)

Bevis. Det räcker med att överväga fallet när tangenspunkten ligger i den första eller andra fjärdedelen av koordinatplanet:
. Ellipsens ekvation i det övre halvplanet har formen:

. (9)

Låt oss använda tangentekvationen till grafen för funktionen
vid punkten
:

Var
– värdet av derivatan av en given funktion vid en punkt
. Ellipsen under det första kvartalet kan betraktas som en graf över funktion (8). Låt oss hitta dess derivata och dess värde vid tangenspunkten:

,

. Här utnyttjade vi att tangeringspunkten
är en punkt på ellipsen och därför uppfyller dess koordinater ellipsekvationen (9), dvs.

.

Vi ersätter det funna värdet av derivatan i tangentekvationen (10):

,

var får vi:

Detta innebär:

Låt oss dela denna jämlikhet med
:

.

Det återstår att notera
, därför att punkt
tillhör ellipsen och dess koordinater uppfyller dess ekvation.

Tangentekvationen (8) bevisas på liknande sätt vid tangenspunkten som ligger i koordinatplanets tredje eller fjärde fjärdedel.

Och slutligen kan vi enkelt verifiera att ekvation (8) ger tangentekvationen vid punkterna
,
:

eller
, Och
eller
.

Teoremet är bevisat.

klausul 6. Spegelegenskap för en ellips.

Sats. Tangensen till ellipsen har lika stora vinklar med tangenspunktens fokalradier.

Låta
- kontaktpunkt,
,
är tangenspunktens fokala radier, P och Q är projektionerna av brännpunkterna på tangenten som dras till ellipsen vid punkten
.

Teoremet säger det

. (11)

Denna jämlikhet kan tolkas som likheten mellan infallsvinklarna och reflektionen av en ljusstråle från en ellips som frigörs från dess fokus. Denna egenskap kallas ellipsens spegelegenskap:

En ljusstråle som frigörs från ellipsens fokus, efter reflektion från ellipsens spegel, passerar genom ett annat fokus av ellipsen.

Bevis för satsen. För att bevisa vinklarnas likhet (11) bevisar vi likheten mellan trianglar
Och
, där parterna
Och
kommer att vara liknande. Eftersom trianglarna är rätvinkliga räcker det för att bevisa likheten

. (12)

Sedan av konstruktion
– avstånd från fokus till tangent L (se fig. 7),
. Låt oss använda formeln för avståndet från en punkt till en linje på ett plan:

Eftersom ekvationen för tangenten till ellipsen vid punkten
ser ut som

,

,

.

Här använde vi formler (5) för ellipspunktens fokala radier.

Teoremet är bevisat.

Andra beviset på satsen:

,
,
är normalvektorn för tangenten L.

. Härifrån,
.

På samma sätt finner vi,
Och
, etc.

klausul 7. Riktlinjer för en ellips.

Definition. Riktlinjerna för en ellips är två räta linjer, som i det kanoniska koordinatsystemet för ellipsen har ekvationerna

eller
. (13)

Sats. Låt M vara en godtycklig punkt på ellipsen, , – dess fokalradier, – avstånd från punkt M till vänster riktlinje, - till höger. Sedan

, (14)

Var – ellipsens excentricitet.

Bevis.

Låt M(x, y) vara koordinaterna för en godtycklig punkt på ellipsen. Sedan

,
,

varifrån jämställdhet (14) följer.

Teoremet är bevisat.

klausul 8. Fokal parameter för ellipsen.

Definition. Fokalparametern för en ellips är längden på den vinkelräta som återställs vid dess fokus innan den skär ellipsen.

Fokalparametern betecknas vanligtvis med bokstaven p.

Av definitionen följer att fokalparametern

.

Sats. Fokalparametern för ellipsen är lika med

. (15)

Bevis. Eftersom punkten N(–с; р) är en punkt på ellipsen
, då uppfyller dess koordinater hans ekvation:

.

Härifrån finner vi

,

varifrån följer (15).

Teoremet är bevisat.

klausul 9. Andra definitionen av en ellips.

Sats från klausul 7. kan fungera som en definition av en ellips.

Definition. En ellips är en GMT för vilken förhållandet mellan avståndet till en fast punkt i planet, kallad fokus, och avståndet till en fast rät linje, som kallas riktlinjen, är ett konstant värde mindre än en och kallade dess excentricitet:

.

Naturligtvis, i det här fallet är den första definitionen av eoips ett teorem som måste bevisas.

Rader av andra ordningen.
Ellips och dess kanoniska ekvation. Cirkel

Efter grundliga studier raka linjer i planet Vi fortsätter att studera den tvådimensionella världens geometri. Insatserna fördubblas och jag inbjuder dig att besöka ett pittoreskt galleri med ellipser, hyperboler, paraboler, som är typiska representanter andra ordningens rader. Utflykten har redan börjat, och först kort information om hela utställningen på olika våningar i museet:

Begreppet en algebraisk linje och dess ordning

En linje på ett plan kallas algebraisk, om i affint koordinatsystem dess ekvation har formen , där är ett polynom som består av termer av formen ( – reella tal, – icke-negativa heltal).

Som du kan se innehåller ekvationen för en algebraisk linje inte sinus, cosinus, logaritmer och andra funktionella beau monde. Endast X och Y är med icke-negativa heltal grader.

Radorder lika med det maximala värdet av de termer som ingår i den.

Enligt motsvarande teorem beror begreppet en algebraisk linje, liksom dess ordning, inte på valet affint koordinatsystem, därför, för att underlätta existensen, antar vi att alla efterföljande beräkningar äger rum i kartesiska koordinater.

Allmän ekvation den andra orderraden har formen , där – godtyckliga reella tal (Det är vanligt att skriva det med en faktor två), och koefficienterna är inte lika med noll samtidigt.

Om , då förenklas ekvationen till , och om koefficienterna inte är lika med noll samtidigt, så är detta exakt generell ekvation för en "plat" linje, som representerar första orderraden.

Många har förstått innebörden av de nya termerna, men ändå, för att behärska materialet till 100%, sticker vi in ​​fingrarna i uttaget. För att bestämma radordningen måste du iterera alla villkor dess ekvationer och hitta för var och en av dem summan av grader inkommande variabler.

Till exempel:

termen innehåller "x" i 1:a potens;
termen innehåller "Y" i 1:a potens;
Det finns inga variabler i termen, så summan av deras potenser är noll.

Låt oss nu ta reda på varför ekvationen definierar linjen andra beställa:

termen innehåller "x" till 2:a potensen;
summan har summan av potenserna av variablerna: 1 + 1 = 2;
termen innehåller "Y" till 2:a potensen;
alla andra termer - mindre grader.

Maximalt värde: 2

Om vi ​​dessutom lägger till, säg, till vår ekvation, kommer den redan att avgöra tredje beställningsraden. Det är uppenbart att den allmänna formen av 3:e ordningens linjeekvation innehåller en "full uppsättning" termer, summan av potenserna av variablerna i vilka är lika med tre:
, där koefficienterna inte är lika med noll samtidigt.

Om du lägger till en eller flera lämpliga termer som innehåller , då ska vi redan prata om 4:e ordningens rader, etc.

Vi kommer att behöva stöta på algebraiska linjer av 3:e, 4:e och högre ordningen mer än en gång, särskilt när vi bekantar oss med polärt koordinatsystem.

Men låt oss återgå till den allmänna ekvationen och komma ihåg dess enklaste skolvariationer. Som exempel uppstår en parabel, vars ekvation lätt kan reduceras till en generell form, och en hyperbel med en ekvivalent ekvation. Men allt är inte så smidigt...

En betydande nackdel med den allmänna ekvationen är att det nästan alltid är oklart vilken linje den definierar. Även i det enklaste fallet kommer du inte omedelbart att inse att detta är en överdrift. Sådana layouter är bara bra på en maskerad, så under analytisk geometri överväger vi typisk uppgift föra 2:a ordningens linjeekvation till kanonisk form.

Vilken är den kanoniska formen av en ekvation?

Detta är den allmänt accepterade standardformen av en ekvation, när det inom några sekunder blir klart vilket geometriskt objekt den definierar. Dessutom är den kanoniska formen mycket bekväm för att lösa många praktiska problem. Så till exempel enligt den kanoniska ekvationen "platt" rak, för det första är det omedelbart tydligt att detta är en rak linje, och för det andra är punkten som hör till den och riktningsvektorn lätt synliga.

Uppenbarligen vilken som helst 1:a beställningsradenär en rak linje. På andra våningen är det inte längre väktaren som väntar på oss, utan ett mycket mer mångsidigt sällskap med nio statyer:

Klassificering av andra ordningens rader

Med hjälp av en speciell uppsättning åtgärder reduceras varje ekvation av en andra ordningens rad till en av följande former:

(och är positiva reella tal)

1) – ellipsens kanoniska ekvation;

2) – kanonisk ekvation för en hyperbel;

3) – kanonisk ekvation för en parabel;

4) – imaginär ellips;

5) – ett par korsande linjer;

6) – par imaginär skärande linjer (med en enda giltig skärningspunkt vid utgångspunkten);

7) – ett par parallella linjer;

8) – par imaginär parallella linjer;

9) – ett par sammanfallande linjer.

Vissa läsare kan ha intrycket att listan är ofullständig. Till exempel, i punkt nr 7, anger ekvationen paret direkt, parallellt med axeln, och frågan uppstår: var är ekvationen som bestämmer linjerna parallella med ordinataaxeln? Svara på det inte anses kanoniskt. Raka linjer representerar samma standardfall, roterat 90 grader, och den extra posten i klassificeringen är överflödig, eftersom den inte ger något fundamentalt nytt.

Det finns alltså nio och bara nio olika typer linjer av 2:a ordningen, men i praktiken finns de oftast ellips, hyperbel och parabel.

Låt oss först titta på ellipsen. Som vanligt fokuserar jag på de punkter som har stor betydelse för att lösa problem, och om du behöver en detaljerad härledning av formler, bevis på satser, hänvisa till exempel till läroboken av Bazylev/Atanasyan eller Aleksandrov.

Ellips och dess kanoniska ekvation

Stavning... vänligen upprepa inte misstagen hos vissa Yandex-användare som är intresserade av "hur man bygger en ellips", "skillnaden mellan en ellips och en oval" och "excentriciteten hos en ellips".

Den kanoniska ekvationen för en ellips har formen , där är positiva reella tal, och . Jag kommer att formulera själva definitionen av en ellips senare, men nu är det dags att ta en paus från den pratande butiken och lösa ett vanligt problem:

Hur bygger man en ellips?

Ja, bara ta den och rita den. Uppgiften förekommer ofta, och en betydande del av eleverna klarar inte av ritningen korrekt:

Exempel 1

Konstruera ellipsen som ges av ekvationen

Lösning: Låt oss först ta ekvationen till kanonisk form:

Varför ta med? En av fördelarna med den kanoniska ekvationen är att den låter dig avgöra omedelbart ellipsens hörn, som finns på punkter. Det är lätt att se att koordinaterna för var och en av dessa punkter uppfyller ekvationen.

I detta fall :


Linjesegmentet kallad huvudaxel ellips;
linjesegmentet – mindre axel;
siffra kallad halvstor axel ellips;
siffra – mindre axel.
i vårt exempel: .

För att snabbt föreställa dig hur en viss ellips ser ut, titta bara på värdena för "a" och "be" i dess kanoniska ekvation.

Allt är fint, snyggt och vackert, men det finns en varning: jag gjorde ritningen med programmet. Och du kan göra ritningen med vilken applikation som helst. Men i den hårda verkligheten ligger det ett rutigt papper på bordet, och möss dansar i cirklar på våra händer. Människor med konstnärlig talang kan förstås argumentera, men du har också möss (fast mindre). Det är inte förgäves att mänskligheten uppfann linjalen, kompassen, gradskivan och andra enkla anordningar för att rita.

Av denna anledning är det osannolikt att vi kommer att kunna rita en ellips noggrant genom att bara känna till hörnen. Det är okej om ellipsen är liten, till exempel med halvaxlar. Alternativt kan du minska skalan och följaktligen dimensionerna på ritningen. Men generellt sett är det mycket önskvärt att hitta ytterligare poäng.

Det finns två sätt att konstruera en ellips - geometrisk och algebraisk. Jag gillar inte att bygga med en kompass och linjal eftersom algoritmen inte är den kortaste och ritningen är betydligt rörig. I nödfall, se läroboken, men i verkligheten är det mycket mer rationellt att använda algebras verktyg. Från ellipsekvationen i utkastet uttrycker vi snabbt:

Ekvationen delas sedan upp i två funktioner:
– definierar ellipsens övre båge;
– definierar ellipsens nedre båge.

Ellipsen som definieras av den kanoniska ekvationen är symmetrisk med avseende på koordinataxlar, och även i förhållande till ursprunget. Och det här är bra - symmetri är nästan alltid ett förebud om freebies. Uppenbarligen räcker det med att ta itu med 1:a koordinatkvartalet, så vi behöver funktionen . Det ber att hittas för ytterligare punkter med abskissar . Låt oss trycka på tre SMS-meddelanden på räknaren:

Naturligtvis är det också trevligt att om ett allvarligt misstag görs i beräkningarna så kommer det genast att bli tydligt under bygget.

Låt oss markera punkter i ritningen (röd), symmetriska punkter på de återstående bågarna ( Blå färg) och anslut försiktigt hela företaget med en linje:


Det är bättre att rita den första skissen mycket tunt och först därefter applicera tryck med en penna. Resultatet borde bli en ganska anständig ellips. Vill du förresten veta vad den här kurvan är?

Definition av en ellips. Ellipshärdar och ellipsexcentricitet

Ellipse är specialfall oval Ordet "oval" ska inte förstås i filistinsk betydelse ("barnet ritade en oval", etc.). Detta är en matematisk term som har en detaljerad formulering. Syftet med denna lektion är inte att överväga teorin om ovaler och deras olika typer, som praktiskt taget inte uppmärksammas i standardkursen för analytisk geometri. Och i enlighet med mer aktuella behov går vi omedelbart vidare till den strikta definitionen av en ellips:

Ellipsär mängden av alla punkter i planet, summan av avstånden till var och en av vilka från två givna punkter, kallas knep ellips, är en konstant storhet, numeriskt lika med längden av denna ellips huvudaxel: .
I det här fallet är avstånden mellan fokuserna mindre än detta värde: .

Nu blir allt tydligare:

Föreställ dig att den blå pricken "färdas" längs en ellips. Så, oavsett vilken punkt på ellipsen vi tar, kommer summan av längderna på segmenten alltid att vara densamma:

Låt oss se till att i vårt exempel är värdet på summan verkligen lika med åtta. Mentalt placera punkten "um" vid högra hörnet av ellipsen, sedan: , vilket är vad som behövde kontrolleras.

En annan metod för att rita den är baserad på definitionen av en ellips. Högre matematik är ibland orsaken till spänningar och stress, så det är dags att ta ett nytt avlastningspass. Vänligen ta whatman-papper eller ett stort ark kartong och nåla fast det på bordet med två spikar. Det här kommer att vara knep. Knyt en grön tråd på de utskjutande spikhuvudena och dra den hela vägen med en penna. Blyertspennan kommer att hamna vid en viss punkt som hör till ellipsen. Börja nu flytta pennan längs papperet, håll den gröna tråden spänd. Fortsätt processen tills du återgår till startpunkten... jättebra... ritningen kan kontrolleras av läkare och lärare =)

Hur hittar man brännpunkterna för en ellips?

I exemplet ovan avbildade jag "färdiga" fokuspunkter, och nu kommer vi att lära oss hur man extraherar dem från geometrins djup.

Om en ellips ges av en kanonisk ekvation, har dess foci koordinater , var är det avstånd från varje fokus till ellipsens symmetricentrum.

Beräkningarna är enklare än enkla:

! De specifika koordinaterna för foci kan inte identifieras med betydelsen av "tse"! Jag upprepar att det är så DISTANCE från varje fokus till mitten(vilket i det allmänna fallet inte behöver ligga exakt vid ursprunget).
Och därför kan avståndet mellan brännpunkterna inte heller bindas till ellipsens kanoniska position. Med andra ord kan ellipsen flyttas till en annan plats och värdet kommer att förbli oförändrat, medan brännpunkterna naturligt kommer att ändra sina koordinater. Kan du överväga det här ögonblicket under fortsatta studier av ämnet.

Ellipsexcentricitet och dess geometriska betydelse

Excentriciteten hos en ellips är ett förhållande som kan ta värden inom intervallet.

I vårat fall:

Låt oss ta reda på hur formen på en ellips beror på dess excentricitet. För detta fixa vänster och höger hörn av ellipsen i fråga, det vill säga värdet på halvhuvudaxeln kommer att förbli konstant. Då kommer excentricitetsformeln att ha formen: .

Låt oss börja föra excentricitetsvärdet närmare enhet. Detta är endast möjligt om . Vad betyder det? ...kom ihåg tricken . Detta innebär att ellipsens fokus kommer att "flytta isär" längs abskissaxeln till sidohörnen. Och eftersom "de gröna segmenten inte är gummi", kommer ellipsen oundvikligen att börja plattas ut, och förvandlas till en tunnare och tunnare korv uppträdd på en axel.

Således, ju närmare ellipsexcentricitetsvärdet är enhet, desto mer långsträckt ellips.

Låt oss nu modellera den motsatta processen: ellipsens foci gick mot varandra, närmade sig mitten. Detta innebär att värdet på "ce" blir mindre och mindre och följaktligen tenderar excentriciteten till noll: .
I det här fallet kommer de "gröna segmenten" tvärtom att "bli trångt" och de kommer att börja "skjuta" ellipslinjen upp och ner.

Således, Ju närmare excentricitetsvärdet är noll, desto mer lik är ellipsen... titta på det begränsande fallet när fokuserna framgångsrikt återförenas vid ursprunget:

En cirkel är ett specialfall av en ellips

I fallet med halvaxlarnas jämlikhet tar den kanoniska ekvationen av ellipsen faktiskt formen , som reflexmässigt förvandlas till ekvationen av en cirkel med ett centrum vid utgångspunkten för radien "a", välkänd från skolan.

I praktiken används beteckningen med den "talande" bokstaven "er" oftare: . Radien är längden på ett segment, med varje punkt i cirkeln borttagen från mitten med ett radieavstånd.

Observera att definitionen av en ellips förblir helt korrekt: brännpunkterna sammanfaller, och summan av längderna av de sammanfallande segmenten för varje punkt på cirkeln är en konstant. Eftersom avståndet mellan brännpunkterna är , alltså excentriciteten för varje cirkel är noll.

Att konstruera en cirkel är enkelt och snabbt, använd bara en kompass. Men ibland är det nödvändigt att ta reda på koordinaterna för några av dess punkter, i det här fallet går vi den välbekanta vägen - vi tar ekvationen till den glada Matanov-formen:

– funktion av den övre halvcirkeln;
– funktion av den nedre halvcirkeln.

Sedan hittar vi de nödvändiga värdena, skilja, integrera och göra andra bra saker.

Artikeln är givetvis endast för referens, men hur kan man leva i världen utan kärlek? Kreativ uppgift för självständigt beslut

Exempel 2

Komponera den kanoniska ekvationen för en ellips om en av dess foci och semi-mollaxel är känd (centrum är i origo). Hitta hörn, ytterligare punkter och rita en linje i ritningen. Beräkna excentricitet.

Lösning och ritning i slutet av lektionen

Låt oss lägga till en åtgärd:

Rotera och parallellförvandla en ellips

Låt oss återgå till ellipsens kanoniska ekvation, nämligen till tillståndet vars mysterium plågar nyfikna sinnen sedan första omnämnandet av denna kurva. Så vi tittade på ellipsen , men är det inte möjligt i praktiken att uppfylla ekvationen ? Trots allt, här verkar det dock vara en ellips också!

Den här typen av ekvation är sällsynt, men den förekommer. Och det definierar faktiskt en ellips. Låt oss avmystifiera:

Som ett resultat av konstruktionen erhölls vår inhemska ellips, roterad 90 grader. Det är, - Det här icke-kanoniskt inträde ellips . Spela in!- ekvationen definierar inte någon annan ellips, eftersom det inte finns några punkter (foci) på axeln som skulle uppfylla definitionen av en ellips.

Andra ordningens kurvor på ett plan är linjer definierade av ekvationer där variabeln koordinerar x Och y finns i andra graden. Dessa inkluderar ellipsen, hyperbeln och parabeln.

Den allmänna formen av andra ordningens kurvekvation är följande:

Var A, B, C, D, E, F- tal och minst en av koefficienterna A, B, C inte lika med noll.

När man löser problem med andra ordningens kurvor beaktas oftast de kanoniska ekvationerna för ellipsen, hyperbeln och parabeln. Det är lätt att gå vidare till dem från allmänna ekvationer; exempel 1 på problem med ellipser kommer att ägnas åt detta.

Ellips ges av den kanoniska ekvationen

Definition av en ellips. En ellips är mängden av alla punkter på planet för vilka summan av avstånden till de punkter som kallas brännpunkter är ett konstant värde som är större än avståndet mellan brännpunkterna.

Fokusen anges som i figuren nedan.

Den kanoniska ekvationen för en ellips har formen:

Var a Och b (a > b) - halvaxlarnas längder, dvs halva längderna av segmenten avskurna av ellipsen på koordinataxlarna.

Den raka linjen som går genom ellipsens brännpunkter är dess symmetriaxel. En annan symmetriaxel för en ellips är en rät linje som går genom mitten av ett segment vinkelrätt mot detta segment. Punkt HANDLA OM skärningspunkten mellan dessa linjer fungerar som ellipsens symmetricentrum eller helt enkelt ellipsens centrum.

Ellipsens abskissaxel skär vid punkterna ( a, HANDLA OM) Och (- a, HANDLA OM), och ordinataaxeln är i punkter ( b, HANDLA OM) Och (- b, HANDLA OM). Dessa fyra punkter kallas ellipsens hörn. Segmentet mellan ellipsens hörn på x-axeln kallas dess huvudaxel, och på ordinataaxeln - dess mindre axel. Deras segment från toppen till mitten av ellipsen kallas halvaxlar.

Om a = b, då antar ellipsens ekvation formen . Detta är ekvationen för en cirkel med radie a, och en cirkel är ett specialfall av en ellips. En ellips kan erhållas från en cirkel med radie a, om du komprimerar den till a/b gånger längs axeln Oj .

Exempel 1. Kontrollera om en linje som ges av en generell ekvation är , ellips.

Lösning. Vi transformerar den allmänna ekvationen. Vi använder överföringen av den fria termen till höger sida, term-för-term division av ekvationen med samma antal och reduktion av bråk:

Svar. Ekvationen som erhålls som ett resultat av transformationerna är ellipsens kanoniska ekvation. Därför är denna linje en ellips.

Exempel 2. Komponera den kanoniska ekvationen för en ellips om dess halvaxlar är 5 respektive 4.

Lösning. Vi tittar på formeln för den kanoniska ekvationen för en ellips och substitut: halvhuvudaxeln är a= 5, den halva axeln är b= 4 . Vi får den kanoniska ekvationen för ellipsen:

Punkter och , indikerade i grönt på huvudaxeln, där

kallas knep.

kallad excentricitet ellips.

Attityd b/a kännetecknar ellipsens "oblateness". Ju mindre detta förhållande är, desto mer förlängs ellipsen längs huvudaxeln. Men graden av förlängning av en ellips uttrycks oftare genom excentricitet, formeln för vilken ges ovan. För olika ellipser varierar excentriciteten från 0 till 1, och förblir alltid mindre än enhet.

Exempel 3. Komponera den kanoniska ekvationen för ellipsen om avståndet mellan brännpunkterna är 8 och huvudaxeln är 10.

Lösning. Låt oss dra några enkla slutsatser:

Om huvudaxeln är lika med 10, så är dess halva, dvs halvaxeln a = 5 ,

Om avståndet mellan brännpunkterna är 8, då siffran c av fokalkoordinaterna är lika med 4.

Vi ersätter och beräknar:

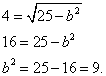
Resultatet är ellipsens kanoniska ekvation:

Exempel 4. Komponera den kanoniska ekvationen för en ellips om dess huvudaxel är 26 och dess excentricitet är .

Lösning. Som följer av både storleken på storaxeln och excentricitetsekvationen, ellipsens semimajoraxel a= 13. Från excentricitetsekvationen uttrycker vi talet c, behövs för att beräkna längden på den mindre halvaxeln:

.

Vi beräknar kvadraten på längden på den mindre halvaxeln:

Vi komponerar den kanoniska ekvationen för ellipsen:

Exempel 5. Bestäm brännpunkterna för ellipsen som ges av den kanoniska ekvationen.

Lösning. Hitta numret c, som bestämmer de första koordinaterna för ellipsens fokus:

.

Vi får fokus på ellipsen:

Exempel 6. Ellipsens brännpunkter är belägna på axeln Oxe symmetriskt om ursprunget. Komponera den kanoniska ekvationen för ellipsen om:

1) avståndet mellan brännpunkterna är 30 och huvudaxeln är 34

2) mindre axel 24, och ett av fokuserna är vid punkten (-5; 0)

3) excentricitet, och en av brännpunkterna är vid punkt (6; 0)

Låt oss fortsätta att lösa ellipsproblem tillsammans

Om är en godtycklig punkt på ellipsen (indikerad i grönt i den övre högra delen av ellipsen på ritningen) och är avståndet till denna punkt från brännpunkterna, så är formlerna för avstånden följande:

För varje punkt som hör till ellipsen är summan av avstånden från brännpunkterna ett konstant värde lika med 2 a.

Linjer definierade av ekvationer

kallas föreståndarinnor ellips (på ritningen finns röda linjer längs kanterna).

Av de två ekvationerna ovan följer det för vilken punkt som helst på ellipsen

,

var och är avstånden för denna punkt till riktningarna och .

Exempel 7. Med tanke på en ellips. Skriv en ekvation för dess riktlinjer.

Lösning. Vi tittar på direktrix-ekvationen och finner att vi behöver hitta ellipsens excentricitet, d.v.s. Vi har all data för detta. Vi beräknar:

.

Vi får ekvationen för ellipsens riktningar:

Exempel 8. Komponera den kanoniska ekvationen för en ellips om dess fokus är punkter och riktlinjer är linjer.

Det kan visas (det gör vi inte) att ekvation (2) är ekvivalent med ekvation (1), även om den härleds från (1) av ingen motsvarighet transformationer. Detta betyder att ekvation (2) är ekvationen för denna ellips. Det heter kanonisk(dvs det enklaste).

Man kan se att ellipsens ekvation är en 2:a ordningens ekvation, dvs. ellipslinje av 2:a ordningen.

För en ellips introducerar vi konceptet excentricitet. Detta är kvantiteten. För en ellips är excentricitet . Därför att Med Och A känd, då också känd. Uttrycket för fokalradier för punkten M(x, y) på ellipsen erhålls enkelt från de tidigare argumenten: . r 2 kommer att hittas från jämlikhet (3)

Kommentar Om du slår in två spikar (F1 och F2) i bordet, knyt ett snöre till dem i båda ändarna, vars längd är större än avståndet mellan spikarna ( 2a), dra i snöret och rita en bit krita längs bordet, så kommer den att rita en sluten ellipskurva som är symmetrisk om båda axlarna och origo.

4. Studie av formen på en ellips med hjälp av dess kanoniska ekvation.

I anmärkningen drog vi av tydlighetsskäl slutsatsen om ellipsens form. Låt oss nu studera formen på ellipsen genom att analysera dess kanoniska ekvation:

Låt oss hitta skärningspunkterna med koordinataxlarna. Om ,y=0, då , , dvs. vi har två punkter A1(-a,0) och A2(a,0). Om x=0, då , . De där. vi har två punkter B1(0,-b) och B2(0,b) (eftersom , då ). Punkterna A1, A2, B1, B2 kallas ellipsens hörn.

2) Platsområdet för ellipsen kan bestämmas utifrån följande överväganden:

a) av ellipsekvationen följer att, dvs. , dvs. eller .

b) på liknande sätt, dvs. eller . Detta visar att hela ellipsen ligger i rektangeln som bildas av linjerna och .

3) Vidare anger variablerna x och y ellipsekvationen endast i jämna potenser, vilket betyder att kurvan är symmetrisk med avseende på var och en av axlarna och med avseende på origo. D-men, om en punkt (x, y) hör till radien, så hör även punkterna (x, -y), (-x, y) och (-x, -y) till den. Därför räcker det att bara beakta den del av ellipsen som ligger i det första kvartalet, var och .

4) Från ekvationen av ellipsen har vi , och i första kvartalet . Om x=0 så är y=b. Detta är punkt B2(0,b). Låt x öka från 0 till a, sedan minskar y från b till 0. Således kommer punkt M(x, y), med utgångspunkt från punkt B2(0, b) som beskriver en båge, till punkt A(a,0). Det kan strikt bevisas att bågen är konvext riktad uppåt. Genom att spegla denna båge i koordinataxlarna och origo får vi hela ellipsen. Symmetriaxlarna för en ellips kallas dess axlar. punkten O i deras skärningspunkt är ellipsens centrum. Längden på segmenten OA1=OA2=a kallas ellipsens halvstoraxel, segmenten OB1, OB2=b är ellipsens halvmollaxel, (a>b), c är halvfokalen distans. Storleken är lätt att förklara geometriskt.

När a=b får vi från ellipsens kanoniska ekvation cirkelekvationen. För en cirkel, d.v.s. F1=F2=0. .

Således är en cirkel ett specialfall av en ellips, när dess brännpunkter sammanfaller med centrum och excentricitet = 0. Ju större excentricitet, desto mer långsträckt ellips.

Kommentar. Från ellipsens kanoniska ekvation är det lätt att dra slutsatsen att ellipsen kan specificeras i parametrisk form. x=a cos t

y=b sin t, där a, b är de stora och små halvaxlarna, t-vinkel.

5. Definition och härledning av den kanoniska hyperbelekvationen.

Överdrift kallas HMT-plan, för vilka skillnaden i avstånd från två fasta punkter F1F2 i planet, kallade foci, är ett konstant värde (inte lika med 0 och mindre än brännvidden F1F2).

Vi kommer att beteckna, som tidigare, F1F2 = 2c, och skillnaden i avstånd är 2a (a<с). Систему координат выберем как и в случае эллипса.

Låt M (x,y) vara den aktuella punkten för hyperbeln. Per definition MF1-MF2= eller ri-r2 = = eller --(1). – detta är ekvationen för en hyperbel.

Vi blir av med irrationalitet i (1): vi isolerar en rot, kvadrerar båda delarna, vi får: eller , kvadrat igen:

Var .

Dela med . Låt oss presentera beteckningen. Sedan --(2). Ekvation (2), som kan visas, är ekvivalent med ekvation (1), och är därför ekvationen för en given hyperbel. Han heter den kanoniska ekvationen för en hyperbel. Vi ser att hyperbelekvationen också är av andra graden, vilket betyder hyperbellinje av andra ordningen.

Excentricitet hos en hyperbel. Uttrycket för fokalradier igenom är lätt att få från den föregående, då hittar vi det från .

6. Studie av formen på en hyperbel med hjälp av dess kanoniska ekvation.

Vi resonerar på samma sätt som när vi studerar en ellips.

1. Hitta skärningspunkterna med hyperbelns axlar. Om x=0, då . Det finns inga skärningspunkter med op-amp-axeln. Om y=0, då . Skärningspunkter , . De kallas hörn av en hyperbel.

2. Lokaliseringsområde för hyperbeln: , dvs. eller . Detta innebär att hyperbeln är belägen utanför remsan som begränsas av raka linjer x=-a Och x=a.

3. Hyperbel har alla typer av symmetri, eftersom x och y förekommer i jämna potenser. Därför räcker det med att beakta den del av hyperbeln som finns i det första kvartalet.

4. Från hyperbelekvationen (2) i första kvartalet har vi . För x=a, y=0 har vi punkten ; en slips. kurvan går upp till höger. För att föreställa dig rörelsen tydligare, överväg två hjälplinjer som går genom koordinaternas ursprung och är diagonalerna för en rektangel med sidorna 2a och 2b: BCB'C'. De har ekvationer och . Låt oss bevisa att den aktuella punkten för hyperbeln M(x,y) går till oändlighet och närmar sig den räta linjen utan gräns. Låt oss ta en godtycklig poäng X och jämför motsvarande ordinata för hyperbelns punkt och linjen. Det är uppenbart att Å>å. MN=Y-y= .

Vi ser att när , d.v.s. kurvan närmar sig den räta linjen på obestämd tid när den rör sig bort från origo. Detta bevisar att linjen är en asymptot av hyperbeln. Dessutom skär hyperbeln inte asymptoten. Detta är tillräckligt för att konstruera en del av hyperbeln. Den är konvext vänd uppåt. De återstående delarna är färdiga i symmetri. Observera att symmetriaxlarna för en hyperbel (koordinataxlar) kallas dess yxor, skärningspunkten för axlarna- Centrumöverdrift. En axel skär hyperbeln (verklig axel), den andra inte (imaginär). Linjesegmentet A kallas den verkliga halvaxeln, segmentet b- imaginär halvaxel. Rektangeln BCB'C' kallas hyperbelns grundläggande rektangel.

Om a=b, då bildar asymptoterna vinklar med koordinataxlarna längs . Då kallas hyperbolen liksidig eller liksidig. Huvudrektangeln förvandlas till en kvadrat. Dess asymptoter är vinkelräta mot varandra.

Kommentar.

Ibland betraktar vi en hyperbel vars kanoniska ekvation är (3). De ringer henne konjugera i förhållande till överdrift (2). Hyperbel (3) har en reell axel som är vertikal och en imaginär axel som är horisontell. Dess utseende etableras omedelbart om du arrangerar om X Och på, A Och b(hon vänder sig tillbaka till sitt gamla jag). Men då har hyperbel (3) formen:

Den pratar.

5. Som redan nämnts, ekvationen för en liksidig hyperbel ( a=b), när koordinataxlarna sammanfaller med hyperbelns axlar, har formen . (4)

Därför att asymptoterna för en liksidig hyperbel är vinkelräta, då kan de också tas som koordinataxlarna OX 1 och OU 1. Detta motsvarar att vända det tidigare OXY-systemet en vinkel. Vinkelrotationsformlerna är följande:

Sedan i nytt system koordinater OX 1 Y 1 ekvation (4) kommer att skrivas om:

Eller eller . Betecknar , vi får eller (5) - detta är ekvationen liksidig hyperbel, klassificerade som asymptoter (det var denna typ av hyperbel som övervägdes i skolan).

Kommentar: Av ekvationen följer att arean av varje rektangel konstruerad på koordinaterna för någon punkt i hyperbeln M(x,y) är densamma: S= k 2 .

7. Definition och härledning av den kanoniska ekvationen för en parabel.

Parabel kallas planets GMT, för var och en av vilka avståndet från en fast punkt F i planet, kallas fokus, är lika med avståndet från en fast rät linje som kallas rektor(fokus utanför rektorn).

Vi kommer att beteckna avståndet från F till riktningen med p och kalla det parametern för parabeln. Låt oss välja koordinatsystemet enligt följande: rita OX-axeln genom punkten F vinkelrät mot riktningen NP. Låt oss välja ursprunget för koordinaterna i mitten av segmentet FP.

I detta system: .

Låt oss ta en godtycklig punkt M(x,y) med nuvarande koordinater (x,y). Det är därför

Därför är (1) parabelns ekvation. Låt oss förenkla:

Eller (2) - det här är det kanonisk ekvation för en parabel. Det kan visas att (1) och (2) är likvärdiga.

Ekvation (2) är en 2:a ordningens ekvation, dvs. parabel är en rad av andra ordningen.

8. Studie av formen på en parabel med hjälp av dess kanoniska ekvation.

(p>0).

1) x=0, y=0 går parabeln genom origo för koordinatpunkten O. Den kallas parabelns vertex.

2), dvs. parabeln är placerad till höger om op-amp-axeln, i det högra halvplanet.

3) på ingår i en jämn grad, därför är parabeln symmetrisk kring OX-axeln, därför räcker det att konstruera den under första kvartalet.

4) i 1:a kvartalet kl , d.v.s. parabeln går upp till höger. Det kan visas att konvexiteten är uppåtgående. Vi bygger i botten efter symmetri. Axeln OU är tangent till parabeln.

Uppenbarligen är brännvidden . Relationen kallas excentricitet: . Symmetriaxeln för en parabel (i vårt fall OX) kallas för parabelns axel.

Observera att ekvationen också är en parabel, men riktad i motsatt riktning. Ekvationerna definierar också paraboler, vars axel är op-förstärkarens axel.

eller i en mer bekant form, där .

Ekvationen definierar en vanlig parabel med en förskjuten vertex.

Anteckningar. 1) Det finns ett nära samband mellan alla fyra linjerna i 2:a ordningen - de är alla koniska sektioner. Om vi ​​tar en kon med två hålrum, då när vi skär den med ett plan vinkelrätt mot konens axel får vi en cirkel om vi lutar sektionsplanet något; om planet är parallellt med generatrisen är sektionen en parabel, om planet skär båda

hålrum-hyperbol.

2) Det kan bevisas att om en ljusstråle som kommer från en parabels fokus reflekteras från den, så går den reflekterade strålen parallellt med parabelns axel - detta används i verkan av spotlights - en parabolisk reflektor, och i fokus - en ljuskälla. Detta resulterar i en riktad ström av ljus.

3) Om vi ​​föreställer oss uppskjutningen av en jordsatellit från punkt T som ligger utanför atmosfären i horisontell riktning, då om initialhastigheten v 0 är otillräckligt, då kommer satelliten inte att rotera runt jorden. När man når 1:an flykthastighet Satelliten kommer att kretsa runt jorden i en cirkulär bana centrerad på jordens mitt. Om den initiala hastigheten ökas, kommer rotationen att ske längs en ellips, jordens centrum kommer att vara vid en av brännpunkterna. När den andra utrymningshastigheten nås, kommer banan att bli parabolisk och satelliten kommer inte att återgå till punkt T, utan kommer att vara inom solsystem. De där. En parabel är en ellips med ett fokus på oändligheten. Med en ytterligare ökning av den initiala hastigheten kommer banan att bli hyperbolisk och ett andra fokus kommer att dyka upp på andra sidan. Jordens centrum kommer alltid att vara i fokus för omloppsbanan. Satelliten kommer att lämna solsystemet.

Omkrets är en sluten plan kurva, vars alla punkter är lika långt från en given punkt (cirkelns centrum). Avståndet från valfri punkt i cirkeln \(P\left((x,y) \right)\) till dess centrum kallas radie. Cirkelns centrum och själva cirkeln ligger i samma plan. Ekvation för en cirkel med radie \(R\) med centrum i origo ( kanonisk ekvation av en cirkel ) har formen
\((x^2) + (y^2) = (R^2)\).

Ekvation av en cirkel radie \(R\) med centrum på en godtycklig punkt \(A\left((a,b) \right)\) skrivs som
\((\left((x - a) \right)^2) + (\left((y - b) \right)^2) = (R^2)\).



Ekvation för en cirkel som går genom tre punkter , skrivet i formen: \(\left| (\begin(array)(*(20)(c)) ((x^2) + (y^2)) & x & y & 1\\ (x_1^ 2 + y_1^2) & ((x_1)) & ((y_1)) & 1\\ (x_2^2 + y_2^2) & ((x_2)) & ((y_2)) & 1\\ (x_3^ 2 + y_3^2) & ((x_3)) & ((y_3)) & 1 \end(array)) \right| = 0.\\\)
Här \(A\vänster(((x_1),(y_1)) \höger)\), \(B\vänster(((x_2),(y_2)) \höger)\), \(C\vänster(( (x_3),(y_3)) \right)\) är tre punkter som ligger på cirkeln.



Cirkelekvation i parametrisk form
\(\left\( \begin(aligned) x &= R \cos t \\ y &= R\sin t \end(aligned) \right., \;\;0 \le t \le 2\pi\ ),
där \(x\), \(y\) är koordinaterna för cirkelns punkter, \(R\) är cirkelns radie, \(t\) är parametern.

Generell ekvation för en cirkel
\(A(x^2) + A(y^2) + Dx + Ey + F = 0\)
med förbehåll för \(A \ne 0\), \(D^2 + E^2 > 4AF\).
Cirkelns mittpunkt är belägen vid punkten med koordinaterna \(\left((a,b) \right)\), där
\(a = - \large\frac(D)((2A))\normalstorlek,\;\;b = - \large\frac(E)((2A))\normalstorlek.\)
Cirkelns radie är
\(R = \sqrt (\large\frac(((D^2) + (E^2) - 4AF))((2\left| A \right|))\normalsize) \)

Ellips kallas en plan kurva för varje punkt vars summan av avstånden till två givna poäng (ellipshärdar ) är konstant. Avståndet mellan brännpunkterna kallas brännvidd och betecknas med \(2c\). Mitten av segmentet som förbinder brännpunkterna kallas mitten av ellipsen . En ellips har två symmetriaxlar: den första eller fokalaxeln, som går genom brännpunkterna, och den andra axeln vinkelrät mot den. Skärningspunkterna för dessa axlar med ellipsen kallas toppar. Segmentet som förbinder mitten av ellipsen med vertex kallas ellipsens halvaxel . Den halvstora axeln betecknas med \(a\), den semi-majoraxeln med \(b\). En ellips vars centrum är i origo och vars halvaxlar ligger på koordinatlinjer beskrivs av följande kanonisk ekvation :
\(\large\frac(((x^2)))(((a^2)))\normalsize + \large\frac(((y^2)))(((b^2)))\ normalstorlek = 1.\)



Summan av avstånden från valfri punkt på ellipsen till dess brännpunkter konstant:
\((r_1) + (r_2) = 2a\),
där \((r_1)\), \((r_2)\) är avstånden från en godtycklig punkt \(P\left((x,y) \right)\) till brännpunkten \((F_1)\) och \(( F_2)\), \(a\) är ellipsens halvhuvudaxel.



Förhållandet mellan ellipsens halvaxlar och brännvidden
\((a^2) = (b^2) + (c^2)\),
där \(a\) är ellipsens halvstora axel, \(b\) är halvmollaxeln, \(c\) är halva brännvidden.

Ellipsexcentricitet
\(e = \large\frac(c)(a)\normalstorlek

Ekvationer av ellipsriktlinjer
Riktlinjen för en ellips är en rät linje vinkelrät mot dess fokalaxel och skär den på ett avstånd \(\large\frac(a)(e)\normalsize\) från centrum. Ellipsen har två riktlinjer placerade på motsatta sidor av mitten. Directricekvationerna skrivs i formen
\(x = \pm \large\frac(a)(e)\normalstorlek = \pm \large\frac(((a^2)))(c)\normalstorlek.\)

Ekvation för en ellips i parametrisk form
\(\left\( \begin(aligned) x &= a\cos t \\ y &= b\sin t \end(aligned) \right., \;\;0 \le t \le 2\pi\ ),
där \(a\), \(b\) är ellipsens halvaxlar, \(t\) är parametern.

Allmän ellipsekvation
\(A(x^2) + Bxy + C(y^2) + Dx + Ey + F = 0\),
där \((B^2) - 4AC

Allmän ekvation för en ellips vars halvaxlar är parallella med koordinataxlarna
\(A(x^2) + C(y^2) + Dx + Ey + F = 0\),
där \(AC > 0\).

Ellips omkrets
\(L = 4aE\vänster(e \höger)\),
där \(a\) är ellipsens halvstora axel, \(e\) är excentriciteten, \(E\) är komplett elliptisk integral av det andra slaget.

Ungefärliga formler för omkretsen av en ellips
\(L \approx \pi \left[ (\large\frac(3)(2)\normalsize\left((a + b) \right) - \sqrt (ab) ) \right],\;\;L \approx \pi \sqrt (2\left(((a^2) + (b^2)) \right)),\)
där \(a\), \(b\) är ellipsens halvaxlar.

Området av ellipsen
\(S = \pi ab\)