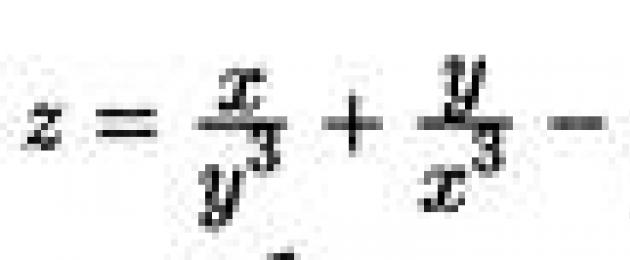Modul 2.
Föreläsning 17. Funktion av flera variabler
Avsnitt 17.1. n-dimensionellt utrymme
1. Flerdimensionella utrymmen
2. Begreppet avstånd (metrics). Metriskt utrymme
3. Principer för klusteranalys
Avsnitt 17.2 Funktion för flera variabler
1. Funktion av flera variabler
2. Partiella derivat
3. Dubbel integral
4. Polära koordinater och Euler-Poisson-integralen
Föreläsningen diskuterar frågor relaterade till utrymmen med dimensioner större än två: introduktionen av begreppet avstånd, användningen av avstånd i klusteranalys, en funktion av flera (i vårt fall, två) variabler, dess karakterisering med hjälp av partiella derivator, samt som beräkningar av area och volym. Funktionsbegrepp för två variabler och dubbel integral Vi kommer att behöva dem när vi studerar slumpmässiga vektorer i sannolikhetsteorin. Föreläsningsmaterialet avslutas med beräkningen av Euler-Poisson-integralen - en av de viktigaste inom sannolikhetsteorin ( obestämd integral från Gauss-funktionen klassificeras som icke-integrerbar, och i fallet med integrationsgränser kräver beräkningen av sådana integraler användning av icke-uppenbara metoder, varav en ges här).
Innan du studerar föreläsningsmaterialet, upprepa definitionen av en funktion, derivata och integral.
Litteratur
B.P. Demidovich, V.A. Kudryavtsev " Kort kurs högre matematik" Kapitel XX (§1, 2.3,10), Kapitel XXIV (§1, 2,3,4,7)
Frågor för självkontroll
1. Vilket rum kallas n-dimensionellt?
2. Vilka villkor måste avståndet uppfylla?
3. Vilket utrymme kallas metriskt?
4. Vad används klusteranalys till?
5. Vad är grafen för en funktion av 2 variabler? Vad är nivålinjer?
6. Vad är en partiell derivata?
7. Ge definitionen av en dubbelintegral. Hur kan du använda den för att beräkna area och volym?
8. Hitta avståndet mellan punkterna A(1,2,3) och B(5,1,0) (med olika avstånd)
9. Hitta funktionsnivålinjer
z = x + y.
10. Hitta partiella derivator av en funktion ![]()
11. Hitta arean av figuren avgränsad av linjer
12. Beräkna
Avsnitt 17.1. Begreppet multidimensionellt utrymme
Definition 17.1.1. n-dimensionellt utrymme.
Om R2 är fixerad på planet rektangulärt system koordinater, sedan mellan planets punkter och alla möjliga talpar (x, y) (x och y är punkternas koordinater) finns en en-till-en-överensstämmelse. Om ett liknande koordinatsystem ges i rymden, så finns det också en en-till-en-överensstämmelse mellan rymdens punkter och deras koordinater - alla möjliga tripletter (x, y, z).
Avstånd (metriskt). Metriskt utrymme
Definition 17.1.2
Metriskt utrymme ( M ,d) är en uppsättning punkter M, på vars kvadrat (det vill säga för alla punkter från M) en avståndsfunktion (metrisk) ges. Den definieras enligt följande:
För alla poäng x, y, z från M denna funktion måste uppfylla följande villkor:
Dessa axiom återspeglar det intuitiva konceptet avstånd. Till exempel måste avståndet vara icke-negativt och avståndet från x innan y samma som från y innan x. Triangelojämlikheten betyder att man ska gå ifrån x innan z kan vara kortare, eller åtminstone inte längre än den första promenaden x innan y, och sedan från y innan z.
Det mest bekanta för oss är det euklidiska avståndet. Detta är dock långt ifrån det enda sättet att ställa in det. Till exempel kommer följande avstånd att uppfylla ovanstående axiom: d(x,y) = 1, Om x ≠ y Och d(x,y) = 0, Om x = y.
Beroende på utrymmets specifika behov eller egenskaper kan olika mått övervägas.
Låt oss titta på några exempel på avstånd:
Definitioner 17.1.3.
Euklidiskt avstånd. Detta verkar vara det mesta allmän typ avstånd. Det är helt enkelt ett geometriskt avstånd i flerdimensionellt utrymme och beräknas enligt följande:
d(x,y) = (i (xi - y i)2) 1/2
Observera att det euklidiska avståndet (och dess kvadrat) beräknas från originaldata, inte standardiserade data. Detta är ett vanligt sätt att beräkna det, vilket har vissa fördelar (till exempel ändras inte avståndet mellan två objekt när ett nytt objekt introduceras i analysen, vilket kan vara en extremvärde). Avstånden kan dock i hög grad påverkas av skillnader mellan de axlar från vilka avstånden beräknas. Till exempel, om en av axlarna mäts i centimeter och du sedan omvandlar den till millimeter (multiplicerar värdena med 10), kommer det slutliga euklidiska avståndet (eller kvadraten på det euklidiska avståndet) beräknat från koordinaterna att ändras mycket, och som ett resultat av detta kan resultaten av klusteranalysen skilja sig mycket från tidigare.
Kvadrat euklidiskt avstånd. Det euklidiska standardavståndet är kvadratiskt för att ge större vikt åt föremål som är längre ifrån varandra. Detta avstånd beräknas enligt följande (detta gäller även anmärkningen om påverkan av måttenheter från föregående stycke):
d(x,y) = i (x i - y i) 2
Stadsblocksavstånd (Manhattan-avstånd). Detta avstånd är helt enkelt medelvärdet av skillnaderna över koordinaterna. I de flesta fall ger detta avståndsmått samma resultat som det vanliga euklidiska avståndet. Vi noterar dock att för detta mått reduceras inflytandet av individuella stora skillnader (extrema) (eftersom de inte är kvadratiska). Manhattan-avståndet beräknas med formeln:
d(x,y) = i |x i - y i |
Chebyshev avstånd. Detta avstånd kan vara användbart när man vill definiera två objekt som "olika" om de skiljer sig åt i en koordinat (i valfri dimension). Chebyshev-avståndet beräknas med formeln:
d(x,y) = max |x i - y i |
(max betyder max - det största av alla värden för differensmoduler)
Kraftavstånd. Ibland vill man successivt öka eller minska en vikt relaterad till en dimension för vilken motsvarande föremål är mycket olika. Detta kan uppnås med hjälp av kraftavstånd. Effektavståndet beräknas med formeln:
d(x,y) = (i |xi - yi | p) 1/r
Var r Och p- användardefinierade parametrar. Några exempel på beräkningar kan visa hur denna åtgärd "fungerar". Parameter sid ansvarar för den gradvisa vägningen av skillnader längs individuella koordinater, parametern r ansvarig för att successivt väga stora avstånd mellan föremål. Om båda parametrarna är r Och sid, är lika med två, så sammanfaller detta avstånd med det euklidiska avståndet.
Grundläggande funktionella utrymmen
Föreläsning 5
En av de viktigaste operationerna i analys är passage till gränsen. Denna operation är baserad på det faktum att avståndet från en punkt till en annan definieras på tallinjen. Många grundläggande analysfakta är inte relaterade till reella tals algebraiska natur (det vill säga det faktum att de bildar ett fält), utan förlitar sig endast på begreppet avstånd. Genom att generalisera idén om reella tal som en uppsättning där avståndet mellan element introduceras, kommer vi till begreppet metriskt utrymme - ett av de viktigaste begreppen i modern matematik.
Definition.
Ett metriskt utrymme är ett par (X, ρ), bestående av någon uppsättning (mellanrum) X element (punkter) och avstånd, det vill säga en envärdig, icke-negativ, reell funktion ρ(x,y), definierad för någon x Och y från X och föremål för följande axiom;
1. ρ(x,y) ≥ 0 för alla x,y,
2. ρ(x,y) = 0 då och bara när x=y,
3. ρ(x,y) = ρ(y,x)(symmetriaxiom),
4. ρ(x,z) £ ρ(x,y) + ρ(y,z)(triangelaxiom).
Själva metriska utrymmet, dvs paret (X, ρ), kommer vi vanligtvis att beteckna med en bokstav R = (X, ρ).
I de fall där missförstånd är uteslutna kommer vi ofta att beteckna det metriska utrymmet med samma symbol som själva "poängbeståndet". X.
Låt oss ge exempel på metriska utrymmen. Vissa av dessa utrymmen spelar en mycket viktig roll i analysen. viktig roll.
1. Inställning för element i en godtycklig uppsättning
vi får uppenbarligen ett metriskt utrymme. Det kan kallas utrymmet för isolerade punkter.
2. Uppsättning reella tal med avstånd
bildar ett metriskt utrymme R 1.
3. Uppsättningen av beställda grupper av n reella tal x = (x 1, …, x n) med avstånd
kallad n-dimensionell aritmetisk euklidisk rymd Rn. Giltigheten av axiom 1) - 3) för Rn uppenbar. Låt oss visa det Rn triangelaxiomet är också uppfyllt.
Låta x = (x 1 ,…, x n), y = (y 1 ,…, y n),
z = (z 1,…, z n);
då skrivs triangelaxiomet som
Förutsatt att vi får , och ojämlikhet (2) tar formen
Men denna ojämlikhet följer omedelbart av den välkända Cauchy-Bunyakovsky-ojämlikheten
På grund av denna ojämlikhet har vi faktiskt
Således är ojämlikhet (3), och därför (2), bevisad.
4. Betrakta samma uppsättning beställda grupper från n riktiga nummer x = (x 1 ,…, x n) men vi definierar avståndet i den med formeln
Giltigheten av axiomen här är uppenbar.
Uppgift. Bevisa axiom 4.
Låt oss beteckna detta metriska utrymme med symbolen.
5. Ta igen samma uppsättning som i exempel 3 och 4, och bestäm avståndet mellan dess element med formeln
Giltigheten av axiom 1) - 3) är uppenbar.
Uppgift. Bevisa axiom 4.
Detta utrymme, som vi betecknar med , är inte mindre praktiskt i många analysfrågor än det euklidiska rummet Rn.
De tre sista exemplen visar att det ibland verkligen är viktigt att ha olika notationer för själva det metriska rummet och för uppsättningen av dess punkter, eftersom samma lager av punkter kan mätas på olika sätt.
6. Massor C allt kontinuerligt verkliga funktioner, definierad på segmentet , med avstånd
bildar också ett metriskt utrymme. Axiom 1) - 3) verifieras direkt.
Uppgift. Bevisa axiom 4.
Detta utrymme spelar en mycket viktig roll i analysen. Vi kommer att beteckna det med samma symbol C, som är uppsättningen av punkter för detta utrymme själv. Istället för C vi kommer att skriva enkelt MED.
7. Låt oss beteckna med l 2 metriskt utrymme vars punkter alla är möjliga sekvenser x=(x 1,...,x n,...) reella tal som uppfyller villkoret,
och avståndet bestäms av formeln
Av den elementära ojämlikheten följer att funktionen ρ(x,y) vettigt för alla konvergerar om
Låt oss nu visa att funktion (8) uppfyller det metriska rummets axiom. Axiom 1) - 3) är uppenbara, och triangelaxiomet här tar formen
På grund av ovanstående konvergerar var och en av de tre serierna som skrivs här. Å andra sidan, varje gång n ojämlikhet är sant
(se exempel 4). Passerar här till gränsen kl n®∞ vi får (8), dvs. triangelojämlikhet i l 2.
8. Betrakta, som i exempel 6, uppsättningen av alla funktioner kontinuerliga på intervallet , men låt oss definiera avståndet annorlunda, nämligen låt oss sätta
Vi kommer att beteckna ett sådant metriskt utrymme C 2 och kalla det utrymmet för kontinuerliga funktioner med kvadratisk metrisk. Här är alla det metriska rummets axiom uppenbara, och triangelaxiomet följer direkt av den integrala formen av Cauchy-Bunyakovsky-ojämlikheten
9. Tänk på uppsättningen av alla begränsade sekvenser x = (x 1 ,…, x n, …) reella tal.
vi får ett metriskt utrymme, som vi betecknar m. Giltigheten av axiomen är uppenbar.
10. Uppsättningen av beställda grupper av n reella tal med avstånd
Var R- valfritt fast nummer ≥ 1 , är ett metriskt utrymme, som vi betecknar med .
Låt oss kolla axiom 4.
Låta x=(xl,…,xn), y=(y1,…,yn), z=(zi,…,zn).
Antag då ojämlikheten
vars rättvisa vi måste etablera kommer att ta formen
Detta är den så kallade Minkowski-ojämlikheten. På p= 1 Minkowskis olikhet är uppenbar (modulen för summan överstiger inte summan av modulerna), så vi antar att p > 1.
Bevis på ojämlikhet (13) med p>1 baserad på den så kallade Hölder-ojämlikheten
var är siffrorna p > 1 Och q > 1 bunden av villkor
Observera att ojämlikhet (14) är homogen. Detta betyder att om det är uppfyllt för två vektorer a = (a 1 ,…, a n), Och b = (b 1 ,..., b n), då gäller det även för vektorer λa Och μb, Var λ Och μ - godtyckliga siffror. Därför är det tillräckligt att bevisa ojämlikhet (14) för fallet när
Så låt villkor (16) vara uppfyllt; låt oss bevisa det
Tänk på planet (ξ,η) kurva definierad av ekvationen η = ξ p -1 (ξ>0), eller, vad är detsamma, enligt ekvationen ξ p -1 (η >0)(Figur 1). Det framgår av figuren att för alla val av positiva värden a Och b kommer S1 + S2 > ab. Låt oss beräkna arean S 1 Och S 2:
Således är den numeriska ojämlikheten sann
Byter ut här a på |a k | Och b på |b k | och summerar k från 1 till n, får vi, med hänsyn till (15) och (16),
Ojämlikhet (17) och följaktligen allmän ojämlikhet (14) har bevisats.
På p = 2 Hölders ojämlikhet (14) övergår i Cauchy-Bunyakovsky-ojämlikheten (4).
Låt oss nu gå vidare till beviset på Minkowskis ojämlikhet. För att göra detta, överväg identiteten
Ersätter i den skriftliga identiteten a på ett k Och b på b k och summerar k från 1 innan n vi får
Tillämpar nu Hölders ojämlikhet på var och en av de två beloppen till höger och tar hänsyn till det (p - 1)q = p, vi får x(t) , vi får
Således har det bevisats att formel (18), som bestämmer avståndet in l sid verkligen vettigt för vem som helst. Samtidigt visar ojämlikhet (19) att i l sid triangelaxiomet är uppfyllt. De återstående axiomen är uppenbara.
Följande teknik ger ett obegränsat antal ytterligare exempel. Låta R = (X, ρ)- metriskt utrymme och M- någon delmängd i X. Sedan M med samma funktion ρ(x,y), som vi nu anser vara definierade för x Och på från M, är också ett metriskt utrymme; det kallas ett underrum av rymden R.
Innan Riemann, Lobachevsky, Einstein och några andra kamrater byggdes geometrin från plan, osynliga punkter och raka linjer oändliga i båda riktningarna. Tiden svävade stolt över den platta tredimensionella världen, av oss uppfattad som en viss process, kvantifierad för bekvämlighets skull till hjärtslag och tickande av en klocka. Allt är bekant, okomplicerat, begripligt, krafter verkar, tre koordinater i rymden kan bestämmas var som helst - bara kör i en tapp.
Slutet på idyllen kom med tillkomsten av matematiker som utforskade flerdimensionella utrymmen på spetsen av sin penna. De byggde komplexa, flerkoordinerade objekt och system som var ofattbara för det mänskliga ögat och sinnena, till exempel den berömda fyrdimensionella kuben, Mobius-remsan och så vidare. Det blev efterhand tydligt att det imaginära rummet inte nödvändigtvis behöver bestå av plan och räta linjer med processtid, det kan t.ex. bestå av en oregelbunden form platt ark, och tiden är längden på axeln som ritas i mitten av röret. En punkt placerad i ett så "fel" utrymme kommer aldrig mer att ha de tre koordinaterna vi är vana vid, eftersom en driven pinne inte hjälper till att mäta dem. Positionen för en given punkt i det icke-euklidiska rummet kommer att behöva representeras som en hel rad av tal, som också kontinuerligt ändras i enlighet med vissa regler. Själva reglerna i varje fiktivt utrymme är olika. En sådan array av siffror kallas en tensor; den lagrar data om punkter i rymden ungefär i den form som den välkända leksaken "bild av spikar" lagrar en bild: längden på varje stav är en vektor som pekar mot en punkt längs med en av koordinaterna, deras kombination ger en bild av den, den enda.
Tensorer är komplexa objekt, men de har en sak gemensam plats- en tensor som en array av stavvektorer kan "skäras över" genom att definiera den så kallade tensormatrisen - en tvådimensionell tabell där det, istället för vanliga tal, finns formler som beskriver reglerna för dess transformation. En matris är ett enkelt objekt, vars operationer var väl utvecklade för århundraden sedan. Cheferna för matematiker började arbeta hårt, de ersatte en mängd olika formler och konstruerade tensorer för punkter i de mest ofattbara utrymmen. Till slut, genom ansträngningar av Minkowski, Riemann, Lorentz och Einstein, upptäcktes de enklaste tensorerna som med tillräcklig noggrannhet beskriver den tredimensionella euklidiska rymd- och tidsprocess vi uppfattar. Deras matriser kallas mått.
Därefter förstod man att på grund av ljusets hastighets konstanta i vakuum, tagen som grund av Einstein, blir Minkowski-metriken otillämplig på mycket stora avstånd mellan punkter, eller vid mycket högater. Cheferna för matematiker började arbeta igen, nu i allians med fysiker som letade efter experimentell bekräftelse av teorier. Så här uppstod till exempel Schwarzschild-metriken, som beskriver vår värld genom multiplikation av matriser av tensorer i ett tvådimensionellt rektangulärt plan och en tvådimensionell sfär (det är också en bekant cirkel, men i form av en hela utrymmet). Schwarzschild-metriken gjorde det möjligt att beskriva varför vi uppfattar rörelsen av föremål på detta sätt och inte på annat sätt. himmelssfären. Tiden i den är ett konstant värde(!), som införs separat i varje beräkning, och avståndet från en punkt till en observatör är faktiskt en sorts vektor som beskriver omfattningen av utrymmet (tiden) mellan två inte objekt, utan händelser.
Vad är ett mått? Vad används det till? Är det ett fysiskt fält?
Metrik i vår tid är fast förknippad med gravitationsteorin, tack vare Hilberts och Einsteins verk tillsammans med Grossman. Det introducerades dock i matematik långt innan detta. Om jag inte misstar mig så var Riemann och Gauss bland de första som använde det explicit på ett eller annat sätt. Först ska vi försöka förstå dess roll i geometrin och först då kommer vi att se hur metriken blev huvudstruktur OTO, Allmän teori Relativitet.
Idag finns det en ganska detaljerad och tydlig definition av metriska utrymmen av en ganska allmän form:
Ett metriskt utrymme ("utrustat med ett mått") i matematik är ett utrymme där ett reellt tal för två av dess ordnade punkter (det vill säga en av dem kallas den första och den andra kallas den andra) definieras så att den är lika med noll, om och endast om , när punkterna sammanfaller, och "triangel"-olikheten är uppfylld - för alla tre punkter (x,y,z) är detta tal för valfritt par (x,y) lika med eller mindre än summan av dessa tal för de andra två paren, (x,z) och (y,z). Det följer också av definitionen att detta tal är icke-negativt och inte ändras (måttet är symmetriskt) när ordningen på punkterna i paret ändras.
Som vanligt, så snart något är definierat, utökas denna definition och namnet utökas till andra liknande utrymmen. Så det är här. Till exempel, strikt formellt kommer inte att vara metrisk enligt definitionen ovan, eftersom i dem kan det "metriska" talet, intervallet, vara noll för två olika punkter, och dess kvadrat kan också vara ett negativt reellt tal. Men de ingår i familjen av metriska utrymmen nästan från början, helt enkelt ta bort motsvarande krav i definitionen, utöka definitionen.
Dessutom kan måtten också bestämmas inte för alla punkter i rymden, utan bara för oändligt nära (lokalt). Sådana utrymmen kallas riemannska och i vardagen kallas de även metriska. Dessutom, Det var Riemannska utrymmen som gjorde metriken så berömd och väckte uppmärksamhet från både matematiker och fysiker, och bekant till och med för många människor som har liten koppling till dessa vetenskaper.
I slutändan kommer vi här att diskutera metriken i relation specifikt till Riemannska rum, d.v.s. i lokal mening. Och även lokalt signalmässigt obestämd.
Den formella matematiska definitionen och dess förlängningar är resultatet av att förstå och förtydliga begreppet metrisk. Låt oss se var detta koncept växte ifrån och med vilka egenskaper verkliga världen den var ursprungligen kopplad.
All geometri uppstod från de begrepp som ursprungligen formaliserades av Euklid. Det är även metriken. I euklidisk geometri (för enkelhetens skull och tydlighetens skull kommer vi att tala om tvådimensionell geometri, och därför geometrin hos ett plan) finns begreppet avståndet mellan två punkter. Mycket ofta, även nu, kallas måtten avstånd. För för det euklidiska planet är avstånd ett mått och ett mått är avstånd. Och det är precis så det konceptualiserades i början. Även om, som jag ska försöka visa, att modernt koncept Detta gäller endast måtten i en mycket begränsad mening, med många reservationer och villkor.
Avstånd på det euklidiska planet (på ett papper) verkar vara en extremt enkel och självklar sak. Med hjälp av en linjal kan du faktiskt rita en rak linje mellan två valfria punkter och mäta dess längd. Det resulterande talet blir avståndet. Om du tar den tredje punkten kan du rita en triangel och se till att detta avstånd (för valfria två punkter på planet) exakt motsvarar definitionen ovan. Egentligen kopierades definitionen en-till-en från egenskaperna för det euklidiska avståndet på ett plan. Och ordet "metrics" är initialt associerat med mätning (med hjälp av en mätare), "metrisering" av ett plan.
Varför var det nödvändigt att mäta avstånd, för att utföra just denna metrisering av planet? Tja, alla har förmodligen sin egen uppfattning om varför avstånd mäts i verkligheten. Och inom geometri började de verkligen tänka på detta när de introducerade koordinater för att beskriva varje punkt på planet separat och unikt från andra. Koordinatsystemet på planet kommer helt klart att vara mer komplext än bara avståndet mellan två punkter. Här är origo, och koordinataxlarna, och avstånden (hur kan vi klara oss utan dem?) från origo till projektionerna av punkten på axeln. Det verkar tydligt varför ett koordinatsystem behövs - det är ett kontinuerligt rutnät av linjer vinkelräta mot varandra (om koordinaterna är kartesiska), som helt fyller planet och löser därmed problemet med att adressera vilken punkt som helst på det.
Det visar sig att måttet är avstånd och koordinater är avstånd. Finns det någon skillnad? Angivna koordinater. Varför då ett mått? Det finns en skillnad, och en mycket betydande sådan. Valet av koordinatsystem innebär en viss frihet. I kartesiska system använder vi raka linjer som axlar. Men vi kan också använda kurvor? Burk. Och alla möjliga krångliga sådana också. Kan vi mäta avstånd längs sådana linjer? Säkert. Att mäta avstånd, längd längs en linje är inte relaterad till vilken sorts linje det är. Den krökta banan har också en längd och milstolpar kan placeras på den. Men metriken i det euklidiska rymden är inte ett godtyckligt avstånd. Detta är längden på en rät linje som förbinder två punkter. Hetero. Och vad är det? Vilken linje är rak och vilken är krökt? I skolkurser är räta linjer ett axiom. Vi ser dem och får idén. Men i allmän geometri kan raka linjer (i sig är detta ett namn, en etikett, inget mer!) definieras som några speciella linjer bland alla möjliga som förbinder två punkter. Nämligen som den kortaste, med den kortaste längden. (Och i vissa fall, för vissa matematiska utrymmen, tvärtom, den längsta, som har störst längd.) Det verkar som om vi har fattat skillnaden mellan ett metriskt och ett godtyckligt avstånd mellan två punkter. Inte så. Vi tog fel väg. Ja, det stämmer, raka linjer är de kortaste i det euklidiska rymden. Men måtten är inte bara längden på den kortaste vägen. Nej. Detta är dess sekundära egenskap. I det euklidiska rymden är metriken inte bara avståndet mellan två punkter. Metriken är först och främst en bild av Pythagoras sats. Ett teorem som låter dig beräkna avståndet mellan två punkter om du känner till deras koordinater och två andra avstånd. Dessutom beräknas det mycket specifikt, som kvadratroten av summan av kvadraterna av koordinatavstånden. Den euklidiska metriken är inte en linjär form av koordinatavstånd, utan en kvadratisk! Endast de specifika egenskaperna hos det euklidiska planet gör anslutningen av metriken med de kortaste vägarna som förbinder punkter så enkel. Avstånd är alltid linjära funktioner för förskjutning längs banan. Metriken är en kvadratisk funktion av dessa förskjutningar. Och här ligger den grundläggande skillnaden mellan det metriska och det intuitivt förstådda avståndet, som linjär funktion förskjutningar från en punkt. Dessutom, för oss i allmänhet, är avstånd direkt förknippat med själva förskjutningen.
Varför, varför i hela friden är den kvadratiska förskjutningsfunktionen så viktig? Och har den verkligen rätt att kallas en distans av i alla avseenden det här ordet? Eller är detta en ganska specifik egenskap för endast det euklidiska utrymmet (nåja, eller någon familj av utrymmen nära euklidiskt)?
Låt oss ta ett litet steg åt sidan och prata mer i detalj om egenskaperna hos måttenheter. Låt oss ställa oss frågan: hur ska linjalerna vara för att kunna applicera ett koordinatnät på ett pappersark? Solid, tuff och oföränderlig, säger du. Och varför "härskare"? En är tillräckligt! Sant, om det kan roteras som önskat i papprets plan och flyttas längs det. Har du märkt "om"? Ja, vi har möjlighet att använda en sådan linjal i förhållande till ett plan. Linjalen är på egen hand, planet är på egen hand, men planet tillåter oss att "fästa" vår linjal till sig själv. Och i förhållande till sfärisk yta? Oavsett hur du applicerar det sticker allt ut utanför ytan. Jag vill bara böja den, ge upp dess hårdhet och styvhet. Låt oss lämna denna tankegång för nu. Vad mer vill vi ha av linjen? Hårdhet och styvhet innebär faktiskt något annat, mycket viktigare för oss när vi tar mätningar - en garanti för den valda linjalens oföränderlighet. Vi vill mäta med samma skala. Varför är detta nödvändigt? Vad menar du varför?! Att kunna jämföra mätresultat överallt i planet. Oavsett hur vi vänder linjalen, hur vi än flyttar den, måste några av dess egenskaper, längden, garanteras förbli oförändrade. Längd är avståndet mellan två punkter (i en rät linje) på en linjal. Mycket lik metrisk. Men metriken introduceras (eller finns) i planet, för punkter på planet, och vad har linjalen med det att göra? Och trots det metriken är just bilden av den konstanta längden av en abstrakt linjal som tagits till sin logiska slutsats, riven av från den yttersta linjalen och tilldelad varje punkt på planet.
Även om våra linjaler alltid är externa objekt för de avstånd de mäter på ett plan, tänker vi också på dem som inre skalor som hör till planet. Följaktligen talar vi om en allmän egenskap hos både de yttre och interna härskarna. Och denna egenskap är en av de två huvudsakliga - magnitud, vilket är det som gör skalan till en måttenhet (skalans andra egenskap är riktning). För det euklidiska rummet verkar denna egenskap vara oberoende av linjalens riktning och dess position (från en punkt i rymden). Det finns två sätt att uttrycka detta oberoende. Den första metoden, en passiv syn på saker och ting, talar om en kvantitets invarians, dess enhetlighet under ett godtyckligt val av tillåtna koordinater. Den andra metoden, aktiv blick, talar om invarians under translation och rotation, som ett resultat av en explicit övergång från punkt till punkt. Dessa metoder är inte likvärdiga med varandra. Den första är helt enkelt en formalisering av påståendet att den kvantitet som finns på en given plats (punkt) är densamma oavsett synvinkel. Den andra anger också att värdena för kvantiteter vid olika punkter är desamma. Det är klart att detta är ett mycket starkare uttalande.
Låt oss nu uppehålla oss vid invariansen av skalvärdet för ett godtyckligt val av koordinater. hoppsan! Så här? För att tilldela koordinater till punkter måste du redan ha skalor. De där. just denna rad. Vad är andra koordinater? Andra rader? Det är faktiskt precis vad det är! Men! Det faktum att vi i det euklidiska planet kan rotera vår linjal vid en punkt som vi vill, skapar intrycket att koordinaterna kan ändras utan att linjalen ändras. Det är en illusion, men en så trevlig illusion! Vad vana vi är vid det! Vi säger alltid – ett roterat koordinatsystem. Och denna illusion är baserad på en viss postulerad skalegenskap i det euklidiska planet - invariansen av dess "längd" under godtycklig rotation vid en punkt, dvs. med en godtycklig förändring av den andra skalegenskapen, riktning. Och denna egenskap äger rum var som helst på det euklidiska planet. Skalan har överallt en "längd" som inte beror på det lokala valet av koordinataxlarnas riktningar. Detta är ett postulat för det euklidiska rummet. Och hur bestämmer vi denna längd? I ett koordinatsystem där den valda skalan är en måttenhet längs en av axlarna, definierar vi det väldigt enkelt - det här är samma enhet. Och i ett koordinatsystem (rektangulärt), där den valda skalan inte sammanfaller med någon av axlarna? Använder Pythagoras sats. Satser är satser, men det finns lite bedrägeri här. I själva verket borde denna sats ersätta några av de axiom som Euklids formulerade. Hon är likvärdig med dem. Och med ytterligare generalisering av geometri (till exempel för godtyckliga ytor) förlitar de sig exakt på metoden för att beräkna skalans längd. Faktum är att denna metod förpassas till kategorin axiom.
Låt oss nu upprepa något som ligger bakom geometrin, vilket gör att vi kan tilldela koordinater till punkter i planet.
Vi pratar om en måttenhet, en skala. Skalan finns när som helst. Den har magnitud - "längd" och riktning. Längden är invariant (ändras inte) när riktningen i en punkt ändras. I rektangulära koordinater i det euklidiska rymden, kvadraten på längden på skalan riktad från en punkt godtyckligt, lika med summan kvadrater av dess projektioner på axeln. Denna geometriska storhet kallas också en vektor. Så skalan är en vektor. Och vektorns "längd" kallas också normen. Bra. Men var är måttet här? A metrik med detta tillvägagångssätt finns det ett sätt att tilldela en norm till vilken vektor som helst vid varje punkt, en metod för att beräkna denna norm för en godtycklig position för denna vektor i förhållande till vektorerna som utgör basen, referenspunkt(de som bestämmer koordinataxlarnas riktningar från en given punkt och har en enhetsnorm per definition, d.v.s. måttenheter). Det är mycket viktigt att denna metod definieras för varje punkt i rymden (plan i detta fall). Det är alltså en egenskap hos detta utrymme och dess inre vektorer, och inte hos objekt utanför utrymmet.
Ursäkta mig, men redan i början gav vi en definition av metriska utrymmen. Varför en ny definition? Och stämmer det med det gamla? Men varför. Här har vi angett hur exakt detta reella tal sätts och bestäms. Avståndet mellan punkter är nämligen lika med "längden", normen för vektorn som förbinder dessa punkter (i det euklidiska rymden). Det faktum att en vektor har en viss norm, oberoende av synvinkeln på den (valet av referenspunkt) är definitionen av en vektor. Det viktigaste villkoret, som gör rymden metrisk, är kravet på att vektorer med en given norm finns vid varje punkt i rymden i alla riktningar. Och denna definition överensstämmer helt med den som gavs i början. Är det möjligt att definiera ett mått på ett visst utrymme annorlunda? I princip är det möjligt. Och till och med på många sätt. Endast dessa kommer att vara helt olika klasser av utrymmen som inte inkluderar det euklidiska rummet ens som ett specialfall.
Varför är det euklidiska utrymmet speciellt för oss? Tja, hur är det? Vid första anblicken har själva utrymmet vi lever i just dessa egenskaper. Ja, vid närmare granskning, inte riktigt så. Men det är skillnad på "inte riktigt så" och "inte alls så"?! Även om uppsättningen av ord verkar vara densamma. Så vår rumtid, om inte euklidisk, så kan den under vissa förhållanden vara väldigt nära den. Följaktligen måste vi välja från familjen av rum där det euklidiska rummet existerar. Det är vad vi gör. Men ändå, vad är det som är så speciellt med det euklidiska rummet som uttrycks i vissa egenskaper hos dess metriska? Det finns ganska många fastigheter, de flesta av dem har redan nämnts ovan. Jag ska försöka formulera denna funktion ganska kompakt. Det euklidiska rummet är sådant att det är möjligt att välja skalor (det vill säga ange koordinater) så att det fylls helt med ett rektangulärt koordinatnät. Kanske är det när metriken vid varje punkt i rymden är densamma. I huvudsak betyder detta att de skalor som krävs för detta finns på varje punkt i rymden och de är alla identiska med en enda. För hela utrymmet räcker det med en linjal, som kan flyttas till vilken punkt som helst (i aktiv mening) utan att ändra både dess storlek och dess riktning.
Ovan ställde jag frågan varför måtten är kvadratisk funktion offset. Det förblir obesvarat än så länge. Vi kommer definitivt att komma till detta igen. Gör nu en anteckning för dig själv för framtiden - metriken i familjen av utrymmen vi behöver är en kvantitetsinvariant under koordinattransformationer. Vi har hittills pratat om kartesiska koordinater, men jag kommer omedelbart att betona här att detta gäller för alla koordinattransformationer som är tillåtna vid en given punkt i ett givet utrymme. En storhet som är invariant (förändras inte) under koordinattransformationer har ett annat speciellt namn inom geometrin - skalär. Titta hur många namn det finns för samma sak - konstant, invariant, skalär... Kanske finns det något annat, det kommer inte direkt att tänka på. Detta talar för vikten av själva konceptet. Så, ett mått är en skalär i en viss mening. Naturligtvis finns det andra skalärer inom geometri.
Varför i "viss mening"? Eftersom begreppet ett mått innehåller två punkter och inte en! Och vektorn är kopplad (definierad) med endast en punkt. Det visar sig att jag vilselett dig? Nej, jag har bara inte sagt allt som behöver sägas. Men det måste sägas att metriken inte är normen för en godtycklig vektor, utan bara för en vektor med oändligt liten förskjutning från en given punkt i en godtycklig riktning. När denna norm inte beror på förskjutningsriktningen från en punkt, kan dess skalära värde betraktas som en egenskap för endast denna punkt. Samtidigt är det fortfarande regeln för att beräkna normen för vilken annan vektor som helst. Så här.
Något stämmer inte... Normerna är olika för olika vektorer! Och måtten är skalär, värdet är detsamma. Motsägelse!
Det finns ingen motsägelse. Jag sa det tydligt - räkneregeln. För alla vektorer. Och det specifika värdet i sig, som också kallas ett mått, beräknas enligt denna regel endast för en vektor, förskjutningen. Vårt språk är vant vid friheter, utelämnanden, förkortningar... Så vi är vana vid att kalla både en skalär och regeln för att beräkna den för ett mått. Det är faktiskt nästan samma sak. Nästan, men inte riktigt. Det är fortfarande viktigt att se skillnaden mellan en regel och resultatet som erhålls med dess hjälp. Vad är viktigare – regeln eller resultatet? Märkligt nog, i det här fallet, regeln... Därför, mycket oftare inom geometri och fysik, när de pratar om metrik, menar de regeln. Endast mycket envisa matematiker föredrar att prata strikt om resultatet. Och det finns skäl till detta, men mer om dem på annat håll.
Det vill jag också notera på ett mer vanligt sätt att framställa, när begreppen tas till grund vektorutrymmen, introduceras måtten som en skalär parvis produkt av alla bas- och referensvektorer. I detta fall skalär produkt vektorer måste bestämmas i förväg. Och på den väg som jag följde här, är det närvaron av en metrisk tensor i rymden som tillåter oss att introducera och definiera skalärprodukten av vektorer. Här är måttet primärt, dess närvaro tillåter oss att introducera den skalära produkten som en slags invariant som förbinder två olika vektorer. Om en skalär beräknas med hjälp av ett mått för samma vektor, så är detta helt enkelt dess norm. Om denna skalär beräknas för två olika vektorer, så är det deras punktprodukt. Om detta också är normen för en infinitesimal vektor, är det helt acceptabelt att helt enkelt kalla det ett mått vid en given punkt.
Och vad kan vi säga om måtten som regel? Här måste vi använda formler. Låt koordinaterna längs axelnumret i betecknas som x i. Och förskjutningen från en given punkt till den intilliggande dx i. Observera att koordinater inte är en vektor! Och förskjutningen är bara en vektor! I en sådan notation kommer det metriska "avståndet" mellan en given punkt och den intilliggande, enligt Pythagoras sats, att beräknas med hjälp av formeln
ds 2 = g ik dx i dx k
Till vänster här är kvadraten på det metriska "avståndet" mellan punkter, "koordinat" (det vill säga längs varje enskild koordinatlinje) mellan vilket avståndet specificeras av förskjutningsvektorn dx i. Till höger är summan över de sammanfallande indexen för alla parvisa produkter av komponenterna i förskjutningsvektorn med motsvarande koefficienter. Och deras tabell, matrisen av koefficienter g ik, som sätter regeln för beräkning av den metriska normen, kallas metrisk tensor. Och det är denna tensor som i de flesta fall kallas metrisk. Termen "" är extremt viktig här. Och det betyder att i ett annat koordinatsystem kommer formeln som skrivits ovan att vara densamma, bara tabellen kommer att innehålla andra (i det allmänna fallet) koefficienter, som beräknas på ett strikt definierat sätt genom dessa ochter. Det euklidiska rummet kännetecknas av det faktum att i kartesiska koordinater är formen av denna tensor extremt enkel och densamma i alla kartesiska koordinater. Matrisen g ik innehåller bara ettor på diagonalen (för i=k), och de återstående talen är nollor. Om icke-kartesiska koordinater används i det euklidiska rummet, kommer matrisen inte att se så enkel ut i dem.
Så vi har skrivit ner en regel som bestämmer det metriska "avståndet" mellan två punkter i det euklidiska rummet. Denna regel är skriven för två godtyckligt nära punkter. I det euklidiska rummet, dvs. i en där den metriska tensorn kan vara diagonal med enheter på diagonalen i något koordinatsystem vid varje punkt, finns det ingen fundamental skillnad mellan finita och infinitesimala förskjutningsvektorer. Men vi är mer intresserade av fallet med riemannska rum (som ytan på en boll, till exempel), där denna skillnad är signifikant. Så vi antar att den metriska tensorn i allmänhet inte är diagonal och ändras när den rör sig från punkt till punkt i rymden. Men resultatet av dess tillämpning, ds 2, förblir vid varje punkt oberoende av valet av förskjutningsriktningen och av själva punkten. Detta är ett mycket strängt villkor (mindre strängt än det euklidiska villkoret) och det är när det är uppfyllt som utrymmet kallas Riemannskt.
Du har säkert märkt att jag väldigt ofta sätter orden "längd" och avstånd inom citattecken." Det är därför jag gör det här. När det gäller det plana och tredimensionella euklidiska rummet verkar metriskt "avstånd" och "längd" vara exakt samma som vanliga avstånd mätt med linjaler. Dessutom introducerades dessa koncept för att formalisera arbetet med mätresultat. Varför då "tycks sammanfalla"? Det är roligt, men detta är exakt fallet när matematiker, tillsammans med det smutsiga (de behövde inte) vattnet, kastade barnet ur badet. Nej, de lämnade något, men det som var kvar upphörde att vara ett barn (avstånd). Detta är lätt att se även med det euklidiska planet som exempel.
Låt mig påminna dig om att det metriska "avståndet" inte beror på valet av kartesiska (och inte bara) koordinater, till exempel på ett pappersark. Låt in några koordinater detta avstånd mellan två punkter på koordinataxeln vara lika med 10. Är det möjligt att ange andra koordinater där avståndet mellan dessa samma punkter blir lika med 1? Inga problem. Rita helt enkelt som en enhet längs samma axlar en ny enhet lika med 10 tidigare. Har det euklidiska rummet förändrats på grund av detta? Vad är problemet? Men faktum är att när vi mäter något så räcker det inte för oss att veta siffran. Vi måste också veta vilka enheter som användes för att få detta nummer. Matematik i den form som är bekant för alla idag är inte intresserad av detta. Hon sysslar bara med siffror. Valet av måttenheter gjordes innan matematik tillämpades och bör inte ändras längre! Men våra avstånd och längder utan att indikera skalor säger oss ingenting! Matematik bryr sig inte. När det kommer till metriskt "avstånd" är dess formella tillämpning likgiltig för valet av skala. Till och med meter, till och med famnar. Bara siffror spelar roll. Det är därför jag sätter citattecken. Vet du vilken? bieffekt har ett sådant tillvägagångssätt i matematiken i Riemannska utrymmen? Här är vad det är. Det är ingen mening att överväga förändringen i skala från punkt till punkt. Bara en förändring i dess riktning. Och detta trots att det är en helt vanlig sak att ändra skalor med hjälp av koordinattransformationer i sådan geometri. Är det möjligt att i geometrin inkludera en konsekvent hänsyn till skalornas egenskaper i sin helhet? Burk. Endast För att göra detta måste du ta bort många konventioner och lära dig att kalla saker vid deras rätta namn. Ett av de första stegen kommer att vara att inse det faktum att inget mått i huvudsak är ett avstånd och inte kan vara det. Hon har säkert några fysisk mening, och en mycket viktig sådan. Men annorlunda.
Inom fysiken uppmärksammades metrikens roll med tillkomsten av relativitetsteorier - först speciella, sedan generella, där metriken blev teorins centrala struktur. Den speciella relativitetsteorin bildades på basis av det faktum att tredimensionellt avstånd inte är en skalär ur synvinkeln av en uppsättning tröghetsfysiska referenssystem som rör sig i förhållande till varandra enhetligt och rätlinjigt. En annan storhet visade sig vara en skalär, en invariant, som kallades ett intervall. Intervall mellan händelser. Och för att beräkna dess värde måste du ta hänsyn till tidsintervallet mellan dessa händelser. Dessutom visade det sig att regeln för beräkning av metriken (och intervallet började omedelbart betraktas som en metrik i den förenade rum-tiden, händelsernas rum) skiljer sig från den vanliga euklidiska regeln i tredimensionellt rum. Liknande, men lite annorlunda. Motsvarande metriska utrymme med fyra dimensioner introduceras Herman Minkowski, började kallas. Det var Minkowskis arbete som uppmärksammade fysiker, inklusive Einstein, på betydelsen av begreppet metrisk som en fysisk storhet, och inte bara en matematisk.
Den allmänna relativitetsteorin tog också hänsyn till fysiska referenssystem som accelererade i förhållande till varandra. Och därmed kunde hon ge en beskrivning av gravitationsfenomen på en ny nivå i förhållande till Newtons teori. Och hon kunde uppnå detta genom att ge mening åt det fysiska fältet specifikt till metriken - både värdet och regeln, den metriska tensorn. Samtidigt använder den den matematiska konstruktionen av Riemannska rymden som en bild av rum-tid. Vi ska inte gå för långt in på detaljerna i denna teori. Bland annat säger denna teori att världen (rum-tid), där det finns massiva kroppar, det vill säga kroppar som attraherar varandra, har en metrik som skiljer sig från den euklidiska metriken som är så behaglig för oss. Alla påståenden nedan är likvärdiga:
Fysiskt uttalande. Punktkroppar med massa attraheras av varandra.
I rum-tid, där det finns massiva kroppar, är det omöjligt att införa ett styvt rektangulärt rutnät överallt. Det finns inga mätinstrument som tillåter detta. Alltid, oavsett hur små, kommer "cellerna" i det resulterande rutnätet att vara böjda fyrkanter.
Du kan välja en skala med samma värde (norm) för hela rumtiden. Vilken skala som helst kan flyttas från sin punkt till vilken annan punkt som helst och jämföras med vad som redan finns där. MEN! Även om förskjutningen är oändlig, kommer riktningarna för de jämförda skalorna i allmänhet inte att sammanfalla. Ju starkare desto närmare skalan är kroppen med massa och desto större är samma massa. Endast där det inte finns några massor (men här är en fråga till dig - hur är det med själva vågen?) kommer anvisningarna att sammanfalla.
I det område av rum-tid som innehåller massiva kroppar finns det inget koordinatsystem där den metriska tensorn vid varje punkt representeras av en matris som är noll överallt förutom diagonalen där de är placerade.
Skillnaden mellan den metriska och den euklidiska är en manifestation av närvaron av ett gravitationsfält (gravitationsfält). Dessutom är fältet för den metriska tensorn gravitationsfältet.
Många fler liknande uttalanden skulle kunna citeras, men nu vill jag uppmärksamma er på det sista. Krökning. Detta är något vi inte har diskuterat ännu. Vad har det med mått att göra? I det stora hela - ingen! är ett mer allmänt begrepp än metriskt. På vilket sätt?
Familjen av riemannska utrymmen, som också inkluderar euklidiska utrymmen, är själv en del av den mer allmänna familjen. Dessa utrymmen, generellt sett, innebär inte att det finns en sådan kvantitet som ett mått för vart och ett av dess punktpar. Men deras nödvändiga egenskap är förekomsten av två andra strukturer relaterade till varandra - affin anslutning och krökning. Och endast under vissa förhållanden på krökning (eller anslutning) finns ett mått i sådana utrymmen. Då kallas dessa utrymmen Riemannian. Alla Riemannska utrymmen har anslutning och krökning. Men inte tvärtom.
Men det kan inte heller sägas att måttet är sekundärt till anslutning eller krökning. Nej. Förekomsten av ett mått är ett uttalande av vissa egenskaper för anslutning, och därför krökning. I standardtolkningen av allmän relativitet betraktas metriken som en viktigare struktur som bildar teorins form. Och affin anslutning och krökning visar sig vara sekundär, härledd från metriken. Denna tolkning lades fast av Einstein, vid en tidpunkt då matematiken ännu inte hade utvecklat en tillräckligt avancerad och konsekvent förståelse av betydelsehierarkin hos strukturer som bestämmer egenskaperna hos familjen av utrymmen som leder till euklidiska sådana. Efter skapandet av GTR-apparaten, i första hand genom verk av Weyl och Schouten (inte bara dem, naturligtvis), utvecklades matematiken för utrymmen med affin anslutning. Egentligen stimulerades detta arbete av uppkomsten av allmän relativitet. Som du kan se, sammanfaller inte den kanoniska tolkningen av strukturernas betydelse i den allmänna relativitetsteorien med matematikens nuvarande syn på deras förhållande. Denna kanoniska tolkning är inget annat än identifieringen av vissa matematiska strukturer med fysiska fält. Ge dem fysisk mening.
I allmän relativitetsteori finns det två planer för att beskriva rum-tid. Den första av dem är själva rumtiden som ett rum av händelser. Händelser som kontinuerligt fyller varje område av rum-tid karakteriseras med hjälp av fyra koordinater. Därför antas koordinatsystemen vara inmatade. Själva namnet på teorin fokuserar uppmärksamheten just på detta - naturlagarna som äger rum i sådan rumtid måste formuleras identiskt med avseende på vilket som helst tillåtet koordinatsystem. Detta krav kallas principen om allmän relativitet. Notera att denna teoriplan ännu inte säger något om närvaron eller frånvaron av en metrik i rum-tid, men ger redan grunden för förekomsten av affin koppling i den (tillsammans med krökning och andra härledda matematiska strukturer). Naturligtvis finns det redan på denna nivå ett behov av att ge fysisk mening åt teorins matematiska objekt. Här är han. En punkt i rum-tid skildrar en händelse, som kännetecknas å ena sidan av position och tid, å andra sidan av fyra koordinater. Något konstigt? Är de inte samma sak? Men nej. I allmän relativitet är det inte samma sak. Koordinater av den mest allmänna formen, som är tillåtna i teorin, kan inte tolkas som positioner och tidpunkter. Denna möjlighet postuleras endast för en mycket begränsad grupp av koordinater - lokalt tröga sådana, som endast finns i närheten av varje punkt, men inte i hela den region som omfattas av det allmänna koordinatsystemet. Detta är ett annat postulat av teorin. Det här är en sådan hybrid. Jag kommer att notera att det är här många av problemen med allmän relativitet uppstår, men jag kommer inte att ta itu med dem nu.
Teorins andra plan kan betraktas som den del av dess postulat, som introducerar övervägande i rum-tid fysiskt fenomen– gravitation, ömsesidig attraktion av massiva kroppar. Det hävdas att detta fysiska fenomen under vissa förhållanden kan förstöras genom ett enkelt val av en lämplig referensram, nämligen en lokalt tröghetsram. För alla kroppar som har samma acceleration ( fritt fall) på grund av närvaron av en avlägsen massiv kropp i ett litet område av gravitationsfältet, är detta fält inte observerbart i en viss referensram. Formellt slutar postulaten där, men i själva verket hänvisar teorins huvudekvation, som introducerar metriken i beaktande, även till postulaten, både som ett matematiskt påstående och som ett fysiskt. Även om jag inte kommer att gå in på detaljer om ekvationen (egentligen ekvationssystem), är det fortfarande användbart att ha den framför dig:
R ik = -с (T ik – 1/2 T g ik)
Här till vänster finns den så kallade Ricci-tensorn, en viss faltning (kombination av ingående komponenter) av den fullständiga krökningstensorn. Det kan med rätta också kallas krökning. Till höger är en konstruktion av energimomentum-tensorn (rent fysisk kvantitet i GTR, singular för massiva kroppar och yttre för rum-tid, som för energimomentum i denna teori helt enkelt är en bärare) och metriken, som antas existera. Dessutom är detta mått, som en skalär kvantitet som produceras av den metriska tensorn, densamma för alla punkter i regionen. Det finns också en dimensionskonstant c, proportionell mot gravitationskonstanten. Från denna ekvation är det tydligt att krökning i stort sett jämförs med energimomentum och metrisk. Den fysiska betydelsen tilldelas måtten i allmän relativitet efter att ha erhållit en lösning på dessa ekvationer. Eftersom de metriska koefficienterna i denna lösning är linjärt relaterade till potentialen för gravitationsfältet (beräknat genom det), tilldelas betydelsen av potentialerna för detta fält till den metriska tensorn. Med detta tillvägagångssätt bör krökning ha en liknande betydelse. Och affin koppling tolkas som fältstyrka. Denna tolkning är felaktig; dess felslutning är förknippad med paradoxen som noterats ovan i tolkningen av koordinater. Naturligtvis går detta inte obemärkt förbi för teorin och visar sig på en rad bra sätt. kända problem(icke-lokaliserbarhet av gravitationsfältsenergi, tolkning av singulariteter), som helt enkelt inte uppstår när geometriska storheter ges den korrekta fysiska betydelsen. Allt detta diskuteras mer i detalj i boken "".
Men även i den allmänna relativitetsteorien har metriken oundvikligen, utöver den mening som på konstgjord väg påtvingats den, en annan fysisk betydelse. Låt oss komma ihåg vad som kännetecknar metriken i fallet med det euklidiska rummet? En mycket viktig sak för mätningar i rum-tid är möjligheten att i detta utrymme införa ett styvt rektangulärt koordinatnät som likformigt fyller hela området. Detta rutnät kallas en tröghetsreferensram i fysiken. Ett sådant referenssystem (koordinatsystem) motsvarar en och endast en standardform av den metriska tensorn. I referenssystem som rör sig godtyckligt i förhållande till den tröga, är formen på den metriska tensorn annorlunda än den vanliga. Ur en fysisk synvinkel är rollen för "referensnätet" ganska transparent. Om du har en stel referenskropp, vars varje punkt är utrustad med samma klocka, som finns i tiden, implementerar den bara ett sådant rutnät. För tomt utrymme uppfinner vi helt enkelt en sådan referenskropp, och förser den (utrymme) med exakt samma metrik. I denna förståelse säger den metriska tensorn, som skiljer sig från den euklidiska standarden, att referenssystemet (koordinaterna) är konstruerat med hjälp av icke fast, och kanske går klockorna också annorlunda på sina punkter. Vad menar jag med detta? Men det faktum att den metriska tensorn är en matematisk bild av några av referenssystemets viktigaste egenskaper för oss. De egenskaper som absolut karakteriserar själva referenssystemets struktur gör att vi kan bestämma hur "bra" det är, hur annorlunda det är från idealet - tröghetsramen. Så GTR använder den metriska tensorn precis som en sådan bild. Hur en bild av mätinstrument fördelade i ett referensområde, som eventuellt ändrar dess orientering från punkt till punkt, men som överallt har samma norm, gemensam för alla referensvektorer. Metriken, betraktad som en skalär, är denna norm, skalans storlek. Metriken som en tensor tillåter oss att betrakta en godtycklig relativ rörelse i förhållande till varandra av alla skalor som utgör referenskroppen. Och General Relativity beskriver en situation där det i rumtid är möjligt att ha en sådan referensmassa, verklig eller imaginär.
Denna syn på mått är verkligen korrekt. Dessutom är det också produktivt, eftersom det omedelbart fokuserar uppmärksamheten på de återstående avtalen i GTR. Vi har faktiskt tillåtit referensramar där skalor vid olika punkter kan orienteras olika (i en fyrdimensionell värld inkluderar orientering också rörelse). Och vi kräver fortfarande att någon absolut egenskap hos skalan, dess norm (intervall) förblir densamma. Följaktligen är påståendet om allmän relativitet att det tog hänsyn till alla möjliga referenssystem överdrivet. Det är inte så generellt, relativitet i denna teori.
© Gavryusev V.G.
Material som publiceras på webbplatsen kan användas med förbehåll för hänvisningsregler.
Metriskt utrymme.
Metriskt utrymmeär en uppsättning där avståndet mellan ett par element definieras.
Ett metriskt utrymme är ett par, där är en mängd ( ämnesuppsättning metriskt utrymme, set poäng metriskt utrymme), och - numerisk funktion (metrik space), som definieras på den kartesiska produkten och tar värden i uppsättningen av reella tal - så att för poäng
Notera: Axiomen antyder att avståndsfunktionen är icke-negativ, eftersom
Komprimerade displayer en av teorins huvudbestämmelser metriska utrymmen om existensen och det unika hos en fast punkt i en uppsättning under någon speciell (”kompressiv”) kartläggning av den i sig själv. S. o. s. används främst i teorin om differentialekvationer och integralekvationer.
Anpassad display A metriskt utrymme M in i dig själv, som vid varje punkt X från M matchar någon punkt y = Ax från M, genererar i rymden M ekvationen
Ax = x. (*)
Visa åtgärd A per poäng X kan tolkas som att det flyttas till en punkt y = Ax. Punkt X kallas en fast punkt i kartläggningen A, om jämställdhet (*) är uppfylld. Den där. frågan om lösbarheten av ekvationen (*) är en fråga om att hitta fasta punkter i kartläggningen A.
Visa A metriskt utrymme M in i sig själv kallas komprimerad om det finns en sådan Positivt nummer a< 1, что для любых точек X Och på från M ojämlikheten håller
d ( Yxa, ja) £a d(x, y),
var är symbolen d(u, u) betyder avstånd mellan punkter u och u av metriskt utrymme M.
S. o. P. hävdar att varje komprimerad avbildning av ett fullständigt metriskt utrymme i sig själv har, och dessutom bara en, fixpunkt. Dessutom för alla startpunkt x 0 från M efterföljd ( x n), definierade av återkommande relationer
xn = Axe n-1, n = 1,2,...,
har som sin gräns en fast punkt X visa A. I det här fallet är följande feluppskattning giltig:
![]() .
.
S. o. s. låter en bevisa viktiga satser om existensen och unikheten hos lösningar till differential-, integralekvationer och andra ekvationer med hjälp av en enhetlig metod. Under tillämplighetsvillkoren för S. o. lösningen kan beräknas med en förutbestämd noggrannhet successiva approximationsmetod.
Genom ett visst val av hela metriska utrymmet M och kartläggning A Dessa problem reduceras först till ekvation (*), och sedan hittas förhållanden under vilka avbildningen A verkar komprimerad.
Konvergensen av mappningar med avseende på detta mått är ekvivalent med deras enhetliga konvergens över hela utrymmet.
I det speciella fallet när är ett kompakt rum och är tallinjen, får vi rummet för alla kontinuerliga funktioner på rymden X med metriken för enhetlig konvergens.

För att den här funktionen ska bli ett mått, är det i de två första utrymmena nödvändigt att identifiera funktioner som skiljer sig åt på mängden mått 0. Annars kommer denna funktion bara att vara en semimetrisk. (I utrymmet för funktioner som är kontinuerliga på ett intervall, är funktioner som skiljer sig åt på en uppsättning av mått 0 redan desamma.)
- I kontakt med 0
- Google+ 0
- OK 0
- Facebook 0