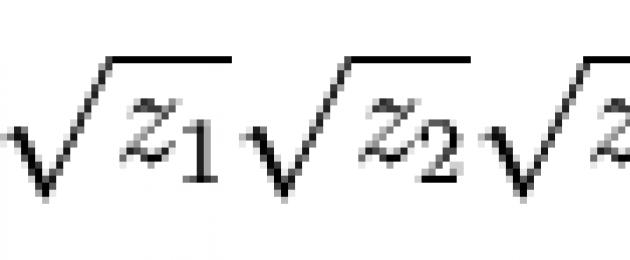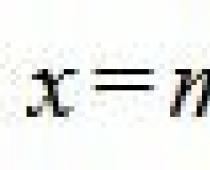На канал на youtube нашего сайта сайт, чтобы быть в курсе всех новых видео уроков.
Для начала вспомним основные формулы степеней и их свойства.
Произведение числа a само на себя происходит n раз, это выражение мы можем записать как a a … a=a n
1. a 0 = 1 (a ≠ 0)
3. a n a m = a n + m
4. (a n) m = a nm
5. a n b n = (ab) n
7. a n /a m = a n — m
Степенные или показательные уравнения – это уравнения в которых переменные находятся в степенях (или показателях), а основанием является число.
Примеры показательных уравнений:
В данном примере число 6 является основанием оно всегда стоит внизу, а переменная x степенью или показателем.
Приведем еще примеры показательных уравнений.
2 x *5=10
16 x — 4 x — 6=0
Теперь разберем как решаются показательные уравнения?
Возьмем простое уравнение:
2 х = 2 3
Такой пример можно решить даже в уме. Видно, что x=3. Ведь чтобы левая и правая часть были равны нужно вместо x поставить число 3.
А теперь посмотрим как нужно это решение оформить:
2 х = 2 3
х = 3
Для того, чтобы решить такое уравнение, мы убрали одинаковые основания (то есть двойки) и записали то что осталось, это степени. Получили искомый ответ.
Теперь подведем итоги нашего решения.
Алгоритм решения показательного уравнения:
1. Нужно проверить одинаковые
ли основания у уравнения справа и слева. Если основания не одинаковые ищем варианты для решения данного примера.
2. После того как основания станут одинаковыми, приравниваем
степени и решаем полученное новое уравнение.
Теперь прорешаем несколько примеров:
Начнем с простого.
Основания в левой и правой части равны числу 2, значит мы можем основание отбросить и приравнять их степени.
x+2=4 Получилось простейшее уравнение.
x=4 — 2
x=2
Ответ: x=2
В следующем примере видно, что основания разные это 3 и 9.
3 3х — 9 х+8 = 0
Для начала переносим девятку в правую сторону, получаем:
Теперь нужно сделать одинаковые основания. Мы знаем что 9=3 2 . Воспользуемся формулой степеней (a n) m = a nm .
3 3х = (3 2) х+8
Получим 9 х+8 =(3 2) х+8 =3 2х+16
3 3х = 3 2х+16 теперь видно что в левой и правой стороне основания одинаковые и равные тройке, значит мы их можем отбросить и приравнять степени.
3x=2x+16 получили простейшее уравнение
3x — 2x=16
x=16
Ответ: x=16.
Смотрим следующий пример:
2 2х+4 — 10 4 х = 2 4
В первую очередь смотрим на основания, основания разные два и четыре. А нам нужно, чтобы были — одинаковые. Преобразовываем четверку по формуле (a n) m = a nm .
4 х = (2 2) х = 2 2х
И еще используем одну формулу a n a m = a n + m:
2 2х+4 = 2 2х 2 4
Добавляем в уравнение:
2 2х 2 4 — 10 2 2х = 24
Мы привели пример к одинаковым основаниям. Но нам мешают другие числа 10 и 24. Что с ними делать? Если приглядеться видно, что в левой части у нас повторяется 2 2х,вот и ответ — 2 2х мы можем вынести за скобки:
2 2х (2 4 — 10) = 24
Посчитаем выражение в скобках:
2 4 — 10 = 16 — 10 = 6
Все уравнение делим на 6:
Представим 4=2 2:
2 2х = 2 2 основания одинаковые, отбрасываем их и приравниваем степени.
2х = 2 получилось простейшее уравнение. Делим его на 2 получаем
х = 1
Ответ: х = 1.
Решим уравнение:
9 х – 12*3 х +27= 0
Преобразуем:
9 х = (3 2) х = 3 2х
Получаем уравнение:
3 2х — 12 3 х +27 = 0
Основания у нас одинаковы равны трем.В данном примере видно, что у первой тройки степень в два раза (2x) больше, чем у второй (просто x). В таком случаем можно решить методом замены . Число с наименьшей степенью заменяем:
Тогда 3 2х = (3 х) 2 = t 2
Заменяем в уравнении все степени с иксами на t:
t 2 — 12t+27 = 0
Получаем квадратное уравнение. Решаем через дискриминант, получаем:
D=144-108=36
t 1 = 9
t 2 = 3
Возвращаемся к переменной x .
Берем t 1:
t 1 = 9 = 3 х
Стало быть,
3 х = 9
3 х = 3 2
х 1 = 2
Один корень нашли. Ищем второй, из t 2:
t 2 = 3 = 3 х
3 х = 3 1
х 2 = 1
Ответ: х 1 = 2; х 2 = 1.
На сайте Вы можете в разделе ПОМОГИТЕ РЕШИТЬ задавать интересующие вопросы мы Вам обязательно ответим.
Вступайте в группу
Решение Декарта - Эйлера
Сделав подстановку , получим уравнение в следующем виде (он называется «неполным»):
y 4 + p y 2 + q y + r = 0 .Корни y 1 , y 2 , y 3 , y 4 такого уравнения равны одному из следующих выражений:
в которых сочетания знаков выбираются таким образом, чтобы выполнялось следующее соотношение:
,
причём z 1 , z 2 и z 3 - это корни кубического уравнения
Решение Феррари
Основная статья : Метод Феррари
Представим уравнение четвёртой степени в виде:
A x 4 + B x 3 + C x 2 + D x + E = 0,Его решение может быть найдено из следующих выражений:
если β = 0
, решив u
4 + αu
2 + γ = 0
и, сделав подстановку 
, найдём корни:
.
, (любой знак квадратного корня подойдёт)
, (три комплексных корня, один из которых подойдёт)
Два ± s должны иметь одинаковый знак, ± t - независимы. Для того, чтобы найти все корни, надо найти x для знаковых комбинаций ± s ,± t = +,+ для +,− для −,+ для −,−. Двойные корни появятся два раза, тройные корни - три раза и корни четвёртого порядка - четыре раза. Порядок корней зависит от того, какой из кубических корней U
выбран.
См. также
- Легко решаемые типы уравнений 4 степени: Биквадратное уравнение , возвратное уравнение четвёртой степени
Литература
- Корн Г., Корн Т. (1974) Справочник по математике.
Ссылки
- Решение Феррари (англ.)
Wikimedia Foundation . 2010 .
Смотреть что такое "Уравнение четвертой степени" в других словарях:
уравнение четвертой степени - — [Л.Г.Суменко. Англо русский словарь по информационным технологиям. М.: ГП ЦНИИС, 2003.] Тематики информационные технологии в целом EN quartic equation … Справочник технического переводчика
График многочлена 4 ой степени с четырьмя корнями и тремя критическими точками. Уравнение четвёртой степени в математике алгебраическое уравнение вида: Четвёртая степень для алгебраических уравнений является наивысшей, при которой… … Википедия
Уравнение вида: anxn + an − 1xn − 1 + ... + a1x + a0 = 0 называется возвратным, если его коэффициенты, стоящие на симметричных позициях, равны, то есть если an − k = ak, при k = 0, 1, …, n. Содержание 1 Уравнение четвёртой степени … Википедия
В котором неизвестный член в четвертой степени. Полный словарь иностранных слов, вошедших в употребление в русском языке. Попов М., 1907. БИКВАДРАТНОЕ УРАВНЕНИЕ от лат. bis, дважды, и quadratum, квадрат. Уравнение, в котором наибольшая степень… … Словарь иностранных слов русского языка
Вместе с арифметикой есть наука о числах и через посредство чисел о величинах вообще. Не занимаясь изучением свойств каких нибудь определенных, конкретных величин, обе эти науки исследуют свойства отвлеченных величин как таковых, независимо от… … Энциклопедический словарь Ф.А. Брокгауза и И.А. Ефрона
Совокупность прикладных знаний, позволяющих авиационным инженерам на занятий в области аэродинамики, проблем прочности, двигателестроения и динамики полета летательных аппаратов (т.е. теории) создать новый летательный аппарат или улучшить… … Энциклопедия Кольера
Самой древней математической деятельностью был счет. Счет был необходим, чтобы следить за поголовьем скота и вести торговлю. Некоторые первобытные племена подсчитывали количество предметов, сопоставляя им различные части тела, главным образом… … Энциклопедия Кольера
История технологий По периодам и регионам: Неолитическая революция Древние технологии Египта Наука и технологии древней Индии Наука и технологии древнего Китая Технологии Древней Греции Технологии Древнего Рима Технологии исламского мира… … Википедия
Уравнением называется математическое соотношение, выражающее равенство двух алгебраических выражений. Если равенство справедливо для любых допустимых значений входящих в него неизвестных, то оно называется тождеством; например, соотношение вида… … Энциклопедия Кольера
Теорема Абеля Руффини утверждает, что общее уравнение степени при неразрешимо в радикалах. Содержание 1 Подробности … Википедия
В общем случае решение уравнения четвёртой степени осуществляется с использованием методов решения уравнений для высших степеней, например, методом Феррари или с помощью схемы Горнера. Но некоторые уравнения 4-ой степени имеют более простое решение.
Существует несколько особых типов уравнений четвертой степени, со способами решения которых вы познакомитесь ниже:
- Биквадратное уравнения $ax^4+bx^2+c=0$;
- Возвратные уравнения вида $ax^4+bx^3+cx^2 +bx+ a=0$;
- Уравнения вида $ax^4+b=0$.
Решение биквадратных уравнений четвёртой степени
Биквадратные уравнения $ax^4+bx^2+c=0$ сводятся к квадратным путём замены переменной $x^2$ на новую, например, на $y$. После замены решается новое полученное уравнение, а затем значение найденной переменной подставляется в уравнение $x^2=y$. Результатом решения будут корни уравнения $x^2=y$.
Пример 1
Решите уравнение $x(x-1)(x-2)(x-3)=24$:
Раскроем скобки в многочлене:
$(x^2-3x)(x^2-3x+2)=24$
В таком виде становится очевидно, что в качестве новой переменной можно выбрать выражение $y=x^2-3x$, подставим её:
$y \cdot (y+2)=24$
Теперь решим два квадратных уравнения $x^2-3x=-4$ и $x^2-3x=-6$.
Корни первого уравнения $x_1{1,2}=4;-1$, второе решений не имеет.
Решение возвратных уравнений 4 степени
Эти уравнения вида $ax^4+bx^3+cx^2 +bx+ a=0$ повторяют своими коэффициентами при младших членах коэффициенты при многочленах со старшими степенями. Для решения такого уравнения сначала делят его на $x^2$:
$ax^4+bx^3+cx^2 +bx+ a=0|:x^2$
$ax^2+bx+c+\frac{b}{x} + \frac{a}{x^2}=0$
$a(x^2+\frac{1}{x^2})+b(x+\frac{1}{x}) + c=0$
Затем заменяют $(x+\frac{1}{x})$ на новую переменную, тогда $(x^2+\frac{1}{x^2})=y^2-2$, после подстановки получаем следующее квадратное уравнение:
$a(y^2-2)+by+c=0$
После этого ищем корни уравнений $x+\frac{1}{x}=y_1$ и $x+\frac{1}{x}=y_2$.
Аналогичным методом решаются возвратные уравнения вида $ax^4+bx^3+cx^2 +kbx+ k^2a=0$.
Пример 2
Решите уравнение:
$3x^4-2x^3-9x^2-4x+12=0$
Данное уравнение – возвратное уравнение вида $ax^4+bx^3+cx^2 +kbx+ k^2a=0$. Поэтому разделим всё уравнение на $x^2$:
$3x^2-2x-9 \cdot \frac{2 \cdot 2}{x}+3 \cdot (\frac{2}{x})^2=0$
$3(x^2+\frac{4}{x^2})-2(x+\frac{2}{x}-9=0$
Произведём замену выражения $x+\frac{2}{x}$: $3(y^2-4)-2y-9=0$
Рассчитаем корни данного уравнения, они равны $y_1=3$ и $y_2=-\frac{7}{3}$.
Соответственно, теперь необходимо решить два уравнения $x+\frac{2}{x}=3$ и $x+\frac{2}{x}=-\frac{7}{3}$. Решение первого уравнения - $x_1=1, x_2=2$, второе уравнение не имеет корней.
Следовательно, корнями исходного уравнения являются $x_1=1, x_2=2$.
Уравнения вида $ax^4+b=0$
Корни уравнения такой разновидности находятся с помощью применения формул сокращённого умножения.
Вскоре после того, как Кардано опубликовал способ решения кубических уравнений, его ученики и последователи нашли способы сведения общего уравнения четвертой степени к кубическому уравнению. Изложим наиболее простой способ, принадлежащий Л. Феррари.
При изложении способа нужно будет воспользоваться следующей элементарной леммой.
Лемма. Для того чтобы квадратный трехчлен был квадратом линейного двучлена, необходимо и достаточно, чтобы его дискриминант равнялся нулю.
Доказательство. Необходимость. Пусть . Тогда Достаточность. Пусть Тогда
Идея излагаемого способа состоит в том, чтобы представить левую часть уравнения в виде разности двух квадратов. Тогда ее можно будет разложить на два множителя второй степени, и решение уравнения приведется к решению двух квадратных уравнений. Для достижения цели левую часть представим в виде:
Здесь у - вспомогательная неизвестная, которую нужно подобрать так, чтобы выражение в квадратных скобках оказалось квадратом линейного двучлена. В силу леммы для этого необходимо и достаточно выполнения условия
Это условие есть уравнение третьей степени относительно у. После раскрытия скобок оно преобразуется к виду
Пусть - один из корней этого уравнения. Тогда при условие будет выполнено, так что имеет место
при некоторых k и I. Исходное уравнение примет вид
Приравнивая нулю каждый из сомножителей, мы найдем четыре корня исходного уравнения.
Сделаем еще одно замечание. Пусть - корни первого сомножителя, и - корни второго. Тогда Сложив эти равенства, получим, что
Таким образом, мы получили выражение корня вспомогательного кубического уравнения через корни исходного уравнения четвертой степени.
Пример. Решить уравнение . Согласно изложенному выше методу преобразуем левую часть:
Теперь положим . После образований получим уравнение
Легко видеть, что одним из корней этого уравнения является число . Подставив его в преобразованную левую часть исходного уравнения, получим:
Приравнивая сомножители нулю, получим
Что касается уравнений выше четвертой степени, то здесь были известны некоторые классы уравнений сравнительно частного вида, допускающих алгебраические решения в радикалах, т. е. в виде результатов арифметических действий и действия извлечения корня. Однако попытки дать решение общих уравнений пятой степени и выше были безуспешны, пока, наконец, в начале 19 в. Руффини и Абель не доказали, что решение такого рода для общих уравнений выше четвертой степени невозможно. Наконец, в 1830 г. гениальному французскому математику Э. Галуа удалось найти необходимые и достаточные условия (проверяемые довольно сложно) для разрешимости в радикалах конкретно заданного уравнения. При этом Галуа создал и использовал новую для своего времени теорию групп подстановок.
2x 4 + 5x 3 - 11x 2 - 20x + 12 = 0
Для начала нужно методом подбора найти один корень. Обычно он является делителем свободного члена. В данном случае делителями числа 12 являются ±1, ±2, ±3, ±4, ±6, ±12. Начнем их подставлять по-очереди:
1: 2 + 5 - 11 - 20 + 12 = -12 ⇒ число 1
-1: 2 - 5 - 11 + 20 + 12 = 18 ⇒ число -1 не является корнем многочлена
2: 2 ∙ 16 + 5 ∙ 8 - 11 ∙ 4 - 20 ∙ 2 + 12 = 0 ⇒ число 2 является корнем многочлена
Мы нашли 1 из корней многочлена. Корнем многочлена является 2, а значит исходный многочлен должен делиться на x - 2 . Для того, чтобы выполнить деление многочленов, воспользуемся схемой Горнера:
| 2 | 5 | -11 | -20 | 12 | |
| 2 |
В верхней строке выставляются коэффициенты исходного многочлена. В первой ячейке второй строки ставится найденный нами корень 2. Во второй строке пишутся коэффициенты многочлена, который получится в результате деления. Они считаются так:
| Во вторую ячейку второй строки запишем число 2, просто перенеся его из соответствующей ячейки первой строки. | ||||||||||||
| 2 ∙ 2 + 5 = 9 | ||||||||||||
| 2 ∙ 9 - 11 = 7 | ||||||||||||
| 2 ∙ 7 - 20 = -6 | ||||||||||||
| 2 ∙ (-6) + 12 = 0 |
Последнее число - это остаток от деления. Если он равен 0, значит мы все верно посчитали.
2x 4 + 5x 3 - 11x 2 - 20x + 12 = (x - 2)(2x 3 + 9x 2 + 7x - 6)
Но это еще не конец. Можно попробовать разложить таким же способом многочлен 2x 3 + 9x 2 + 7x - 6.
Опять ищем корень среди делителей свободного члена. Делителями числа -6 являются ±1, ±2, ±3, ±6.
1: 2 + 9 + 7 - 6 = 12 ⇒ число 1 не является корнем многочлена
-1: -2 + 9 - 7 - 6 = -6 ⇒ число -1 не является корнем многочлена
2: 2 ∙ 8 + 9 ∙ 4 + 7 ∙ 2 - 6 = 60 ⇒ число 2 не является корнем многочлена
-2: 2 ∙ (-8) + 9 ∙ 4 + 7 ∙ (-2) - 6 = 0 ⇒ число -2 является корнем многочлена
Напишем найденный корень в нашу схему Горнера и начнем заполнять пустые ячейки:
| Во вторую ячейку третьей строки запишем число 2, просто перенеся его из соответствующей ячейки второй строки. | ||||||||||||||||||
| -2 ∙ 2 + 9 = 5 | ||||||||||||||||||
| -2 ∙ 5 + 7 = -3 | ||||||||||||||||||
| -2 ∙ (-3) - 6 = 0 |
Таким образом мы исходный многочлен разложили на множители:
2x 4 + 5x 3 - 11x 2 - 20x + 12 = (x - 2)(x + 2)(2x 2 + 5x - 3)
Многочлен 2x 2 + 5x - 3 тоже можно разложить на множители. Для этого можно решить квадратное уравнение через дискриминант , а можно поискать корень среди делителей числа -3. Так или иначе, мы придем к выводу, что корнем этого многочлена является число -3
| Во вторую ячейку четвертой строки запишем число 2, просто перенеся его из соответствующей ячейки третьей строки. | ||||||||||||||||||||||||
| -3 ∙ 2 + 5 = -1 | ||||||||||||||||||||||||
| -3 ∙ (-1) - 3 = 0 |
Таким образом мы исходный многочлен разложили на линейные множители.
