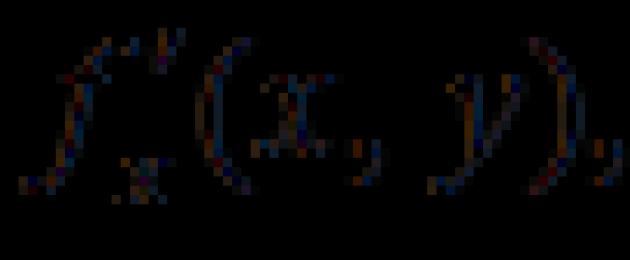Considere una función de dos variables:
Como las variables $x$ y $y$ son independientes, podemos introducir el concepto de derivada parcial para tal función:
La derivada parcial de la función $f$ en el punto $M=\left(((x)_(0));((y)_(0)) \right)$ con respecto a la variable $x$ es el límite
\[(((f)")_(x))=\underset(\Delta x\to 0)(\mahop(\lim ))\,\frac(f\left(((x)_(0) )+\Delta x;((y)_(0)) \right))(\Delta x)\]
De manera similar, podemos definir la derivada parcial con respecto a la variable $y$ :
\[(((f)")_(y))=\underset(\Delta y\to 0)(\mahop(\lim ))\,\frac(f\left(((x)_(0) );((y)_(0))+\Delta y \right))(\Delta y)\]
En otras palabras, para encontrar la derivada parcial de una función de varias variables, debe fijar todas las demás variables excepto la deseada y luego encontrar la derivada ordinaria con respecto a esta variable deseada.
De aquí se sigue la técnica principal para calcular tales derivadas: simplemente considere que todas las variables, excepto la dada, son constantes, y luego diferencie la función como diferenciaría la función "ordinaria", con una variable. Por ejemplo:
$\begin(alinear)& ((\left(((x)^(2))+10xy \right))_(x))^(\prime )=((\left(((x)^(2 )) \right))^(\prime ))_(x)+10y\cdot ((\left(x \right))^(\prime ))_(x)=2x+10y, \\& (( \left(((x)^(2))+10xy \right))_(y))^(\prime )=((\left(((x)^(2)) \right))^(\ prime ))_(y)+10x\cdot ((\left(y \right))^(\prime ))_(y)=0+10x=10x. \\\end(alinear)$
Obviamente, las derivadas parciales con respecto a diferentes variables dan respuestas diferentes; esto es normal. Es mucho más importante entender por qué, digamos, en el primer caso, quitamos tranquilamente $10y$ de debajo del signo de la derivada, y en el segundo caso, anulamos completamente el primer término. Todo esto se debe a que todas las letras, excepto la variable por la que se realiza la diferenciación, se consideran constantes: se pueden sacar, "quemar", etc.
¿Qué es una "derivada parcial"?
Hoy hablaremos de funciones de varias variables y sus derivadas parciales. Primero, ¿qué es una función de múltiples variables? Hasta ahora, nos hemos acostumbrado a pensar en una función como $y\left(x \right)$ o $t\left(x \right)$, o cualquier variable y una sola función a partir de ella. Ahora tendremos una función y varias variables. Cuando $y$ y $x$ cambian, el valor de la función cambiará. Por ejemplo, si $x$ se duplica, el valor de la función cambiará, mientras que si $x$ cambia y $y$ no cambia, el valor de la función cambiará de la misma manera.
Por supuesto, una función de varias variables, al igual que una función de una variable, se puede derivar. Sin embargo, dado que hay varias variables, es posible diferenciar según diferentes variables. En este caso surgen reglas específicas que no existían al diferenciar una variable.
En primer lugar, cuando consideramos la derivada de una función de cualquier variable, debemos indicar de qué variable consideramos la derivada; esto se llama derivada parcial. Por ejemplo, tenemos una función de dos variables, y podemos calcularla tanto en $x$ como en $y$, dos derivadas parciales de cada una de las variables.
En segundo lugar, en cuanto hayamos fijado una de las variables y empecemos a calcular la derivada parcial con respecto a ella, todas las demás incluidas en esta función se considerarán constantes. Por ejemplo, en $z\left(xy \right)$, si consideramos la derivada parcial con respecto a $x$, entonces donde sea que encontremos $y$, la consideramos una constante y la tratamos exactamente como una constante. En particular, al calcular la derivada de un producto, podemos sacar $y$ del paréntesis (tenemos una constante), y al calcular la derivada de la suma, si obtenemos en alguna parte la derivada de una expresión que contiene $y$ y no contiene $x$, entonces la derivada de esta expresión será igual a "cero" como la derivada de la constante.
A primera vista, puede parecer que estoy hablando de algo complejo y muchos estudiantes se confunden al principio. Sin embargo, no hay nada sobrenatural en las derivadas parciales, y ahora lo veremos en el ejemplo de problemas específicos.
Problemas con radicales y polinomios
Tarea 1
Para no perder el tiempo en vano, desde el principio comenzaremos con ejemplos serios.
Permítanme comenzar con la siguiente fórmula:
Este es el valor de tabla estándar que conocemos del curso estándar.
En este caso, la derivada $z$ se calcula de la siguiente manera:
\[(((z)")_(x))=((\left(\sqrt(\frac(y)(x)) \right))^(\prime ))_(x)=\frac( 1)(2\sqrt(\frac(y)(x)))((\left(\frac(y)(x) \right))^(\prime ))_(x)\]
Repitamos, dado que la raíz no es $x$, sino alguna otra expresión, en este caso $\frac(y)(x)$, primero usaremos el valor estándar de la tabla, y luego, dado que la raíz no es $ x $ y otra expresión, necesitamos multiplicar nuestra derivada por una más de esta expresión con respecto a la misma variable. Comencemos con lo siguiente:
\[((\left(\frac(y)(x) \right))^(\prime )))_(x)=\frac(((((y)"))_(x))\cdot xy \cdot ((((x)"))_(x)))(((x)^(2)))=\frac(0\cdot xy\cdot 1)(((x)^(2)) )=-\frac(y)(((x)^(2)))\]
Volvemos a nuestra expresión y escribimos:
\[(((z)")_(x))=((\left(\sqrt(\frac(y)(x)) \right))^(\prime ))_(x)=\frac( 1)(2\sqrt(\frac(y)(x)))((\left(\frac(y)(x) \right))^(\prime ))_(x)=\frac(1) (2\sqrt(\frac(y)(x)))\cdot \left(-\frac(y)(((x)^(2))) \right)\]
Básicamente, eso es todo. Sin embargo, es incorrecto dejarlo en esta forma: tal construcción es inconveniente de usar para cálculos posteriores, así que transformémoslo un poco:
\[\frac(1)(2\sqrt(\frac(y)(x)))\cdot \left(-\frac(y)(((x)^(2))) \right)=\frac (1)(2)\cdot \sqrt(\frac(x)(y))\cdot \frac(y)(((x)^(2)))=\]
\[=-\frac(1)(2)\cdot \sqrt(\frac(x)(y))\cdot \sqrt(\frac(((y)^(2)))(((x)^ (4))))=-\frac(1)(2)\sqrt(\frac(x\cdot ((y)^(2)))(y\cdot ((x)^(4)))) =-\frac(1)(2)\sqrt(\frac(y)(((x)^(3))))\]
Respuesta encontrada. Ahora tratemos con $y$:
\[(((z)")_(y))=((\left(\sqrt(\frac(y)(x)) \right))^(\prime ))_(y)=\frac( 1)(2\sqrt(\frac(y)(x)))\cdot ((\left(\frac(y)(x) \right))^(\prime ))_(y)\]
Escribamos por separado:
\[((\left(\frac(y)(x) \right))^(\prime )))_(y)=\frac(((((y)"))_(y))\cdot xy \cdot ((((x)"))_(y)))(((x)^(2)))=\frac(1\cdot xy\cdot 0)(((x)^(2)) )=\frac(1)(x)\]
Ahora escribimos:
\[(((z)")_(y))=((\left(\sqrt(\frac(y)(x)) \right))^(\prime ))_(y)=\frac( 1)(2\sqrt(\frac(y)(x)))\cdot ((\left(\frac(y)(x) \right))^(\prime ))_(y)=\frac( 1)(2\sqrt(\frac(y)(x)))\cdot \frac(1)(x)=\]
\[=\frac(1)(2)\cdot \sqrt(\frac(x)(y))\cdot \sqrt(\frac(1)(((x)^(2))))=\frac (1)(2)\sqrt(\frac(x)(y\cdot ((x)^(2))))=\frac(1)(2\sqrt(xy))\]
Hecho.
Tarea 2
Este ejemplo es más simple y más complejo que el anterior. Más difícil, porque hay más acciones, pero más fácil, porque no hay raíz y, además, la función es simétrica con respecto a $x$ y $y$, es decir si intercambiamos $x$ y $y$, la fórmula no cambia. Esta observación simplificará aún más el cálculo de la derivada parcial, es decir basta con calcular uno de ellos, y en el segundo intercambiar $x$ y $y$.
Vamos a ir al grano:
\[(((z)")_(x))=((\left(\frac(xy)(((x)^(2))+((y)^(2))+1) \right ))^(\prime ))_(x)=\frac(((\left(xy \right))^(\prime )))_(x)\left(((x)^(2))+( (y)^(2))+1 \right)-xy((\left(((x)^(2))+((y)^(2))+1 \right))^(\prime ) )_(x))(((\izquierda(((x)^(2))+((y)^(2))+1 \derecha))^(2)))\]
Contemos:
\[((\left(xy \right))^(\prime ))_(x)=y\cdot ((\left(x \right))^(\prime ))=y\cdot 1=y\ ]
Sin embargo, muchos estudiantes no entienden tal registro, por lo que lo escribimos así:
\[((\left(xy \right))^(\prime ))_(x)=((\left(x \right))^(\prime ))_(x)\cdot y+x\cdot ((\left(y \right))^(\prime ))_(x)=1\cdot y+x\cdot 0=y\]
Así, volvemos a estar convencidos de la universalidad del algoritmo de derivadas parciales: no importa cómo las consideremos, si todas las reglas se aplican correctamente, la respuesta será la misma.
Ahora tratemos con una derivada parcial más de nuestra gran fórmula:
\[((\left(((x)^(2))+((y)^(2))+1 \right))^(\prime ))_(x)=((\left((( x)^(2)) \right))^(\prime ))_(x)+((\left(((y)^(2)) \right))^(\prime ))_(x) +(((1)")_(x))=2x+0+0\]
Sustituimos las expresiones resultantes en nuestra fórmula y obtenemos:
\[\frac(((\left(xy \right))^(\prime ))_(x)\left(((x)^(2))+((y)^(2))+1 \ derecha)-xy((\left(((x)^(2))+((y)^(2))+1 \right))^(\prime ))_(x))(((\left (((x)^(2))+((y)^(2))+1 \derecho))^(2)))=\]
\[=\frac(y\cdot \left(((x)^(2))+((y)^(2))+1 \right)-xy\cdot 2x)(((\left((( x)^(2))+((y)^(2))+1 \right))^(2)))=\]
\[=\frac(y\left(((x)^(2))+((y)^(2))+1-2((x)^(2)) \right))(((\ izquierda (((x)^(2))+((y)^(2))+1 \derecha))^(2)))=\frac(y\izquierda(((y)^(2)) -((x)^(2))+1 \right))(((\left(((x)^(2))+((y)^(2))+1 \right))^(2 )))\]
$x$ contados. Y para calcular $y$ a partir de la misma expresión, no realicemos la misma secuencia de acciones, sino que usemos la simetría de nuestra expresión original: simplemente reemplazamos todos los $y$ en nuestra expresión original con $x$ y viceversa:
\[(((z)")_(y))=\frac(x\left(((x)^(2))-((y)^(2))+1 \right))((( \izquierda(((x)^(2))+((y)^(2))+1 \derecha))^(2)))\]
Debido a la simetría, calculamos esta expresión mucho más rápido.
Matices de la solución.
Para las derivadas parciales funcionan todas las fórmulas estándar que usamos para las ordinarias, a saber, la derivada de la privada. En este caso, sin embargo, surgen sus propias características específicas: si consideramos la derivada parcial de $x$, entonces cuando la obtenemos de $x$, la consideramos como una constante y, por lo tanto, su derivada será igual a " cero".
Como en el caso de las derivadas ordinarias, el cociente (el mismo) se puede calcular de varias formas diferentes. Por ejemplo, la misma construcción que acabamos de calcular se puede reescribir de la siguiente manera:
\[((\left(\frac(y)(x) \right))^(\prime ))_(x)=y\cdot ((\left(\frac(1)(x) \right)) ^(\primo))_(x)=-y\frac(1)(((x)^(2)))\]
\[((\left(xy \right))^(\prime ))_(x)=y\cdot (((x)")_(x))=y\cdot 1=y\]
Sin embargo, por otro lado, puede usar la fórmula de la suma derivada. Como sabemos, es igual a la suma de derivadas. Por ejemplo, escribamos lo siguiente:
\[((\left(((x)^(2))+((y)^(2))+1 \right))^(\prime ))_(x)=2x+0+0=2x \]
Ahora, sabiendo todo esto, intentemos trabajar con expresiones más serias, ya que las derivadas parciales reales no se limitan solo a polinomios y raíces: hay trigonometría, y logaritmos, y una función exponencial. Ahora hagamos esto.
Problemas con funciones trigonométricas y logaritmos
Tarea 1
Escribimos las siguientes fórmulas estándar:
\[((\left(\sqrt(x) \right))^(\prime ))_(x)=\frac(1)(2\sqrt(x))\]
\[((\left(\cos x \right))^(\prime ))_(x)=-\sin x\]
Armados con este conocimiento, intentemos resolver:
\[(((z)")_(x))=((\left(\sqrt(x)\cdot \cos \frac(x)(y) \right))^(\prime ))_(x )=((\left(\sqrt(x) \right))^(\prime ))_(x)\cdot \cos \frac(x)(y)+\sqrt(x)\cdot ((\left (\cos \frac(x)(y) \right))^(\prime ))_(x)=\]
Escribamos una variable por separado:
\[((\left(\cos \frac(x)(y) \right))^(\prime ))_(x)=-\sin \frac(x)(y)\cdot ((\left( \frac(x)(y) \right))^(\prime ))_(x)=-\frac(1)(y)\cdot \sin \frac(x)(y)\]
Volvamos a nuestro diseño:
\[=\frac(1)(2\sqrt(x))\cdot \cos \frac(x)(y)+\sqrt(x)\cdot \left(-\frac(1)(y)\cdot \sin \frac(x)(y) \right)=\frac(1)(2\sqrt(x))\cdot \cos \frac(x)(y)-\frac(\sqrt(x))( y)\cdot\sin\frac(x)(y)\]
Hemos encontrado todo para $x$, ahora hagamos los cálculos para $y$:
\[(((z)")_(y))=((\left(\sqrt(x)\cdot \cos \frac(x)(y) \right))^(\prime ))_(y )=((\left(\sqrt(x) \right))^(\prime ))_(y)\cdot \cos \frac(x)(y)+\sqrt(x)\cdot ((\left (\cos \frac(x)(y) \right))^(\prime ))_(y)=\]
Nuevamente, considere una expresión:
\[((\left(\cos \frac(x)(y) \right))^(\prime ))_(y)=-\sin \frac(x)(y)\cdot ((\left( \frac(x)(y) \right))^(\prime ))_(y)=-\sin \frac(x)(y)\cdot x\cdot \left(-\frac(1)(( (y)^(2))) \derecha)\]
Volvemos a la expresión original y continuamos la solución:
\[=0\cdot \cos \frac(x)(y)+\sqrt(x)\cdot \frac(x)(((y)^(2)))\sin \frac(x)(y) =\frac(x\sqrt(x))(((y)^(2)))\cdot \sin \frac(x)(y)\]
Hecho.
Tarea 2
Escribamos la fórmula que necesitamos:
\[((\left(\ln x \right))^(\prime ))_(x)=\frac(1)(x)\]
Ahora vamos a contar por $x$:
\[(((z)")_(x))=((\left(\ln \left(x+\ln y \right) \right))^(\prime ))_(x)=\frac( 1)(x+\ln y).((\left(x+\ln y \right))^(\prime ))_(x)=\]
\[=\frac(1)(x+\ln y)\cdot \left(1+0 \right)=\frac(1)(x+\ln y)\]
Encontrado por $x$. Contando por $y$:
\[(((z)")_(y))=((\left(\ln \left(x+\ln y \right) \right))^(\prime ))_(y)=\frac( 1)(x+\ln y).((\left(x+\ln y \right))^(\prime ))_(y)=\]
\[=\frac(1)(x+\ln y)\left(0+\frac(1)(y) \right)=\frac(1)(y\left(x+\ln y \right))\ ]
Problema resuelto.
Matices de la solución.
Entonces, no importa de qué función saquemos una derivada parcial, las reglas siguen siendo las mismas, sin importar si estamos trabajando con trigonometría, con raíces o con logaritmos.
Las reglas clásicas para trabajar con derivadas estándar permanecen sin cambios, a saber, la derivada de la suma y la diferencia, el cociente y la función compleja.
La última fórmula se encuentra con mayor frecuencia en la resolución de problemas con derivadas parciales. Los encontramos en casi todas partes. Todavía no ha habido una sola tarea que no nos hayamos encontrado allí. Pero no importa qué fórmula usemos, aún agregamos un requisito más, a saber, la característica de trabajar con derivadas parciales. Tan pronto como fijamos una variable, todas las demás son constantes. En particular, si consideramos la derivada parcial de la expresión $\cos \frac(x)(y)$ con respecto a $y$, entonces $y$ es la variable, y $x$ permanece constante en todas partes. Lo mismo funciona al revés. Se puede sacar del signo de la derivada, y la derivada de la constante misma será igual a "cero".
Todo esto lleva al hecho de que las derivadas parciales de la misma expresión, pero con respecto a diferentes variables, pueden verse completamente diferentes. Por ejemplo, considere las siguientes expresiones:
\[((\left(x+\ln y \right))^(\prime ))_(x)=1+0=1\]
\[((\left(x+\ln y \right))^(\prime ))_(y)=0+\frac(1)(y)=\frac(1)(y)\]
Problemas con funciones exponenciales y logaritmos
Tarea 1
Comencemos escribiendo la siguiente fórmula:
\[((\left(((e)^(x)) \right))^(\prime ))_(x)=((e)^(x))\]
Conociendo este hecho, así como la derivada de una función compleja, intentemos calcular. Ahora voy a resolver de dos maneras diferentes. La primera y más obvia es la derivada del producto:
\[(((z)")_(x))=((\left(((e)^(x))\cdot ((e)^(\frac(x)(y))) \right) )^(\prime ))_(x)=((\left(((e)^(x)) \right))^(\prime ))_(x)\cdot ((e)^(\frac (x)(y)))+((e)^(x))\cdot ((\left(((e)^(\frac(x)(y))) \right))^(\prime ) )_(x)=\]
\[=((e)^(x))\cdot ((e)^(\frac(x)(y)))+((e)^(x))\cdot ((e)^(\frac (x)(y)))\cdot ((\left(\frac(x)(y) \right))^(\prime ))_(x)=\]
Resolvamos la siguiente expresión por separado:
\[((\left(\frac(x)(y) \right))^(\prime ))_(x)=\frac(((((x)"))_(x))\cdot yx .((((y)"))_(x)))(((y)^(2)))=\frac(1\cdot yx\cdot 0)(((y)^(2))) =\frac(y)(((y)^(2)))=\frac(1)(y)\]
Volvemos a nuestro diseño original y continuamos con la solución:
\[=((e)^(x))\cdot ((e)^(\frac(x)(y)))+((e)^(x))\cdot ((e)^(\frac (x)(y)))\cdot \frac(1)(y)=((e)^(x))\cdot ((e)^(\frac(x)(y)))\left(1 +\frac(1)(y)\derecha)\]
Todo, $x$ contado.
Sin embargo, como prometí, ahora intentaremos calcular la misma derivada parcial de otra manera. Para hacer esto, tenga en cuenta lo siguiente:
\[((e)^(x))\cdot ((e)^(\frac(x)(y)))=((e)^(x+\frac(x)(y)))\]
Escribámoslo así:
\[((\left(((e)^(x))\cdot ((e)^(\frac(x)(y))) \right))^(\prime ))_(x)=( (\left(((e)^(x+\frac(x)(y))) \right))^(\prime ))_(x)=((e)^(x+\frac(x)(y) )))\cdot ((\left(x+\frac(x)(y) \right))^(\prime ))_(x)=((e)^(x+\frac(x)(y)) )\cdot \left(1+\frac(1)(y) \right)\]
Como resultado, obtuvimos exactamente la misma respuesta, pero la cantidad de cálculos resultó ser menor. Para ello, bastó notar que cuando se multiplica el producto, se pueden sumar los exponentes.
Ahora vamos a contar por $y$:
\[(((z)")_(y))=((\left(((e)^(x))\cdot ((e)^(\frac(x)(y))) \right) )^(\prime ))_(y)=((\left(((e)^(x)) \right))^(\prime ))_(y)\cdot ((e)^(\frac (x)(y)))+((e)^(x))\cdot ((\left(((e)^(\frac(x)(y))) \right))^(\prime ) )_(y)=\]
\[=0\cdot ((e)^(\frac(x)(y)))+((e)^(x))\cdot ((e)^(\frac(x)(y))) \cdot ((\left(\frac(x)(y) \right))^(\prime ))_(y)=\]
Resolvamos una expresión por separado:
\[((\left(\frac(x)(y) \right))^(\prime )))_(y)=\frac(((((x)"))_(y))\cdot yx \cdot ((((y)"))_(y)))(((y)^(2)))=\frac(0-x\cdot 1)(((y)^(2))) =-\frac(1)(((y)^(2)))=-\frac(x)(((y)^(2)))\]
Continuemos con la solución de nuestra construcción original:
\[=((e)^(x))\cdot ((e)^(\frac(x)(y)))\cdot \left(-\frac(x)(((y)^(2) )) \right)=-\frac(x)(((y)^(2)))\cdot ((e)^(x))\cdot ((e)^(\frac(x)(y) ))\]
Por supuesto, la misma derivada podría calcularse de la segunda manera, la respuesta sería la misma.
Tarea 2
Contemos por $x$:
\[(((z)")_(x))=((\left(x \right))_(x))\cdot \ln \left(((x)^(2))+y \right )+x\cdot ((\left(\ln \left(((x)^(2))+y \right) \right))^(\prime ))_(x)=\]
Contemos una expresión por separado:
\[((\left(\ln \left(((x)^(2))+y \right) \right))^(\prime ))_(x)=\frac(1)(((x )^(2))+y)\cdot ((\left(((x)^(2))+y \right))^(\prime ))_(x)=\frac(2x)((( x)^(2))+y)\]
Sigamos con la solución de la construcción original: $$
Aquí está la respuesta.
Queda por encontrar por analogía por $y$:
\[(((z)")_(y))=((\left(x \right))^(\prime ))_(y).\ln \left(((x)^(2)) +y \right)+x\cdot ((\left(\ln \left(((x)^(2))+y \right) \right))^(\prime ))_(y)=\]
Contemos una expresión por separado como siempre:
\[((\left(((x)^(2))+y \right))^(\prime ))_(y)=((\left(((x)^(2)) \right) )^(\principal))_(y)+(((y)")_(y))=0+1=1\]
Continuamos la solución de la estructura principal:
Todo está contado. Como puede ver, dependiendo de qué variable se tome para la diferenciación, las respuestas son completamente diferentes.
Matices de la solución.
Aquí hay un vívido ejemplo de cómo la derivada de la misma función se puede calcular de dos maneras diferentes. Mira aquí:
\[(((z)")_(x))=\left(((e)^(x))\cdot ((e)^(\frac(x)(y))) \right)=( (\left(((e)^(x)) \right))^(\prime ))_(x)\cdot ((e)^(\frac(x)(y)))+((e) ^(x))\cdot ((\left(((e)^(\frac(x)(y))) \right))^(\prime ))_(x)=\]
\[=((e)^(x))\cdot ((e)^(\frac(x)(y)))+((e)^(x))\cdot ((e)^(\frac (x)(y)))\cdot \frac(1)(y)=((e)^(x))\cdot ((e)^(^(\frac(x)(y))))\ izquierda(1+\frac(1)(y)\derecha)\]
\[(((z)")_(x))=((\left(((e)^(x)).((e)^(\frac(x)(y))) \right)) ^(\prime ))_(x)=((\left(((e)^(x+\frac(x)(y))) \right))^(\prime ))_(x)=(( e)^(x+\frac(x)(y))).((\left(x+\frac(x)(y) \right))^(\prime ))_(x)=\]
\[=((e)^(x))\cdot ((e)^(^(\frac(x)(y))))\left(1+\frac(1)(y) \right)\ ]
Al elegir diferentes caminos, la cantidad de cálculos puede ser diferente, pero la respuesta, si todo se hace correctamente, será la misma. Esto se aplica tanto a las derivadas clásicas como a las parciales. Al mismo tiempo, les recuerdo una vez más: dependiendo de qué variable se toma la derivada, es decir diferenciación, la respuesta puede ser completamente diferente. Mirar:
\[((\left(\ln \left(((x)^(2))+y \right) \right))^(\prime ))_(x)=\frac(1)(((x )^(2))+y)\cdot ((\left(((x)^(2))+y \right))^(\prime ))_(x)=\frac(1)((( x)^(2))+y)\cdot 2x\]
\[((\left(\ln \left(((x)^(2))+y \right) \right))^(\prime ))_(y)=\frac(1)(((x )^(2))+y)\cdot ((\left(((x)^(2))+y \right))^(\prime ))_(y)=\frac(1)((( x)^(2))+y)\cpunto 1\]
En conclusión, para consolidar todo este material, intentemos contar dos ejemplos más.
Problemas con una función trigonométrica y una función de tres variables
Tarea 1
Escribamos estas fórmulas:
\[((\left(((a)^(x)) \right))^(\prime ))=((a)^(x))\cdot \ln a\]
\[((\left(((e)^(x)) \right))^(\prime ))=((e)^(x))\]
Ahora resolvamos nuestra expresión:
\[(((z)")_(x))=((\left(((3)^(x\sen y)) \right))^(\prime ))_(x)=((3 )^(x.\sin y))\cdot \ln 3\cdot ((\left(x\cdot \sin y \right))^(\prime ))_(x)=\]
Por separado, considere la siguiente construcción:
\[((\left(x\cdot \sin y \right))^(\prime ))_(x)=(((x)")_(x))\cdot \sin y+x((\ izquierda(\sin y \right))^(\prime ))_(x)=1\cdot \sin y+x\cdot 0=\sin y\]
Seguimos resolviendo la expresión original:
\[=((3)^(x\sin y))\cdot \ln 3\cdot \sin y\]
Esta es la respuesta final de la variable privada en $x$. Ahora vamos a contar por $y$:
\[(((z)")_(y))=((\left(((3)^(x\sen y)) \right))^(\prime ))_(y)=((3 )^(x\sin y))\cdot \ln 3\cdot ((\left(x\sin y \right))^(\prime ))_(y)=\]
Resolvamos una expresión por separado:
\[((\left(x\cdot \sin y \right))^(\prime ))_(y)=(((x)")_(y))\cdot \sin y+x((\ izquierda(\sin y \right))^(\prime ))_(y)=0\cdot \sin y+x\cdot \cos y=x\cdot \cos y\]
Resolvemos nuestra construcción hasta el final:
\[=((3)^(x\cdot \sin y))\cdot \ln 3\cdot x\cos y\]
Tarea 2
A primera vista, este ejemplo puede parecer bastante complicado, porque hay tres variables. De hecho, esta es una de las tareas más fáciles del video tutorial de hoy.
Buscar por $x$:
\[(((t)")_(x))=((\left(x((e)^(y))+y((e)^(z)) \right))^(\prime ) )_(x)=((\left(x\cdot ((e)^(y)) \right))^(\prime ))_(x)+((\left(y\cdot ((e) ^(z)) \right))^(\prime ))_(x)=\]
\[=((\left(x \right))^(\prime ))_(x)\cdot ((e)^(y))+x\cdot ((\left(((e)^(y )) \right))^(\prime ))_(x)=1\cdot ((e)^(y))+x\cdot o=((e)^(y))\]
Ahora tratemos con $y$:
\[(((t)")_(y))=((\left(x\cdot ((e)^(y))+y\cdot ((e)^(z)) \right))^ (\prime ))_(y)=((\left(x\cdot ((e)^(y)) \right))^(\prime ))_(y)+((\left(y\cdot ((e)^(z)) \right))^(\prime ))_(y)=\]
\[=x\cdot ((\left(((e)^(y)) \right))^(\prime ))_(y)+((e)^(z))\cdot ((\left (y \right))^(\prime ))_(y)=x\cdot ((e)^(y))+((e)^(z))\]
Hemos encontrado la respuesta.
Ahora queda encontrar por $z$:
\[(((t)")_(z))=((\left(x\cdot ((e)^(y))+((y)^(z)) \right))^(\prime ))_(z)=((\left(x\cdot ((e)^(y)) \right))^(\prime ))_(z)+((\left(y\cdot ((e )^(z)) \right))^(\prime ))_(z)=0+y\cdot ((\left(((e)^(z)) \right))^(\prime )) _(z)=y\cdot ((e)^(z))\]
Hemos calculado la tercera derivada, sobre la cual se completa por completo la solución del segundo problema.
Matices de la solución.
Como puede ver, no hay nada complicado en estos dos ejemplos. Lo único que hemos visto es que la derivada de una función compleja se usa con frecuencia, y dependiendo de qué derivada parcial consideremos, obtenemos diferentes respuestas.
En la última tarea, se nos pidió que tratáramos con una función de tres variables a la vez. No hay nada de malo en esto, pero al final nos aseguramos de que todos difieran significativamente entre sí.
Puntos clave
Las conclusiones finales del videotutorial de hoy son las siguientes:
- Las derivadas parciales se consideran de la misma forma que las ordinarias, mientras que para calcular la derivada parcial con respecto a una variable, todas las demás variables incluidas en esta función, las tomamos como constantes.
- Cuando trabajamos con derivadas parciales, usamos todas las mismas fórmulas estándar que con las derivadas ordinarias: la suma, la diferencia, la derivada del producto y el cociente y, por supuesto, la derivada de una función compleja.
Por supuesto, ver este video tutorial por sí solo no es suficiente para comprender completamente este tema, por lo que ahora mismo en mi sitio web para este video en particular hay un conjunto de tareas dedicadas al tema de hoy: vaya, descargue, resuelva estas tareas y verifique la respuesta. Y después de eso, no hay problemas con las derivadas parciales ni en los exámenes ni en Trabajo independiente no lo harás Por supuesto, esta no es la última lección de matemáticas superiores, así que visite nuestro sitio web, agregue VKontakte, suscríbase a YouTube, ponga Me gusta y quédese con nosotros.
Sea dada una función de dos variables. Incrementemos el argumento y dejemos el argumento sin cambios. Entonces la función recibirá un incremento, que se llama incremento parcial con respecto a la variable y se denota:
De manera similar, al arreglar el argumento y darle un incremento, obtenemos un incremento parcial de la función con respecto a la variable:
El valor se llama el incremento completo de la función en el punto.
Definición 4. La derivada parcial de una función de dos variables con respecto a una de estas variables es el límite de la razón del incremento parcial correspondiente de la función al incremento de la variable dada cuando esta última tiende a cero (si este límite existe). La derivada parcial se denota como: o, o.
Así, por definición, tenemos:
Las derivadas parciales de una función se calculan según las mismas reglas y fórmulas que una función de una variable, teniendo en cuenta que al derivar con respecto a una variable se considera constante, y al derivar con respecto a una variable se considera constante.
Ejemplo 3. Hallar derivadas parciales de funciones:
Solución. a) Para encontrar asumimos un valor constante y diferenciamos en función de una variable:
De manera similar, asumiendo un valor constante, encontramos:

Definición 5. La diferencial total de una función es la suma de los productos de las derivadas parciales de esta función y los incrementos de las correspondientes variables independientes, es decir
Dado que los diferenciales de las variables independientes coinciden con sus incrementos, es decir , la fórmula para el diferencial total se puede escribir como

Ejemplo 4 Buscar diferencial total funciones

Solución. Dado que, entonces por la fórmula del diferencial total encontramos

Derivadas parciales de órdenes superiores
Las derivadas parciales también se denominan derivadas parciales de primer orden o primeras derivadas parciales.
Definición 6. Las derivadas parciales de segundo orden de una función son derivadas parciales de derivadas parciales de primer orden.
Hay cuatro derivadas parciales de segundo orden. Se designan de la siguiente manera:




Las derivadas parciales de orden 3, 4 y superiores se definen de manera similar. Por ejemplo, para una función tenemos:


Derivadas parciales de la segunda o más alto orden tomadas sobre diferentes variables se llaman derivadas parciales mixtas. Para una función, estos son derivados. Tenga en cuenta que en el caso de que las derivadas mixtas sean continuas, entonces se produce la igualdad.
Ejemplo 5. Hallar las derivadas parciales de segundo orden de una función
Solución. Las derivadas parciales de primer orden para esta función se encuentran en el ejemplo 3:
Derivando y con respecto a las variables x e y, obtenemos
Para resumir, cuál es la diferencia entre encontrar derivadas parciales y encontrar derivadas "ordinarias" de una función de una variable:
1) Cuando encontramos la derivada parcial, entonces variable considerado una constante.
2) Cuando encontramos la derivada parcial, entonces variable considerado una constante.
3) Las reglas y la tabla de funciones elementales derivadas son válidas y aplicables para cualquier variable ( , o alguna otra) respecto de la cual se realiza la diferenciación.
Segundo paso. Encontramos derivadas parciales de segundo orden. Hay cuatro de ellos.
Designaciones:
O - la segunda derivada con respecto a "X"
O - la segunda derivada con respecto a "y"
O - mezclado derivada "con respecto a x y"
O - mezclado derivada "con respecto a x"
No hay nada complicado en el concepto de la segunda derivada. hablando lenguaje simple, La segunda derivada es la derivada de la primera derivada.
Para mayor claridad, reescribiré las derivadas parciales de primer orden ya encontradas:
![]()
Primero encontramos las derivadas mixtas:
Como ves, todo es sencillo: sacamos la derivada parcial y la volvemos a derivar, pero en este caso ya por “y”.
Similar:
Para ejemplos prácticos, cuando todas las derivadas parciales son continuas, se cumple la siguiente igualdad:
Así, mediante derivadas mixtas de segundo orden, es muy conveniente comprobar si hemos hallado correctamente las derivadas parciales de primer orden.
Encontramos la segunda derivada con respecto a "x".
Sin inventos, tomamos ![]() y diferenciarlo por "X" de nuevo:
y diferenciarlo por "X" de nuevo:
Similar:
Cabe señalar que al encontrar , debe mostrar mayor atención, ya que no hay igualdades milagrosas que comprobar.
Ejemplo 2
Hallar derivadas parciales de primer y segundo orden de una función
Este es un ejemplo de auto-resolución (respuesta al final de la lección).
Con algo de experiencia, resolverás oralmente las derivadas parciales de los ejemplos No. 1, 2.
Pasemos a ejemplos más complejos.
Ejemplo 3
Mira esto . Escriba la diferencial total de primer orden.
Solución: Encontramos derivadas parciales de primer orden:

Preste atención al subíndice: al lado de la "x" no está prohibido escribir entre paréntesis que es una constante. Esta marca puede ser muy útil para los principiantes para facilitar la navegación por la solución.
Más comentarios:
(1) Sacamos todas las constantes fuera del signo de la derivada. En este caso, y , y, por lo tanto, su producto se considera un número constante.
(2) No olvides cómo diferenciar adecuadamente las raíces.

(1) Sacamos todas las constantes del signo de la derivada, en este caso la constante es .
(2) Bajo el primo, tenemos el producto de dos funciones, por lo tanto, necesitamos usar la regla de diferenciación del producto ![]() .
.
(3) No olvides que es una función compleja (aunque la más simple de las complejas). Usamos la regla correspondiente: ![]() .
.
Ahora encontramos derivadas mixtas de segundo orden:


Esto significa que todos los cálculos son correctos.
Escribamos el diferencial total. En el contexto de la tarea bajo consideración, no tiene sentido decir cuál es el diferencial total de una función de dos variables. Es importante que este diferencial muy a menudo necesite ser escrito en problemas prácticos.
La diferencial total de primer orden de una función de dos variables tiene la forma:
En este caso:
Es decir, en la fórmula solo necesita sustituir las derivadas parciales de primer orden ya encontradas. Iconos diferenciales y en esta y otras situaciones similares, si es posible, es mejor escribir en numeradores:
Ejemplo 4
Encontrar derivadas parciales de primer orden de una función ![]() . Mira esto . Escriba la diferencial total de primer orden.
. Mira esto . Escriba la diferencial total de primer orden.
Este es un ejemplo de bricolaje. Una solución completa y un ejemplo de diseño del problema se encuentran al final de la lección.
Considere una serie de ejemplos que incluyen funciones complejas.
Ejemplo 5
Hallar derivadas parciales de primer orden de la función.
(1) Aplicamos la regla de diferenciación de una función compleja ![]() . de la lección Derivada de una función compuesta debe recordarse un punto muy importante: cuando convertimos el seno (función externa) en un coseno de acuerdo con la tabla, entonces la inversión (función interna) que tenemos no cambia.
. de la lección Derivada de una función compuesta debe recordarse un punto muy importante: cuando convertimos el seno (función externa) en un coseno de acuerdo con la tabla, entonces la inversión (función interna) que tenemos no cambia.
(2) Aquí usamos la propiedad de las raíces: , quitamos la constante del signo de la derivada y representamos la raíz en la forma necesaria para la derivación.
Similar: 
Escribimos la diferencial total de primer orden:
Ejemplo 6
Encontrar derivadas parciales de primer orden de una función ![]() .
.
Anote el diferencial total.
Este es un ejemplo de auto-resolución (respuesta al final de la lección). No publicaré la solución completa porque es bastante simple.
Muy a menudo, todas las reglas anteriores se aplican en combinación.
Ejemplo 7
Encontrar derivadas parciales de primer orden de una función ![]() .
.

(1) Usamos la regla de diferenciar la suma.
(2) El primer término en este caso se considera una constante, ya que no hay nada en la expresión que dependa de "x", solo "y".
(Sabes, siempre es bueno cuando puedes convertir una fracción en cero).
Para el segundo término, aplicamos la regla de diferenciación de productos. Por cierto, nada cambiaría en el algoritmo si en su lugar se diera una función; es importante que aquí tengamos producto de dos funciones, CADA una de las cuales depende de "x", por lo que debe utilizar la regla de diferenciación de productos. Para el tercer término, aplicamos la regla de derivación de una función compleja.
Cada derivada parcial (sobre X y por y) de una función de dos variables es la derivada ordinaria de una función de una variable con un valor fijo de la otra variable:
(donde y= constante),
(donde X= constante).
Por lo tanto, las derivadas parciales se calculan a partir de fórmulas y reglas para calcular derivadas de funciones de una variable, considerando la otra variable como una constante (constante).
Si no necesita un análisis de ejemplos y la teoría mínima necesaria para esto, pero solo necesita una solución a su problema, entonces proceda a calculadora de derivadas parciales en línea .
Si es difícil concentrarse en hacer un seguimiento de dónde está la constante en la función, puede sustituir cualquier número en el borrador de la solución del ejemplo en lugar de una variable con un valor fijo; luego puede calcular rápidamente la derivada parcial como la ordinaria. derivada de una función de una variable. Solo es necesario no olvidar devolver la constante (una variable con un valor fijo) a su lugar al terminar.
La propiedad de las derivadas parciales descrita anteriormente se deriva de la definición de derivada parcial, que se puede encontrar en las preguntas del examen. Por lo tanto, para familiarizarse con la definición a continuación, puede abrir la referencia teórica.
El concepto de continuidad de una función. z= F(X, y) en un punto se define de manera similar a este concepto para una función de una variable.
Función z = F(X, y) se llama continua en un punto si
La diferencia (2) se llama incremento total de la función z(se obtiene incrementando ambos argumentos).
Deja que la función z= F(X, y) y punto
Si la función cambia z ocurre cuando solo uno de los argumentos cambia, por ejemplo, X, con un valor fijo del otro argumento y, entonces la función se incrementará
llamado incremento parcial de la función F(X, y) sobre X.
Teniendo en cuenta el cambio de función z dependiendo del cambio de solo uno de los argumentos, en realidad pasamos a una función de una variable.
Si hay un límite finito
entonces se llama derivada parcial de la función F(X, y) por argumento X y se denota por uno de los símbolos
![]()
![]() (4)
(4)
El incremento parcial se define de manera similar z sobre y:
y derivada parcial F(X, y) sobre y:
![]() (6)
(6)
Ejemplo 1
Solución. Encontramos la derivada parcial con respecto a la variable "x":
![]() (y reparado);
(y reparado);
Encontramos la derivada parcial con respecto a la variable "y":
(X reparado).
Como puedes ver, no importa en qué medida la variable que es fija: en este caso, es sólo un número que es un factor (como en el caso de la derivada habitual) con la variable por la que encontramos el parcial. derivado. Si la variable fija no se multiplica por la variable con respecto a la cual encontramos la derivada parcial, entonces esta solitaria constante, no importa en qué medida, como en el caso de una derivada ordinaria, se desvanece.
Ejemplo 2 Dada una función
Encontrar derivadas parciales
(por x) y (por y) y calcula sus valores en el punto A (1; 2).
Solución. en un fijo y la derivada del primer término se encuentra como la derivada de la función potencia ( tabla de funciones derivadas de una variable):
![]() .
.
en un fijo X la derivada del primer término se encuentra como derivada funcion exponencial, y el segundo - como un derivado de una constante:
Ahora calculamos los valores de estas derivadas parciales en el punto A (1; 2):

Puedes comprobar la solución de problemas con derivadas parciales en calculadora de derivadas parciales en línea .
Ejemplo 3 Hallar derivadas parciales de funciones
Solución. En un paso encontramos
![]()
(y X, como si el argumento del seno fuera 5 X: del mismo modo, 5 aparece antes del signo de la función);
![]()
(X es fijo y es en este caso un factor en y).
Puedes comprobar la solución de problemas con derivadas parciales en calculadora de derivadas parciales en línea .
Las derivadas parciales de una función de tres o más variables se definen de manera similar.
Si cada conjunto de valores ( X; y; ...; t) variables independientes del conjunto D corresponde a un valor específico tu desde muchos mi, entonces tu se llama función de variables X, y, ..., t y denota tu= F(X, y, ..., t).
Para funciones de tres o más variables, no hay interpretación geométrica.
Las derivadas parciales de una función de varias variables también se definen y calculan bajo el supuesto de que solo una de las variables independientes cambia, mientras que las demás son fijas.
Ejemplo 4 Hallar derivadas parciales de funciones
![]() .
.
Solución. y y z reparado:
X y z reparado:
X y y reparado:
Encuentre derivadas parciales por su cuenta y luego vea soluciones
Ejemplo 5
Ejemplo 6 Hallar derivadas parciales de una función.
La derivada parcial de una función de varias variables tiene el mismo significado mecánico como la derivada de una función de una variable, es la velocidad a la que cambia la función en relación con un cambio en uno de los argumentos.
Ejemplo 8 cantidad de flujo PAGS pasajeros vias ferreas se puede expresar como una función
donde PAGS- el número de pasajeros, norte- el número de residentes de los puntos correspondientes, R– distancia entre puntos.
Derivada parcial de una función PAGS sobre R igual a
muestra que la disminución en el flujo de pasajeros es inversamente proporcional al cuadrado de la distancia entre los puntos correspondientes para el mismo número de habitantes en los puntos.
Derivada parcial PAGS sobre norte igual a
muestra que el aumento en el flujo de pasajeros es proporcional al doble del número de habitantes asentamientos con la misma distancia entre puntos.
Puedes comprobar la solución de problemas con derivadas parciales en calculadora de derivadas parciales en línea .
diferencial completo
El producto de la derivada parcial y el incremento de la variable independiente correspondiente se llama diferencial parcial. Los diferenciales parciales se denotan de la siguiente manera:
![]()
La suma de diferenciales parciales sobre todas las variables independientes da el diferencial total. Para una función de dos variables independientes, el diferencial total se expresa por la igualdad
![]() (7)
(7)
Ejemplo 9 Hallar la diferencial completa de una función
Solución. El resultado de usar la fórmula (7):
![]()
Una función que tiene un diferencial total en cada punto de algún dominio se llama diferenciable en ese dominio.
Encuentre el diferencial total por su cuenta y luego vea la solución
Al igual que en el caso de una función de una variable, la diferenciabilidad de una función en una determinada región implica su continuidad en esta región, pero no al revés.
Formulemos sin demostración una condición suficiente para la derivabilidad de una función.
Teorema. Si la función z= F(X, y) tiene derivadas parciales continuas
en una región dada, entonces es diferenciable en esta región y su diferencial se expresa mediante la fórmula (7).
Se puede demostrar que, así como en el caso de una función de una variable, la diferencial de la función es la parte lineal principal del incremento de la función, así en el caso de una función de varias variables, la diferencial total es la principal, lineal con respecto a incrementos de independientes parte variable incremento total de la función.
Para una función de dos variables, el incremento total de la función tiene la forma
 (8)
(8)
donde α y β son infinitesimales para y .
Derivadas parciales de órdenes superiores
Derivadas parciales y funciones F(X, y) son a su vez algunas funciones de las mismas variables y, a su vez, pueden tener derivadas con respecto a diferentes variables, que se denominan derivadas parciales de órdenes superiores.
El concepto de una función de muchas variables.
Sean n-variables ya cada x 1, x 2 ... x n de un cierto conjunto x se le asigna una definición. el número Z, luego en el conjunto x se da la función Z \u003d f (x 1, x 2 ... x n) de muchas variables.
X - área de funciones definidas
x 1, x 2 ... x n - variable independiente (argumentos)
Z - función Ejemplo: Z \u003d P x 2 1 * x 2 (Volumen del cilindro)
Considere Z \u003d f (x; y) - f-ción de 2 variables x (x 1, x 2 reemplazadas por x, y). Los resultados se transfieren por analogía a otras funciones de muchas variables. El área de definición de la función de 2 variables es toda la cuerda del cuadrado (ooh) o parte de él. Mn-en el valor de la función th de 2 variables - la superficie en un espacio tridimensional.
Técnicas de construcción de grafos: - Sección Rassm-t sobre la superficie del cuadrado || cuadrados coordinados.
Ejemplo: x \u003d x 0, zn. cuadrado X || 0yz y \u003d y 0 0xz Tipo de función: Z \u003d f (x 0, y); Z=f(x, y 0)
Por ejemplo: Z=x 2 +y 2 -2y
Z= x 2 +(y-1) 2 -1 x=0 Z=(y-1) 2 -1 y=1 Z= x 2 -1 Z=0 x 2 +(y-1) 2 -1
Círculo de parábola (centro (0; 1)
Límites y continuidad de funciones de dos variables
Sea Z = f (x; y), entonces A es el límite de la f-ción en m (x 0, y 0), si para cualquier put arbitrariamente pequeño. número E>0 sustantivo-t número positivo b>0, que para todo x,y que satisface |x-x 0 |<б; |y-y 0 |<б выполняется нерав-во |f(x,y)-A| Z \u003d f (x; y) es continuo en t (x 0, y 0), si: - está definido en este t .; - tiene un finito límite en x, tendiendo a x 0 yy a y 0; - este límite = valor funciones en t (x 0, y 0), es decir límf (x; y) \u003d f (x 0, y 0) Si la función es continua en cada uno. t.mn-va X, entonces es continuo en esta área Función diferencial, su geosignificado. El uso de dif-la en valores aproximados. dy=f’(x)∆x – función diferencial dy=dx, es decir dy=f '(x)dx si y=x Desde el punto de vista de un geólogo, una función diferencial es un incremento en la ordenada de la tangente trazada a la gráfica de la función en un punto con la abscisa x 0 Dif-l se utiliza en el cálculo de aprox. valores de función según la fórmula: f(x 0 +∆x)~f(x 0)+f’(x 0)∆x Cuanto más cerca esté ∆x de x, más preciso será el resultado. Derivadas parciales de primer y segundo orden Derivada de primer orden (que se llama privada) O. Sean x, y los incrementos de las variables independientes x e y en algún punto de la región X. Entonces el valor igual a z = f(x + x, y + y) = f(x, y) se llama incremento total en el punto x 0, y 0. Si la variable x es fija y la variable y se incrementa en y, entonces obtenemos zу = f(x, y, + y) – f(x, y) La derivada parcial de la variable y se define de manera similar, es decir, La derivada parcial de una función de 2 variables se calcula siguiendo las mismas reglas que para las funciones de una variable. La diferencia es que al derivar una función con respecto a la variable x, y se considera const, y al derivar con respecto a y, x se considera const. Las constantes aisladas están conectadas a la función con operaciones de suma/resta. Las constantes asociadas están conectadas a la función con operaciones de multiplicación/división. Derivada de constante aislada = 0 1.4.Diferencial total de una función de 2 variables y sus aplicaciones
Sea z = f(x,y), entonces tz = Derivada parcial de segundo orden Para funciones continuas de 2 variables, las derivadas parciales mixtas de 2º orden y coinciden. El uso de derivadas parciales para determinar las derivadas parciales de funciones máximas y mínimas se denomina extremos. A. Los puntos se denominan max o min z = f(x,y) si hay algunos segmentos tales que para todo x e y de esta vecindad f(x,y) T. Si se da un punto extremo de una función de 2 variables, entonces el valor de las derivadas parciales en este punto es igual a 0, es decir , Los puntos en los que las derivadas parciales de primer orden se denominan estacionarias o críticas. Por lo tanto, para encontrar los puntos extremos de una función de 2 variables, se utilizan condiciones extremas suficientes. Sea la función z = f(x,y) dos veces diferenciable, y sea el punto estacionario, 1), y maxA<0, minA>0. 1.4.(*)diferencial completo. El significado geométrico del diferencial. Aplicación del diferencial en cálculos aproximados
O. Sea definida la función y = f(x) en alguna vecindad en los puntos . Una función f(x) se llama diferenciable en un punto si su incremento en este punto Donde A es un valor constante independiente de , en un punto fijo x, - infinitamente pequeño en . Una función A relativamente lineal se denomina diferencial de la función f(x) en un punto y se denota por df() o dy. Por lo tanto, la expresión (1) se puede escribir como La función diferencial en la expresión (1) tiene la forma dy = A . Como cualquier función lineal, se define para cualquier valor Para facilitar la notación de la diferencial, el incremento se denota por dx y se denomina diferencial de la variable independiente x. Por lo tanto, el diferencial se escribe como dy = Adx. Si la función f(x) es diferenciable en cada punto de algún intervalo, entonces su diferencial es una función de dos variables: el punto x y la variable dx: T. Para que la función y = g(x) sea diferenciable en algún punto, es necesario y suficiente que tenga derivada en ese punto, mientras que (*)Prueba. Necesitar. Sea la función f(x) diferenciable en el punto , es decir, Por lo tanto, la derivada f'() existe y es igual a A. Por lo tanto, dy = f'()dx Adecuación. Sea una derivada f'(), es decir = f'(). Entonces la curva y = f(x) es un segmento tangente. Para calcular el valor de una función en un punto x, tome un punto en alguna de sus vecindades, tal que no sea difícil encontrar f() y f'()/![]() - se llama un incremento completo
- se llama un incremento completo![]()
![]()
![]()
![]()
![]()
![]() , donde se representa en la forma (1)
, donde se representa en la forma (1)![]() ().
().![]() mientras que el incremento de la función debe ser considerado solo para aquellos para los cuales + pertenece al dominio de la función f(x).
mientras que el incremento de la función debe ser considerado solo para aquellos para los cuales + pertenece al dominio de la función f(x).![]() . Entonces
. Entonces![]()