1. Definición de paralelogramo.
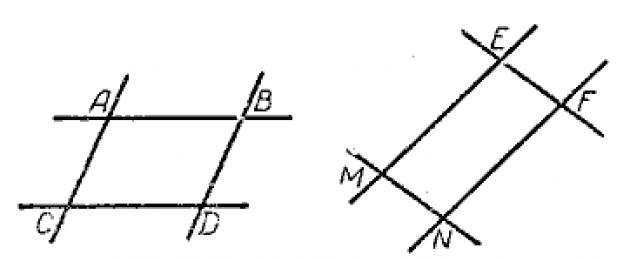
Si cortamos un par de rectas paralelas con otro par de rectas paralelas, obtenemos un cuadrilátero cuyos lados opuestos son paralelos por pares.
En los cuadriláteros ABDC y EFNM (Fig. 224) ВD || AC y AB || CD;
FE || MN y EM || FN.
Un cuadrilátero cuyos lados opuestos son paralelos en pares se llama paralelogramo.
2. Propiedades de un paralelogramo.
Teorema. La diagonal de un paralelogramo lo divide en dos triángulos iguales.
Sea un paralelogramo ABDC (Fig. 225), en el que AB || CD y aire acondicionado || ВD.
Necesitas demostrar que la diagonal lo divide en dos triángulos iguales.
Dibujemos la diagonal CB en el paralelogramo ABDC. Demostremos que \(\Delta\)CAB = \(\Delta\)СДВ.
El lado NE es común a estos triángulos; ∠ABC = ∠BCD, como ángulos transversales internos con AB y CD paralelos y CB secante; ∠ACB = ∠СВD, también como ángulos transversales internos con AC y BD paralelos y CB secante.
Por lo tanto \(\Delta\)CAB = \(\Delta\)СДВ.
De la misma forma, se puede demostrar que la diagonal AD dividirá el paralelogramo en dos triángulos iguales ACD y ABD.
Consecuencias:
1 . Los ángulos opuestos de un paralelogramo son iguales entre sí.
∠A = ∠D, esto se desprende de la igualdad de los triángulos CAB y CDB.
Asimismo, ∠C = ∠B.
2. Los lados opuestos de un paralelogramo son iguales entre sí.
AB = CD y AC = BD, ya que estos son lados de triángulos iguales y están opuestos ángulos iguales.
Teorema 2. Las diagonales de un paralelogramo se dividen por la mitad en el punto de su intersección.
Sean BC y AD las diagonales del paralelogramo ABC (figura 226). Demostremos que AO = OD y CO = OB.
Para hacer esto, compare algún par de triángulos ubicados en direcciones opuestas, por ejemplo \(\Delta\)AOB y \(\Delta\)COD.
En estos triángulos AB = CD, como lados opuestos de un paralelogramo;
∠1 = ∠2, como ángulos internos transversales a los paralelos AB y CD y secante AD;
∠3 = ∠4 por la misma razón, ya que AB || CD y SV son sus secantes.
De ello se deduce que \(\Delta\)AOB = \(\Delta\)СOD. Y en triángulos iguales se encuentran ángulos iguales opuestos lados iguales. Por tanto, AO = OD y CO = OB.
Teorema 3. La suma de los ángulos adyacentes a un lado de un paralelogramo es igual a 180°.
En el paralelogramo ABCD trazamos la diagonal AC y obtenemos dos triángulos ABC y ADC.
Los triángulos son iguales, ya que ∠1 = ∠4, ∠2 = ∠3 (ángulos transversales para rectas paralelas) y el lado AC es común.
De la igualdad \(\Delta\)ABC = \(\Delta\)ADC se deduce que AB = CD, BC = AD, ∠B = ∠D.
La suma de los ángulos adyacentes a un lado, por ejemplo los ángulos A y D, es igual a 180° como ángulos unilaterales para rectas paralelas.
El curso en vídeo "Obtén una A" incluye todos los temas que necesitas completar con exito Examen Estatal Unificado de Matemáticas por 60-65 puntos. Completamente todos los problemas 1-13 Perfil Examen estatal unificado matemáticas. También apto para aprobar el Examen Estatal Unificado Básico de Matemáticas. Si quieres aprobar el Examen Estatal Unificado con 90-100 puntos, ¡debes resolver la parte 1 en 30 minutos y sin errores!
Curso de preparación para el Examen del Estado Unificado para los grados 10-11, así como para docentes. Todo lo que necesitas para resolver la Parte 1 del Examen Estatal Unificado de Matemáticas (los primeros 12 problemas) y el Problema 13 (trigonometría). Y esto son más de 70 puntos en el Examen Estatal Unificado, y ni un estudiante de 100 puntos ni un estudiante de humanidades pueden prescindir de ellos.
Toda la teoría necesaria. Maneras rápidas soluciones, dificultades y secretos del examen estatal unificado. Se han analizado todas las tareas actuales de la parte 1 del Banco de tareas FIPI. El curso cumple plenamente con los requisitos del Examen Estatal Unificado 2018.
El curso contiene 5 grandes temas, de 2,5 horas cada uno. Cada tema se da desde cero, de forma sencilla y clara.
Cientos de tareas del Examen Estatal Unificado. Problemas de palabras y teoría de la probabilidad. Algoritmos simples y fáciles de recordar para la resolución de problemas. Geometría. Teoría, material de referencia, análisis de todo tipo de tareas del Examen Estatal Unificado. Estereometría. Soluciones complicadas, trucos útiles, desarrollo de la imaginación espacial. Trigonometría desde cero hasta el problema 13. Comprender en lugar de abarrotar. Explicación visual conceptos complejos. Álgebra. Raíces, potencias y logaritmos, función y derivada. Una base para resolver problemas complejos de la Parte 2 del Examen Estatal Unificado.
Presupuesto municipal institución educativa
escuela secundaria savinskaya
Paralelogramo y sus nuevas propiedades.
Completado por: estudiante de 8B
Escuela secundaria MBOU Savinskaya
Kuznetsova Svetlana, 14 años
Responsable: profesor de matemáticas
Tulchevskaya N.A.
p.Savino
Región de Ivanovo, Rusia
2016
I. Introducción ___________________________________________________página 3
II. De la historia del paralelogramo ___________________________________página 4
III Propiedades adicionales de un paralelogramo ____________________________página 4
IV. Prueba de propiedades _____________________________________ página 5
v. Resolver problemas usando propiedades adicionales __________página 8
VI. Aplicación de las propiedades de un paralelogramo en la vida ___________________página 11
VII. Conclusión _________________________________________________página 12
VIII. Literatura _________________________________________________página 13
Introducción
"Entre mentes iguales
en igualdad de otras condiciones
el que sabe geometría es superior"
(Blaise Pascal).
Mientras estudiamos el tema "Paralelogramo" en las lecciones de geometría, observamos dos propiedades de un paralelogramo y tres características, pero cuando comenzamos a resolver problemas, resultó que esto no era suficiente.
Tenía una pregunta: ¿tiene un paralelogramo otras propiedades y cómo ayudarán a resolver problemas?
Y decidí estudiar propiedades adicionales del paralelogramo y mostrar cómo se pueden aplicar para resolver problemas.
Tema de estudio : paralelogramo
Objeto de estudio
: propiedades de un paralelogramo
Objetivo del trabajo:
formulación y prueba de propiedades adicionales de un paralelogramo que no se estudian en la escuela;
Aplicación de estas propiedades a la resolución de problemas.
Tareas:
Estudiar la historia de la aparición del paralelogramo y la historia del desarrollo de sus propiedades;
Encontrar Otras lecturas sobre el tema en estudio;
Estudiar propiedades adicionales de un paralelogramo y demostrarlas;
Mostrar la aplicación de estas propiedades para resolver problemas;
Considere la aplicación de las propiedades de un paralelogramo en la vida.
Métodos de búsqueda:
Trabajar con literatura educativa y de divulgación científica, recursos de Internet;
Estudio de material teórico;
Identificación de una variedad de problemas que pueden resolverse utilizando propiedades adicionales de un paralelogramo;
Observación, comparación, análisis, analogía.
Duración del estudio : 3 meses: enero-marzo 2016
De la historia del paralelogramo.
En un libro de texto de geometría leemos la siguiente definición de paralelogramo: Un paralelogramo es un cuadrilátero cuyos lados opuestos son paralelos en pares.
La palabra "paralelogramo" se traduce como "líneas paralelas" (de las palabras griegas Parallelos - paralelo y gramme - línea), este término fue introducido por Euclides. En su libro Elementos, Euclides demostró las siguientes propiedades de un paralelogramo: los lados y ángulos opuestos de un paralelogramo son iguales y la diagonal lo biseca. Euclides no menciona el punto de intersección de un paralelogramo. Sólo a finales de la Edad Media se desarrolló una teoría completa de los paralelogramos y sólo en el siglo XVII aparecieron en los libros de texto teoremas sobre los paralelogramos, que se demuestran utilizando el teorema de Euclides sobre las propiedades del paralelogramo.
III Propiedades adicionales de un paralelogramo
En el libro de texto de geometría, solo se dan 2 propiedades de un paralelogramo:
Los ángulos opuestos y los lados son iguales.
Las diagonales de un paralelogramo se cortan y son bisecadas por el punto de intersección.
En varias fuentes sobre geometría puede encontrar las siguientes propiedades adicionales:
La suma de los ángulos adyacentes de un paralelogramo es 180 0
La bisectriz del ángulo de un paralelogramo se corta de él. triángulo isósceles;
Las bisectrices de los ángulos opuestos de un paralelogramo se encuentran en rectas paralelas;
Las bisectrices de los ángulos adyacentes de un paralelogramo se cortan en ángulos rectos;
Cuando las bisectrices de todos los ángulos de un paralelogramo se cruzan, forman un rectángulo;
Las distancias desde las esquinas opuestas de un paralelogramo a la misma diagonal son iguales.
Si conectas los vértices opuestos de un paralelogramo con los puntos medios de los lados opuestos, obtienes otro paralelogramo.
La suma de los cuadrados de las diagonales de un paralelogramo es igual al doble de la suma de los cuadrados de sus lados adyacentes.
Si dibujas altitudes desde dos ángulos opuestos en un paralelogramo, obtienes un rectángulo.
IV Prueba de las propiedades de un paralelogramo.
La suma de los ángulos adyacentes de un paralelogramo es 180. 0
Dado:
ABCD – paralelogramo
Probar:
A+ B= 
Prueba:
un y B – ángulos internos unilaterales con rectas paralelas BC 
AD y secante AB, lo que significa A+ B=
2
Dado: A B C D - paralelogramo,
bisectriz AK 
A.
Probar: 
AVK – isósceles
Prueba:
1) 1=3 (cruzado en BC AD y secante AK ),
2) 2=3 porque AK es una bisectriz,
significa 1= 2.
3) ABC - isósceles porque 2 ángulos de un triángulo son iguales
3
Dado: ABCD es un paralelogramo,
AK – bisectriz A,
CP - bisectriz C.
Probar: AK ║ SR
Prueba:
1) 1=2 porque AK es una bisectriz
2) 4=5 porque CP – bisectriz
3) 3=1 (ángulos transversales en
BC ║ AD y AK-secante),
4) A =C (por la propiedad de un paralelogramo), lo que significa 2=3=4=5.
4) De los párrafos 3 y 4 se deduce que 1 = 4, y estos ángulos corresponden a las rectas AK y CP y a la secante BC,
esto significa AK ║ CP (basado en el paralelismo de líneas)
. Las bisectrices de ángulos opuestos de un paralelogramo se encuentran en rectas paralelas.
Las bisectrices de ángulos adyacentes de un paralelogramo se cortan en ángulos rectos.
Dado: ABCD - paralelogramo,
AK-bisectriz A,
bisectriz DP D
Probar: PD 
ALASKA.
Prueba:
1) 1=2, porque AK - bisectriz
Sea 1=2=x, entonces A=2x,
2) 3=4, porque D Р – bisectriz
Sea 3=4=y, entonces D=2y
3) A + D =180 0, porque la suma de los ángulos adyacentes de un paralelogramo es 180
2) Considere una sobredosis
1+3=90 0 , entonces <5=90 0 (сумма углов треугольников равна 180 0)
5. Las bisectrices de todos los ángulos de un paralelogramo cuando se cruzan forman un rectángulo.
Dado: ABCD - paralelogramo, AK-bisectriz A,
DP-bisectriz D,
CM bisectriz C,
BF - bisectriz B .
Probar: KRNS - rectángulo
Prueba:
Basado en la propiedad anterior 8=7=6=5=90 0,
significa que KRNS es un rectángulo.
Las distancias desde las esquinas opuestas de un paralelogramo a la misma diagonal son iguales.
Dado: ABCD-paralelogramo, AC-diagonal.
VC C.A, DP C.A.
Probar: BC=PD
Prueba: 1) DCP = KAB, como cruces internos con AB ║ CD y secante AC.
2) batería = CDР (a lo largo del lado y dos ángulos adyacentes AB=CD CD P=AB K).
Y en triángulos iguales los lados correspondientes son iguales, lo que significa DP=BK.
Si conectas los vértices opuestos de un paralelogramo con los puntos medios de los lados opuestos, obtienes otro paralelogramo.
Dado: Paralelogramo ABCD.
Probar: VKDP es un paralelogramo.
Prueba:
1) BP=KD (AD=BC, puntos K y P
divide estos lados por la mitad)
2) BP ║ KD (acostado en AD ANTES DE CRISTO)
Si los lados opuestos de un cuadrilátero son iguales y paralelos, entonces el cuadrilátero es un paralelogramo.
Si dibujas altitudes desde dos ángulos opuestos en un paralelogramo, obtienes un rectángulo.
La suma de los cuadrados de las diagonales de un paralelogramo es igual al doble de la suma de los cuadrados de sus lados adyacentes.
Dado: ABCD es un paralelogramo. BD y AC son diagonales.
Probar: C.A. 2 +ВD 2 =2(AB 2 + ANUNCIO 2 )
Prueba: 1)PREGUNTAR:
C.A.
²=
+
2)B RD : BD 2 = B R 2 +RD 2 (según el teorema de Pitágoras)
3) C.A. ²+ BD ²=SK²+A K²+B Р²+РD ²
4) SC = BP = N(altura )
5) aire acondicionado 2 +BD 2 = h 2 + A A 2 + h 2 +PD 2
6)
Dejar
D
k=A
p=x, Entonces C
AD
:
h
2
=
CD
2
- X 2
según el teorema de pitágoras )
7) CA²+BD ² = CD 2 - x²+ AK 1 ²+ CD 2 -X 2 +PD 2 ,
CA²+BD ²=2СD 2 -2x 2 + A A 2 +PD 2
8) Un A=AD+ X, RD=AD- X,
CA²+BD ² =2CD 2 -2x 2 +(ANUNCIO +x) 2 +(ANUNCIO -X) 2 ,
C.A.²+
END²=2
COND²-2
X² + ANUNCIO
2
+2AD
X+
X 2
+ANUNCIO
2
-2AD
X+
X 2
,
C.A.²+
END²=2CD
2
+2AD
2
=2(CD
2
+ANUNCIO
2
).
V . Resolver problemas usando estas propiedades.
El punto de intersección de las bisectrices de dos ángulos de un paralelogramo adyacentes a un lado pertenece al lado opuesto. El lado más corto de un paralelogramo es 5 . Encuentra su lado grande.
Dado: ABCD es un paralelogramo,
AK – bisectriz A,
DK – bisectriz D , AB=5
Encontrar: Sol
decisión Solución
Porque AK - bisectriz Y entonces ABC es isósceles.
Porque DK – bisectriz D, entonces DCK - isósceles
CC =C K= 5
Entonces, BC=VC+SC=5+5 = 10
Respuesta: 10
2. Calcula el perímetro de un paralelogramo si la bisectriz de uno de sus ángulos divide el lado del paralelogramo en segmentos de 7 cm y 14 cm.
1 caso
Dado: A,
VK=14 cm, KS=7 cm
Encontrar: paralelogramo P
Solución
VS=VK+KS=14+7=21 (cm)
Porque AK – bisectriz Y entonces ABC es isósceles.
AB=BK= 14cm
Entonces P=2 (14+21) =70 (cm)
Dado: ABCD es un paralelogramo,
DK – bisectriz D
VK=14 cm, KS=7 cm
Encontrar: P paralelogramo
Solución
VS=VK+KS=14+7=21 (cm)
Porque DK – bisectriz D, entonces DCK - isósceles
CC =C K= 7
Entonces, P= 2 (21+7) = 56 (cm)
Respuesta: 70cm o 56cm
3. Los lados de un paralelogramo miden 10 cm y 3 cm. Las bisectrices de dos ángulos adyacentes al lado mayor dividen el lado opuesto en tres segmentos. Encuentra estos segmentos.
1 caso: bisectrices se cortan fuera del paralelogramo
Dado: ABCD – paralelogramo, AK – bisectriz A,
DK – bisectriz D , AB=3 cm, BC=10 cm
Encontrar: VM, MN, Carolina del Norte
Solución
Porque soy - bisectriz Y entonces la AVM es isósceles.
Porque DN - bisectriz D, entonces DCN - isósceles
CC=CN=3
Entonces, MN = 10 – (BM +NC) = 10 – (3+3)=4 cm
Caso 2: las bisectrices se cortan dentro de un paralelogramo
Porque AN - bisectriz Y entonces ABN es isósceles.
AB=Bnorte = 3 D
Y la rejilla corrediza debe moverse a la distancia requerida en la entrada.
Mecanismo de paralelogramo- un mecanismo de cuatro barras, cuyos eslabones forman un paralelogramo. Se utiliza para implementar el movimiento de traslación mediante mecanismos articulados.
Paralelogramo con un enlace fijo.- un eslabón está inmóvil, el opuesto hace un movimiento de balanceo, permaneciendo paralelo al inmóvil. Dos paralelogramos conectados uno detrás del otro le dan al eslabón final dos grados de libertad, dejándolo paralelo al eslabón estacionario.
Ejemplos: limpiaparabrisas de autobuses, montacargas, trípodes, perchas, suspensiones de automóviles.
Paralelogramo con articulación fija- Se utiliza la propiedad del paralelogramo de mantener una relación constante de distancias entre tres puntos. Ejemplo: pantógrafo de dibujo: un dispositivo para escalar dibujos.
Rombo- todos los eslabones tienen la misma longitud, la aproximación (contracción) de un par de bisagras opuestas provoca la separación de las otras dos bisagras. Todos los enlaces funcionan en compresión.
Ejemplos: gato de automóvil en forma de diamante, pantógrafo de tranvía.
Cortar con tijeras o Mecanismo en forma de X, también conocido como tijeras de nuremberg- versión rombo - dos eslabones conectados en el medio por una bisagra. Las ventajas del mecanismo son la compacidad y la simplicidad, la desventaja es la presencia de dos pares deslizantes. Dos (o más) de estos mecanismos conectados en serie forman un diamante en el medio. Utilizado en ascensores y juguetes infantiles.
VII Conclusión
¿Quién ha estudiado matemáticas desde pequeño?
desarrolla la atención, entrena su cerebro,
propia voluntad, cultiva la perseverancia
y perseverancia en el logro de objetivos.
A. Markushevich
Durante el trabajo demostré propiedades adicionales del paralelogramo.
Estaba convencido de que utilizando estas propiedades se pueden resolver problemas más rápido.
Mostré cómo se aplican estas propiedades usando ejemplos de resolución de problemas específicos.
Aprendí mucho sobre el paralelogramo, que no está en nuestro libro de texto de geometría.
Me convencí de que el conocimiento de la geometría es muy importante en la vida a través de ejemplos de la aplicación de las propiedades de un paralelogramo.
El propósito de mi trabajo de investigación se ha cumplido.
La importancia del conocimiento matemático se evidencia en el hecho de que se estableció un premio para quien publique un libro sobre una persona que vivió toda su vida sin la ayuda de las matemáticas. Ninguna persona ha recibido todavía este premio.
VIII Literatura
Pogorelov A.V. Geometría 7-9: libro de texto para educación general. instituciones - M.: Educación, 2014
L.S.Atanasyan y otros Geometría. Agregar. Capítulos para el libro de texto de 8º grado: libro de texto. manual para estudiantes de escuelas y clases avanzadas. Estudió matemáticas. – M.: Vita-press, 2003
recursos de Internet
Materiales de Wikipedia
Prueba
En primer lugar, dibujemos la diagonal AC. Obtenemos dos triángulos: ABC y ADC.
Como ABCD es un paralelogramo, se cumple lo siguiente:
ANUNCIO || BC \Flecha derecha \ángulo 1 = \ángulo 2 como tumbarse transversalmente.
AB || CD\Flecha derecha\ángulo3 =\ángulo 4 como tumbarse transversalmente.
Por lo tanto, \triangle ABC = \triangle ADC (según el segundo criterio: y AC es común).
Y, por lo tanto, \triangle ABC = \triangle ADC, luego AB = CD y AD = BC.
¡Probado!
2. Los ángulos opuestos son idénticos.
Prueba
Según la prueba propiedades 1 Lo sabemos \ángulo 1 = \ángulo 2, \ángulo 3 = \ángulo 4. Entonces la suma de los ángulos opuestos es: \ángulo 1 + \ángulo 3 = \ángulo 2 + \ángulo 4. Considerando que \triangle ABC = \triangle ADC obtenemos \angle A = \angle C , \angle B = \angle D .
¡Probado!
3. Las diagonales se dividen por la mitad por el punto de intersección.
Prueba
Dibujemos otra diagonal.
Por propiedad 1 sabemos que los lados opuestos son idénticos: AB = CD. Una vez más, observe los ángulos iguales que se encuentran transversalmente.
Así, está claro que \triangle AOB = \triangle COD según el segundo criterio de igualdad de triángulos (dos ángulos y el lado entre ellos). Es decir, BO = OD (opuesto a las esquinas \angle 2 y \angle 1) y AO = OC (opuesto a las esquinas \angle 3 y \angle 4, respectivamente).
¡Probado!
Signos de un paralelogramo
Si solo hay una característica presente en tu problema, entonces la figura es un paralelogramo y puedes usar todas las propiedades de esta figura.
Para una mejor memorización, tenga en cuenta que el signo del paralelogramo responderá la siguiente pregunta: "¿Cómo saberlo?". Es decir, cómo saber que una figura dada es un paralelogramo.
1. Un paralelogramo es un cuadrilátero cuyos dos lados son iguales y paralelos.
AB = CD ; AB || CD\Rightarrow ABCD es un paralelogramo.
Prueba
Miremos más de cerca. Por qué AD || ¿ANTES DE CRISTO?
\triángulo ABC = \triángulo ADC por propiedad 1: AB = CD, AC - común y \angle 1 = \angle 2 transversal a las paralelas AB y CD y secante AC.
Pero si \triangle ABC = \triangle ADC , entonces \angle 3 = \angle 4 (se encuentran frente a AB y CD, respectivamente). Y por lo tanto AD || BC (\angle 3 y \angle 4 - los que se encuentran en forma transversal también son iguales).
La primera señal es correcta.
2. Un paralelogramo es un cuadrilátero cuyos lados opuestos son iguales.
AB = CD, AD = BC \Rightarrow ABCD es un paralelogramo.
Prueba
Consideremos este signo. Dibujemos nuevamente la diagonal AC.
Por propiedad 1\triángulo ABC = \triángulo ACD .
Resulta que: \ángulo 1 = \ángulo 2 \Rightarrow AD || ANTES DE CRISTO. Y \ángulo 3 = \ángulo 4 \Rightarrow AB || CD, es decir, ABCD es un paralelogramo.
La segunda señal es correcta.
3. Un paralelogramo es un cuadrilátero cuyos ángulos opuestos son iguales.
\ángulo A = \ángulo C , \ángulo B = \ángulo D \Rightarrow ABCD- paralelogramo.
Prueba
2 \alfa + 2 \beta = 360^(\circ)(dado que ABCD es un cuadrilátero y \angle A = \angle C , \angle B = \angle D por condición).
Resulta que \alpha + \beta = 180^(\circ) . Pero \alpha y \beta son unilaterales internos en la secante AB.
Y el hecho de que \alpha + \beta = 180^(\circ) también significa que AD || ANTES DE CRISTO.
Además, \alpha y \beta son unilaterales internos en la secante AD. Y eso significa AB || CD.
El tercer signo es correcto.
4. Un paralelogramo es un cuadrilátero cuyas diagonales se dividen por la mitad por el punto de intersección.
AO = OC ; BO = OD\paralelogramo de flecha derecha.
Prueba
BO = DO; AO = OC , \angle 1 = \angle 2 como vertical \Rightarrow \triangle AOB = \triangle COD, \Flecha derecha \ángulo 3 = \ángulo 4 y \Rightarrow AB || CD.
De manera similar BO = OD; AO = OC, \angle 5 = \angle 6 \Rightarrow \triangle AOD = \triangle BOC \Rightarrow \angle 7 = \angle 8 y \Rightarrow AD || ANTES DE CRISTO.
El cuarto signo es correcto.
- En contacto con 0
- Google+ 0
- DE ACUERDO 0
- Facebook 0
