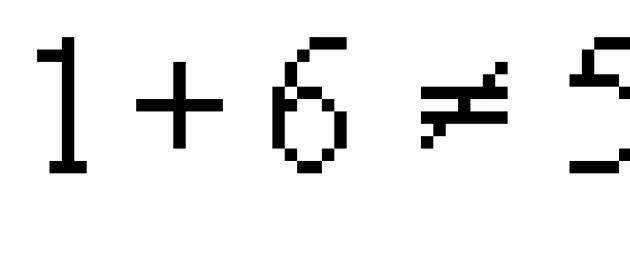Võrrandite lahendamine Vieta teoreemi näidete abil. Viet teoreem, pöördvieti valem ja näited mannekeenide lahendustega

François Vieta (1540-1603) - matemaatik, kuulsate Vieta valemite looja

Vieta teoreem vajalik ruutvõrrandite kiireks lahendamiseks (lihtsamalt öeldes).

Täpsemalt t Vieta teoreem - see ruutvõrrandi juurte summa on võrdne teise koefitsiendiga, mis võetakse vastupidise märgiga, ja korrutis on võrdne vaba liikmega. Sellel omadusel on mis tahes ruutvõrrand, millel on juured.

Vieta teoreemi kasutades saate ruutvõrrandid lihtsalt valiku teel lahendada, nii et ütleme mõõk käes olevale matemaatikule meie õnneliku 7. klassi eest "aitäh".

Vieta teoreemi tõestus

Teoreemi tõestamiseks saab kasutada tuntud juurvalemeid, tänu millele koostame ruutvõrrandi juurte summa ja korrutise. Alles pärast seda saame veenduda, et need on võrdsed ja vastavalt .

Oletame, et meil on võrrand: . Sellel võrrandil on järgmised juured: ja . Tõestame, et .

Ruuvvõrrandi juurte valemite järgi:

1. Leidke juurte summa:

Analüüsime seda võrrandit, kuna saime selle täpselt nii:

= .

Samm 1. Vähendame murrud ühise nimetajani, selgub:

= = .

2. samm. Saime murdosa, kus peate sulgud avama:

Vähendame murdosa 2 võrra ja saame:

Oleme tõestanud ruutvõrrandi juurte summa seose Vieta teoreemi abil.

2. Leidke juurte korrutis:

= = = = = .

Tõestame seda võrrandit:

Samm 1. Murdude korrutamiseks on reegel, mille kohaselt korrutame selle võrrandi:

Nüüd tuletame meelde ruutjuure määratlust ja kaalume:

= .

3. samm. Tuletame meelde ruutvõrrandi diskriminanti: . Seetõttu asendame D (diskriminant) asemel viimase murruga, siis saame:

= .

4. samm. Avage sulud ja lisage murdudele sarnased terminid:

5. samm. Vähendame "4a" ja saame.

Seega oleme tõestanud seose juurte korrutisega vastavalt Vieta teoreemile.

TÄHTIS!Kui diskriminant on null, on ruutvõrrandil ainult üks juur.

Teoreem on Vieta teoreemi pöördvõrdeline

Vastavalt teoreemile, Vieta teoreemi pöördväärtusele, saame kontrollida, kas meie võrrand on õigesti lahendatud. Teoreemi enda mõistmiseks peame seda üksikasjalikumalt käsitlema.

Kui numbrid on:

Ja siis on need ruutvõrrandi juured.

Vieta pöördteoreemi tõestus

Samm 1.Asendame võrrandis selle koefitsientide avaldised:

2. sammTeisendame võrrandi vasaku külje:

3. samm. Leiame võrrandi juured ja selleks kasutame omadust, et korrutis on võrdne nulliga:

Või . Kust see tuleb: või.

Näited lahendustega Vieta teoreemi järgi

Näide 1

Ülesanne

Leia ruutvõrrandi juurte summa, korrutis ja ruutude summa ilma võrrandi juuri leidmata.

Lahendus

Samm 1. Tuletage meelde diskrimineeriva valemit. Asendame oma numbrid tähtede all. See tähendab, , on asendaja , ja . See tähendab:

Selgub:

Title="(!LANG: Renderdab QuickLaTeX.com" height="13" width="170" style="vertical-align: -1px;">. Если дискриминант больше нуля, тогда у уравнения есть корни. По теореме Виета их сумма , а произведение . !}

Me väljendame juurte ruutude summat nende summa ja korrutise kaudu:

Vastus

7; 12; 25.

Näide 2

Ülesanne

Lahenda võrrand. Sel juhul ärge kasutage ruutvõrrandi valemeid.

Lahendus

Selle võrrandi juured on diskriminandi (D) poolest suuremad kui null. Vastavalt Vieta teoreemile on selle võrrandi juurte summa 4 ja korrutis 5. Esiteks määrame arvu jagajad, mille summa on 4. Need on arvud "5" ja "-1". Nende korrutis on – 5 ja summa – 4. Seega vastavalt teoreemile, mis on Vieta teoreemi vastupidine, on nad selle võrrandi juured.

Vastus

JA Näide 4

Ülesanne

Kirjutage võrrand, kus iga juur on kaks korda suurem kui võrrandi vastav juur:

Lahendus

Vieta teoreemi järgi on selle võrrandi juurte summa 12 ja korrutis = 7. Seega on need kaks juurt positiivsed.

Uue võrrandi juurte summa on võrdne:

Ja töö.

Vieta teoreemile vastupidise teoreemi järgi on uuel võrrandil vorm:

Vastus

Tulemuseks oli võrrand, mille iga juur on kaks korda suurem:

Niisiis, vaatasime, kuidas lahendada võrrandit Vieta teoreemi abil. Seda teoreemi on väga mugav kasutada, kui lahendatakse ülesandeid, mis on seotud ruutvõrrandite juurte märkidega. See tähendab, et kui valemis olev vaba liige on positiivne arv ja kui ruutvõrrandis on reaaljuured, võivad need mõlemad olla negatiivsed või positiivsed.

Ja kui vaba liige on negatiivne arv ja kui ruutvõrrandis on reaalsed juured, on mõlemad märgid erinevad. See tähendab, et kui üks juur on positiivne, on teine ​​juur ainult negatiivne.

Kasulikud allikad:

1. Dorofejev G. V., Suvorova S. B., Bunimovitš E. A. Algebra 8. klass: Moskva “Valgustus”, 2016 – 318 lk.
2. Rubin A. G., Chulkov P. V. - õpik Algebra 8. klass: Moskva "Balass", 2015 - 237 lk.
3. Nikolsky S. M., Potopav M. K., Reshetnikov N. N., Shevkin A. V. – algebra 8. klass: Moskva “Valgustus”, 2014 – 300

Vieta teoreem, Vieta pöördvalem ja näited lahendustega mannekeenide jaoks värskendatud: 22. novembril 2019: Teaduslikud artiklid.Ru

Vieta teoreemi sõnastamine ja tõestamine ruutvõrrandite jaoks. Vieta pöördteoreem. Vieta teoreem kuupvõrrandite ja suvalise järjestusega võrrandite jaoks.

Sisu

Vaata ka: Ruutvõrrandi juured

Ruutvõrrandid

Vieta teoreem

Olgu ja tähistatakse taandatud ruutvõrrandi juuri
(1) .
Siis võrdub juurte summa koefitsiendiga, mis on võetud vastupidise märgiga. Juurte korrutis võrdub vaba terminiga:
;
.

Märkus mitme juure kohta

Kui võrrandi (1) diskriminant on null, on sellel võrrandil üks juur. Kuid selleks, et vältida tülikaid sõnastusi, on üldtunnustatud, et antud juhul on võrrandil (1) kaks mitmekordset või võrdset juurt:
.

Tõestus üks

Leiame võrrandi (1) juured. Selleks kasutage ruutvõrrandi juurte valemit:
;
;
.

Juurte summa leidmine:
.

Toote leidmiseks kasutame valemit:
.
Siis

.

Teoreem on tõestatud.

Tõestus kaks

Kui arvud ja on ruutvõrrandi (1) juured, siis
.
Avame sulgud.

.
Seega on võrrand (1) järgmisel kujul:
.
Võrreldes punktiga (1) leiame:
;
.

Teoreem on tõestatud.

Vieta pöördteoreem

Olgu suvalised arvud. Siis ja on ruutvõrrandi juured
,
kus
(2) ;
(3) .

Vieta pöördteoreemi tõestus

Mõelge ruutvõrrandile
(1) .
Peame tõestama, et kui ja , siis ja on võrrandi (1) juured.

Asendage (2) ja (3) punktiga (1):
.
Rühmitame võrrandi vasaku poole liikmed:
;
;
(4) .

Asendage punktis (4):
;
.

Asendage punktis (4):
;
.
Võrrand on täidetud. See tähendab, et arv on võrrandi (1) juur.

Teoreem on tõestatud.

Vieta teoreem täieliku ruutvõrrandi jaoks

Nüüd kaaluge täielikku ruutvõrrandit
(5) ,
kus , ja on mõned numbrid. Ja .

Jagame võrrandi (5) järgmisega:
.
See tähendab, et oleme saanud ülaltoodud võrrandi
,
kus; .

Siis on täieliku ruutvõrrandi Vieta teoreemil järgmine kuju.

Olgu ja tähistatakse täieliku ruutvõrrandi juuri
.
Seejärel määratakse juurte summa ja korrutis valemitega:
;
.

Vieta teoreem kuupvõrrandi jaoks

Samamoodi saame luua seoseid kuupvõrrandi juurte vahel. Mõelge kuupvõrrandile
(6) ,
kus , , , on mõned arvud. Ja .
Jagame selle võrrandi järgmisega:
(7) ,
kus , , .
Olgu , , võrrandi (7) (ja võrrandi (6)) juurteks. Siis

.

Võrreldes võrrandiga (7) leiame:
;
;
.

Vieta teoreem n-nda astme võrrandi jaoks

Samamoodi saab n-nda astme võrrandi jaoks leida seoseid juurte , , ... , , vahel
.

Vieta teoreem n-nda astme võrrandi jaoks on järgmisel kujul:
;
;
;

.

Nende valemite saamiseks kirjutame võrrandi järgmisel kujul:
.
Seejärel võrdsustame koefitsiendid punktis , , , ... ja võrdleme vaba liiget.

Viited:
I.N. Bronstein, K.A. Semendjajev, Matemaatika käsiraamat inseneridele ja kõrgkoolide üliõpilastele, Lan, 2009.
CM. Nikolsky, M.K. Potapov jt, Algebra: õpik õppeasutuste 8. klassile, Moskva, Haridus, 2006.

Vaata ka:

Kaheksandas klassis tutvustatakse õpilastele ruutvõrrandeid ja nende lahendamist. Samal ajal, nagu kogemus näitab, kasutab enamik õpilasi täielike ruutvõrrandite lahendamisel ainult ühte meetodit - ruutvõrrandi juurte valemit. Hea suulise loendamise oskusega õpilaste jaoks on see meetod selgelt irratsionaalne. Tihti peavad õpilased gümnaasiumis lahendama ruutvõrrandeid ja seal on lihtsalt kahju diskriminandi arvutamisele aega kulutada. Minu arvates tuleks ruutvõrrandite uurimisel rohkem aega ja tähelepanu pöörata Vieta teoreemi rakendamisele (AG Mordkovich Algebra-8 programmi järgi on kavas vaid kaks tundi õppida teemat “Vieta teoreem. ruuttrinoom lineaarseteks teguriteks).

Enamikus algebraõpikutes on see teoreem sõnastatud taandatud ruutvõrrandi jaoks ja ütleb, et kui võrrandil on juured ja , siis nad vastavad võrdsustele , . Seejärel formuleeritakse väide, mis on vastupidine Vieta teoreemile, ja pakutakse mitmeid näiteid selle teemaga töötamiseks.

Võtame konkreetsed näited ja jälgime nende peal oleva lahenduse loogikat Vieta teoreemi abil.

Näide 1. Lahenda võrrand.

Oletame, et sellel võrrandil on juured, nimelt ja . Seejärel Vieta teoreemi järgi võrdsused

Pange tähele, et juurte korrutis on positiivne arv. Seega on võrrandi juurtel sama märk. Ja kuna juurte summa on samuti positiivne arv, järeldame, et võrrandi mõlemad juured on positiivsed. Läheme tagasi juurte toote juurde. Oletame, et võrrandi juurteks on positiivsed täisarvud. Siis saab õige esimese võrdsuse saada ainult kahel viisil (kuni tegurite järjekorrani): või . Kontrollime pakutud arvupaaride puhul Vieta teoreemi teise väite teostatavust: . Seega vastavad numbrid 2 ja 3 mõlemale võrdsusele ja on seega antud võrrandi juured.

Vastus: 2; 3.

Toome välja peamised arutlemise etapid antud ruutvõrrandi lahendamisel Vieta teoreemi abil:

kirjutage üles Vieta teoreemi väide

(*)

• määrake võrrandi juurte märgid (Kui korrutis ja juurte summa on positiivsed, siis on mõlemad juured positiivsed arvud. Kui juurte korrutis on positiivne arv ja juurte summa on negatiivne, siis mõlemad juured on negatiivsed arvud.Kui juurte korrutis on negatiivne arv, siis on juurtel erinevad märgid.Pealegi, kui juurte summa on positiivne, siis suurema mooduliga juur on positiivne arv ja kui juurte summa on väiksem kui null, siis suurema mooduliga juur on negatiivne arv);
• vali täisarvude paarid, mille korrutis annab tähistuses õige esimese võrdsuse (*);
• leitud arvupaaride hulgast vali paar, mis tähises (*) teise võrrandisse asendamisel annab õige võrdsuse;
• märkige vastuses võrrandi leitud juured.

Toome veel mõned näited.

Näide 2: lahendage võrrand .

Lahendus.

Olgu ja on antud võrrandi juured. Seejärel Vieta teoreemi järgi Pane tähele, et korrutis on positiivne ja summa negatiivne. Seega on mõlemad juured negatiivsed arvud. Valime tegurite paarid, mis annavad korrutiseks 10 (-1 ja -10; -2 ja -5). Teine numbripaar annab kokku -7. Nii et arvud -2 ja -5 on selle võrrandi juured.

Vastus: -2; -5.

Näide 3. Lahenda võrrand .

Lahendus.

Olgu ja on antud võrrandi juured. Seejärel Vieta teoreemi järgi Pange tähele, et korrutis on negatiivne. Nii et juured on erineva märgiga. Ka juurte summa on negatiivne arv. Seega on suurima mooduliga juur negatiivne. Valime tegurite paarid, mis annavad tootele -10 (1 ja -10; 2 ja -5). Teine numbripaar annab kokku -3. Nii et arvud 2 ja -5 on selle võrrandi juured.

Vastus: 2; -5.

Pange tähele, et Vieta teoreemi saab põhimõtteliselt formuleerida täieliku ruutvõrrandi jaoks: kui ruutvõrrand on juured ja , siis nad vastavad võrdsustele , . Selle teoreemi rakendamine on aga üsna problemaatiline, kuna täisruutvõrrandis on vähemalt üks juurtest (muidugi kui on) murdarv. Ja fraktsioonide valikuga töötamine on pikk ja raske. Kuid ikkagi on väljapääs.

Vaatleme täielikku ruutvõrrandit . Korrutage võrrandi mõlemad pooled esimese koefitsiendiga aga ja kirjutage võrrand vormile . Tutvustame uut muutujat ja saame redutseeritud ruutvõrrandi , mille juured ja (kui on) on leitavad Vieta teoreemi abil. Siis on algvõrrandi juurteks . Pange tähele, et redutseeritud abivõrrandi kirjutamine on väga lihtne: teine ​​koefitsient säilib ja kolmas koefitsient võrdub korrutisega äss. Teatud oskusega koostavad õpilased kohe abivõrrandi, leiavad Vieta teoreemi abil selle juured ja näitavad ette antud tervikvõrrandi juured. Toome näiteid.

Näide 4. Lahenda võrrand .

Koostame abivõrrandi ja Vieta teoreemi abil leiame selle juured. Nii et algvõrrandi juured .

Vastus: .

Näide 5. Lahenda võrrand .

Abivõrrandil on vorm . Vieta teoreemi järgi on selle juured . Leiame algse võrrandi juured .

Vastus: .

Ja veel üks juhtum, kui Vieta teoreemi rakendamine võimaldab verbaalselt leida täieliku ruutvõrrandi juured. Seda on lihtne tõestada arv 1 on võrrandi juur , kui ja ainult kui. Võrrandi teine ​​juur leitakse Vieta teoreemiga ja on võrdne . Veel üks väide: nii et arv -1 on võrrandi juur vajalik ja piisav. Siis on võrrandi teine ​​juur Vieta teoreemi järgi võrdne . Samasuguseid väiteid saab sõnastada ka taandatud ruutvõrrandi jaoks.

Näide 6. Lahenda võrrand.

Pange tähele, et võrrandi koefitsientide summa on null. Seega võrrandi juured .

Vastus: .

Näide 7. Lahenda võrrand.

Selle võrrandi koefitsiendid vastavad omadusele (tõepoolest, 1-(-999)+(-1000)=0). Seega võrrandi juured .

Vastus: ..

Näited Vieta teoreemi rakendamiseks

Ülesanne 1. Lahenda etteantud ruutvõrrand Vieta teoreemi abil.

1.	6.	11.	16.
2.	7.	12.	17.
3.	8.	13.	18.
4.	9.	14.	19.
5.	10.	15.	20.

Ülesanne 2. Lahendage täielik ruutvõrrand, kasutades üleminekut abivähendatud ruutvõrrandile.

1.	6.	11.	16.
2.	7.	12.	17.
3.	8.	13.	18.
4.	9.	14.	19.
5.	10.	15.	20.

Ülesanne 3. Lahenda ruutvõrrand omaduse abil.

Ruutvõrrandi juurte ja kordajate vahel on lisaks juurvalemitele ka muid kasulikke seoseid, mis on antud Vieta teoreem. Selles artiklis esitame ruutvõrrandi Vieta teoreemi sõnastuse ja tõestuse. Järgmisena käsitleme teoreemi, mis on vastupidine Vieta teoreemile. Pärast seda analüüsime kõige iseloomulikumate näidete lahendusi. Lõpuks kirjutame üles Vieta valemid, mis määratlevad seose tegelike juurte vahel algebraline võrrand aste n ja selle koefitsiendid.

Leheküljel navigeerimine.

Vieta teoreem, sõnastus, tõestus

Ruutvõrrandi juurte valemitest a x 2 +b x+c=0 vormi , kus D=b 2 −4 a c , seosed x 1 +x 2 = −b/a, x 1 x 2 = c/a . Need tulemused on kinnitatud Vieta teoreem:

Teoreem.

Kui x 1 ja x 2 on ruutvõrrandi ax 2 +b x+c=0 juured, siis võrdub juurte summa vastasmärgiga koefitsientide b ja a suhtega ja korrutisega juur võrdub koefitsientide c ja a suhtega, see tähendab .

Tõestus.

Tõestame Vieta teoreemi järgmise skeemi järgi: koostame ruutvõrrandi juurte summa ja korrutise teadaolevate juurvalemite abil, seejärel teisendame saadud avaldised ja veendume, et need on võrdsed -b /a ja c/a vastavalt.

Alustame juurte summast, koostame selle. Nüüd viime murrud ühise nimetaja juurde, meil on. Saadud murru lugejas , mille järel : . Lõpuks, pärast 2, saame . See tõestab Vieta teoreemi esimest seost ruutvõrrandi juurte summa kohta. Liigume teise juurde.

Koostame ruutvõrrandi juurte korrutise:. Murdude korrutamise reegli järgi võib viimase korrutise kirjutada kujul. Nüüd korrutame sulu lugejas oleva suuga, kuid seda toodet on kiirem ahendada ruutude erinevuse valem, Nii et. Seejärel, pidades meeles, teostame järgmise ülemineku. Ja kuna valem D=b 2 −4 a·c vastab ruutvõrrandi diskriminandile, siis saab b 2 −4·a·c asendada D asemel viimaseks murruks, saame . Pärast sulgude avamist ja sarnaste terminite vähendamist jõuame murduni ja selle vähendamine 4·a võrra annab . See tõestab Vieta teoreemi teist seost juurte korrutise kohta.

Kui jätame seletused välja, on Vieta teoreemi tõestus kokkuvõtlik:
,
.

Jääb vaid märkida, et kui diskriminant on võrdne nulliga, on ruutvõrrandil üks juur. Kui aga eeldada, et võrrandil on sel juhul kaks identset juurt, siis kehtivad ka Vieta teoreemi võrrandid. Tõepoolest, kui D=0 ruutvõrrandi juur on , siis ja , ning kuna D=0, st b 2 −4·a·c=0 , kust b 2 =4·a·c , siis .

Praktikas kasutatakse Vieta teoreemi kõige sagedamini seoses taandatud ruutvõrrandiga (kõrgeima koefitsiendiga a on 1) kujul x 2 +p·x+q=0 . Mõnikord on see sõnastatud just seda tüüpi ruutvõrranditele, mis ei piira üldistust, kuna iga ruutvõrrandi saab asendada samaväärse võrrandiga, jagades selle mõlemad osad nullist erineva arvuga a. Siin on Vieta teoreemi vastav sõnastus:

Teoreem.

Redutseeritud ruutvõrrandi juurte summa x 2 + px + q \u003d 0 on võrdne koefitsiendiga punktis x, mis on võetud vastupidise märgiga, ja juurte korrutis on vaba liige, see tähendab x 1 + x 2 \u003d −p, x 1 x 2 = q.

Teoreem on Vieta teoreemi pöördvõrdeline

Vieta teoreemi teine ​​sõnastus, mis on toodud eelmises lõigus, näitab, et kui x 1 ja x 2 on taandatud ruutvõrrandi x 2 +p x+q=0 juured, siis seosed x 1 +x 2 = − p , x 1 x 2 = q. Seevastu kirjutatud seostest x 1 +x 2 =−p, x 1 x 2 =q järeldub, et x 1 ja x 2 on ruutvõrrandi x 2 +p x+q=0 juured. Teisisõnu, väide, mis on vastupidine Vieta teoreemile, on tõene. Sõnastame selle teoreemi kujul ja tõestame.

Teoreem.

Kui arvud x 1 ja x 2 on sellised, et x 1 +x 2 =−p ja x 1 x 2 =q, siis on x 1 ja x 2 taandatud ruutvõrrandi x 2 +p x+q=0 juured. .

Tõestus.

Pärast koefitsientide p ja q asendamist nende avaldises võrrandis x 2 +p x+q=0 läbi x 1 ja x 2 teisendatakse see samaväärseks võrrandiks.

Asendame saadud võrrandis x asemel arvu x 1, meil on võrdsus x 1 2 −(x 1 + x 2) x 1 + x 1 x 2 =0, mis iga x 1 ja x 2 korral on õige arvuline võrdus 0=0, kuna x 1 2 −(x 1 + x 2) x 1 + x 1 x 2 = x 1 2 −x 1 2 −x 2 x 1 + x 1 x 2 =0. Seetõttu on x 1 võrrandi juur x 2 − (x 1 + x 2) x + x 1 x 2 \u003d 0, mis tähendab, et x 1 on ekvivalentvõrrandi x 2 +p x+q=0 juur.

Kui võrrandis x 2 − (x 1 + x 2) x + x 1 x 2 \u003d 0 asenda x asemel arv x 2, siis saame võrdsuse x 2 2 −(x 1 + x 2) x 2 + x 1 x 2 =0. See on õige võrrand, sest x 2 2 −(x 1 + x 2) x 2 + x 1 x 2 = x 2 2 −x 1 x 2 −x 2 2 +x 1 x 2 =0. Seetõttu on x 2 ka võrrandi juur x 2 − (x 1 + x 2) x + x 1 x 2 \u003d 0, ja seega võrrandid x 2 +p x+q=0 .

See lõpetab Vieta teoreemile vastupidise teoreemi tõestamise.

Näiteid Vieta teoreemi kasutamisest

On aeg rääkida Vieta teoreemi ja selle pöördteoreemi praktilisest rakendamisest. Selles alapeatükis analüüsime mitmete kõige tüüpilisemate näidete lahendusi.

Alustuseks rakendame Vieta teoreemile vastupidise teoreemi. Selle abil on mugav kontrollida, kas antud kaks arvu on antud ruutvõrrandi juured. Sel juhul arvutatakse nende summa ja vahe, misjärel kontrollitakse seoste kehtivust. Kui mõlemad seosed on täidetud, siis Vieta teoreemile vastupidise teoreemi alusel järeldatakse, et need arvud on võrrandi juured. Kui vähemalt üks seostest ei ole täidetud, ei ole need arvud ruutvõrrandi juured. Seda lähenemist saab kasutada ruutvõrrandite lahendamisel leitud juurte kontrollimiseks.

Näide.

Milline arvupaaridest 1) x 1 =−5, x 2 =3 või 2) või 3) on ruutvõrrandi 4 x 2 −16 x+9=0 juurte paar?

Lahendus.

Antud ruutvõrrandi 4 x 2 −16 x+9=0 koefitsiendid on a=4 , b=−16 , c=9 . Vieta teoreemi järgi peab ruutvõrrandi juurte summa olema võrdne −b/a, see tähendab 16/4=4 ja juurte korrutis peab olema võrdne c/a, see tähendab 9 /4.

Nüüd arvutame kõigis kolmes antud paaris olevate arvude summa ja korrutise ning võrdleme neid äsja saadud väärtustega.

Esimesel juhul on meil x 1 +x 2 =−5+3=−2 . Saadud väärtus erineb 4-st, seetõttu ei saa täiendavat kontrollimist läbi viia, kuid teoreemi, Vieta teoreemi pöördväärtuse põhjal saame kohe järeldada, et esimene arvupaar ei ole antud ruutvõrrandi juurte paar. .

Liigume edasi teise juhtumi juurde. Siin on esimene tingimus täidetud. Kontrollime teist tingimust: , saadud väärtus erineb 9/4-st. Seetõttu ei ole teine ​​arvupaar ruutvõrrandi juurte paar.

Jääb viimane juhtum. Siin ja . Mõlemad tingimused on täidetud, seega on need arvud x 1 ja x 2 antud ruutvõrrandi juurteks.

Vastus:

Teoreemi, Vieta teoreemi vastupidist, saab praktikas kasutada ruutvõrrandi juurte valimiseks. Tavaliselt valitakse antud ruutvõrrandi täisarvuliste koefitsientidega täisjuured, kuna muudel juhtudel on seda üsna raske teha. Samal ajal kasutavad nad seda, et kui kahe arvu summa on võrdne ruutvõrrandi teise koefitsiendiga, mis on võetud miinusmärgiga, ja nende arvude korrutis on võrdne vaba liikmega, siis need arvud on selle ruutvõrrandi juured. Käsitleme seda näitega.

Võtame ruutvõrrandi x 2 −5 x+6=0 . Et arvud x 1 ja x 2 oleksid selle võrrandi juured, peavad olema täidetud kaks võrdsust x 1 +x 2 \u003d 5 ja x 1 x 2 \u003d 6. Jääb üle valida sellised numbrid. Sel juhul on seda üsna lihtne teha: sellised arvud on 2 ja 3, kuna 2+3=5 ja 2 3=6 . Seega on 2 ja 3 selle ruutvõrrandi juured.

Vieta teoreemile vastupidine teoreem on eriti mugav redutseeritud ruutvõrrandi teise juure leidmiseks, kui üks juurtest on juba teada või ilmne. Sel juhul leitakse mis tahes seostest teine ​​juur.

Näiteks võtame ruutvõrrandi 512 x 2 −509 x−3=0 . Siin on lihtne näha, et ühik on võrrandi juur, kuna selle ruutvõrrandi kordajate summa on null. Seega x 1 = 1. Teise juure x 2 võib leida näiteks seosest x 1 x 2 =c/a. Meil on 1 x 2 = −3/512 , kust x 2 = −3/512 . Seega oleme defineerinud ruutvõrrandi mõlemad juured: 1 ja −3/512.

On selge, et juurte valik on otstarbekas ainult kõige lihtsamatel juhtudel. Muudel juhtudel saab juurte leidmiseks rakendada ruutvõrrandi juurte valemeid läbi diskriminandi.

Teine teoreemi praktiline rakendus, Vieta teoreemi pöördväärtus, on ruutvõrrandite koostamine antud juurte x 1 ja x 2 jaoks. Selleks piisab, kui arvutada juurte summa, mis annab antud ruutvõrrandi vastasmärgiga kordaja x, ja juurte korrutis, mis annab vaba liikme.

Näide.

Kirjutage ruutvõrrand, mille juurteks on arvud −11 ja 23.

Lahendus.

Tähistame x 1 =−11 ja x 2 =23 . Arvutame nende arvude summa ja korrutise: x 1 + x 2 \u003d 12 ja x 1 x 2 \u003d −253. Seetõttu on need arvud antud ruutvõrrandi juurteks teise koefitsiendiga -12 ja vaba liikmega -253. See tähendab, et x 2 −12·x−253=0 on soovitud võrrand.

Vastus:

x 2 −12 x −253=0 .

Vieta teoreemi kasutatakse väga sageli ruutvõrrandite juurte märkidega seotud ülesannete lahendamisel. Kuidas on Vieta teoreem seotud taandatud ruutvõrrandi x 2 +p x+q=0 juurte märkidega? Siin on kaks asjakohast väidet:

• Kui vaba liige q on positiivne arv ja ruutvõrrandil on reaaljuured, siis on need mõlemad positiivsed või mõlemad negatiivsed.
• Kui vaba liige q on negatiivne arv ja kui ruutvõrrandil on reaaljuured, siis on nende märgid erinevad ehk teisisõnu üks juur on positiivne ja teine ​​negatiivne.

Need väited tulenevad valemist x 1 x 2 =q, samuti positiivsete, negatiivsete ja erinevate märkidega arvude korrutamise reeglitest. Mõelge nende rakendamise näidetele.

Näide.

R on positiivne. Diskriminandi valemi järgi leiame D=(r+2) 2 −4 1 (r−1)= r 2 +4 r+4−4 r+4=r 2 +8 , avaldise r 2 väärtuse +8 on positiivne iga reaalse r korral, seega D>0 iga reaalse r korral. Seetõttu on algsel ruutvõrrandil parameetri r mis tahes tegelike väärtuste jaoks kaks juurt.

Nüüd uurime välja, millal on juurtel erinevad märgid. Kui juurte märgid on erinevad, siis on nende korrutis negatiivne ja Vieta teoreemi järgi on antud ruutvõrrandi juurte korrutis võrdne vaba liikmega. Seetõttu oleme huvitatud nendest r väärtustest, mille vaba liige r−1 on negatiivne. Seega, selleks, et leida meile huvi pakkuvad r väärtused, peame seda tegema lahendada lineaarne võrratus r-1<0 , откуда находим r<1 .

Vastus:

aadressil r<1 .

Vieta valemid

Eespool rääkisime Vieta ruutvõrrandi teoreemist ja analüüsisime selles väidetavaid seoseid. Kuid on valemeid, mis ühendavad mitte ainult ruutvõrrandite, vaid ka kuupvõrrandite, neljakordsete võrrandite ja üldiselt, algebralised võrrandid aste n. Neid nimetatakse Vieta valemid.

Kirjutame Vieta valemid vormi n astme algebralise võrrandi jaoks, eeldades, et sellel on n reaaljuurt x 1, x 2, ..., x n (nende hulgas võivad olla samad):

Hankige Vieta valemid võimaldavad polünoomifaktorisatsiooni teoreem, samuti võrdsete polünoomide määratlus kõigi neile vastavate koefitsientide võrdsuse kaudu. Seega on polünoom ja selle laienemine vormi lineaarseteks teguriteks võrdsed. Avades viimases korrutis olevad sulud ja võrdsustades vastavad koefitsiendid, saame Vieta valemid.

Täpsemalt, n=2 puhul oleme juba tuttavad Ruutvõrrandi Vieta valemid.

Kuupvõrrandi jaoks on Vieta valemitel vorm

Jääb üle vaid märkida, et Vieta valemite vasakul küljel on nn elementaar sümmeetrilised polünoomid.

Bibliograafia.

• Algebra:õpik 8 raku jaoks. Üldharidus institutsioonid / [Yu. N. Makarychev, N. G. Mindjuk, K. I. Neshkov, S. B. Suvorova]; toim. S. A. Teljakovski. - 16. väljaanne. - M. : Haridus, 2008. - 271 lk. : haige. - ISBN 978-5-09-019243-9.
• Mordkovitš A.G. Algebra. 8. klass. Kell 14 1. osa. Õpik õppeasutuste õpilastele / A. G. Mordkovich. - 11. väljaanne, kustutatud. - M.: Mnemozina, 2009. - 215 lk.: ill. ISBN 978-5-346-01155-2.
• Algebra ja matemaatilise analüüsi algus. 10. klass: õpik. üldhariduse jaoks institutsioonid: põhi- ja profiil. tasemed / [Yu. M. Koljagin, M. V. Tkatšova, N. E. Fedorova, M. I. Šabunin]; toim. A. B. Žižtšenko. - 3. väljaanne - M.: Valgustus, 2010.- 368 lk. : haige. - ISBN 978-5-09-022771-1.

Vieta teoreemi kasutatakse sageli juba leitud juurte testimiseks. Kui olete juured leidnud, saate väärtuste arvutamiseks kasutada valemeid \(\begin(cases)x_1+x_2=-p \\x_1 \cdot x_2=q\end(cases)\) ) ja \(q\ ). Ja kui need osutuvad samaks, mis algses võrrandis, siis leitakse juured õigesti.

Näiteks kasutame , lahendame võrrandi \(x^2+x-56=0\) ja saame juured: \(x_1=7\), \(x_2=-8\). Kontrollime, kas me tegime lahendamise käigus vea. Meie puhul \(p=1\) ja \(q=-56\). Vieta teoreemi järgi on meil:

\(\begin(cases)x_1+x_2=-p \\x_1 \cdot x_2=q\end(cases)\) \(\Leftparemnool\) \(\begin(cases)7+(-8)=-1 \\7\cdot(-8)=-56\end(cases)\) \(\Leftparemnool\) \(\begin(cases)-1=-1\\-56=-56\end(cases)\ )

Mõlemad väited lähenesid, mis tähendab, et lahendasime võrrandi õigesti.

Seda testi saab teha suuliselt. See võtab 5 sekundit ja säästab teid rumalate vigade eest.

Vieta pöördteoreem

Kui \(\begin(cases)x_1+x_2=-p \\x_1 \cdot x_2=q\end(cases)\), siis \(x_1\) ja \(x_2\) on ruutvõrrandi juured \ (x^ 2+px+q=0\).

Või lihtsal viisil: kui teil on võrrand kujul \(x^2+px+q=0\), siis lahendades süsteemi \(\begin(cases)x_1+x_2=-p \\x_1 \ cdot x_2=q\ end(cases)\) leiad selle juured.

Tänu sellele teoreemile saate kiiresti leida ruutvõrrandi juured, eriti kui need juured on . See oskus on oluline, kuna säästab palju aega.

Näide . Lahendage võrrand \(x^2-5x+6=0\).

Lahendus : Kasutades pöördvõrdelist Vieta teoreemi, saame, et juured vastavad tingimustele: \(\begin(cases)x_1+x_2=5 \\x_1 \cdot x_2=6\end(cases)\).
Vaadake süsteemi \(x_1 \cdot x_2=6\) teist võrrandit. Milliseks kaheks saab arvu \(6\) lagundada? \(2\) ja \(3\), \(6\) ja \(1\) või \(-2\) ja \(-3\) ja \(-6\) ja \(- üks\). Ja millist paari valida, ütleb süsteemi esimene võrrand: \(x_1+x_2=5\). \(2\) ja \(3\) on sarnased, kuna \(2+3=5\).
Vastus : \(x_1=2\), \(x_2=3\).

Näited . Kasutades Vieta teoreemi pöördväärtust, leidke ruutvõrrandi juured:
a) \(x^2-15x+14=0\); b) \(x^2+3x-4=0\); c) \(x^2+9x+20=0\); d) \(x^2-88x+780=0\).

Lahendus :
a) \(x^2-15x+14=0\) - millisteks teguriteks \(14\) laguneb? \(2\) ja \(7\), \(-2\) ja \(-7\), \(-1\) ja \(-14\), \(1\) ja \(14\ ). Millised arvupaarid annavad kokku \(15\)? Vastus: \(1\) ja \(14\).

b) \(x^2+3x-4=0\) - millisteks teguriteks \(-4\) laguneb? \(-2\) ja \(2\), \(4\) ja \(-1\), \(1\) ja \(-4\). Millised arvupaarid annavad kokku \(-3\)? Vastus: \(1\) ja \(-4\).

c) \(x^2+9x+20=0\) – millisteks teguriteks \(20\) laguneb? \(4\) ja \(5\), \(-4\) ja \(-5\), \(2\) ja \(10\), \(-2\) ja \(-10\ ), \(-20\) ja \(-1\), \(20\) ja \(1\). Millised arvupaarid annavad kokku \(-9\)? Vastus: \(-4\) ja \(-5\).

d) \(x^2-88x+780=0\) – millisteks teguriteks \(780\) laguneb? \(390\) ja \(2\). Kas nende summa on \(88\)? Ei. Milliseid kordajaid \(780\) veel on? \(78\) ja \(10\). Kas nende summa on \(88\)? Jah. Vastus: \(78\) ja \(10\).

Viimast liiget ei ole vaja kõigiks võimalikeks teguriteks lagundada (nagu viimases näites). Saate kohe kontrollida, kas nende summa annab \(-p\).

Tähtis! Vieta teoreem ja vastupidine teoreem töötavad ainult , st sellisega, mille koefitsient \(x^2\) ees on võrdne ühega. Kui meil on algselt taandamata võrrand, siis saame selle redutseerida, jagades lihtsalt koefitsiendiga \ (x ^ 2 \) ees.

Näiteks, olgu võrrand \(2x^2-4x-6=0\) antud ja soovime kasutada üht Vieta teoreemi. Kuid me ei saa, sest koefitsient enne \(x^2\) on võrdne \(2\). Vabaneme sellest, jagades kogu võrrandi arvuga \(2\).

\(2x^2-4x-6=0\) \(|:2\)
\(x^2-2x-3=0\)

Valmis. Nüüd saame kasutada mõlemat teoreemi.

Vastused korduma kippuvatele küsimustele

küsimus: Vieta teoreemi järgi saate lahendada mis tahes ?
Vastus: Kahjuks ei. Kui võrrandis ei ole täisarve või võrrandil pole üldse juuri, siis Vieta teoreem ei aita. Sel juhul peate kasutama diskrimineeriv . Õnneks on kooli matemaatikakursusel 80% võrranditest täisarvulised lahendid.