Examen och dess egenskaper. Bestämning av examen

Grader formler används i processen för minskning och förenkling komplexa uttryck, vid lösning av ekvationer och ojämlikheter.

siffra cär n-te potensen av ett tal a När:

Verksamhet med examina.

1. Genom att multiplicera grader med samma bas läggs deras indikatorer till:

en m·a n = a m + n .

2. När man dividerar grader med samma bas, subtraheras deras exponenter:

3. Effekten av produkten av 2 eller Mer faktorer är lika med produkten av styrkorna hos dessa faktorer:

(abc...) n = a n · b n · c n …

4. Graden av ett bråk är lika med förhållandet mellan graderna av utdelningen och divisorn:

(a/b) n = a n/b n .

5. Genom att höja en potens till en potens multipliceras exponenterna:

(a m) n = a m n .

Varje formel ovan är sann i riktningarna från vänster till höger och vice versa.

Till exempel. (2 3 5/15)² = 2² 3² 5²/15² = 900/225 = 4.

Verksamhet med rötter.

1. Roten av produkten av flera faktorer är lika med produkten av rötterna av dessa faktorer:

2. Roten av ett förhållande är lika med förhållandet mellan utdelningen och rötternas divisor:

3. När man höjer en rot till en makt räcker det att höja det radikala talet till denna makt:

4. Om du ökar graden av roten in n en gång och samtidigt bygga in n potensen är ett radikalt tal, då ändras inte rotens värde:

5. Om du minskar graden av roten in n extrahera roten samtidigt n-te potensen av ett radikalt tal, då ändras inte rotens värde:

En grad med negativ exponent. Potensen för ett visst tal med en icke-positiv (heltals) exponent definieras som en dividerad med potensen av samma tal med en exponent lika med det absoluta värdet av den icke-positiva exponenten:

Formel en m:a n =a m - n kan användas inte bara för m> n, men också med m< n.

Till exempel. a4:a 7 = a 4 - 7 = a -3.

Till formel en m:a n =a m - n blev rättvist när m=n, krävs närvaro av noll grader.

En grad med nollindex. Potensen för ett tal som inte är lika med noll med en nollexponent är lika med ett.

Till exempel. 2 0 = 1,(-5) 0 = 1,(-3/5) 0 = 1.

Grad med bråkexponent. Att höja ett reellt tal A till den grad m/n, måste du extrahera roten n e graden av m-e potensen av detta tal A.

Om vi ignorerar åttonde potensen, vad ser vi här? Låt oss komma ihåg 7:e klassprogrammet. Så, kommer du ihåg? Detta är formeln för förkortad multiplikation, nämligen skillnaden på kvadrater! Vi får:

Låt oss titta noga på nämnaren. Det ser mycket ut som en av täljarfaktorerna, men vad är det för fel? Ordningen på termerna är felaktig. Om de var omvända skulle regeln kunna gälla.

Men hur gör man det? Det visar sig att det är väldigt enkelt: den jämna graden av nämnaren hjälper oss här.

På magiskt sätt bytte termerna plats. Detta "fenomen" gäller alla uttryck i jämn grad: vi kan enkelt ändra tecknen inom parentes.

Men det är viktigt att komma ihåg: alla tecken ändras samtidigt!

Låt oss gå tillbaka till exemplet:

Och återigen formeln:

Hela vi kallar de naturliga talen, deras motsatser (det vill säga taget med tecknet " ") och talet.

positivt heltal, och det är inte annorlunda än naturligt, då ser allt ut precis som i föregående avsnitt.

Låt oss nu titta på nya fall. Låt oss börja med en indikator lika med.

Varje tal till nollpotensen är lika med ett:

Låt oss som alltid fråga oss själva: varför är det så?

Låt oss överväga en viss grad med en bas. Ta till exempel och multiplicera med:

Så vi multiplicerade talet med, och vi fick samma sak som det var - . Vilket tal ska man multiplicera med så att inget förändras? Det stämmer, på. Betyder att.

Vi kan göra detsamma med ett godtyckligt tal:

Låt oss upprepa regeln:

Varje tal till nollpotensen är lika med ett.

Men det finns undantag från många regler. Och här finns det också - det här är ett tal (som bas).

Å ena sidan måste det vara lika med vilken grad som helst - hur mycket du än multiplicerar noll med sig själv kommer du fortfarande att få noll, det är klart. Men å andra sidan, som vilket tal som helst med nollpotens, måste det vara lika. Så hur mycket av detta är sant? Matematikerna bestämde sig för att inte engagera sig och vägrade att höja noll till nollpotentialen. Det vill säga, nu kan vi inte bara dividera med noll, utan också höja den till nollpotentialen.

Låt oss gå vidare. Bortsett från naturliga tal och tal till heltal inkluderar negativa tal. För att förstå vad en negativ potens är, låt oss göra som förra gången: multiplicera ett normalt tal med samma tal till en negativ potens:

Härifrån är det lätt att uttrycka vad du letar efter:

Låt oss nu utöka den resulterande regeln till en godtycklig grad:

Så låt oss formulera en regel:

Ett tal med en negativ potens är det reciproka av samma tal med en positiv potens. Men samtidigt Basen kan inte vara null:(eftersom du inte kan dividera med).

Låt oss sammanfatta:

I. Uttrycket är inte definierat i målet. Om då.

II. Varje tal till nollpotensen är lika med ett: .

III. Ett tal som inte är lika med noll till en negativ potens är inversen av samma tal till en positiv potens: .

Uppgifter för oberoende lösning:

Tja, som vanligt, exempel på oberoende lösningar:

Analys av problem för oberoende lösning:

Jag vet, jag vet, siffrorna är skrämmande, men på Unified State Exam måste du vara beredd på vad som helst! Lös dessa exempel eller analysera deras lösningar om du inte kunde lösa dem och du kommer att lära dig att hantera dem lätt i provet!

Låt oss fortsätta att utöka antalet siffror "lämpliga" som exponent.

Låt oss nu överväga rationella nummer. Vilka tal kallas rationella?

Svar: allt som kan representeras som ett bråk, var och är heltal, och.

För att förstå vad det är "fraktionell grad", överväg bråket:

Låt oss höja båda sidor av ekvationen till en potens:

Låt oss nu komma ihåg regeln om "grad till grad":

Vilket nummer måste höjas till en makt för att få?

Denna formulering är definitionen av roten till den e graden.

Låt mig påminna dig: roten till den e potensen av ett tal () är ett tal som, när det höjs till en potens, är lika med.

Det vill säga roten till den e potensen är den omvända operationen av att höja till en potens: .

Det visar sig att. Uppenbarligen detta specialfall kan utökas: .

Nu lägger vi till täljaren: vad är det? Svaret är lätt att få med hjälp av power-to-power-regeln:

Men kan basen vara vilket tal som helst? När allt kommer omkring kan roten inte extraheras från alla tal.

Ingen!

Låt oss komma ihåg regeln: alla tal som höjs till en jämn potens är ett positivt tal. Det vill säga, det är omöjligt att extrahera jämna rötter från negativa tal!

Det betyder att sådana tal inte kan höjas till en bråkpotens med en jämn nämnare, det vill säga uttrycket är inte vettigt.

Hur är det med uttrycket?

Men här uppstår ett problem.

Talet kan representeras i form av andra, reducerbara bråk, till exempel, eller.

Och det visar sig att det finns, men inte existerar, utan det här är bara två olika poster med samma antal.

Eller ett annat exempel: en gång, då kan du skriva ner det. Men om vi skriver ner indikatorn annorlunda kommer vi återigen att hamna i problem: (det vill säga vi fick ett helt annat resultat!).

För att undvika sådana paradoxer överväger vi endast positiv basexponent med bråkdelsexponent.

Så om:

- naturligt nummer;
- heltal;

Exempel:

Rationella exponenter är mycket användbara för att transformera uttryck med rötter, till exempel:

5 exempel att öva på

Analys av 5 exempel för träning

1. Glöm inte de vanliga egenskaperna hos grader:

2. . Här minns vi att vi glömde att lära oss tabellen över grader:

trots allt - det här är eller. Lösningen hittas automatiskt: .

Nåväl, nu kommer det svåraste. Nu ska vi reda ut det grad med irrationell exponent.

Alla regler och egenskaper hos grader här är exakt samma som för en examen med en rationell exponent, med undantag

När allt kommer omkring, per definition är irrationella tal tal som inte kan representeras som ett bråk, där och är heltal (det vill säga irrationella tal är alla reella tal utom rationella).

När vi studerade examina med naturliga, heltals och rationella exponenter skapade vi varje gång en viss "bild", "analogi" eller beskrivning i mer bekanta termer.

Till exempel är en grad med en naturlig exponent ett tal multiplicerat med sig själv flera gånger;

...nummer till noll potens- det här är så att säga ett tal multiplicerat med sig själv en gång, det vill säga de har ännu inte börjat multiplicera det, vilket betyder att själva talet inte ens har dykt upp ännu - därför är resultatet bara ett visst "tomt tal" , nämligen ett nummer;

...negativ heltalsgrad- det är som om någon "omvänd process" hade inträffat, det vill säga att talet inte multiplicerades med sig självt, utan dividerades.

Förresten, inom vetenskap används ofta en examen med en komplex exponent, det vill säga exponenten är inte ens ett reellt tal.

Men i skolan tänker vi inte på sådana svårigheter, du kommer att ha möjlighet att förstå dessa nya koncept på institutet.

DÄR VI ÄR SÄKRA ATT DU GÅR! (om du lär dig att lösa sådana exempel :))

Till exempel:

Bestäm själv:

Analys av lösningar:

1. Låt oss börja med den vanliga regeln för att höja en makt till en makt:

Titta nu på indikatorn. Påminner han dig inte om något? Låt oss komma ihåg formeln för förkortad multiplikation av skillnaden mellan kvadrater:

I detta fall,

Det visar sig att:

Svar: .

2. Vi reducerar bråk i exponenter till samma form: antingen båda decimaler eller båda vanliga. Vi får till exempel:

Svar: 16

3. Inget speciellt, vi använder de vanliga egenskaperna för grader:

AVANCERAD NIVÅ

Bestämning av examen

En examen är ett uttryck för formen: , där:

— gradbas;
- exponent.

Grad med naturlig indikator (n = 1, 2, 3,...)

Att höja ett tal till den naturliga potensen n innebär att multiplicera talet med sig själv gånger:

Grad med en heltalsexponent (0, ±1, ±2,...)

Om exponenten är positivt heltal siffra:

Konstruktion till nollgraden:

Uttrycket är obestämt, eftersom, å ena sidan, i vilken grad som helst är detta, och å andra sidan, vilket tal som helst till den e graden är detta.

Om exponenten är negativt heltal siffra:

(eftersom du inte kan dividera med).

Återigen om nollor: uttrycket är inte definierat i fallet. Om då.

Exempel:

Makt med rationell exponent

- naturligt nummer;
- heltal;

Exempel:

Egenskaper för grader

För att göra det lättare att lösa problem, låt oss försöka förstå: var kom dessa egenskaper ifrån? Låt oss bevisa dem.

Låt oss se: vad är och?

A-priory:

Så, på höger sida av detta uttryck får vi följande produkt:

Men per definition är det en potens av ett tal med en exponent, det vill säga:

Q.E.D.

Exempel : Förenkla uttrycket.

Lösning : .

Exempel : Förenkla uttrycket.

Lösning : Det är viktigt att notera att i vår regel Nödvändigtvis det måste finnas samma skäl. Därför kombinerar vi krafterna med basen, men det förblir en separat faktor:

En annan viktig anmärkning: denna regel - endast för produkt av makt!

Det kan du under inga omständigheter skriva.

Precis som med den tidigare egenskapen, låt oss gå till definitionen av grad:

Låt oss omgruppera detta arbete så här:

Det visar sig att uttrycket multipliceras med sig själv gånger, det vill säga enligt definitionen är detta talets: e potens:

I huvudsak kan detta kallas "att ta indikatorn ur parentes." Men du kan aldrig göra detta totalt: !

Låt oss komma ihåg de förkortade multiplikationsformlerna: hur många gånger ville vi skriva? Men detta är trots allt inte sant.

Kraft med negativ bas.

Hittills har vi bara diskuterat hur det borde vara index grader. Men vad ska ligga till grund? I krafter av naturlig indikator grunden kan vara vilket nummer som helst .

Vi kan faktiskt multiplicera alla tal med varandra, vare sig de är positiva, negativa eller jämna. Låt oss fundera på vilka tecken ("" eller "") som kommer att ha grader av positiva och negativa tal?

Till exempel, är talet positivt eller negativt? A? ?

Med den första är allt klart: oavsett hur många positiva tal vi multiplicerar med varandra kommer resultatet att bli positivt.

Men de negativa är lite mer intressanta. Vi minns den enkla regeln från 6:e klass: "minus för minus ger ett plus." Det vill säga eller. Men om vi multiplicerar med (), får vi - .

Och så vidare i oändlighet: med varje efterföljande multiplikation kommer tecknet att ändras. Följande enkla regler kan formuleras:

även grad, - antal positiv.
Negativt tal höjts till udda grad, - antal negativ.
Positivt nummer i någon grad är ett positivt tal.
Noll till valfri potens är lika med noll.

Bestäm själv vilket tecken följande uttryck kommer att ha:

1.	2.	3.
4.	5.	6.

Klarade du dig? Här är svaren:

1) ; 2) ; 3) ; 4) ; 5) ; 6) .

I de fyra första exemplen hoppas jag att allt är klart? Vi tittar helt enkelt på basen och exponenten och tillämpar lämplig regel.

I exempel 5) är allt inte heller så skrämmande som det verkar: trots allt spelar det ingen roll vad basen är lika med - graden är jämn, vilket betyder att resultatet alltid kommer att vara positivt. Tja, förutom när basen är noll. Basen är väl inte lika? Uppenbarligen inte, eftersom (eftersom).

Exempel 6) är inte längre så enkelt. Här måste du ta reda på vilket som är mindre: eller? Om vi kommer ihåg det, blir det tydligt att, vilket betyder att basen är mindre än noll. Det vill säga vi tillämpar regel 2: resultatet blir negativt.

Och återigen använder vi definitionen av grad:

Allt är som vanligt - vi skriver ner definitionen av grader och delar dem med varandra, delar upp dem i par och får:

Innan vi tittar på den sista regeln, låt oss lösa några exempel.

Beräkna uttrycken:

Lösningar :

Vi får:

Låt oss titta noga på nämnaren. Det ser mycket ut som en av täljarfaktorerna, men vad är det för fel? Ordningen på termerna är felaktig. Om de ändrades skulle regel 3 kunna gälla. Men hur? Det visar sig att det är väldigt enkelt: den jämna graden av nämnaren hjälper oss här.

Om du multiplicerar det med förändras ingenting, eller hur? Men nu blir det så här:

På magiskt sätt bytte termerna plats. Detta "fenomen" gäller alla uttryck i jämn grad: vi kan enkelt ändra tecknen inom parentes. Men det är viktigt att komma ihåg: Alla tecken ändras samtidigt! Du kan inte ersätta den med genom att bara ändra en nackdel som vi inte gillar!

Låt oss gå tillbaka till exemplet:

Och återigen formeln:

Så nu den sista regeln:

Hur ska vi bevisa det? Naturligtvis, som vanligt: låt oss utöka begreppet grad och förenkla det:

Nåväl, låt oss nu öppna parenteserna. Hur många bokstäver är det totalt? gånger med multiplikatorer - vad påminner detta dig om? Detta är inget annat än en definition av en operation multiplikation: Det fanns bara multiplikatorer där. Det vill säga, detta är per definition en potens av ett tal med en exponent:

Exempel:

Grad med irrationell exponent

Förutom information om examina för medelnivån kommer vi att analysera graden med en irrationell exponent. Alla regler och egenskaper för grader här är exakt desamma som för en grad med en rationell exponent, med undantag - trots allt, per definition är irrationella tal tal som inte kan representeras som ett bråk, där och är heltal (det vill säga irrationella tal är alla reella tal utom rationella tal).

När vi studerade examina med naturliga, heltals och rationella exponenter skapade vi varje gång en viss "bild", "analogi" eller beskrivning i mer bekanta termer. Till exempel är en grad med en naturlig exponent ett tal multiplicerat med sig själv flera gånger; ett tal till nollpotensen är så att säga ett tal multiplicerat med sig själv en gång, det vill säga de har ännu inte börjat multiplicera det, vilket betyder att talet i sig inte ens har dykt upp ännu - därför är resultatet bara ett visst ”blankt nummer”, nämligen ett nummer; en grad med en heltals negativ exponent - det är som om någon "omvänd process" hade inträffat, det vill säga att talet inte multiplicerades med sig självt, utan dividerades.

Det är extremt svårt att föreställa sig en grad med en irrationell exponent (precis som det är svårt att föreställa sig ett 4-dimensionellt utrymme). Det är snarare ett rent matematiskt objekt som matematiker skapade för att utvidga begreppet grad till hela talrymden.

Förresten, inom vetenskap används ofta en examen med en komplex exponent, det vill säga exponenten är inte ens ett reellt tal. Men i skolan tänker vi inte på sådana svårigheter, du kommer att ha möjlighet att förstå dessa nya koncept på institutet.

Så vad gör vi om vi ser en irrationell exponent? Vi gör vårt bästa för att bli av med det! :)

Till exempel:

Bestäm själv:

Svar:

Låt oss komma ihåg formeln för skillnaden mellan kvadrater. Svar: .
Vi reducerar bråken till samma form: antingen båda decimalerna eller båda vanliga. Vi får till exempel: .
Inget speciellt, vi använder de vanliga egenskaperna för grader:

SAMMANFATTNING AV AVSNITTET OCH GRUNDFORMLER

Grad kallas ett uttryck av formen: , där:

Grad med en heltalsexponent

en grad vars exponent är ett naturligt tal (d.v.s. heltal och positivt).

Makt med rationell exponent

grad, vars exponent är negativa tal och bråktal.

Grad med irrationell exponent

grad vars exponent är oändlig decimal eller rot.

Egenskaper för grader

Funktioner av grader.

Negativt tal höjts till även grad, - antal positiv.
Negativt tal höjts till udda grad, - antal negativ.
Ett positivt tal i vilken grad som helst är ett positivt tal.
Noll är lika med vilken makt som helst.
Alla tal till nollpotensen är lika.

NU HAR DU ORDET...

Hur gillar du artikeln? Skriv nedan i kommentarerna om du gillade det eller inte.

Berätta för oss om din erfarenhet av att använda examensegenskaper.

Kanske har du frågor. Eller förslag.

Skriv i kommentarerna.

Och lycka till på dina tentor!

Lektionens ämne: Att höja produktens makt, kvot och makt

Lektionstyp: Lektion om generalisering och systematisering av kunskap

Genererade resultat:

Ämne. Stärka färdigheterna att använda egenskaperna hos grader med naturliga exponenter

Personlig. Utveckla förmågan att planera ditt agerande i enlighet med den pedagogiska uppgiften

Metasubjekt. Utveckla förstå essensen av algebraiska recept och förmågan att agera i enlighet med den föreslagna algoritmen

Förväntade resultat: Eleverna lär sig att använda egenskaperna hos exponenter med naturliga exponenter för att beräkna betydelsen av uttryck och konvertera uttryck som innehåller exponenter.

Utrustning: kort, multimediaprojektor, signalkort för reflektion.

Organisationsstruktur för lektionen:

1 . Att organisera tid.

Hej kära killar! Jag är väldigt glad att se dig. Låt oss börja mattelektionen

Vilka svårigheter hade du när du utförde uppgiften?

Reflexion.

Framför varje elev finns det muggar i tre färger: röd, grön, blå.

Berätta för mig om ditt humör med hjälp av färgade cirklar (röd– glad, jag är säker på att jag kommer att lära mig många nya saker på lektionen, jag är säker på min kunskap.

Grön -lugna; Jag är säker på min kunskap.

Blå– alarmerande; Jag är inte säker på mig själv).

Jag kommer att muntra upp dig lite med Poissons ord: "Livet förskönas av två saker: att göra matematik och lära ut det."

Låt oss dekorera våra liv!

2. Redogörelse för ämnet och syftet med lektionen.

Idag kommer vi att fortsätta att studera ämnet: "Exponentiering av produkten av en kvot och en examen",

vi kommer att konsolidera alla lärda handlingar med grader,

Vi kommer att lära oss att resonera, tänka logiskt och bevisa vår synpunkt.

3. Blitzundersökning enligt ämnets regler.

Hur multiplicerar man potenser med samma baser? Ge exempel.

Hur delar man grader med samma baser?

Vad är potensen av ett tal a, inte lika med 0, med en nollexponent?

Hur höjer man en produkt till en makt?

Hur höjer man en examen till en makt?

4. Muntlig räkning.

Vem äger dessa ord?

"Bland alla vetenskaper som öppnar vägen för människan att förstå naturlagarna, är den mest kraftfulla, den största vetenskapen matematik."

/Sofya Vasilievna Kovalevskaya/

Den första kvinnan är matematiker.

Du lär dig genom att utföra huvudräkningsuppgifter.

K – Vilken sida har kvadraten om dess area är 49 cm 2. (7 cm)

O – kvadraten på vilket tal är lika med ? ()

B – x 3 x 4 (x 7)

A – x 6 : x 2 (x 4)

L – (x 3) 3 (x 9)

E -
(m 3 )

I -
(m 8 )

MED -
(m 10 )

K – (- 2) 3 (-8)

A - - 2 2 (-4)

I - 2 0 (1)

5. Konsolidering av det som har lärts.

Vi upprepade reglerna för att höja en produkt till en makt och en makt till en makt.

Låt oss nu fokusera på praktiska uppgifter.

Flera personer kommer att passa påforskning. (Glida)

Arbeta i par.

1) Bevisa att kvadraterna av motsatta tal är lika.

2) Bevisa att kuberna med motsatta tal är motsatser.

3) Hur kommer arean på en kvadrat att förändras om dess sida fördubblas; 3 gånger; 10 gånger; n gånger?

4) Hur kommer volymen på en kub att förändras om dess kant fördubblas; 3 gånger; 10 gånger; n gånger?

6. Reflektion: visa mig ditt humör.

7. Fysisk träning: "Jag håller med - jag håller inte med"

Skaka på huvudet om du håller med mig eller inte.

1) (y 2) 3 = y 5 (nej)

2) (-3) 3 = -27 (ja)

3) (-x) 2 = -x 2 (nej)

4) Grafen för funktionen y = 1,3x går genom origo. (Ja)

3 · () 2 – 0,5 2

a) -1; b) - 1 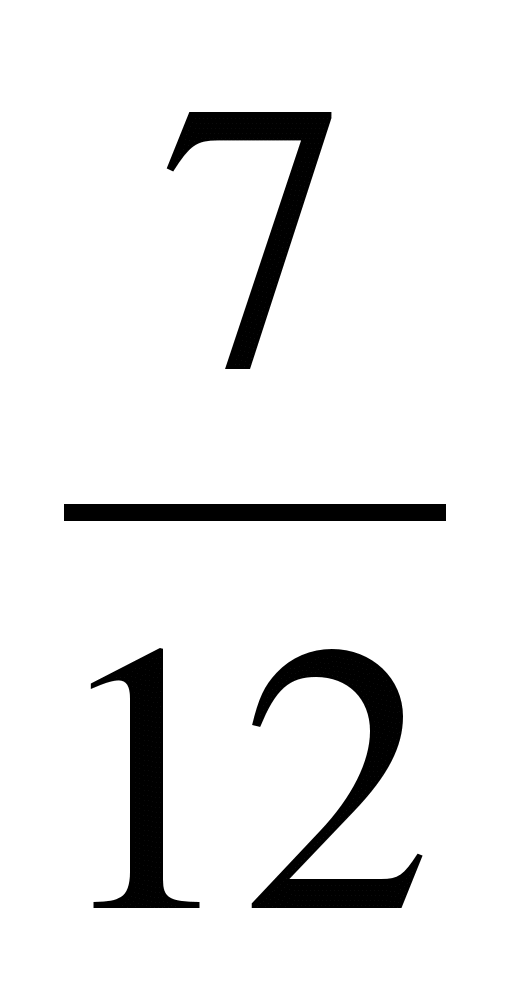; i 1 ; d) 1

2) Förenkla uttrycket:

a) m 10; b)m4; c) m2; d) m 8.

3) Beräkna:

A) 3; b) 9; CD)

4) Vilket uttryck ska ersättas istället för (*) för att få en identitet:

X 8 : (*) = x 4

A) x 4; b) x 2; c) x 8; d) x 12

Kontrollera glidtestet:

9. Låt oss spela "Hitta felet!"

1) en 15 : en 3 = en 5

2) -z · z 5 · z 0 = - z 6 - höger

3)
=

4)(y 4 y) 2 = y 10 - sant

Skriv ner fel uppgifter och lös dem korrekt.

10. Lektionssammanfattning.

Vad lärde du dig på lektionen?

11. D/z

nr 458, 457 (bild)

Rapporter om S.V. Kovalevskaya.

12. Reflektion.

Visa mig hur du känner när du lämnar lektionen?

Slide: Lycka till!

FI:

Självständigt arbete. (testa)

1) Hitta betydelsen av uttrycket:

3· () 2 – 0,5 2

a) -1; b) - 1 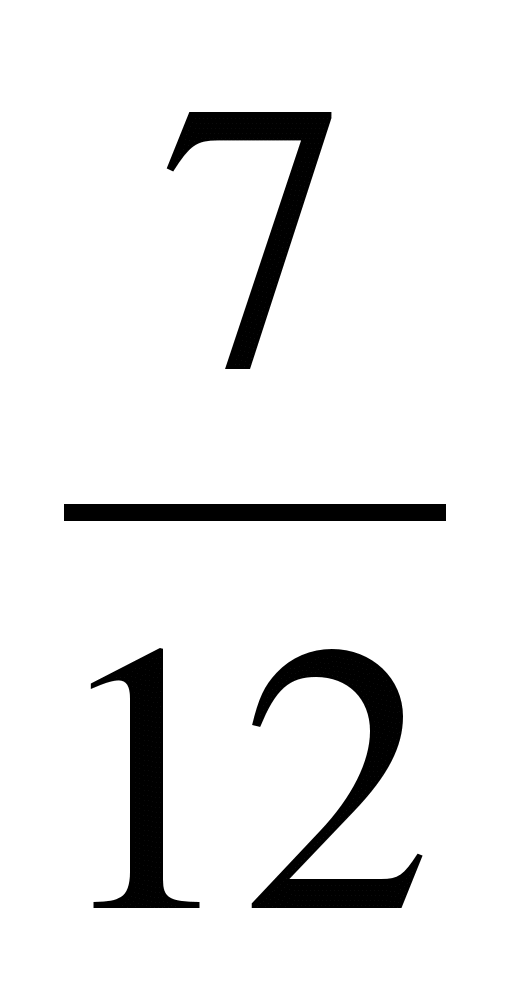; i 1 ; d) 1

2) Förenkla uttrycket:

a) m 10; b)m4; c) m2; d) m 8.

3) Beräkna:

a) 3; b) 9; CD)

4) Vilket uttryck ska ersättas istället för (*) för att få en identitet:

x 8: (*) = x 4

a) x 4; b) x 2; c) x 8; d) x 12

Kvalitet:

Självständigt arbete. (testa)

1) Hitta betydelsen av uttrycket:

3· () 2 – 0,5 2

a) -1; b) - 1 ; i 1 ; d) 1

2) Förenkla uttrycket:

primärt mål

Att bekanta eleverna med graders egenskaper med naturliga exponenter och lära dem hur man utför operationer med grader.

Ämne "Examen och dess egenskaper" innehåller tre frågor:

Bestämning av grad med en naturlig indikator.
Multiplikation och division av potenser.
Exponentiering av produkt och grad.

Kontrollfrågor

Formulera definitionen av en grad med en naturlig exponent större än 1. Ge ett exempel.
Formulera definitionen av grad med exponent 1. Ge ett exempel.
Vilken är operationsordningen när man beräknar värdet på ett uttryck som innehåller potenser?
Formulera examens huvudsakliga egenskap. Ge ett exempel.
Formulera regeln för att multiplicera potenser med samma baser. Ge ett exempel.
Formulera en regel för att dividera potenser med samma baser. Ge ett exempel.
Formulera regeln för exponentiering av en produkt. Ge ett exempel. Bevisa identiteten (ab) n = a n b n .
Formulera regeln för att höja en makt till en makt. Ge ett exempel. Bevisa identiteten (a m) n = a m n .

Definition av examen.

Talets makt a med naturlig indikator n, större än 1, är produkten av n faktorer, som var och en är lika A. Talets makt A med exponent 1 är själva talet A.

Grad med bas A och indikator när skrivet så här: och n. Det står " A till en viss grad n”; " n:te potens av ett tal A ”.

Per definition av examen:

a 4 = a a a a

. . . . . . . . . . . .

Att hitta värdet på en potens kallas genom exponentiering .

1. Exempel på exponentiering:

3 3 = 3 3 3 = 27

0 4 = 0 0 0 0 = 0

(-5) 3 = (-5) (-5) (-5) = -125

25 ; 0,09 ;

25 = 5 2 ; 0,09 = (0,3) 2 ; .

27 ; 0,001 ; 8 .

27 = 3 3 ; 0,001 = (0,1) 3 ; 8 = 2 3 .

4. Hitta betydelsen av uttrycken:

a) 3 10 3 = 3 10 10 10 = 3 1000 = 3000

b) -24 + (-3)2 = 7
2 4 = 16
(-3) 2 = 9
-16 + 9 = 7

Alternativ 1

a) 0,3 0,3 0,3

c) b b b b b b b

d) (-x) (-x) (-x) (-x)

e) (ab) (ab) (ab)

2. Presentera talet som en kvadrat:

3. Presentera talen som en kub:

4. Hitta betydelsen av uttrycken:

c) -14 + (-2) 3

d) -4 3 + (-3) 2

e) 100 - 5 2 4

Multiplikation av potenser.

För alla tal a och godtyckliga tal m och n gäller följande:

a m a n = a m + n .

Bevis:

Regel : När potenser multipliceras med samma baser lämnas baserna desamma, och potensernas exponenter adderas.

a m a n a k = a m + n a k = a (m + n) + k = a m + n + k

a) x 5 x 4 = x 5 + 4 = x 9

b) y y 6 = y 1 y 6 = y 1 + 6 = y 7

c) b 2 b 5 b 4 = b 2 + 5 + 4 = b 11

d) 3 4 9 = 3 4 3 2 = 3 6

e) 0,01 0,1 3 = 0,1 2 0,1 3 = 0,1 5

a) 2 3 2 = 2 4 = 16

b) 3 2 3 5 = 3 7 = 2187

Alternativ 1

1. Presentera som examen:

a) x 3 x 4 e) x 2 x 3 x 4

b) a 6 a 2 g) 3 3 9

c) å 4 å h) 7 4 49

d) a a 8 i) 16 2 7

e) 2 3 2 4 j) 0,3 3 0,09

2. Presentera som en grad och hitta värdet från tabellen:

a) 2 2 2 3 c) 8 2 5

b) 3 4 3 2 d) 27 243

Indelning av examina.

För alla tal a0 och godtyckliga naturliga tal m och n, så att m>n gäller följande:

a m: a n = a m - n

Bevis:

a m - n a n = a (m - n) + n = a m - n + n = a m

per definition av kvot:

a m: a n = a m - n .

Regel: När man dividerar potenser med samma bas, lämnas basen densamma, och exponenten för divisorn subtraheras från exponenten för utdelningen.

Definition: Potensen för ett tal a, inte lika med noll, med en nollexponent är lika med ett:

därför att a n: a n = 1 vid a0.

a) x 4: x 2 = x 4 - 2 = x 2

b) y 8: y 3 = y 8 - 3 = y 5

c) a 7:a = a 7:a 1 = a 7 - 1 = a 6

d) från 5:från 0 = från 5:1 = från 5

a) 5 7:5 5 = 5 2 = 25

b) 10 20:10 17 = 10 3 = 1000

V)

G)

d)

Alternativ 1

1. Presentera kvoten som en potens:

2. Hitta betydelsen av uttrycken:

Att höja kraften i en produkt.

För alla a och b och ett godtyckligt naturligt tal n:

(ab) n = a n b n

Bevis:

Per definition av examen

(ab)n=

Om vi grupperar faktorerna a och faktorerna b separat får vi:

Den bevisade egenskapen hos en produkts kraft sträcker sig till produktens kraft av tre eller flera faktorer.

Till exempel:

(abc)n = anbncn;

(a b c d) n = a n b n c n d n .

Regel: När man höjer en produkt till en makt, höjs varje faktor till den makten och resultatet multipliceras.

1. Höj till en makt:

a) (a b) 4 = a 4 b 4

b) (2 x y) 3 =2 3 x 3 y 3 = 8 x 3 y 3

c) (3 a) 4 = 3 4 a 4 = 81 a 4

d) (-5 y) 3 = (-5) 3 y 3 = -125 y 3

e) (-0,2 x y) 2 = (-0,2) 2 x 2 y 2 = 0,04 x 2 y 2

e) (-3 a b c) 4 = (-3) 4 a 4 b 4 c 4 = 81 a 4 b 4 c 4

2. Hitta värdet på uttrycket:

a) (2 10) 4 = 2 4 10 4 = 16 1000 = 16 000

b) (3 5 20) 2 = 3 2 100 2 = 9 10000= 90000

c) 2 4 5 4 = (2 5) 4 = 10 4 = 10 000

d) 0,25 11 4 11 = (0,25 4) 11 = 1 11 = 1

d)

Alternativ 1

1. Höj till en makt:

b) (2 a c) 4

e) (-0,1 x y) 3

2. Hitta värdet på uttrycket:

b) (5 7 20) 2

Att höja sig till en makts makt.

För alla tal a och godtyckliga naturliga tal m och n:

(a m) n = a m n

Bevis:

Per definition av examen

(a m) n =

Regel: När man höjer en potens till en potens, lämnas basen densamma, och exponenterna multipliceras.

1. Höj till en makt:

(a 3) 2 = a 6 (x 5) 4 = x 20

(y 5) 2 = y 10 (b 3) 3 = b 9

2. Förenkla uttrycken:

a) a 3 (a 2) 5 = a 3 a 10 = a 13

b) (b 3) 2 b 7 = b 6 b 7 = b 13

c) (x 3) 2 (x 2) 4 = x 6 x 8 = x 14

d) (y 7) 3 = (y 8) 3 = y 24

A)

b)

Alternativ 1

1. Höj till en makt:

a) (a 4) 2 b) (x 4) 5

c) (y 3) 2 d) (b 4) 4

2. Förenkla uttrycken:

a) a 4 (a 3) 2

b) (b 4) 3 b 5+

c) (x 2) 4 (x 4) 3

d) (y 9) 2

3. Hitta betydelsen av uttrycken:

Ansökan

Definition av examen.

Alternativ 2

1. Skriv produkten som en kraft:

a) 0,4 0,4 0,4

c) a a a a a a a a

d) (-y) (-y) (-y) (-y)

e) (bс) (bс) (bс)

2. Presentera talet som en kvadrat:

3. Presentera talen som en kub:

4. Hitta betydelsen av uttrycken:

c) -13 + (-2) 4

d) -6 2 + (-3) 2

e) 4 5 2 – 100

Alternativ 3

1. Skriv produkten som en kraft:

a) 0,5 0,5 0,5

c) med med med med med med med med

d) (-x) (-x) (-x) (-x)

e) (ab) (ab) (ab)

2. Presentera talet som en kvadrat: 100; 0,49; .

3. Presentera talen som en kub:

4. Hitta betydelsen av uttrycken:

c) -15 + (-3) 2

d) -5 3 + (-4) 2

e) 5 4 2 - 100

Alternativ 4

1. Skriv produkten som en kraft:

a) 0,7 0,7 0,7

c) x x x x x x

d) (-a) (-a) (-a)

e) (bc) (bc) (bc) (bc)

2. Presentera talet som en kvadrat:

3. Presentera talen som en kub:

4. Hitta betydelsen av uttrycken:

c) -14 + (-3) 3

d) -3 4 + (-5) 2

e) 100 - 3 2 5

Multiplikation av potenser.

Alternativ 2

1. Presentera som examen:

a) x 4 x 5 e) x 3 x 4 x 5

b) a 7 a 3 g) 2 3 4

c) å 5 å h) 4 3 16

d) a a 7 i) 4 2 5

e) 2 2 2 5 j) 0,2 3 0,04

2. Presentera som en grad och hitta värdet från tabellen:

a) 3 2 3 3 c) 16 2 3

b) 2 4 2 5 d) 9 81

Alternativ 3

1. Presentera som examen:

a) a 3 a 5 f) y 2 y 4 y 6

b) x 4 x 7 g) 3 5 9

c) b 6 b h) 5 3 25

d) y 8 i) 49 7 4

e) 2 3 2 6 j) 0,3 4 0,27

2. Presentera som en grad och hitta värdet från tabellen:

a) 3 3 3 4 c) 27 3 4

b) 2 4 2 6 d) 16 64

Alternativ 4

1. Presentera som examen:

a) a 6 a 2 e) x 4 x x 6

b) x 7 x 8 g) 3 4 27

c) å 6 å h) 4 3 16

d) x x 10 i) 36 6 3

e) 2 4 2 5 j) 0,2 2 0,008

2. Presentera som en grad och hitta värdet från tabellen:

a) 2 6 2 3 c) 64 2 4

b) 3 5 3 2 d) 81 27

Indelning av examina.

Alternativ 2

1. Presentera kvoten som en potens:

2. Hitta betydelsen av uttrycken:

Vi påminner dig om att i den här lektionen kommer vi att förstå egenskaper hos grader med naturliga indikatorer och noll. Grader med rationella indikatorer och deras egenskaper kommer att diskuteras i lektioner för årskurs 8.

En potens med naturlig exponent har flera viktiga egenskaper som gör att vi kan förenkla beräkningar i exempel med potenser.

Fastighet nr 1
Produkt av makter

Kom ihåg!

När potenser multipliceras med samma baser förblir basen oförändrad, och potensernas exponenter adderas.

a m · a n = a m + n, där "a" är valfritt tal och "m", "n" är alla naturliga tal.

Denna egenskap hos makter gäller även produkten av tre eller flera potenser.

Förenkla uttrycket.
b b 2 b 3 b 4 b 5 = b 1 + 2 + 3 + 4 + 5 = b 15
Presentera det som en examen.
6 15 36 = 6 15 6 2 = 6 15 6 2 = 6 17
Presentera det som en examen.
(0,8) 3 · (0,8) 12 = (0,8) 3 + 12 = (0,8) 15

Viktig!

Observera att vi i den angivna egenskapen bara pratade om att multiplicera potenser med på samma grunder . Det gäller inte deras tillägg.

Du kan inte ersätta summan (3 3 + 3 2) med 3 5. Detta är förståeligt om
beräkna (3 3 + 3 2) = (27 + 9) = 36 och 3 5 = 243

Fastighet nr 2
Partiella examina

Kom ihåg!

När man dividerar potenser med samma baser förblir basen oförändrad, och divisorns exponent subtraheras från exponenten för utdelningen.

= 11 3 − 2 4 2 − 1 = 11 4 = 44

Exempel. Lös ekvationen. Vi använder egenskapen kvotbefogenheter.
3 8: t = 3 4

T = 3 8 − 4

Svar: t = 3 4 = 81

Med hjälp av egenskaper nr 1 och nr 2 kan du enkelt förenkla uttryck och utföra beräkningar.

Exempel. Förenkla uttrycket.
4 5m + 6 4 m + 2: 4 4m + 3 = 4 5m + 6 + m + 2: 4 4m + 3 = 4 6m + 8 − 4m − 3 = 4 2m + 5
Exempel. Hitta värdet på ett uttryck med hjälp av egenskaperna hos exponenter.
= = = 2 9 + 2
2 5
= 2 11
2 5
= 2 11 − 5 = 2 6 = 64
Viktig!
Observera att vi i fastighet 2 bara pratade om att dela potenser med samma baser.

Du kan inte ersätta skillnaden (4 3 −4 2) med 4 1. Detta är förståeligt om man räknar (4 3 −4 2) = (64 − 16) = 48 och 4 1 = 4

Var försiktig!

Fastighet nr 3
Att höja en grad till en makt

Kom ihåg!
När man höjer en grad till en potens förblir gradens bas oförändrad och exponenterna multipliceras.
(a n) m = a n · m, där "a" är valfritt tal och "m", "n" är alla naturliga tal.

Egenskaper 4
Produktkraft

Kom ihåg!
När man höjer en produkt till en makt, höjs var och en av faktorerna till en makt. De erhållna resultaten multipliceras sedan.
(a b) n = a n b n, där "a", "b" är alla rationella tal; "n" är vilket naturligt tal som helst.
- Exempel 1.
  (6 a 2 b 3 c) 2 = 6 2 a 2 2 b 3 2 c 1 2 = 36 a 4 b 6 c 2
- Exempel 2.
  (−x 2 y) 6 = ((−1) 6 x 2 6 y 1 6) = x 12 y 6
Viktig!
Observera att egenskap nr 4, liksom andra egenskaper för grader, också tillämpas i omvänd ordning.
(a n · b n)= (a · b) n
Det vill säga, för att multiplicera potenser med samma exponenter kan du multiplicera baserna, men lämna exponenten oförändrad.
- Exempel. Beräkna.
  2 4 5 4 = (2 5) 4 = 10 4 = 10 000
- Exempel. Beräkna.
  0,5 16 2 16 = (0,5 2) 16 = 1
I mer komplexa exempel Det kan finnas fall då multiplikation och division måste utföras på potenser med olika baser och olika exponenter. I det här fallet rekommenderar vi att du gör följande.

Till exempel, 4 5 3 2 = 4 3 4 2 3 2 = 4 3 (4 3) 2 = 64 12 2 = 64 144 = 9216

Ett exempel på att höja en decimal till en potens.
4 21 (−0,25) 20 = 4 4 20 (−0,25) 20 = 4 (4 (−0,25)) 20 = 4 (−1) 20 = 4 1 = 4
Egenskaper 5
Kraften i en kvot (bråkdel)

Kom ihåg!
För att höja en kvot till en potens kan du höja utdelningen och divisorn separat till denna potens och dividera det första resultatet med det andra.
(a: b) n = a n: b n, där "a", "b" är alla rationella tal, b ≠ 0, n är vilket naturligt tal som helst.
- Exempel. Presentera uttrycket som en maktkvot.
  (5: 3) 12 = 5 12: 3 12
Vi påminner om att en kvot kan representeras som en bråkdel. Därför kommer vi att uppehålla oss vid ämnet att höja en bråkdel till en makt mer detaljerat på nästa sida.