Modulärt schema. Funktionsdiagram med modul

Modulen är en av de saker som alla verkar ha hört talas om, men i verkligheten är det ingen som riktigt förstår. Därför kommer det idag att finnas en stor lektion tillägnad att lösa ekvationer med moduler.

Jag säger genast: lektionen kommer inte att vara svår. Och generellt sett är moduler ett relativt enkelt ämne. "Ja, självklart, det är inte komplicerat! Det får mig att bli förbannad!" – kommer många elever att säga, men alla dessa hjärnbrott uppstår på grund av att de flesta inte har kunskap i huvudet, utan någon form av skit. Och målet med den här lektionen är att förvandla skit till kunskap. :)

Lite teori

Låt oss gå. Låt oss börja med det viktigaste: vad är en modul? Låt mig påminna dig om att modulen för ett tal helt enkelt är samma tal, men taget utan minustecknet. Det är till exempel $\left| -5 \right|=5$. Eller $\left| -129,5 \right|=129,5 $.

Är det så enkelt? Ja, enkelt. Vad är då det absoluta värdet av ett positivt tal? Det är ännu enklare här: modulen för ett positivt tal är lika med detta tal: $\left| 5 \right|=5$; $\left| 129,5 \right|=$129,5 osv.

\[\vänster| -a \höger|=\vänster| a\right|\]

Ett annat viktigt faktum: modul är aldrig negativ. Vilket tal vi än tar - vare sig det är positivt eller negativt - visar sig dess modul alltid vara positiv (eller, i extrema fall, noll). Det är därför som modulen ofta kallas för det absoluta värdet av ett tal.

Dessutom, om vi kombinerar definitionen av modulen för ett positivt och negativt tal, får vi en global definition av modulen för alla tal. Nämligen: modulen för ett tal är lika med själva talet om talet är positivt (eller noll), eller lika med det motsatta talet om talet är negativt. Du kan skriva detta som en formel:

Det finns också en modul på noll, men den är alltid lika med noll. Dessutom är noll det enda tal som inte har en motsats.

Alltså, om vi betraktar funktionen $y=\left| x \right|$ och försök rita dess graf, får du något sånt här:

Modulgraf och exempel på att lösa ekvationen

Från denna bild är det omedelbart tydligt att $\left| -m \höger|=\vänster| m \right|$, och modulgrafen faller aldrig under x-axeln. Men det är inte allt: den röda linjen markerar den raka linjen $y=a$, som, för positiv $a$, ger oss två rötter samtidigt: $((x)_(1))$ och $((x) _(2)) $, men vi pratar om det senare. :)

Förutom den rent algebraiska definitionen finns det en geometrisk. Låt oss säga att det finns två punkter på tallinjen: $((x)_(1))$ och $((x)_(2))$. I det här fallet uttrycket $\left| ((x)_(1))-((x)_(2)) \right|$ är helt enkelt avståndet mellan de angivna punkterna. Eller, om du föredrar, längden på segmentet som förbinder dessa punkter:

Modul är avståndet mellan punkter på en tallinje

Denna definition innebär också att modulen alltid är icke-negativ. Men tillräckligt med definitioner och teorier - låt oss gå vidare till riktiga ekvationer. :)

Grundformel

Okej, vi har reda ut definitionen. Men det gjorde det inte lättare. Hur löser man ekvationer som innehåller just denna modul?

Lugn, bara lugn. Låt oss börja med de enklaste sakerna. Tänk på något i stil med detta:

\[\vänster| x\right|=3\]

Så modulen för $x$ är 3. Vad kan $x$ vara lika med? Tja, av definitionen att döma är vi ganska nöjda med $x=3$. Verkligen:

\[\vänster| 3\höger|=3\]

Finns det andra siffror? Cap verkar antyda att det finns. Till exempel är $x=-3$ också $\left| -3 \right|=3$, dvs. den erforderliga jämlikheten är uppfylld.

Så kanske om vi letar och tänker så hittar vi fler siffror? Men bryt det: fler siffror Nej. Ekvation $\vänster| x \right|=3$ har bara två rötter: $x=3$ och $x=-3$.

Låt oss nu komplicera uppgiften lite. Låt funktionen $f\left(x \right)$ hänga ut under modultecknet istället för variabeln $x$, och sätt ett godtyckligt tal $a$ i stället för trippeln till höger. Vi får ekvationen:

\[\vänster| f\left(x \right) \right|=a\]

Så hur kan vi lösa detta? Låt mig påminna dig: $f\left(x \right)$ är en godtycklig funktion, $a$ är vilket tal som helst. De där. Vad som helst! Till exempel:

\[\vänster| 2x+1 \right|=5\]

\[\vänster| 10x-5 \right|=-65\]

Låt oss uppmärksamma den andra ekvationen. Du kan genast säga om honom: han har inga rötter. Varför? Allt är korrekt: eftersom det kräver att modulen är lika med ett negativt tal, vilket aldrig händer, eftersom vi redan vet att modulen alltid är ett positivt tal eller, i extrema fall, noll.

Men med den första ekvationen är allt roligare. Det finns två alternativ: antingen finns det ett positivt uttryck under modultecknet och sedan $\left| 2x+1 \right|=2x+1$, eller så är uttrycket fortfarande negativt, och sedan $\left| 2x+1 \höger|=-\vänster(2x+1 \höger)=-2x-1$. I det första fallet kommer vår ekvation att skrivas om enligt följande:

\[\vänster| 2x+1 \höger|=5\högerpil 2x+1=5\]

Och plötsligt visar det sig att det submodulära uttrycket $2x+1$ verkligen är positivt - det är lika med siffran 5. Dvs. vi kan säkert lösa denna ekvation - den resulterande roten kommer att vara en del av svaret:

De som är särskilt misstroende kan försöka ersätta den hittade roten i den ursprungliga ekvationen och se till att modulen faktiskt blir Positivt nummer.

Låt oss nu titta på fallet med ett negativt submodulärt uttryck:

\[\left\( \begin(align)& \left| 2x+1 \right|=5 \\& 2x+1 \lt 0 \\\end(align) \right.\Rightarrow -2x-1=5 \Högerpil 2x+1=-5\]

hoppsan! Återigen, allt är klart: vi antog att $2x+1 \lt 0$, och som ett resultat fick vi att $2x+1=-5$ - verkligen, detta uttryck är mindre än noll. Vi löser den resulterande ekvationen, samtidigt som vi redan vet säkert att den hittade roten kommer att passa oss:

Totalt fick vi återigen två svar: $x=2$ och $x=3$. Ja, mängden beräkningar visade sig vara lite större än i den mycket enkla ekvationen $\left| x \right|=3$, men ingenting har förändrats i grunden. Så det kanske finns någon form av universell algoritm?

Ja, en sådan algoritm finns. Och nu ska vi analysera det.

Att bli av med modultecknet

Låt oss ges ekvationen $\left| f\left(x \right) \right|=a$, och $a\ge 0$ (annars, som vi redan vet, finns det inga rötter). Då kan du bli av med modultecknet med hjälp av följande regel:

\[\vänster| f\vänster(x \höger) \höger|=a\högerpil f\vänster(x \höger)=\pm a\]

Således delas vår ekvation med en modul i två, men utan en modul. Det är allt tekniken är! Låt oss försöka lösa ett par ekvationer. Låt oss börja med detta

\[\vänster| 5x+4 \right|=10\Högerpil 5x+4=\pm 10\]

Låt oss överväga separat när det finns ett tio plus till höger, och separat när det finns ett minus. Vi har:

\[\begin(align)& 5x+4=10\Högerpil 5x=6\Högerpil x=\frac(6)(5)=1,2; \\& 5x+4=-10\Högerpil 5x=-14\Högerpil x=-\frac(14)(5)=-2.8. \\\end(align)\]

Det är allt! Vi fick två rötter: $x=1.2$ och $x=-2.8$. Hela lösningen tog bokstavligen två rader.

Okej, ingen fråga, låt oss titta på något lite mer allvarligt:

\[\vänster| 7-5x\höger|=13\]

Återigen öppnar vi modulen med plus och minus:

\[\begin(align)& 7-5x=13\Högerpil -5x=6\Högerpil x=-\frac(6)(5)=-1,2; \\& 7-5x=-13\Högerpil -5x=-20\Högerpil x=4. \\\end(align)\]

Ett par rader igen - och svaret är klart! Som sagt, det är inget komplicerat med moduler. Du behöver bara komma ihåg några regler. Därför går vi vidare och börjar med verkligt mer komplexa uppgifter.

Fallet med en variabel på höger sida

Tänk nu på denna ekvation:

\[\vänster| 3x-2 \right|=2x\]

Denna ekvation skiljer sig fundamentalt från alla tidigare. Hur? Och det faktum att till höger om likhetstecknet står uttrycket $2x$ – och vi kan inte på förhand veta om det är positivt eller negativt.

Vad ska man göra i det här fallet? Först måste vi förstå det en gång för alla om den högra sidan av ekvationen visar sig vara negativ, kommer ekvationen inte att ha några rötter- Vi vet redan att modulen inte kan vara lika med ett negativt tal.

Och för det andra, om den högra delen fortfarande är positiv (eller lika med noll), kan du agera på exakt samma sätt som tidigare: öppna helt enkelt modulen separat med ett plustecken och separat med ett minustecken.

Således formulerar vi en regel för godtyckliga funktioner $f\left(x \right)$ och $g\left(x \right)$:

\[\vänster| f\left(x \right) \right|=g\left(x \right)\Högerpil \left\( \begin(align)& f\left(x \right)=\pm g\left(x \right ), \\& g\left(x \right)\ge 0. \\\end(align) \right.\]

I relation till vår ekvation får vi:

\[\vänster| 3x-2 \right|=2x\Högerpil \left\( \begin(align)& 3x-2=\pm 2x, \\& 2x\ge 0. \\\end(align) \right.\]

Tja, vi kommer på något sätt att klara av kravet $2x\ge 0$. I slutändan kan vi dumt ersätta rötterna som vi får från den första ekvationen och kontrollera om ojämlikheten håller eller inte.

Så låt oss lösa själva ekvationen:

\[\begin(align)& 3x-2=2\Högerpil 3x=4\Högerpil x=\frac(4)(3); \\& 3x-2=-2\Högerpil 3x=0\Högerpil x=0. \\\end(align)\]

Tja, vilken av dessa två rötter uppfyller kravet $2x\ge 0$? Ja båda! Därför blir svaret två siffror: $x=(4)/(3)\;$ och $x=0$. Det är lösningen. :)

Jag misstänker att några av eleverna redan börjar bli uttråkade? Tja, låt oss titta på en ännu mer komplex ekvation:

\[\vänster| ((x)^(3))-3((x)^(2))+x \höger|=x-((x)^(3))\]

Även om det ser ondskefullt ut, är det i själva verket fortfarande samma ekvation av formen "modul är lika med funktion":

\[\vänster| f\vänster(x \höger) \höger|=g\vänster(x \höger)\]

Och det är löst på exakt samma sätt:

\[\vänster| ((x)^(3))-3((x)^(2))+x \höger|=x-((x)^(3))\Högerpil \left\( \begin(align)& ( (x)^(3))-3((x)^(2))+x=\pm \vänster(x-((x)^(3)) \höger), \\& x-((x) )^(3))\ge 0. \\\end(align) \right.\]

Vi kommer att ta itu med ojämlikhet senare - det är på något sätt för ondskefullt (i själva verket är det enkelt, men vi kommer inte att lösa det). För nu är det bättre att ta itu med de resulterande ekvationerna. Låt oss överväga det första fallet - det här är när modulen utökas med ett plustecken:

\[((x)^(3))-3((x)^(2))+x=x-((x)^(3))\]

Tja, det är enkelt att du behöver samla allt från vänster, ta med liknande och se vad som händer. Och detta är vad som händer:

\[\begin(align)& ((x)^(3))-3((x)^(2))+x=x-((x)^(3)); \\& 2((x)^(3))-3((x)^(2))=0; \\\end(align)\]

Vi tar ut den gemensam multiplikator$((x)^(2))$ utanför parentes och vi får en mycket enkel ekvation:

\[((x)^(2))\left(2x-3 \right)=0\Högerpil \left[ \begin(align)& ((x)^(2))=0 \\& 2x-3 =0 \\\end(align) \right.\]

\[((x)_(1))=0;\quad ((x)_(2))=\frac(3)(2)=1.5.\]

Här utnyttjade vi en viktig egenskap hos produkten, för vilken vi faktoriserade det ursprungliga polynomet: produkten är lika med noll när minst en av faktorerna är lika med noll.

Låt oss nu ta itu med den andra ekvationen på exakt samma sätt, som erhålls genom att expandera modulen med ett minustecken:

\[\begin(align)& ((x)^(3))-3((x)^(2))+x=-\left(x-((x)^(3)) \right); \\& ((x)^(3))-3((x)^(2))+x=-x+((x)^(3)); \\& -3((x)^(2))+2x=0; \\& x\vänster(-3x+2 \höger)=0. \\\end(align)\]

Återigen samma sak: produkten är lika med noll när minst en av faktorerna är lika med noll. Vi har:

\[\left[ \begin(align)& x=0 \\& -3x+2=0 \\\end(align) \right.\]

Tja, vi har tre rötter: $x=0$, $x=1.5$ och $x=(2)/(3)\;$. Tja, vilken av denna uppsättning kommer att gå in i det slutliga svaret? För att göra detta, kom ihåg att vi har en ytterligare begränsning i form av ojämlikhet:

Hur tar man hänsyn till detta krav? Låt oss bara ersätta de hittade rötterna och kontrollera om ojämlikheten gäller för dessa $x$ eller inte. Vi har:

\[\begin(align)& x=0\Högerpil x-((x)^(3))=0-0=0\ge 0; \\& x=1,5\Högerpil x-((x)^(3))=1,5-((1,5)^(3)) \lt 0; \\& x=\frac(2)(3)\Högerpil x-((x)^(3))=\frac(2)(3)-\frac(8)(27)=\frac(10) (27)\ge 0; \\\end(align)\]

Roten $x=1.5$ passar oss alltså inte. Och som svar kommer det bara att finnas två rötter:

\[((x)_(1))=0;\quad ((x)_(2))=\frac(2)(3).\]

Som du kan se, även i det här fallet var det inget komplicerat - ekvationer med moduler löses alltid med en algoritm. Du behöver bara ha en god förståelse för polynom och ojämlikheter. Därför går vi vidare till mer komplexa uppgifter - det kommer redan att finnas inte en, utan två moduler.

Ekvationer med två moduler

Hittills har vi bara studerat mest enkla ekvationer— det fanns en modul och något annat. Vi skickade detta "något annat" till en annan del av ojämlikheten, bort från modulen, så att allt i slutändan skulle reduceras till en ekvation av formen $\left| f\left(x \right) \right|=g\left(x \right)$ eller ännu enklare $\left| f\left(x \right) \right|=a$.

Men dagis slutade - det är dags att överväga något mer seriöst. Låt oss börja med ekvationer så här:

\[\vänster| f\vänster(x \höger) \höger|=\vänster| g\vänster(x \höger) \höger|\]

Detta är en ekvation av formen "modul lika med modul" En fundamentalt viktig punkt är frånvaron av andra termer och faktorer: bara en modul till vänster, en modul till till höger - och inget mer.

Någon kommer nu att tycka att sådana ekvationer är svårare att lösa än vad vi har studerat hittills. Men nej: dessa ekvationer är ännu lättare att lösa. Här är formeln:

\[\vänster| f\vänster(x \höger) \höger|=\vänster| g\vänster(x \höger) \höger|\Högerpil f\vänster(x \höger)=\pm g\vänster(x \höger)\]

Allt! Vi sätter helt enkelt likhetstecken mellan submodulära uttryck genom att sätta ett plus- eller minustecken framför ett av dem. Och sedan löser vi de två resulterande ekvationerna - och rötterna är klara! Inga ytterligare begränsningar, inga ojämlikheter osv. Allt är väldigt enkelt.

Låt oss försöka lösa det här problemet:

\[\vänster| 2x+3 \höger|=\vänster| 2x-7 \right|\]

Elementär Watson! Utöka modulerna:

\[\vänster| 2x+3 \höger|=\vänster| 2x-7 \höger|\högerpil 2x+3=\pm \left(2x-7 \höger)\]

Låt oss överväga varje fall separat:

\[\begin(align)& 2x+3=2x-7\Högerpil 3=-7\Högerpil \emptyset ; \\& 2x+3=-\vänster(2x-7 \höger)\Högerpil 2x+3=-2x+7. \\\end(align)\]

Den första ekvationen har inga rötter. För när är $3=-7$? Vid vilka värden på $x$? "Vad fan är $x$? Är du hög? Det finns inga $x$ där alls", säger du. Och du kommer att ha rätt. Vi har fått en likhet som inte är beroende av variabeln $x$, och samtidigt är själva likheten felaktig. Det är därför det inte finns några rötter. :)

Med den andra ekvationen är allt lite mer intressant, men också väldigt, väldigt enkelt:

Som du kan se löstes allt bokstavligen på ett par rader - vi förväntade oss inget annat från en linjär ekvation. :)

Som ett resultat blir det slutliga svaret: $x=1$.

Så hur? Svår? Självklart inte. Låt oss prova något annat:

\[\vänster| x-1 \höger|=\vänster| ((x)^(2))-3x+2 \höger|\]

Återigen har vi en ekvation av formen $\left| f\vänster(x \höger) \höger|=\vänster| g\left(x \right) \right|$. Därför skriver vi om det omedelbart och avslöjar modultecknet:

\[((x)^(2))-3x+2=\pm \left(x-1 \höger)\]

Kanske kommer någon nu att fråga: ”Hej, vilka dumheter? Varför visas "plus-minus" på det högra uttrycket och inte till vänster?" Lugn, jag ska förklara allt nu. På ett bra sätt borde vi faktiskt ha skrivit om vår ekvation enligt följande:

Sedan måste du öppna parenteserna, flytta alla termer till ena sidan av likhetstecknet (eftersom ekvationen uppenbarligen kommer att vara kvadratisk i båda fallen) och sedan hitta rötterna. Men du måste erkänna: när "plus-minus" förekommer före tre termer (särskilt när en av dessa termer är ett kvadratiskt uttryck), ser det på något sätt mer komplicerat ut än situationen när "plus-minus" förekommer endast före två termer.

Men ingenting hindrar oss från att skriva om den ursprungliga ekvationen enligt följande:

Vad hände? Inget speciellt: de har precis bytt den vänstra och höger sida på några ställen. En liten sak som i slutändan kommer att göra vårt liv lite lättare. :)

I allmänhet löser vi denna ekvation, med tanke på alternativ med plus och minus:

\[\begin(align)& ((x)^(2))-3x+2=x-1\Högerpil ((x)^(2))-4x+3=0; \\& ((x)^(2))-3x+2=-\vänster(x-1 \höger)\Högerpil ((x)^(2))-2x+1=0. \\\end(align)\]

Den första ekvationen har rötter $x=3$ och $x=1$. Den andra är i allmänhet en exakt kvadrat:

\[((x)^(2))-2x+1=((\vänster(x-1 \höger))^(2))\]

Därför har den bara en rot: $x=1$. Men vi har redan fått denna rot tidigare. Således kommer endast två siffror att gå in i det slutliga svaret:

\[((x)_(1))=3;\quad ((x)_(2))=1.\]

Uppdrag slutfört! Du kan ta en paj från hyllan och äta den. Det finns 2 av dem, din är den mellersta. :)

Viktig notering. Närvaron av identiska rötter för olika varianter av expansion av modulen innebär att de ursprungliga polynomen faktoriseras, och bland dessa faktorer kommer det definitivt att finnas en gemensam sådan. Verkligen:

\[\begin(align)& \left| x-1 \höger|=\vänster| ((x)^(2))-3x+2 \höger|; \\& \vänster| x-1 \höger|=\vänster| \left(x-1 \right)\left(x-2 \right) \right|. \\\end(align)\]

En av modulegenskaperna: $\left| a\cdot b \höger|=\vänster| en \right|\cdot \left| b \right|$ (dvs. produktens modul är lika med produkten av modulerna), så den ursprungliga ekvationen kan skrivas om enligt följande:

\[\vänster| x-1 \höger|=\vänster| x-1 \right|\cdot \left| x-2 \right|\]

Som ni ser har vi verkligen en gemensam faktor. Nu, om du samlar alla moduler på ena sidan, kan du ta bort denna faktor ur fästet:

\[\begin(align)& \left| x-1 \höger|=\vänster| x-1 \right|\cdot \left| x-2 \right|; \\& \vänster| x-1 \höger|-\vänster| x-1 \right|\cdot \left| x-2 \right|=0; \\& \vänster| x-1 \right|\cdot \left(1-\left| x-2 \right| \right)=0. \\\end(align)\]

Tja, kom nu ihåg att produkten är lika med noll när minst en av faktorerna är lika med noll:

\[\left[ \begin(align)& \left| x-1 \right|=0, \\& \left| x-2 \right|=1. \\\end(align) \right.\]

Därmed har den ursprungliga ekvationen med två moduler reducerats till de två enklaste ekvationerna som vi pratade om alldeles i början av lektionen. Sådana ekvationer kan lösas bokstavligen på ett par rader. :)

Denna kommentar kan tyckas onödigt komplicerad och otillämplig i praktiken. Men i verkligheten kan du stöta på mycket mer komplexa problem än de vi tittar på idag. I dem kan moduler kombineras med polynom, aritmetiska rötter, logaritmer etc. Och i sådana situationer kan möjligheten att sänka ekvationens övergripande grad genom att ta något utanför parentes vara väldigt, väldigt användbar. :)

Nu skulle jag vilja titta på en annan ekvation, som vid första anblicken kan verka galen. Många studenter fastnar för det, även de som tror att de har god förståelse för modulerna.

Denna ekvation är dock ännu lättare att lösa än vad vi tittade på tidigare. Och om du förstår varför, får du ett annat knep för snabb lösning ekvationer med moduler.

Så ekvationen är:

\[\vänster| x-((x)^(3)) \höger|+\vänster| ((x)^(2))+x-2 \right|=0\]

Nej, det här är inget stavfel: det är ett plus mellan modulerna. Och vi måste hitta vid vilken $x$ summan av två moduler är lika med noll. :)

Vad är problemet egentligen? Men problemet är att varje modul är ett positivt tal, eller i extrema fall noll. Vad händer om du lägger till två positiva tal? Uppenbarligen en positiv siffra igen:

\[\begin(align)& 5+7=12 \gt 0; \\& 0,004+0,0001=0,0041 \gt 0; \\& 5+0=5 \gt 0. \\\end(align)\]

Den sista raden kan ge dig en idé: den enda gången summan av modulerna är noll är om varje modul är noll:

Och när är modulen lika med noll? Endast i ett fall - när det submodulära uttrycket är lika med noll:

\[((x)^(2))+x-2=0\Högerpil \vänster(x+2 \höger)\vänster(x-1 \höger)=0\Högerpil \vänster[ \begin(align)& x=-2 \\& x=1 \\\end(align) \right.\]

Således har vi tre punkter där den första modulen nollställs: 0, 1 och −1; samt två punkter där den andra modulen nollställs: −2 och 1. Vi behöver dock båda modulerna nollställas samtidigt, så bland de hittade numren måste vi välja de som ingår i båda uppsättningarna. Uppenbarligen finns det bara ett sådant nummer: $x=1$ - detta kommer att vara det slutliga svaret.

Klyvningsmetod

Tja, vi har redan täckt en massa problem och lärt oss många tekniker. Tror du att det är allt? Men nej! Nu ska vi titta på den slutliga tekniken – och samtidigt den viktigaste. Vi kommer att prata om att dela ekvationer med modul. Vad ska vi ens prata om? Låt oss gå tillbaka lite och titta på någon enkel ekvation. Till exempel detta:

\[\vänster| 3x-5 \right|=5-3x\]

I princip vet vi redan hur man löser en sådan ekvation, eftersom det är en standardkonstruktion av formen $\left| f\vänster(x \höger) \höger|=g\vänster(x \höger)$. Men låt oss försöka se på denna ekvation från en lite annan vinkel. Mer exakt, betrakta uttrycket under modultecknet. Låt mig påminna dig om att modulen för vilket tal som helst kan vara lika med själva talet, eller så kan det vara motsatt det här talet:

\[\vänster| a \right|=\left\( \begin(align)& a,\quad a\ge 0, \\& -a,\quad a \lt 0. \\\end(align) \right.\]

Egentligen är denna tvetydighet hela problemet: eftersom talet under modulen ändras (det beror på variabeln), är det inte klart för oss om det är positivt eller negativt.

Men vad händer om du initialt kräver att denna siffra är positiv? Till exempel kräver vi att $3x-5 \gt 0$ - i det här fallet är vi garanterade att få ett positivt tal under modultecknet, och vi kan helt bli av med just denna modul:

Således kommer vår ekvation att förvandlas till en linjär, som lätt kan lösas:

Det är sant att alla dessa tankar är meningsfulla endast under villkoret $3x-5 \gt 0$ - vi införde själva detta krav för att otvetydigt avslöja modulen. Låt oss därför ersätta den hittade $x=\frac(5)(3)$ i detta tillstånd och kontrollera:

Det visar sig att för det angivna värdet på $x$ uppfylls inte vårt krav, eftersom uttrycket visade sig vara lika med noll, och vi behöver det vara strikt större än noll. Tråkigt. :(

Men det är okej! Det finns trots allt ett annat alternativ $3x-5 \lt 0$. Dessutom: det finns också fallet $3x-5=0$ - detta måste också beaktas, annars kommer lösningen att vara ofullständig. Så, överväg fallet $3x-5 \lt 0$:

Uppenbarligen kommer modulen att öppnas med ett minustecken. Men då uppstår en märklig situation: både till vänster och till höger i den ursprungliga ekvationen kommer samma uttryck att sticka ut:

Jag undrar vid vilken $x$ uttrycket $5-3x$ kommer att vara lika med uttrycket $5-3x$? Även Captain Obviousness skulle kvävas av sin saliv av sådana ekvationer, men vi vet: denna ekvation är en identitet, d.v.s. det är sant för alla värden på variabeln!

Det betyder att alla $x$ passar oss. Vi har dock en begränsning:

Med andra ord, svaret kommer inte att vara ett enda nummer, utan ett helt intervall:

Slutligen finns det ytterligare ett fall kvar att överväga: $3x-5=0$. Allt är enkelt här: under modulen kommer det att finnas noll, och nollmodulen är också lika med noll (detta följer direkt av definitionen):

Men sedan den ursprungliga ekvationen $\left| 3x-5 \right|=5-3x$ kommer att skrivas om enligt följande:

Vi fick redan denna rot ovan när vi övervägde fallet med $3x-5 \gt 0$. Dessutom är denna rot en lösning på ekvationen $3x-5=0$ - detta är begränsningen som vi själva införde för att återställa modulen. :)

Så, förutom intervallet, kommer vi också att vara nöjda med siffran som ligger i slutet av detta intervall:

Kombinera rötter i modulo-ekvationer

Totalt slutligt svar: $x\in \left(-\infty ;\frac(5)(3) \right]$ Det är inte särskilt vanligt att se sådan skit i svaret på en ganska enkel (i huvudsak linjär) ekvation med modul , Tja, vänja dig vid det: svårigheten med modulen är att svaren i sådana ekvationer kan visa sig vara helt oförutsägbara.

Något annat är mycket viktigare: vi har just analyserat en universell algoritm för att lösa en ekvation med en modul! Och denna algoritm består av följande steg:

Jämställ varje modul i ekvationen med noll. Vi får flera ekvationer;
Lös alla dessa ekvationer och markera rötterna på tallinjen. Som ett resultat kommer den räta linjen att delas upp i flera intervall, vid var och en av vilka alla moduler avslöjas unikt;
Lös den ursprungliga ekvationen för varje intervall och kombinera dina svar.

Det är allt! Det finns bara en fråga kvar: vad ska man göra med rötterna som erhölls i steg 1? Låt oss säga att vi har två rötter: $x=1$ och $x=5$. De kommer att dela upp tallinjen i 3 delar:

Dela upp tallinjen i intervaller med hjälp av punkter

Så vad är intervallen? Det är tydligt att det finns tre av dem:

Den längst till vänster: $x \lt 1$ — själva enheten ingår inte i intervallet;
Central: $1\le x \lt 5$ - här ingår en i intervallet, men fem ingår inte;
Längst till höger: $x\ge 5$ - fem ingår bara här!

Jag tror att du redan förstår mönstret. Varje intervall inkluderar den vänstra änden och inkluderar inte den högra.

Vid första anblicken kan ett sådant inlägg verka obekvämt, ologiskt och generellt något slags galet. Men tro mig: efter lite övning kommer du att upptäcka att detta tillvägagångssätt är det mest tillförlitliga och inte stör otvetydigt att öppna modulerna. Det är bättre att använda ett sådant schema än att tänka varje gång: ge vänster/höger ände till det aktuella intervallet eller "kasta" det i nästa.

Detta avslutar lektionen. Ladda ner problem att lösa på egen hand, öva, jämför med svaren - så ses vi i nästa lektion, som kommer att ägnas åt ojämlikheter med moduli. :)

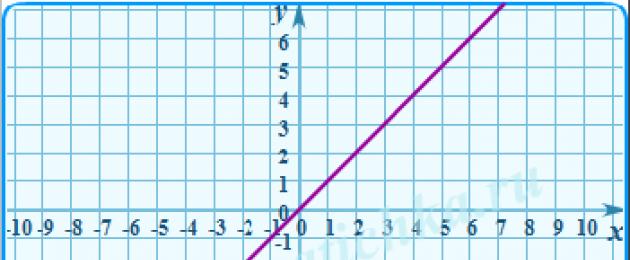
Funktion av formen y=|x|.
Grafen för en funktion på ett intervall är med grafen för funktionen y=-x.

Låt oss först betrakta det enklaste fallet - funktionen y=|x|. Per definition av en modul har vi:

Således, för x≥0 funktionen y=|x| sammanfaller med funktionen y=x, och för x Med denna förklaring är det lätt att plotta funktionen y=|x| (Fig. 1).

Det är lätt att se att denna graf är en kombination av den del av grafen för funktionen y = x som inte ligger under OX-axeln och linjen som erhålls genom spegelreflektion i förhållande till OX-axeln, den del som ligger under OX axel.
Denna metod är också lämplig för att plotta funktionen y=|kx+b|.
Om grafen för funktionen y=kx+b visas i fig. 2, då grafen för funktionen y=|kx+b| är linjen som visas i fig. 3.

Exempel 1. Rita funktionen y=||1-x 2 |-3|.
Låt oss bygga en graf av funktionen y=1-x 2 och tillämpa "modul"-operationen på den (den del av grafen som ligger under OX-axeln reflekteras symmetriskt i förhållande till OX-axeln).

Låt oss flytta ner grafen med 3.

Låt oss tillämpa "modulus"-operationen och få den slutliga grafen för funktionen y=||1-x 2 |-3|

Exempel 2. Rita funktionen y=||x 2 -2x|-3|.
Som ett resultat av transformationen får vi y=|x 2 -2x|=|(x-1) 2 -1|. Låt oss bygga en graf av funktionen y=(x-1) 2 -1: bygg en parabel y=x 2 och skifta åt höger med 1 och nedåt med 1.

Låt oss tillämpa "modul"-operationen på den (den del av grafen som ligger under OX-axeln reflekteras symmetriskt i förhållande till OX-axeln).

Låt oss flytta ner grafen med 3 och tillämpa "modulus"-operationen, vilket resulterar i den slutliga grafen.

Exempel 3. Konstruera en graf över funktionen.
För att utöka modulen måste vi överväga två fall:
1)x>0, då öppnas modulen med ett "+"-tecken =
2)x =

Låt oss bygga en graf för det första fallet.

Låt oss kassera den del av grafen där x

Låt oss bygga en graf för det andra fallet och på samma sätt kassera delen där x>0, som ett resultat får vi.

Låt oss koppla ihop de två graferna och få den sista.

Exempel 4. Konstruera en graf över funktionen.
Låt oss först konstruera en graf över funktionen. För att göra detta är det bekvämt att markera hela delen, vi får . Bygger vi på värdetabellen får vi en graf.

Låt oss tillämpa moduloperationen (den del av grafen som ligger under OX-axeln reflekteras symmetriskt i förhållande till OX-axeln). Vi får det slutgiltiga schemat

Exempel 5. Rita funktionen y=|-x 2 +6x-8|. Låt oss först förenkla funktionen till y=1-(x-3) 2 och bygga dess graf

Nu kommer vi att tillämpa "modul"-operationen och visa delen av grafen under OX-axeln, i förhållande till OX-axeln

Exempel 6. Rita en graf över funktionen y=-x 2 +6|x|-8. Låt oss också förenkla funktionen till y=1-(x-3) 2 och plotta den

Nu kommer vi att tillämpa "modulus" operationen och reflektera delen av grafen till höger om oY-axeln, till vänster sida

Exempel 7. Plotta funktionen . Låt oss plotta funktionen

Låt oss plotta funktionen

Låt oss utföra en parallell översättning av 3 enhetssegment till höger och 2 uppåt. Grafen kommer att se ut så här:

Låt oss tillämpa "modul"-operationen och reflektera den del av grafen till höger om den räta linjen x=3 i det vänstra halvplanet.

Transkript

1 Regional vetenskaplig-praktisk konferens utbildnings- och forskningsarbeten av elever i årskurs 6-11 "Tillämpade och grundläggande frågor om matematik" Metodologiska aspekter av att studera matematik Konstruktion av grafer för funktioner som innehåller modulen Gabova Angela Yuryevna, 10:e klass, MOBU "Gymnasium 3" Kudymkar, Pikuleva Nadezhda Ivanovna, matematiklärare MOBU “ Gymnasium 3" Kudymkar Perm, 2016

2 Innehåll: Inledning...3 s. I. Huvuddel...6 s. 1.1 Historisk referens.. 6 sida 2. Grundläggande definitioner och egenskaper för funktioner sida 2.1 Kvadratisk funktion..7 sid 2.2 Linjär funktion...8 sid 2.3 Bråkrationell funktion 8 sid 3. Algoritmer för att konstruera grafer med en modul 9 sidor 3.1 Definition av modulen.. 9 sidor 3.2 Algoritm för att konstruera en graf linjär funktion med modul...9 s. 3.3 Konstruera grafer av funktioner som innehåller ”kapslade moduler” i formeln.10 s. 3.4 Algoritm för att konstruera grafer av funktioner av formen y = a 1 x x 1 + a 2 x x a n x x n + ax + b. ..13 s. 3.5 Algoritm för att konstruera en graf av en kvadratisk funktion med modul 14 s. 3.6 Algoritm för att konstruera en graf av en bråkdel rationell funktion med modul. 15 sid. 4. Förändringar i grafen för en kvadratisk funktion beroende på placeringen av tecknet för det absoluta värdet..17p. II. Slutsats...26 s. III. Förteckning över referenser och källor...27 s. IV. Bilaga....28pp. 2

3 Inledning Graffunktioner är en av dem de mest intressanta ämnena i skolans matematik. Vår tids största matematiker, Israel Moiseevich Gelfand, skrev: ”Processen att konstruera grafer är ett sätt att omvandla formler och beskrivningar till geometriska bilder. Den här grafen är ett sätt att se formler och funktioner och se hur dessa funktioner förändras. Till exempel, om det skrivs y =x 2, så ser du omedelbart en parabel; om y = x 2-4, ser du en parabel sänkt med fyra enheter; om y = -(x 2 4), så ser du den föregående parabeln nedslagen. Denna förmåga att omedelbart se en formel och dess geometriska tolkning är viktig inte bara för att studera matematik, utan också för andra ämnen. Det är en färdighet som stannar med dig hela livet, som att cykla, skriva eller köra bil." Grunderna i att lösa ekvationer med moduler fick man i årskurserna 6-7. Jag valde just det här ämnet för att jag anser att det kräver djupare och grundligare forskning. Jag vill få mer kunskap om talmodulen, på olika sätt konstruera grafer som innehåller tecknet för det absoluta värdet. När modultecknet ingår i "standard"-ekvationer för linjer, paraboler och hyperboler, blir deras grafer ovanliga och till och med vackra. För att lära dig hur man bygger sådana grafer måste du behärska teknikerna för att konstruera grundläggande figurer, samt känna till och förstå definitionen av modulen för ett tal. I skolmatematikkursen diskuteras inte grafer med modulen tillräckligt på djupet, varför jag ville utöka mina kunskaper om detta ämne och bedriva egen forskning. Utan att känna till definitionen av en modul är det omöjligt att konstruera ens den enklaste grafen som innehåller ett absolut värde. Karakteristiskt drag grafer över funktioner som innehåller uttryck med ett modultecken, 3

4 är förekomsten av veck vid de punkter där uttrycket under modultecknet byter tecken. Syfte med arbetet: att överväga konstruktionen av en graf av linjära, kvadratiska och bråkrationella funktioner som innehåller en variabel under modultecknet. Mål: 1) Studera litteraturen om egenskaperna hos det absoluta värdet av linjära, kvadratiska och bråk-rationell funktioner. 2) Undersök förändringar i funktionsgrafer beroende på placeringen av tecknet för det absoluta värdet. 3) Lär dig att rita ekvationer. Studieobjekt: grafer över linjära, kvadratiska och bråkrationella funktioner. Forskningsämne: förändringar i grafen för linjära, kvadratiska och bråkrationella funktioner beroende på placeringen av tecknet för det absoluta värdet. Den praktiska betydelsen av mitt arbete ligger i: 1) att använda den förvärvade kunskapen om detta ämne, samt att fördjupa den och tillämpa den på andra funktioner och ekvationer; 2) i användningen av färdigheter forskningsarbete i framtiden utbildningsverksamhet. Relevans: Att rita uppgifter är traditionellt ett av de svåraste ämnena inom matematik. Våra studenter står inför problemet med att klara State Exam och Unified State Exam. Forskningsproblem: att konstruera grafer av funktioner som innehåller modultecknet från den andra delen av GIA. Forskningshypotes: användningen av en metod för att lösa uppgifter i den andra delen av GIA, utvecklad på basis av allmänna metoder för att konstruera grafer av funktioner som innehåller ett modultecken, kommer att tillåta eleverna att lösa dessa uppgifter 4

5 på en medveten grund, välj den mest rationella lösningsmetoden, tillämpa olika lösningsmetoder och klara State Examen mer framgångsrikt. Forskningsmetoder som används i arbetet: 1. Analys av matematisk litteratur och internetresurser om detta ämne. 2. Reproduktiv reproduktion av det studerade materialet. 3. Kognitiva och sökaktiviteter. 4.Analys och jämförelse av data i jakt på lösningar på problem. 5. Angivande av hypoteser och verifiering av dem. 6. Jämförelse och generalisering av matematiska fakta. 7. Analys av de erhållna resultaten. När detta arbete skrevs användes följande källor: Internetresurser, OGE-tester, matematisk litteratur. 5

6 I. Huvuddel 1.1 Historisk bakgrund. Under första hälften av 1600-talet, idén om funktion som ett beroende av en variabel storlek från en annan. De franska matematikerna Pierre Fermat () och Rene Descartes () föreställde sig således en funktion som beroendet av ordinatan för en punkt på en kurva på dess abskiss. Och den engelske vetenskapsmannen Isaac Newton () förstod en funktion som koordinaten för en rörlig punkt som förändras beroende på tid. Termen "funktion" (från latinets funktionsutförande, fullbordan) introducerades först av den tyske matematikern Gottfried Leibniz(). Han associerade en funktion med en geometrisk bild (grafen för en funktion). Därefter ansåg den schweiziske matematikern Johann Bernoulli() och en medlem av Sankt Petersburgs vetenskapsakademi, den berömde 1700-talsmatematikern Leonard Euler(), funktionen som ett analytiskt uttryck. Euler har också en allmän förståelse av en funktion som beroendet av en variabel av en annan. Ordet "modul" kommer från det latinska ordet "modulus", som betyder "mått". Detta tvetydigt ord(homonym), som har många betydelser och används inte bara inom matematik, utan även inom arkitektur, fysik, teknik, programmering och andra exakta vetenskaper. Inom arkitektur är detta den initiala måttenheten som fastställts för en given arkitektonisk struktur och används för att uttrycka flera förhållanden av dess beståndsdelar. Inom teknik är detta en term som används inom olika teknikområden, som inte har en universell betydelse och tjänar till att beteckna olika koefficienter och kvantiteter, till exempel ingreppsmodul, elasticitetsmodul, etc. 6

7 Bulkmodul (i fysik) är förhållandet mellan normal spänning i ett material och relativ töjning. 2. Grundläggande definitioner och egenskaper hos funktioner Funktion är ett av de viktigaste matematiska begreppen. En funktion är ett beroende av variabeln y på variabeln x så att varje värde på variabeln x motsvarar ett enda värde på variabeln y. Metoder för att specificera en funktion: 1) analytisk metod (funktionen specificeras med hjälp av matematisk formel); 2) tabellform (funktionen specificeras med hjälp av en tabell); 3) beskrivande metod (funktionen är specificerad verbal beskrivning); 4) grafisk metod (funktionen specificeras med hjälp av en graf). Grafen för en funktion är mängden av alla punkter koordinatplan, vars abskiss är lika med värdet på argumentet, och ordinaterna är lika med motsvarande värden för funktionen. 2.1 Kvadratisk funktion En funktion definierad av formeln y = ax 2 + in + c, där x och y är variabler, och parametrarna a, b och c är valfria reella tal, och a = 0, kallas kvadratisk. Grafen för funktionen y=ax 2 +in+c är en parabel; parabelns symmetriaxel y=ax 2 +in+c är en rät linje, för a>0 är parabelns "grenar" riktade uppåt, för a<0 вниз. Чтобы построить график квадратичной функции, нужно: 1) найти координаты вершины параболы и отметить её в координатной плоскости; 2) построить ещё несколько точек, принадлежащих параболе; 3) соединить отмеченные точки плавной линией.,. 2.2Линейная функция функция вида 7

8 (för funktioner av en variabel). Den huvudsakliga egenskapen för linjära funktioner: ökningen av funktionen är proportionell mot ökningen av argumentet. Det vill säga att funktionen är en generalisering av direkt proportionalitet. Grafen för en linjär funktion är en rak linje, vilket är där dess namn kommer ifrån. Detta gäller en reell funktion av en reell variabel. 1) När den räta linjen bildar en spetsig vinkel med abskissaxelns positiva riktning. 2) När den räta linjen bildar en trubbig vinkel med x-axelns positiva riktning. 3) är ordinataindikatorn för skärningspunkten för linjen med ordinataaxeln. 4) När den räta linjen går genom origo. , 2.3 En bråk-rationell funktion är ett bråk vars täljare och nämnare är polynom. Den har formen where, polynom i valfritt antal variabler. Ett specialfall är rationella funktioner av en variabel:, där och är polynom. 1) Alla uttryck som kan erhållas från variabler med fyra aritmetiska operationer är en rationell funktion. 8

9 2) Uppsättningen av rationella funktioner är sluten under aritmetiska operationer och sammansättningsoperationen. 3) Vilken rationell funktion som helst kan representeras som en summa av enkla bråk - detta används i analytisk integration.. , 3. Algoritmer för att konstruera grafer med modul 3.1 Definition av modul Modulen för ett reellt tal a är talet a själv, om det är icke-negativt, och talet mittemot a, om a är negativt. a = 3.2 Algoritm för att konstruera en graf för en linjär funktion med modul För att konstruera grafer för funktionerna y = x måste du veta att för positivt x har vi x = x. Detta betyder att för positiva värden av argumentet sammanfaller grafen y= x med grafen y=x, det vill säga denna del av grafen är en stråle som kommer ut från origo i en vinkel på 45 grader mot abskissaxeln . Vid x< 0 имеем x = -x; значит, для отрицательных x график y= x совпадает с биссектрисой второго координатного угла. Впрочем, вторую половину графика (для отрицательных X) легко получить из первой, если заметить, что функция y= x чётная, так как -a = a. Значит, график функции y= x симметричен относительно оси Oy, и вторую половину графика можно приобрести, отразив относительно оси ординат часть, начерченную для положительных x. Получается график:y= x 9

10 För att konstruera tar vi poäng (-2; 2) (-1; 1) (0; 0) (1; 1) (2; 2). Låt oss nu bygga en graf y= x-1. Om A är en punkt på grafen y= x med koordinater (a; a), så kommer punkten på grafen y= x-1 med samma värde på Y-ordinaten vara punkt A1(a+1; a). Denna punkt i den andra grafen kan erhållas från punkt A(a; a) i den första grafen genom att flytta parallellt med Ox-axeln till höger. Det betyder att hela grafen för funktionen y= x-1 erhålls från grafen för funktionen y= x genom att skifta parallellt med Ox-axeln till höger med 1. Låt oss konstruera graferna: y= x-1 För att konstruera , ta poängen (-2; 3) (-1; 2) (0; 1) (1; 0) (2; 1). 3.3 Konstruera grafer för funktioner som innehåller "kapslade moduler" i formeln Låt oss betrakta konstruktionsalgoritmen med ett specifikt exempel Konstruera en graf för en funktion: 10

11 y=i-2-ix+5ii 1. Bygg en graf över funktionen. 2. Vi visar grafen för det nedre halvplanet uppåt symmetriskt i förhållande till OX-axeln och erhåller grafen för funktionen. elva

12 3. Vi visar grafen för funktionen nedåt symmetriskt i förhållande till OX-axeln och erhåller grafen för funktionen. 4. Vi visar grafen för funktionen nedåt symmetriskt i förhållande till OX-axeln och får en graf över funktionen 5. Vi visar grafen för funktionen i förhållande till OX-axeln och får en graf. 12

13 6. Som ett resultat ser grafen för funktionen ut så här 3.4. Algoritm för att konstruera grafer för funktioner av formen y = a 1 x x 1 + a 2 x x a n x x n + ax + b. I det föregående exemplet var det ganska lätt att avslöja modultecknen. Om det finns fler summor av moduler är det problematiskt att överväga alla möjliga kombinationer av tecken på submodulära uttryck. Hur, i detta fall, konstruera en graf av funktionen? Observera att grafen är en streckad linje, med hörn i punkter som har abskissorna -1 och 2. Vid x = -1 och x = 2 är de submodulära uttrycken lika med noll. På ett praktiskt sätt har vi kommit närmare regeln för att konstruera sådana grafer: Grafen för en funktion av formen y = a 1 x x 1 + a 2 x x a n x x n + ax + b är en streckad linje med oändliga extremlänkar. För att konstruera en sådan bruten linje räcker det att känna till alla dess hörn (punkternas abskiss är nollorna i de submodulära uttrycken) och en kontrollpunkt på vänster och höger oändliga länkar. 13

14 Problem. Rita funktionen y = x + x 1 + x + 1 och hitta dess minsta värde. Lösning: 1. Nollor av submodulära uttryck: 0; -1; Vertices av polylinjen (0; 2); (-13); (1; 3) (vi ersätter nollorna för de submodulära uttrycken i ekvationen) 3 Kontrollpunkt till höger (2; 6), till vänster (-2; 6). Vi bygger en graf (fig. 7), det minsta värdet på funktionen är Algoritm för att konstruera en graf av en kvadratisk funktion med modulen Rita upp algoritmer för att konvertera funktionsgrafer. 1. Rita en graf för funktionen y= f(x). Per definition av en modul är denna funktion uppdelad i en uppsättning av två funktioner. Följaktligen består grafen för funktionen y= f(x) av två grafer: y= f(x) i det högra halvplanet, y= f(-x) i det vänstra halvplanet. Utifrån detta kan en regel (algoritm) formuleras. Grafen för funktionen y= f(x) erhålls från grafen för funktionen y= f(x) enligt följande: vid x 0 bevaras grafen och vid x< 0полученная часть графика отображается симметрично относительно оси ОУ. 2.Построение графика функции y= f(x). а). Строим график функции y= f(x). б). Часть графика y= f(x), лежащая над осью ОХ, сохраняется, часть его, лежащая под осью ОХ, отображается симметрично относительно оси ОХ. 14

15 3. För att bygga en graf av funktionen y= f(x) måste du först bygga en graf av funktionen y= f(x) för x> 0, sedan för x< 0 построить изображение, симметричное ему относительно оси ОУ, а затем на интервалах, где f(x) <0,построить изображение, симметричное графику y= f(x) относительно оси ОХ. 4.Для построения графиков вида y = f(x)достаточно построить график функции y= f(x) для тех х из области определения, при которых f(х) 0, и отобразить полученную часть графика симметрично относительно оси абсцисс. Пример Построим график функции у = х 2 6х +5. Сначала построим параболу у= х 2 6х +5. Чтобы получить из неё график функции у = х 2-6х + 5, нужно каждую точку параболы с отрицательной ординатой заменить точкой с той же абсциссой, но с противоположной (положительной) ординатой. Иными словами, часть параболы, расположенную ниже оси Ох, нужно заменить линией, ей симметричной относительно оси Ох (Рис.1). Рис Алгоритм построения графика дробно рациональной функции с модулем 1. Начнем с построения графика В основе его лежит график функции и все мы знаем, как он выглядит: Теперь построим график 15

16 För att få denna graf behöver du bara flytta den tidigare erhållna grafen tre enheter åt höger. Observera att om nämnaren för bråket innehöll uttrycket x + 3, så skulle vi flytta grafen åt vänster: Nu måste vi multiplicera alla ordinater med två för att få grafen för funktionen. Slutligen flyttar vi grafen uppåt med två enheter: Det sista vi måste göra är att konstruera en graf för en given funktion om den är innesluten under modultecknet. För att göra detta reflekterar vi symmetriskt uppåt hela den del av grafen vars ordinater är negativa (den del som ligger under x-axeln): Fig. 4 16

17 4.Förändringar i grafen för en kvadratisk funktion beroende på placeringen av tecknet för det absoluta värdet. Konstruera en graf av funktionen y = x 2 - x -3 1) Eftersom x = x vid x 0, sammanfaller den nödvändiga grafen med parabeln y = 0,25 x 2 - x - 3. Om x<0, то поскольку х 2 = х 2, х =-х и требуемый график совпадает с параболой у=0,25 х 2 + х) Если рассмотрим график у=0,25 х 2 - х - 3 при х 0 и отобразить его относительно оси ОУ мы получим тот же самый график. (0; - 3) координаты точки пересечения графика функции с осью ОУ. у =0, х 2 -х -3 = 0 х 2-4х -12 = 0 Имеем, х 1 = - 2; х 2 = 6. (-2; 0) и (6; 0) - координаты точки пересечения графика функции с осью ОХ. Если х<0, ордината точки требуемого графика такая же, как и у точки параболы, но с положительной абсциссой, равной х. Такие точки симметричны относительно оси ОУ(например, вершины (2; -4) и -(2; -4). Значит, часть требуемого графика, соответствующая значениям х<0, симметрична относительно оси ОУ его же части, соответствующей значениям х>0. b) Därför slutför jag konstruktionen för x<0 часть графика, симметричную построенной относительно оси ОУ. 17

18 Fig. 4 Grafen för funktionen y = f (x) sammanfaller med grafen för funktionen y = f (x) på uppsättningen av icke-negativa värden för argumentet och är symmetrisk till den med avseende på axeln för argumentet OU på uppsättningen negativa värden för argumentet. Bevis: Om x 0, då f (x) = f (x), dvs. på uppsättningen av icke-negativa värden för argumentet sammanfaller graferna för funktionerna y = f (x) och y = f (x). Eftersom y = f (x) är en jämn funktion, är dess graf symmetrisk med avseende på op-amp. Således kan grafen för funktionen y = f (x) erhållas från grafen för funktionen y = f (x) enligt följande: 1. konstruera en graf för funktionen y = f (x) för x>0; 2. För x<0, симметрично отразить построенную часть относительно оси ОУ. Вывод: Для построения графика функции у = f (х) 1. построить график функции у = f(х) для х>0; 2. För x<0, симметрично отразить построенную часть относительно оси ОУ. Построить график функции у = х 2-2х Освободимся от знака модуля по определению Если х 2-2х 0, т.е. если х 0 и х 2, то х 2-2х = х 2-2х Если х 2-2х<0, т.е. если 0<х< 2, то х 2-2х =- х 2 + 2х Видим, что на множестве х 0 и х 2 графики функции у = х 2-2х и у = х 2-2х совпадают, а на множестве (0;2) графики функции у = -х 2 + 2х и у = х 2-2х совпадают. Построим их. График функции у = f (х) состоит из части графика функции у = f(х) при у?0 и симметрично отражённой части у = f(х) при у <0 относительно оси ОХ. Построить график функции у = х 2 - х -6 1) Если х 2 - х -6 0, т.е. если х -2 и х 3, то х 2 - х -6 = х 2 - х

19 Om x 2 - x -6<0, т.е. если -2<х< 3, то х 2 - х -6 = -х 2 + х +6. Построим их. 2) Построим у = х 2 - х -6. Нижнюю часть графика симметрично отбражаем относительно ОХ. Сравнивая 1) и 2), видим что графики одинаковые. Работа на тетрадях. Докажем, что график функции у = f (х) совпадает с графиком функции у = f (х) для f(х) >0 och symmetriskt reflekterad del y = f(x) vid y<0 относительно оси ОХ. Действительно, по определению абсолютной величины, можно данную функцию рассмотреть как совокупность двух линий: у = f(х), если f(х) 0; у = - f(х), если f(х) <0 Для любой функции у = f(х), если f(х) >0, då f (x) = f (x), vilket betyder i denna del att grafen för funktionen y = f (x) sammanfaller med grafen för själva funktionen y = f (x). Om f(x)<0, то f (х) = - f(х),т.е. точка (х; - f(х)) симметрична точке (х; f (х)) относительно оси ОХ. Поэтому для получения требуемого графика отражаем симметрично относительно оси ОХ "отрицательную" часть графика у = f(х). Вывод: действительно для построения графика функции у = f(х) достаточно: 1.Построить график функции у = f(х) ; 2. На участках, где график расположен в нижней полуплоскости, т.е., где f(х) <0, симметрично отражаем относительно оси абсцисс. (Рис.5) 19

20 Fig.5 Slutsats: Att bygga en graf av funktionen y= f(x) 1. Bygg en graf av funktionen y=f(x) ; 2. I områden där grafen är placerad i det nedre halvplanet, d.v.s. där f(x)<0, строим кривые, симметричные построенным графикам относительно оси абсцисс. (Рис.6, 7.) 20

21 Forskningsarbete om att konstruera grafer för funktionen y = f (x) Med hjälp av definitionen av absolutvärde och tidigare diskuterade exempel kommer vi att konstruera grafer för funktionen: y = 2 x - 3 y = x 2-5 x y = x 2 -2 och dra slutsatser. För att bygga en graf av funktionen y = f (x) behöver du: 1. Bygga en graf av funktionen y = f (x) för x>0. 2. Konstruera den andra delen av grafen, d.v.s. spegla den konstruerade grafen symmetriskt i förhållande till op-förstärkaren, eftersom Denna funktion är jämn. 3. Konvertera sektioner av den resulterande grafen i det nedre halvplanet till det övre halvplanet symmetriskt mot OX-axeln. Konstruera en graf av funktionen y = 2 x - 3 (1:a metoden för att bestämma modulen) 1. Konstruera y = 2 x - 3, för 2 x - 3 > 0, x >1,5 d.v.s. X< -1,5 и х>1,5 a) y = 2x - 3, för x>0 b) för x<0, симметрично отражаем построенную часть относительно оси ОУ. 2. Строим у = -2 х + 3, для 2 х - 3 < 0. т.е. -1,5<х<1,5 а) у = -2х + 3, для х>0 b) för x<0, симметрично отражаем построенную часть относительно оси ОУ. У = 2 х - 3 1) Строим у = 2х-3, для х>0. 2) Vi konstruerar en rät linje, symmetrisk mot den som är konstruerad i förhållande till op-förstärkarens axel. 3) Jag visar sektioner av grafen placerade i det nedre halvplanet symmetriskt i förhållande till OX-axeln. När vi jämför båda graferna ser vi att de är likadana. 21

22 Exempel på problem Exempel 1. Betrakta grafen för funktionen y = x 2 6x +5. Eftersom x är kvadratiskt, oavsett tecknet för talet x, blir det efter kvadrering positivt. Det följer att grafen för funktionen y = x 2-6x +5 kommer att vara identisk med grafen för funktionen y = x 2-6x +5, d.v.s. graf över en funktion som inte innehåller ett absolutvärdestecken (Fig. 2). Fig.2 Exempel 2. Betrakta grafen för funktionen y = x 2 6 x +5. Med hjälp av definitionen av modulen för ett tal ersätter vi formeln y = x 2 6 x +5 Nu har vi att göra med den för oss bekanta bitvisa beroendetilldelningen. Vi bygger en graf så här: 1) bygger en parabel y = x 2-6x +5 och ringa in delen som är 22

23 motsvarar icke-negativa värden på x, dvs. den del som ligger till höger om Oy-axeln. 2) i samma koordinatplan, konstruera en parabel y = x 2 +6x +5 och ringa in den del som motsvarar negativa värden på x, dvs. den del som ligger till vänster om Oy-axeln. De inringade delarna av parabolerna bildar tillsammans en graf över funktionen y = x 2-6 x +5 (Fig. 3). Fig.3 Exempel 3. Betrakta grafen för funktionen y = x 2-6 x +5. Därför att grafen för ekvationen y = x 2 6x +5 är densamma som grafen för funktionen utan modultecknet (behandlas i exempel 2), det följer att grafen för funktionen y = x 2 6 x +5 är identisk till grafen för funktionen y = x 2 6 x +5 , betraktad i exempel 2 (fig. 3). Exempel 4. Låt oss bygga en graf av funktionen y = x 2 6x +5. För att göra detta, låt oss bygga en graf av funktionen y = x 2-6x. För att få en graf av funktionen y = x 2-6x från den måste du ersätta varje punkt i parabeln med en negativ ordinata med en punkt med samma abskissa, men med den motsatta (positiva) ordinatan. Med andra ord måste den del av parabeln som ligger under x-axeln ersättas med en linje som är symmetrisk mot den i förhållande till x-axeln. Därför att vi behöver bygga en graf av funktionen y = x 2-6x +5, sedan behöver grafen för funktionen vi ansåg y = x 2-6x bara höjas längs y-axeln med 5 enheter upp (fig. 4) ). 23

24 Fig.4 Exempel 5. Låt oss bygga en graf av funktionen y = x 2-6x+5. För att göra detta kommer vi att använda den välkända styckvisa funktionen. Låt oss hitta nollorna för funktionen y = 6x +5 6x + 5 = 0 at. Låt oss överväga två fall: 1) Om, då kommer ekvationen att ha formen y = x 2 6x -5. Låt oss konstruera denna parabel och ringa in delen där. 2) Om, då har ekvationen formen y = x 2 + 6x +5. Låt oss stå denna parabel och ringa in den del av den som ligger till vänster om punkten med koordinater (fig. 5). 24

25 Fig.5 Exempel6. Låt oss bygga en graf av funktionen y = x 2 6 x +5. För att göra detta kommer vi att bygga en graf av funktionen y = x 2-6 x +5. Vi byggde denna graf i exempel 3. Eftersom vår funktion är helt under modultecknet, för att bygga en graf av funktionen y = x 2 6 x +5, behöver vi varje punkt i grafen för funktionen y = x 2 6 x + 5 med negativ ordinata ska ersättas med en punkt med samma abskissa, men med motsatt (positiv) ordinatan, dvs. den del av parabeln som ligger under Ox-axeln måste ersättas med en linje som är symmetrisk mot den i förhållande till Ox-axeln (fig. 6). Fig.6 25

26 II. Slutsats "Matematisk information kan endast användas skickligt och användbart om den bemästras kreativt, så att eleven själv ser hur han skulle kunna komma till det på egen hand." EN. Kolmogorov. Dessa problem är av stort intresse för elever i nian, eftersom de är mycket vanliga i OGE-test. Möjligheten att konstruera datagrafer för funktioner gör att du klarar provet mer framgångsrikt. De franska matematikerna Pierre Fermat () och Rene Descartes () föreställde sig en funktion som beroendet av ordinatan för en punkt på en kurva på dess abskiss. Och den engelske vetenskapsmannen Isaac Newton () förstod en funktion som koordinaten för en rörlig punkt som förändras beroende på tid. 26

27 III Lista över referenser och källor 1. Galitsky M. L., Goldman A. M., Zvavich L. I. Samling av problem i algebra för årskurs 8-9: Lärobok. manual för skolelever. och avancerade klasser studerat Matematik 2:a uppl. M.: Enlightenment, Dorofeev G.V. Mathematics. Algebra. Funktioner. Dataanalys. 9:e klass: m34 Pedagogisk. för allmänna pedagogiska studier. etablering 2:a uppl., stereotyp. M.: Bustard, Solomonik V.S. Samling av frågor och problem i matematik M.: "Higher School", Yashchenko I.V. GIA. Matematik: standardprovalternativ: Om alternativ.m.: ”Nationell utbildning”, sid. 5. Jasjtjenko I.V. OGE. Matematik: standardprovalternativ: Om alternativ.m.: ”Nationell utbildning”, sid. 6. Jasjtjenko I.V. OGE. Matematik: standardexamensalternativ: Om alternativ.m.: ”Nationell utbildning”, med

28 Bilaga 28

29 Exempel 1. Rita funktionen y = x 2 8 x Lösning. Låt oss bestämma funktionens paritet. Värdet för y(-x) är detsamma som värdet för y(x), så denna funktion är jämn. Då är dess graf symmetrisk kring Oy-axeln. Vi plottar funktionen y = x 2 8x + 12 för x 0 och visar symmetriskt grafen med avseende på Oy för negativt x (Fig. 1). Exempel 2. Följande graf av formen y = x 2 8x Detta innebär att grafen för funktionen erhålls på följande sätt: bygg en graf över funktionen y = x 2 8x + 12, lämna den del av grafen som ligger ovanför Ox-axeln oförändrad, och den del av grafen som ligger under abskissaxeln och visas symmetriskt i förhållande till Ox-axeln (fig. 2). Exempel 3. För att rita en graf av funktionen y = x 2 8 x + 12, utförs en kombination av transformationer: y = x 2 8x + 12 y = x 2 8 x + 12 y = x 2 8 x Svar: Figur 3. Exempel 4 Uttryck under modultecknet byter tecken vid punkten x=2/3. Vid x<2/3 функция запишется так: 29

30 För x>2/3 kommer funktionen att skrivas så här: Det vill säga punkten x=2/3 delar upp vårt koordinatplan i två områden, i det ena (till höger) bygger vi en funktion och i det andra (till vänster) bygger vi en graf av funktionen: Exempel 5 Nästa Grafen är också bruten, men har två brytpunkter, eftersom den innehåller två uttryck under modultecknen: Låt oss se vid vilka punkter de submodulära uttrycken byter tecken: Låt oss ordna tecknen för de submodulära uttrycken på koordinatlinjen: 30

31 Vi utökar modulerna på det första intervallet: På det andra intervallet: På det tredje intervallet: Således, på intervallet (- ; 1,5] har vi en graf skriven av den första ekvationen, på intervallet en graf skriven av den andra ekvationen , och på intervallet)

Total:0
I kontakt med 0
Google+ 0
OK 0
Facebook 0