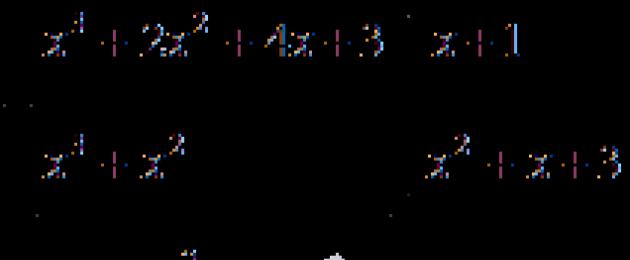Lösning av 5:e gradens ekvation i radikaler. Lösa ekvationer av högre grader

På vår webbplatss youtube-kanal för att hålla dig à jour med alla nya videolektioner.

Till att börja med, låt oss komma ihåg de grundläggande formlerna för grader och deras egenskaper.

Produkt av antal a händer n gånger kan vi skriva detta uttryck som a ... a = a n

1.a 0 = 1 (a ≠ 0)

3.a n a m = a n + m

4. (a n) m = a nm

5.a n b n = (ab) n

7.a n / a m = a n - m

Ström eller exponentiella ekvationer - dessa är ekvationer där variablerna är i potenser (eller exponenter), och basen är ett tal.

Exempel på exponentiella ekvationer:

I det här exemplet är siffran 6 basen, den står alltid längst ner och variabeln x grad eller indikator.

Här är några fler exempel på exponentiella ekvationer.
2 x * 5 = 10
16 x - 4 x - 6 = 0

Låt oss nu titta på hur exponentiella ekvationer löses?

Låt oss ta en enkel ekvation:

2 x = 2 3

Ett sådant exempel kan lösas även i sinnet. Man ser att x = 3. När allt kommer omkring, för att vänster och höger sida ska vara lika, måste du sätta siffran 3 istället för x.
Låt oss nu se hur den här lösningen måste formaliseras:

2 x = 2 3
x = 3

För att lösa en sådan ekvation tog vi bort identiska grunder(det vill säga tvåor) och skrev ner vad som var kvar, det är grader. Vi fick det önskade svaret.

Låt oss nu sammanfatta vårt beslut.

Algoritm för att lösa exponentialekvationen:
1. Behöver kontrollera det samma om ekvationen har baser till höger och vänster. Om grunderna inte är desamma letar vi efter alternativ för att lösa detta exempel.
2. Efter att baserna är desamma, likställa grad och lös den resulterande nya ekvationen.

Låt oss nu lösa några exempel:

Låt oss börja enkelt.

Baserna på vänster och höger sida är lika med siffran 2, vilket betyder att vi kan kassera basen och likställa deras grader.

x + 2 = 4 Detta är den enklaste ekvationen.
x = 4 - 2
x = 2
Svar: x = 2

I följande exempel kan du se att baserna är olika, de är 3 och 9.

3 3x - 9x + 8 = 0

Till att börja med överför vi de nio till höger sida, vi får:

Nu måste du göra samma baser. Vi vet att 9 = 3 2. Låt oss använda formeln grader (a n) m = a nm.

3 3x = (3 2) x + 8

Vi får 9 x + 8 = (3 2) x + 8 = 3 2x + 16

3 3x = 3 2x + 16 nu kan du se att baserna på vänster och höger sida är lika och lika med de tre, så vi kan kassera dem och likställa graderna.

3x = 2x + 16 fick den enklaste ekvationen
3x - 2x = 16
x = 16
Svar: x = 16.

Se följande exempel:

2 2x + 4 - 10 4 x = 2 4

Först och främst tittar vi på baserna, baser är olika två och fyra. Och vi behöver att de är likadana. Konvertera de fyra med formeln (a n) m = a nm.

4 x = (2 2) x = 2 2x

Och vi använder också en formel a n a m = a n + m:

2 2x + 4 = 2 2x 2 4

Lägg till i ekvationen:

2 2x 2 4 - 10 2 2x = 24

Vi har fört exemplet till samma grund. Men vi hindras av andra nummer 10 och 24. Vad ska man göra med dem? Om du tittar noga kan du se att vi på vänster sida upprepar 2 2x, här är svaret - 2 2x kan vi ta ut ur parentesen:

2 2x (2 4 - 10) = 24

Låt oss beräkna uttrycket inom parentes:

2 4 — 10 = 16 — 10 = 6

Dividera hela ekvationen med 6:

Låt oss föreställa oss 4 = 2 2:

2 2x = 2 2 baser är lika, kassera dem och jämför potenserna.
2x = 2 får vi den enklaste ekvationen. Vi delar det med 2 får vi
x = 1
Svar: x = 1.

Låt oss lösa ekvationen:

9 x - 12 * 3 x + 27 = 0

Låt oss förvandla:
9 x = (3 2) x = 3 2x

Vi får ekvationen:
3 2x - 12 3x +27 = 0

Våra baser är lika med 3. I det här exemplet kan du se att de tre första har en grad två gånger (2x) än den andra (bara x). I det här fallet kan du lösa ersättningsmetod... Ersätt siffran med den minsta graden:

Sedan 3 2x = (3x) 2 = t 2

Ersätt alla potenser med x i ekvationen med t:

t 2 - 12t + 27 = 0
Vi får en andragradsekvation. Vi löser genom diskriminanten, vi får:
D = 144-108 = 36
t 1 = 9
t 2 = 3

Återgår till variabeln x.

Vi tar t 1:
ti = 9 = 3 x

Det är,

3 x = 9
3 x = 3 2
x 1 = 2

Hittade en rot. Vi letar efter den andra, från t 2:
t2 = 3 = 3 x
3 x = 3 1
x 2 = 1
Svar: x 1 = 2; x 2 = 1.

På sidan kan du ställa frågor av intresse i avsnittet HJÄLP ATT LÖSA, vi kommer definitivt att svara dig.

Gå med i gruppen

I allmänhet kan en ekvation med en grad högre än 4 inte lösas i radikaler. Men ibland kan vi fortfarande hitta rötterna till polynomet till vänster i ekvationen av högsta grad, om vi representerar det som en produkt av polynom i grad 4. Lösningen på sådana ekvationer är baserad på att faktorisera ett polynom i faktorer, så vi råder dig att upprepa detta ämne innan du studerar den här artikeln.

Oftast har man att göra med ekvationer av högre grader med heltalskoefficienter. I dessa fall kan vi försöka hitta rationella rötter, och faktorisera sedan polynomet för att sedan omvandla det till en ekvation av lägre grad, som blir lätt att lösa. Inom ramen för detta material kommer vi att överväga just sådana exempel.

Ekvationer av högsta grad med heltalskoefficienter

Alla ekvationer av formen a n x n + a n - 1 x n - 1 +. ... ... + a 1 x + a 0 = 0, vi kan reducera till en ekvation av samma grad genom att multiplicera båda sidor med a n n - 1 och ändra en variabel av formen y = a n x:

a n x n + a n - 1 x n - 1 +. ... ... + a 1 x + a 0 = 0 ann xn + an - 1 ann - 1 xn - 1 +... + a 1 (an) n - 1 x + a 0 (an) n - 1 = 0 y = anx ⇒ yn + bn - 1 yn - 1 +... + b 1 y + b 0 = 0

De resulterande koefficienterna kommer också att vara hela. Därför måste vi lösa den reducerade ekvationen för den n:e graden med heltalskoefficienter, som har formen x n + a n x n - 1 +... + a 1 x + a 0 = 0.

Vi beräknar hela rötterna till ekvationen. Om ekvationen har heltalsrötter måste du leta efter dem bland divisorerna för den fria termen a 0. Låt oss skriva ner dem och ersätta dem med den ursprungliga jämlikheten i sin tur och kontrollera resultatet. När vi har fått en identitet och hittat en av rötterna till ekvationen kan vi skriva den på formen x - x 1 · P n - 1 (x) = 0. Här är x 1 roten till ekvationen, och P n - 1 (x) är kvoten för att dividera x n + a n x n - 1 +... + a 1 x + a 0 med x - x 1.

Ersätt resten av divisorerna skrivna i P n - 1 (x) = 0, börja med x 1, eftersom rötterna kan upprepas. Efter att ha erhållit identiteten anses roten x 2 hittad, och ekvationen kan skrivas som (x - x 1) (x - x 2) P n - 2 (x) = 0. Här P n - 2 (x) kommer att vara kvoten för att dividera P n - 1 (x) med x - x 2.

Vi fortsätter att iterera över divisorerna. Hitta alla hela rötter och ange deras antal som m. Därefter kan den ursprungliga ekvationen representeras som x - x 1 x - x 2 · ... · x - x m · P n - m (x) = 0. Här är P n - m (x) ett polynom med graden n - m. Det är bekvämt att använda Horners schema för att räkna.

Om vår ursprungliga ekvation har heltalskoefficienter kan vi inte sluta med bråkrötter.

Som ett resultat fick vi ekvationen P n - m (x) = 0, vars rötter kan hittas på vilket bekvämt sätt som helst. De kan vara irrationella eller komplexa.

Låt oss visa på specifikt exempel hur ett sådant lösningssystem tillämpas.

Exempel 1

Skick: hitta lösningen till ekvationen x 4 + x 3 + 2 x 2 - x - 3 = 0.

Lösning

Låt oss börja med att hitta hela rötter.

Vi har en friperiod lika med minus tre. Den har delare 1, - 1, 3 och - 3. Låt oss ersätta dem i den ursprungliga ekvationen och se vilka av dem som kommer att resultera i identiteter.

Med x lika med ett får vi 1 4 + 1 3 + 2 · 1 2 - 1 - 3 = 0, vilket betyder att en kommer att vara roten till denna ekvation.

Nu utför vi division av polynomet x 4 + x 3 + 2 x 2 - x - 3 med (x - 1) i en kolumn:

Alltså x 4 + x 3 + 2 x 2 - x - 3 = x - 1 x 3 + 2 x 2 + 4 x + 3.

1 3 + 2 1 2 + 4 1 + 3 = 10 ≠ 0 (- 1) 3 + 2 (- 1) 2 + 4 - 1 + 3 = 0

Vi har fått en identitet, vilket betyder att vi har hittat en annan rot till ekvationen, lika med - 1.

Dividera polynomet x 3 + 2 x 2 + 4 x + 3 med (x + 1) i en kolumn:

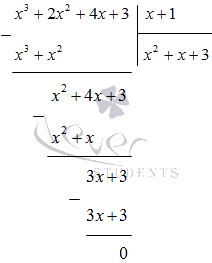
Det förstår vi

x 4 + x 3 + 2 x 2 - x - 3 = (x - 1) (x 3 + 2 x 2 + 4 x + 3) = = (x - 1) (x + 1) (x 2 + x + 3)

Byt ut nästa delare i likheten x 2 + x + 3 = 0, börja med - 1:

1 2 + (- 1) + 3 = 3 ≠ 0 3 2 + 3 + 3 = 15 ≠ 0 (- 3) 2 + (- 3) + 3 = 9 ≠ 0

De resulterande likheterna blir felaktiga, vilket innebär att ekvationen inte längre har integralrötter.

De återstående rötterna kommer att vara rötterna till uttrycket x 2 + x + 3.

D = 1 2 - 4 1 3 = - 11< 0

Det följer av detta att detta kvadratiska trinomium inte har några egentliga rötter, utan har komplexa konjugerade sådana: x = - 1 2 ± i 11 2.

Låt oss förtydliga att istället för lång division kan vi använda Horners schema. Detta görs så här: efter att vi har bestämt den första roten av ekvationen fyller vi i tabellen.

I koefficienttabellen kan vi omedelbart se koefficienterna för kvoten för divisionen av polynom, vilket betyder att x 4 + x 3 + 2 x 2 - x - 3 = x - 1 x 3 + 2 x 2 + 4 x + 3.

Efter att ha hittat nästa rot lika med - 1 får vi följande:

Svar: x = - 1, x = 1, x = - 1 2 ± i 11 2.

Exempel 2

Skick: Lös ekvationen x 4 - x 3 - 5 x 2 + 12 = 0.

Lösning

Fritiden har delare 1, - 1, 2, - 2, 3, - 3, 4, - 4, 6, - 6, 12, - 12.

Vi kontrollerar dem i ordning:

1 4 - 1 3 - 5 1 2 + 12 = 7 ≠ 0 (- 1) 4 - (- 1) 3 - 5 (- 1) 2 + 12 = 9 ≠ 0 2 4 2 3 - 5 2 2 + 12 = 0

Därför kommer x = 2 att vara roten till ekvationen. Dela x 4 - x 3 - 5 x 2 + 12 med x - 2 med hjälp av Horners schema:

Som ett resultat får vi x - 2 (x 3 + x 2 - 3 x - 6) = 0.

2 3 + 2 2 - 3 2 - 6 = 0

Därför kommer 2 återigen att vara en rot. Dividera x 3 + x 2 - 3 x - 6 = 0 med x - 2:

Som ett resultat får vi (x - 2) 2 (x 2 + 3 x + 3) = 0.

Det är ingen mening att kontrollera de återstående divisorerna, eftersom likheten x 2 + 3 x + 3 = 0 är snabbare och bekvämare att lösa med hjälp av diskriminanten.

Låt oss lösa andragradsekvationen:

x 2 + 3 x + 3 = 0 D = 3 2 - 4 1 3 = - 3< 0

Vi får ett komplext konjugerat rötterpar: x = - 3 2 ± i 3 2.

Svar: x = - 3 2 ± i 3 2.

Exempel 3

Skick: hitta de reella rötterna för ekvationen x 4 + 1 2 x 3 - 5 2 x - 3 = 0.

Lösning

x 4 + 1 2 x 3 - 5 2 x - 3 = 0 2 x 4 + x 3 - 5 x - 6 = 0

Vi utför multiplikation 2 3 på båda sidor av ekvationen:

2 x 4 + x 3 - 5 x - 6 = 0 2 4 x 4 + 2 3 x 3 - 20 2 x - 48 = 0

Byt ut variablerna y = 2 x:

2 4 x 4 + 2 3 x 3 - 20 2 x - 48 = 0 y 4 + y 3 - 20 y - 48 = 0

Som ett resultat fick vi en standard 4:e gradens ekvation, som kan lösas enligt standardschemat. Låt oss kontrollera divisorerna, dividera och få som ett resultat att den har 2 reella rötter y = - 2, y = 3 och två komplexa rötter. Vi kommer inte att presentera den kompletta lösningen här. På grund av utbytet kommer de reella rötterna till denna ekvation att vara x = y 2 = - 2 2 = - 1 och x = y 2 = 3 2.

Svar: x 1 = - 1, x 2 = 3 2

Om du märker ett fel i texten, markera det och tryck på Ctrl + Enter

På 1500-talet stötte matematiker på komplexa tal nästan av en slump (se kapitel 11). TILL XVIII-talet komplexa tal ansågs vara en förlängning av omfånget av reella tal, men arbetet med dem ledde ändå till ett paritetsfel, eftersom han i Leonard E:s stora verk om talteori, Arithmetic Investigations (1801), undvek användningen av så kallade "imaginära" tal." Det förefaller mig som om den viktigaste delen av detta arbete är det första beviset på algebras grundläggande sats. Gauss insåg hur viktig denna sats var och skapade flera ytterligare bevis genom åren. 1849 reviderade han den första versionen, denna gång med hjälp av komplexa tal. Med moderna termer kan vi säga att för alla ändliga polynomekvationer med reella eller komplexa koefficienter kommer alla dess rötter att vara reella eller komplexa tal. Således får vi ett negativt svar på den långvariga frågan om huruvida lösa polynomekvationer av högre ordning kräver skapandet av högre ordningens tal än komplexa.

Ett av den tidens mest törstiga problem inom algebra var frågan om femte ordningens polynom – kvintik – gick att lösa med algebraiska metoder, det vill säga med hjälp av ett ändligt antal algebraiska steg. Nu får skolan lära sig formeln för att lösa andragradsekvationer och sedan 1500-talet har liknande metoder varit kända för att lösa ekvationer av tredje och fjärde graden (kapitel 11). Men ingen metod hittades för Quintics. Det kan tyckas som om algebras grundläggande sats innehåller möjligheten till ett jakande svar, men i själva verket garanterar den helt enkelt att lösningar finns, den säger ingenting om förekomsten av formler som ger exakta lösningar (vid den tiden fanns det redan ungefärliga numeriska och grafiska metoder). Och så fanns det två matematiska genier med ett tragiskt öde.

Niels Henrik Abel (1802–1829) föddes i en stor fattig familj som bodde i en liten by i Norge, ett land ödelagt av de långa åren av krig med England och Sverige. Läraren, vänligt inställd mot pojken, gav honom privatlektioner, men efter faderns död, vid arton års ålder, trots ung ålder och med bräcklig hälsa tvingades Abel försörja sin familj. År 1824 publicerade han en vetenskaplig artikel där han konstaterade att kvintiken inte är lösbar med algebraiska medel, som faktiskt vilket polynom som helst av högre ordning. Abel trodde att denna artikel skulle fungera som hans pass till den vetenskapliga världen och skickade den till Gauss vid universitetet i Göttingen. Tyvärr tänkte Gauss inte skära sidorna med en kniv (på den tiden var alla läsare tvungna att göra detta) och läste inte artikeln. År 1826 anslog den norska regeringen slutligen medel för att Abel skulle resa till Europa. Av rädsla för att personlig kontakt med Gauss inte skulle ge honom mycket glädje, bestämde sig matematikern för att inte besöka Göttingen och åkte istället till Berlin. Där blev han vän med August Leopold Crelle (1780–1855), en matematiker, arkitekt och ingenjör som var rådgivare till det preussiska utbildningsministeriet om matematik. Krell var på väg att grunda Journal of Clean och tillämpad matematik". Så Abel fick möjlighet att sprida sitt arbete och publicerade mycket, särskilt i de tidiga numren av "Tidskriften", som omedelbart började betraktas som en mycket prestigefylld och auktoritativ vetenskaplig publikation. Norrmannen publicerade där en utökad version av sitt bevis på att quintic är obestämbart med algebraiska metoder. Och sedan reste han till Paris. Denna resa upprörde Abel mycket, eftersom han praktiskt taget inte fick stöd från de franska matematikerna som han behövde så mycket. Han kom nära Augustin Louis Cauchy (1789-1857), som vid den tiden var den främsta ljusaren matematisk analys, men hade en mycket komplex karaktär. Som Abel själv uttryckte det, "Cauchy är galen, och ingenting kan göras åt det, även om han för närvarande är den ende som är kapabel till någonting i matematik." Om vi ​​försöker hitta ursäkter för de yttringar av respektlöshet och förakt som utgick från Gauss och Cauchy, kan vi säga att quinticen uppnådde en viss berömmelse och väckte uppmärksamhet från både respekterade matematiker och original. Abel återvände till Norge, där han led mer och mer av tuberkulos. Han fortsatte att skicka sina verk till Crelle, men dog 1829, utan att veta hur mycket hans rykte hade vuxit i den vetenskapliga världen... Två dagar efter sin död fick Abel ett erbjudande om att ta en vetenskaplig position i Berlin.

Abel visade att alla polynom högre än fjärde ordningen inte kan lösas med radikaler som kvadrat-, kubiska eller högre rötter. Men de explicita villkoren under vilka dessa polynom kunde lösas i speciella fall och metoden för deras lösning formulerades av Galois. Evariste Galois (1811-1832) levde ett kort och händelserikt liv. Han var en otroligt begåvad matematiker. Galois var oförsonlig mot dem som han ansåg vara mindre begåvade än han själv, och samtidigt kunde han inte tolerera social orättvisa. Han visade ingen talang för matematik förrän han läste Legendre's Principles of Geometry (publicerad 1794, denna bok var den viktigaste läroboken för de kommande hundra åren). Sedan svalde han bokstavligen resten av verken av Legendre och, senare, Abel. Hans entusiasm, självförtroende och intolerans ledde till verkligt fruktansvärda konsekvenser i hans förhållande till lärare och examinatorer. Galois deltog i tävlingen om antagning till Ecole Polytechnique - den franska matematikens vagga, men misslyckades på grund av bristande förberedelser på provet. Under en tid efter att ha träffat en ny lärare, som kände igen hans talang, lyckades han hålla humöret under kontroll. I mars 1829 publicerade Galois sin första artikel om fortsatta bråk, som han ansåg vara hans mest betydelsefulla arbete. Han skickade ett meddelande om sina upptäckter till Vetenskapsakademin, och Cauchy lovade att presentera dem, men glömde det. Dessutom tappade han helt enkelt manuskriptet.

Galois andra misslyckande när han gick in på Ecole Polytechnique gick in i matematisk folklore. Han var så van vid att ständigt ha komplexa matematiska idéer i huvudet att han blev upprörd över examinatorernas småkvistar. Eftersom examinatorerna hade svårt att förstå hans förklaring kastade han en whiteboardtrasa i ansiktet på en av dem. Kort därefter dog hans far, som begick självmord till följd av kyrkans intriger. Vid hans begravning utbröt nästan ett bråk. I februari 1830 skrev Galois följande tre artiklar och skickade dem till Vetenskapsakademin för Grand Prix i matematik. Joseph Fourier, då akademins sekreterare, dog utan att ha läst dem, och efter hans död hittades inga artiklar bland hans tidningar. En sådan flod av besvikelser skulle ha dumpat vem som helst. Galois gjorde uppror mot makthavarna, eftersom han kände: de erkände inte hans förtjänster och ruinerade hans far. Han kastade sig huvudstupa in i politiken och blev en ivrig republikan - inte det klokaste beslutet i Frankrike 1830. I ett sista desperat försök skickade han en vetenskaplig artikel till den berömde franske fysikern och matematikern Simeon Denis Poisson (1781-1840), som som svar krävde ytterligare bevis.

Detta var droppen. 1831 arresterades Galois två gånger - första gången för att ha uppmanat till mordet på kung Louis Philippe, och sedan för att skydda honom - fruktade myndigheterna en republikansk revolt! Den här gången dömdes han till sex månaders fängelse på förfalskade anklagelser för att olagligt bära uniformen från den upplösta artilleribataljon han gick med i. Släppt på sitt hedersord tog han ett jobb som orsakade honom samma avsky som allt annat i livet. I brev till sin hängivne vän Chevalier kan man känna hans besvikelse. Den 29 maj 1832 accepterade han en utmaning till en duell, vars orsaker inte är helt klarlagda. "Jag blev offer för en ohederlig kokett. Mitt liv är utsläckt i ett ynkligt bråk”, skriver han i sitt brev till alla republikaner. Mest berömt verk Galois draftades kvällen före den ödesdigra duellen. Klagomålen är utspridda i fälten: "Jag har inte mer tid, jag har inte mer tid." Han var tvungen att överlåta till andra en detaljerad presentation av de mellanliggande stegen, som inte var nödvändiga för att förstå huvudidén. Han behövde sprida på papper grunden för sina upptäckter - ursprunget till vad som nu kallas Galois' teorem. Han avslutade sitt testamente med att be Chevalier "be Jacobi och Gauss att offentligt uttrycka sin åsikt, inte om riktigheten, utan om vikten av dessa satser." Tidigt på morgonen gick Galois för att träffa sin rival. De fick skjuta från ett avstånd av 25 steg. Galois skadades och dog på sjukhuset nästa morgon. Han var bara tjugo år gammal.

Galois förlitade sig på Lagranges och Cauchys arbete, men han utvecklade en mer allmän metod. Det var extremt viktig prestation inom området för att lösa quintics. Forskaren ägnade mindre uppmärksamhet åt de ursprungliga ekvationerna eller den grafiska tolkningen och tänkte mer på själva rötternas natur. För att förenkla betraktade Galois endast de så kallade irreducible quintics, det vill säga de som inte kunde faktoriseras i form av polynom av lägre ordning (som vi sa, för alla polynomekvationer upp till fjärde ordningen finns det formler för att hitta deras rötter). I allmänhet är ett irreducerbart polynom med rationella koefficienter ett polynom som inte kan dekomponeras till enklare polynom med rationella koefficienter. Till exempel, (x 5 - 1) kan faktoriseras (x-1) (x 4 + x 3 + x 2 + x + 1), medan (x 5 - 2) oreducerbar. Galois mål var att definiera villkor under vilka alla lösningar av en allmän irreducerbar polynomekvation kan hittas i termer av radikaler.

Nyckeln till lösningen ligger i det faktum att rötterna till alla irreducerbara algebraiska ekvationer inte är oberoende, de kan uttryckas den ena genom den andra. Dessa relationer formaliserades till gruppen av alla möjliga permutationer, den så kallade rotsymmetrigruppen - för en quintic innehåller denna grupp 5! = 5 x 4 x 3 x 2 x 1 = 120 element. De matematiska algoritmerna för Galois-teorin är mycket komplexa, och troligen, delvis på grund av detta, förstods de till en början med stor svårighet. Men efter att abstraktionsnivån gjorde det möjligt att övergå från de algebraiska lösningarna av ekvationer till den algebraiska strukturen för de grupper som var associerade med dem, kunde Galois förutsäga ekvationens lösbarhet baserat på egenskaperna hos sådana grupper. Dessutom tillhandahöll hans teori också en metod genom vilken dessa rötter kunde hittas. När det gäller quintics, matematikern Joseph Liouville (1809-1882), som 1846 publicerade mest Galois verk i hans "Journal of Pure and Applied Mathematics", noterade att den unge vetenskapsmannen hade bevisat ett "vackert teorem", och för att "för att en irreducerbar ekvation av den ursprungliga graden ska vara lösbar i termer av radikaler, är det nödvändigt och tillräckligt för att alla dess rötter är rationella funktioner vilka som helst av dem." Eftersom detta är omöjligt för en quintic, kan det inte lösas med hjälp av radikaler.

På tre år har den matematiska världen förlorat två av sina ljusaste nya stjärnor. Anklagelser och en omvärdering av värderingar följde, och Abel och Galois uppnådde det erkännande de förtjänade, men bara postumt. År 1829 fick Karl Jacobi, genom Legendre, veta om det "försvunna" manuskriptet av Abel, och 1830 utbröt en diplomatisk skandal när den norske konsuln i Paris krävde att hitta en artikel av sin landsman. Till slut hittade Cauchy artikeln, men bara för att gå vilse igen på akademin! Samma år tilldelades Abel Grand Prix i matematik (tillsammans med Jacobi) – men han var redan död. Hans biografi publicerades 1841. År 1846 redigerade Liouville några av Galois manuskript för publicering och uttryckte i inledningen att han beklagade att akademin till en början hade förkastat Galois verk på grund av dess komplexitet - "det behövs verkligen klarhet när författaren tar läsaren utanför den slagna vägen in i okända vildmarker ." Han fortsätter: ”Galois är borta! Låt oss inte ägna oss åt värdelös kritik. Låt oss kasta bort nackdelarna och titta på fördelarna!" Frukt kort liv Galois rymde bara sextio sidor. Redaktören för den matematiska tidskriften för kandidater till Ecole Normal och École Polytechnique kommenterade Galois-fallet på följande sätt: ”En sökande med hög intelligens såldes bort av en examinator med lägre tänkande. Barbarus hic ego sum, quia non intelligor illis."

För det första är den andra sidan i detta verk inte belastad med namn, efternamn, beskrivningar av situationen i samhället, titlar och elegier för att hedra någon snål prins, vars plånbok kommer att öppnas med hjälp av dessa rökelser - med hotet att stänga den när lovsången är över. Du kommer inte att se här respektfulla lovord, skrivna med tre gånger större bokstäver än själva texten, riktade till dem som har en hög ställning inom vetenskapen, någon vis beskyddare - något obligatoriskt (jag skulle säga, oundvikligt) för någon i tjugoårsåldern som vill skriva något. Jag säger inte till någon här att jag är skyldig deras råd och stöd till allt som är bra i mitt arbete. Jag säger inte detta för att det skulle vara en lögn. Om jag var tvungen att nämna någon av de stora i samhället eller inom vetenskapen (för närvarande är skillnaden mellan de två klasserna av människor nästan omärklig), jag svär, det skulle inte vara ett tecken på tacksamhet. Jag är skyldig dem att jag publicerade den första av dessa två artiklar så sent, och att jag skrev det hela i fängelset - på en plats som knappast kan anses lämplig för vetenskaplig reflektion, och jag blir ofta förvånad över min återhållsamhet och förmåga att hålla min mun på slottet i förhållande till dumma och elaka zoils. Det förefaller mig som att jag kan använda ordet "zoiles" utan rädsla för att bli anklagad för oanständighet, eftersom det är vad jag kallar mina motståndare. Jag tänker inte skriva här om hur och varför jag sattes i fängelse, men jag måste säga att mina manuskript oftast bara försvann i mappar av herrar från akademimedlemmarna, även om jag i sanning inte kan föreställa mig sådana indiskretion hos personer på vars samvete Abels död. Enligt min mening skulle vem som helst vilja bli jämförd med denna briljanta matematiker. Det räcker med att säga att min uppsats om ekvationsteori skickades till Vetenskapsakademien i februari 1830, att utdrag ur den skickades i februari 1829, och inget av detta publicerades, och till och med manuskriptet var omöjligt att återlämna.

Galois, opublicerat förord, 1832

Klass: 9

Grundläggande mål:

1. Att konsolidera begreppet en hel rationell ekvation av den e graden.
2. Formulera de viktigaste metoderna för att lösa ekvationer av högre grader (n > 3).
3. Att lära ut grundläggande metoder för att lösa ekvationer av högre grader.
4. Att undervisa efter typen av ekvation för att bestämma mest effektiv metod hans beslut.

Former, metoder och pedagogiska tekniker som används av läraren i lektionen:

• Föreläsning-seminarie utbildningssystem (föreläsningar - förklaring av nytt material, seminarier - problemlösning).
• Informations- och kommunikationsteknik (frontalundersökning, muntligt arbete med klassen).
• Differentierad undervisning, grupp- och individuella former.
• Utforskande lärande i utvecklingsundervisning matematiska apparater och varje enskild elevs tankeförmåga.
• Tryckt material - en individuell kort sammanfattning av lektionen (grundbegrepp, formler, påståenden, föreläsningsmaterial komprimeras i form av diagram eller tabeller).

Lektionsplanering:

1. Organisera tid.
   Etappmål: att inkludera elever i lärandeaktiviteter, bestämma den meningsfulla ramen för lektionen.
2. Uppdatering av elevernas kunskaper.
   Syftet med scenen: att uppdatera elevernas kunskaper om tidigare studerade relaterade ämnen
3. Studie av ett nytt ämne (föreläsning). Syftet med steget: att formulera de viktigaste metoderna för att lösa ekvationer av högre grader (n > 3)
4. Sammanfattande.
   Syftet med steget: återigen lyfta fram nyckelpunkterna i materialet som studeras i lektionen.
5. Läxa.
   Etappmål: att formulera läxa för studenter.

Lektionssammanfattning

1. Organisatoriskt ögonblick.

Formulering av ämnet för lektionen: ”Ekvationer av högsta grader. Metoder för deras lösning ”.

2. Förverkligande av elevernas kunskaper.

Teoretisk undersökning – samtal. Upprepning av en del tidigare studerad information från teorin. Eleverna formulerar grundläggande definitioner och formulerar nödvändiga satser. Exempel ges för att visa den kunskapsnivå som förvärvats tidigare.

• Konceptet med en ekvation i en variabel.
• Begreppet roten till ekvationen, ekvationens lösning.
• Begrepp linjär ekvation med en variabel, konceptet med en andragradsekvation i en variabel.
• Begreppet ekvationers ekvivalens, ekvationskonsekvensen (begreppet med främmande rötter), övergången inte av följden (fallet med förlust av rötter).
• Konceptet med ett helt rationellt uttryck med en variabel.
• Konceptet med en hel rationell ekvation n-e graden. Standardformen för hela den rationella ekvationen. Reducerad hela rationella ekvationen.
• Övergång till en uppsättning ekvationer med lägre grader genom att faktorisera den ursprungliga ekvationen i faktorer.
• Polynom koncept n-e graden från x... Bezouts teorem. Konsekvenser från Bezouts sats. Rotsatser ( Z-rötter och F-rötter) av en hel rationell ekvation med heltalskoefficienter (reducerade respektive icke-reducerade).
• Horners plan.

3. Studera ett nytt ämne.

Vi kommer att överväga hela den rationella ekvationen n-th graden av standardformen med en okänd variabel x: P n (x)= 0, där P n (x) = a n x n + a n-1 x n-1 + a 1 x + a 0- polynom n-e graden från x, a n ≠ 0. Om a n = 1 så kallas en sådan ekvation för den reducerade hela rationella ekvationen n-e graden. Betrakta sådana ekvationer för olika värden n och lista de viktigaste metoderna för att lösa dem.

n= 1 - linjär ekvation.

n= 2 - andragradsekvation. Diskriminerande formel. Formel för att beräkna rötter. Vietas sats. Att välja en komplett ruta.

n= 3 - kubikekvation.

Grupperingsmetod.

Exempel: x 3 - 4x 2 - x+ 4 = 0 (x - 4) (x 2– 1) = 0 x 1 = 4 , x 2 = 1,x 3 = -1.

Omvänd kubikekvation av formen yxa 3 + bx 2 + bx + a= 0. Lös genom att kombinera termer med samma koefficienter.

Exempel: x 3 – 5x 2 – 5x + 1 = 0 (x + 1)(x 2 – 6x + 1) = 0 x 1 = -1, x 2 = 3 + 2, x 3 = 3 – 2.

Val av Z-rötter baserat på satsen. Horners plan. När du tillämpar denna metod är det nödvändigt att betona att sökningen i detta fall är ändlig, och vi väljer rötterna enligt en viss algoritm i enlighet med satsen på Z-rötter av den reducerade hela rationella ekvationen med heltalskoefficienter.

Exempel: x 3 – 9x 2 + 23x- 15 = 0. Ekvation given. Låt oss skriva ned divisorerna för den fria termen ( + 1; + 3; + 5; + 15). Låt oss tillämpa Horners schema:

	x 3	x 2	x 1	x 0	slutsats
	1	-9	23	-15
1	1	1 x 1 - 9 = -8	1 x (-8) + 23 = 15	1 x 15 - 15 = 0	1 - rot
	x 2	x 1	x 0

Vi får ( x – 1)(x 2 – 8x + 15) = 0 x 1 = 1, x 2 = 3, x 3 = 5.

Ekvation med heltalskoefficienter. Val av Q-rötter baserat på satsen. Horners plan. När man tillämpar denna metod är det nödvändigt att betona att uppräkningen i detta fall är ändlig och vi väljer rötterna enligt en viss algoritm i enlighet med satsen på F-rötter till en irreducerbar hel rationell ekvation med heltalskoefficienter.

Exempel: 9 x 3 + 27x 2 – x- 3 = 0. Ekvationen reduceras inte. Låt oss skriva ned divisorerna för den fria termen ( + 1; + 3). Låt oss skriva ned divisorerna för koefficienten med högsta potensen av det okända. ( + 1; + 3; + 9) Därför kommer vi att leta efter rötterna bland värdena ( + 1; + ; + ; + 3). Låt oss tillämpa Horners schema:

	x 3	x 2	x 1	x 0	slutsats
	9	27	-1	-3
1	9	1 x 9 + 27 = 36	1 x 36 - 1 = 35	1 x 35 - 3 = 32 ≠ 0	1 - inte rot
-1	9	-1 x 9 + 27 = 18	-1 x 18 - 1 = -19	-1 x (-19) - 3 = 16 ≠ 0	-1 - inte rot
	9	x 9 + 27 = 30	x 30 - 1 = 9	x 9 - 3 = 0	rot
	x 2	x 1	x 0

Vi får ( x – )(9x 2 + 30x + 9) = 0 x 1 = , x 2 = - , x 3 = -3.

För att underlätta beräkningen när du väljer Q -rötter det är bekvämt att ändra variabeln, gå till den reducerade ekvationen och välj Z -rötter.

• Om friperioden är 1

.

• Om du kan använda en ersättning av formuläret y = kx

.

Formel Cardano. Det finns en universell metod för att lösa kubiska ekvationer - det här är Cardano-formeln. Denna formel är associerad med namnen på de italienska matematikerna Gerolamo Cardano (1501-1576), Nicolo Tartaglia (1500-1557), Scipione del Ferro (1465-1526). Denna formel ligger utanför vår kurs.

n= 4 - fjärde gradens ekvation.

Grupperingsmetod.

Exempel: x 4 + 2x 3 + 5x 2 + 4x – 12 = 0 (x 4 + 2x 3) + (5x 2 + 10x) – (6x + 12) = 0 (x + 2)(x 3 + 5x - 6) = 0 (x + 2)(x– 1)(x 2 + x + 6) = 0 x 1 = -2, x 2 = 1.

Variabel ersättningsmetod.

• Formens biquadratiska ekvation yxa 4 + bx 2 + s = 0 .

Exempel: x 4 + 5x 2 - 36 = 0. Byte y = x 2. Härifrån y 1 = 4, y 2 = -9. Så x 1,2 = + 2 .

• Omvänd ekvation av formens fjärde grad yxa 4 + bx 3 + c x 2 + bx + a = 0.

Vi löser, genom att kombinera termer med samma koefficienter, genom att ersätta formuläret

• yxa 4 + bx 3 + cx 2 – bx + a = 0.

• Generaliserad fjärdegrads returekvation av formen yxa 4 + bx 3 + cx 2 + kbx + k 2 a = 0.

• Byte av den allmänna uppfattningen. Några standardersättningar.

Exempel 3 . Ersätter den allmänna vyn(följer av formen av en specifik ekvation).

n = 3.

Ekvation med heltalskoefficienter. Montering av Q-rötter n = 3.

Allmän formel. Det finns en universell metod för att lösa ekvationer av fjärde graden. Denna formel är förknippad med namnet Ludovico Ferrari (1522-1565). Denna formel ligger utanför vår kurs.

n > 5 - ekvationer av femte och högre grader.

Ekvation med heltalskoefficienter. Val av Z-rötter baserat på satsen. Horners plan. Algoritmen liknar den som ansågs ovan för n = 3.

Ekvation med heltalskoefficienter. Montering av Q-rötter baserat på satsen. Horners plan. Algoritmen liknar den som ansågs ovan för n = 3.

Symmetriska ekvationer. Varje returekvation av udda grad har en rot x= -1 och efter att ha faktoriserat det i faktorer får vi att en faktor har formen ( x+ 1), och den andra faktorn är returekvationen för en jämn grad (dess grad är en mindre än graden av den ursprungliga ekvationen). Varje returekvation av jämn grad tillsammans med en rot av formen x = φ innehåller artens rot. Med hjälp av dessa påståenden löser vi problemet genom att sänka graden av den studerade ekvationen.

Variabel ersättningsmetod. Använda enhetlighet.

Det finns ingen generell formel för att lösa hela ekvationer av femte graden (detta visades av den italienske matematikern Paolo Ruffini (1765-1822) och den norske matematikern Niels Henrik Abel (1802-1829)) och högre grader (detta visades av franske matematikern Evariste Galois (1811-1832) )).

• Låt oss återigen komma ihåg att det i praktiken är möjligt att använda kombinationer metoder som anges ovan. Det är bekvämt att gå över till en uppsättning ekvationer med lägre grader med faktorisering av den ursprungliga ekvationen.
• Mycket använd i praktiken förblev utanför ramen för vår dagens diskussion. grafiska metoder lösa ekvationer och ungefärliga lösningsmetoder ekvationer av högre grader.
• Det finns situationer när ekvationen inte har några R-rötter.
Sedan reduceras lösningen till att visa att ekvationen inte har några rötter. För att bevisa detta analyserar vi beteendet hos de funktioner som övervägs på intervall av monotoni. Exempel: Ekvation x 8 – x 3 + 1 = 0 har inga rötter.
• Använda funktioners monotoniegenskaper
... Det finns situationer när användningen av olika egenskaper hos funktioner gör det möjligt att förenkla uppgiften.
Exempel 1: ekvation x 5 + 3x- 4 = 0 har en rot x= 1. Genom egenskapen monotoni hos de analyserade funktionerna finns det inga andra rötter.
Exempel 2: Ekvation x 4 + (x- 1) 4 = 97 har rötter x 1 = -2 och x 2 = 3. Efter att ha analyserat beteendet hos motsvarande funktioner på intervaller av monotoni, drar vi slutsatsen att det inte finns några andra rötter.

4. Sammanfattning.

Sammanfattning: Nu har vi bemästrat de grundläggande metoderna för att lösa olika ekvationer av högre grader (för n > 3). Vår uppgift är att lära sig hur man effektivt använder algoritmerna ovan. Beroende på typen av ekvation måste vi lära oss att bestämma vilken lösningsmetod i detta fall som är den mest effektiva, samt att korrekt tillämpa den valda metoden.

5. Läxor.

: s. 7, s. 164-174, nr. 33-36, 39-44, 46,47.

: №№ 9.1–9.4, 9.6–9.8, 9.12, 9.14–9.16, 9.24–9.27.

Möjliga ämnen för rapporter eller sammandrag om detta ämne:

• Formel Cardano
• Grafisk metod för att lösa ekvationer. Lösningsexempel.
• Metoder för ungefärlig lösning av ekvationer.

Analys av assimileringen av materialet och elevernas intresse för ämnet:

Erfarenheten visar att studenterna i första hand är intresserade av möjligheten att rekrytera Z-rötter och F-rötterna av ekvationer med en ganska enkel algoritm som använder Horners schema. Eleverna är också intresserade av olika standardtyper av variabelsubstitutioner som avsevärt kan förenkla problemet. Grafiska lösningsmetoder är vanligtvis av särskilt intresse. I det här fallet kan du dessutom demontera uppgifterna till en grafisk metod för att lösa ekvationer; diskutera den allmänna vyn av grafen för ett polynom på 3, 4, 5 grader; analysera hur antalet rötter av ekvationer på 3, 4, 5 grader är relaterat till typen av motsvarande graf. Nedan finns en lista över böcker där du kan hitta ytterligare information om detta ämne.

Bibliografi:

1. Vilenkin N. Ya. et al. "Algebra. En lärobok för 9:e årskurselever med fördjupning i matematik ”- M., Education, 2007 - 367 sid.
2. Vilenkin N.Ya., Shibasov L.P., Shibasova Z.F.”Bakom sidorna i en lärobok i matematik. Aritmetisk. Algebra. Årskurs 10-11 ”- M., Utbildning, 2008 - 192 sid.
3. Vygodsky M. Ya."Handbok i matematik" - M., AST, 2010 - 1055 sid.
4. Galitsky M.L."Samling av problem i algebra. Handledning för årskurs 8-9 med fördjupning i matematik ”- M., Utbildning, 2008 - 301 sid.
5. Zvavich L.I. et al. ”Algebra och början av analys. 8-11 cl. En manual för skolor och klasser med fördjupning i matematik ”- M., Bustard, 1999 - 352 s.
6. Zvavich L.I., Averyanov D.I., Pigarev B.P., Trushanina T.N."Uppgifter i matematik för att förbereda för skriftlig tentamen i årskurs 9" - M., Utbildning, 2007 - 112 sid.
7. Ivanov A.A., Ivanov A.P.”Tematiska prov för systematisering av kunskap i matematik” del 1 - M., Fizmatkniga, 2006 - 176 sid.
8. Ivanov A.A., Ivanov A.P.”Tematiska prov för systematisering av kunskap i matematik” del 2 - M., Fizmatkniga, 2006 - 176 sid.
9. Ivanov A.P.“Tester och testpapper matematik. Handledning". - M., Fizmatkniga, 2008 - 304 sid.
10. Leibson K.L.”Samling av praktiska övningar i matematik. Del 2-9 årskurs "- M., MCNMO, 2009 - 184 sid.
11. Makarychev Yu.N., Mindyuk N.G."Algebra. Ytterligare kapitel till skolbokÅrskurs 9. En lärobok för elever i skolor och klasser med avancerade studier i matematik." - M., Utbildning, 2006 - 224 sid.
12. Mordkovich A.G."Algebra. Avancerad studie. 8: e klass. Lärobok "- M., Mnemosina, 2006 - 296 s.
13. A.P. Savin “encyklopedisk ordbok ung matematiker "- M., Pedagogy, 1985 - 352 s.
14. Survillo G.S., Simonov A.S. “Didaktiskt material i algebra för årskurs 9 med fördjupning i matematik ”- M., Education, 2006 - 95 sid.
15. Chulkov P.V.”Ekvationer och ojämlikheter i skolmatematikerkursen. Föreläsningar 1–4 ”- M., 1 september 2006 - 88 sid.
16. Chulkov P.V.”Ekvationer och ojämlikheter i skolmatematikerkursen. Föreläsningar 5–8 ”- M., 1 september 2009 - 84 sid.

Överväga lösningar av ekvationer med en variabel av grad högre än den andra.

Graden av ekvationen P (x) = 0 är graden av polynomet P (x), d.v.s. den största av graderna i dess termer med en koefficient som inte är lika med noll.

Så till exempel har ekvationen (x 3 - 1) 2 + x 5 = x 6 - 2 den femte graden, eftersom efter operationerna med att öppna parenteser och ta med liknande, får vi den ekvivalenta ekvationen x 5 - 2x 3 + 3 = 0 av den femte graden.

Låt oss komma ihåg de regler som kommer att behövas för att lösa ekvationer med grader högre än två.

Påståenden om rötterna till ett polynom och dess divisorer:

1. Polynom n:e graden har antalet rötter högst n, och multiplicitetens rötter m förekommer exakt m gånger.

2. Ett polynom med udda grad har minst en reell rot.

3. Om α är en rot av P (x), då P n (x) = (x - α) Q n - 1 (x), där Q n - 1 (x) är ett polynom av grad (n - 1).

4.

5. Det reducerade polynomet med heltalskoefficienter kan inte ha rationella bråkrötter.

6. För ett polynom av grad 3

P 3 (x) = ax 3 + bx 2 + cx + d en av två saker är möjlig: antingen sönderfaller den till en produkt av tre binomialer

Р 3 (x) = а (х - α) (х - β) (х - γ), eller så kan den brytas upp i produkten av ett binomial och ett kvadratiskt trinomium Р 3 (x) = а (х - α) (х 2 + βх + γ ).

7. Vilket polynom som helst av fjärde graden kan dekomponeras till produkten av två kvadratiska trinomial.

8. Polynomet f (x) är delbart med polynomet g (x) utan rest om det finns ett polynom q (x) så att f (x) = g (x) q (x). För att dividera polynom tillämpas regeln "hörndelning".

9. För delbarheten av polynomet P (x) i binomet (x - c) är det nödvändigt och tillräckligt att talet c är en rot från P (x) (Korollary of Bezout's theorem).

10. Vietas sats: Om x 1, x 2, ..., x n är reella rötter till polynomet

P (x) = a 0 x n + a 1 x n - 1 + ... + a n, då gäller följande likheter:

x 1 + x 2 + ... + x n = -a 1 / a 0,

x 1 x 2 + x 1 x 3 + ... + x n - 1 x n = a 2 / a 0,

x 1 x 2 x 3 + ... + x n - 2 x n - 1 x n = -a 3 / a 0,

x 1 x 2 x 3 x n = (-1) n a n / a 0.

Lösningsexempel

Exempel 1.

Hitta resten av att dividera P (x) = x 3 + 2/3 x 2 - 1/9 med (x - 1/3).

Lösning.

Som en följd av Bezouts sats: "Återstoden av att dividera ett polynom med ett binomium (x - c) är lika med värdet av polynomet i c". Låt oss hitta Р (1/3) = 0. Därför är resten 0 och talet 1/3 är roten till polynomet.

Svar: R = 0.

Exempel 2.

Dela med ett hörn 2x 3 + 3x 2 - 2x + 3 med (x + 2). Hitta resten och den ofullständiga kvoten.

Lösning:

2x 3 + 3x 2 - 2x + 3 | x + 2

2x3 + 4 x 2 2x 2 - x

X 2 - 2 x

Svar: R = 3; privat: 2x 2 - x.

Grundläggande metoder för att lösa ekvationer av högre grader

1. Införande av en ny variabel

Metoden för att introducera en ny variabel är redan bekant med ett exempel. biquadratiska ekvationer... Den består i det faktum att för att lösa ekvationen f (x) = 0, införs en ny variabel (substitution) t = xn eller t = g (x) och f (x) uttrycks i termer av t, vilket ger en ny ekvation r(t). Sedan, när man löser ekvationen r (t), hittas rötterna:

(ti, t2, ..., tn). Därefter erhålls en uppsättning av n ekvationer q (x) = t 1, q (x) = t 2, ..., q (x) = t n, från vilka rötterna till den ursprungliga ekvationen hittas.

Exempel 1.

(x 2 + x + 1) 2 - 3x 2 - 3x - 1 = 0.

Lösning:

(x 2 + x + 1) 2 - 3 (x 2 + x) - 1 = 0.

(x 2 + x + 1) 2 - 3 (x 2 + x + 1) + 3 - 1 = 0.

Ersättning (x 2 + x + 1) = t.

t 2 - 3t + 2 = 0.

t 1 = 2, t 2 = 1. Omvänd utbyte:

x 2 + x + 1 = 2 eller x 2 + x + 1 = 1;

x 2 + x - 1 = 0 eller x 2 + x = 0;

Svar: Från den första ekvationen: x 1, 2 = (-1 ± √5) / 2, från den andra: 0 och -1.

2. Faktorisering genom gruppering och reducerade multiplikationsformler

Grunden för denna metod är inte heller ny och består i att gruppera termerna på ett sådant sätt att varje grupp innehåller en gemensam faktor. För att göra detta måste du ibland använda några konstgjorda metoder.

Exempel 1.

x 4 - 3x 2 + 4x - 3 = 0.

Lösning.

Föreställ dig - 3x 2 = -2x 2 - x 2 och grupp:

(x 4 - 2x 2) - (x 2 - 4x + 3) = 0.

(x 4 - 2x 2 +1 - 1) - (x 2 - 4x + 3 + 1 - 1) = 0.

(x 2 - 1) 2 - 1 - (x - 2) 2 + 1 = 0.

(x 2 - 1) 2 - (x - 2) 2 = 0.

(x 2 - 1 - x + 2) (x 2 - 1 + x - 2) = 0.

(x 2 - x + 1) (x 2 + x - 3) = 0.

x 2 - x + 1 = 0 eller x 2 + x - 3 = 0.

Svar: Det finns inga rötter i den första ekvationen, från den andra: x 1, 2 = (-1 ± √13) / 2.

3. Faktorering med metoden med odefinierade koefficienter

Kärnan i metoden är att det ursprungliga polynomet delas upp i faktorer med okända koefficienter. Genom att använda egenskapen att polynomen är lika om deras koefficienter är lika vid samma grader, hittas de okända expansionskoefficienterna.

Exempel 1.

x 3 + 4x 2 + 5x + 2 = 0.

Lösning.

Ett polynom av 3:e graden kan expanderas till produkten av en linjär och en kvadratisk faktor.

x 3 + 4x 2 + 5x + 2 = (x - a) (x 2 + bx + c),

x 3 + 4x 2 + 5x + 2 = x 3 + bx 2 + cx - ax 2 - abx - ac,

x 3 + 4x 2 + 5x + 2 = x 3 + (b - a) x 2 + (cx - ab) x - ac.

Efter att ha löst systemet:

(b - a = 4,
(c - ab = 5,
(-ac = 2,

(a = -1,
(b = 3,
(c = 2, dvs.

x 3 + 4x 2 + 5x + 2 = (x + 1) (x 2 + 3x + 2).

Rötterna till ekvationen (x + 1) (x 2 + 3x + 2) = 0 är lätta att hitta.

Svar: -1; -2.

4. Metod för val av roten med den högsta och den fria koefficienten

Metoden är baserad på tillämpningen av satser:

1) Varje heltalsrot av ett polynom med heltalskoefficienter är en divisor av en skärning.

2) För att det irreducerbara bråket p / q (p är ett heltal, q är ett naturligt) ska vara en rot till en ekvation med heltalskoefficienter, är det nödvändigt att talet p är en heltalsdelare av den fria termen a 0, och q - en naturlig divisor av den ledande koefficienten.

Exempel 1.

6x 3 + 7x 2 - 9x + 2 = 0.

Lösning:

6: q = 1, 2, 3, 6.

Därför är p/q = ± 1, ± 2, ± 1/2, ± 1/3, ± 2/3, ± 1/6.

Efter att ha hittat en rot, till exempel - 2, hittar vi de andra rötterna med hjälp av division med en vinkel, metoden för odefinierade koefficienter eller Horners schema.

Svar: -2; 1/2; 1/3.

Har du fortfarande frågor? Osäker på hur man löser ekvationer?
För att få hjälp av en handledare – registrera dig.
Första lektionen är gratis!

webbplats, med hel eller delvis kopiering av materialet, krävs en länk till källan.