Kui funktsioon on paaris siis. Paaris- ja paaritu funktsioonid

2020. aasta juulis käivitab NASA ekspeditsiooni Marsile. Kosmoselaev toimetab Marsile elektroonilise kandja kõigi ekspeditsiooni registreeritud liikmete nimedega.

Kui see postitus lahendas teie probleemi või teile see lihtsalt meeldis, jagage selle linki oma sõpradega sotsiaalvõrgustikes.

Üks neist koodivalikutest tuleb kopeerida ja kleepida oma veebilehe koodi, eelistatavalt siltide vahele Ja või kohe pärast silti . Esimese variandi järgi laadib MathJax kiiremini ja aeglustab lehte vähem. Kuid teine ​​valik jälgib ja laadib automaatselt MathJaxi uusimad versioonid. Kui sisestate esimese koodi, tuleb seda perioodiliselt värskendada. Kui kleepite teise koodi, laaditakse lehed aeglasemalt, kuid te ei pea pidevalt MathJaxi värskendusi jälgima.

Lihtsaim viis MathJaxi ühendamiseks on Bloggeris või WordPressis: lisage saidi juhtpaneelile vidin, mis on mõeldud kolmanda osapoole JavaScripti koodi sisestamiseks, kopeerige sellesse ülaltoodud laadimiskoodi esimene või teine ​​versioon ja asetage vidin lähemale. malli algusesse (muide, see pole üldse vajalik, kuna MathJaxi skript laaditakse asünkroonselt). See on kõik. Õppige nüüd MathML-i, LaTeX-i ja ASCIIMathML-i märgistuse süntaksit ning olete valmis matemaatilisi valemeid oma veebilehtedele manustama.

Järjekordne aastavahetus... pakane ilm ja lumehelbed aknaklaasil... See kõik ajendas mind uuesti kirjutama... fraktaalidest ja sellest, mida Wolfram Alpha sellest teab. Sedapuhku on huvitav artikkel, kus on näiteid kahemõõtmelistest fraktaalstruktuuridest. Siin käsitleme keerukamaid näiteid kolmemõõtmelistest fraktalidest.

Fraktaali saab visuaalselt kujutada (kirjeldada) geomeetrilise kujundi või kehana (see tähendab, et mõlemad on hulk, antud juhul punktide kogum), mille detailid on sama kujuga kui algkujul endal. See tähendab, et tegemist on isesarnase struktuuriga, mille detaile arvestades näeme suurendamisel sama kuju, mis ilma suurenduseta. Kui tavalise geomeetrilise kujundi (mitte fraktaali) puhul näeme sisse suumides detaile, mis on lihtsama kujuga kui algkuju ise. Näiteks piisavalt suure suurenduse korral näeb osa ellipsist välja sirgjoonelise lõiguna. Fraktaalide puhul seda ei juhtu: nende suurenemise korral näeme jälle sama keerulist kujundit, mis iga suurenemisega kordub ikka ja jälle.

Fraktaaliteaduse rajaja Benoit Mandelbrot kirjutas oma artiklis Fractals and Art for Science: "Fraktalid on geomeetrilised kujundid, mis on oma detailide poolest sama keerulised kui oma üldisel kujul. See tähendab, et kui osa fraktalist tahab Suurendatakse terviku suuruseni, näeb see välja nagu tervik või täpselt või võib-olla väikese deformatsiooniga.

. Selleks kasutage millimeetripaberit või graafilist kalkulaatorit. Valige sõltumatu muutuja jaoks suvaline arv väärtusi x (\displaystyle x) ja ühendage need sõltuva muutuja väärtuste arvutamiseks funktsiooniga y (\displaystyle y). Asetage leitud punktide koordinaadid koordinaatide tasapinnale ja ühendage need punktid funktsiooni graafiku koostamiseks.

• Asendage funktsiooni positiivsed arvväärtused x (\displaystyle x) ja vastavad negatiivsed arvväärtused. Näiteks antud funktsioon f (x) = 2 x 2 + 1 (\displaystyle f(x)=2x^(2)+1). Asendage sellesse järgmised väärtused x (\displaystyle x):

Kontrollige, kas funktsiooni graafik on y-telje suhtes sümmeetriline. Sümmeetria viitab y-telje ümber oleva graafiku peegelpildile. Kui y-teljest paremal olev graafiku osa (sõltumatu muutuja positiivsed väärtused) ühtib y-teljest vasakul oleva graafiku osaga (sõltumatu muutuja negatiivsed väärtused), graafik on sümmeetriline y-telje suhtes.Kui funktsioon on sümmeetriline y-telje suhtes, on funktsioon paaris.

Kontrollige, kas funktsiooni graafik on algpunkti suhtes sümmeetriline. Algpunktiks on punkt koordinaatidega (0,0). Sümmeetria päritolu kohta tähendab positiivset väärtust y (\displaystyle y)(positiivse väärtusega x (\displaystyle x)) vastab negatiivsele väärtusele y (\displaystyle y)(negatiivse väärtusega x (\displaystyle x)), ja vastupidi. Paaritutel funktsioonidel on sümmeetria päritolu suhtes.

Kontrollige, kas funktsiooni graafikul on sümmeetriat. Viimane funktsioonitüüp on funktsioon, mille graafikul puudub sümmeetria, st puudub peegelpilt nii y-telje kui ka alguspunkti suhtes. Näiteks antud funktsioon.

• Asendage funktsiooni mitu positiivset ja vastavat negatiivset väärtust x (\displaystyle x):
• Saadud tulemuste kohaselt sümmeetria puudub. Väärtused y (\displaystyle y) vastandlike väärtuste jaoks x (\displaystyle x) ei sobi kokku ega ole vastandlikud. Seega ei ole funktsioon paaris ega paaritu.
• Pange tähele, et funktsioon f (x) = x 2 + 2 x + 1 (\displaystyle f(x)=x^(2)+2x+1) võib kirjutada nii: f (x) = (x + 1) 2 (\displaystyle f(x)=(x+1)^(2)). Sellisel kujul kirjutatuna näib funktsioon olevat paaris, kuna sellel on paarisaste. Kuid see näide tõestab, et funktsiooni vormi ei saa kiiresti määrata, kui sõltumatu muutuja on sulgudes. Sel juhul peate avama sulud ja analüüsima saadud eksponente.

Funktsioon on üks olulisemaid matemaatilisi mõisteid. Funktsioon – muutuv sõltuvus juures muutujast x, kui iga väärtus X vastab ühele väärtusele juures. muutuv X nimetatakse sõltumatuks muutujaks või argumendiks. muutuv juures nimetatakse sõltuvaks muutujaks. Kõik sõltumatu muutuja väärtused (muutuja x) moodustavad funktsiooni domeeni. Kõik väärtused, mida sõltuv muutuja võtab (muutuja y), moodustavad funktsiooni vahemiku.

Funktsioonigraafik nad kutsuvad koordinaattasandi kõigi punktide hulka, mille abstsissid on võrdsed argumendi väärtustega ja ordinaadid on võrdsed funktsiooni vastavate väärtustega, st. muutujad on kantud piki abstsissi x, ja muutuja väärtused kantakse piki y-telge y. Funktsiooni joonistamiseks peate teadma funktsiooni omadusi. Funktsiooni põhiomadusi käsitletakse allpool!

Funktsioonigraafiku joonistamiseks soovitame kasutada meie programmi - Graphing Functions Online. Kui teil on sellel lehel materjali uurimisel küsimusi, võite neid alati meie foorumis esitada. Samuti aidatakse foorumil lahendada ülesandeid matemaatikas, keemias, geomeetrias, tõenäosusteoorias ja paljudes teistes ainetes!

Funktsioonide põhiomadused.

1) Funktsiooni ulatus ja funktsioonide ulatus.

Funktsiooni ulatus on argumendi kõigi kehtivate väärtuste kogum x(muutuja x), mille jaoks funktsioon y = f(x) määratletud.
Funktsiooni vahemik on kõigi reaalväärtuste hulk y et funktsioon aktsepteerib.

Elementaarmatemaatikas uuritakse funktsioone ainult reaalarvude hulgal.

2) Funktsiooni nullid.

Väärtused X, mille juures y=0, kutsutakse funktsiooni nullid. Need on funktsiooni graafiku ja x-telje lõikepunktide abstsissid.

3) Funktsiooni märgi püsivuse intervallid.

Funktsiooni märgi püsivuse intervallid on sellised väärtuste intervallid x, millel on funktsiooni väärtused y kutsutakse kas ainult positiivseid või ainult negatiivseid funktsiooni märgi püsivuse intervallid.

4) Funktsiooni monotoonsus.

Kasvav funktsioon (mingis intervallis) - funktsioon, milles selle intervalli argumendi suurem väärtus vastab funktsiooni suuremale väärtusele.

Vähenev funktsioon (mingis intervallis) - funktsioon, milles selle intervalli argumendi suurem väärtus vastab funktsiooni väiksemale väärtusele.

5) Paaris (paaritud) funktsioonid.

Paarisfunktsioon on funktsioon, mille määratluspiirkond on sümmeetriline lähtekoha suhtes ja mis tahes jaoks X f(-x) = f(x). Paarisfunktsiooni graafik on y-telje suhtes sümmeetriline.

Paaritu funktsioon on funktsioon, mille määratluspiirkond on sümmeetriline lähtekoha suhtes ja mis tahes jaoks X määratlusvaldkonnast võrdsus f(-x) = - f(x). Paaritu funktsiooni graafik on lähtekoha suhtes sümmeetriline.

Ühtlane funktsioon
1) Määratluspiirkond on punkti (0; 0) suhtes sümmeetriline, st kui punkt a kuulub definitsiooni valdkonda, siis punkt -a kuulub ka definitsiooni valdkonda.
2) Iga väärtuse jaoks x f(-x)=f(x)
3) Paarisfunktsiooni graafik on sümmeetriline Oy telje suhtes.

paaritu funktsioon sellel on järgmised omadused:
1) Määratluspiirkond on punkti (0; 0) suhtes sümmeetriline.
2) mis tahes väärtuse puhul x, mis kuulub definitsiooni, võrdsuse valdkonda f(-x)=-f(x)
3) Paaritu funktsiooni graafik on sümmeetriline lähtepunkti (0; 0) suhtes.

Mitte iga funktsioon pole paaris ega paaritu. Funktsioonid üldine vaade pole paaris ega paaritu.

6) Piiratud ja piiramatud funktsioonid.

Funktsiooni nimetatakse piiritletuks, kui on olemas positiivne arv M, mille puhul |f(x)| ≤ M kõigi x väärtuste korral. Kui sellist arvu pole, on funktsioon piiramata.

7) Funktsiooni perioodilisus.

Funktsioon f(x) on perioodiline, kui on olemas nullist erinev arv T, nii et mis tahes funktsiooni domeeni x jaoks on f(x+T) = f(x). Seda väikseimat arvu nimetatakse funktsiooni perioodiks. Kõik trigonomeetrilised funktsioonid on perioodilised. (Trigonomeetrilised valemid).

Funktsioon f nimetatakse perioodiliseks, kui on olemas selline arv, et mis tahes jaoks x määratlusvaldkonnast võrdsus f(x)=f(x-T)=f(x+T). T on funktsiooni periood.

Igal perioodilisel funktsioonil on lõpmatu arv perioode. Praktikas võetakse tavaliselt arvesse väikseimat positiivset perioodi.

Perioodilise funktsiooni väärtusi korratakse pärast perioodiga võrdset intervalli. Seda kasutatakse graafikute koostamisel.

Paaris- ja paaritu funktsioonid on selle üks peamisi omadusi ning paarsus moodustab muljetavaldava osa matemaatika koolikursusest. See määrab suuresti funktsiooni käitumise olemuse ja hõlbustab oluliselt vastava graafiku koostamist.

Määratleme funktsiooni paarsuse. Üldiselt vaadeldakse uuritavat funktsiooni isegi siis, kui selle määratluspiirkonnas asuva sõltumatu muutuja (x) vastandväärtuste korral on y (funktsiooni) vastavad väärtused võrdsed.

Anname rangema määratluse. Vaatleme mõnda funktsiooni f (x), mis on määratletud domeenis D. See on isegi siis, kui mis tahes punkti x puhul, mis asub definitsioonipiirkonnas:

• -x (vastaspunkt) asub samuti antud ulatuses,

• f(-x) = f(x).

Ülaltoodud definitsioonist tuleneb sellise funktsiooni määratluspiirkonna jaoks vajalik tingimus, nimelt sümmeetria punkti O suhtes, mis on koordinaatide alguspunkt, kuna kui mingi punkt b sisaldub definitsioonipiirkonnas. paarisfunktsioon, siis selles valdkonnas asub ka vastav punkt - b. Eelnevast järeldub seega järeldus: paarisfunktsioonil on vorm, mis on ordinaattelje (Oy) suhtes sümmeetriline.

Kuidas määrata funktsiooni paarsust praktikas?

Olgu see antud valemiga h(x)=11^x+11^(-x). Otseselt definitsioonist tulenevat algoritmi järgides uurime kõigepealt selle definitsioonivaldkonda. Ilmselt on see defineeritud kõigi argumendi väärtuste jaoks, see tähendab, et esimene tingimus on täidetud.

Järgmine samm on argumendi (x) asendamine selle vastupidise väärtusega (-x).
Saame:
h(-x) = 11^(-x) + 11^x.
Kuna liitmine rahuldab kommutatiivse (nihke) seaduse, siis on ilmne, et h(-x) = h(x) ja antud funktsionaalne sõltuvus on paaris.

Kontrollime funktsiooni h(x)=11^x-11^(-x) ühtlust. Sama algoritmi järgides saame h(-x) = 11^(-x) -11^x. Kui miinust välja võtta, siis selle tulemusena on meil
h(-x)=-(11^x-11^(-x))=- h(x). Seega on h(x) paaritu.

Muide, tuleb meeles pidada, et on funktsioone, mida ei saa nende kriteeriumide järgi klassifitseerida, neid ei nimetata paaristeks ega paarituks.

Isegi funktsioonidel on mitmeid huvitavaid omadusi:

• sarnaste funktsioonide lisamise tulemusena saadakse ühtlane;
• selliste funktsioonide lahutamise tulemusena saadakse ühtlane;
• ühtlane, ka ühtlane;
• kahe sellise funktsiooni korrutamise tulemusena saadakse ühtlane;
• paaritute ja paarisfunktsioonide korrutamise tulemusena saadakse paaritu;
• paaritu ja paarisfunktsioonide jagamise tulemusena saadakse paaritu;
• sellise funktsiooni tuletis on paaritu;
• Kui paneme paaritu funktsiooni ruutu, saame paarisfunktsiooni.

Funktsiooni paarsust saab kasutada võrrandite lahendamisel.

Sellise võrrandi nagu g(x) = 0 lahendamiseks, kus võrrandi vasak pool on paarisfunktsioon, piisab muutuja mittenegatiivsete väärtuste lahenduste leidmisest. Saadud võrrandi juured tuleb kombineerida vastandarvudega. Üks neist kuulub kontrollimisele.

Sama kasutatakse edukalt parameetriga mittestandardsete probleemide lahendamiseks.

Näiteks, kas parameetril a on mõni väärtus, mis muudaks võrrandil 2x^6-x^4-ax^2=1 kolme juure?

Kui arvestada, et muutuja siseneb võrrandisse paarisastmetes, siis on selge, et x asendamine -x-ga antud võrrandit ei muuda. Sellest järeldub, et kui teatud arv on selle juur, siis on ka vastupidine arv. Järeldus on ilmne: võrrandi juured, välja arvatud null, sisalduvad selle lahendite komplektis "paarides".

On selge, et arv 0 ise ei ole, see tähendab, et sellise võrrandi juurte arv saab olla ainult paaris ja loomulikult ei saa see ühegi parameetri väärtuse korral olla kolme juurega.

Kuid võrrandi 2^x+ 2^(-x)=ax^4+2x^2+2 juurte arv võib olla paaritu ja seda parameetri mis tahes väärtuse korral. Tõepoolest, on lihtne kontrollida, et antud võrrandi juurte hulk sisaldab lahendusi "paarides". Kontrollime, kas 0 on juur. Asendades selle võrrandisse, saame 2=2. Seega on 0 lisaks "paaritud" ka juur, mis tõestab nende paaritut arvu.

Peida saade

Funktsiooni seadistamise viisid

Olgu funktsioon antud valemiga: y=2x^(2)-3 . Määrates sõltumatule muutujale x mis tahes väärtuse, saate selle valemi abil arvutada sõltuva muutuja y vastavad väärtused. Näiteks kui x=-0.5 , siis valemit kasutades saame, et y vastav väärtus on y=2 \cdot (-0.5)^(2)-3=-2.5 .

Arvestades mis tahes väärtust, mis on võetud argumendiga x valemis y=2x^(2)-3 , saab arvutada ainult ühe funktsiooni väärtuse, mis sellele vastab. Funktsiooni saab esitada tabelina:

x	−2	−1	0	1	2	3
y	−4	−3	−2	−1	0	1

Seda tabelit kasutades saate aru, et argumendi väärtusele -1 vastab funktsiooni -3 väärtus; ja väärtus x=2 vastab y=0-le ja nii edasi. Samuti on oluline teada, et iga argumendi väärtus tabelis vastab ainult ühele funktsiooni väärtusele.

Graafikute abil saab määrata rohkem funktsioone. Graafiku abil tehakse kindlaks, milline funktsiooni väärtus korreleerub teatud x väärtusega. Enamasti on see funktsiooni ligikaudne väärtus.

Paaris ja paaritu funktsioon

Funktsioon on ühtlane funktsioon, kui f(-x)=f(x) mis tahes domeeni x jaoks. Selline funktsioon on sümmeetriline Oy telje suhtes.

Funktsioon on paaritu funktsioon kui f(-x)=-f(x) domeeni mis tahes x jaoks. Selline funktsioon on sümmeetriline lähtepunkti O suhtes (0;0) .

Funktsioon on mitte isegi, ega veider ja helistas üldine funktsioon kui sellel puudub sümmeetria telje või alguspunkti suhtes.

Pariteedi jaoks uurime järgmist funktsiooni:

f(x)=3x^(3)-7x^(7)

D(f)=(-\infty ; +\infty) sümmeetrilise definitsioonipiirkonnaga lähtekoha kohta. f(-x)= 3 \cdot (-x)^(3)-7 \cdot (-x)^ (7)= -3x^(3)+7x^(7)= -(3x^(3)-7x^(7))= -f(x).

Seega on funktsioon f(x)=3x^(3)-7x^(7) paaritu.

Perioodiline funktsioon

Funktsiooni y=f(x) , mille domeenis f(x+T)=f(x-T)=f(x) on tõene mis tahes x korral, nimetatakse perioodiline funktsioon perioodiga T \neq 0 .

Funktsiooni graafiku kordamine abstsisstelje mis tahes segmendil, mille pikkus on T .

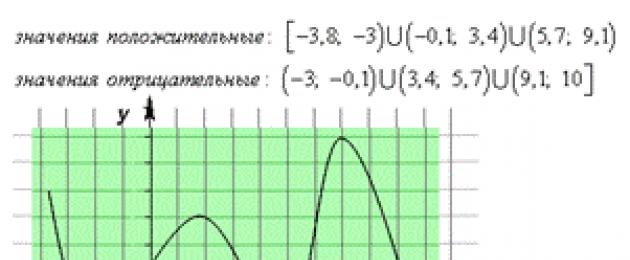
Intervallid, kus funktsioon on positiivne, st f (x) > 0 - abstsisstelje lõigud, mis vastavad funktsiooni graafiku punktidele, mis asuvad abstsisstelje kohal.

f(x) > 0 sees (x_(1); x_(2)) \tass (x_(3); +\infty)

Lüngad, kus funktsioon on negatiivne, st f(x)< 0 - отрезки оси абсцисс, которые отвечают точкам графика функции, лежащих ниже оси абсцисс.

f(x)< 0 на (-\infty; x_(1)) \tass (x_(2); x_(3))

Funktsiooni piiratus

altpoolt piiratud on tavaks kutsuda funktsiooni y=f(x), x \in X, kui on olemas arv A, mille puhul kehtib võrratus f(x) \geq A mis tahes x \in X korral.

Näide funktsioonist, mis on piiratud allpool: y=\sqrt(1+x^(2)), kuna y=\sqrt(1+x^(2)) \geq 1 mis tahes x .

ülalt piiratud funktsioon y=f(x), x \in X kutsutakse välja, kui on olemas arv B, mille võrratus f(x) \neq B kehtib mis tahes x \in X korral.

Allpool piiritletud funktsiooni näide: y=\sqrt(1-x^(2)), x \in [-1;1] kuna y=\sqrt(1+x^(2)) \neq 1 iga x \in [-1;1] jaoks.

Piiratud on tavaks kutsuda funktsiooni y=f(x), x \in X, kui on olemas arv K > 0, mille puhul ebavõrdsus \vasak | f(x) \parem | \neq K mis tahes x \in X .

Piiratud funktsiooni näide: y=\sin x on täisarvu real piiratud, sest \vasakul | \sin x \right | \neq 1.

Funktsiooni suurendamine ja vähenemine

Tavapäraselt räägitakse funktsioonist, mis suureneb vaadeldaval intervallil as funktsiooni suurendamine kui suurem x väärtus vastab funktsiooni y=f(x) suuremale väärtusele. Siit selgub, et kui võtta vaadeldavast intervallist argumendi x_(1) ja x_(2) kaks suvalist väärtust ning x_(1) > x_(2) , on see y(x_(1)) > y(x_(2)) .

Kutsutakse funktsiooni, mis väheneb vaadeldaval intervallil vähenev funktsioon kui suurem x väärtus vastab funktsiooni y(x) väiksemale väärtusele. Siit selgub, et kui võtta vaadeldavast intervallist argumendi x_(1) ja x_(2) kaks suvalist väärtust ning x_(1) > x_(2) , on see y(x_(1))< y(x_{2}) .

Funktsiooni juured on tavaks nimetada punkte, kus funktsioon F=y(x) lõikub abstsissteljega (need saadakse võrrandi y(x)=0 lahendamise tulemusena).

a) Kui paarisfunktsioon x > 0 korral suureneb, siis x korral see väheneb< 0

b) Kui paarisfunktsioon x > 0 korral väheneb, siis see x korral suureneb< 0

c) Kui paaritu funktsioon suureneb x > 0 korral, suureneb see ka x korral< 0

d) Kui paaritu funktsioon väheneb x > 0 korral, väheneb see ka x korral< 0

Funktsiooni äärmused

Funktsiooni miinimumpunkt y=f(x) on tavaks nimetada sellist punkti x=x_(0) , milles selle naabruses on teised punktid (v.a punkt x=x_(0) ) ja nende jaoks siis võrratus f( x) > f (x_(0)) . y_(min) - funktsiooni tähistus punktis min.

Funktsiooni maksimumpunkt y=f(x) on tavaks nimetada sellist punkti x=x_(0) , milles selle naabruses on teised punktid (v.a punkt x=x_(0) ) ja siis võrratus f(x) jääks nendega rahule< f(x^{0}) . y_{max} - обозначение функции в точке max.

Vajalik seisukord

Vastavalt Fermat' teoreemile: f"(x)=0, siis kui funktsioon f(x) , mis on diferentseeruv punktis x_(0) , tekib selles punktis ekstreemum.

Piisav seisukord

1. Kui tuletise märk muutub plussist miinusesse, siis x_(0) on miinimumpunkt;
2. x_(0) - on maksimumpunkt ainult siis, kui tuletis muudab statsionaarse punkti x_(0) läbimisel märgi miinusest plussiks.

Funktsiooni suurim ja väikseim väärtus intervallil

Arvutamise etapid:

1. Otsin tuletist f"(x) ;
2. Leitakse funktsiooni statsionaarsed ja kriitilised punktid ning valitakse intervalli kuuluvad;
3. Funktsiooni f(x) väärtused leitakse segmendi statsionaarsetes ja kriitilistes punktides ja otstes. Tulemustest on väikseim funktsiooni väikseim väärtus, ja veel - suurim.