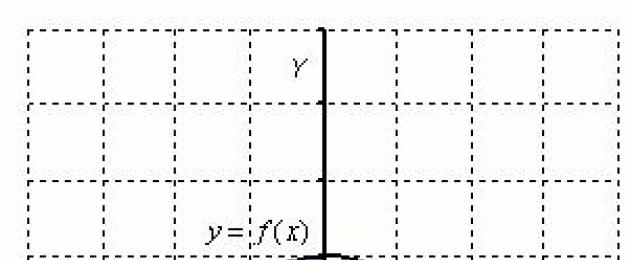Hakkame kaaluma topeltintegraali arvutamise tegelikku protsessi ja tutvume selle geomeetrilise tähendusega.

Topeltintegraal on arvuliselt võrdne lameda kujundi pindalaga (integratsioonipiirkond). See on topeltintegraali kõige lihtsam vorm, kui kahe muutuja funktsioon on võrdne ühega: .

Mõelgem kõigepealt probleemile üldiselt. Nüüd olete üllatunud, kui lihtne see tegelikult on! Arvutame joontega piiratud tasase kujundi pindala. Kindluse huvides eeldame, et intervallil . Selle joonise pindala on arvuliselt võrdne:

Kujutame ala joonisel:

Valime esimese võimaluse piirkonnast mööda hiilimiseks:

Sellel viisil:

Ja kohe oluline tehniline nipp: itereeritud integraale võib käsitleda eraldi. Kõigepealt sisemine integraal, seejärel välimine integraal. See meetod on väga soovitatav teekannud algajatele.

1) Arvutage sisemine integraal, samal ajal kui integreerimine toimub muutuja "y" kaudu:

Määramatu integraal on siin kõige lihtsam ja siis kasutatakse banaalset Newtoni-Leibnizi valemit, ainsa erinevusega, et integreerimise piirid ei ole numbrid, vaid funktsioonid. Esiteks asendasime ülemise piiri "y"-ga (antiderivatiivne funktsioon), seejärel alumine piir

2) Esimeses lõigus saadud tulemus tuleb asendada välisintegraaliga:

Kogu lahenduse kompaktsem märge näeb välja järgmine:

Saadud valem on täpselt töövalem lameda kujundi pindala arvutamiseks "tavalise" kindla integraali abil! Vaata õppetundi Pindala arvutamine kindla integraali abil, seal ta on igal sammul!

St pindala arvutamise probleem topeltintegraali abil veidi erinev ala leidmise probleemist kindla integraali abil! Tegelikult on need üks ja seesama!

Seetõttu ei tohiks raskusi tekkida! Ma ei käsitle väga palju näiteid, kuna tegelikult olete selle probleemiga korduvalt kokku puutunud.

Näide 9

Lahendus: Kujutame ala joonisel:

Valime järgmise piirkonna läbimise järjekorra:

Siin ja allpool ma ei hakka kirjeldama, kuidas ala läbida, sest esimene lõik oli väga üksikasjalik.

Sellel viisil:

Nagu ma juba märkisin, on algajatele parem itereeritud integraalid eraldi arvutada, järgin sama meetodit:

1) Esiteks, kasutades Newtoni-Leibnizi valemit, käsitleme sisemist integraali:

2) Esimeses etapis saadud tulemus asendatakse välimise integraaliga:

Punkt 2 on tegelikult lameda kujundi pindala leidmine kindla integraali abil.

Vastus:

Siin on nii rumal ja naiivne ülesanne.

Huvitav näide iseseisvast lahendusest:

Näide 10

Arvutage topeltintegraali abil tasapinnalise kujundi pindala, mis on piiratud joontega , ,

Lõpplahenduse näide tunni lõpus.

Näidetes 9-10 on palju tulusam kasutada alast möödasõidu esimest meetodit, uudishimulikud lugejad, muide, saavad ümbersõidu järjekorda muuta ja pindalasid arvutada teisel viisil. Kui te ei eksi, siis loomulikult saadakse samad pindala väärtused.

Kuid mõnel juhul on teine ​​võimalus piirkonnast mööda hiilida tõhusam ja noore nohiku kursuse lõpetuseks vaatame veel paar näidet sel teemal:

Näide 11

Arvutage topeltintegraali abil joontega piiratud tasapinnalise kujundi pindala.

Lahendus: ootame kahte tuulega parabooli, mis nende küljel lebavad. Pole vaja naeratada, sageli kohtab sarnaseid asju mitmes integraalis.

Kuidas on kõige lihtsam joonistada?

Esitame parabooli kahe funktsioonina:
- ülemine haru ja - alumine haru.

Samamoodi kujutame parabooli ülemise ja alumise haruna.

Joonise pindala arvutatakse topeltintegraali abil järgmise valemi järgi:

Mis juhtub, kui valime esimese võimaluse piirkonnast mööda minna? Esiteks tuleb see ala jagada kaheks osaks. Ja teiseks vaatleme seda kurba pilti: . Integraalid pole muidugi ülikeerulise tasemega, aga ... kehtib vana matemaatiline ütlus: kes on juurtega sõbralik, see ei vaja tasaarveldust.

Seetõttu väljendame tingimuses antud arusaamatusest pöördfunktsioonid:

Selle näite pöördfunktsioonide eeliseks on see, et need määravad kohe kogu parabooli ilma lehtede, tammetõrude, okste ja juurteta.

Teise meetodi kohaselt on ala läbimine järgmine:

Sellel viisil:

Nagu öeldakse, tunneta erinevust.

1) Tegeleme sisemise integraaliga:

Asendame tulemuse välimise integraaliga:

Muutuja "y" kohal integreerimine ei tohiks olla piinlik, kui seal oleks täht "zyu" - selle üle oleks suurepärane integreerida. Kuigi kes loeb tunni teist lõiku Kuidas arvutada pöördekeha ruumala, ta ei koge enam vähimatki piinlikkust integreerimisega "y" pärast.

Pöörake tähelepanu ka esimesele sammule: integrand on paaris ja integratsioonisegment on nulli suhtes sümmeetriline. Seetõttu saab segmenti poole võrra vähendada ja tulemust kahekordistada. Seda tehnikat kirjeldatakse tunnis üksikasjalikult. Tõhusad meetodid kindla integraali arvutamiseks.

Mida lisada…. Kõik!

Vastus:

Integreerimistehnika testimiseks võite proovida arvutada . Vastus peaks olema täpselt sama.

Näide 12

Arvutage topeltintegraali abil joontega piiratud tasapinnalise kujundi pindala

See on tee-seda-ise näide. Huvitav on märkida, et kui proovite kasutada esimest võimalust piirkonnast mööda minna, siis ei jagune kuju enam kaheks, vaid kolmeks osaks! Ja vastavalt saame kolm paari itereeritud integraale. Mõnikord juhtub.

Meistriklass on lõppenud ja on aeg liikuda edasi suurmeistri tasemele - Kuidas arvutada topeltintegraali? Lahendusnäited. Püüan teises artiklis mitte nii maniakaalne olla =)

Soovin teile edu!

Lahendused ja vastused:

Näide 2:Lahendus: Joonistage ala joonisel:

Valime järgmise piirkonna läbimise järjekorra:

Sellel viisil:
Liigume edasi pöördfunktsioonide juurde:


Sellel viisil:
Vastus:

Näide 4:Lahendus: Liigume edasi otseste funktsioonide juurde:


Teostame joonise:

Muudame ala läbimise järjekorda:

Vastus:

Piirkonna läbimise järjekord:

Sellel viisil:

1)
2)

Vastus:

Kindel integraal. Kuidas arvutada figuuri pindala

Nüüd käsitleme integraalarvutuse rakendusi. Selles õppetükis analüüsime tüüpilist ja levinumat ülesannet. Kuidas kasutada tasapinnalise kujundi pindala arvutamiseks kindlat integraali. Lõpuks, need, kes otsivad tähendust kõrgemas matemaatikas – leidku see. Ei või iial teada. Reaalses elus peate elementaarsete funktsioonidega suvila ligikaudselt hindama ja leidma selle pindala teatud integraali abil.

Materjali edukaks valdamiseks peate:

1) Mõista määramatut integraali vähemalt kesktasemel. Seega peaksid mannekeenid esmalt õppetunni läbi lugema Mitte.

2) Oskab rakendada Newtoni-Leibnizi valemit ja arvutada kindlat integraali. Lehel teatud integraalidega saate luua soojad sõbralikud suhted Kindel integraal. Lahendusnäited.

Tegelikult pole figuuri pindala leidmiseks vaja nii palju teadmisi määramata ja kindla integraali kohta. Ülesanne "arvuta pindala kindla integraali abil" hõlmab alati joonise koostamist, seega on teie teadmised ja joonistamisoskused palju asjakohasem. Sellega seoses on kasulik värskendada põhiliste elementaarfunktsioonide graafikuid mälus ja vähemalt osata koostada sirgjoont, parabooli ja hüperbooli. Seda saab teha (paljudel on seda vaja) metoodilise materjali ja graafikute geomeetrilisi teisendusi käsitleva artikli abil.

Tegelikult on ala leidmise probleem kindla integraali abil kõigile tuttav juba kooliajast ja läheme kooli õppekavast veidi ette. Seda artiklit ei pruugi üldse eksisteerida, kuid tõsiasi on see, et probleem esineb 99 juhul 100-st, kui õpilast piinab vihatud torn entusiastlikult kõrgema matemaatika kursust omandades.

Selle töötoa materjalid on esitatud lihtsalt, üksikasjalikult ja minimaalse teooriaga.

Alustame kõverjoonelise trapetsiga.

Kurviline trapets nimetatakse tasapinnaliseks kujundiks, mida piiravad telg , sirged jooned ja funktsiooni graafik, mis on pideval lõigul, mis sellel intervallil märki ei muuda. Olgu see kujund asukoht mitte vähem abstsiss:

Siis kõverjoonelise trapetsi pindala on arvuliselt võrdne teatud integraaliga. Igal kindlal integraalil (mis eksisteerib) on väga hea geomeetriline tähendus. Õppetunnis Kindel integraal. LahendusnäitedÜtlesin, et kindel integraal on arv. Ja nüüd on aeg välja tuua veel üks kasulik fakt. Geomeetria seisukohalt on kindel integraal ALA.

St kindel integraal (kui see on olemas) vastab geomeetriliselt mõne kujundi pindalale. Vaatleme näiteks kindlat integraali . Integrand määratleb kõvera tasapinnal, mis asub telje kohal (soovijad saavad joonist täiendada) ja kindel integraal ise on numbriliselt võrdne vastava kõverjoonelise trapetsi pindalaga.

Näide 1

See on tüüpiline ülesande avaldus. Otsuse esimene ja kõige olulisem hetk on joonise konstrueerimine. Pealegi tuleb joonis ehitada ÕIGE.

Plaani koostamisel soovitan järgmist järjekorda: Esiteks parem on konstrueerida kõik read (kui neid on) ja ainult Siis- paraboolid, hüperboolid, muude funktsioonide graafikud. Funktsioonigraafikute koostamine on tulusam punkt punkti haaval, punktkonstruktsiooni tehnikaga võib leida võrdlusmaterjalist Elementaarfunktsioonide graafikud ja omadused. Sealt leiate ka materjali, mis on väga kasulik seoses meie tunniga - kuidas kiiresti parabooli ehitada.

Selle probleemi puhul võib lahendus välja näha selline.
Teeme joonise (pange tähele, et võrrand määrab telje):

Kurvilist trapetsi ma hauduma ei hakka, on ilmselge, mis alast siin jutt käib. Lahendus jätkub järgmiselt:

Segmendil paikneb funktsiooni graafik üle telje, sellepärast:

Vastus:

Kellel on raskusi kindla integraali arvutamisega ja Newtoni-Leibnizi valemi rakendamisega , viidata loengule Kindel integraal. Lahendusnäited.

Pärast ülesande täitmist on alati kasulik vaadata joonist ja aru saada, kas vastus on tõeline. Sel juhul loendame "silma järgi" joonisel olevate lahtrite arvu - noh, umbes 9 trükitakse, see näib olevat tõsi. On täiesti selge, et kui meil oleks, ütleme, vastus: 20 ruutühikut, siis ilmselgelt tehti kuskil viga - 20 lahtrit ilmselt ei mahu kõnealusele joonisele, kõige rohkem kümmekond. Kui vastus osutus eitavaks, siis oli ka ülesanne valesti lahendatud.

Näide 2

Arvutage joonise pindala, mis on piiratud joontega , ja teljega

See on tee-seda-ise näide. Täislahendus ja vastus tunni lõpus.

Mida teha, kui kõverjooneline trapets asub telje all?

Näide 3

Arvutage joonise pindala, mis on piiratud joonte ja koordinaattelgedega.

Lahendus: Teeme joonise:

Kui kõverjooneline trapets asub telje all(või vähemalt mitte kõrgem antud telg), siis selle pindala saab leida valemiga:
Sel juhul:

Tähelepanu! Ärge ajage kahte tüüpi ülesandeid segamini:

1) Kui teil palutakse lahendada ainult kindel integraal ilma geomeetrilise tähenduseta, võib see olla negatiivne.

2) Kui teil palutakse leida figuuri pindala kindla integraali abil, siis on pindala alati positiivne! Seetõttu ilmub just vaadeldavas valemis miinus.

Praktikas paikneb joonis enamasti nii ülemisel kui alumisel pooltasandil ja seetõttu liigume lihtsamate kooliülesannete juurest edasi sisukamate näidete juurde.

Näide 4

Leidke tasapinnalise kujundi pindala, mis on piiratud joontega , .

Lahendus: Kõigepealt peate joonise lõpetama. Üldiselt huvitab meid pindalaülesannetes joonise konstrueerimisel enim sirgete lõikepunktid. Leiame parabooli ja sirge lõikepunktid. Seda saab teha kahel viisil. Esimene viis on analüütiline. Lahendame võrrandi:

Seega integratsiooni alumine piir, integratsiooni ülempiir.
Võimaluse korral on parem seda meetodit mitte kasutada..

Punkthaaval on liine palju tulusam ja kiirem ehitada, samas kui integratsiooni piirid selgitatakse välja justkui “iseenesest”. Erinevate diagrammide punkt-punkti ehitustehnikat käsitletakse üksikasjalikult abis Elementaarfunktsioonide graafikud ja omadused. Sellegipoolest tuleb piiride leidmise analüütilist meetodit mõnikord siiski kasutada, kui näiteks graafik on piisavalt suur või keermestatud konstruktsioon ei toonud esile integreerimise piire (need võivad olla murdosalised või irratsionaalsed). Ja me kaalume ka sellist näidet.

Pöördume tagasi oma ülesande juurde: ratsionaalsem on kõigepealt konstrueerida sirge ja alles seejärel parabool. Teeme joonise:

Kordan, et punktkonstruktsiooniga selgitatakse integratsiooni piirid kõige sagedamini välja “automaatselt”.

Ja nüüd töövalem: kui intervallil on pidev funktsioon suurem või võrdne mõne pideva funktsiooni, siis nende funktsioonide graafikute ja sirgjoontega piiratud joonise pindala saab leida valemiga:

Siin pole enam vaja mõelda, kus kujund asub - telje kohal või telje all ja jämedalt öeldes on oluline, milline diagramm on ÜLAL(teise graafiku suhtes), ja milline neist on ALL.

Vaadeldavas näites on ilmne, et lõigul asub parabool sirgest kõrgemal ja seetõttu tuleb sellest lahutada

Lahenduse valmimine võib välja näha järgmine:

Soovitud figuuri piirab ülevalt parabool ja altpoolt sirgjoon.
Segmendil vastavalt vastavale valemile:

Vastus:

Tegelikult on alumise pooltasandi kõverjoonelise trapetsi pindala koolvalem (vt lihtsat näidet nr 3) valemi erijuht . Kuna telg on antud võrrandiga , ja funktsiooni graafik asub mitte kõrgem kirved siis

Ja nüüd paar näidet iseseisvaks lahenduseks

Näide 5

Näide 6

Leidke joontega ümbritsetud joonise pindala , .

Pindala arvutamise ülesannete lahendamise käigus teatud integraali abil juhtub mõnikord naljakas juhtum. Joonis tehti õigesti, arvutused olid õiged, kuid tähelepanematuse tõttu ... leidis vale kujundi ala, nõnda ajas su kuulekas sulane mitu korda sassi. Siin on tõsielu juhtum:

Näide 7

Arvutage joonise pindala, mis on piiratud joontega , , , .

Lahendus: Teeme kõigepealt joonise:

…Eh, joonistus tuli jama, aga kõik tundub olevat loetav.

Joonis, mille ala peame leidma, on varjutatud sinisega.(vaadake hoolikalt seisukorda - kuidas figuur on piiratud!). Kuid praktikas juhtub tähelepanematuse tõttu sageli "tõrge", et peate leidma roheliseks varjutatud figuuri ala!

See näide on kasulik ka selle poolest, et selles arvutatakse joonise pindala kahe kindla integraali abil. Tõesti:

1) Lõigul telje kohal on sirge graafik;

2) Telje kohal lõigul on hüperboolgraafik.

On üsna ilmne, et piirkondi saab (ja tuleks) lisada, seega:

Vastus:

Liigume edasi ühe sisukama ülesande juurde.

Näide 8

Arvutage joontega piiratud kujundi pindala,
Esitame võrrandid "kooli" kujul ja teostame punkt-punkti joonise:

Jooniselt on näha, et meie ülempiir on “hea”: .
Aga mis on alumine piir? On selge, et see pole täisarv, aga mis? Võib olla ? Aga kus on garantii, et joonis on tehtud täiusliku täpsusega, see võib ka selguda. Või juur. Mis siis, kui me ei saanud graafikust üldse õiget?

Sellistel juhtudel tuleb kulutada lisaaega ja integreerimise piire analüütiliselt täpsustada.

Leiame sirge ja parabooli lõikepunktid.
Selleks lahendame võrrandi:


,

Tõesti,.

Edasine lahendus on triviaalne, peaasi, et asendustes ja märkides segadusse ei läheks, siin pole arvutused just kõige lihtsamad.

Segmendil , vastavalt vastavale valemile:

Vastus:

Tunni kokkuvõttes käsitleme kahte ülesannet raskemaks.

Näide 9

Arvutage joonise pindala, mis on piiratud joontega , ,

Lahendus: joonistage see joonis joonisele.

Kurat, ma unustasin graafikule alla kirjutada ja pilti uuesti teha, vabandust, mitte hotz. Mitte joonistus, ühesõnaga täna on see päev =)

Punkthaaval ehitamiseks on vaja teada sinusoidi välimust (ja üldiselt on kasulik teada kõigi elementaarfunktsioonide graafikud), samuti mõned siinusväärtused, need leiate trigonomeetriline tabel. Mõnel juhul (nagu antud juhul) on lubatud konstrueerida skemaatiline joonis, millel tuleb põhimõtteliselt õigesti kuvada graafikud ja integreerimispiirid.

Integratsioonipiirangutega siin probleeme pole, need tulenevad otse tingimusest: - "x" muutub nullist "pi"-ks. Teeme järgmise otsuse:

Segmendil asub funktsiooni graafik telje kohal, seega:

Selles õppetükis õpime arvutama lamedate figuuride alad, mida nimetatakse kõverjoonelised trapetsid .

Selliste jooniste näited on toodud alloleval joonisel.

Ühest küljest on kindla integraali abil lameda kujundi pindala leidmine äärmiselt lihtne. Me räägime joonise pindalast, mis on ülalt piiratud teatud kõveraga, altpoolt - abstsissteljega ( Ox) ning vasakul ja paremal on mõned sirged jooned. Lihtsus seisneb selles funktsiooni kindel integraal, millele kõver on antud, ja seal on sellise kujundi pindala(kõverjooneline trapets).

Figuuri pindala arvutamiseks vajame:

1. Kõverat defineeriva funktsiooni kindel integraal , mis piirab kõverjoonelist trapetsi ülalt. Ja siit tuleb esimene oluline nüanss: kõverjoonelist trapetsi saab piirata kõveraga mitte ainult ülalt, vaid ka altpoolt . Kuidas sel juhul toimida? Lihtne, kuid oluline meeles pidada: integraal võetakse sel juhul miinusmärgiga .
2. Integratsiooni piirid a Ja b, mille leiame joonte võrranditest, mis piiravad joonist vasakul ja paremal: x = a , x = b, kus a Ja b- numbrid.

Eraldi veel mõned nüansid.

Kõver, mis piirab kõverjoonelist trapetsi ülalt (või altpoolt), peab olema pideva ja mittenegatiivse funktsiooni graafik y = f(x) .

X väärtused peavad kuuluma segmendile [a, b] . See tähendab, et arvesse ei võeta näiteks selliseid jooni nagu seenelõik, mille jalg sobib ideaalselt sellesse segmenti ja kork on palju laiem.

Külgmised segmendid võivad degenereeruda punktideks . Kui nägite joonisel sellist kujundit, ei tohiks see teid segadusse ajada, kuna sellel punktil on x-teljel alati oma väärtus. Nii et integratsiooni piiridega on kõik korras.

Nüüd saate liikuda valemite ja arvutuste juurde. Seega piirkond s kõverjoonelist trapetsi saab arvutada valemiga

Kui f(x) ≤ 0 (funktsiooni graafik asub telje all Ox), siis kõvera trapetsi pindala saab arvutada valemiga

On ka juhtumeid, kus nii joonise ülemine kui ka alumine piir on vastavalt funktsioonid y = f(x) Ja y = φ (x) , siis arvutatakse sellise joonise pindala valemiga

. (3)

Lahendame probleeme koos

Alustame juhtudest, kus joonise pindala saab arvutada valemi (1) abil.

Näide 1Ox) ja otsene x = 1 , x = 3 .

Lahendus. Sest y = 1/x> 0 lõigul , siis leitakse kõverjoonelise trapetsi pindala valemiga (1):

.

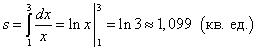Näide 2 Leidke joonise pindala, mis on piiratud funktsiooni graafikuga, sirgjoon x= 1 ja x-telg ( Ox ).

Lahendus. Valemi (1) rakendamise tulemus:

Kui siis s= 1/2; kui siis s= 1/3 jne.

Näide 3 Leidke funktsiooni graafikuga piiratud joonise pindala, x-telg ( Ox) ja otsene x = 4 .

Lahendus. Ülesande tingimusele vastav kujund on kõverjooneline trapets, milles vasakpoolne lõik on taandunud punktiks. Integreerimispiirid on 0 ja 4. Kuna valemi (1) järgi leiame kõverjoonelise trapetsi pindala:

.

Näide 4 Leidke joonise pindala, mis on piiratud joontega , , ja asub 1. kvartalis.

Lahendus. Valemi (1) kasutamiseks esindame näite tingimustega antud joonise pindala kolmnurga pindalade summana OAB ja kõverjooneline trapets ABC. Kolmnurga pindala arvutamisel OAB integreerimise piirid on punktide abstsissid O Ja A, ja figuuri jaoks ABC- punktide abstsissid A Ja C (A on sirge lõikepunkt OA ja paraboolid ja C- parabooli ja telje lõikepunkt Ox). Lahendades ühiselt (süsteemina) sirge ja parabooli võrrandid, saame (punkti abstsiss A) ja (teise sirge ja parabooli lõikepunkti abstsiss, mida lahenduse jaoks pole vaja). Samamoodi saame , (punktide abstsissid C Ja D). Nüüd on meil kõik, et leida figuuri pindala. Leiame:

Näide 5 Leidke kõverjoonelise trapetsi pindala ACDB, kui kõvera võrrand CD ja abstsiss A Ja B vastavalt 1 ja 2.

Lahendus. Avaldame seda kõvera võrrandit Y kaudu: Kõverajoonelise trapetsi pindala leitakse valemiga (1):

.

Liigume edasi juhtumite juurde, kus joonise pindala saab arvutada valemi (2) abil.

Näide 6 Leidke parabooli ja x-teljega piiratud kujundi pindala ( Ox ).

Lahendus. See joonis asub x-telje all. Seetõttu kasutame selle pindala arvutamiseks valemit (2). Integratsiooni piirid on abstsissid ja parabooli lõikepunktid teljega Ox. Järelikult

Näide 7 Leidke ala x-telje ( Ox) ja kaks naabersiinuslainet.

Lahendus. Selle joonise pindala saab leida valemiga (2):

.

Leiame iga termini eraldi:

.

.

Lõpuks leiame piirkonna:

.

Näide 8 Leidke parabooli ja kõvera vahele jääva kujundi pindala.

Lahendus. Avaldame sirgete võrrandid Y-ga:

Valemile (2) vastav pindala saadakse kui

,

kus a Ja b- punktide abstsissid A Ja B. Leiame need võrrandite koos lahendamisega:

Lõpuks leiame piirkonna:

Ja lõpuks on juhtumeid, kus joonise pindala saab arvutada valemi (3) abil.

Näide 9 Leidke paraboolide vahele jääva kujundi pindala Ja .

Mõtlesime välja, kuidas leida kõverjoonelise trapetsi G pindala. Siin on saadud valemid:
pideva ja mittenegatiivse funktsiooni y=f(x) korral lõigul ,
pideva ja mittepositiivse funktsiooni y=f(x) korral lõigul .

Ala leidmise probleemide lahendamisel tuleb aga sageli tegeleda keerukamate kujunditega.

Selles artiklis räägime nende kujundite pindala arvutamisest, mille piirid on funktsioonidega selgelt määratletud, st y=f(x) või x=g(y) , ja analüüsime üksikasjalikult tüüpiliste näidete lahendust. .

Leheküljel navigeerimine.

Valem joontega y=f(x) või x=g(y) piiratud joonise pindala arvutamiseks.

Teoreem.

Olgu funktsioonid ja defineeritud ja pidevad segmendil ja mis tahes väärtuse x korral alates . Siis joonise G ala, mis on piiratud joontega x=a , x=b , ja arvutatakse valemiga .

Sarnane valem kehtib joonise ala kohta, mis on piiratud joontega y \u003d c, y \u003d d ja: .

Tõestus.

Näitame valemi kehtivust kolmel juhul:

Esimesel juhul, kui mõlemad funktsioonid on mittenegatiivsed, võrdub pindala liitmisomaduse tõttu algse joonise G pindala ja kõverjoonelise trapetsi pindala summa joonise pindalaga. Järelikult

Sellepärast, . Viimane üleminek on võimalik tänu kindla integraali kolmandale omadusele.

Samamoodi kehtib võrdsus teisel juhul. Siin on graafiline illustratsioon:

Kolmandal juhul, kui mõlemad funktsioonid on mittepositiivsed, on meil . Illustreerime seda:

Nüüd saame liikuda üldise juhtumi juurde, kui funktsioonid ristuvad Härg-teljega.

Tähistame ristumispunkte. Need punktid jagavad segmendi n osaks , kus . Joonist G saab esitada kujundite ühendusena . On ilmne, et selle intervall langeb ühe kolmest varem käsitletud juhtumist, seetõttu leitakse nende alad kui

Järelikult

Viimane üleminek kehtib kindla integraali viienda omaduse tõttu.

Üldjuhu graafiline illustratsioon.

Seega valem tõestatud.

On aeg liikuda edasi näidete lahendamise juurde joontega y=f(x) ja x=g(y) piiratud kujundite pindala leidmiseks.

Näited joontega y=f(x) või x=g(y) piiratud joonise pindala arvutamiseks.

Iga ülesande lahendamist alustame tasapinnale joonise konstrueerimisega. See võimaldab meil kujutada keerulist kujundit lihtsamate kujundite liiduna. Ehitusraskuste korral vaadake artikleid:; Ja .

Näide.

Arvutage parabooliga piiratud kujundi pindala ja sirged , x=1 , x=4 .

Lahendus.

Ehitame need jooned lennukile.

Kõikjal lõigul parabooli graafik üleval sirge. Seetõttu rakendame pindala jaoks eelnevalt saadud valemit ja arvutame Newtoni-Leibnizi valemi abil kindla integraali:

Teeme näite veidi keerulisemaks.

Näide.

Arvutage joontega piiratud joonise pindala.

Lahendus.

Kuidas see erineb eelmistest näidetest? Varem oli meil alati kaks sirget paralleelselt x-teljega ja nüüd ainult üks x=7 . Kohe tekib küsimus: kust võtta lõimumise teine ​​piir? Vaatame selle jaoks joonist.

Selgus, et joonise pindala leidmisel on integratsiooni alumine piir sirge y \u003d x ja poolparabooli graafiku lõikepunkti abstsiss. Selle abstsissi leiame võrdsusest:

Seetõttu on lõikepunkti abstsiss x=2 .

Märge.

Meie näitel ja joonisel on näha, et sirged ja y=x ristuvad punktis (2;2) ning eelnevad arvutused tunduvad üleliigsed. Kuid muudel juhtudel ei pruugi asjad nii ilmsed olla. Seetõttu soovitame alati analüütiliselt arvutada sirgete lõikepunktide abstsissid ja ordinaadid.

Ilmselt asub funktsiooni y=x graafik intervalli funktsiooni graafiku kohal. Pindala arvutamiseks kasutame valemit:

Teeme ülesande veelgi keerulisemaks.

Näide.

Arvutage joonise pindala, mis on piiratud funktsioonide graafikutega ja .

Lahendus.

Koostame pöördproportsionaalsuse graafiku ja parabooli .

Enne joonise pindala leidmise valemi rakendamist peame otsustama integreerimise piirid. Selleks leiame joonte lõikepunktide abstsissid, võrdsustades avaldised ja .

Nullist erinevate x väärtuste korral võrdsus samaväärne kolmanda astme võrrandiga täisarvu koefitsientidega. Selle lahendamise algoritmi meeldetuletamiseks võite vaadata jaotist.

Lihtne on kontrollida, kas x=1 on selle võrrandi juur: .

Väljendi jagamine binoomarvu x-1 jaoks on meil:

Seega leitakse võrrandist ülejäänud juured :

Nüüd sai jooniselt selgeks, et joonis G on intervallis sinise kohal ja punase joone all . Seega on nõutav ala võrdne

Vaatame veel üht tüüpilist näidet.

Näide.

Arvutage kõveratega piiratud kujundi pindala ja abstsisstelg.

Lahendus.

Teeme joonise.

See on tavaline astmefunktsioon, mille astendaja on üks kolmandik, funktsiooni graafik saab graafikult, kuvades selle sümmeetriliselt x-telje ümber ja tõstes seda ühe võrra üles.

Leia kõigi sirgete lõikepunktid.

X-teljel on võrrand y=0 .

Funktsioonide ja y=0 graafikud lõikuvad punktis (0;0), kuna x=0 on võrrandi ainus reaalne juur.

Funktsioonigraafikud ja y=0 lõikuvad punktis (2;0), kuna x=2 on võrrandi ainus juur .

Funktsioonigraafikud ja lõikuvad punktis (1;1), kuna x=1 on võrrandi ainus juur . See väide ei ole täiesti ilmne, kuid see on rangelt kasvav funktsioon ja - võrrandit rangelt vähendades on kõige rohkem üks juur.

Ainus märkus: sel juhul peate piirkonna leidmiseks kasutama vormi valemit . See tähendab, et piirdejooned tuleb esitada argumendi funktsioonidena y , kuid musta joonega .

Määratleme sirgete lõikepunktid.

Alustame funktsioonide graafikutega ja:

Leiame funktsioonide ja graafikute lõikepunkti:

Jääb leida joonte lõikepunkt ja:

Nagu näete, väärtused ühtivad.

Tehke kokkuvõte.

Oleme analüüsinud kõiki levinumaid juhtumeid, kus leitakse selgesõnaliselt etteantud joontega piiratud kujundi pindala. Selleks peate suutma ehitada tasapinnal sirgeid, leidma sirgete lõikepunktid ja rakendama pindala leidmiseks valemit, mis eeldab teatud integraalide arvutamise võimalust.

Näide1 . Arvutage joonise pindala, mis on piiratud joontega: x + 2y - 4 = 0, y = 0, x = -3 ja x = 2

Ehitame joonise (vt joonis.) Ehitame sirge x + 2y - 4 \u003d 0 mööda kahte punkti A (4; 0) ja B (0; 2). Väljendades y-d x-iga, saame y \u003d -0,5x + 2. Vastavalt valemile (1), kus f (x) \u003d -0,5x + 2, a \u003d -3, b \u003d 2, me leida

S \u003d \u003d [-0,25 \u003d 11,25 ruutmeetrit ühikut

Näide 2 Arvutage joontega piiratud joonise pindala: x - 2y + 4 \u003d 0, x + y - 5 \u003d 0 ja y \u003d 0.

Lahendus. Ehitame figuuri.

Ehitame sirge x - 2y + 4 = 0: y = 0, x = - 4, A (-4; 0); x = 0, y = 2, B(0; 2).

Ehitame sirge x + y - 5 = 0: y = 0, x = 5, С(5; 0), x = 0, y = 5, D(0; 5).

Leidke sirgete lõikepunkt, lahendades võrrandisüsteemi:

x = 2, y = 3; M(2; 3).

Vajaliku pindala arvutamiseks jagame AMC kolmnurga kaheks kolmnurgaks AMN ja NMC, kuna kui x muutub A-st N-ks, on pindala piiratud sirgjoonega ja kui x muutub N-st C-ks, on see sirgjoon.

Kolmnurga AMN jaoks on meil: ; y = 0,5x + 2, st f (x) = 0,5x + 2, a = 4, b = 2.

NMC kolmnurga jaoks on meil: y = - x + 5, st f(x) = - x + 5, a = 2, b = 5.

Arvutades iga kolmnurga pindala ja liites tulemused, leiame:

ruut ühikut

ruut ühikut

9 + 4, 5 = 13,5 ruutmeetrit ühikut Kontrollige: = 0,5AC = 0,5 ruutmeetrit. ühikut

Näide 3 Arvutage joontega piiratud kujundi pindala: y = x 2 , y = 0, x = 2, x = 3.

Sel juhul on vaja arvutada kõverjoonelise trapetsi pindala, mis on piiratud parabooliga y = x 2 , sirgjooned x \u003d 2 ja x \u003d 3 ning Ox telg (vt joonis.) Valemi (1) järgi leiame kõverjoonelise trapetsi pindala

= = 6kv. ühikut

Näide 4 Arvutage joontega piiratud joonise pindala: y \u003d - x 2 + 4 ja y = 0

Ehitame figuuri. Soovitud ala on ümbritsetud parabooli y \u003d - x vahele 2 + 4 ja telg Oh.

Leidke parabooli ja x-telje lõikepunktid. Eeldades y \u003d 0, leiame x \u003d Kuna see arv on Oy telje suhtes sümmeetriline, arvutame Oy teljest paremal asuva joonise pindala ja kahekordistame tulemuse: \u003d + 4x] ruut. ühikut 2 = 2 ruutmeetrit ühikut

Näide 5 Arvutage joontega piiratud kujundi pindala: y 2 = x, yx = 1, x = 4

Siin on vaja arvutada kõverjoonelise trapetsi pindala, mis on piiratud parabooli y ülemise haruga 2 \u003d x, härja telg ja sirgjooned x \u003d 1x \u003d 4 (vt joonis).

Vastavalt valemile (1), kus f(x) = a = 1 ja b = 4, on meil = (= ruutühikud

Näide 6 . Arvutage joonise pindala, mis on piiratud joontega: y = sinx, y = 0, x = 0, x = .

Soovitud ala on piiratud poollaine sinusoidi ja Ox-teljega (vt joonis).

Meil on - cosx \u003d - cos \u003d 1 + 1 \u003d 2 ruutmeetrit. ühikut

Näide 7 Arvutage joonise pindala, mis on piiratud joontega: y \u003d - 6x, y \u003d 0 ja x \u003d 4.

Joonis asub Ox-telje all (vt joonis).

Seetõttu leitakse selle pindala valemiga (3)

= =

Näide 8 Arvutage joonise pindala, mis on piiratud joontega: y \u003d ja x \u003d 2. Koostame punktide kaupa kõvera y \u003d (vt joonist). Seega leitakse joonise pindala valemiga (4)

Näide 9 .

X 2 + y 2 = r 2 .

Siin tuleb arvutada ala, mis on piiratud ringiga x 2 + y 2 = r 2 st ringi pindala raadiusega r, mille keskpunkt on alguspunktis. Leiame selle ala neljanda osa, võttes integratsiooni piirid 0-st

dor; meil on: 1 = = [

Järelikult 1 =

Näide 10 Arvutage joontega piiratud joonise pindala: y \u003d x 2 ja y = 2x

Seda arvu piirab parabool y \u003d x 2 ja sirge y \u003d 2x (vt joonis.) Antud sirgete lõikepunktide määramiseks lahendame võrrandisüsteemi: x 2 – 2x = 0 x = 0 ja x = 2

Valemi (5) abil pindala leidmiseks saame

= }