Moodul on üks neist asjadest, millest kõik on justkui kuulnud, aga tegelikult ei saa keegi sellest õieti aru. Seetõttu toimub täna suur õppetund, mis on pühendatud võrrandite lahendamisele moodulite abil.
Ma ütlen teile kohe: õppetund saab olema lihtne. Üldiselt on moodulid üldiselt suhteliselt lihtne teema. "Jah, muidugi, see on lihtne! See paneb mu aju plahvatama!" - ütlevad paljud õpilased, aga kõik need ajumurrud on tingitud sellest, et enamikul pole mitte teadmised peas, vaid mingi jama. Ja selle tunni eesmärk on muuta jama teadmisteks. :)
Natuke teooriat
Nii et lähme. Alustame kõige olulisemast: mis on moodul? Tuletan meelde, et arvu moodul on lihtsalt sama arv, kuid võetud ilma miinusmärgita. See on näiteks $\left| -5 \parem|=5 $. Või $\left| -129,5\parem|=129,5$.
Kas see on nii lihtne? Jah, lihtne. Mis on siis positiivse arvu moodul? Siin on asi veelgi lihtsam: positiivse arvu moodul on võrdne selle arvu endaga: $\left| 5\right|=5$; $\left| 129,5 \right|=129,5 $ jne.
Selgub kurioosne asi: erinevatel numbritel võib olla sama moodul. Näiteks: $\left| -5 \right|=\left| 5\right|=5$; $\left| -129,5 \right|=\left| 129,5 \right|=129,5 $. On lihtne näha, mis tüüpi need arvud on, milles moodulid on samad: need numbrid on vastandlikud. Seega märgime ise, et vastandarvude moodulid on võrdsed:
\[\left| -a \right|=\left| a\right|\]
Veel üks oluline fakt: moodul ei ole kunagi negatiivne. Ükskõik millise arvu me võtame – isegi positiivse, isegi negatiivse –, selle moodul osutub alati positiivseks (või äärmisel juhul nulliks). Seetõttu nimetatakse moodulit sageli arvu absoluutväärtuseks.
Lisaks, kui kombineerime positiivse ja negatiivse arvu mooduli definitsiooni, saame kõigi arvude mooduli globaalse definitsiooni. Nimelt: arvu moodul on võrdne selle arvu endaga, kui arv on positiivne (või null), või võrdne vastupidise arvuga, kui arv on negatiivne. Selle saate kirjutada valemina:
Samuti on olemas nullmoodul, kuid see on alati võrdne nulliga. Samuti on null ainus arv, millel pole vastandit.
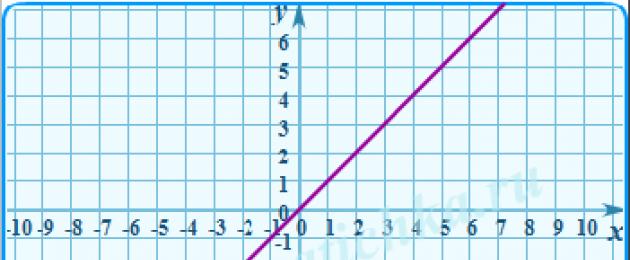
Seega, kui arvestada funktsiooni $y=\left| x \right|$ ja proovige joonistada selle graafik, saate sellise "daw":
Mooduligraafiku ja võrrandilahenduse näide
Sellelt pildilt on kohe näha, et $\left| -m \right|=\left| m \right|$ ja mooduli graafik ei jää kunagi x-teljest allapoole. Kuid see pole veel kõik: punane joon tähistab sirget $y=a$, mis positiivse $a$ korral annab meile kaks juurt korraga: $((x)_(1))$ ja $((x) _(2)) $, aga sellest räägime hiljem. :)
Lisaks puhtalt algebralisele määratlusele on olemas ka geomeetriline. Oletame, et arvureal on kaks punkti: $((x)_(1))$ ja $((x)_(2))$. Sel juhul avaldis $\left| ((x)_(1))-((x)_(2)) \right|$ on vaid määratud punktide vaheline kaugus. Või soovi korral neid punkte ühendava segmendi pikkus:
 Moodul on arvujoone punktide vaheline kaugus
Moodul on arvujoone punktide vaheline kaugus Sellest definitsioonist järeldub ka, et moodul on alati mittenegatiivne. Aga piisavalt definitsioone ja teooriat – liigume edasi reaalvõrrandite juurde. :)
Põhivalem
Olgu, oleme määratluse välja mõelnud. Kuid see ei muutunud lihtsamaks. Kuidas lahendada võrrandeid, mis sisaldavad just seda moodulit?
Rahune, lihtsalt rahu. Alustame kõige lihtsamatest asjadest. Kaaluge midagi sellist:
\[\left| x\right|=3\]
Seega on moodul$x$ 3. Millega saab $x$ olla võrdne? Noh, definitsiooni järgi otsustades, $x=3$ sobib meile täpselt. Tõesti:
\[\left| 3\right|=3\]
Kas on muid numbreid? Kork näib vihjavat, et on olemas. Näiteks $x=-3$ — $\left| -3 \right|=3$, st. nõutav võrdsus on täidetud.
Ehk kui otsime, mõtleme, leiame veel numbreid? Aga katkesta: numbreid enam pole. Võrrand $\left| x \right|=3$ on ainult kaks juurt: $x=3$ ja $x=-3$.
Teeme nüüd ülesande pisut keerulisemaks. Laske muutuja $x$ asemel rippuda mooduli märgi all funktsioon $f\left(x \right)$ ja paremale asetame kolmiku asemel suvalise arvu $a$. Saame võrrandi:
\[\left| f\left(x \right) \right|=a\]
No kuidas sa otsustad? Tuletan teile meelde: $f\left(x \right)$ on suvaline funktsioon, $a$ on suvaline arv. Need. üldse mis tahes! Näiteks:
\[\left| 2x+1 \right|=5\]
\[\left| 10x-5 \parem|=-65\]
Vaatame teist võrrandit. Tema kohta võib kohe öelda: tal pole juuri. Miks? See on õige: kuna see nõuab, et moodul oleks võrdne negatiivse arvuga, mida kunagi ei juhtu, kuna me juba teame, et moodul on alati positiivne arv või äärmisel juhul null.
Kuid esimese võrrandiga on kõik lõbusam. On kaks võimalust: kas mooduli märgi all on positiivne avaldis ja seejärel $\left| 2x+1 \right|=2x+1$ või see avaldis on ikkagi negatiivne, sel juhul $\left| 2x+1 \right|=-\left(2x+1 \right)=-2x-1$. Esimesel juhul kirjutatakse meie võrrand ümber järgmiselt:
\[\left| 2x+1 \right|=5\Paremnool 2x+1=5\]
Ja äkki selgub, et alammooduli avaldis $2x+1$ on tõepoolest positiivne – see on võrdne arvuga 5. See tähendab, saame selle võrrandi ohutult lahendada - saadud juur on osa vastusest:
Need, kes on eriti umbusklikud, võivad proovida asendada leitud juur algvõrrandiga ja veenduda, et mooduli all on tõesti positiivne arv.
Vaatame nüüd negatiivse alammooduli avaldise juhtumit:
\[\left\( \begin(joona)& \left| 2x+1 \right|=5 \\& 2x+1 \lt 0 \\\end(joonda) \right.\Rightnarrow -2x-1=5 \Paremnool 2x+1=-5\]
Oih! Jällegi on kõik selge: eeldasime, et $2x+1 \lt 0$ ja tulemuseks saime, et $2x+1=-5$ – tõepoolest, see avaldis on väiksem kui null. Lahendame saadud võrrandi, teades juba kindlalt, et leitud juur meile sobib:
Kokku saime taas kaks vastust: $x=2$ ja $x=3$. Jah, arvutuste maht osutus veidi suuremaks kui väga lihtsas võrrandis $\left| x \right|=3$, kuid põhimõtteliselt pole midagi muutunud. Ehk on mingi universaalne algoritm?
Jah, selline algoritm on olemas. Ja nüüd analüüsime seda.
Mooduli märgist vabanemine
Olgu meile antud võrrand $\left| f\left(x \right) \right|=a$ ja $a\ge 0$ (muidu, nagu me juba teame, pole juuri). Seejärel saate moodulmärgist lahti saada vastavalt järgmisele reeglile:
\[\left| f\left(x \right) \right|=a\Rightnarrow f\left(x \right)=\pm a\]
Seega jaguneb meie võrrand mooduliga kaheks, kuid ilma moodulita. See on kogu tehnoloogia! Proovime lahendada paar võrrandit. Alustame sellest
\[\left| 5x+4 \right|=10\Paremnool 5x+4=\pm 10\]
Eraldi kaalume, millal on kümme plussiga paremal ja eraldi, millal on miinus. Meil on:
\[\begin(joona)& 5x+4=10\Paremnool 5x=6\Paremnool x=\frac(6)(5)=1,2; \\& 5x+4=-10\Paremnool 5x=-14\Paremnool x=-\frac(14)(5)=-2,8. \\\lõpp(joonda)\]
See on kõik! Saime kaks juurt: $x=1,2$ ja $x=-2,8$. Kogu lahendus võttis sõna otseses mõttes kaks rida.
Ok, pole kahtlust, vaatame midagi veidi tõsisemat:
\[\left| 7-5x \right|=13\]
Jällegi avage moodul pluss- ja miinusmärgiga:
\[\begin(align)& 7-5x=13\Rightnarrow -5x=6\Rightarrow x=-\frac(6)(5)=-1,2; \\& 7-5x=-13\Paremnool -5x=-20\Paremnool x=4. \\\lõpp(joonda)\]
Jälle paar rida – ja vastus ongi valmis! Nagu ma ütlesin, pole moodulites midagi keerulist. Peate lihtsalt meeles pidama mõnda reeglit. Seetõttu läheme kaugemale ja jätkame tõesti raskemate ülesannetega.
Muutuv parempoolne ümbris
Nüüd kaaluge seda võrrandit:
\[\left| 3x-2 \right|=2x\]
See võrrand erineb põhimõtteliselt kõigist eelmistest. Kuidas? Ja see, et avaldis $2x$ asub võrdusmärgist paremal – ja me ei saa ju ette teada, kas see on positiivne või negatiivne.
Kuidas sel juhul olla? Esiteks peame sellest lõplikult aru saama kui võrrandi parem pool on negatiivne, pole võrrandil juuri- me juba teame, et moodul ei saa olla võrdne negatiivse arvuga.
Ja teiseks, kui parempoolne osa on ikka positiivne (või võrdne nulliga), siis saab edasi minna täpselt samamoodi nagu enne: lihtsalt ava moodul eraldi plussmärgiga ja eraldi miinusmärgiga.
Seega formuleerime reegli suvaliste funktsioonide $f\left(x \right)$ ja $g\left(x \right)$ jaoks:
\[\left| f\left(x \right) \right|=g\left(x \right)\Rightnarrow \left\( \begin (joonda)& f\left(x \right)=\pm g\left(x \right) ), \\& g\left(x \right)\ge 0. \\\end(joonda) \right.\]
Seoses võrrandiga saame:
\[\left| 3x-2 \right|=2x\Paremnool \left\( \begin(joona)& 3x-2=\pm 2x, \\& 2x\ge 0. \\\end(joonda) \right.\]
Noh, me saame kuidagi hakkama $2x\ge 0$ nõudega. Lõpuks võime rumalalt asendada esimesest võrrandist saadud juured ja kontrollida, kas ebavõrdsus kehtib või mitte.
Lahendame siis võrrandi enda:
\[\begin(align)& 3x-2=2\Rightnarrow 3x=4\Rightarrow x=\frac(4)(3); \\& 3x-2=-2\Paremnool 3x=0\Paremnool x=0. \\\lõpp(joonda)\]
Noh, milline neist kahest juurtest täidab nõuet $2x\ge 0$? Jah, mõlemad! Seetõttu on vastuseks kaks numbrit: $x=(4)/(3)\;$ ja $x=0$. See on lahendus. :)
Kahtlustan, et ühel õpilastest on juba igav hakanud? Noh, kaaluge veelgi keerulisemat võrrandit:
\[\left| ((x)^(3))-3((x)^(2))+x \parem|=x-((x)^(3))\]
Kuigi see näeb välja kurja, on see tegelikult sama võrrand kujul "moodul võrdub funktsiooniga":
\[\left| f\left(x \right) \right|=g\left(x \right)\]
Ja see lahendatakse samal viisil:
\[\left| ((x)^(3))-3((x)^(2))+x \parem|=x-((x)^(3))\Paremnool \vasak\( \begin(joon)& ( (x)^(3))-3((x)^(2))+x=\pm \left(x-((x)^(3)) \right), \\& x-((x) )^(3))\ge 0. \\\end(joonda) \paremale.\]
Ebavõrdsusega tegeleme hiljem - see on kuidagi liiga tige (tegelikult lihtne, aga me ei lahenda seda). Praegu vaatame saadud võrrandeid. Mõelge esimesele juhtumile - see on siis, kui moodulit laiendatakse plussmärgiga:
\[((x)^(3))-3((x)^(2))+x=x-((x)^(3))\]
Noh, siin pole mõtet, et peate koguma kõik vasakpoolsed, tooma sarnased ja vaadake, mis juhtub. Ja see juhtub:
\[\begin(joona)& ((x)^(3))-3((x)^(2))+x=x-((x)^(3)); \\& 2((x)^(3))-3((x)^(2))=0; \\\lõpp(joonda)\]
Pannes ühisteguri $((x)^(2))$ sulust välja, saame väga lihtsa võrrandi:
\[((x)^(2))\left(2x-3 \right)=0\Paremnool \vasak[ \begin(joona)& ((x)^(2))=0 \\& 2x-3 =0 \\\lõpp(joondamine) \paremale.\]
\[((x)_(1))=0;\quad ((x)_(2))=\frac(3)(2)=1,5.\]
Siin kasutasime korrutise olulist omadust, mille huvides faktoreerisime algse polünoomi: korrutis on võrdne nulliga, kui vähemalt üks teguritest on võrdne nulliga.
Nüüd käsitleme samamoodi teist võrrandit, mis saadakse mooduli laiendamisel miinusmärgiga:
\[\begin(joona)& ((x)^(3))-3((x)^(2))+x=-\left(x-((x)^(3)) \right); \\& ((x)^(3))-3((x)^(2))+x=-x+((x)^(3)); \\& -3((x)^(2))+2x=0; \\& x\left(-3x+2 \right)=0. \\\lõpp(joonda)\]
Jällegi sama: korrutis on null, kui vähemalt üks teguritest on null. Meil on:
\[\left[ \begin(align)& x=0 \\& -3x+2=0 \\\end(joonda) \right.\]
Noh, saime kolm juurt: $x=0$, $x=1.5$ ja $x=(2)/(3)\;$. Noh, mis selle komplekti lõplikuks vastuseks läheb? Selleks pidage meeles, et meil on täiendav ebavõrdsuse piirang:
Kuidas seda nõuet arvesse võtta? Asendame leitud juured ja kontrollime, kas ebavõrdsus kehtib nende $x$ kohta või mitte. Meil on:
\[\begin(align)& x=0\Paremnool x-((x)^(3))=0-0=0\ge 0; \\& x=1,5\Paremnool x-((x)^(3))=1,5-((1,5)^(3)) \lt 0; \\& x=\frac(2)(3)\Paremnool x-((x)^(3))=\frac(2)(3)-\frac(8)(27)=\frac(10) (27)\ge 0; \\\lõpp(joonda)\]
Seega juur $x=1,5$ meile ei sobi. Ja vastuseks lähevad ainult kaks juurt:
\[((x)_(1))=0;\quad ((x)_(2))=\frac(2) (3).\]
Nagu näha, polnud ka sel juhul midagi keerulist – moodulitega võrrandid lahendatakse alati vastavalt algoritmile. Peate lihtsalt polünoomidest ja ebavõrdsustest hästi aru saama. Seetõttu liigume edasi keerukamate ülesannete juurde - mooduleid pole juba üks, vaid kaks.
Kahe mooduliga võrrandid
Siiani oleme uurinud ainult kõige lihtsamaid võrrandeid - oli üks moodul ja midagi muud. Saatsime selle “midagi veel” ebavõrdsuse teise ossa, moodulist eemale, et lõpuks taandataks kõik selliseks võrrandiks nagu $\left| f\left(x \right) \right|=g\left(x \right)$ või veelgi lihtsam $\left| f\left(x \right) \right|=a$.
Aga lasteaed on läbi – aeg on mõelda millegi tõsisema üle. Alustame selliste võrranditega:
\[\left| f\left(x \right) \right|=\left| g\left(x \right) \right|\]
See on võrrand kujul "moodul on võrdne mooduliga". Põhimõtteliselt oluline punkt on muude terminite ja tegurite puudumine: ainult üks moodul vasakul, veel üks moodul paremal - ja ei midagi muud.
Nüüd võiks arvata, et selliseid võrrandeid on keerulisem lahendada kui seni uurituid. Aga ei: neid võrrandeid lahendatakse veelgi lihtsamalt. Siin on valem:
\[\left| f\left(x \right) \right|=\left| g\left(x \right) \right|\Rightarrow f\left(x \right)=\pm g\left(x \right)\]
Kõik! Me lihtsalt võrdsustame alammooduli avaldised, lisades ühele neist pluss- või miinusmärgi. Ja siis lahendame saadud kaks võrrandit - ja juured on valmis! Ei mingeid lisapiiranguid, ebavõrdsust jne. Kõik on väga lihtne.
Proovime seda probleemi lahendada:
\[\left| 2x+3 \right|=\left| 2x-7 \right|\]
Elementaarne Watson! Moodulite avamine:
\[\left| 2x+3 \right|=\left| 2x-7 \right|\Paremnool 2x+3=\pm \left(2x-7 \right)\]
Vaatleme iga juhtumit eraldi:
\[\begin(align)& 2x+3=2x-7\Rightarrow 3=-7\Rightarrow \emptyset ; \\& 2x+3=-\left(2x-7 \right)\Paremnool 2x+3=-2x+7. \\\lõpp(joonda)\]
Esimesel võrrandil pole juuri. Sest millal on $3=-7$? Milliste väärtuste jaoks $x$? "Mis kurat on $x$? Kas sa oled kividega visatud? $x$ pole üldse olemas," ütlete te. Ja sul on õigus. Oleme saanud võrdsuse, mis ei sõltu muutujast $x$ ja samas on võrdsus ise vale. Sellepärast pole juuri.
Teise võrrandiga on kõik veidi huvitavam, aga ka väga-väga lihtne:
Nagu näete, otsustati kõik sõna otseses mõttes paari reaga - me ei oodanud lineaarvõrrandist midagi muud. :)
Selle tulemusena on lõplik vastus: $x=1$.
No kuidas? Keeruline? Muidugi mitte. Proovime midagi muud:
\[\left| x-1 \right|=\left| ((x)^(2))-3x+2 \parem|\]
Jällegi on meil selline võrrand nagu $\left| f\left(x \right) \right|=\left| g\left(x \right) \right|$. Seetõttu kirjutame selle kohe ümber, paljastades mooduli märgi:
\[((x)^(2))-3x+2=\pm \left(x-1 \right)\]
Võib-olla küsib keegi nüüd: “Kuule, mis jama? Miks on pluss-miinus paremal pool ja mitte vasakul? Rahune maha, ma seletan kõik ära. Tõepoolest, heas mõttes oleksime pidanud oma võrrandi ümber kirjutama järgmiselt:
Seejärel peate avama sulud, nihutama kõik terminid võrdusmärgist ühes suunas (kuna võrrand on ilmselgelt mõlemal juhul ruut) ja seejärel leidma juured. Kuid peate tunnistama: kui "pluss-miinus" on kolme liikme ees (eriti kui üks neist on ruudukujuline avaldis), tundub see kuidagi keerulisem kui olukord, kus "pluss-miinus" on ainult kahe ees. tingimustele.
Kuid miski ei takista meil algset võrrandit järgmiselt ümber kirjutamast:
\[\left| x-1 \right|=\left| ((x)^(2))-3x+2 \right|\Paremnool \vasak| ((x)^(2))-3x+2 \right|=\left| x-1 \right|\]
Mis juhtus? Jah, ei midagi erilist: lihtsalt vasak ja parem pool vahetatud. Pisiasi, mis kokkuvõttes meie elu natukenegi lihtsustab. :)
Üldiselt lahendame selle võrrandi, võttes arvesse pluss- ja miinusvõimalusi:
\[\begin(joona)& ((x)^(2))-3x+2=x-1\Paremnool ((x)^(2))-4x+3=0; \\& ((x)^(2))-3x+2=-\left(x-1 \right)\Paremnool ((x)^(2))-2x+1=0. \\\lõpp(joonda)\]
Esimesel võrrandil on juured $x=3$ ja $x=1$. Teine on üldiselt täpne ruut:
\[((x)^(2))-2x+1=((\left(x-1 \right))^(2))\]
Seetõttu on sellel üks juur: $x=1$. Aga selle juure oleme juba varem saanud. Seega läheb lõplikku vastust ainult kaks numbrit:
\[((x)_(1))=3;\quad ((x)_(2))=1.\]
Ülesanne täidetud! Saab riiulilt võtta ja pirukat süüa. Neid on 2, sinu keskmine. :)
Oluline märkus. Samade juurte olemasolu mooduli laiendamise erinevate versioonide jaoks tähendab, et algsed polünoomid jaotatakse teguriteks ja nende tegurite hulgas on tingimata ühine. Tõesti:
\[\begin(joona)& \left| x-1 \right|=\left| ((x)^(2))-3x+2 \parem|; \\&\left| x-1 \right|=\left| \left(x-1 \right)\left(x-2 \right) \right|. \\\lõpp(joonda)\]
Üks mooduli atribuutidest: $\left| a\cdot b \right|=\left| a \right|\cdot \left| b \right|$ (see tähendab, et korrutise moodul on võrdne mooduli korrutisega), seega saab algse võrrandi ümber kirjutada
\[\left| x-1 \right|=\left| x-1 \right|\cdot \left| x-2 \right|\]
Nagu näete, on meil tõesti ühine tegur. Nüüd, kui kogute kõik moodulid ühele küljele, saate selle kordaja sulust välja võtta:
\[\begin(joona)& \left| x-1 \right|=\left| x-1 \right|\cdot \left| x-2 \parem|; \\&\left| x-1 \right|-\left| x-1 \right|\cdot \left| x-2 \right|=0; \\&\left| x-1 \right|\cdot \left(1-\left| x-2 \right| \right)=0. \\\lõpp(joonda)\]
Noh, nüüd tuletame meelde, et korrutis on võrdne nulliga, kui vähemalt üks teguritest on võrdne nulliga:
\[\left[ \begin(align)& \left| x-1 \right|=0, \\& \left| x-2 \right|=1. \\\lõpp(joonda) \paremale.\]
Seega on algne kahe mooduliga võrrand taandatud kahele kõige lihtsamale võrrandile, millest me juba tunni alguses rääkisime. Selliseid võrrandeid saab lahendada vaid paari reaga. :)
See märkus võib tunduda tarbetult keeruline ja praktikas kohaldamatu. Kuid tegelikkuses võite kokku puutuda palju keerukamate ülesannetega kui need, mida täna analüüsime. Nendes saab mooduleid kombineerida polünoomide, aritmeetiliste juurte, logaritmidega jne. Ja sellistes olukordades võib võrrandi üldist astet alandada, pannes midagi sulgudest välja, olla väga-väga mugav. :)
Nüüd tahaksin analüüsida teist võrrandit, mis esmapilgul võib tunduda hullumeelne. Paljud õpilased jäävad sellele kinni – isegi need, kes usuvad, et saavad moodulitest hästi aru.
Seda võrrandit on aga veelgi lihtsam lahendada kui seda, mida me varem kaalusime. Ja kui saate aru, miks, saate veel ühe nipi võrrandite kiireks lahendamiseks moodulitega.
Seega võrrand on järgmine:
\[\left| x-((x)^(3)) \right|+\left| ((x)^(2))+x-2 \right|=0\]
Ei, see pole kirjaviga: see on pluss moodulite vahel. Ja me peame leidma, millise $x$ puhul on kahe mooduli summa võrdne nulliga. :)
Milles on probleem? Ja probleem on selles, et iga moodul on positiivne arv või äärmuslikel juhtudel null. Mis juhtub, kui liita kaks positiivset arvu? Ilmselgelt jälle positiivne arv:
\[\begin(joona)& 5+7=12 \gt 0; \\& 0,004+0,0001=0,0041 \gt 0; \\& 5+0=5 \gt 0. \\\end(joonda)\]
Viimane rida võib anda teile aimu: ainus juhtum, kus moodulite summa on null, on siis, kui iga moodul on võrdne nulliga:
\[\left| x-((x)^(3)) \right|+\left| ((x)^(2))+x-2 \right|=0\Paremnool \vasak\( \begin(joon)& \left| x-((x)^(3)) \right|=0, \\& \left|((x)^(2))+x-2 \right|=0. \\\end(joonda) \right.\]
Millal on moodul võrdne nulliga? Ainult ühel juhul - kui alammooduli avaldis on võrdne nulliga:
\[((x)^(2))+x-2=0\Paremnool \left(x+2 \right)\left(x-1 \right)=0\Paremnool \vasak[ \begin(joonda)& x=-2 \\& x=1 \\\end(joonda) \paremale.\]
Seega on meil kolm punkti, kus esimene moodul nullitakse: 0, 1 ja −1; samuti kaks punkti, kus teine moodul nullitakse: −2 ja 1. Siiski on vaja, et mõlemad moodulid nullitaks korraga, seega peame leitud arvude hulgast valima need, mis sisalduvad mõlemas komplektis. Ilmselgelt on ainult üks selline arv: $x=1$ – see on lõplik vastus.
poolitamise meetod
Noh, me oleme juba läbinud hulga ülesandeid ja õppinud palju nippe. Kas sa arvad, et see on kõik? Kuid mitte! Nüüd kaalume lõplikku tehnikat - ja samal ajal kõige olulisemat. Räägime võrrandite jagamisest mooduliga. Mida arutatakse? Lähme veidi tagasi ja kaalume mõnda lihtsat võrrandit. Näiteks see:
\[\left| 3x-5\parem|=5-3x\]
Põhimõtteliselt me juba teame, kuidas sellist võrrandit lahendada, sest see on standard $\left| f\left(x \right) \right|=g\left(x \right)$. Kuid proovime seda võrrandit veidi teise nurga alt vaadata. Täpsemalt mõelge väljendile mooduli märgi all. Lubage mul teile meelde tuletada, et mis tahes arvu moodul võib olla võrdne arvu endaga või olla sellele arvule vastupidine:
\[\left| a \right|=\left\( \begin(align)& a,\quad a\ge 0, \\& -a,\quad a \lt 0. \\\end(joonda) \right.\]
Tegelikult on see ebaselgus kogu probleem: kuna mooduli all olev arv muutub (see sõltub muutujast), pole meile selge, kas see on positiivne või negatiivne.
Aga mis siis, kui me esialgu nõuame, et see arv oleks positiivne? Näiteks nõuame, et $3x-5 \gt 0$ – sellisel juhul saame garanteeritult moodulimärgi alla positiivse arvu ja saame sellest moodulist täielikult lahti:
Seega muutub meie võrrand lineaarseks, mida on lihtne lahendada:
Tõsi, kõik need kaalutlused on mõttekad ainult tingimusel $3x-5 \gt 0$ - me ise kehtestasime selle nõude, et moodulit ühemõtteliselt paljastada. Asendame leitud $x=\frac(5)(3)$ selle tingimusega ja kontrollime:
Selgub, et määratud väärtuse $x$ puhul ei ole meie nõue täidetud, sest avaldis osutus võrdseks nulliga ja me peame olema rangelt suurem kui null. Kurb. :(
Aga pole midagi! On ju veel üks variant $3x-5 \lt 0$. Veelgi enam: on ka juhtum $3x-5=0$ - sedagi tuleb arvestada, muidu jääb lahendus poolikuks. Niisiis, kaaluge juhtumit $3x-5 \lt 0$:
On ilmne, et moodul avaneb miinusmärgiga. Kuid siis tekib kummaline olukord: algses võrrandis jääb nii vasakul kui ka paremal välja sama avaldis:
Huvitav, mille puhul selline $x$ avaldis $5-3x$ võrdub avaldisega $5-3x$? Selliste võrrandite järgi lämbuks isegi Kapten ilmselgelt süljesse, aga me teame, et see võrrand on identiteet, s.t. see kehtib muutuja mis tahes väärtuse kohta!
Ja see tähendab, et meile sobib iga $x$. Meil on aga piirang:
Teisisõnu, vastus ei ole üks arv, vaid terve intervall:
Lõpuks on veel üks juhtum, mida kaaluda: $3x-5=0$. Siin on kõik lihtne: mooduli all on null ja nullmoodul on samuti võrdne nulliga (see tuleneb otseselt definitsioonist):
Aga siis algne võrrand $\left| 3x-5 \right|=5-3x$ kirjutatakse ümber järgmiselt:
Selle juure saime juba eespool, kui kaalusime juhtumit $3x-5 \gt 0$. Pealegi on see juur lahendus võrrandile $3x-5=0$ - see on piirang, mille me ise mooduli nullimiseks kasutusele võtsime. :)
Seega jääme lisaks intervallile rahule ka selle intervalli lõpus oleva numbriga:
 Juurte ühendamine võrrandites mooduliga
Juurte ühendamine võrrandites mooduliga Lõplik vastus kokku: $x\in \left(-\infty ;\frac(5)(3) \right]$. Üsna lihtsa (sisuliselt lineaarse) mooduliga võrrandi vastuses pole sellist jama väga sageli näha No harjuge ära: mooduli keerukus seisneb selles, et vastused sellistes võrrandites võivad olla täiesti ettearvamatud.
Palju olulisem on midagi muud: me võtsime just lahti universaalse algoritmi mooduliga võrrandi lahendamiseks! Ja see algoritm koosneb järgmistest sammudest:
- Võrdsusta iga võrrandi moodul nulliga. Võtame mõned võrrandid;
- Lahendage kõik need võrrandid ja märkige arvujoonele juured. Selle tulemusena jagatakse sirgjoon mitmeks intervalliks, millest igaühel on kõik moodulid ainulaadselt laiendatud;
- Lahendage iga intervalli algne võrrand ja ühendage vastused.
See on kõik! Jääb vaid üks küsimus: mida teha esimeses etapis saadud juurtega? Oletame, et meil on kaks juurt: $x=1$ ja $x=5$. Nad jagavad numbrirea kolmeks osaks:
 Arvrea jagamine intervallideks punktide abil
Arvrea jagamine intervallideks punktide abil Millised on siis intervallid? On selge, et neid on kolm:
- Kõige vasakpoolsem: $x \lt 1$ - ühik ise ei kuulu intervalli;
- Keskne: $1\le x \lt 5$ - siin sisaldub intervallis üks, aga viit ei arvestata;
- Parempoolseim: $x\ge 5$ — viis on kaasatud ainult siin!
Ma arvan, et sa juba mõistad mustrit. Iga intervall sisaldab vasakut otsa ja ei sisalda paremat otsa.
Esmapilgul võib selline plaat tunduda ebamugav, ebaloogiline ja üldiselt mingi hull. Kuid uskuge mind: pärast väikest harjutamist avastate, et see on kõige usaldusväärsem lähenemine ja samal ajal ei sega moodulite üheselt paljastamist. Parem on kasutada sellist skeemi kui mõelda iga kord: anda praegusele intervallile vasak / parem ots või "viska" see järgmisele.
Siin lõpeb õppetund. Laadige alla ülesanded ise lahendamiseks, harjutamiseks, vastustega võrdlemiseks - ja kohtumiseni järgmises õppetunnis, mis on pühendatud moodulitega ebavõrdsusele. :)
Funktsioon kujul y=|x|.
Funktsiooni graafik intervallil - funktsiooni y \u003d -x graafikuga.
Vaatleme esmalt lihtsaimat juhtu – funktsiooni y=|x|. Mooduli määratluse järgi on meil:
Seega x≥0 korral funktsioon y=|x| langeb kokku funktsiooniga y \u003d x ja x jaoks Seda selgitust kasutades on lihtne joonistada funktsiooni y \u003d | x | (joonis 1).

On lihtne näha, et see graafik on ühendus funktsiooni y \u003d x graafiku selle osaga, mis ei asu OX-telje all, ja joonest, mis saadakse peegelpeegeldusega ümber OX-telje, selle osa, mis asub OX-telje all.
See meetod sobib ka funktsiooni y=|kx+b| graafiku joonistamiseks.
Kui funktsiooni y=kx+b graafik on kujutatud joonisel 2, siis funktsiooni y=|kx+b| on joonisel 3 näidatud joon.
(!LANG:Näide 1. Joonistage funktsioon y=||1-x 2 |-3|.
Koostame funktsiooni y=1-x 2 graafiku ja rakendame sellele operatsiooni "moodul" (OX-telje all asuv graafiku osa peegeldub sümmeetriliselt OX-telje suhtes).

Nihutame diagrammi 3 võrra allapoole.

Rakendame operatsiooni "moodul" ja saame lõpliku graafiku funktsioonist y=||1-x 2 |-3|

Näide 2 Joonistage funktsioon y=||x 2 -2x|-3|.
Teisenduse tulemusena saame y=|x 2 -2x|=|(x-1) 2 -1|. Koostame funktsiooni y=(x-1) 2 -1 graafiku: koostame parabooli y=x 2 ja nihutame 1 võrra paremale ja 1 võrra alla.

Rakendame sellele operatsiooni "moodul" (OX-telje all asuv graafiku osa peegeldub sümmeetriliselt OX-telje suhtes).

Nihutame graafikut 3 võrra allapoole ja rakendame operatsiooni "moodul", mille tulemusena saame lõpliku graafiku.

Näide 3 Joonistage funktsioon.
Mooduli laiendamiseks peame kaaluma kahte juhtumit:
1)x>0, siis avaneb moodul märgiga "+" =
2) x =
Koostame esimese juhtumi jaoks graafiku.

Jätame kõrvale graafiku osa, kus x

Koostame teise juhtumi jaoks graafiku ja jätame samamoodi kõrvale osa, kus x>0, mille tulemusena saame.

Kombineerime kaks graafikut ja saame lõpliku.

Näide 4 Joonistage funktsioon.
Kõigepealt koostame funktsiooni graafiku, mille jaoks on mugav valida täisarvuline osa, saame. Väärtuste tabelile tuginedes saame graafiku.

Rakendame moodulitehet (OX-telje all asuv graafiku osa peegeldub sümmeetriliselt OX-telje suhtes). Saame lõpliku diagrammi

Näide 5 Joonistage funktsioon y=|-x 2 +6x-8|. Esiteks lihtsustame funktsiooni väärtuseks y=1-(x-3) 2 ja koostame selle graafiku

Nüüd rakendame operatsiooni "moodul" ja kajastame OX-telje all olevat graafiku osa OX-telje suhtes

Näide 6 Joonistage funktsioon y=-x 2 +6|x|-8. Samuti lihtsustame funktsiooni y=1-(x-3) 2 ja koostame selle graafiku

Nüüd rakendame operatsiooni "moodul" ja kajastame oY teljest paremale jäävat graafiku osa vasakule küljele

Näide 7 Joonistage funktsioon ![]() . Joonistame funktsiooni
. Joonistame funktsiooni

Joonistame funktsiooni

Teeme paralleelülekande 3 ühikulise segmendi võrra paremale ja 2 ülespoole. Graafik näeb välja selline:

Rakendame operatsiooni "moodul" ja peegeldame sirgest x=3 paremale jäävat graafiku osa vasakpoolsesse pooltasandisse.
ärakiri
1 6.-11. klassi õpilaste õppe- ja uurimistöö piirkondlik teaduslik ja praktiline konverents "Matemaatika rakendus- ja põhiküsimused" Matemaatika õppimise metoodilised aspektid Gabova Anzhela Yurievna moodulit sisaldavate funktsioonide graafikute koostamine, 10. klass, MOBU "Gümnaasium 3" " Kudymkar, Pikuleva Nadežda Ivanovna, matemaatikaõpetaja, MOBU "Gymnasium 3", Kudymkar, Perm, 2016
2 Sisu: Sissejuhatus...3 lk I. Põhiosa... 6 lk 1.1Ajalooline taust.. 6 lk 2.Funktsioonide põhidefinitsioonid ja omadused lk .8 lk 2.3 Murd-ratsionaalfunktsioon 8 lk. 3. Algoritmid moodulitega graafikute joonistamiseks 9 lk 3.1 Mooduli määramine .. 9 p valemis "pesastatud moodulid".10 lk 3.4 Algoritm funktsioonide graafikute joonistamiseks kujul y = a 1 x x 1 + a 2 x x a n x x n + ax + b...13 lk 3.5 Algoritm mooduliga ruutfunktsiooni graafiku joonistamiseks.14 lk 3.6 Algoritm mooduliga murdratsionaalfunktsiooni joonistamiseks. 15p. 4. Ruutfunktsiooni graafiku muutused olenevalt absoluutväärtuse märgi asukohast ..17str. II. Järeldus ... 26 lk III. Kasutatud kirjanduse ja allikate loetelu...27 lk IV. Taotlus....28lk. 2
3 Sissejuhatus Funktsioonide joonistamine on koolimatemaatika üks huvitavamaid teemasid. Meie aja suurim matemaatik Israel Moiseevich Gelfand kirjutas: "Joonistamise protsess on viis valemite ja kirjelduste muutmiseks geomeetrilisteks kujutisteks. See joonistamine on vahend valemite ja funktsioonide nägemiseks ning nende funktsioonide muutumise nägemiseks. Näiteks kui y \u003d x 2 on kirjutatud, näete kohe parabooli; kui y = x 2-4, näete nelja ühiku võrra langetatud parabooli; kui y \u003d - (x 2 4), siis näete eelmist parabooli alla keeratuna. See valemi korraga nägemise ja selle geomeetrilise tõlgendamise võimalus on oluline mitte ainult matemaatika, vaid ka teiste ainete õppimisel. See on oskus, mis jääb teiega kaasa kogu eluks, nagu näiteks rattaga sõitma, trükkima või autot juhtima õppimine." Moodulitega võrrandite lahendamise alused saadi 6. 7. klassist. Valisin selle konkreetse teema, sest usun, et see nõuab sügavamat ja põhjalikumat uurimist. Soovin saada rohkem teadmisi arvu moodulitest, erinevatest absoluutväärtuse märki sisaldavate graafikute joonistamise viisidest. Kui joonte, paraboolide, hüperboolide “standardvõrrandid” sisaldavad mooduli märki, muutuvad nende graafikud ebatavaliseks ja isegi ilusaks. Selliste graafikute koostamise õppimiseks peate valdama põhifiguuride koostamise tehnikaid, samuti teadma ja mõistma kindlalt arvu mooduli määratlust. Kooli matemaatikakursusel ei käsitleta mooduliga graafikuid piisavalt süvitsi, mistõttu tekkis soov sel teemal oma teadmisi täiendada, oma uurimistööd läbi viia. Ilma mooduli definitsiooni teadmata on võimatu koostada isegi kõige lihtsamat absoluutväärtust sisaldavat graafikut. Moodulimärgiga avaldisi sisaldavate funktsioonide graafikute iseloomulik tunnus, 3
4 on keerdude olemasolu kohtades, kus mooduli märgi all olev avaldis märki muudab. Töö eesmärk: käsitleda lineaarsete, ruut- ja murdratsionaalsete funktsioonide graafiku koostamist, mis sisaldab muutujat moodulmärgi all. Ülesanded: 1) Tutvuda kirjandusega lineaar-, ruut- ja murdratsionaalfunktsioonide absoluutväärtuse omaduste kohta. 2) Uurige funktsioonide graafikute muutusi sõltuvalt absoluutväärtuse märgi asukohast. 3) Õppige joonistama võrrandite graafikuid. Õppeobjekt: lineaar-, ruut- ja murdratsionaalfunktsioonide graafikud. Õppeaine: muutused lineaar-, ruut- ja murdratsionaalfunktsioonide graafikus sõltuvalt absoluutväärtuse märgi asukohast. Minu töö praktiline tähendus seisneb: 1) antud teemal omandatud teadmiste kasutamises, samuti nende süvendamises ja rakendamises teiste funktsioonide ja võrrandite puhul; 2) uurimisoskuste kasutamisel edasises õppetegevuses. Asjakohasus: Graafikusülesanded on traditsiooniliselt üks raskemaid teemasid matemaatikas. Meie lõpetajad seisavad silmitsi GIA ja ühtse riigieksami eduka sooritamise probleemiga. Uurimisprobleem: moodulmärki sisaldavate funktsioonide joonistamine GIA teisest osast. Uurimistöö hüpotees: GIA teise osa ülesannete lahendamise metoodika rakendamine, mis on välja töötatud mooduli märki sisaldavate funktsioonide graafikute koostamise üldiste meetodite alusel, võimaldab õpilastel neid ülesandeid lahendada.
5 teadlikult, valida ratsionaalseim lahendusviis, rakendada erinevaid lahendusviise ja läbida GIA edukamalt. Töös kasutatud uurimismeetodid: 1. Selleteemalise matemaatilise kirjanduse ja internetiavaruste analüüs. 2. Uuritava materjali paljunemine. 3. Kognitiiv-otsingutegevus. 4. Andmete analüüs ja võrdlemine probleemidele lahenduse otsimisel. 5. Hüpoteeside püstitamine ja nende kontrollimine. 6. Matemaatiliste faktide võrdlemine ja üldistamine. 7. Saadud tulemuste analüüs. Selle töö kirjutamisel kasutati järgmisi allikaid: Interneti-ressursid, OGE testid, matemaatiline kirjandus. 5
6 I. Põhiosa 1.1 Ajalooline taust. 17. sajandi esimesel poolel hakkas funktsiooni mõiste kujunema ühe muutuja sõltuvusena teisest. Niisiis kujutasid prantsuse matemaatikud Pierre Fermat () ja Rene Descartes () funktsiooni ette kõvera punkti ordinaadi sõltuvusena selle abstsissist. Ja inglise teadlane Isaac Newton () mõistis funktsiooni liikuva punkti koordinaadina, mis muutub sõltuvalt ajast. Mõiste "funktsioon" (ladina sõnast funktsiooni jõudlus, komisjon) võttis esmakordselt kasutusele saksa matemaatik Gottfried Leibniz (). Ta seostas funktsiooni geomeetrilise kujutisega (funktsiooni graafik). Hiljem pidasid funktsiooni analüütiliseks väljendiks Šveitsi matemaatik Johann Bernoulli () ja Peterburi Teaduste Akadeemia liige, 18. sajandi kuulus matemaatik Leonard Euler (). Euleril on ka üldine arusaam funktsioonist kui ühe muutuja sõltuvusest teisest. Sõna "moodul" tuleb ladinakeelsest sõnast "modulus", mis tõlkes tähendab "mõõta". See on mitme väärtusega sõna (homonüüm), millel on palju tähendusi ja mida kasutatakse mitte ainult matemaatikas, vaid ka arhitektuuris, füüsikas, inseneriteaduses, programmeerimises ja teistes täppisteadustes. Arhitektuuris on see algne mõõtühik, mis määratakse antud arhitektuurilise struktuuri jaoks ja mida kasutatakse selle koostisosade mitmekordse suhte väljendamiseks. Inseneriteaduses on see erinevates tehnoloogiavaldkondades kasutatav termin, millel pole universaalset tähendust ja mis tähistab erinevaid koefitsiente ja suurusi, näiteks haardemoodulit, elastsusmoodulit jne. 6
7 Mahumoodul (füüsikas) on materjali normaalpinge ja suhtelise pikenemise suhe. 2. Funktsioonide põhidefinitsioonid ja omadused Funktsioon on üks olulisemaid matemaatilisi mõisteid. Funktsioon on muutuja y selline sõltuvus muutujast x, milles muutuja x iga väärtus vastab muutuja y ühele väärtusele. Funktsiooni seadmise viisid: 1) analüütiline meetod (funktsioon seatakse matemaatilise valemi abil); 2) tabelimeetod (funktsioon täpsustatakse tabeli abil); 3) kirjeldav meetod (funktsioon antakse sõnalise kirjeldusega); 4) graafiline meetod (funktsioon seatakse graafiku abil). Funktsiooni graafik on koordinaattasandi kõigi punktide kogum, mille abstsissid on võrdsed argumendi väärtusega ja ordinaadid on võrdsed funktsiooni vastavate väärtustega. 2.1 Ruutfunktsioon Funktsiooni, mis on defineeritud valemiga y=ax 2 +in+c, kus x ja y on muutujad ning parameetrid a, b ja c on mis tahes reaalarvud ning a = 0, nimetatakse ruutarvuks. Funktsiooni y \u003d ax 2 + in + c graafik on parabool; parabooli sümmeetriatelg y \u003d ax 2 + in + c on sirgjoon, kui a> 0 on parabooli "oksad" suunatud ülespoole, a<0 вниз. Чтобы построить график квадратичной функции, нужно: 1) найти координаты вершины параболы и отметить её в координатной плоскости; 2) построить ещё несколько точек, принадлежащих параболе; 3) соединить отмеченные точки плавной линией.,. 2.2Линейная функция функция вида 7
8 (ühe muutuja funktsioonide jaoks). Lineaarfunktsioonide peamine omadus on see, et funktsiooni juurdekasv on proportsionaalne argumendi juurdekasvuga. See tähendab, et funktsioon on otsese proportsionaalsuse üldistus. Lineaarfunktsiooni graafik on sirgjoon, sellest ka selle nimi. See puudutab ühe reaalmuutuja reaalfunktsiooni. 1) Punktis, sirge moodustab teravnurga x-telje positiivse suunaga. 2) Millal, joon moodustab nürinurga x-telje positiivse suunaga. 3) on sirge ja y-telje lõikepunkti ordinaadi indikaator. 4) Millal, joon läbib alguspunkti. , 2.3 Murd-ratsionaalfunktsioon on murd, mille lugeja ja nimetaja on polünoomid. Sellel on vorm kus polünoomid suvalises arvus muutujates. Ühe muutuja ratsionaalsed funktsioonid on erijuhtum: kus ja on polünoomid. 1) Iga avaldis, mida saab nelja aritmeetilise tehte abil muutujatest saada, on ratsionaalne funktsioon. kaheksa
9 2) Ratsionaalfunktsioonide hulk on aritmeetiliste tehtete ja kompositsioonitehte all suletud. 3) Iga ratsionaalfunktsiooni saab esitada lihtmurdude summana - seda kasutatakse analüütilises integratsioonis .., 3. Graafikusalgoritmid mooduliga, kui a on negatiivne. a = 3.2 Algoritm mooduliga lineaarfunktsiooni graafiku koostamiseks Funktsioonide y= x graafikute joonistamiseks peate teadma, et positiivse x korral on meil x = x. See tähendab, et argumendi positiivsete väärtuste korral langeb graafik y=x kokku graafikuga y=x, see tähendab, et see graafiku osa on kiir, mis väljub algpunktist abstsisstelje suhtes 45 kraadise nurga all. . x jaoks< 0 имеем x = -x; значит, для отрицательных x график y= x совпадает с биссектрисой второго координатного угла. Впрочем, вторую половину графика (для отрицательных X) легко получить из первой, если заметить, что функция y= x чётная, так как -a = a. Значит, график функции y= x симметричен относительно оси Oy, и вторую половину графика можно приобрести, отразив относительно оси ординат часть, начерченную для положительных x. Получается график:y= x 9
10 Ehituse jaoks võtame punktid (-2; 2) (-1; 1) (0; 0) (1; 1) (2; 2). Nüüd koostame graafiku y= x-1. Kui A on graafiku punkt y= x koordinaatidega (a; a), siis graafiku punkt y= x-1, mille Y ordinaadi väärtus on sama, on punkt A1( a+1; a). Selle teise graafiku punkti saab esimese graafiku punktist A(a; a), nihutades paralleelselt Ox-teljega paremale. See tähendab, et funktsiooni y= x-1 kogu graafik saadakse funktsiooni y= x graafikust, nihkudes paralleelselt Ox-teljega paremale 1 võrra. Koostame graafikud: y= x-1 Ehitamiseks, võtame punkte (-2; 3) (-1; 2) (0; 1) (1; 0) (2; 1). 3.3 Valemis "pesastatud mooduleid" sisaldavate funktsioonide graafikute koostamine Vaatleme konstrueerimisalgoritmi konkreetse näite abil.
11 y \u003d i-2-ix + 5ii 1. Koostame funktsiooni graafiku. 2. Kuvame alumise pooltasandi graafiku ülespoole sümmeetriliselt OX-telje suhtes ja saame funktsiooni graafiku. üksteist
12 3. Kuvame funktsiooni graafiku sümmeetriliselt OX-telje suhtes allapoole ja saame funktsiooni graafiku. 4. Kuvame funktsiooni graafiku sümmeetriliselt allapoole OX-telje suhtes ja saame funktsiooni graafiku 5. Kuvame funktsiooni graafiku OX-telje suhtes ja saame graafiku. 12
13 6. Selle tulemusena näeb funktsiooni graafik välja selline 3.4. Algoritm funktsioonide graafikute koostamiseks kujul y = a 1 x x 1 + a 2 x x a n x x n + ax + b. Eelmises näites oli moodulimärkide laiendamine piisavalt lihtne. Kui moodulite summasid on rohkem, siis on problemaatiline võtta arvesse kõiki võimalikke alammooduli avaldiste märkide kombinatsioone. Kuidas saame antud juhul funktsiooni graafiku kujutada? Pange tähele, et graaf on polüline, mille tippude punktides on abstsissid -1 ja 2. Kui x = -1 ja x = 2, on alammooduli avaldised võrdsed nulliga. Praktiliselt lähenesime selliste graafikute koostamise reeglile: funktsiooni y \u003d a 1 x x 1 + a 2 x x a n x x n + ax + b graaf on lõpmatute äärmuslike linkidega polüjoon. Sellise polüliini konstrueerimiseks piisab, kui on teada kõik selle tipud (tipu abstsissid on alammooduli avaldiste nullid) ja üks kontrollpunkt mõlemal vasakul ja paremal lõpmatul lingil. kolmteist
14 Ülesanne. Joonistage funktsioon y = x + x 1 + x + 1 ja leidke selle väikseim väärtus. Lahendus: 1. Alammooduli avaldiste nullid: 0; -üks; Polüliini tipud (0; 2); (-kolmteist); (1; 3). (Alammooduli avaldiste nullid asendatakse võrrandis) Ehitame graafiku (joonis 7), funktsiooni väikseim väärtus on Algoritm ruutfunktsiooni graafiku joonistamiseks mooduliga Funktsioonide graafikute teisendamise algoritmide koostamine. 1.Funktsiooni y= f(x) graafiku koostamine. Vastavalt mooduli definitsioonile on see funktsioon jaotatud kahe funktsiooni komplektiks. Seetõttu koosneb funktsiooni y= f(x) graafik kahest graafikust: y= f(x) paremal pooltasandil, y= f(-x) vasakul pooltasandil. Selle põhjal saame sõnastada reegli (algoritmi). Funktsiooni y= f(x) graafik saadakse funktsiooni y= f(x) graafikust järgmiselt: x 0 korral graafik säilib ja x juures< 0полученная часть графика отображается симметрично относительно оси ОУ. 2.Построение графика функции y= f(x). а). Строим график функции y= f(x). б). Часть графика y= f(x), лежащая над осью ОХ, сохраняется, часть его, лежащая под осью ОХ, отображается симметрично относительно оси ОХ. 14
15 3. Funktsiooni y= f(x) graafiku koostamiseks tuleb esmalt joonistada funktsioon y= f(x) x> 0, seejärel x jaoks.< 0 построить изображение, симметричное ему относительно оси ОУ, а затем на интервалах, где f(x) <0,построить изображение, симметричное графику y= f(x) относительно оси ОХ. 4.Для построения графиков вида y = f(x)достаточно построить график функции y= f(x) для тех х из области определения, при которых f(х) 0, и отобразить полученную часть графика симметрично относительно оси абсцисс. Пример Построим график функции у = х 2 6х +5. Сначала построим параболу у= х 2 6х +5. Чтобы получить из неё график функции у = х 2-6х + 5, нужно каждую точку параболы с отрицательной ординатой заменить точкой с той же абсциссой, но с противоположной (положительной) ординатой. Иными словами, часть параболы, расположенную ниже оси Ох, нужно заменить линией, ей симметричной относительно оси Ох (Рис.1). Рис Алгоритм построения графика дробно рациональной функции с модулем 1. Начнем с построения графика В основе его лежит график функции и все мы знаем, как он выглядит: Теперь построим график 15
16 Selle graafiku saamiseks piisab, kui nihutada eelnevalt saadud graafikut kolme ühiku võrra paremale. Pange tähele, et kui murdosa nimetaja oleks x + 3, siis nihutaksime graafikut vasakule: Nüüd peame funktsiooni graafiku saamiseks kõik ordinaadid korrutama kahega. Lõpuks nihutame graafikut kahe ühiku võrra ülespoole. : Viimane asi, mida peame tegema, on joonistada antud funktsioon, kui see on mooduli märgi all. Selleks peegeldame sümmeetriliselt ülespoole kogu graafiku osa, mille ordinaadid on negatiivsed (osa, mis jääb allapoole x-telge): Joon.4 16
17 4. Muutused ruutfunktsiooni graafikus sõltuvalt absoluutväärtuse märgi asukohast. Joonistage funktsioon y \u003d x 2 - x -3 1) Kuna x \u003d x punktis x 0, langeb nõutav graafik kokku parabooliga y \u003d 0,25 x 2 - x - 3. Kui x<0, то поскольку х 2 = х 2, х =-х и требуемый график совпадает с параболой у=0,25 х 2 + х) Если рассмотрим график у=0,25 х 2 - х - 3 при х 0 и отобразить его относительно оси ОУ мы получим тот же самый график. (0; - 3) координаты точки пересечения графика функции с осью ОУ. у =0, х 2 -х -3 = 0 х 2-4х -12 = 0 Имеем, х 1 = - 2; х 2 = 6. (-2; 0) и (6; 0) - координаты точки пересечения графика функции с осью ОХ. Если х<0, ордината точки требуемого графика такая же, как и у точки параболы, но с положительной абсциссой, равной х. Такие точки симметричны относительно оси ОУ(например, вершины (2; -4) и -(2; -4). Значит, часть требуемого графика, соответствующая значениям х<0, симметрична относительно оси ОУ его же части, соответствующей значениям х>0. b) Seetõttu lõpetan x jaoks<0 часть графика, симметричную построенной относительно оси ОУ. 17
18 Joon. 4 Funktsiooni y \u003d f (x) graafik langeb kokku argumendi mittenegatiivsete väärtuste hulgal oleva funktsiooni y \u003d f (x) graafikuga ja on selle suhtes sümmeetriline y suhtes. -telg argumendi negatiivsete väärtuste komplektil. Tõestus: Kui x 0, siis f (x) = f (x), st. argumendi mittenegatiivsete väärtuste hulgal langevad funktsioonide y = f (x) ja y = f (x) graafikud kokku. Kuna y \u003d f (x) on paarisfunktsioon, on selle graafik OS-i suhtes sümmeetriline. Seega saab funktsiooni y \u003d f (x) graafiku saada funktsiooni y \u003d f (x) graafikult järgmiselt: 1. joonistage funktsioon y \u003d f (x) x>0 jaoks; 2. X jaoks<0, симметрично отразить построенную часть относительно оси ОУ. Вывод: Для построения графика функции у = f (х) 1. построить график функции у = f(х) для х>0; 2. X jaoks<0, симметрично отразить построенную часть относительно оси ОУ. Построить график функции у = х 2-2х Освободимся от знака модуля по определению Если х 2-2х 0, т.е. если х 0 и х 2, то х 2-2х = х 2-2х Если х 2-2х<0, т.е. если 0<х< 2, то х 2-2х =- х 2 + 2х Видим, что на множестве х 0 и х 2 графики функции у = х 2-2х и у = х 2-2х совпадают, а на множестве (0;2) графики функции у = -х 2 + 2х и у = х 2-2х совпадают. Построим их. График функции у = f (х) состоит из части графика функции у = f(х) при у?0 и симметрично отражённой части у = f(х) при у <0 относительно оси ОХ. Построить график функции у = х 2 - х -6 1) Если х 2 - х -6 0, т.е. если х -2 и х 3, то х 2 - х -6 = х 2 - х
19 Kui x 2 - x -6<0, т.е. если -2<х< 3, то х 2 - х -6 = -х 2 + х +6. Построим их. 2) Построим у = х 2 - х -6. Нижнюю часть графика симметрично отбражаем относительно ОХ. Сравнивая 1) и 2), видим что графики одинаковые. Работа на тетрадях. Докажем, что график функции у = f (х) совпадает с графиком функции у = f (х) для f(х) >0 ja sümmeetriliselt peegeldunud osa y \u003d f (x) punktis y<0 относительно оси ОХ. Действительно, по определению абсолютной величины, можно данную функцию рассмотреть как совокупность двух линий: у = f(х), если f(х) 0; у = - f(х), если f(х) <0 Для любой функции у = f(х), если f(х) >0, siis f (x) \u003d f (x), mis tähendab, et selles osas langeb funktsiooni y \u003d f (x) graafik kokku funktsiooni enda graafikuga y \u003d f (x). Kui f(x)<0, то f (х) = - f(х),т.е. точка (х; - f(х)) симметрична точке (х; f (х)) относительно оси ОХ. Поэтому для получения требуемого графика отражаем симметрично относительно оси ОХ "отрицательную" часть графика у = f(х). Вывод: действительно для построения графика функции у = f(х) достаточно: 1.Построить график функции у = f(х) ; 2. На участках, где график расположен в нижней полуплоскости, т.е., где f(х) <0, симметрично отражаем относительно оси абсцисс. (Рис.5) 19
20 Joonis 5. Järeldus: Funktsiooni y= f(x) joonistamiseks 1. Joonistage funktsioon y=f(x) ; 2. Piirkondades, kus graafik asub alumisel pooltasandil, st kus f (x)<0, строим кривые, симметричные построенным графикам относительно оси абсцисс. (Рис.6, 7.) 20
21 Uurimistöö funktsioonide graafikute y \u003d f (x) rakendamisel absoluutväärtuse definitsiooni ja eelnevalt vaadeldud näidete abil joonistame funktsioonigraafikud: y \u003d 2 x - 3 y \u003d x 2-5 x y \ u003d x 2-2 ja tegi järeldused. Funktsiooni y = f (x) graafiku koostamiseks on vaja: 1. Koostada funktsiooni y = f (x) graafik x>0 korral. 2. Ehitage graafiku teine osa, st peegeldage konstrueeritud graafikut sümmeetriliselt OS-i suhtes, kuna see funktsioon on ühtlane. 3. Saadud graafiku lõigud, mis asuvad alumisel pooltasandil, tuleks teisendada ülemiseks pooltasandiks sümmeetriliselt OX-telje suhtes. Koostage funktsiooni y \u003d 2 x - 3 graafik (mooduli määramise esimene meetod) X< -1,5 и х>1,5 a) y = 2x - 3, x>0 korral b) x korral<0, симметрично отражаем построенную часть относительно оси ОУ. 2. Строим у = -2 х + 3, для 2 х - 3 < 0. т.е. -1,5<х<1,5 а) у = -2х + 3, для х>0 b) x jaoks<0, симметрично отражаем построенную часть относительно оси ОУ. У = 2 х - 3 1) Строим у = 2х-3, для х>0. 2) Ehitame sirge, mis on sümmeetriline OS-i telje suhtes ehitatud sirgjoonega. 3) Graafiku alumisel pooltasandil asuvad lõigud kuvatakse sümmeetriliselt OX-telje suhtes. Mõlemat graafikut võrreldes näeme, et need on samad. 21
22 Ülesannete näited Näide 1. Vaatleme funktsiooni y = x 2 6x +5 graafikut. Kuna x on ruudus, siis olenemata arvu x märgist pärast ruudustamist on see positiivne. Sellest järeldub, et funktsiooni y \u003d x 2-6x +5 graafik on identne funktsiooni y \u003d x 2-6x +5 graafikuga, st. funktsiooni graafik, mis ei sisalda absoluutväärtuse märki (joonis 2). Joonis 2 Näide 2. Vaatleme funktsiooni y \u003d x 2 6 x +5 graafikut. Kasutades arvu mooduli definitsiooni, asendame valemi y \u003d x 2 6 x +5 Nüüd tegeleme meile hästi tuntud tükipõhise sõltuvuse määramisega. Koostame sellise graafiku: 1) koostame parabooli y \u003d x 2-6x +5 ja teeme ringiga selle osa, mis on 22
23 vastab mittenegatiivsetele x väärtustele, st. y-teljest paremal olev osa. 2) konstrueerime samal koordinaattasandil parabooli y \u003d x 2 +6x +5 ja teeme ringiga selle osa, mis vastab x negatiivsetele väärtustele, s.o. y-teljest vasakule jääv osa. Paraboolide ringiga ümbritsetud osad moodustavad koos funktsiooni y \u003d x 2-6 x +5 graafiku (joonis 3). Joonis 3 Näide 3. Vaatleme funktsiooni y \u003d x 2-6 x +5 graafikut. Sest võrrandi y \u003d x 2 6x +5 graafik on sama mis funktsiooni graafik ilma moodulmärgita (vaadatud näites 2), sellest järeldub, et funktsiooni y \u003d x 2 6 x +5 graafik on identne näites 2 vaadeldava funktsiooni y \u003d x 2 6 x +5 graafikuga (joonis 3). Näide 4. Koostame funktsiooni y \u003d x 2 6x +5 graafiku. Selleks koostame funktsiooni y \u003d x 2-6x graafiku. Sellest funktsiooni y \u003d x 2-6x graafiku saamiseks peate parabooli iga punkti asendama negatiivse ordinaadiga sama abstsissiga punktiga, kuid vastupidise (positiivse) ordinaadiga. Teisisõnu tuleb x-telje all asuv parabooli osa asendada x-telje suhtes sümmeetrilise joonega. Sest peame koostama funktsiooni y \u003d x 2-6x +5 graafiku, siis tuleb funktsiooni y \u003d x 2-6x graafik lihtsalt piki y-telge tõsta 5 ühiku võrra ülespoole (joonis fig. . 4). 23
24 Joon.4 Näide 5. Koostame funktsiooni y \u003d x 2-6x + 5 graafiku. Selleks kasutame tuntud tükipõhise funktsiooni. Leidke funktsiooni y \u003d 6x +5 6x + 5 \u003d 0 nullpunktid. Vaatleme kahte juhtumit: 1) Kui, siis on võrrand kujul y = x 2 6x -5. Ehitame selle parabooli ja teeme ringiga selle osa, kus. 2) Kui, siis on võrrand kujul y \u003d x 2 + 6x +5. Koostame selle parabooli ja teeme ringjoonega selle osa, mis asub koordinaatidega punktist vasakul (joonis 5). 24
25 Joon.5 Näide6. Joonistame funktsiooni y \u003d x 2 6 x +5. Selleks joonistame funktsiooni y \u003d x 2-6 x +5. Joonistasime selle graafiku näites 3. Kuna meie funktsioon on täielikult mooduli märgi all, on funktsiooni graafiku y \u003d x 2 6 x +5 joonistamiseks vaja funktsiooni y \u003d x 2 graafiku iga punkti 6 x + 5 negatiivse ordinaadiga, asenda sama abstsissiga punktiga, aga vastupidise (positiivse) ordinaadiga, s.t. parabooli Härg-telje all asuv osa tuleb asendada joonega, mis on Hrja telje suhtes sümmeetriline (joonis 6). Joon.6 25
26 II Järeldus "Matemaatilist teavet saab oskuslikult ja tulusalt kasutada ainult siis, kui seda valdatakse loovalt, nii et õpilane näeb ise, kuidas oleks võimalik selleni iseseisvalt jõuda." A.N. Kolmogorov. Need ülesanded pakuvad suurt huvi üheksanda klassi õpilastele, kuna need on OGE testides väga levinud. Nende funktsioonide graafikute koostamise võimalus võimaldab teil eksami edukamalt sooritada. Prantsuse matemaatikud Pierre Fermat () ja Rene Descartes () kujutasid funktsiooni ette kui kõvera punkti ordinaadi sõltuvust selle abstsissist. Ja inglise teadlane Isaac Newton () mõistis funktsiooni liikuva punkti koordinaadina, mis muutub sõltuvalt ajast. 26
27 III Viidete ja allikate loetelu 1. Galitsky M. L., Goldman A. M., Zvavich L. I. Algebra ülesannete kogumik 8. 9. klassidele: Proc. toetus kooliõpilastele. ja süvenemisega tunnid. Uuring Matemaatika 2. väljaanne. M .: Valgustus, Dorofejev G.V. Matemaatika. Algebra. Funktsioonid. Andmete analüüs. 9. klass: m34 Proc. üldharidusõppeks. juht 2. väljaanne, stereotüüp. M .: Bustard, Solomonik V.S. Matemaatika küsimuste ja probleemide kogumik M .: "Kõrgkool", Yashchenko I.V. GIA. Matemaatika: tüüpilised eksamivalikud: Optsioonidest.m .: "Rahvusharidus", lk. 5. Jaštšenko I.V. OGE. Matemaatika: tüüpilised eksamivalikud: Optsioonidest.m .: "Rahvusharidus", lk. 6. Jaštšenko I.V. OGE. Matemaatika: tüüpilised eksamivalikud: Optsioonidest.m .: "Rahvusharidus", lk.
28 Lisa 28
29 Näide 1. Joonistage funktsioon y = x 2 8 x Lahendus. Määratleme funktsiooni paarsuse. Y(-x) väärtus on sama, mis y(x) väärtus, seega on see funktsioon paaris. Siis on selle graafik Oy telje suhtes sümmeetriline. Koostame funktsiooni y \u003d x 2 8x + 12 graafiku x 0 korral ja kuvame graafiku sümmeetriliselt Oy suhtes negatiivse x korral (joonis 1). Näide 2. Järgmine graafik kujul y \u003d x 2 8x See tähendab, et funktsiooni graafik saadakse järgmiselt: nad koostavad funktsiooni y \u003d x 2 8x + 12 graafiku, lahkuvad graafiku osast mis asub Hrja telje kohal muutumatuna ja graafiku osa, mis asub abstsisstelje all, kuvatakse sümmeetriliselt Hrja telje suhtes (joonis 2). Näide 3. Funktsiooni y \u003d x 2 8 x + 12 joonistamiseks viiakse läbi teisenduste kombinatsioon: y \u003d x 2 8x + 12 y \u003d x 2 8 x + 12 y \u003d x 2 8 x Vastus : Joonis 3. Näide 4 Mooduli märgi all olev avaldis muudab märki punktis x=2/3. Kell x<2/3 функция запишется так: 29
30 Kui x>2/3, kirjutatakse funktsioon järgmiselt: See tähendab, et punkt x=2/3 jagab meie koordinaattasandi kaheks piirkonnaks, millest ühes (paremal) ehitame funktsiooni ja teine (vasakul) funktsiooni Me ehitame graafik: Näide 5 Järgmisena on graafik katki, kuid sellel on kaks katkestuspunkti, kuna see sisaldab kahte avaldist mooduli märkide all:
31 Laiendage mooduleid esimesel intervallil: Teisel intervallil: Kolmandal intervallil: Seega on meil intervallil (- ; 1.5] graaf kirjutatud esimese võrrandiga, intervallil teise võrrandiga, ja intervallil)
- Kokkupuutel 0
- Google Plus 0
- Okei 0
- Facebook 0