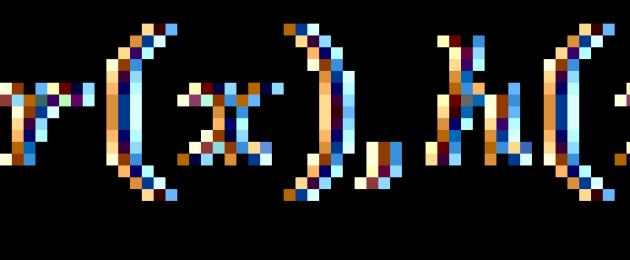Ratsionaalvõrrandite näited koolituseks. Videotund "Ratsionaalvõrrandid

Ratsionaalvõrrandid on võrrandid, mis sisaldavad ratsionaalseid avaldisi.

Definitsioon 1

Sel juhul on ratsionaalsed avaldised avaldised, mida saab kirjutada tavalise murruna kujul $\frac(m)(n)$, samas kui $m$ ja $n$ on täisarvud ja $n$ ei saa olla võrdne nulliga. Ratsionaalväljendid ei hõlma mitte ainult avaldisi, mis sisaldavad murde kujul $\frac(2)(3)$, vaid ka avaldisi, mis sisaldavad ainult täisarve, kuna iga täisarvu saab esitada vale murduna.

Vaatame nüüd lähemalt, mis on ratsionaalvõrrandid.

Nagu eespool mainitud, on ratsionaalvõrrandid võrrandid, mis sisaldavad ratsionaalseid avaldisi ja muutujaid.

Vastavalt muutuja asukohale ratsionaalvõrrandis võib see olla kas murdosaline ratsionaalvõrrand või terve ratsionaalvõrrand.

Murdvõrrandid võivad sisaldada muutujaga murdosa ainult ühes võrrandi osas, samas kui terved võrrandid ei sisalda muutujaga murdosavaldisi.

Tervete ratsionaalsete võrrandite näited: $5x+2= 12$; $3 a = -7 (-4 a + 5) $; $7a-14=256$.

Murdratsionaalvõrrandite näited: $\frac(3x-2)(x+3)+\frac(1)(2)=\frac(5)(x)$; $\frac(7)(2y-3)=5$;

Väärib märkimist, et murdartsionaalvõrranditeks nimetatakse ainult neid võrrandeid, mille nimetajas on murdosa, kuna muutujateta murdosavaldisi sisaldavaid võrrandeid saab hõlpsasti taandada lineaarseteks täisarvulisteks võrranditeks.

Kuidas lahendada ratsionaalseid võrrandeid?

Olenevalt sellest, kas tegemist on täisarvulise ratsionaalvõrrandiga või murdosaga, kasutatakse selle lahendamiseks veidi erinevaid algoritme.

Algoritm tervete ratsionaalvõrrandite lahendamiseks

1. Esiteks peate määrama kogu võrdsuse väikseima ühisnimetaja.
2. Seejärel peate määrama tegurid, millega peate korrutama iga võrdsuse liikme.
3. Järgmine etapp on taandamine kogu võrdsuse ühiseks nimetajaks.
4. Lõpuks saadud täisarvulise ratsionaalse võrdsuse juurte otsimise rakendamine.

Näide 1

Lahendage võrrand: $\frac(5x+9)(2)=\frac(x)(4)$

Esiteks leiame ühise teguri – antud juhul numbri $4$. Nimetajast vabanemiseks korrutage vasak pool $\frac(2)(2)$-ga, saame:

$10x+18=x$ - saadud võrrand on lineaarne, selle juur on $x=-2$.

Kuidas lahendada murdratsionaalvõrrandeid?

Murdratsionaalvõrrandite puhul on lahendusjärjestus sarnane täisarvuliste ratsionaalsete lahendamise algoritmiga ehk punktid 1-4 säilivad, kuid pärast eeldatavate juurte leidmist mitteekvivalentsete teisenduste kasutamise korral, juured tuleb kontrollida, asendades need võrrandisse.

Näide 2

Lahendage murdarvuline ratsionaalvõrrand: $\frac(x-3)(x-5)+\frac(1)(x)=\frac(x+5)(x \cdot (x-5))$

Murru taandamiseks ühiseks nimetajaks, siin on see $x \cdot (x-5)$, korrutame iga murdosa ühega, mis on esindatud tegurina, mis on vajalik ühisnimetajaks taandamiseks:

$\frac((x-3) \cdot x)((x-5)\cdot x)+\frac(1 \cdot (x-5))(x \cdot (x-5))=\frac( x+5)(x \cdot (x-5))$

Nüüd, kui kogu murrul on ühine nimetaja, saate sellest lahti saada:

$(x-3) \cdot x+(x-5)=x+5$

$x^2 ​​​​- 3x+x-5 = x+5$

Saadud ruutvõrrandi lahendamiseks kasutame Vieta teoreemi:

$\begin(cases) x_1 + x_2 = 3 \\ x_1 \cdot x_2 = -10 \\ \end(cases)$

$\begin(cases) x_1=5 \\ x_2=-2 \\ \end(cases)$

Kuna võrrandi lihtsustamiseks kasutatav teisendus ei ole ekvivalentne, tuleb saadud juured kontrollida algses võrrandis, selleks asendame need:

$\frac(-2-3)(-2-5) +\frac(1)(-2)=\frac(-2+5)((-2) \cdot (-2-5))$

$\frac(5)(7)-\frac(1)(2)=\frac(3)(14)$

$\frac(3)(14)=\frac(3)(14)$ - järelikult on juur $x_2=-2$ õige.

$\frac(5-3)(5-5) +\frac(1)(5)=\frac(5+5)((-2) \cdot (5-5))$

Siin on kohe selge, et nimetajas moodustub null, seega on juur $x_1=5$ autsaider.

Tuleb meeles pidada, et kui võrrand, mis sisaldab avaldist kujul $\frac(m)(n)$ vasakul või paremal küljel, on võrdne nulliga, saab ainult murdosa lugeja olla võrdne nulliga. See on tingitud asjaolust, et kui nimetajas moodustatakse kuskil null, siis kontrollitav juur ei ole võrrandi juur, kuna kogu võrdsus kaotab sel juhul oma tähenduse. Juureid, mis toovad nimetaja nulli, nimetatakse kõrvalisteks.

Kui murdratsionaalvõrrandil on üsna keerukas kuju, on selle edasiseks lihtsustamiseks ja lahendamiseks võimalik kasutada võrrandi osa asendamist uue muutujaga, ilmselt olete juba näinud näiteid sellistest murdratsionaalvõrranditest:

Näide 3

Lahenda võrrand:

$\frac(1)(x^2+3x-3)+\frac(2)(x^2+3x+1)=\frac(7)(5)$

Lahenduse lihtsustamiseks võtame kasutusele muutuja $t= x^2+3x$:

$\frac(1)(t-3)+\frac(2)(t+1)=\frac(7)(5)$

Ühisnimetaja on siin $5 \cdot (t-3)(t+1)$, korrutame võrrandi kõik osad vajalike teguritega, et sellest lahti saada:

$\frac(5(t+1))(5(t-3)(t+1))+\frac(2 \cdot 5(t-3))(5(t+1)(t-3) )=\frac(7(t+1)(t-3))(5(t-3)(t+1))$

$5(t+1)+10(t-3)=7(t+1)(t-3)$

$5t+5+10t-30=7(t^2-3t+t-3)$

$15t-25=7t^2-14t-21$

Diskriminandi kaudu arvutame juured:

$t_1=4;t_2=\frac(1)(7)$

Kuna kasutasime mitteekvivalentseid teisendusi, siis on vaja kontrollida saadud juuri nimetajas, need peavad täitma tingimust $5(t-3)(t+1)≠0$. Mõlemad juured vastavad sellele tingimusele.

Nüüd asendame saadud juurtega $t$ ja saame kaks võrrandit:

$x^2+3x=4$ ja $x^2+3x=\frac(1)(7)$.

Vieta teoreemi järgi esimese võrrandi juured $x_1=-4; x_2=1$, arvutame teise juured diskriminandi järgi ja saame $x_(1,2)=\frac(-3±\sqrt(\frac(67)(7)))(2) $.

Kõik võrrandi juured on: $x_1=-4; x_2=1, x_(3,4)=\frac(-3±\sqrt(\frac(67)(7)))(2)$.

Teisendused võrrandivormi lihtsustamiseks

Nagu ülalt näha, kasutatakse ratsionaalsete võrrandite lahendamiseks erinevaid teisendusi.

Võrranditeisendusi on kahte tüüpi: ekvivalentsed (identsed) ja ebavõrdsed.

Teisendusi nimetatakse ekvivalentseteks, kui need viivad uut tüüpi võrrandini, mille juured on samad, mis originaalil.

Identiteedi teisendused, mida saab kasutada algse võrrandi kuju muutmiseks ilma täiendava kontrollita, on järgmised:

• Kogu võrrandi korrutamine või jagamine mõne nullist erineva arvuga;
• Võrrandi osade ülekandmine vasakult küljelt paremale ja vastupidi.

Mitteekvivalentsed teisendused on teisendused, mille käigus võivad ilmneda kõrvalised juured. Mitteekvivalentsed teisendused hõlmavad järgmist:

• Võrrandi mõlema poole ruudustamine;
• Muutujat sisaldavatest nimetajatest vabanemine;

Mitteekvivalentsete teisenduste abil lahendatud ratsionaalsete võrrandite juuri tuleb kontrollida algse võrrandiga asendamise teel, kuna mitteekvivalentsete teisenduste käigus võivad ilmneda kõrvalised juured. Mittevõrdväärsed teisendused ei too alati kaasa kõrvaliste juurte ilmnemist, kuid sellegipoolest on vaja sellega arvestada.

Kahest suuremate astmetega ratsionaalsete võrrandite lahendus

Kõige sagedamini kasutatavad meetodid võrrandite lahendamiseks, mille astmed on suuremad kui kaks, on muutuja muutmise meetod, mida arutasime eespool murdratsionaalvõrrandi näitel, samuti faktoriseerimise meetodit.

Vaatleme faktoriseerimise meetodit üksikasjalikumalt.

Olgu antud võrrand kujul $P(x)= 0$, kus $P(x)$ on polünoom, mille aste on suurem kui kaks. Kui seda võrrandit saab faktoriseerida nii, et see võtab kuju $P_1(x)P_2(x)P_3(x)..\cdot P_n(x)=0$, siis on selle võrrandi lahenduseks võrrandid $P_1(x)=0, P_2(x)=0, P_3(x)=0...P_n(x)=0$.

Neile, kes ei mäleta: võrrandi vaba liige on võrrandi liige, mis ei sisalda muutujat tegurina. Samal ajal, olles leidnud sellise võrrandi ühe juurtest, saab seda kasutada võrrandi edasiseks faktoriseerimiseks.

Näide 5

Lahenda võrrand:

Vaba liikme jagajad on numbrid $±1, ±2, ±3, ±4, ±6, ±8, ±12$ ja $±24$. Nende kontrollimisel osutus sobivaks juureks $x=2$. See tähendab, et seda polünoomi saab laiendada, kasutades seda juurt: $(x-2)(x^2+6+12)=0$.

Teises juursulgude paaris oleval polünoomil pole juuri, mis tähendab, et selle võrrandi ainus juur on $x=2$.

Teist tüüpi võrrandid, mille aste on suurem kui kaks, on bikvadraatvõrrandid kujul $ax^4+bx^2+ c=0$. Sellised võrrandid lahendatakse, asendades $x^2$ väärtusega $y$, rakendades seda, saame võrrandi kujul $ay^2+y+c=0$ ja seejärel kasutatakse uue muutuja saadud väärtust arvutage algne muutuja.

On ka teist tüüpi võrrand, mida nimetatakse tagastatav. Sellised võrrandid näevad välja järgmised: $ax^4+bx^3+cx^2+bx+a=0$. Neil on selline nimi koefitsientide kordumise tõttu kõrgematel ja madalamatel kraadidel.

Täisarvuline avaldis on matemaatiline avaldis, mis koosneb arvudest ja literaalsetest muutujatest, kasutades liitmise, lahutamise ja korrutamise toiminguid. Täisarvud hõlmavad ka avaldisi, mis sisaldavad jagamist mõne muu arvuga kui null.

Murdarvulise ratsionaalse avaldise mõiste

Murdravaldis on matemaatiline avaldis, mis lisaks arvude ja literaalsete muutujatega tehtavatele liitmis-, lahutamis- ja korrutamisoperatsioonidele, samuti arvuga, mis ei võrdu nulliga, sisaldab ka jagamist literaalsete muutujatega avaldisteks.

Ratsionaalväljendid on kõik täis- ja murdavaldised. Ratsionaalvõrrandid on võrrandid, mille vasak ja parem pool on ratsionaalsed avaldised. Kui ratsionaalses võrrandis on vasak ja parem osa täisarvulised avaldised, siis sellist ratsionaalset võrrandit nimetatakse täisarvuks.

Kui ratsionaalvõrrandis on vasak või parem osa murdosa avaldised, siis sellist ratsionaalset võrrandit nimetatakse murdosaliseks.

Näited murdosa ratsionaalsetest avaldistest

1,x-3/x=-6*x+19

2. (x-4)/(2*x+5) = (x+7)/(x-2)

3. (x-3)/(x-5) + 1/x = (x+5)/(x*(x-5))

Murdratsionaalvõrrandi lahendamise skeem

1. Leidke kõigi võrrandisse kuuluvate murdude ühisnimetaja.

2. Korrutage võrrandi mõlemad pooled ühise nimetajaga.

3. Lahendage saadud koguvõrrand.

4. Kontrollige juuri ja välistage need, mis muudavad ühise nimetaja nulliks.

Kuna me lahendame murdarvulisi ratsionaalvõrrandeid, on murdude nimetajates muutujad. Seega on need ühises nimetajas. Ja algoritmi teises lõigus korrutame ühise nimetajaga, siis võivad ilmneda kõrvalised juured. Mille korral on ühisnimetaja võrdne nulliga, mis tähendab, et sellega korrutamine on mõttetu. Seetõttu kontrollige lõpus kindlasti saadud juuri.

Kaaluge näidet:

Lahendage murdarvuline ratsionaalvõrrand: (x-3)/(x-5) + 1/x = (x+5)/(x*(x-5)).

Peame kinni üldisest skeemist: kõigepealt leiame kõigi murdude ühise nimetaja. Saame x*(x-5).

Korrutage iga murdosa ühise nimetajaga ja kirjutage saadud koguvõrrand.

(x-3)/(x-5) * (x*(x-5))= x*(x+3);
1/x * (x*(x-5)) = (x-5);
(x+5)/(x*(x-5)) * (x*(x-5)) = (x+5);
x*(x+3) + (x-5) = (x+5);

Lihtsustame saadud võrrandit. Saame:

x^2+3*x + x-5 - x -5 =0;
x^2+3*x-10=0;

Saime lihtsa taandatud ruutvõrrandi. Lahendame selle mistahes tuntud meetoditega, saame juurteks x=-2 ja x=5.

Nüüd kontrollime saadud lahendusi:

Asendame ühisnimetajas arvud -2 ja 5. Kui x=-2, ühisnimetaja x*(x-5) ei kao, -2*(-2-5)=14. Seega on arv -2 algse murdarvulise ratsionaalvõrrandi juur.

Kui x=5, muutub ühisnimetaja x*(x-5) nulliks. Seetõttu ei ole see arv algse murdarvulise ratsionaalvõrrandi juur, kuna toimub jagamine nulliga.

Oleme juba õppinud ruutvõrrandeid lahendama. Laiendame nüüd uuritud meetodeid ratsionaalsetele võrranditele.

Mis on ratsionaalne väljend? Oleme selle kontseptsiooniga juba kokku puutunud. Ratsionaalsed väljendid nimetatakse avaldisteks, mis koosnevad arvudest, muutujatest, nende astmetest ja matemaatiliste tehete märkidest.

Sellest lähtuvalt on ratsionaalvõrrandid võrrandid kujul: , kus - ratsionaalsed väljendid.

Varem käsitlesime ainult neid ratsionaalseid võrrandeid, mis taanduvad lineaarseteks. Vaatleme nüüd neid ratsionaalseid võrrandeid, mida saab taandada ruutvõrranditeks.

Näide 1

Lahenda võrrand:.

Otsus:

Murd on 0 siis ja ainult siis, kui selle lugeja on 0 ja nimetaja ei ole 0.

Saame järgmise süsteemi:

Süsteemi esimene võrrand on ruutvõrrand. Enne selle lahendamist jagame kõik selle koefitsiendid 3-ga.

Saame kaks juurt: ; .

Kuna 2 ei võrdu kunagi 0-ga, peavad olema täidetud kaks tingimust: . Kuna ükski ülaltoodud võrrandi juurtest ei ühti teise võrratuse lahendamisel saadud muutuja kehtetute väärtustega, on need mõlemad selle võrrandi lahendid.

Vastus:.

Niisiis, formuleerime ratsionaalsete võrrandite lahendamise algoritmi:

1. Liigutage kõik terminid vasakule poole, nii et paremal küljel saadakse 0.

2. Teisenda ja lihtsusta vasak pool, vii kõik murrud ühisele nimetajale.

3. Võrdsusta saadud murd 0-ga vastavalt järgmisele algoritmile: .

4. Kirjutage üles need juured, mis on saadud esimeses võrrandis ja rahuldavad vastuseks teise võrratuse.

Vaatame teist näidet.

Näide 2

Lahenda võrrand: .

Otsus

Kohe alguses kanname kõik terminid vasakule poole nii, et paremale jääks 0. Saame:

Nüüd toome võrrandi vasaku poole ühise nimetaja juurde:

See võrrand on samaväärne süsteemiga:

Süsteemi esimene võrrand on ruutvõrrand.

Selle võrrandi koefitsiendid: . Arvutame diskriminandi:

Saame kaks juurt: ; .

Nüüd lahendame teise võrratuse: tegurite korrutis ei võrdu 0-ga siis ja ainult siis, kui ükski tegur ei ole võrdne 0-ga.

Täidetud peavad olema kaks tingimust: . Saame, et esimese võrrandi kahest juurest sobib ainult üks - 3.

Vastus:.

Selles tunnis meenutasime, mis on ratsionaalne avaldis, ja õppisime ka lahendama ratsionaalseid võrrandeid, mis on taandatud ruutvõrranditeks.

Järgmises õppetükis käsitleme ratsionaalseid võrrandeid reaalsete olukordade mudelitena ja käsitleme ka liikumisprobleeme.

Bibliograafia

1. Bashmakov M.I. Algebra, 8. klass. - M.: Valgustus, 2004.
2. Dorofejev G.V., Suvorova S.B., Bunimovitš E.A. jt Algebra, 8. 5. väljaanne. - M.: Haridus, 2010.
3. Nikolski S.M., Potapov M.A., Reshetnikov N.N., Ševkin A.V. Algebra, 8. klass. Õpik haridusasutustele. - M.: Haridus, 2006.

1. Pedagoogiliste ideede festival "Avatud tund" ().
2. School.xvatit.com().
3. Rudocs.exdat.com().

Kodutöö

Selle võrrandi lihtsustamiseks kasutatakse vähimat ühist nimetajat. See meetod on rakendatav juhul, kui seda võrrandit ei ole võimalik kirjutada ühe ratsionaalse avaldisega võrrandi mõlemale poolele (ja kasutada ristkorrutamise meetodit). Seda meetodit kasutatakse kolme või enama murruga ratsionaalvõrrandi esitamisel (kahe murru puhul on parem kasutada ristikorrutamist).

Leidke murdude vähim ühisosa (või vähim ühiskordne). NOZ on väikseim arv, mis jagub ühtlaselt iga nimetajaga.

• Mõnikord on NOZ ilmne number. Näiteks kui on antud võrrand: x/3 + 1/2 = (3x + 1)/6, siis on ilmne, et arvude 3, 2 ja 6 vähim ühiskordne on 6.
• Kui NOD ei ole ilmne, kirjutage üles suurima nimetaja kordsed ja leidke nende hulgast selline, mis on ka teiste nimetajate kordne. Sageli saate NOD-i leida, korrutades lihtsalt kaks nimetajat kokku. Näiteks kui on antud võrrand x/8 + 2/6 = (x - 3)/9, siis NOZ = 8*9 = 72.
• Kui üks või mitu nimetajat sisaldavad muutujat, on protsess mõnevõrra keerulisem (kuid mitte võimatu). Sel juhul on NOZ avaldis (sisaldab muutujat), mis jagub iga nimetajaga. Näiteks võrrandis 5/(x-1) = 1/x + 2/(3x) NOZ = 3x(x-1), kuna see avaldis jagub iga nimetajaga: 3x(x-1)/(x -1 ) = 3x; 3x(x-1)/3x = (x-1); 3x(x-1)/x = 3(x-1).

Korrutage nii iga murdosa lugeja kui ka nimetaja arvuga, mis on võrdne NOZ-i jagamisel iga murdosa vastava nimetajaga. Kuna korrutate nii lugeja kui ka nimetaja sama arvuga, korrutate murdosa 1-ga (näiteks 2/2 = 1 või 3/3 = 1).

• Nii et meie näites korrutage x/3 2/2-ga, et saada 2x/6, ja korrutage 1/2 3/3-ga, et saada 3/6 (3x + 1/6 ei pea korrutama, kuna nimetaja on 6).
• Kui muutuja on nimetajas, toimige samamoodi. Meie teises näites NOZ = 3x(x-1), seega 5/(x-1) korda (3x)/(3x) on 5(3x)/(3x)(x-1); 1/x korda 3(x-1)/3(x-1), et saada 3(x-1)/3x(x-1); 2/(3x) korrutage (x-1)/(x-1) ja saad 2(x-1)/3x(x-1).

Otsige "x". Nüüd, kui olete murded ühiseks nimetajaks taandanud, saate nimetajast lahti saada. Selleks korrutage võrrandi mõlemad pooled ühise nimetajaga. Seejärel lahendage saadud võrrand, see tähendab, leidke "x". Selleks eraldage muutuja võrrandi ühel küljel.

• Meie näites: 2x/6 + 3/6 = (3x +1)/6. Saate lisada kaks sama nimetajaga murru, seega kirjutage võrrand järgmiselt: (2x+3)/6=(3x+1)/6. Korrutage võrrandi mõlemad pooled 6-ga ja vabanege nimetajatest: 2x+3 = 3x +1. Lahendage ja saage x = 2.
• Meie teises näites (nimetajas muutujaga) näeb võrrand välja (pärast ühiseks nimetajaks taandamist): 5(3x)/(3x)(x-1) = 3(x-1)/3x(x) -1) + 2 (x-1)/3x (x-1). Korrutades võrrandi mõlemad pooled NOZ-iga, vabanete nimetajast ja saate: 5(3x) = 3(x-1) + 2(x-1) või 15x = 3x - 3 + 2x -2 või 15x = x - 5 Lahenda ja saad: x = -5/14.

Teie privaatsus on meile oluline. Sel põhjusel oleme välja töötanud privaatsuspoliitika, mis kirjeldab, kuidas me teie teavet kasutame ja säilitame. Palun lugege meie privaatsuspoliitikat ja andke meile teada, kui teil on küsimusi.

Isikuandmete kogumine ja kasutamine

Isikuandmete all mõeldakse andmeid, mille abil saab tuvastada konkreetse isiku või temaga ühendust võtta.

Teil võidakse paluda esitada oma isikuandmed igal ajal, kui võtate meiega ühendust.

Järgnevalt on toodud mõned näited selle kohta, millist tüüpi isikuandmeid võime koguda ja kuidas seda teavet kasutada.

Milliseid isikuandmeid me kogume:

• Kui esitate saidil avalduse, võime koguda erinevat teavet, sealhulgas teie nime, telefoninumbrit, e-posti aadressi jne.

Kuidas me teie isikuandmeid kasutame:

• Kogutavad isikuandmed võimaldavad meil teiega ühendust võtta ja teid teavitada ainulaadsetest pakkumistest, tutvustustest ja muudest sündmustest ning eelseisvatest sündmustest.
• Aeg-ajalt võime kasutada teie isikuandmeid teile oluliste teadete ja teadete saatmiseks.
• Võime kasutada isikuandmeid ka sisemistel eesmärkidel, näiteks auditite, andmeanalüüsi ja erinevate uuringute läbiviimiseks, et täiustada pakutavaid teenuseid ja anda teile meie teenuste kohta soovitusi.
• Kui osalete loosimises, võistluses või sarnases stiimulis, võime kasutada teie esitatud teavet selliste programmide haldamiseks.

Avalikustamine kolmandatele isikutele

Me ei avalda teilt saadud teavet kolmandatele isikutele.

Erandid:

• Kui see on vajalik - vastavalt seadusele, kohtukorraldusele, kohtumenetluses ja/või avalike taotluste või Vene Föderatsiooni territooriumil asuvate riigiasutuste taotluste alusel - avaldage oma isikuandmed. Samuti võime avaldada teie kohta teavet, kui leiame, et selline avaldamine on vajalik või asjakohane turvalisuse, õiguskaitse või muudel avalikes huvides.
• Ümberkorraldamise, ühinemise või müügi korral võime edastada kogutud isikuandmed vastavale kolmandale isikule õigusjärglasele.

Isikuandmete kaitse

Me rakendame ettevaatusabinõusid – sealhulgas halduslikke, tehnilisi ja füüsilisi –, et kaitsta teie isikuandmeid kaotsimineku, varguse ja väärkasutuse, samuti volitamata juurdepääsu, avalikustamise, muutmise ja hävitamise eest.

Teie privaatsuse säilitamine ettevõtte tasandil

Teie isikuandmete turvalisuse tagamiseks edastame oma töötajatele privaatsus- ja turvatavade ning rakendame rangelt privaatsuspõhimõtteid.