Figuuri pindala arvutamine See on võib-olla üks piirkonnateooria kõige keerulisemaid probleeme. Kooligeomeetrias õpetatakse leidma geomeetriliste põhikujundite pindalasid nagu näiteks kolmnurk, romb, ristkülik, trapets, ring jne. Tihti tuleb aga tegeleda keerukamate kujundite pindalade arvutamisega. Just selliste ülesannete lahendamisel on väga mugav kasutada integraalarvutust.
Definitsioon.
Kurviline trapets kutsutakse välja mõni joonis G, mis on piiratud joontega y \u003d f (x), y \u003d 0, x \u003d a ja x \u003d b ning funktsioon f (x) on segmendil [a] pidev; b] ja ei muuda sellel olevat märki (joonis 1). Kõverajoonelise trapetsi pindala võib tähistada tähega S(G).
Funktsiooni f(x) kindel integraal ʃ a b f(x)dx, mis on pidev ja mittenegatiivne lõigul [a; b] ja on vastava kõverjoonelise trapetsi pindala.
See tähendab, et joonise G pindala leidmiseks, mis on piiratud joontega y \u003d f (x), y \u003d 0, x \u003d a ja x \u003d b, on vaja arvutada kindel integraal ʃ abf (x) dx.
Sellel viisil, S(G) = ʃ a b f(x)dx.
Kui funktsioon y = f(x) ei ole positiivne [a; b], siis saab kõverjoonelise trapetsi pindala leida valemiga S(G) = -ʃ a b f(x)dx.
Näide 1
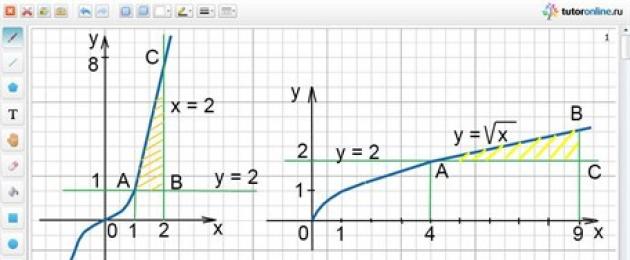
Arvutage joonise pindala, mis on piiratud joontega y \u003d x 3; y = 1; x = 2.
Lahendus.
Antud jooned moodustavad joonise ABC, mida näidatakse viirutusega riis. 2.
Soovitud pindala on võrdne kõverjoonelise trapetsi DACE ja ruudu DABE pindalade vahega.
Kasutades valemit S = ʃ a b f(x)dx = S(b) – S(a), leiame integratsiooni piirid. Selleks lahendame kahe võrrandi süsteemi:
(y \u003d x 3,
(y = 1.
Seega on meil x 1 \u003d 1 - alumine piir ja x \u003d 2 - ülempiir.
Niisiis, S = S DACE - S DABE = ʃ 1 2 x 3 dx - 1 = x 4 /4| 1 2 - 1 \u003d (16 - 1) / 4 - 1 \u003d 11/4 (ruutühikud).
Vastus: 11/4 ruutmeetrit. ühikut

Näide 2
Arvutage joonise pindala, mis on piiratud joontega y \u003d √x; y = 2; x = 9.
Lahendus.
Antud jooned moodustavad joonise ABC, mis on ülalt piiratud funktsiooni graafikuga
y \u003d √x ja altpoolt funktsiooni y \u003d 2 graafikut. Saadud joonist näidatakse viirutusega riis. 3.
Soovitud pindala on võrdne S = ʃ a b (√x - 2). Leiame integreerimise piirid: b = 9, a leidmiseks lahendame kahe võrrandi süsteemi:
(y = √x,
(y = 2.
Seega on x = 4 = a alumine piir.
Niisiis, S = ∫ 4 9 (√x – 2)dx = ∫ 4 9 √x dx –∫ 4 9 2dx = 2/3 x√x| 4 9 - 2x| 4 9 \u003d (18 - 16/3) - (18 - 8) \u003d 2 2/3 (ruutühikud).
Vastus: S = 2 2/3 ruutmeetrit. ühikut
Näide 3
Arvutage joonise pindala, mis on piiratud joontega y \u003d x 3 - 4x; y = 0; x ≥ 0.
Lahendus.
Joonistame funktsiooni y \u003d x 3 - 4x x ≥ 0 korral. Selleks leiame tuletise y ':
y’ = 3x 2 – 4, y’ = 0, kui х = ±2/√3 ≈ 1,1 on kriitilised punktid.
Kui joonistada kriitilised punktid reaalteljele ja asetada tuletise märgid, saame, et funktsioon kahaneb nullist 2/√3 ja suureneb 2/√3 pluss lõpmatuseni. Siis x = 2/√3 on miinimumpunkt, funktsiooni y minimaalne väärtus on min = -16/(3√3) ≈ -3.
Määrame graafiku lõikepunktid koordinaattelgedega:
kui x \u003d 0, siis y \u003d 0, mis tähendab, et A (0; 0) on Oy telje lõikepunkt;
kui y \u003d 0, siis x 3 - 4x \u003d 0 või x (x 2 - 4) \u003d 0 või x (x - 2) (x + 2) \u003d 0, kust x 1 \u003d 0, x 2 \u003d 2, x 3 \u003d -2 (ei sobi, kuna x ≥ 0).
Punktid A(0; 0) ja B(2; 0) on graafiku lõikepunktid Ox-teljega.
Antud jooned moodustavad OAB joonise, mida näidatakse viirutusega riis. 4.
Kuna funktsioon y \u003d x 3 - 4x võtab (0; 2) negatiivse väärtuse, siis
S = |ʃ 0 2 (x 3 – 4x)dx|.
Meil on: ʃ 0 2 (x 3 - 4x)dx = (x 4 /4 - 4x 2 /2)| 0 2 \u003d -4, kust S = 4 ruutmeetrit. ühikut
Vastus: S = 4 ruutmeetrit. ühikut

Näide 4
Leidke joonise pindala, mida piiravad parabool y \u003d 2x 2 - 2x + 1, sirged x \u003d 0, y \u003d 0 ja selle parabooli puutuja punktis, mille abstsiss on x 0 \u003d 2.
Lahendus.
Esiteks koostame parabooli y \u003d 2x 2 - 2x + 1 puutuja võrrandi punktis, mille abstsiss on x₀ \u003d 2.
Kuna tuletis y' = 4x - 2, siis x 0 = 2 korral saame k = y'(2) = 6.
Leidke puutepunkti ordinaat: y 0 = 2 2 2 – 2 2 + 1 = 5.
Seetõttu on puutuja võrrandi vorm: y - 5 \u003d 6 (x - 2) või y \u003d 6x - 7.
Ehitame joontega piiratud joonise:
y \u003d 2x 2 - 2x + 1, y \u003d 0, x \u003d 0, y = 6x - 7.
Г y \u003d 2x 2 - 2x + 1 - parabool. Lõikepunktid koordinaattelgedega: A(0; 1) - Oy teljega; Ox teljega - ristumispunkte pole, sest võrrandil 2x 2 - 2x + 1 = 0 pole lahendeid (D< 0). Найдем вершину параболы:
x b \u003d 2/4 \u003d 1/2;
y b \u003d 1/2, see tähendab, et parabooli punkti B tipul on koordinaadid B (1/2; 1/2).
Niisiis, joonis, mille pindala määratakse, on näidatud viirutusega riis. viis.
Meil on: S O A B D \u003d S OABC - S ADBC.
Leidke punkti D koordinaadid tingimusest:
6x - 7 = 0, st. x \u003d 7/6, siis DC \u003d 2 - 7/6 \u003d 5/6.
Leiame kolmnurga DBC pindala valemiga S ADBC = 1/2 · DC · BC. Sellel viisil,
S ADBC = 1/2 5/6 5 = 25/12 ruutmeetrit. ühikut
S OABC = ʃ 0 2 (2x 2 - 2x + 1)dx = (2x 3 /3 - 2x 2 /2 + x)| 0 2 \u003d 10/3 (ruutühikud).
Lõpuks saame: S O A B D \u003d S OABC - S ADBC \u003d 10/3 - 25/12 \u003d 5/4 \u003d 1 1/4 (ruutühikud).
Vastus: S = 1 1/4 ruutmeetrit. ühikut
Vaatasime näiteid üle etteantud joontega piiratud kujundite pindalade leidmine. Selliste ülesannete edukaks lahendamiseks peate suutma ehitada tasapinnal sirgeid ja funktsioonide graafikuid, leida sirgete lõikepunkte, rakendada pindala leidmiseks valemit, mis eeldab teatud integraalide arvutamise oskust ja oskusi.
saidil, materjali täieliku või osalise kopeerimise korral on nõutav link allikale.
Selles õppetükis õpime arvutama lamedate figuuride alad, mida nimetatakse kõverjoonelised trapetsid .
Selliste jooniste näited on toodud alloleval joonisel.
Ühest küljest on kindla integraali abil lameda kujundi pindala leidmine äärmiselt lihtne. Me räägime joonise pindalast, mis on ülalt piiratud teatud kõveraga, altpoolt - abstsissteljega ( Ox) ning vasakul ja paremal on mõned sirged jooned. Lihtsus seisneb selles funktsiooni kindel integraal, millele kõver on antud, ja seal on sellise kujundi pindala(kõverjooneline trapets).
Figuuri pindala arvutamiseks vajame:
- Kõverat defineeriva funktsiooni kindel integraal , mis piirab kõverjoonelist trapetsi ülalt. Ja siit tuleb esimene oluline nüanss: kõverjoonelist trapetsi saab piirata kõveraga mitte ainult ülalt, vaid ka altpoolt . Kuidas sel juhul toimida? Lihtne, kuid oluline meeles pidada: integraal võetakse sel juhul miinusmärgiga .
- Integratsiooni piirid a Ja b, mille leiame joonte võrranditest, mis piiravad joonist vasakul ja paremal: x = a , x = b, kus a Ja b- numbrid.
Eraldi veel mõned nüansid.
Kõver, mis piirab kõverjoonelist trapetsi ülalt (või altpoolt), peab olema pideva ja mittenegatiivse funktsiooni graafik y = f(x) .
X väärtused peavad kuuluma segmendile [a, b] . See tähendab, et arvesse ei võeta näiteks selliseid jooni nagu seenelõik, mille jalg sobib ideaalselt sellesse segmenti ja kork on palju laiem.
Külgmised segmendid võivad degenereeruda punktideks . Kui nägite joonisel sellist kujundit, ei tohiks see teid segadusse ajada, kuna sellel punktil on x-teljel alati oma väärtus. Nii et integratsiooni piiridega on kõik korras.
Nüüd saate liikuda valemite ja arvutuste juurde. Seega piirkond s kõverjoonelist trapetsi saab arvutada valemiga
Kui f(x) ≤ 0 (funktsiooni graafik asub telje all Ox), siis kõvera trapetsi pindala saab arvutada valemiga
On ka juhtumeid, kus nii joonise ülemine kui ka alumine piir on vastavalt funktsioonid y = f(x) Ja y = φ (x) , siis arvutatakse sellise joonise pindala valemiga
![]() . (3)
. (3)
Lahendame probleeme koos
Alustame juhtudest, kus joonise pindala saab arvutada valemi (1) abil.
Näide 1Ox) ja otsene x = 1 , x = 3 .

Lahendus. Sest y = 1/x> 0 lõigul , siis leitakse kõverjoonelise trapetsi pindala valemiga (1):
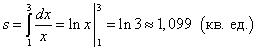 .
.
Näide 2 Leidke joonise pindala, mis on piiratud funktsiooni graafikuga, sirgjoon x= 1 ja x-telg ( Ox ).

Lahendus. Valemi (1) rakendamise tulemus:
![]()
Kui siis s= 1/2; kui siis s= 1/3 jne.
Näide 3 Leidke funktsiooni graafikuga piiratud joonise pindala, x-telg ( Ox) ja otsene x = 4 .

Lahendus. Ülesande tingimusele vastav kujund on kõverjooneline trapets, milles vasakpoolne lõik on taandunud punktiks. Integreerimispiirid on 0 ja 4. Kuna valemi (1) järgi leiame kõverjoonelise trapetsi pindala:
 .
.
Näide 4 Leidke joonise pindala, mis on piiratud joontega , , ja asub 1. kvartalis.

Lahendus. Valemi (1) kasutamiseks esindame näite tingimustega antud joonise pindala kolmnurga pindalade summana OAB ja kõverjooneline trapets ABC. Kolmnurga pindala arvutamisel OAB integreerimise piirid on punktide abstsissid O Ja A, ja figuuri jaoks ABC- punktide abstsissid A Ja C (A on sirge lõikepunkt OA ja paraboolid ja C- parabooli ja telje lõikepunkt Ox). Lahendades ühiselt (süsteemina) sirge ja parabooli võrrandid, saame (punkti abstsiss A) ja (teise sirge ja parabooli lõikepunkti abstsiss, mida lahenduse jaoks pole vaja). Samamoodi saame , (punktide abstsissid C Ja D). Nüüd on meil kõik, et leida figuuri pindala. Leiame:

Näide 5 Leidke kõverjoonelise trapetsi pindala ACDB, kui kõvera võrrand CD ja abstsiss A Ja B vastavalt 1 ja 2.

Lahendus. Avaldame seda kõvera võrrandit Y kaudu: Kõverajoonelise trapetsi pindala leitakse valemiga (1):
 .
.
Liigume edasi juhtumite juurde, kus joonise pindala saab arvutada valemi (2) abil.
Näide 6 Leidke parabooli ja x-teljega piiratud kujundi pindala ( Ox ).

Lahendus. See joonis asub x-telje all. Seetõttu kasutame selle pindala arvutamiseks valemit (2). Integratsiooni piirid on abstsissid ja parabooli lõikepunktid teljega Ox. Järelikult

Näide 7 Leidke ala x-telje ( Ox) ja kaks naabersiinuslainet.

Lahendus. Selle joonise pindala saab leida valemiga (2):
![]() .
.
Leiame iga termini eraldi:
 .
.
 .
.
Lõpuks leiame piirkonna:
![]() .
.
Näide 8 Leidke parabooli ja kõvera vahele jääva kujundi pindala.

Lahendus. Avaldame sirgete võrrandid Y-ga:
Valemile (2) vastav pindala saadakse kui
![]() ,
,
kus a Ja b- punktide abstsissid A Ja B. Leiame need võrrandite koos lahendamisega:

Lõpuks leiame piirkonna:

Ja lõpuks on juhtumeid, kus joonise pindala saab arvutada valemi (3) abil.
Näide 9 Leidke paraboolide vahele jääva kujundi pindala ![]() Ja .
Ja .
Arvutage joontega piiratud kujundi pindala.
Lahendus.
Leiame antud sirgete lõikepunktid. Selleks lahendame võrrandisüsteemi:
Antud sirgete lõikepunktide abstsisside leidmiseks lahendame võrrandi:
Leiame: x 1 = -2, x 2 = 4.
Niisiis, need sirged, mis on parabool ja sirgjoon, ristuvad punktides A(-2; 0), B(4; 6).

Need jooned moodustavad suletud joonise, mille pindala arvutatakse ülaltoodud valemi abil:



Newtoni-Leibnizi valemi järgi leiame:



Leidke ellipsiga piiratud ala pindala.
Lahendus.

I kvadrandi ellipsi võrrandist saame . Siit saame valemi järgi
Rakendame asendust x = a patt t, dx = a cos t dt. Uued integratsiooni piirid t = α Ja t = β määratakse võrranditest 0 = a patt t, a = a patt t. Saab panna α = 0 ja β = π /2.
Leiame nõutavast pinnast neljandiku
![]()
Siit S = pab.
Leidke joontega piiratud kujundi pindalay = - x 2 + x + 4 jay = - x + 1.
Lahendus.
Leidke sirgete lõikepunktid y = -x 2 + x + 4, y = -x+ 1, võrdsustades joonte ordinaate: - x 2 + x + 4 = -x+ 1 või x 2 - 2x- 3 = 0. Leia juured x 1 = -1, x 2 = 3 ja neile vastavad ordinaadid y 1 = 2, y 2 = -2.

Joonise pindala valemit kasutades saame
Leidke parabooliga ümbritsetud alay = x 2 + 1 ja otsenex + y = 3.
Lahendus.
Võrrandisüsteemi lahendamine
leida ristumispunktide abstsissid x 1 = -2 ja x 2 = 1.

Eeldusel y 2 = 3 - x Ja y 1 = x 2 + 1, saadud valemi põhjal
Arvutage Bernoulli lemniskaadi pindalar 2 = a 2 cos 2 φ .
Lahendus.

Polaarkoordinaatide süsteemis on joonise pindala, mis on piiratud kõvera kaarega r = f(φ ) ja kaks polaarraadiust φ 1 = ʅ Ja φ 2 = ʆ , väljendatakse integraaliga
Kõvera sümmeetria tõttu määrame kõigepealt ühe neljandiku soovitud pindalast
Seega on kogupindala S = a 2 .
Arvutage astroidi kaare pikkusx 2/3 + y 2/3 = a 2/3 .
Lahendus.

Kirjutame astroidi võrrandi kujule
(x 1/3) 2 + (y 1/3) 2 = (a 1/3) 2 .
Paneme x 1/3 = a 1/3 kulu t, y 1/3 = a 1/3 patt t.
Siit saame astroidi parameetrilised võrrandid
x = a cos 3 t, y = a patt 3 t, (*)
kus 0 ≤ t ≤ 2π .
Kõvera (*) sümmeetriat silmas pidades piisab, kui leida neljandiku kaare pikkusest L parameetri muutusele vastav t 0 kuni π /2.
Saame
dx = -3a cos 2 t patt t dt, dy = 3a patt 2 t cos t dt.
Siit leiame
![]()
Saadud avaldise integreerimine vahemikus 0 kuni π /2, saame
![]()
![]()
Siit L = 6a.
Leidke Archimedese spiraaliga piiratud alar = aφ ja kaks raadiusvektorit, mis vastavad polaarnurkadeleφ 1 Jaφ 2 (φ 1 < φ 2 ).
Lahendus.

Kõveraga piiratud ala r = f(φ ) arvutatakse valemiga , kus α Ja β - polaarnurga muutumise piirid.
Seega saame

 (*)
(*)
Alates (*) järeldub, et ala, mis on piiratud polaartelje ja Archimedese spiraali esimese pöördega ( φ 1 = 0; φ 2 = 2π ):
Samamoodi leiame ala, mis on piiratud polaartelje ja Archimedese spiraali teise pöördega ( φ 1 = 2π ; φ 2 = 4π ):
![]()
Nõutav pindala on võrdne nende alade erinevusega
Arvutage ümber telje pöörlemisel saadud keha ruumalaOx paraboolidega piiratud kujundy = x 2 Jax = y 2 .
Lahendus.

Lahendame võrrandisüsteemi
ja saada x 1 = 0, x 2 = 1, y 1 = 0, y 2 = 1, kust kõverate lõikepunktid O(0; 0), B(üksteist). Nagu jooniselt näha, on pöördekeha soovitud ruumala võrdne ümber telje pöörlemisel tekkiva kahe ruumala vahega Ox kõverjoonelised trapetsid OCBA Ja ODBA:

Arvutage teljega piiratud pindalaOx ja sinusoidy = pattx segmentide kohta: a); b) .
Lahendus.

a) Lõigul funktsioon sin x säilitab märgi ja seega valemiga , eeldades y= patt x, leiame


b) Lõigul funktsioon sin x muudab märki. Ülesande õigeks lahendamiseks on vaja segment jagada kaheks ja [ π , 2π ], millest igaühes säilitab funktsioon oma märgi.
Vastavalt märkide reeglile on lõigul [ π , 2π ] ala on võetud miinusmärgiga.
Selle tulemusena on soovitud ala võrdne
![]()
![]()
![]()
![]()
![]()
Määrake ellipsi pöörlemisel saadud pinnaga piiratud keha ruumalaümber suurteljea .
Lahendus.

Arvestades, et ellips on sümmeetriline koordinaattelgede suhtes, piisab, kui leida ümber telje pöörlemisel tekkiva ruumala Ox ala OAB, võrdub ühe neljandikuga ellipsi pindalast ja kahekordistage tulemust.
Tähistagem läbi pöördekeha mahtu V x; siis on meil valemi põhjal , kus 0 ja a- punktide abstsissid B Ja A. Ellipsi võrrandist leiame . Siit
Seega on nõutav maht võrdne . (Kui ellips pöörleb ümber väiketelje b, keha maht on )
Leidke paraboolidega piiratud alay 2 = 2 px Jax 2 = 2 py .
Lahendus.

Esiteks leiame paraboolide lõikepunktide koordinaadid, et määrata integreerimisintervall. Algsed võrrandid teisendades saame ja . Võrdsustades need väärtused, saame või x 4 - 8lk 3 x = 0.
x 4 - 8lk 3 x = x(x 3 - 8lk 3) = x(x - 2lk)(x 2 + 2px + 4lk 2) = 0.
Leiame võrrandite juured:
![]()
![]()
Arvestades asjaolu, et punkt A paraboolide ristumiskoht on esimesel veerandil, siis lõimumise piirid x= 0 ja x = 2lk.
Soovitud ala leitakse valemiga
aga)
Lahendus.
Otsuse esimene ja kõige olulisem hetk on joonise konstrueerimine.
Teeme joonise:
Võrrand y=0 määrab x-telje;
- x=-2 Ja x=1 - sirge, paralleelne teljega OU;
- y \u003d x 2 +2 - parabool, mille harud on suunatud ülespoole, tipuga (0;2).
kommenteerida. Parabooli konstrueerimiseks piisab, kui leida selle lõikepunktid koordinaatide telgedega, s.t. panemine x=0 leidke ristmik teljega OU ja lahendades vastava ruutvõrrandi, leidke lõikekoht teljega Oh .
Parabooli tipu saab leida valemite abil:
Saate joonistada jooni ja punkt-punkti haaval.
Intervallil [-2;1] funktsiooni graafik y = x 2 +2 asub üle telje Ox , sellepärast:
Vastus: S \u003d 9 ruutühikut
Pärast ülesande täitmist on alati kasulik vaadata joonist ja aru saada, kas vastus on tõeline. Sel juhul loendame "silma järgi" joonisel olevate lahtrite arvu - noh, umbes 9 kirjutatakse, see tundub olevat tõsi. On täiesti selge, et kui meil oleks näiteks vastus: 20 ruutühikut, siis ilmselgelt tehti kuskil viga - 20 lahtrit ei mahu ilmselgelt kõnealusele joonisele, kõige rohkem kümmekond. Kui vastus osutus eitavaks, siis oli ka ülesanne valesti lahendatud.
Mida teha, kui kõverjooneline trapets asub telje all Oh?
b) Arvutage joontega piiratud kujundi pindala y=-e x , x=1 ja koordinaatteljed.
Lahendus.
Teeme joonise.
Kui kõverjooneline trapets täiesti silla all Oh , siis selle pindala saab leida valemiga:
Vastus: S=(e-1) ruutühik" 1,72 ruutühik
Tähelepanu! Ärge ajage kahte tüüpi ülesandeid segamini:
1) Kui teil palutakse lahendada ainult kindel integraal ilma geomeetrilise tähenduseta, võib see olla negatiivne.
2) Kui teil palutakse leida figuuri pindala kindla integraali abil, siis on pindala alati positiivne! Seetõttu ilmub just vaadeldavas valemis miinus.
Praktikas asub kujund enamasti nii ülemisel kui alumisel pooltasandil.
alates) Leidke joontega piiratud tasapinnalise kujundi pindala y \u003d 2x-x 2, y \u003d -x.
Lahendus.
Kõigepealt peate tegema joonise. Üldiselt huvitab meid pindalaülesannetes joonise konstrueerimisel enim sirgete lõikepunktid. Leiame parabooli ja sirge lõikepunktid Seda saab teha kahel viisil. Esimene viis on analüütiline.
Lahendame võrrandi:
Seega integratsiooni alumine piir a=0 , integreerimise ülempiir b = 3 .
|
Ehitame etteantud sirged: 1. Parabool - tipp punktis (1;1); telje ristumiskoht Oh - punktid (0;0) ja (0;2). 2. Sirge - 2. ja 4. koordinaatnurga poolitaja. Ja nüüd Tähelepanu! Kui intervallil [ a;b] mingi pidev funktsioon f(x) suurem või võrdne mõne pideva funktsiooniga g(x), siis saab vastava joonise pindala leida valemiga: . Ja pole tähtis, kus joonis asub - telje kohal või all, vaid oluline on, milline diagramm on KÕRGEM (teise diagrammi suhtes) ja kumb ALL. Vaadeldavas näites on ilmne, et lõigul asub parabool sirgest kõrgemal ja seetõttu tuleb sellest lahutada |
Joone on võimalik konstrueerida punkt-punkti haaval, samas kui lõimimise piirid selgitatakse välja justkui "iseenesest". Sellegipoolest tuleb piiride leidmise analüütilist meetodit mõnikord siiski kasutada, kui näiteks graafik on piisavalt suur või keermestatud konstruktsioon ei toonud esile integreerimise piire (need võivad olla murdosalised või irratsionaalsed).
Soovitud figuuri piirab ülevalt parabool ja altpoolt sirgjoon.
Segmendil vastavalt vastavale valemile:
Vastus: S \u003d 4,5 ruutmeetrit
Tegelikult pole figuuri pindala leidmiseks vaja nii palju teadmisi määramata ja kindla integraali kohta. Ülesanne "arvuta pindala kindla integraali abil" hõlmab alati joonise koostamist, seega on teie teadmised ja joonistamisoskused palju asjakohasem. Sellega seoses on kasulik värskendada põhiliste elementaarfunktsioonide graafikute mälu ja vähemalt osata ehitada sirgjoont ja hüperbooli.
Kõverjooneline trapets on lame kujund, mis on piiratud telje, sirgjoonte ja pideva funktsiooni graafikuga lõigul, mis sellel intervallil märki ei muuda. Olgu see kujund asukoht mitte vähem abstsiss:
Siis kõverjoonelise trapetsi pindala on arvuliselt võrdne teatud integraaliga. Igal kindlal integraalil (mis eksisteerib) on väga hea geomeetriline tähendus.
Geomeetria seisukohalt on kindel integraal ALA.
St kindel integraal (kui see on olemas) vastab geomeetriliselt mõne kujundi pindalale. Vaatleme näiteks kindlat integraali . Integrand määratleb kõvera tasapinnal, mis asub telje kohal (soovijad saavad joonist täiendada) ja kindel integraal ise on numbriliselt võrdne vastava kõverjoonelise trapetsi pindalaga.
Näide 1
See on tüüpiline ülesande avaldus. Otsuse esimene ja kõige olulisem hetk on joonise konstrueerimine. Pealegi tuleb joonis ehitada ÕIGE.
Plaani koostamisel soovitan järgmist järjekorda: Esiteks parem on konstrueerida kõik read (kui neid on) ja ainult Siis- paraboolid, hüperboolid, muude funktsioonide graafikud. Funktsioonigraafikute koostamine on tulusam punktsuunas.
Selle probleemi puhul võib lahendus välja näha selline.
Teeme joonise (pange tähele, et võrrand määrab telje):
Segmendil paikneb funktsiooni graafik üle telje, sellepärast:
Vastus:
Pärast ülesande täitmist on alati kasulik vaadata joonist ja aru saada, kas vastus on tõeline. Sel juhul loendame "silma järgi" joonisel olevate lahtrite arvu - noh, umbes 9 kirjutatakse, see tundub olevat tõsi. On täiesti selge, et kui meil oleks näiteks vastus: 20 ruutühikut, siis ilmselgelt tehti kuskil viga - 20 lahtrit ei mahu ilmselgelt kõnealusele joonisele, kõige rohkem kümmekond. Kui vastus osutus eitavaks, siis oli ka ülesanne valesti lahendatud.
Näide 3
Arvutage joonise pindala, mis on piiratud joonte ja koordinaattelgedega.
Lahendus: Teeme joonise:
Kui kõverjooneline trapets asub telje all(või vähemalt mitte kõrgem antud telg), siis selle pindala saab leida valemiga:
Sel juhul:
Tähelepanu! Ärge ajage kahte tüüpi ülesandeid segamini:
1) Kui teil palutakse lahendada ainult kindel integraal ilma geomeetrilise tähenduseta, võib see olla negatiivne.
2) Kui teil palutakse leida figuuri pindala kindla integraali abil, siis on pindala alati positiivne! Seetõttu ilmub just vaadeldavas valemis miinus.
Praktikas paikneb joonis enamasti nii ülemisel kui alumisel pooltasandil ja seetõttu liigume lihtsamate kooliülesannete juurest edasi sisukamate näidete juurde.
Näide 4
Leidke tasapinnalise kujundi pindala, mis on piiratud joontega , .
Lahendus: Kõigepealt peate joonise lõpetama. Üldiselt huvitab meid pindalaülesannetes joonise konstrueerimisel enim sirgete lõikepunktid. Leiame parabooli ja sirge lõikepunktid. Seda saab teha kahel viisil. Esimene viis on analüütiline. Lahendame võrrandi:
Seega integratsiooni alumine piir, integratsiooni ülempiir.
Võimaluse korral on parem seda meetodit mitte kasutada..
Punkthaaval on liine palju tulusam ja kiirem ehitada, samas kui integratsiooni piirid selgitatakse välja justkui “iseenesest”. Sellegipoolest tuleb piiride leidmise analüütilist meetodit mõnikord siiski kasutada, kui näiteks graafik on piisavalt suur või keermestatud konstruktsioon ei toonud esile integreerimise piire (need võivad olla murdosalised või irratsionaalsed). Ja me kaalume ka sellist näidet.
Pöördume tagasi oma ülesande juurde: ratsionaalsem on kõigepealt konstrueerida sirge ja alles seejärel parabool. Teeme joonise:
Ja nüüd töövalem: kui intervallil on pidev funktsioon suurem või võrdne mõne pideva funktsiooni, siis nende funktsioonide graafikute ja sirgjoontega piiratud joonise pindala saab leida valemiga:
Siin pole enam vaja mõelda, kus kujund asub - telje kohal või telje all ja jämedalt öeldes on oluline, milline diagramm on ÜLAL(teise graafiku suhtes), ja milline neist on ALL.
Vaadeldavas näites on ilmne, et lõigul asub parabool sirgest kõrgemal ja seetõttu tuleb sellest lahutada
Lahenduse valmimine võib välja näha järgmine:
Soovitud figuuri piirab ülevalt parabool ja altpoolt sirgjoon.
Segmendil vastavalt vastavale valemile:
Vastus:
Näide 4
Arvutage joonise pindala, mis on piiratud joontega , , , .
Lahendus: Teeme kõigepealt joonise:
Joonis, mille ala peame leidma, on varjutatud sinisega.(vaadake hoolikalt seisukorda - kuidas figuur on piiratud!). Kuid praktikas juhtub tähelepanematuse tõttu sageli "tõrge", et peate leidma roheliseks varjutatud figuuri ala!
See näide on kasulik ka selle poolest, et selles arvutatakse joonise pindala kahe kindla integraali abil.
Tõesti:
1) Lõigul telje kohal on sirge graafik;
2) Telje kohal lõigul on hüperboolgraafik.
On üsna ilmne, et piirkondi saab (ja tuleks) lisada, seega:
Kuidas arvutada pöördekeha ruumalakasutades kindlat integraali?
Kujutage ette mingit lamedat kujundit koordinaattasandil. Oleme selle ala juba leidnud. Kuid lisaks saab seda joonist pöörata ja pöörata kahel viisil:
X-telje ümber;
Ümber y-telje .
Käesolevas artiklis käsitletakse mõlemat juhtumit. Eriti huvitav on teine pööramisviis, see tekitab kõige suuremaid raskusi, kuid tegelikult on lahendus peaaegu sama, mis tavalisemal ümber x-telje pööramisel.
Alustame kõige populaarsema pöörlemisviisiga.
- Kokkupuutel 0
- Google Plus 0
- Okei 0
- Facebook 0