Lavoro di prova per reparto corrispondenza
Danko, P.E. Matematica superiore in esercizi e compiti: in 2 ore / P.E. Danko, AG Popov, T. Ya. Kozhevnikova. - 5a ed., Rev. - M.: Scuola superiore Parte 1.-1998.-304s.
Bermant AF, Aramanovich I.G. Corso breve analisi matematica. -12a edizione. - San Pietroburgo: Lan, 2005.- 736 p.
BM Vladimirsky, AB Gorstko, Ya.M. Gerusalemme. Matematica: corso generale. - San Pietroburgo: casa editrice "Lan", 2002. - 954 p.
Kudryavtsev VA, Demidovich B.P. Un breve corso di matematica superiore. - 5a ed., Stereotipo. - M.: Nauka, 1978. - 632 pag.
Demidovich B.P. Corso breve di matematica superiore: Esercitazione per le università - M.: Astrel Publishing House LLC: AST Publishing House LLC, 2001. - 656s.
Piskunov NS Calcolo differenziale e integrale: Proc. per le università. In 2-h Vol. T. II: - M.: Integral-Press, 2004. -544 p.
Introduzione.
Esaudire test segue un programma rigoroso. Ogni studente esegue un test sotto l'opzione, il cui numero corrisponde al suo numero di serie nel diario di gruppo. La soluzione dei problemi deve essere fornita per iscritto su fogli separati (formato A 4, rilegato). Puoi inviare il tuo lavoro sia in forma cartacea che scritta. Esecuzione di k.r. , lo studente deve riscrivere la condizione del problema corrispondente, scrivere soluzione dettagliata evidenziando la risposta. Se necessario, fornire brevi spiegazioni lungo il percorso.
"SERIE NUMERICHE E FUNZIONALI"
Linee numeriche. Criteri sufficienti per la loro convergenza
Lascia stare tu 1 , tu 2 , tu 3 , … , u n, …, dove u n = F(n), è una sequenza numerica infinita. Espressione tu 1 + tu 2 + tu 3 + … + u n+ ... si chiama infinito serie numerica, e i numeri tu 1 , tu 2 , tu 3 , … , u n, … sono membri della serie; u n = F(n) è chiamato membro comune. La serie è spesso scritta come .
La somma del primo n i membri della serie numerica sono indicati con S n e chiama n th somma parziale di una serie:
La riga è chiamata convergente se n-esima somma parziale S n con aumento illimitato n tende al limite finale, cioè Se . Numero S chiamata la somma delle serie. Se n-esima somma parziale della serie a non tende a un limite finito, allora si chiama la serie divergente.
Una serie composta da termini di qualsiasi progressione geometrica decrescente è convergente e ha somma .
La fila ha chiamato armonico, diverge.
Segno necessario di convergenza. Se la serie converge, allora , cioè per , il limite del termine comune della serie convergente è uguale a zero.
Quindi, se , allora la serie diverge.
Elenchiamo i criteri più importanti per la convergenza e la divergenza di serie con termini positivi.
Il primo segno di confronto. Lascia che ci siano due righe
inoltre, ogni termine della serie (1) non eccede il corrispondente termine della serie (2), cioè . Allora se la serie (2) converge, allora converge anche la serie (1); se la serie (1) diverge, diverge anche la serie (2).
Questa caratteristica rimane valida se le disuguaglianze non sono soddisfatte per tutti n, ma solo a partire da un certo numero n = n.
Il secondo segno di confronto. Se esiste un limite finito diverso da zero, allora la serie ed entrambi convergono o divergono.
Segno radicale di Cauchy. Se per una serie
esiste, allora questa serie converge a , diverge a .
Segno di d'Alembert. Se esiste una serie, allora questa serie converge in , diverge in .
Test di Cauchy integrale. Se F(X) for è una funzione continua positiva e monotonicamente decrescente, quindi la serie , dove converge o diverge a seconda che l'integrale converge o diverga.
Consideriamo ora serie i cui membri hanno segni alternati, ad es. righe del modulo, dove .
Test di convergenza per una serie alternata (test di Leibniz). Una serie alternata converge se i valori assoluti dei suoi termini decrescono monotonicamente e il termine comune tende a zero. Ovvero, se sono soddisfatte le seguenti due condizioni: 1) e 2) .
Prendiamo n-esima somma parziale di una serie alternata convergente per la quale è soddisfatto il criterio di Leibniz:
Sia -- n-esimo resto della riga. Può essere scritto come la differenza tra la somma delle serie S e n-esima somma parziale S n, cioè. . È facile vederlo
Il valore viene stimato utilizzando la disuguaglianza.
Soffermiamoci ora su alcune proprietà delle serie alternate di segni (cioè serie e serie alternate di segni con un'alternanza arbitraria dei segni dei loro membri).
Una serie alternata converge se la serie converge.
In questo caso, viene chiamata la serie originale assolutamente convergente.
Si chiama la serie convergente condizionatamente convergente se la serie diverge.
Esempio 1. Indagare la convergenza di una serie
Soluzione. Questa serie è composta da membri di una progressione geometrica infinitamente decrescente e quindi converge. Troviamo la sua somma. Qui , (il denominatore della progressione). Di conseguenza,
Esempio 2. Indagare la convergenza della serie.
Soluzione. Questa serie si ottiene dall'armonica scartando i primi dieci termini. Pertanto, diverge.
Esempio 3. Indagare la convergenza della serie., – la serie converge.
$\sum \limits _(n=1)^(\infty )a_(n) $ i cui membri soddisfano tre condizioni:
- $a_(n) >0,\, \, \, n\ge 1$, ovvero serie originale con membri positivi;
- i termini della serie decrescono monotonicamente, cioè $a_(1) >a_(2) >\lpunti >a_(n-1) >a_(n) >\lpunti >0$;
- il termine comune della serie tende a zero: $\mathop(\lim )\limits_(n\to \infty ) a_(n) =0$.
Sia definita una funzione f(x) continua e monotonicamente decrescente definita per $x\ge 1$ tale che $f\left(1\right)=a_(1) ,\, \, \, f\left(2 \right )=a_(2) ,\, \, \, \ldots ;\, \, \, f\left(n\right)=a_(n) ,\, \, \, \ldots $, cioè e. $\sum \limits _(n=1)^(\infty )a_(n) =\sum \limits _(n=1)^(\infty )f(n) $. Quindi se l'integrale improprio $\int \limits _(1)^(+\infty )f\left(x\right)(\rm d)x $ converge, allora la serie $\sum \limits _(n=1 ) ^(\infty )a_(n) $ converge anche; se l'integrale indicato diverge, allora questa serie diverge.
Nota 1
Il teorema rimane vero anche quando le sue condizioni sono soddisfatte non per tutti i membri della serie, ma solo a partire dalla kth ($n\ge k$), nel qual caso l'integrale $\int \limits _(k)^(+ \ infty )f\sinistra(x\destra)\, (\rm d)x $.
Nota 2
Il criterio integrale di Cauchy semplifica enormemente lo studio della convergenza di una serie, poiché ci permette di ridurre questa domanda alla ricerca della convergenza dell'integrale di una funzione corrispondente ben scelta $f(x)$, cosa che si può fare facilmente usando il metodo metodi di calcolo integrale.
Teorema 2 (test di Cauchy radicale)
Sia data una serie con termini positivi $\sum \limits _(n=1)^(\infty )a_(n) ,\, \, \, a_(n) >0$ e sia presente un limite finito $ \mathop(\ lim )\limits_(n\to \infty ) \sqrt[(n)](a_(n) ) =l.$Allora:
- se $ l
- se $l>1$, la serie diverge,
- se $l=1$, allora il criterio di Cauchy radicale non è applicabile per determinare la convergenza delle serie.
Prova
- Sia $\mathop(\lim )\limits_(n\to \infty ) \sqrt[(n)](a_(n) ) =l0$, allora $l\ge 0$. Si consideri un numero q tale che $l 0$ esista $N=N((\rm \varepsilon ))\in $N, a partire da cui $\forall n \ge N$ la disuguaglianza $\left|\sqrt[( n )](a_(n) ) -l\destra|
$\sum \limits _(n=1)^(\infty )a_(n) =\, a_(1) +\, a_(2) +\ldots +\, a_(N) +\, a_(N +1) +a_(N+2) +...$ . (uno)
Creiamo una nuova riga
$\sum \limits _(k=0)^(\infty )q^(N+k) =q^(N) +\, q^(N+1) +q^(N+2) +\lpunti $(2)
La serie (2) è una serie di progressioni geometriche con denominatore $q$: $0\le q
- Sia $\mathop(\lim )\limits_(n\to \infty ) \sqrt[(n)](a_(n) ) =l>1$ esiste. A partire da alcuni $N=N((\rm \varepsilon ))\in (\rm N)$ $\forall n\ge N$, $\, \, \sqrt[(n)](a_(n) ) >1\, \, \, \Freccia destra \, \, \, \, a_(n) >1$, ovvero $\mathop(\lim )\limits_(n\to \infty ) a_(n) \ne 0$, allora la serie originale diverge secondo il criterio di convergenza richiesto.
- Se $\mathop(\lim )\limits_(n\to \infty ) \sqrt[(n)](a_(n) ) =l=1$ (o non esiste), il criterio di Cauchy radicale non è applicabile .
Il teorema è stato dimostrato.
Teorema 3 (test di d'Alembert)
Sia data una serie con termini positivi $\sum \limits _(n=1)^(\infty )a_(n) \, \, \, (a_(n) >0) $, e sia finita limit $\mathop( \lim )\limits_(n\to \infty ) \frac(a_(n+1) )(a_(n) ) =l$, quindi:
- la serie $\sum \limits _(n=1)^(\infty )a_(n) $ converge se $l
- la serie $\sum \limits _(n=1)^(\infty )a_(n) $ diverge se $l>1$,
- se $l=1$, allora il criterio di d'Alembert non è applicabile per determinare la convergenza delle serie.
Prova
- Lascia che il limite $\mathop(\lim )\limits_(n\to \infty ) \frac(a_(n+1) )(a_(n) ) =l$ esista e $0\le l 0$ esista $N( ( \rm \varepsilon ))\in $N, a partire da cui $\forall n\ge N=N((\rm \varepsilon ))$ $\left|\frac(a_(n+1)) (a_n ) -l\destra|
Scriviamo la serie originale $\sum \limits _(n=1)^(\infty )a_(n) \, \, \, (a_(n) >0) $ come: $\sum \limits _( n= 1)^(\infty )a_(n) =a_(1) +a_(2) +\ldots +a_(N) +a_(N+1) +a_(N+2) \, +.. .$ . Considera una nuova serie $\sum \limits _(k=0)^(\infty )a_(N) \cdot q^(k) =a_(N) +qa_(N) +q^(2) a_(N ) +\lpunti $ . Questa serie è una serie di progressioni geometriche con $b_(1) =a_(N) $ e $0
- Sia $\mathop(\lim )\limits_(n\to \infty ) \frac(a_(n+1) )(a_(n) ) =l>1$. Si consideri un numero q tale che $l>q>1$. $(\rm \varepsilon )=lq>0$, dalla definizione del limite segue: $-(\rm \varepsilon ) q > 1.$Quindi, $a_(n+1) >a_n > 0$ e per $n \to \infty $ il membro comune della serie $a_(n) $ non tende a 0, cioè la serie $\sum \limits _(n=1)^(\infty )a_n $ diverge perché non vale condizione necessaria convergenza in serie. Si dimostra la seconda parte del teorema.
- Se $l=1$,$\mathop(\lim )\limits_(n\to \infty ) \frac(a_(n+1) )(a_(n) ) $ è uguale a uno o non esiste, in quale caso per il criterio di d'Alembert non è applicabile per determinare la convergenza di una serie.
Esempio 1
Esaminare la serie $\sum \limits _(n=1)^(\infty )\, \frac(n)(2^(n) ) $ per la convergenza.
Soluzione. Denota $\frac(n)(2^(n) ) =a_(n) $, $a_(n) >0$; trova $a_(n+1) =\frac(n+1)(2^(n+1) ) $. Componi il limite $l=\mathop(\lim )\limits_(n\to \infty ) \frac(a_(n+1) )(a_(n) ) =\mathop(\lim )\limits_(n\to \ infty ) \frac((n+1)\cdot 2^(n) )(2^(n) \cdot 2\cdot n) =\frac(1)(2) \mathop(\lim )\limits_( n \to \infty ) \frac(n+1)(n) =\frac(1)(2)
Risposta: la serie $\sum \limits _(n=1)^(\infty )\, \frac(n)(2^(n) ) $converge.
Esempio 2
Esamina la serie $\sum \limits _(n=1)^(\infty )\, \frac(n{5^{n} } $.!}
Soluzione. Denota $\frac(n{5^{n} } =a_{n} ,a_{n} >0$; найдём $a_{n+1} =\frac{(n+1)!}{5^{n+1} } $. Составим предел!}
quelli. secondo il test d'Alembert, la serie diverge.
Risposta: serie $\sum \limits _(n=1)^(\infty )\, \frac(n{5^{n} } $ расходится.!}
Esempio 3
Esamina la serie $\sum \limits _(n=1)^(\infty )\, \left(\frac(n)(2n+1) \right)^(n) $ per la convergenza
Soluzione. Denota $\left(\frac(n)(2n+1) \right)^(n) =a_(n) ,^() a_(n) >0$. Facciamo un limite:
$l=\mathop(\lim )\limits_(n\to \infty ) \sqrt[(n)](a_(n) ) =\mathop(\lim )\limits_(n\to ) \frac(n) (2n+1)=\frac(1)(2)
Risposta: la serie $\sum \limits _(n=1)^(\infty )\, \left(\frac(n)(2n+1) \right)^(n) $converges.
MATEMATICA SUPERIORE
Serie numerica
Conferenza.Serie numerica
1. Definizione di una serie numerica. Convergenza
2. Proprietà di base delle serie numeriche
3. Serie con termini positivi. Segni di convergenza
4. File alternati. Test di convergenza di Leibniz
5. Serie alternata
Domande per l'autoesame
Letteratura
Conferenza. SERIE NUMERICA
1. Definizione di una serie numerica. Convergenza.
2. Proprietà di base delle serie numeriche.
3. Serie con termini positivi. Segni di convergenza.
4. File alternati. Test di convergenza di Leibniz.
5. Serie alternata.
1. Definizione di una serie numerica. Convergenza
Nelle applicazioni matematiche, oltre che nella risoluzione di alcuni problemi di economia, statistica e altro, vengono considerate somme con un numero infinito di termini. Definiamo qui cosa si intende per tali importi.
Sia data una sequenza numerica infinita
, , …, , …Definizione 1.1. Serie numeriche o semplicemente nelle vicinanzeè chiamata espressione (somma) della forma
. (1.1) sono chiamati membri di un numero, – generale o n – m un membro della fila.Per definire la serie (1.1), è sufficiente definire la funzione dell'argomento naturale
calcolo del esimo termine della serie per il suo numeroEsempio 1.1. Lascia stare
. Riga (1.2)chiamata serie armonica .
Esempio 1.2. Lascia stare
, Serie (1.3)chiamata serie armonica generalizzata. In un caso particolare, quando
si ottiene una serie armonica.Esempio 1.3. Lascia stare
= . Riga (1.4)chiamata accanto a una progressione geometrica.
Dai termini della serie (1.1) formiamo un numero sequenza di parzialeimporti dove
è la somma dei primi termini della serie, che si chiama n-e somma parziale, cioè. , , ,…………………………….
, (1.5)…………………………….
Sequenza numerica
con un aumento illimitato del numero può:1) avere un limite finito;
2) non hanno un limite finito (il limite non esiste o è uguale all'infinito).
Definizione 1.2. Viene chiamata la serie (1.1). convergente, se la successione delle sue somme parziali (1.5) ha un limite finito, cioè
In questo caso, il numero
chiamata somma serie (1.1) e si scrive .Definizione 1.3.Viene chiamata la serie (1.1). divergente, se la successione delle sue somme parziali non ha limite finito.
Nessuna somma è assegnata alla serie divergente.
Pertanto, il problema di trovare la somma delle serie convergenti (1.1) equivale a calcolare il limite della successione delle sue somme parziali.
Diamo un'occhiata ad alcuni esempi.
Esempio 1.4. Dimostralo la serie
converge e trova la sua somma.
Cerchiamo n- la somma parziale della serie data
.Membro comune
rappresentiamo la serie nella forma .Quindi abbiamo:
. Pertanto, questa serie converge e la sua somma è uguale a 1:Esempio 1.5. Indagare per serie di convergenza
(1.6)Per questa riga
. Pertanto, questa serie diverge.Commento. In
la serie (1.6) è la somma di un numero infinito di zeri ed è ovviamente convergente.Esempio 1.6. Indagare per serie di convergenza
(1.7)Per questa riga
In questo caso, il limite della sequenza delle somme parziali
non esiste e la serie diverge.Esempio 1.7. Indagare la convergenza delle serie di progressione geometrica (1.4):
È facile mostrarlo n-esima somma parziale di una serie di progressioni geometriche per
dato dalla formula.Considera i casi:
Poi e .Pertanto, la serie converge e la sua somma è uguale a
Definizione di serie numerica e sua convergenza.
Criterio necessario per la convergenza
Sia una sequenza infinita di numeri.
Definizione. Espressione
, (1)
o, qual è lo stesso, si chiama serie numerica e i numeri https://pandia.ru/text/79/302/images/image005_146.gif" width="53" height="31"> – membri della serie. Viene chiamato un membro con un numero arbitrarion-m, o membro comune della serie.
Di per sé, l'espressione (1) non ha un significato numerico definito, perché quando calcoliamo la somma, ogni volta abbiamo a che fare solo con un numero finito di termini. È del tutto naturale determinare il significato di questa espressione come segue.
Sia data la serie (1).
Definizione. Sommani primi membri della serie

chiamata n -esima somma parziale riga. Formiamo una sequenza di somme parziali:
font-size:14.0pt">Incremento infinitontutto conta in totale di più membri di fila. Pertanto, è ragionevole dare una definizione del genere.
Definizione. Se esiste un limite finito della sequenza di somme parziali https://pandia.ru/text/79/302/images/image011_76.gif" width="103" height="41"> si chiama somma.
Se la sequenza è https://pandia.ru/text/79/302/images/image013_77.gif" width="80" height="31">, 2) se è fluttuante. In entrambi i casi, la serie è detto di non avere somma.
Esempio 1 Consideriamo una serie composta da membri di una progressione geometrica:
 , (2)
, (2)
dove - è chiamato il primo membro della progressione, e font-size:14.0pt"> Somma parziale di questa serie a font-size:14.0pt">font-size:14.0pt"> Da qui:
1) se , allora
font-size:14.0pt">cioè la serie geometrica converge e la sua somma è .
In particolare, se  , riga
, riga  converge e la sua somma.
converge e la sua somma.
Su https://pandia.ru/text/79/302/images/image026_42.gif" width="307" height="59 src="> converge anche la sua somma.
2) se , allora  , cioè la serie (2) diverge.
, cioè la serie (2) diverge.
3) se , la riga (2) diventa font-size:14.0pt"> e![]() , cioè la serie diverge(con font-size:18.0pt">) .
, cioè la serie diverge(con font-size:18.0pt">) .
4) se https://pandia.ru/text/79/302/images/image036_32.gif" width="265" height="37"> . Per questa riga
https://pandia.ru/text/79/302/images/image038_28.gif" width="253" height="31 src=">,
cioè..gif" width="67" height="41"> non esiste, quindi anche la serie diverge(a ) .
Calcolare la somma di una serie direttamente per definizione è molto scomodo a causa della difficoltà di calcolare esplicitamente font-size:14.0pt"> somme parziali e trovare il limite della loro sequenza. Ma, se è stabilito che la serie converge, la sua somma può essere calcolato approssimativamente, perché dalla definizione del limite della sequenza, ne consegue che per sufficientemente grande. Pertanto, quando si studiano le serie, è sufficiente
1) conoscere le tecniche che consentono di stabilire la convergenza di una serie senza trovarne la somma;
2) essere in grado di identificarefont-size:14.0pt">.gif" width="16 height=24" height="24"> con una certa precisione.
La convergenza delle serie numeriche viene stabilita con l'ausilio di teoremi, che prendono il nome di criteri di convergenza.
Caratteristica richiesta convergenza
Se la serie converge, il suo termine comune tende a zero, cioè font-size:14.0pt">.gif" width="61 height=63" height="63"> diverge.
Esempio 2 Dimostra la riga 0 " style="border-collapse:collapse">
 ;
;
 ;
;
 ;
;
 .
.
Soluzione.
A) https://pandia.ru/text/79/302/images/image051_28.gif" width="176" height="81 src="> diverge.

e quindi la serie diverge. Nel risolvere, abbiamo usato il secondo notevole
limite:  (per i dettagli vedere).
(per i dettagli vedere).
C) font-size:14.0pt">, ovvero la sequenza
 - infinitamente
- infinitamente
piccolo. Dal momento che con font-size:14.0pt">~ (vedi ), allora
~ .Considerando questo, otteniamo:
quindi la serie diverge.
D) dimensione del carattere: 14.0pt">,
quindi la serie diverge.
Condizione ![]() è un necessario, ma non abbastanza condizione di convergenza delle serie: esiste un insieme di serie per cui
è un necessario, ma non abbastanza condizione di convergenza delle serie: esiste un insieme di serie per cui![]() , ma che tuttavia divergono.
, ma che tuttavia divergono.
Esempio 3 Esplora la convergenza della serie font-size:14.0pt"> Soluzione. notare che https://pandia.ru/text/79/302/images/image066_20.gif" width="119" height="59 src="> , cioè la condizione di convergenza necessaria è soddisfatta. somma parziale
sinistra">
- una volta
quindi font-size:14.0pt"> il che significa che la serie diverge per definizione.
Condizioni sufficienti per la convergenza di serie di segno positivo
Lascia stare. Poi la seriefont-size:14.0pt"> Segno di confronto
Lascia stare e sono serie di segno positivo. Se la disuguaglianza è soddisfatta per tutti, allora la convergenza della serie segue dalla convergenza della serie e dalla divergenza della serie
Questo segno rimane valido se la disuguaglianza https://pandia.ru/text/79/302/images/image072_18.gif" width="60" height="24">, ma solo a partire da un numero . Può essere interpretato come segue: se la serie maggiore converge, la serie minore converge ancora di più; se la serie minore diverge, diverge anche quella maggiore.
Esempio 4 Esplora la convergenza delle righe 0 " style="margin-left:50.4pt;border-collapse:collapse">
 ;
;
Soluzione.
A) Nota che font-size:14.0pt"> per tutti ![]() . Serie con un termine comune
. Serie con un termine comune
 converge per confronto.
converge per confronto.
B) Confronta riga con riga ..gif" width="91" height="29 src=">.gif" width="87" height="59"> diverge, quindi diverge anche la serie.
Nonostante la semplicità di formulazione del criterio di confronto, in pratica risulta più conveniente il seguente teorema, che ne è la conseguenza.
Limite segno di confronto
Lascia stare https://pandia.ru/text/79/302/images/image071_17.gif" width="53" height="60 src="> – serie positiva. Se esiste finito e diverso da zero limit , quindi entrambe le righe e
convergere contemporaneamente o divergere contemporaneamente.
Come serie utilizzata per il confronto con i dati, una serie del modulo  . Si chiama tale serie vicino a Dirichlet. Negli esempi 3 e 4 è stato mostrato che la serie di Dirichlet con e diverge. Posso per ora-
. Si chiama tale serie vicino a Dirichlet. Negli esempi 3 e 4 è stato mostrato che la serie di Dirichlet con e diverge. Posso per ora-

 .
.
Se , allora la riga  chiamata armonico. La serie armonica diverge.
chiamata armonico. La serie armonica diverge.
Esempio 5 Indagare per serie di convergenzautilizzando il criterio di confronto dei limiti, se
|
|
|
Soluzione. a) Poiché per https://pandia.ru/text/79/302/images/image101_9.gif" width="31" height="23 src="> e
![]() ~ , allora
~ , allora  ~ font-size:14.0pt">confronto con una data serie armonica font-size:14.0pt">, ovvero .
~ font-size:14.0pt">confronto con una data serie armonica font-size:14.0pt">, ovvero .
font-size:14.0pt"> Poiché il limite è finito e diverso da zero e la serie armonica diverge, anche questa serie diverge.
B) Per https://pandia.ru/text/79/302/images/image109_10.gif" width="111" height="31 src=">.gif" width="129" height="31" sufficientemente grandi src=">.gif" width="132" height="64 src="> è il membro comune della serie per confrontare questo con:
Font-size:14.0pt">La serie converge ( Riga Dirichlet con font-size:16.0pt">), quindi anche questa serie converge.
IN)  , così infinitesimale font-size:14.0pt"> puoi
, così infinitesimale font-size:14.0pt"> puoi
essere sostituito dal valore equivalente a(https://pandia.ru/text/79/302/images/image058_20.gif" width="13" height="21 src="> con font-size: 20.0pt">). ;
 ;
;
 ;
;
G )
 ;
;
 .
.
In pratica, spesso non è così importante trovare la somma di una serie quanto rispondere alla domanda sulla convergenza delle serie. A tal fine vengono utilizzati criteri di convergenza basati sulle proprietà del termine comune delle serie.
Un criterio necessario per la convergenza di una serie
TEOREMA 1
Se la filaconverge, quindi il suo termine comune  tende a zero a
tende a zero a  ,
quelli.
,
quelli.
 .
.
Brevemente: se la serie converge, allora il suo termine comune tende a zero.
Prova. Lascia che la serie converga e la sua somma sia uguale a  . Per chiunque
. Per chiunque  somma parziale
somma parziale


 .
.
Quindi .
Dal comprovato criterio necessario per la convergenza segue un criterio sufficiente per la divergenza delle serie:
se a  il termine comune della serie non tende a zero, quindi la serie diverge.
il termine comune della serie non tende a zero, quindi la serie diverge.
Esempio 4

Per questa serie, il termine comune  e
e  .
.
Pertanto, questa serie diverge.
Esempio 5 Indagare per serie di convergenza

È ovvio che il termine comune di questa serie, la cui forma non è indicata per l'ingombrante espressione, tende a zero in  , cioè. il criterio necessario per la convergenza della serie è soddisfatto, ma questa serie diverge, poiché la sua somma
tende all'infinito.
, cioè. il criterio necessario per la convergenza della serie è soddisfatto, ma questa serie diverge, poiché la sua somma
tende all'infinito.
Serie di segni positivi
Viene chiamata una serie di numeri i cui membri sono tutti positivi segno positivo.
TEOREMA 2 (Criterio per la convergenza di una serie positiva)
Perché una serie positiva converga, è necessario e sufficiente che tutte le sue somme parziali siano limitate superiormente dallo stesso numero.
Prova. Dal momento che per qualsiasi 
 , quindi, cioè sotto sequenza
, quindi, cioè sotto sequenza  - monotonicamente crescente, quindi, per l'esistenza di un limite, è necessario e sufficiente restringere di un certo numero la sequenza dall'alto.
- monotonicamente crescente, quindi, per l'esistenza di un limite, è necessario e sufficiente restringere di un certo numero la sequenza dall'alto.
Questo teorema in di più ha un'importanza teorica piuttosto che pratica. I seguenti sono altri criteri di convergenza che sono di maggiore utilità.
Condizioni sufficienti per la convergenza di serie di segno positivo
TEOREMA 3 (Prima prova di confronto)
Si danno due serie positive:
 (1)
(1)
 (2)
(2)
e, partendo da un certo numero  , per chiunque
, per chiunque  la disuguaglianza
la disuguaglianza  Quindi:
Quindi:

Notazione schematica del primo segno di confronto:

discesa discesa.
flussoflusso
Prova. 1) Poiché l'eliminazione di un numero finito di termini della serie non pregiudica la sua convergenza, dimostreremo il teorema per il caso  . Lascia per chiunque
. Lascia per chiunque  noi abbiamo
noi abbiamo
 , (3)
, (3)
dove  e
e
 sono rispettivamente le somme parziali delle serie (1) e (2).
sono rispettivamente le somme parziali delle serie (1) e (2).
Se la serie (2) converge, allora c'è un numero  .
Dalla sequenza
.
Dalla sequenza  - aumentando, il suo limite è maggiore di qualsiasi suo membro, cioè
- aumentando, il suo limite è maggiore di qualsiasi suo membro, cioè  per chiunque
per chiunque  .
Quindi dalla disuguaglianza (3) segue
.
Quindi dalla disuguaglianza (3) segue
 .
Pertanto, tutte le somme parziali della serie (1) sono limitate dall'alto dal numero
.
Pertanto, tutte le somme parziali della serie (1) sono limitate dall'alto dal numero  .
Secondo il Teorema 2, questa serie converge.
.
Secondo il Teorema 2, questa serie converge.
2) Infatti, se la serie (2) convergesse, convergerebbe anche la serie (1) per confronto.
Per applicare questa caratteristica, vengono spesso utilizzate tali serie standard, la cui convergenza o divergenza è nota in anticipo, ad esempio:

3)
 -
serie di Dirichlet (converge a
-
serie di Dirichlet (converge a  e diverge a
e diverge a  ).
).
Inoltre, vengono spesso utilizzate serie, che possono essere ottenute utilizzando le seguenti ovvie disuguaglianze:

 ,
,

 ,
, ,
, .
.
Considera esempi concreti uno schema per studiare una serie di segni positivi per la convergenza utilizzando il primo segno di confronto.
Esempio 6 Esplora un numero  per convergenza.
per convergenza.
Passaggio 1. Controlliamo il segno positivo della serie:  per
per 
Passaggio 2. Verifichiamo il soddisfacimento del criterio necessario per la convergenza delle serie:  . Perché
. Perché  , poi
, poi 
(se il calcolo del limite è difficile, allora questo passaggio può essere saltato).
Passaggio 3. Usiamo il primo segno di confronto. Per fare ciò, selezioniamo una serie standard per questa serie. Perché  , quindi come standard possiamo prendere la serie
, quindi come standard possiamo prendere la serie  , cioè. Fila di Dirichlet. Questa serie converge perché l'esponente
, cioè. Fila di Dirichlet. Questa serie converge perché l'esponente  . Pertanto, secondo il primo criterio di confronto, converge anche la serie in esame.
. Pertanto, secondo il primo criterio di confronto, converge anche la serie in esame.
Esempio 7 Esplora un numero  per convergenza.
per convergenza.
1) Questa serie è di segno positivo, poiché  per
per 
2) Il criterio necessario per la convergenza delle serie è soddisfatto, perché
3) Selezioniamo uno standard di serie. Perché  , quindi come standard possiamo prendere le serie geometriche
, quindi come standard possiamo prendere le serie geometriche

 . Questa serie converge, quindi converge anche la serie in esame.
. Questa serie converge, quindi converge anche la serie in esame.
TEOREMA 4 (Seconda prova comparativa)
Se per serie con segno positivo
 e
e
 esiste un limite finito diverso da zero
esiste un limite finito diverso da zero  , poi
le righe convergono o divergono allo stesso tempo.
, poi
le righe convergono o divergono allo stesso tempo.
Prova. Sia la serie (2) convergere; Dimostriamo che allora converge anche la serie (1). Scegliamo un numero  ,
più di
,
più di  .
Dalla condizione
.
Dalla condizione
 l'esistenza di un tale numero
l'esistenza di un tale numero
 quello per tutti
quello per tutti  la disuguaglianza
la disuguaglianza  ,
oppure, che è lo stesso,
,
oppure, che è lo stesso,
 (4)
(4)
Scartando nelle righe (1) e (2) la prima
 termini (che non pregiudica la convergenza), possiamo supporre che la disuguaglianza (4) sia valida per tutti
termini (che non pregiudica la convergenza), possiamo supporre che la disuguaglianza (4) sia valida per tutti  Ma una serie con un termine comune
Ma una serie con un termine comune  converge per la convergenza della serie (2). Secondo il primo criterio di confronto, la disuguaglianza (4) implica la convergenza delle serie (1).
converge per la convergenza della serie (2). Secondo il primo criterio di confronto, la disuguaglianza (4) implica la convergenza delle serie (1).
Ora converga la serie (1); Dimostriamo la convergenza della serie (2). Per fare ciò, invertire semplicemente i ruoli delle righe indicate. Perché

allora, per quanto sopra dimostrato, la convergenza della serie (1) dovrebbe implicare la convergenza della serie (2).
Se  a
a  (un criterio necessario per la convergenza), quindi dalla condizione
(un criterio necessario per la convergenza), quindi dalla condizione  , segue quello
, segue quello  e
e  sono infinitesimi dello stesso ordine di piccolezza (equivalenti a
sono infinitesimi dello stesso ordine di piccolezza (equivalenti a  ). Pertanto, se data una serie
). Pertanto, se data una serie
 , dove
, dove  a
a  , quindi per questa serie possiamo prendere la serie standard
, quindi per questa serie possiamo prendere la serie standard
 , dove il termine comune
, dove il termine comune  ha lo stesso ordine di piccolezza del termine comune della serie data.
ha lo stesso ordine di piccolezza del termine comune della serie data.
Quando si sceglie una serie standard, è possibile utilizzare la seguente tabella di infinitesimi equivalenti per  :
:
1)
 ; 4)
; 4) ;
;
2)
 ; 5)
; 5) ;
;
3)
 ; 6)
; 6) .
.
Esempio 8 Indagare per serie di convergenza
 .
.
 per chiunque
per chiunque  .
.

Perché  , quindi prendiamo come serie di riferimento la serie armonica divergente
, quindi prendiamo come serie di riferimento la serie armonica divergente  . Dal limite del rapporto dei termini comuni
. Dal limite del rapporto dei termini comuni  e
e  è finita e diversa da zero (è uguale a 1), quindi in base al secondo criterio di confronto, questa serie diverge.
è finita e diversa da zero (è uguale a 1), quindi in base al secondo criterio di confronto, questa serie diverge.
Esempio 9 per due motivi di confronto.
per due motivi di confronto.
Questa serie è positiva, perché  , E
, E  . Nella misura in cui
. Nella misura in cui  , allora la serie armonica può essere presa come serie di riferimento
, allora la serie armonica può essere presa come serie di riferimento  . Questa serie diverge e, quindi, secondo il primo segno di confronto, diverge anche la serie in esame.
. Questa serie diverge e, quindi, secondo il primo segno di confronto, diverge anche la serie in esame.
Poiché per la serie data e la serie di riferimento, la condizione  (qui viene utilizzato il 1° limite notevole), quindi in base al secondo criterio di confronto, la serie
(qui viene utilizzato il 1° limite notevole), quindi in base al secondo criterio di confronto, la serie  - diverge.
- diverge.
TEOREMA 5 (prova di D'Alembert)
 c'è un limite finito
c'è un limite finito  , allora la serie converge a
, allora la serie converge a  e diverge a
e diverge a  .
.
Prova. Lascia stare  . Prendiamo qualsiasi numero
. Prendiamo qualsiasi numero  ,
concluso tra
,
concluso tra  e 1:
e 1:  . Dalla condizione
. Dalla condizione
 ne consegue che partendo da un certo numero
ne consegue che partendo da un certo numero  la disuguaglianza
la disuguaglianza
 ;
;
 ;
; (5)
(5)
Considera la serie
Secondo (5), tutti i termini della serie (6) non superano i termini corrispondenti di una progressione geometrica infinita  Nella misura in cui
Nella misura in cui  , questa progressione è convergente. Da qui, in virtù del primo segno di confronto, segue la convergenza delle serie
, questa progressione è convergente. Da qui, in virtù del primo segno di confronto, segue la convergenza delle serie
Succede  considera per te stesso.
considera per te stesso.
Osservazioni :

ne consegue che il resto della serie 
 .
.
Il test d'Alembert è conveniente in pratica quando contiene il termine comune della serie funzione esponenziale o fattoriale.
Esempio 10 Indagare per serie di convergenza  secondo d'Alembert.
secondo d'Alembert.
Questa serie è positiva e
 .
.
(Qui, nel calcolo, la regola L'Hopital viene applicata due volte).

allora questa serie converge per il criterio d'Alembert.
Esempio 11. .
.
Questa serie è positiva e  . Nella misura in cui
. Nella misura in cui
quindi la serie converge.
TEOREMA 6 (test di Cauchy)
Se per una serie di segno positivo
 c'è un limite finito
c'è un limite finito  , poi a
, poi a  la serie converge, e
la serie converge, e  la fila diverge.
la fila diverge.
La dimostrazione è simile al Teorema 5.
Osservazioni :

Esempio 12. Indagare per serie di convergenza  .
.
Questa serie è positiva, perché  per chiunque
per chiunque  . Dal calcolo del limite
. Dal calcolo del limite  causa alcune difficoltà, omettiamo la verifica della fattibilità del criterio necessario per la convergenza delle serie.
causa alcune difficoltà, omettiamo la verifica della fattibilità del criterio necessario per la convergenza delle serie.
allora la serie data diverge secondo il criterio di Cauchy.
TEOREMA 7 (Test integrale per la convergenza di Maclaurin-Cauchy)
Sia data una riga
i cui termini sono positivi e non aumentano:

Lascia andare oltre
 è una funzione definita per tutti i reali
è una funzione definita per tutti i reali  , è continuo, non aumenta e
, è continuo, non aumenta e
- In contatto con 0
- Google+ 0
- ok 0
- Facebook 0

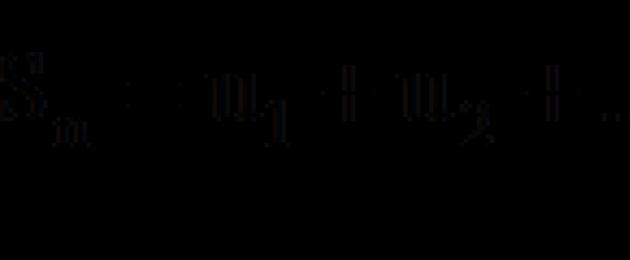
 ;
;
 ;
;
 ;
;