Om funktionen är jämn då. Jämna och udda funktioner

I juli 2020 lanserar NASA en expedition till Mars. Rymdfarkosten kommer att leverera till Mars en elektronisk bärare med namnen på alla registrerade medlemmar i expeditionen.

Om det här inlägget löste ditt problem eller om du bara gillade det, dela länken till det med dina vänner på sociala nätverk.

Ett av dessa kodalternativ måste kopieras och klistras in i koden på din webbsida, helst mellan taggarna Och eller direkt efter taggen . Enligt det första alternativet laddas MathJax snabbare och saktar ner sidan mindre. Men det andra alternativet spårar och laddar automatiskt de senaste versionerna av MathJax. Om du sätter in den första koden måste den uppdateras med jämna mellanrum. Om du klistrar in den andra koden kommer sidorna att laddas långsammare, men du behöver inte ständigt övervaka MathJax-uppdateringar.

Det enklaste sättet att ansluta MathJax är i Blogger eller WordPress: i webbplatsens kontrollpanel, lägg till en widget som är utformad för att infoga JavaScript-kod från tredje part, kopiera den första eller andra versionen av laddningskoden som presenteras ovan i den och placera widgeten närmare. till början av mallen (förresten, detta är inte alls nödvändigt eftersom MathJax-skriptet laddas asynkront). Det är allt. Lär dig nu MathML-, LaTeX- och ASCIIMathML-markeringssyntaxen och du är redo att bädda in matematiska formler på dina webbsidor.

Ännu en nyårsafton... frostväder och snöflingor på fönsterrutan... Allt detta fick mig att skriva igen om... fraktaler, och vad Wolfram Alpha vet om det. Vid detta tillfälle finns det en intressant artikel där det finns exempel på tvådimensionella fraktala strukturer. Här kommer vi att överväga mer komplexa exempel på tredimensionella fraktaler.

En fraktal kan visuellt representeras (beskrivs) som en geometrisk figur eller kropp (vilket betyder att båda är en uppsättning, i detta fall en uppsättning punkter), vars detaljer har samma form som själva originalfiguren. Det vill säga, det är en självliknande struktur, med tanke på vars detaljer, när vi förstoras, kommer vi att se samma form som utan förstoring. Medan i fallet med en vanlig geometrisk figur (inte en fraktal), när vi zoomar in, kommer vi att se detaljer som har en enklare form än själva originalfiguren. Till exempel, vid en tillräckligt hög förstoring, ser en del av en ellips ut som ett rakt linjesegment. Detta händer inte med fraktaler: med någon ökning av dem kommer vi igen att se samma komplexa form, som med varje ökning kommer att upprepas om och om igen.

Benoit Mandelbrot, grundaren av vetenskapen om fraktaler, skrev i sin artikel Fractals and Art for Science: "Fractals är geometriska former som är lika komplexa i sina detaljer som de är i sin övergripande form. Det vill säga om en del av fraktal kommer förstoras till storleken på helheten, kommer det att se ut som helheten, eller exakt, eller kanske med en liten deformation.

. För att göra detta, använd millimeterpapper eller en grafisk miniräknare. Välj valfritt antal numeriska värden för den oberoende variabeln x (\displaystyle x) och koppla in dem i funktionen för att beräkna värdena för den beroende variabeln y (\displaystyle y). Sätt de hittade koordinaterna för punkterna på koordinatplanet och koppla sedan ihop dessa punkter för att bygga en graf över funktionen.

• Ersätt positiva numeriska värden i funktionen x (\displaystyle x) och motsvarande negativa numeriska värden. Till exempel givet en funktion f (x) = 2 x 2 + 1 (\displaystyle f(x)=2x^(2)+1). Ersätt följande värden i den x (\displaystyle x):

Kontrollera om grafen för funktionen är symmetrisk kring y-axeln. Symmetri avser spegelbilden av grafen kring y-axeln. Om delen av grafen till höger om y-axeln (positiva värden för den oberoende variabeln) matchar delen av grafen till vänster om y-axeln (negativa värden för den oberoende variabeln), grafen är symmetrisk kring y-axeln Om funktionen är symmetrisk kring y-axeln är funktionen jämn.

Kontrollera om grafen för funktionen är symmetrisk om ursprunget. Ursprunget är punkten med koordinater (0,0). Symmetri om ursprunget innebär att ett positivt värde y (\displaystyle y)(med ett positivt värde x (\displaystyle x)) motsvarar ett negativt värde y (\displaystyle y)(med ett negativt värde x (\displaystyle x)), och vice versa. Udda funktioner har symmetri med avseende på ursprunget.

Kontrollera om grafen för funktionen har någon symmetri. Den sista typen av funktion är en funktion vars graf inte har symmetri, det vill säga det finns ingen spegelbild både i förhållande till y-axeln och i förhållande till origo. Till exempel givet en funktion.

• Ersätt flera positiva och motsvarande negativa värden i funktionen x (\displaystyle x):
• Enligt de erhållna resultaten finns det ingen symmetri. Värderingar y (\displaystyle y) för motsatta värden x (\displaystyle x) stämmer inte överens och är inte motsatta. Funktionen är alltså varken jämn eller udda.
• Observera att funktionen f (x) = x 2 + 2 x + 1 (\displaystyle f(x)=x^(2)+2x+1) kan skrivas så här: f (x) = (x + 1) 2 (\displaystyle f(x)=(x+1)^(2)). Skrivet i denna form verkar funktionen vara jämn eftersom det finns en jämn exponent. Men det här exemplet bevisar att formen på en funktion inte kan bestämmas snabbt om den oberoende variabeln är omgiven av parentes. I det här fallet måste du öppna parenteserna och analysera de resulterande exponenterna.

Fungeraär ett av de viktigaste matematiska begreppen. Funktion - variabelberoende på från en variabel x, om varje värde X matchar ett enskilt värde på. variabel X kallas den oberoende variabeln eller argumentet. variabel på kallas den beroende variabeln. Alla värden för den oberoende variabeln (variabel x) utgör funktionens domän. Alla värden som den beroende variabeln tar (variabel y), bildar intervallet för funktionen.

Funktionsdiagram de kallar uppsättningen av alla punkter i koordinatplanet, vars abskiss är lika med värdena för argumentet, och ordinaterna är lika med motsvarande värden för funktionen, det vill säga värdena på variabeln plottas längs abskissan x, och variabelns värden plottas längs y-axeln y. För att plotta en funktion behöver du känna till funktionernas egenskaper. Funktionens huvudsakliga egenskaper kommer att diskuteras nedan!

För att rita en funktionsgraf rekommenderar vi att du använder vårt program - Graphing Functions Online. Om du har några frågor när du studerar materialet på denna sida kan du alltid ställa dem på vårt forum. Även på forumet får du hjälp att lösa problem inom matematik, kemi, geometri, sannolikhetsteori och många andra ämnen!

Grundläggande egenskaper hos funktioner.

1) Funktionsomfång och funktionsomfång.

Omfattningen av en funktion är uppsättningen av alla giltiga giltiga värden för argumentet x(variabel x) för vilken funktionen y = f(x) definierat.
Omfånget för en funktion är mängden av alla reella värden y som funktionen accepterar.

I elementär matematik studeras funktioner endast på uppsättningen av reella tal.

2) Funktionsnollor.

Värderingar X, vid vilken y=0, kallas funktion nollor. Dessa är abskissorna för skärningspunkterna för grafen för funktionen med x-axeln.

3) Intervaller för teckenkonstans för en funktion.

Intervallet för teckenkonstans för en funktion är sådana värdeintervall x, där funktionens värden y antingen bara positiva eller bara negativa kallas intervaller för teckenkonstans för funktionen.

4) Monotonicitet hos funktionen.

Ökande funktion (i något intervall) - en funktion där ett större värde på argumentet från detta intervall motsvarar ett större värde på funktionen.

Minskande funktion (i något intervall) - en funktion där ett större värde på argumentet från detta intervall motsvarar ett mindre värde på funktionen.

5) Jämna (udda) funktioner.

En jämn funktion är en funktion vars definitionsdomän är symmetrisk med avseende på ursprunget och för eventuella X f(-x) = f(x). Grafen för en jämn funktion är symmetrisk kring y-axeln.

En udda funktion är en funktion vars definitionsdomän är symmetrisk med avseende på ursprunget och för alla X från definitionsdomänen jämlikheten f(-x) = - f(x). Grafen för en udda funktion är symmetrisk om ursprunget.

Jämn funktion
1) Definitionsdomänen är symmetrisk med avseende på punkten (0; 0), det vill säga om punkten a hör till definitionsdomänen, då punkten -a hör också till definitionsdomänen.
2) För vilket värde som helst x f(-x)=f(x)
3) Grafen för en jämn funktion är symmetrisk kring Oy-axeln.

udda funktion har följande egenskaper:
1) Definitionsdomänen är symmetrisk med avseende på punkten (0; 0).
2) för vilket värde som helst x, som hör till definitionsdomänen, jämlikheten f(-x)=-f(x)
3) Grafen för en udda funktion är symmetrisk med avseende på origo (0; 0).

Alla funktioner är inte jämna eller udda. Funktioner allmän synär varken jämna eller udda.

6) Begränsade och obegränsade funktioner.

En funktion kallas bounded om det finns ett positivt tal M så att |f(x)| ≤ M för alla värden på x . Om det inte finns något sådant nummer är funktionen obegränsad.

7) Funktionens periodicitet.

En funktion f(x) är periodisk om det finns ett icke-nolltal T så att för valfritt x från funktionens domän, f(x+T) = f(x). Detta minsta tal kallas perioden för funktionen. Alla trigonometriska funktioner är periodiska. (Trigonometriska formler).

Fungera f kallas periodisk om det finns ett tal så att för någon x från definitionsdomänen jämlikheten f(x)=f(x-T)=f(x+T). Tär funktionens period.

Varje periodisk funktion har ett oändligt antal perioder. I praktiken brukar man räkna med den minsta positiva perioden.

Värdena för den periodiska funktionen upprepas efter ett intervall lika med perioden. Detta används när du ritar grafer.

Jämna och udda funktioner är en av dess huvudegenskaper, och paritet upptar en imponerande del av skolkursen i matematik. Det bestämmer till stor del arten av funktionens beteende och underlättar avsevärt konstruktionen av motsvarande graf.

Låt oss definiera funktionens paritet. Generellt sett anses funktionen som studeras även om för motsatta värden av den oberoende variabeln (x) som finns i dess definitionsdomän, motsvarande värden för y (funktion) är lika.

Låt oss ge en mer rigorös definition. Tänk på någon funktion f (x), som är definierad i domänen D. Det kommer att vara även om för någon punkt x som finns i definitionsdomänen:

• -x (motsatt punkt) ligger också i det givna omfånget,

• f(-x) = f(x).

Av definitionen ovan följer det villkor som krävs för definitionsdomänen för en sådan funktion, nämligen symmetri med avseende på punkten O, som är ursprunget till koordinaterna, eftersom om någon punkt b finns i definitionsdomänen för en jämn funktion, då ligger motsvarande punkt - b också i denna domän. Av det föregående följer därför slutsatsen: en jämn funktion har en form som är symmetrisk med avseende på ordinataaxeln (Oy).

Hur bestämmer man en funktions paritet i praktiken?

Låt det ges med formeln h(x)=11^x+11^(-x). Efter algoritmen som följer direkt av definitionen studerar vi först och främst dess definitionsdomän. Uppenbarligen är det definierat för alla värden i argumentet, det vill säga det första villkoret är uppfyllt.

Nästa steg är att ersätta argumentet (x) med dess motsatta värde (-x).
Vi får:
h(-x) = 11^(-x) + 11^x.
Eftersom addition uppfyller den kommutativa (förskjutnings) lagen är det uppenbart att h(-x) = h(x) och det givna funktionella beroendet är jämnt.

Låt oss kontrollera jämnheten för funktionen h(x)=11^x-11^(-x). Efter samma algoritm får vi h(-x) = 11^(-x) -11^x. Att ta ut minus, som ett resultat, har vi
h(-x)=-(11^x-11^(-x))=- h(x). Därför är h(x) udda.

Det bör förresten påminnas om att det finns funktioner som inte kan klassificeras enligt dessa kriterier, de kallas varken jämna eller udda.

Även funktioner har ett antal intressanta egenskaper:

• som ett resultat av tillägget av liknande funktioner erhålls en jämn;
• som ett resultat av att subtrahera sådana funktioner erhålls en jämn;
• jämn, även jämn;
• som ett resultat av att multiplicera två sådana funktioner erhålls en jämn;
• som ett resultat av multiplikation av udda och jämna funktioner erhålls en udda;
• som ett resultat av att dela de udda och jämna funktionerna erhålls en udda;
• derivatan av en sådan funktion är udda;
• Om vi ​​kvadrerar en udda funktion får vi en jämn.

En funktions paritet kan användas för att lösa ekvationer.

För att lösa en ekvation som g(x) = 0, där den vänstra sidan av ekvationen är en jämn funktion, räcker det med att hitta dess lösningar för variabelns icke-negativa värden. De erhållna rötterna av ekvationen måste kombineras med motsatta tal. En av dem är föremål för verifiering.

Detsamma används framgångsrikt för att lösa icke-standardiserade problem med en parameter.

Till exempel, finns det något värde för parametern a som skulle få ekvationen 2x^6-x^4-ax^2=1 att ha tre rötter?

Om vi ​​tar med i beräkningen att variabeln kommer in i ekvationen i jämna potenser, så är det tydligt att byte av x med -x inte kommer att ändra den givna ekvationen. Det följer att om ett visst tal är dess rot, så är det motsatta talet också. Slutsatsen är uppenbar: rötterna till ekvationen, andra än noll, ingår i uppsättningen av dess lösningar i "par".

Det är tydligt att talet 0 i sig inte är det, det vill säga antalet rötter i en sådan ekvation kan bara vara jämnt och naturligtvis kan det inte ha tre rötter för något värde på parametern.

Men antalet rötter i ekvationen 2^x+ 2^(-x)=ax^4+2x^2+2 kan vara udda, och för valfritt värde på parametern. Det är faktiskt lätt att kontrollera att uppsättningen av rötter i en given ekvation innehåller lösningar i "par". Låt oss kontrollera om 0 är en rot. När vi sätter in det i ekvationen får vi 2=2. Således, förutom "parad" är 0 också en rot, vilket bevisar deras udda tal.

Gömma visa

Sätt att ställa in en funktion

Låt funktionen ges av formeln: y=2x^(2)-3 . Genom att tilldela valfritt värde till den oberoende variabeln x kan du använda den här formeln för att beräkna motsvarande värden för den beroende variabeln y . Till exempel, om x=-0,5 , då vi använder formeln, får vi att motsvarande värde för y är y=2 \cdot (-0,5)^(2)-3=-2,5 .

Givet vilket värde som helst som tas av x-argumentet i formeln y=2x^(2)-3 , kan endast ett funktionsvärde beräknas som motsvarar det. Funktionen kan representeras som en tabell:

x	−2	−1	0	1	2	3
y	−4	−3	−2	−1	0	1

Med den här tabellen kan du räkna ut att för värdet av argumentet -1 kommer värdet för funktionen -3 att motsvara; och värdet x=2 kommer att motsvara y=0, och så vidare. Det är också viktigt att veta att varje argumentvärde i tabellen endast motsvarar ett funktionsvärde.

Fler funktioner kan ställas in med hjälp av grafer. Med hjälp av grafen fastställs vilket värde på funktionen som korrelerar med ett visst värde på x. Oftast kommer detta att vara ett ungefärligt värde för funktionen.

Jämn och udda funktion

Funktionen är jämn funktion, när f(-x)=f(x) för valfritt x från domänen. En sådan funktion kommer att vara symmetrisk kring Oy-axeln.

Funktionen är udda funktion när f(-x)=-f(x) för valfritt x i domänen. En sådan funktion kommer att vara symmetrisk kring origo O (0;0) .

Funktionen är inte ens, inte heller udda och ringde allmän funktion när den inte har symmetri kring axeln eller ursprunget.

Vi undersöker följande funktion för paritet:

f(x)=3x^(3)-7x^(7)

D(f)=(-\infty ; +\infty) med en symmetrisk definitionsdomän om ursprunget. f(-x)= 3 \cdot (-x)^(3)-7 \cdot (-x)^(7)= -3x^(3)+7x^(7)= -(3x^(3)-7x^(7))= -f(x).

Därför är funktionen f(x)=3x^(3)-7x^(7) udda.

Periodisk funktion

Funktionen y=f(x) , i vars domän f(x+T)=f(x-T)=f(x) är sann för alla x, kallas periodisk funktion med period T \neq 0 .

Upprepning av grafen för funktionen på valfritt segment av abskissaxeln, som har längden T .

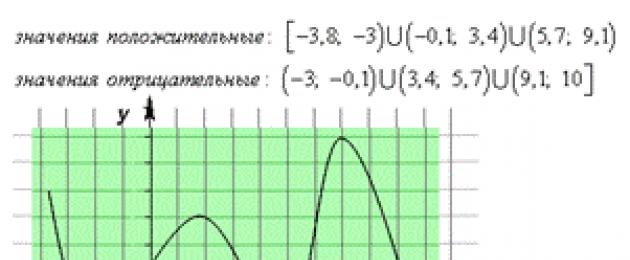
Intervaller där funktionen är positiv, det vill säga f (x) > 0 - segment av abskissaxeln, som motsvarar de punkter i grafen för funktionen som ligger ovanför abskissaxeln.

f(x) > 0 på (x_(1); x_(2)) \cup (x_(3); +\infty)

Luckor där funktionen är negativ, dvs f(x)< 0 - отрезки оси абсцисс, которые отвечают точкам графика функции, лежащих ниже оси абсцисс.

f(x)< 0 на (-\infty; x_(1)) \cup (x_(2); x_(3))

Funktionsbegränsning

avgränsad underifrån det är vanligt att anropa en funktion y=f(x), x \in X när det finns ett tal A för vilket olikheten f(x) \geq A gäller för alla x \in X .

Ett exempel på en funktion som avgränsas nedan: y=\sqrt(1+x^(2)) eftersom y=\sqrt(1+x^(2)) \geq 1 för alla x .

avgränsad från ovan en funktion y=f(x), x \in X anropas om det finns ett tal B för vilket olikheten f(x) \neq B gäller för alla x \in X .

Ett exempel på en funktion som avgränsas nedan: y=\sqrt(1-x^(2)), x \in [-1;1] eftersom y=\sqrt(1+x^(2)) \neq 1 för valfritt x \i [-1;1] .

Begränsad det är vanligt att anropa en funktion y=f(x), x \i X när det finns ett tal K > 0 för vilket olikheten \left | f(x) \höger | \neq K för valfritt x \i X .

Exempel på en begränsad funktion: y=\sin x är avgränsad på hela tallinjen eftersom \vänster | \sin x \right | \neq 1.

Ökande och minskande funktion

Det är vanligt att tala om en funktion som ökar på det aktuella intervallet som ökande funktion när ett större värde på x kommer att motsvara ett större värde på funktionen y=f(x) . Härifrån visar det sig att om man tar från det betraktade intervallet två godtyckliga värden av argumentet x_(1) och x_(2) och x_(1) > x_(2) blir det y(x_(1)) > y(x_(2)) .

En funktion som minskar på det aktuella intervallet kallas minskande funktion när ett större värde på x kommer att motsvara ett mindre värde på funktionen y(x) . Härifrån visar det sig att om man tar från det betraktade intervallet två godtyckliga värden av argumentet x_(1) och x_(2) och x_(1) > x_(2) blir det y(x_(1))< y(x_{2}) .

Funktionsrötter det är vanligt att namnge de punkter där funktionen F=y(x) skär abskissaxeln (de erhålls som ett resultat av att lösa ekvationen y(x)=0 ).

a) Om en jämn funktion ökar för x > 0, så minskar den för x< 0

b) När en jämn funktion minskar för x > 0, så ökar den för x< 0

c) När en udda funktion ökar för x > 0, så ökar den också för x< 0

d) När en udda funktion minskar för x > 0, kommer den också att minska för x< 0

Funktion extremer

Funktionsminimumspunkt y=f(x) är det vanligt att kalla en sådan punkt x=x_(0) , där dess grannskap kommer att ha andra punkter (förutom punkten x=x_(0) ), och sedan olikheten f(x) > f (x_(0)) . y_(min) - beteckning för funktionen vid punkten min.

Funktions maxpunkt y=f(x) är det vanligt att kalla en sådan punkt x=x_(0) , där dess grannskap kommer att ha andra punkter (förutom punkten x=x_(0) ), och sedan olikheten f(x) kommer att vara nöjd för dem< f(x^{0}) . y_{max} - обозначение функции в точке max.

Nödvändigt skick

Enligt Fermats sats: f"(x)=0, så kommer då funktionen f(x) , som är differentierbar vid punkten x_(0) , ett extremum att dyka upp vid denna punkt.

Tillräckligt skick

1. När tecknet på derivatan ändras från plus till minus kommer x_(0) att vara minimipunkten;
2. x_(0) - kommer att vara en maxpunkt endast när derivatan ändrar tecken från minus till plus när den passerar genom den stationära punkten x_(0) .

Funktionens största och minsta värde på intervallet

Beräkningssteg:

1. Letar efter derivatan f"(x) ;
2. Stationära och kritiska punkter för funktionen hittas och de som hör till intervallet väljs;
3. Värdena för funktionen f(x) finns vid de stationära och kritiska punkterna och ändarna av segmentet. Det minsta av resultaten kommer att vara det minsta värdet på funktionen, och mer - störst.