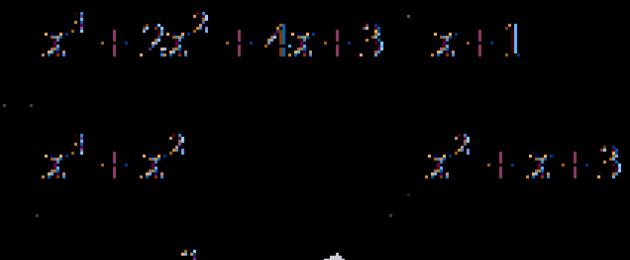Solution of the 5th degree equation in radicals. Solving equations of higher degrees

On the youtube channel of our site, to keep abreast of all the new video lessons.

To begin with, let's recall the basic formulas of degrees and their properties.

Product of number a happens to itself n times, we can write this expression as a a ... a = a n

1.a 0 = 1 (a ≠ 0)

3.a n a m = a n + m

4. (a n) m = a nm

5.a n b n = (ab) n

7.a n / a m = a n - m

Power or exponential equations - these are equations in which the variables are in powers (or exponents), and the base is a number.

Examples of exponential equations:

In this example, the number 6 is the base, it always stands at the bottom, and the variable x degree or indicator.

Here are some more examples of exponential equations.
2 x * 5 = 10
16 x - 4 x - 6 = 0

Now let's look at how the exponential equations are solved?

Let's take a simple equation:

2 x = 2 3

Such an example can be solved even in the mind. It is seen that x = 3. After all, in order for the left and right sides to be equal, you need to put the number 3 instead of x.
Now let's see how this solution needs to be formalized:

2 x = 2 3
x = 3

In order to solve such an equation, we removed identical grounds(that is, two's) and wrote down what was left, these are degrees. We got the desired answer.

Now let's summarize our decision.

Algorithm for solving the exponential equation:
1. Need to check the same whether the equation has bases on the right and left. If the grounds are not the same, we are looking for options to solve this example.
2. After the bases are the same, equate degree and solve the resulting new equation.

Now let's solve a few examples:

Let's start simple.

The bases on the left and right sides are equal to the number 2, which means we can discard the base and equate their degrees.

x + 2 = 4 This is the simplest equation.
x = 4 - 2
x = 2
Answer: x = 2

In the following example, you can see that the bases are different, they are 3 and 9.

3 3x - 9x + 8 = 0

To begin with, we transfer the nine to the right side, we get:

Now you need to make the same bases. We know that 9 = 3 2. Let's use the formula of degrees (a n) m = a nm.

3 3x = (3 2) x + 8

We get 9 x + 8 = (3 2) x + 8 = 3 2x + 16

3 3x = 3 2x + 16 now you can see that the bases on the left and right sides are the same and equal to the three, so we can discard them and equate the degrees.

3x = 2x + 16 got the simplest equation
3x - 2x = 16
x = 16
Answer: x = 16.

See the following example:

2 2x + 4 - 10 4 x = 2 4

First of all, we look at the bases, bases are different two and four. And we need them to be the same. Convert the four by the formula (a n) m = a nm.

4 x = (2 2) x = 2 2x

And we also use one formula a n a m = a n + m:

2 2x + 4 = 2 2x 2 4

Add to the equation:

2 2x 2 4 - 10 2 2x = 24

We have brought the example to the same grounds. But we are hindered by other numbers 10 and 24. What to do with them? If you look closely, you can see that on the left side we repeat 2 2x, here is the answer - 2 2x we can take out of the brackets:

2 2x (2 4 - 10) = 24

Let's calculate the expression in brackets:

2 4 — 10 = 16 — 10 = 6

Divide the whole equation by 6:

Let's imagine 4 = 2 2:

2 2x = 2 2 bases are the same, discard them and equate the powers.
2x = 2 we get the simplest equation. We divide it by 2 we get
x = 1
Answer: x = 1.

Let's solve the equation:

9 x - 12 * 3 x + 27 = 0

Let's transform:
9 x = (3 2) x = 3 2x

We get the equation:
3 2x - 12 3x +27 = 0

Our bases are the same equal to 3. In this example, you can see that the first three has a degree twice (2x) than the second (just x). In this case, you can solve replacement method... Replace the number with the smallest degree:

Then 3 2x = (3x) 2 = t 2

Replace all powers with x in the equation with t:

t 2 - 12t + 27 = 0
We get a quadratic equation. We solve through the discriminant, we get:
D = 144-108 = 36
t 1 = 9
t 2 = 3

Returning to the variable x.

We take t 1:
t 1 = 9 = 3 x

That is,

3 x = 9
3 x = 3 2
x 1 = 2

Found one root. We are looking for the second, from t 2:
t 2 = 3 = 3 x
3 x = 3 1
x 2 = 1
Answer: x 1 = 2; x 2 = 1.

On the site you can ask questions of interest in the HELP TO SOLVE section, we will definitely answer you.

Join the group

In general, an equation with a degree higher than 4 cannot be solved in radicals. But sometimes we can still find the roots of the polynomial on the left in the equation of the highest degree, if we represent it as a product of polynomials in degree at most 4. The solution to such equations is based on factoring a polynomial into factors, so we advise you to repeat this topic before studying this article.

Most often, one has to deal with equations of higher degrees with integer coefficients. In these cases, we can try to find rational roots, and then factor the polynomial in order to then transform it into an equation of a lower degree, which will be easy to solve. Within the framework of this material, we will consider just such examples.

Equations of the highest degree with integer coefficients

All equations of the form a n x n + a n - 1 x n - 1 +. ... ... + a 1 x + a 0 = 0, we can reduce to an equation of the same degree by multiplying both sides by a n n - 1 and changing a variable of the form y = a n x:

a n x n + a n - 1 x n - 1 +. ... ... + a 1 x + a 0 = 0 ann xn + an - 1 ann - 1 xn - 1 +… + a 1 (an) n - 1 x + a 0 (an) n - 1 = 0 y = anx ⇒ yn + bn - 1 yn - 1 +… + b 1 y + b 0 = 0

The resulting coefficients will also be whole. Thus, we will need to solve the reduced equation of the n-th degree with integer coefficients, which has the form x n + a n x n - 1 +… + a 1 x + a 0 = 0.

We calculate the whole roots of the equation. If the equation has integer roots, you need to look for them among the divisors of the free term a 0. Let us write them down and substitute them into the original equality in turn, checking the result. Once we have obtained an identity and found one of the roots of the equation, we can write it in the form x - x 1 · P n - 1 (x) = 0. Here x 1 is the root of the equation, and P n - 1 (x) is the quotient of dividing x n + a n x n - 1 +… + a 1 x + a 0 by x - x 1.

Substitute the rest of the divisors written out in P n - 1 (x) = 0, starting with x 1, since the roots can be repeated. After obtaining the identity, the root x 2 is considered found, and the equation can be written as (x - x 1) (x - x 2) P n - 2 (x) = 0. Here P n - 2 (x) will be the quotient of dividing P n - 1 (x) by x - x 2.

We continue to iterate over the divisors. Find all whole roots and denote their number as m. After that, the original equation can be represented as x - x 1 x - x 2 · ... · x - x m · P n - m (x) = 0. Here P n - m (x) is a polynomial of degree n - m. It is convenient to use Horner's scheme for counting.

If our original equation has integer coefficients, we cannot end up with fractional roots.

As a result, we got the equation P n - m (x) = 0, the roots of which can be found in any convenient way. They can be irrational or complex.

Let's show on specific example how such a solution scheme is applied.

Example 1

Condition: find the solution to the equation x 4 + x 3 + 2 x 2 - x - 3 = 0.

Solution

Let's start by finding whole roots.

We have a free term equal to minus three. It has divisors of 1, - 1, 3, and - 3. Let's substitute them in the original equation and see which of them will result in identities.

With x equal to one, we get 1 4 + 1 3 + 2 · 1 2 - 1 - 3 = 0, which means that one will be the root of this equation.

Now we perform division of the polynomial x 4 + x 3 + 2 x 2 - x - 3 by (x - 1) in a column:

Hence, x 4 + x 3 + 2 x 2 - x - 3 = x - 1 x 3 + 2 x 2 + 4 x + 3.

1 3 + 2 1 2 + 4 1 + 3 = 10 ≠ 0 (- 1) 3 + 2 (- 1) 2 + 4 - 1 + 3 = 0

We have obtained an identity, which means that we have found another root of the equation, equal to - 1.

Divide the polynomial x 3 + 2 x 2 + 4 x + 3 by (x + 1) in a column:

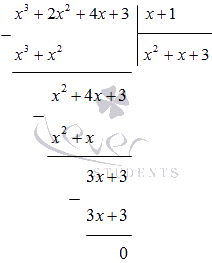
We get that

x 4 + x 3 + 2 x 2 - x - 3 = (x - 1) (x 3 + 2 x 2 + 4 x + 3) = = (x - 1) (x + 1) (x 2 + x + 3)

Substitute the next divisor into the equality x 2 + x + 3 = 0, starting with - 1:

1 2 + (- 1) + 3 = 3 ≠ 0 3 2 + 3 + 3 = 15 ≠ 0 (- 3) 2 + (- 3) + 3 = 9 ≠ 0

The resulting equalities will be incorrect, which means that the equation no longer has integral roots.

The remaining roots will be the roots of the expression x 2 + x + 3.

D = 1 2 - 4 1 3 = - 11< 0

It follows from this that this square trinomial has no real roots, but has complex conjugate ones: x = - 1 2 ± i 11 2.

Let us clarify that instead of long division, we can use Horner's scheme. This is done like this: after we have determined the first root of the equation, we fill in the table.

In the table of coefficients, we can immediately see the coefficients of the quotient of the division of polynomials, which means that x 4 + x 3 + 2 x 2 - x - 3 = x - 1 x 3 + 2 x 2 + 4 x + 3.

After finding the next root equal to - 1, we get the following:

Answer: x = - 1, x = 1, x = - 1 2 ± i 11 2.

Example 2

Condition: Solve the equation x 4 - x 3 - 5 x 2 + 12 = 0.

Solution

The free term has divisors 1, - 1, 2, - 2, 3, - 3, 4, - 4, 6, - 6, 12, - 12.

We check them in order:

1 4 - 1 3 - 5 1 2 + 12 = 7 ≠ 0 (- 1) 4 - (- 1) 3 - 5 (- 1) 2 + 12 = 9 ≠ 0 2 4 2 3 - 5 2 2 + 12 = 0

Hence, x = 2 will be the root of the equation. Divide x 4 - x 3 - 5 x 2 + 12 by x - 2 using Horner's scheme:

As a result, we get x - 2 (x 3 + x 2 - 3 x - 6) = 0.

2 3 + 2 2 - 3 2 - 6 = 0

Hence, 2 will again be a root. Divide x 3 + x 2 - 3 x - 6 = 0 by x - 2:

As a result, we get (x - 2) 2 (x 2 + 3 x + 3) = 0.

It makes no sense to check the remaining divisors, since the equality x 2 + 3 x + 3 = 0 is faster and more convenient to solve using the discriminant.

Let's solve the quadratic equation:

x 2 + 3 x + 3 = 0 D = 3 2 - 4 1 3 = - 3< 0

We get a complex conjugate pair of roots: x = - 3 2 ± i 3 2.

Answer: x = - 3 2 ± i 3 2.

Example 3

Condition: find the real roots for the equation x 4 + 1 2 x 3 - 5 2 x - 3 = 0.

Solution

x 4 + 1 2 x 3 - 5 2 x - 3 = 0 2 x 4 + x 3 - 5 x - 6 = 0

We carry out multiplication 2 3 of both sides of the equation:

2 x 4 + x 3 - 5 x - 6 = 0 2 4 x 4 + 2 3 x 3 - 20 2 x - 48 = 0

Replace the variables y = 2 x:

2 4 x 4 + 2 3 x 3 - 20 2 x - 48 = 0 y 4 + y 3 - 20 y - 48 = 0

As a result, we got a standard 4th degree equation, which can be solved according to the standard scheme. Let's check the divisors, divide and get as a result that it has 2 real roots y = - 2, y = 3 and two complex roots. We will not present the complete solution here. Due to the replacement, the real roots of this equation will be x = y 2 = - 2 2 = - 1 and x = y 2 = 3 2.

Answer: x 1 = - 1, x 2 = 3 2

If you notice an error in the text, please select it and press Ctrl + Enter

In the 16th century, mathematicians came across complex numbers almost by accident (see Chapter 11). TO XVIII century complex numbers were considered an extension of the range of real numbers, but working with them still led to a parity error, as in Leonard E's great work on number theory, Arithmetic Investigations (1801), he avoided the use of so-called "imaginary numbers." It seems to me that the most important part of this work is the first proof of the fundamental theorem of algebra. Gauss realized how important this theorem was, creating several additional proofs over the years. In 1849 he revised the first version, this time using complex numbers. Using modern terms, we can say that for any finite polynomial equation with real or complex coefficients, all its roots will be real or complex numbers. Thus, we get a negative answer to the long-standing question of whether solving higher-order polynomial equations requires the creation of higher-order numbers than complex ones.

One of the most thorny problems in algebra of that time was the question of whether the fifth-order polynomial, the quintic, was solvable by algebraic methods, that is, with the help of a finite number of algebraic steps. Now the school is taught the formula for solving quadratic equations, and since the 16th century, similar methods have been known for solving equations of the third and fourth degrees (Chapter 11). But no method was found for the Quintics. It may seem that the fundamental theorem of algebra contains the prospect of an affirmative answer, but in fact it simply guarantees that solutions exist, it does not say anything about the existence of formulas that give exact solutions (by that time there were already approximate numerical and graphical methods). And then there were two mathematical geniuses with a tragic fate.

Niels Henrik Abel (1802–1829) was born into a large poor family living in a small village in Norway, a country devastated by the long years of war with England and Sweden. The teacher, kindly disposed towards the boy, gave him private lessons, but after the death of his father, at the age of eighteen, despite young age and in fragile health, Abel was forced to support his family. In 1824, he published a scientific article in which he stated that the quintic is not solvable by algebraic means, as, indeed, any polynomial of a higher order. Abel believed that this article would serve as his pass to the scientific world, and sent it to Gauss at the University of Göttingen. Unfortunately, Gauss was not going to cut the pages with a knife (in those days any reader had to do this) and did not read the article. In 1826, the Norwegian government finally allocated funds for Abel to travel to Europe. Fearing that personal contact with Gauss would not give him much joy, the mathematician decided not to visit Göttingen and instead went to Berlin. There he became friends with August Leopold Crelle (1780–1855), a mathematician, architect and engineer who advised the Prussian Ministry of Education on mathematics. Krell was about to found the Journal of Clean and applied mathematics". So Abel got the opportunity to spread his work and published a lot, especially in the early issues of the "Journal", which immediately began to be considered a very prestigious and authoritative scientific publication. The Norwegian published there an extended version of his proof that quintic is undecidable by algebraic methods. And then he left for Paris. This trip upset Abel very much, because he practically did not receive the support of the French mathematicians that he needed so much. He became close to Augustin Louis Cauchy (1789-1857), who at that time was the main luminary mathematical analysis, but had a very complex character. As Abel himself put it, "Cauchy is insane, and nothing can be done about it, although at present he is the only one who is capable of anything in mathematics." If we try to find excuses for the manifestations of disrespect and disregard emanating from Gauss and Cauchy, we can say that the quintic has achieved a certain fame and attracted the attention of both respected mathematicians and originals. Abel returned to Norway, where he suffered more and more from tuberculosis. He continued to send his works to Crelle, but died in 1829, not knowing how much his reputation had grown in the scientific world... Two days after his death, Abel received an offer to take a scientific position in Berlin.

Abel showed that any polynomial higher than the fourth order cannot be solved using radicals like square, cubic, or higher roots. However, the explicit conditions under which these polynomials could be solved in special cases and the method for their solution were formulated by Galois. Evariste Galois (1811-1832) lived a short and eventful life. He was an incredibly gifted mathematician. Galois was implacable to those whom he considered less talented than himself, and at the same time he could not tolerate social injustice. He showed no talent for mathematics until he read Legendre's Principles of Geometry (published in 1794, this book was the main textbook for the next hundred years). Then he literally swallowed the rest of the works of Legendre and, later, Abel. His enthusiasm, self-confidence and intolerance led to truly dire consequences in his relationship with teachers and examiners. Galois took part in the competition for admission to the Ecole Polytechnique - the cradle of French mathematics, but due to lack of preparation failed the exam. For some time after meeting a new teacher, who recognized his talent, he managed to keep his temper under control. In March 1829, Galois published his first paper on continued fractions, which he considered his most significant work. He sent a message about his discoveries to the Academy of Sciences, and Cauchy promised to present them, but forgot. Moreover, he simply lost the manuscript.

Galois's second failure when entering the Ecole Polytechnique entered mathematical folklore. He was so used to constantly having complex mathematical ideas in his head that he was infuriated by the petty quibbles of the examiners. Since the examiners had a hard time understanding his explanation, he threw a whiteboard rag in the face of one of them. Soon after, his father died, who committed suicide as a result of church intrigues. At his funeral, a riot almost broke out. In February 1830, Galois wrote the following three articles, sending them to the Academy of Sciences for the Grand Prix in Mathematics. Joseph Fourier, then the secretary of the academy, died without reading them, and after his death, no articles were found among his papers. Such a flood of disappointments would have dumped anyone. Galois rebelled against those in power, because he felt: they did not recognize his merits and ruined his father. He plunged headlong into politics, becoming an ardent republican - not the wisest decision in France in 1830. In a last desperate attempt, he sent a scientific article to the famous French physicist and mathematician Simeon Denis Poisson (1781-1840), who in response demanded additional proof.

This was the last straw. In 1831, Galois was arrested twice - the first time for allegedly calling for the assassination of King Louis Philippe, and then in order to protect him - the authorities feared a republican revolt! This time, he was sentenced to six months in prison on trumped-up charges of illegally wearing the uniform of the disbanded artillery battalion he joined. Released on his word of honor, he took up a job that caused him the same disgust as everything else in life. In letters to his devoted friend Chevalier, one can feel his disappointment. On May 29, 1832, he accepted a challenge to a duel, the reasons for which are not fully understood. “I fell victim to a dishonorable coquette. My life is extinguished in a pitiful quarrel, ”he writes in his Letter to All Republicans. The most famous work Galois was drafted on the night before the fateful duel. Complaints are scattered in the fields: "I have no more time, I have no more time." He was forced to leave to others a detailed presentation of the intermediate steps, which were not essential for understanding the main idea. He needed to splash out on paper the basis of his discoveries - the origins of what is now called Galois's theorem. He ended his will by asking Chevalier "to ask Jacobi and Gauss to publicly express their opinion, not on the correctness, but on the importance of these theorems." Early in the morning Galois went to meet his rival. They had to shoot from a distance of 25 steps. Galois was injured and died in the hospital the next morning. He was only twenty years old.

Galois relied on the work of Lagrange and Cauchy, but he developed a more general method. It was extremely important achievement in the field of solving quintics. The scientist paid less attention to the original equations or graphical interpretation, and thought more about the nature of the roots themselves. To simplify, Galois considered only the so-called irreducible quintics, that is, those that could not be factorized in the form of polynomials of a lower order (as we said, for any polynomial equations up to the fourth order there are formulas for finding their roots). In general, an irreducible polynomial with rational coefficients is a polynomial that cannot be decomposed into simpler polynomials with rational coefficients. For example, (x 5 - 1) can be factorized (x-1) (x 4 + x 3 + x 2 + x + 1), whereas (x 5 - 2) irreducible. Galois's goal was to define conditions under which all solutions of a general irreducible polynomial equation can be found in terms of radicals.

The key to the solution lies in the fact that the roots of any irreducible algebraic equation are not independent, they can be expressed one through the other. These relations were formalized into the group of all possible permutations, the so-called root symmetry group - for a quintic, this group contains 5! = 5 x 4 x 3 x 2 x 1 = 120 elements. The mathematical algorithms of Galois theory are very complex, and, most likely, partly because of this, they were initially understood with great difficulty. But after the level of abstraction made it possible to pass from the algebraic solutions of equations to the algebraic structure of the groups associated with them, Galois was able to predict the solvability of the equation based on the properties of such groups. Moreover, his theory also provided a method by which these roots could be found. As for the quintics, the mathematician Joseph Liouville (1809-1882), who in 1846 published most Galois's works in his "Journal of Pure and Applied Mathematics", noted that the young scientist had proved a "beautiful theorem", and in order "for an irreducible equation of the original degree to be solvable in terms of radicals, it is necessary and sufficient that all its roots are rational functions any two of them. " Since this is impossible for a quintic, it cannot be solved with the help of radicals.

In three years, the mathematical world has lost two of its brightest new stars. Accusations and a reassessment of values ​​followed, and Abel and Galois achieved the recognition they deserved, but only posthumously. In 1829, Karl Jacobi, through Legendre, learned about the "lost" manuscript of Abel, and in 1830 a diplomatic scandal erupted when the Norwegian consul in Paris demanded to find an article by his compatriot. In the end, Cauchy found the article, but only to be lost again at the Academy! In the same year, Abel was awarded the Grand Prix in Mathematics (together with Jacobi) - but he was already dead. His biography was published in 1841. In 1846, Liouville edited some of Galois's manuscripts for publication and, in the introduction, expressed regret that the academy had initially rejected Galois's work because of its complexity - "indeed clarity is needed when the author takes the reader off the beaten path into uncharted wilderness." He continues: “Galois is gone! Let's not indulge in useless criticism. Let's cast aside the disadvantages and look at the merits! " Fruit short life Galois fit only sixty pages. The editor of the mathematical journal for candidates for the Ecole Normal and École Polytechnique commented on the Galois case as follows: “An applicant with high intelligence was screened out by an examiner with a lower level of thinking. Barbarus hic ego sum, quia non intelligor illis. "

First of all, the second page of this work is not burdened with names, surnames, descriptions of the position in society, titles and elegies in honor of some miserly prince, whose wallet will be opened with the help of these incenses - with the threat of closing it when the praises are over. You will not see here respectful praises, written in letters three times larger than the text itself, addressed to those who have a high position in science, to some wise patron - something obligatory (I would say, inevitable) for someone in the age of twenty who wants to write something. I am not telling anyone here that I owe their advice and support to all that is good in my work. I am not saying this because it would be a lie. If I had to mention any of the greats in society or in science (at present, the difference between the two classes of people is almost imperceptible), I swear, it would not be a token of gratitude. I owe them the fact that I published the first of these two articles so late, and that I wrote it all in prison - in a place that can hardly be considered suitable for scientific reflection, and I am often amazed at my restraint and ability to keep my mouth on castle in relation to stupid and vicious zoils. It seems to me that I can use the word "zoiles" without fear of being accused of indecency, since that is what I call my opponents. I am not going to write here about how and why I was sent to prison, but I must say that my manuscripts most often just got lost in the folders of gentlemen of the members of the academy, although, in truth, I cannot imagine such indiscretion on the part people on whose conscience Abel's death. In my opinion, anyone would like to be compared to this brilliant mathematician. Suffice it to say that my paper on the theory of equations was sent to the Academy of Sciences in February 1830, that extracts from it were sent in February 1829, and none of this was published, and even the manuscript was impossible to return.

Galois, unpublished preface, 1832

Class: 9

Basic goals:

1. To consolidate the concept of a whole rational equation of the th degree.
2. Formulate the main methods for solving equations of higher degrees (n > 3).
3. To teach the basic methods of solving equations of higher degrees.
4. To teach by the type of equation to determine the most effective method his decisions.

Forms, methods and pedagogical techniques that are used by the teacher in the lesson:

• Lecture-seminar training system (lectures - explanation of new material, seminars - problem solving).
• Information and communication technologies (frontal survey, oral work with the class).
• Differentiated teaching, group and individual forms.
• Exploratory learning in developmental teaching mathematical apparatus and the thinking abilities of each individual student.
• Printed material - an individual short summary of the lesson (basic concepts, formulas, statements, lecture material is compressed in the form of diagrams or tables).

Lesson plan:

1. Organizing time.
   Stage goal: to include students in learning activities, determine the meaningful framework of the lesson.
2. Updating students' knowledge.
   The purpose of the stage: to update the knowledge of students on previously studied related topics
3. Study of a new topic (lecture). The purpose of the stage: to formulate the main methods for solving equations of higher degrees (n > 3)
4. Summarizing.
   The purpose of the stage: once again highlight the key points in the material studied in the lesson.
5. Homework.
   Stage goal: to formulate homework for students.

Lesson summary

1. Organizational moment.

Formulation of the topic of the lesson: “Equations of the highest degrees. Methods for their solution ”.

2. Actualization of students' knowledge.

Theoretical survey - conversation. Repetition of some previously studied information from the theory. Students formulate basic definitions and formulate necessary theorems. Examples are given to demonstrate the level of knowledge acquired earlier.

• The concept of an equation in one variable.
• The concept of the root of the equation, the solution of the equation.
• Concept linear equation with one variable, the concept of a quadratic equation in one variable.
• The concept of the equivalence of equations, the equation-consequence (the concept of extraneous roots), the transition not by the corollary (the case of loss of roots).
• The concept of a whole rational expression with one variable.
• The concept of a whole rational equation n-th degree. The standard form of the whole rational equation. Reduced whole rational equation.
• The transition to a set of equations of lower degrees by factoring the original equation into factors.
• Polynomial concept n-th degree from x... Bezout's theorem. Consequences from Bezout's theorem. Root theorems ( Z-roots and Q-roots) of an entire rational equation with integer coefficients (reduced and non-reduced, respectively).
• Horner's scheme.

3. Studying a new topic.

We will consider the whole rational equation n-th degree of the standard form with one unknown variable x: P n (x)= 0, where P n (x) = a n x n + a n-1 x n-1 + a 1 x + a 0- polynomial n-th degree from x, a n ≠ 0. If a n = 1 then such an equation is called the reduced whole rational equation n-th degree. Consider such equations for different values n and list the main methods for solving them.

n= 1 - linear equation.

n= 2 - quadratic equation. Discriminant formula. Formula for calculating roots. Vieta's theorem. Selecting a complete square.

n= 3 - cubic equation.

Grouping method.

Example: x 3 - 4x 2 - x+ 4 = 0 (x - 4) (x 2– 1) = 0 x 1 = 4 , x 2 = 1,x 3 = -1.

Reverse cubic equation of the form ax 3 + bx 2 + bx + a= 0. Solve by combining terms with the same coefficients.

Example: x 3 – 5x 2 – 5x + 1 = 0 (x + 1)(x 2 – 6x + 1) = 0 x 1 = -1, x 2 = 3 + 2, x 3 = 3 – 2.

Selection of Z-roots based on the theorem. Horner's scheme. When applying this method, it is necessary to emphasize that the search in this case is finite, and we select the roots according to a certain algorithm in accordance with the theorem on Z-roots of the reduced whole rational equation with integer coefficients.

Example: x 3 – 9x 2 + 23x- 15 = 0. Equation given. Let us write down the divisors of the free term ( + 1; + 3; + 5; + 15). Let's apply Horner's scheme:

	x 3	x 2	x 1	x 0	conclusion
	1	-9	23	-15
1	1	1 x 1 - 9 = -8	1 x (-8) + 23 = 15	1 x 15 - 15 = 0	1 - root
	x 2	x 1	x 0

We get ( x – 1)(x 2 – 8x + 15) = 0 x 1 = 1, x 2 = 3, x 3 = 5.

Equation with integer coefficients. Selection of Q-roots based on the theorem. Horner's scheme. When applying this method, it is necessary to emphasize that the enumeration in this case is finite and we select the roots according to a certain algorithm in accordance with the theorem on Q-roots of an irreducible entire rational equation with integer coefficients.

Example: 9 x 3 + 27x 2 – x- 3 = 0. The equation is not reduced. Let us write down the divisors of the free term ( + 1; + 3). Let us write down the divisors of the coefficient at the highest power of the unknown. ( + 1; + 3; + 9) Therefore, we will look for the roots among the values ​​( + 1; + ; + ; + 3). Let's apply Horner's scheme:

	x 3	x 2	x 1	x 0	conclusion
	9	27	-1	-3
1	9	1 x 9 + 27 = 36	1 x 36 - 1 = 35	1 x 35 - 3 = 32 ≠ 0	1 - not root
-1	9	-1 x 9 + 27 = 18	-1 x 18 - 1 = -19	-1 x (-19) - 3 = 16 ≠ 0	-1 - not root
	9	x 9 + 27 = 30	x 30 - 1 = 9	x 9 - 3 = 0	root
	x 2	x 1	x 0

We get ( x – )(9x 2 + 30x + 9) = 0 x 1 = , x 2 = - , x 3 = -3.

For the convenience of calculation when selecting Q -roots it is convenient to make a change of variable, go to the reduced equation and select Z -roots.

• If the free term is 1

.

• If you can use a substitution of the form y = kx

.

Formula Cardano. There is a universal method for solving cubic equations - this is the Cardano formula. This formula is associated with the names of the Italian mathematicians Gerolamo Cardano (1501-1576), Nicolo Tartaglia (1500-1557), Scipione del Ferro (1465-1526). This formula is outside the scope of our course.

n= 4 - equation of the fourth degree.

Grouping method.

Example: x 4 + 2x 3 + 5x 2 + 4x – 12 = 0 (x 4 + 2x 3) + (5x 2 + 10x) – (6x + 12) = 0 (x + 2)(x 3 + 5x - 6) = 0 (x + 2)(x– 1)(x 2 + x + 6) = 0 x 1 = -2, x 2 = 1.

Variable replacement method.

• Biquadratic equation of the form ax 4 + bx 2 + s = 0 .

Example: x 4 + 5x 2 - 36 = 0. Substitution y = x 2. From here y 1 = 4, y 2 = -9. So x 1,2 = + 2 .

• Reverse equation of the fourth degree of the form ax 4 + bx 3 + c x 2 + bx + a = 0.

We solve, combining terms with the same coefficients, by replacing the form

• ax 4 + bx 3 + cx 2 – bx + a = 0.

• Generalized fourth-degree return equation of the form ax 4 + bx 3 + cx 2 + kbx + k 2 a = 0.

• Replacement of the general view. Some standard replacements.

Example 3 . Replacing the general view(follows from the form of a specific equation).

n = 3.

Equation with integer coefficients. Fitting Q-roots n = 3.

General formula. There is a universal method for solving equations of the fourth degree. This formula is associated with the name of Ludovico Ferrari (1522-1565). This formula is outside the scope of our course.

n > 5 - equations of the fifth and higher degrees.

Equation with integer coefficients. Selection of Z-roots based on the theorem. Horner's scheme. The algorithm is similar to that considered above for n = 3.

Equation with integer coefficients. Fitting Q-roots based on the theorem. Horner's scheme. The algorithm is similar to that considered above for n = 3.

Symmetric equations. Any return equation of odd degree has a root x= -1 and after factoring it into factors, we obtain that one factor has the form ( x+ 1), and the second factor is the return equation of an even degree (its degree is one less than the degree of the original equation). Any return equation of even degree together with a root of the form x = φ contains the root of the species. Using these statements, we solve the problem by lowering the degree of the equation under study.

Variable replacement method. Using uniformity.

There is no general formula for solving entire equations of the fifth degree (this was shown by the Italian mathematician Paolo Ruffini (1765-1822) and the Norwegian mathematician Niels Henrik Abel (1802-1829)) and higher degrees (this was shown by the French mathematician Evariste Galois (1811-1832) )).

• Let us recall again that in practice it is possible to use combinations methods listed above. It is convenient to go over to a set of equations of lower degrees by factorization of the original equation.
• Widely used in practice remained outside the scope of our today's discussion. graphic methods solving equations and approximate solution methods equations of higher degrees.
• There are situations when the equation has no R-roots.
Then the solution is reduced to showing that the equation has no roots. To prove this, we analyze the behavior of the functions under consideration on intervals of monotonicity. Example: Equation x 8 – x 3 + 1 = 0 has no roots.
• Using the monotonicity property of functions
... There are situations when the use of various properties of functions makes it possible to simplify the task at hand.
Example 1: equation x 5 + 3x- 4 = 0 has one root x= 1. By the property of monotonicity of the analyzed functions, there are no other roots.
Example 2: Equation x 4 + (x- 1) 4 = 97 has roots x 1 = -2 and x 2 = 3. Having analyzed the behavior of the corresponding functions on intervals of monotonicity, we conclude that there are no other roots.

4. Summing up.

Summary: Now we have mastered the basic methods of solving various equations of higher degrees (for n > 3). Our task is to learn how to effectively use the algorithms listed above. Depending on the type of equation, we will have to learn to determine which solution method in this case is the most effective, as well as to correctly apply the chosen method.

5. Homework.

: p. 7, pp. 164-174, No. 33-36, 39-44, 46.47.

: №№ 9.1–9.4, 9.6–9.8, 9.12, 9.14–9.16, 9.24–9.27.

Possible topics of reports or abstracts on this topic:

• Formula Cardano
• Graphical method for solving equations. Solution examples.
• Methods for the approximate solution of equations.

Analysis of the assimilation of the material and the interest of students in the topic:

Experience shows that students are primarily interested in the possibility of recruiting Z-roots and Q-roots of equations using a fairly simple algorithm using Horner's scheme. Students are also interested in various standard types of variable substitutions that can greatly simplify the problem. Graphical solution methods are usually of particular interest. In this case, you can additionally disassemble the tasks into a graphical method for solving equations; discuss the general view of the graph for a polynomial of 3, 4, 5 degrees; analyze how the number of roots of equations of 3, 4, 5 degrees is related to the type of the corresponding graph. Below is a list of books in which you can find additional information on this topic.

Bibliography:

1. Vilenkin N. Ya. et al. “Algebra. A textbook for 9th grade students with in-depth study of mathematics ”- M., Education, 2007 - 367 p.
2. Vilenkin N.Ya., Shibasov L.P., Shibasova Z.F.“Behind the pages of a mathematics textbook. Arithmetic. Algebra. Grade 10-11 ”- M., Education, 2008 - 192 p.
3. Vygodsky M. Ya."Handbook of Mathematics" - M., AST, 2010 - 1055 p.
4. Galitsky M.L.“Collection of problems in algebra. Tutorial for grades 8-9 with in-depth study of mathematics ”- M., Education, 2008 - 301 p.
5. Zvavich L.I. et al. “Algebra and the beginning of analysis. 8-11 cl. A manual for schools and classes with in-depth study of mathematics ”- M., Bustard, 1999 - 352 p.
6. Zvavich L.I., Averyanov D.I., Pigarev B.P., Trushanina T.N."Tasks in mathematics to prepare for the written exam in grade 9" - M., Education, 2007 - 112 p.
7. Ivanov A.A., Ivanov A.P.“Thematic tests for the systematization of knowledge in mathematics” part 1 - M., Fizmatkniga, 2006 - 176 p.
8. Ivanov A.A., Ivanov A.P.“Thematic tests for the systematization of knowledge in mathematics” part 2 - M., Fizmatkniga, 2006 - 176 p.
9. Ivanov A.P.“Tests and test papers mathematics. Tutorial". - M., Fizmatkniga, 2008 - 304 p.
10. Leibson K.L.“Collection of practical exercises in mathematics. Part 2-9 grade "- M., MCNMO, 2009 - 184 p.
11. Makarychev Yu.N., Mindyuk N.G."Algebra. Additional chapters to school textbook Grade 9. A textbook for students in schools and classes with advanced study of mathematics. " - M., Education, 2006 - 224 p.
12. Mordkovich A.G."Algebra. Advanced Study. 8th grade. Textbook "- M., Mnemosina, 2006 - 296 p.
13. A.P. Savin “encyclopedic Dictionary young mathematician "- M., Pedagogy, 1985 - 352 p.
14. Survillo G.S., Simonov A.S. “Didactic materials in algebra for grade 9 with in-depth study of mathematics ”- M., Education, 2006 - 95 p.
15. Chulkov P.V.“Equations and inequalities in the school mathematician course. Lectures 1–4 ”- M., September 1, 2006 - 88 p.
16. Chulkov P.V.“Equations and inequalities in the school mathematician course. Lectures 5–8 ”- M., September 1, 2009 - 84 p.

Consider solutions of equations with one variable of degree higher than the second.

The degree of the equation P (x) = 0 is the degree of the polynomial P (x), i.e. the largest of the degrees of its terms with a coefficient not equal to zero.

So, for example, the equation (x 3 - 1) 2 + x 5 = x 6 - 2 has the fifth degree, since after the operations of opening brackets and bringing similar ones, we get the equivalent equation x 5 - 2x 3 + 3 = 0 of the fifth degree.

Let us recall the rules that will be needed to solve equations of degree higher than two.

Statements about the roots of a polynomial and its divisors:

1. Polynomial nth degree has the number of roots at most n, and the roots of multiplicity m occur exactly m times.

2. An odd degree polynomial has at least one real root.

3. If α is a root of P (x), then P n (x) = (x - α) Q n - 1 (x), where Q n - 1 (x) is a polynomial of degree (n - 1).

4.

5. The reduced polynomial with integer coefficients cannot have fractional rational roots.

6. For a polynomial of degree 3

P 3 (x) = ax 3 + bx 2 + cx + d one of two things is possible: either it decomposes into a product of three binomials

Р 3 (x) = а (х - α) (х - β) (х - γ), or it can be decomposed into the product of a binomial and a square trinomial Р 3 (x) = а (х - α) (х 2 + βх + γ ).

7. Any polynomial of the fourth degree can be decomposed into the product of two square trinomials.

8. The polynomial f (x) is divisible by the polynomial g (x) without a remainder if there is a polynomial q (x) such that f (x) = g (x) q (x). For dividing polynomials, the “corner division” rule is applied.

9. For the divisibility of the polynomial P (x) into the binomial (x - c), it is necessary and sufficient that the number c be a root of P (x) (Corollary of Bezout's theorem).

10. Vieta's theorem: If x 1, x 2, ..., x n are real roots of the polynomial

P (x) = a 0 x n + a 1 x n - 1 + ... + a n, then the following equalities hold:

x 1 + x 2 + ... + x n = -a 1 / a 0,

x 1 x 2 + x 1 x 3 + ... + x n - 1 x n = a 2 / a 0,

x 1 x 2 x 3 + ... + x n - 2 x n - 1 x n = -a 3 / a 0,

x 1 x 2 x 3 x n = (-1) n a n / a 0.

Solution examples

Example 1.

Find the remainder of dividing P (x) = x 3 + 2/3 x 2 - 1/9 by (x - 1/3).

Solution.

By corollary to Bezout's theorem: "The remainder of dividing a polynomial by a binomial (x - c) is equal to the value of the polynomial in c". Let's find Р (1/3) = 0. Therefore, the remainder is 0 and the number 1/3 is the root of the polynomial.

Answer: R = 0.

Example 2.

Divide with a corner 2x 3 + 3x 2 - 2x + 3 by (x + 2). Find the remainder and the incomplete quotient.

Solution:

2x 3 + 3x 2 - 2x + 3 | x + 2

2х 3 + 4 x 2 2x 2 - x

X 2 - 2 x

Answer: R = 3; private: 2x 2 - x.

Basic methods for solving equations of higher degrees

1. Introducing a new variable

The method of introducing a new variable is already familiar with an example. biquadratic equations... It consists in the fact that to solve the equation f (x) = 0, a new variable (substitution) t = x n or t = g (x) is introduced and f (x) is expressed in terms of t, obtaining a new equation r (t). Then, solving the equation r (t), the roots are found:

(t 1, t 2, ..., t n). After that, a set of n equations q (x) = t 1, q (x) = t 2, ..., q (x) = t n is obtained, from which the roots of the original equation are found.

Example 1.

(x 2 + x + 1) 2 - 3x 2 - 3x - 1 = 0.

Solution:

(x 2 + x + 1) 2 - 3 (x 2 + x) - 1 = 0.

(x 2 + x + 1) 2 - 3 (x 2 + x + 1) + 3 - 1 = 0.

Replacement (x 2 + x + 1) = t.

t 2 - 3t + 2 = 0.

t 1 = 2, t 2 = 1. Reverse replacement:

x 2 + x + 1 = 2 or x 2 + x + 1 = 1;

x 2 + x - 1 = 0 or x 2 + x = 0;

Answer: From the first equation: x 1, 2 = (-1 ± √5) / 2, from the second: 0 and -1.

2. Factorization by grouping and reduced multiplication formulas

The basis of this method is also not new and consists in grouping the terms in such a way that each group contains a common factor. To do this, sometimes you have to use some artificial methods.

Example 1.

x 4 - 3x 2 + 4x - 3 = 0.

Solution.

Imagine - 3x 2 = -2x 2 - x 2 and group:

(x 4 - 2x 2) - (x 2 - 4x + 3) = 0.

(x 4 - 2x 2 +1 - 1) - (x 2 - 4x + 3 + 1 - 1) = 0.

(x 2 - 1) 2 - 1 - (x - 2) 2 + 1 = 0.

(x 2 - 1) 2 - (x - 2) 2 = 0.

(x 2 - 1 - x + 2) (x 2 - 1 + x - 2) = 0.

(x 2 - x + 1) (x 2 + x - 3) = 0.

x 2 - x + 1 = 0 or x 2 + x - 3 = 0.

Answer: There are no roots in the first equation, from the second: x 1, 2 = (-1 ± √13) / 2.

3. Factoring by the method of undefined coefficients

The essence of the method is that the original polynomial is decomposed into factors with unknown coefficients. Using the property that the polynomials are equal if their coefficients are equal at the same degrees, the unknown expansion coefficients are found.

Example 1.

x 3 + 4x 2 + 5x + 2 = 0.

Solution.

A polynomial of the 3rd degree can be expanded into the product of a linear and a square factor.

x 3 + 4x 2 + 5x + 2 = (x - a) (x 2 + bx + c),

x 3 + 4x 2 + 5x + 2 = x 3 + bx 2 + cx - ax 2 - abx - ac,

x 3 + 4x 2 + 5x + 2 = x 3 + (b - a) x 2 + (cx - ab) x - ac.

Having solved the system:

(b - a = 4,
(c - ab = 5,
(-ac = 2,

(a = -1,
(b = 3,
(c = 2, i.e.

x 3 + 4x 2 + 5x + 2 = (x + 1) (x 2 + 3x + 2).

The roots of the equation (x + 1) (x 2 + 3x + 2) = 0 are easy to find.

Answer: -1; -2.

4. Root selection method based on the highest and free coefficient

The method is based on the application of theorems:

1) Any integer root of a polynomial with integer coefficients is a divisor of an intercept.

2) In order for the irreducible fraction p / q (p is an integer, q is a natural) to be a root of an equation with integer coefficients, it is necessary that the number p be an integer divisor of the free term a 0, and q - a natural divisor of the leading coefficient.

Example 1.

6x 3 + 7x 2 - 9x + 2 = 0.

Solution:

6: q = 1, 2, 3, 6.

Therefore, p / q = ± 1, ± 2, ± 1/2, ± 1/3, ± 2/3, ± 1/6.

Having found one root, for example - 2, we find the other roots using division with an angle, the method of undefined coefficients or Horner's scheme.

Answer: -2; 1/2; 1/3.

Still have questions? Not sure how to solve equations?
To get help from a tutor - register.
The first lesson is free!

site, with full or partial copying of the material, a link to the source is required.