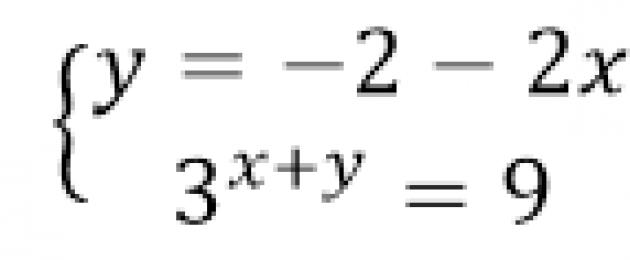Sektsioonid: Matemaatika
Tunni eesmärgid:
Haridus: õpetada lahendama eksponentsiaalvõrrandi süsteeme; kinnistada nendes süsteemides sisalduvaid võrrandite lahendamise oskusi
Haridus: kasvatada täpsust.
Arendamine: arendada kirjaliku ja suulise kõne kultuuri.
Varustus: arvuti; multimeedia projektor.
Tundide ajal
Aja organiseerimine
Õpetaja. Täna jätkame peatüki “Eksponentfunktsioon” uurimist. Tunni teema sõnastatakse veidi hiljem. Tunni ajal täidate vastuste lehti, mis on teie tabelitel ( cm. taotlus number 1 ). Vastused võetakse kokku.
Teadmiste värskendus.
Õpilased vastavad küsimustele:
- Mis on eksponentsiaalfunktsioon?
suuline töö. Töötage slaididega 1 kuni 5.
- Mis on eksponentsiaalvõrrand?
- Milliseid lahendusviise te teate?
Suuline töö slaididel 6 kuni 10.
- Milline vara eksponentsiaalne funktsioon mida kasutatakse eksponentsiaalvõrratuste lahendamisel?
Suuline töö slaididel 11-15.
Harjutus. Kirjuta vastused nendele küsimustele vastuselehele nr 1. ( cm. taotlus number 1 ). (slaidid 16 kuni 31)
Kodutööde kontrollimine
.Kodutöid kontrollime järgmiselt.
Asenda võrrandite juured vastava tähega ja arva ära sõna.
Õpilased vaatavad vastustelehte number 2 ( 1. lisa) . Õpetaja demonstreerib slaidi number 33
(Õpilased nimetavad sõna (slaid nr 34)).
- Millised nähtused toimuvad selle funktsiooni seaduste järgi?
Õpilasi kutsutakse lahendama ühtse riigieksami B12 ülesandeid (slaid 35) ja kirjutama lahendus vastusevormile nr 3 ( 1. lisa).
Kodutööde kontrollimise ja ülesande B12 lahendamise käigus kordame eksponentsiaalvõrrandite lahendamise meetodeid.
Õpilased jõuavad järeldusele, et kahe muutujaga võrrandi lahendamiseks on vaja teist võrrandit.
Seejärel sõnastatakse tunni teema (slaid nr 37).
Süsteem on kirjutatud vihikutesse (slaid nr 38).
Selle süsteemi lahendamiseks kordame asendusmeetodit (slaid nr 39).
Lisamismeetodit korratakse süsteemi lahustamise ajal (slaid 38 kuni 39).
Õpitud materjali esmane konsolideerimine
:Õpilased lahendavad iseseisvalt võrrandisüsteeme vastusevormides nr 4 ( 1. lisa ), saades õpetajalt individuaalset nõu.
Kokkuvõtteid tehes. Peegeldus.
Jätkake fraase.
- Täna klassis tegin...
- Täna klassis parandasin...
- Täna tunnis õppisin...
- Täna tunnis õppisin...
Tunni lõpus kirjutavad õpilased üles oma kodutööd ja esitavad vastuselehed.
Kodutöö:
Nr 59 (paaris) ja nr 62 (paaris).Kirjandus
- Kõik USE rühma ülesanded 3000 ülesannet - Kirjastus "Exam" Moskva, 2011. Toimetanud A.L. Semenova, I.V. Jaštšenko.
- S.A. Šestakov, P.I. Zakharov USE 2010 matemaatikaülesanne C1, toimetanud A.L. Semenova, I.V. Jaštšenko Moskva kirjastus "MTsNMO".
- Õpetus Algebra ja matemaatilise analüüsi algus, 10. klass Yu.M. Kolyagin Moskva “Valgustus”, 2008.
Võrrandisüsteemide lahendamise viisid
Alustuseks tuletagem lühidalt meelde, millised võrrandisüsteemide lahendamise meetodid üldiselt eksisteerivad.
Olemas neli peamist viisi võrrandisüsteemide lahendused:
Asendusmeetod: võtke ükskõik milline neist võrranditest ja väljendage $y$ väärtusega $x$, seejärel asendatakse $y$ süsteemi võrrandiga, kust leitakse muutuja $x.$. Pärast seda saame lihtsalt arvutada muutuja $y.$
Liitmismeetod: selle meetodi puhul on vaja üks või mõlemad võrrandid korrutada selliste arvudega, et mõlema liitmisel üks muutujatest "kaoks".
Graafiline meetod: süsteemi mõlemal võrrandil on kujutatud koordinaattasand ja leidke nende ristumispunkt.
Uute muutujate sisseviimise meetod: selle meetodi puhul asendame süsteemi lihtsustamiseks mõned avaldised ja seejärel rakendame ühte ülaltoodud meetoditest.
Eksponentvõrrandisüsteemid
Definitsioon 1
Eksponentvõrranditest koosnevaid võrrandisüsteeme nimetatakse eksponentsiaalvõrrandisüsteemiks.
Vaatleme eksponentsiaalvõrrandisüsteemide lahendamist näidete abil.
Näide 1
Lahenda võrrandisüsteem
1. pilt.
Otsus.
Selle süsteemi lahendamiseks kasutame esimest meetodit. Esmalt väljendame $y$ esimeses võrrandis väärtusega $x$.

Joonis 2.
Asendage $y$ teises võrrandis:
\ \ \[-2-x=2\] \ \
Vastus: $(-4,6)$.
Näide 2
Lahenda võrrandisüsteem

Joonis 3
Otsus.
See süsteem on süsteemiga samaväärne

Joonis 4
Võrrandite lahendamiseks rakendame neljandat meetodit. Olgu $2^x=u\ (u >0)$ ja $3^y=v\ (v >0)$, saame:

Joonis 5
Lahendame saadud süsteemi liitmismeetodil. Lisame võrrandid:
\ \
Siis saame teisest võrrandist selle
Asenduse juurde tagasi tulles, sain uus süsteem eksponentsiaalvõrrandid:
Joonis 6
Saame:
Joonis 7
Vastus: $(0,1)$.
Eksponentvõrratuste süsteemid
2. definitsioon
Eksponentvõrranditest koosnevaid võrratussüsteeme nimetatakse süsteemiks eksponentsiaalne ebavõrdsus.
Vaatleme eksponentsiaalvõrratuste süsteemide lahendamist näidete abil.
Näide 3
Lahendage võrratuste süsteem

Joonis 8
Otsus:
See ebavõrdsuse süsteem on süsteemiga samaväärne

Joonis 9
Esimese ebavõrdsuse lahendamiseks tuletage meelde järgmine eksponentsiaalvõrratuste samaväärsuse teoreem:
1. teoreem. Võrratus $a^(f(x)) >a^(\varphi (x)) $, kus $a >0,a\ne 1$ on võrdne kahe süsteemi hulgaga
\ \ \
Vastus: $(-4,6)$.
Näide 2
Lahenda võrrandisüsteem

Joonis 3
Otsus.
See süsteem on süsteemiga samaväärne

Joonis 4
Võrrandite lahendamiseks rakendame neljandat meetodit. Olgu $2^x=u\ (u >0)$ ja $3^y=v\ (v >0)$, saame:

Joonis 5
Lahendame saadud süsteemi liitmismeetodil. Lisame võrrandid:
\ \
Siis saame teisest võrrandist selle
Asenduse juurde naastes sain uue eksponentsiaalvõrrandi süsteemi:
Joonis 6
Saame:
Joonis 7
Vastus: $(0,1)$.
Eksponentvõrratuste süsteemid
2. definitsioon
Eksponentvõrranditest koosnevaid võrratussüsteeme nimetatakse eksponentsiaalvõrratuste süsteemiks.
Vaatleme eksponentsiaalvõrratuste süsteemide lahendamist näidete abil.
Näide 3
Lahendage võrratuste süsteem

Joonis 8
Otsus:
See ebavõrdsuse süsteem on süsteemiga samaväärne

Joonis 9
Esimese ebavõrdsuse lahendamiseks tuletage meelde järgmine eksponentsiaalvõrratuste samaväärsuse teoreem:
1. teoreem. Võrratus $a^(f(x)) >a^(\varphi (x)) $, kus $a >0,a\ne 1$ on võrdne kahe süsteemi hulgaga
\}
- Kokkupuutel 0
- Google+ 0
- Okei 0
- Facebook 0