Se la funzione è pari allora. Funzioni pari e dispari

Nel luglio 2020, la NASA lancia una spedizione su Marte. Il veicolo spaziale consegnerà su Marte un vettore elettronico con i nomi di tutti i membri registrati della spedizione.

Se questo post ha risolto il tuo problema o ti è semplicemente piaciuto, condividi il link con i tuoi amici sui social network.

Una di queste opzioni di codice deve essere copiata e incollata nel codice della tua pagina web, preferibilmente tra i tag e o subito dopo il tag . Secondo la prima opzione, MathJax si carica più velocemente e rallenta meno la pagina. Ma la seconda opzione traccia e carica automaticamente le ultime versioni di MathJax. Se inserisci il primo codice, sarà necessario aggiornarlo periodicamente. Se incolli il secondo codice, le pagine verranno caricate più lentamente, ma non dovrai monitorare costantemente gli aggiornamenti di MathJax.

Il modo più semplice per connettere MathJax è in Blogger o WordPress: nel pannello di controllo del sito, aggiungi un widget progettato per inserire codice JavaScript di terze parti, copia al suo interno la prima o la seconda versione del codice di caricamento presentato sopra e avvicina il widget all'inizio del modello (a proposito, questo non è affatto necessario, poiché lo script MathJax viene caricato in modo asincrono). È tutto. Ora impara la sintassi del markup MathML, LaTeX e ASCIIMathML e sei pronto per incorporare formule matematiche nelle tue pagine web.

Un altro capodanno... gelo e fiocchi di neve sui vetri della finestra... Tutto questo mi ha spinto a scrivere di nuovo sui... frattali e su ciò che Wolfram Alpha ne sa. In questa occasione, c'è un articolo interessante in cui ci sono esempi di strutture frattali bidimensionali. Qui considereremo esempi più complessi di frattali tridimensionali.

Un frattale può essere rappresentato visivamente (descritto) come una figura o un corpo geometrico (il che significa che entrambi sono un insieme, in questo caso, un insieme di punti), i cui dettagli hanno la stessa forma della figura originale stessa. Cioè, è una struttura auto-simile, considerando i dettagli di cui, quando ingranditi, vedremo la stessa forma senza ingrandimento. Mentre nel caso di una figura geometrica ordinaria (non un frattale), quando ingrandiamo, vedremo dettagli che hanno una forma più semplice rispetto alla figura originale stessa. Ad esempio, con un ingrandimento sufficientemente elevato, parte di un'ellisse appare come un segmento di linea retta. Questo non accade con i frattali: con ogni loro aumento, vedremo di nuovo la stessa forma complessa, che ad ogni aumento verrà ripetuta ancora e ancora.

Benoit Mandelbrot, il fondatore della scienza dei frattali, nel suo articolo Fractals and Art for Science ha scritto: "I frattali sono forme geometriche tanto complesse nei dettagli quanto nella loro forma complessiva. Cioè, se parte del frattale lo farà essere ingrandito alla dimensione del tutto, sembrerà come il tutto, o esattamente, o forse con una leggera deformazione.

. Per fare ciò, utilizzare carta millimetrata o una calcolatrice grafica. Seleziona un numero qualsiasi di valori numerici per la variabile indipendente x (\ displaystyle x) e inserirli nella funzione per calcolare i valori della variabile dipendente y (\ displaystyle y). Metti le coordinate trovate dei punti sul piano delle coordinate, quindi collega questi punti per costruire un grafico della funzione.

• Sostituisci i valori numerici positivi nella funzione x (\ displaystyle x) e corrispondenti valori numerici negativi. Ad esempio, data una funzione f (x) = 2 x 2 + 1 (\displaystyle f(x)=2x^(2)+1). Sostituisci i seguenti valori in esso x (\ displaystyle x):

Controlla se il grafico della funzione è simmetrico rispetto all'asse y. La simmetria si riferisce all'immagine speculare del grafico sull'asse y. Se la parte del grafico a destra dell'asse y (valori positivi della variabile indipendente) corrisponde alla parte del grafico a sinistra dell'asse y (valori negativi della variabile indipendente), il grafico è simmetrico rispetto all'asse Y. Se la funzione è simmetrica rispetto all'asse Y, la funzione è pari.

Controllare se il grafico della funzione è simmetrico rispetto all'origine. L'origine è il punto con coordinate (0,0). Simmetria sull'origine significa che un valore positivo y (\ displaystyle y)(con valore positivo x (\ displaystyle x)) corrisponde a un valore negativo y (\ displaystyle y)(con valore negativo x (\ displaystyle x)), e viceversa. Le funzioni dispari hanno simmetria rispetto all'origine.

Controllare se il grafico della funzione ha simmetria. L'ultimo tipo di funzione è una funzione il cui grafico non ha simmetria, ovvero non esiste un'immagine speculare sia relativa all'asse y che relativa all'origine. Ad esempio, data una funzione.

• Sostituisci diversi valori positivi e corrispondenti negativi nella funzione x (\ displaystyle x):
• Secondo i risultati ottenuti, non c'è simmetria. I valori y (\ displaystyle y) per valori opposti x (\ displaystyle x) non corrispondono e non sono opposti. Pertanto, la funzione non è né pari né dispari.
• Si prega di notare che la funzione f (x) = x 2 + 2 x + 1 (\displaystyle f(x)=x^(2)+2x+1) si può scrivere così: f (x) = (x + 1) 2 (\displaystyle f(x)=(x+1)^(2)). Scritta in questa forma, la funzione sembra essere pari perché esiste un esponente pari. Ma questo esempio dimostra che la forma di una funzione non può essere determinata rapidamente se la variabile indipendente è racchiusa tra parentesi. In questo caso, è necessario aprire le parentesi e analizzare gli esponenti risultanti.

Funzioneè uno dei concetti matematici più importanti. Funzione: dipendenza dalle variabili a da una variabile X, se ogni valore X corrisponde a un singolo valore a. variabile X chiamato variabile o argomento indipendente. variabile a chiamata variabile dipendente. Tutti i valori della variabile indipendente (variabile X) formano il dominio della funzione. Tutti i valori che assume la variabile dipendente (variabile y), formano l'intervallo della funzione.

Grafico delle funzioni chiamano l'insieme di tutti i punti del piano delle coordinate, le cui ascisse sono uguali ai valori dell'argomento e le ordinate sono uguali ai valori corrispondenti della funzione, ovvero i valori di le variabili sono tracciate lungo l'asse delle ascisse X e i valori della variabile vengono tracciati lungo l'asse y y. Per tracciare una funzione, è necessario conoscere le proprietà della funzione. Le principali proprietà della funzione saranno discusse di seguito!

Per tracciare un grafico di funzione, ti consigliamo di utilizzare il nostro programma - Funzioni di rappresentazione grafica in linea. Se hai domande mentre studi il materiale in questa pagina, puoi sempre farle sul nostro forum. Inoltre sul forum verrai aiutato a risolvere problemi di matematica, chimica, geometria, teoria delle probabilità e molte altre materie!

Proprietà di base delle funzioni.

1) Ambito della funzione e gamma di funzioni.

L'ambito di una funzione è l'insieme di tutti i valori validi validi dell'argomento X(variabile X) per cui la funzione y = f(x) definito.
L'intervallo di una funzione è l'insieme di tutti i valori reali y che la funzione accetta.

Nella matematica elementare, le funzioni sono studiate solo sull'insieme dei numeri reali.

2) Funzione zeri.

I valori X, al quale y=0, è chiamato zeri di funzione. Queste sono le ascisse dei punti di intersezione del grafico della funzione con l'asse x.

3) Intervalli di costanza di segno di una funzione.

Gli intervalli di costanza di segno di una funzione sono tali intervalli di valori X, su cui i valori della funzione y vengono chiamati solo positivi o solo negativi intervalli di costanza di segno della funzione.

4) Monotonia della funzione.

Funzione crescente (in alcuni intervalli): una funzione in cui un valore maggiore dell'argomento di questo intervallo corrisponde a un valore maggiore della funzione.

Funzione decrescente (in alcuni intervalli): una funzione in cui un valore maggiore dell'argomento da questo intervallo corrisponde a un valore minore della funzione.

5) Funzioni pari (dispari)..

Una funzione pari è una funzione il cui dominio di definizione è simmetrico rispetto all'origine e per qualsiasi X f(-x) = f(x). Il grafico di una funzione pari è simmetrico rispetto all'asse y.

Una funzione dispari è una funzione il cui dominio di definizione è simmetrico rispetto all'origine e per qualsiasi X dal dominio di definizione l'uguaglianza f(-x) = - f(x). Il grafico di una funzione dispari è simmetrico rispetto all'origine.

Funzione pari
1) Il dominio di definizione è simmetrico rispetto al punto (0; 0), cioè se il punto un appartiene al dominio della definizione, quindi il punto -un appartiene anche al dominio della definizione.
2) Per qualsiasi valore X f(-x)=f(x)
3) Il grafico di una funzione pari è simmetrico rispetto all'asse Oy.

funzione dispari ha le seguenti proprietà:
1) Il dominio di definizione è simmetrico rispetto al punto (0; 0).
2) per qualsiasi valore X, che appartiene al dominio di definizione, l'uguaglianza f(-x)=-f(x)
3) Il grafico di una funzione dispari è simmetrico rispetto all'origine (0; 0).

Non tutte le funzioni sono pari o dispari. Funzioni vista generale non sono né pari né dispari.

6) Funzioni limitate e illimitate.

Una funzione si dice limitata se esiste un numero positivo M tale che |f(x)| ≤ M per tutti i valori di x . Se non esiste un tale numero, la funzione è illimitata.

7) Periodicità della funzione.

Una funzione f(x) è periodica se esiste un numero T diverso da zero tale che per ogni x dal dominio della funzione, f(x+T) = f(x). Questo numero più piccolo è chiamato periodo della funzione. Tutte le funzioni trigonometriche sono periodiche. (Formule trigonometriche).

Funzione F si dice periodico se esiste un numero tale che per qualsiasi X dal dominio di definizione l'uguaglianza f(x)=f(x-T)=f(x+T). Tè il periodo della funzione.

Ogni funzione periodica ha un numero infinito di periodi. In pratica, di solito viene considerato il periodo positivo più piccolo.

I valori della funzione periodica vengono ripetuti dopo un intervallo pari al periodo. Viene utilizzato quando si tracciano grafici.

L'uniformità e la stranezza di una funzione sono una delle sue proprietà principali e l'uguaglianza occupa una parte impressionante del corso scolastico di matematica. Determina in gran parte la natura del comportamento della funzione e facilita notevolmente la costruzione del grafico corrispondente.

Definiamo la parità della funzione. In generale, la funzione in esame viene considerata anche se per valori opposti della variabile indipendente (x) situata nel suo dominio di definizione, i corrispondenti valori di y (funzione) sono uguali.

Diamo una definizione più rigorosa. Si consideri una qualche funzione f(x), che è definita nel dominio D. Sarà anche se per ogni punto x situato nel dominio di definizione:

• -x (punto opposto) si trova anche nell'ambito dato,

• f(-x) = f(x).

Dalla definizione di cui sopra segue la condizione necessaria per il dominio di definizione di tale funzione, ovvero la simmetria rispetto al punto O, che è l'origine delle coordinate, poiché se un punto b è contenuto nel dominio di definizione di un funzione pari, allora il punto corrispondente - b si trova anche in questo dominio. Da quanto precede, quindi, segue la conclusione: una funzione pari ha una forma simmetrica rispetto all'asse delle ordinate (Oy).

Come determinare in pratica la parità di una funzione?

Sia data usando la formula h(x)=11^x+11^(-x). Seguendo l'algoritmo che segue direttamente dalla definizione, studiamo prima di tutto il suo dominio di definizione. Ovviamente è definito per tutti i valori dell'argomento, cioè la prima condizione è soddisfatta.

Il passaggio successivo consiste nel sostituire l'argomento (x) con il suo valore opposto (-x).
Noi abbiamo:
h(-x) = 11^(-x) + 11^x.
Poiché l'addizione soddisfa la legge commutativa (spostamento), è ovvio che h(-x) = h(x) e la dipendenza funzionale data è pari.

Verifichiamo l'uniformità della funzione h(x)=11^x-11^(-x). Seguendo lo stesso algoritmo, otteniamo h(-x) = 11^(-x) -11^x. Eliminando il meno, di conseguenza, abbiamo
h(-x)=-(11^x-11^(-x))=- h(x). Quindi h(x) è dispari.

A proposito, va ricordato che ci sono funzioni che non possono essere classificate secondo questi criteri, non sono chiamate né pari né dispari.

Anche le funzioni hanno una serie di proprietà interessanti:

• per aggiunta di funzioni simili si ottiene una pari;
• per effetto della sottrazione di tali funzioni si ottiene una pari;
• pari, anche pari;
• moltiplicando due di tali funzioni si ottiene una pari;
• come risultato della moltiplicazione delle funzioni pari e dispari si ottiene una dispari;
• come risultato della divisione delle funzioni pari e dispari si ottiene una dispari;
• la derivata di tale funzione è dispari;
• Se eleviamo al quadrato una funzione dispari, otteniamo una pari.

La parità di una funzione può essere utilizzata per risolvere le equazioni.

Per risolvere un'equazione come g(x) = 0, dove il lato sinistro dell'equazione è una funzione pari, sarà sufficiente trovare le sue soluzioni per valori non negativi della variabile. Le radici ottenute dell'equazione devono essere combinate con numeri opposti. Uno di questi è soggetto a verifica.

Lo stesso viene utilizzato con successo per risolvere problemi non standard con un parametro.

Ad esempio, esiste un valore per il parametro a che renderebbe l'equazione 2x^6-x^4-ax^2=1 con tre radici?

Se prendiamo in considerazione che la variabile entra nell'equazione in potenze pari, allora è chiaro che la sostituzione di x con -x non cambierà l'equazione data. Ne consegue che se un certo numero è la sua radice, allora lo è anche il numero opposto. La conclusione è ovvia: le radici dell'equazione, diverse da zero, sono incluse nell'insieme delle sue soluzioni a “coppie”.

È chiaro che il numero 0 stesso non è, cioè il numero di radici di una tale equazione può essere solo pari e, naturalmente, per qualsiasi valore del parametro non può avere tre radici.

Ma il numero di radici dell'equazione 2^x+ 2^(-x)=ax^4+2x^2+2 può essere dispari, e per qualsiasi valore del parametro. Infatti, è facile verificare che l'insieme delle radici di una data equazione contenga soluzioni a "coppie". Verifichiamo se 0 è una radice. Quando lo sostituiamo nell'equazione, otteniamo 2=2. Quindi, oltre a "accoppiato" 0 è anche una radice, che dimostra il loro numero dispari.

Nascondi spettacolo

Modi per impostare una funzione

Sia data la funzione dalla formula: y=2x^(2)-3 . Assegnando un qualsiasi valore alla variabile indipendente x, puoi utilizzare questa formula per calcolare i valori corrispondenti della variabile dipendente y. Ad esempio, se x=-0.5 , quindi utilizzando la formula, otteniamo che il valore corrispondente di y è y=2 \cdot (-0.5)^(2)-3=-2.5 .

Dato qualsiasi valore preso dall'argomento x nella formula y=2x^(2)-3 , è possibile calcolare solo un valore di funzione che corrisponde ad esso. La funzione può essere rappresentata come una tabella:

X	−2	−1	0	1	2	3
y	−4	−3	−2	−1	0	1

Usando questa tabella, puoi capire che per il valore dell'argomento -1, il valore della funzione -3 corrisponderà; e il valore x=2 corrisponderà a y=0, e così via. È anche importante sapere che ogni valore di argomento nella tabella corrisponde a un solo valore di funzione.

È possibile impostare più funzioni utilizzando i grafici. Con l'aiuto del grafico si stabilisce quale valore della funzione è correlato a un certo valore di x. Molto spesso, questo sarà un valore approssimativo della funzione.

Funzione pari e dispari

La funzione è funzione pari, quando f(-x)=f(x) per qualsiasi x dal dominio. Tale funzione sarà simmetrica rispetto all'asse Oy.

La funzione è funzione dispari quando f(-x)=-f(x) per qualsiasi x nel dominio. Tale funzione sarà simmetrica rispetto all'origine O (0;0) .

La funzione è nemmeno, né dispari e chiamato funzione generale quando non ha simmetria rispetto all'asse o all'origine.

Esaminiamo la seguente funzione di parità:

f(x)=3x^(3)-7x^(7)

D(f)=(-\infty ; +\infty) con un dominio di definizione simmetrico sull'origine. f(-x)= 3 \cpunto (-x)^(3)-7 \cpunto (-x)^(7)= -3x^(3)+7x^(7)= -(3x^(3)-7x^(7))= -f(x).

Quindi, la funzione f(x)=3x^(3)-7x^(7) è dispari.

Funzione periodica

La funzione y=f(x) , nel dominio di cui f(x+T)=f(x-T)=f(x) è vera per ogni x, viene chiamata funzione periodica con periodo T \neq 0 .

Ripetizione del grafico della funzione su un qualsiasi segmento dell'asse delle ascisse, che abbia lunghezza T .

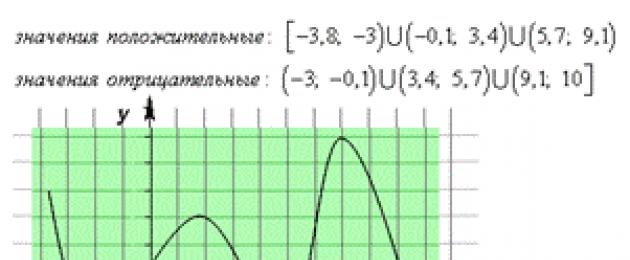
Intervalli in cui la funzione è positiva, cioè f (x) > 0 - segmenti dell'asse delle ascisse, che corrispondono ai punti del grafico della funzione che si trovano sopra l'asse delle ascisse.

f(x) > 0 acceso (x_(1); x_(2)) \cup (x_(3); +\infty)

Lacune in cui la funzione è negativa, cioè f(x)< 0 - отрезки оси абсцисс, которые отвечают точкам графика функции, лежащих ниже оси абсцисс.

f(x)< 0 на (-\infty; x_(1)) \cup (x_(2); x_(3))

Limitazione delle funzioni

delimitata dal bassoè consuetudine chiamare una funzione y=f(x), x \in X quando esiste un numero A per il quale vale la disuguaglianza f(x) \geq A per ogni x \in X .

Un esempio di una funzione delimitata di seguito: y=\sqrt(1+x^(2)) poiché y=\sqrt(1+x^(2)) \geq 1 for any x .

delimitata dall'alto viene chiamata una funzione y=f(x), x \in X se esiste un numero B per il quale vale la disuguaglianza f(x) \neq B per ogni x \in X .

Un esempio di una funzione delimitata di seguito: y=\sqrt(1-x^(2)), x \in [-1;1] poiché y=\sqrt(1+x^(2)) \neq 1 per ogni x \in [-1;1] .

Limitatoè consuetudine chiamare una funzione y=f(x), x \in X quando esiste un numero K > 0 per il quale la disuguaglianza \left | f(x) \right | \neq K per ogni x \in X .

Esempio di funzione limitata: y=\sin x è delimitata sulla retta del numero intero perché \sinistra | \peccato x \destra | \neq 1.

Funzione crescente e decrescente

È consuetudine parlare di una funzione che cresce sull'intervallo considerato come funzione crescente quando un valore maggiore di x corrisponderà a un valore maggiore della funzione y=f(x) . Da qui risulta che prendendo dall'intervallo considerato due valori arbitrari dell'argomento x_(1) e x_(2) , e x_(1) > x_(2) , sarà y(x_(1)) > y(x_(2)) .

Viene chiamata una funzione che decresce sull'intervallo considerato funzione decrescente quando un valore maggiore di x corrisponderà a un valore minore della funzione y(x) . Da qui risulta che prendendo dall'intervallo considerato due valori arbitrari dell'argomento x_(1) e x_(2) , e x_(1) > x_(2) , sarà y(x_(1))< y(x_{2}) .

Radici di funzioneè consuetudine nominare i punti in cui la funzione F=y(x) interseca l'asse delle ascisse (si ottengono risolvendo l'equazione y(x)=0 ).

a) Se una funzione pari aumenta per x > 0, allora diminuisce per x< 0

b) Quando una funzione pari diminuisce per x > 0, aumenta per x< 0

c) Quando una funzione dispari aumenta per x > 0, aumenta anche per x< 0

d) Quando una funzione dispari diminuisce per x > 0, diminuisce anche per x< 0

Estremi di funzione

Punto minimo di funzione y=f(x) è consuetudine chiamare tale punto x=x_(0) , in cui il suo intorno avrà altri punti (tranne il punto x=x_(0) ), e per questi quindi la disuguaglianza f( x) > f (x_(0)) . y_(min) - designazione della funzione nel punto min.

Punto massimo della funzione y=f(x) è consuetudine chiamare tale punto x=x_(0) , in cui il suo intorno avrà altri punti (tranne il punto x=x_(0) ), e quindi la disuguaglianza f(x) sarà soddisfatto per loro< f(x^{0}) . y_{max} - обозначение функции в точке max.

Condizione necessaria

Secondo il teorema di Fermat: f"(x)=0, allora quando la funzione f(x) , che è derivabile nel punto x_(0) , apparirà a questo punto un estremo.

Condizione sufficiente

1. Quando il segno della derivata cambia da più a meno, allora x_(0) sarà il punto minimo;
2. x_(0) - sarà un punto massimo solo quando la derivata cambia segno da meno a più quando passa per il punto stazionario x_(0) .

Il valore più grande e più piccolo della funzione sull'intervallo

Passi di calcolo:

1. Alla ricerca della derivata f"(x) ;
2. Si trovano i punti stazionari e critici della funzione e si scelgono quelli appartenenti all'intervallo;
3. I valori della funzione f(x) si trovano ai punti e alle estremità stazionari e critici del segmento. Il più piccolo dei risultati sarà il valore più piccolo della funzione e altro ancora - più grande.