Formuła kompresji ekscentrycznej. Ekscentryczna kompresja lub rozciąganie

Na wiele elementów konstrukcji budowlanych (słupy, stojaki, podpory) działają siły ściskające działające nie w środku ciężkości przekroju. Na ryc. 12.9 przedstawia słup, na którym spoczywa belka stropowa. Jak widać, siła działa w stosunku do osi kolumny z mimośrodem mi, a więc w dowolnej sekcji Ach słupy wraz z siłą podłużną n = -R występuje moment zginający, którego wielkość jest równa Odnośnie. Mimośrodowe rozciąganie (ściskanie) pręta jest rodzajem odkształcenia, w którym wypadkowa siły zewnętrzne działaj wzdłuż linii prostej równoległej do osi pręta. W dalszej części rozważymy głównie problemy kompresji mimośrodowej. W przypadku rozciągania mimośrodowego we wszystkich podanych wzorach obliczeniowych należy zmienić znak przed siłą r na odwrót.

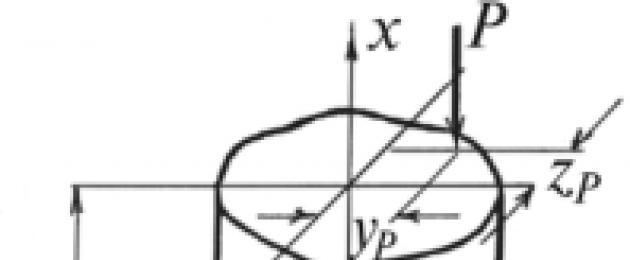
Niech pręt o dowolnym przekroju (rys. 12.10) zostanie obciążony na końcu mimośrodowo przyłożoną siłą ściskającą R, skierowane równolegle do osi Oh. Zaakceptuj pozytywne

kierunki głównych osi bezwładności przekroju OU I Oz tak, że punkt przyłożenia siły r znajdował się w pierwszej ćwiartce osi współrzędnych. Oznaczamy współrzędne punktu przyłożenia siły r w poprzek y r I z p -

Siły wewnętrzne w dowolnym przekroju pręta są równe

Znaki ujemne momentów zginających wynikają z faktu, że w pierwszej ćwiartce osi współrzędnych momenty te powodują ściskanie. Wielkie ilości wewnętrzne wysiłki w tym przykładzie nie zmieniaj się na długości pręta, a co za tym idzie rozkład naprężeń w odcinkach dostatecznie oddalonych od miejsca przyłożenia obciążenia będzie taki sam.

Podstawiając (12.11) do (12.1) otrzymujemy wzór na normalne naprężenia przy mimośrodowym ściskaniu:

Ta formuła może być przekonwertowana do postaci

gdzie ja , ja- główne promienie bezwładności przekroju. W której

Wstawiając (12.12) o = 0 otrzymujemy równanie linia zerowa:

Tutaj o 0 i z 0 - współrzędne punktów linii zerowej (ryc. 12.11). Równanie (12.14) to równanie linii prostej, która nie przechodzi przez środek ciężkości przekroju. Aby narysować linię zerową, znajdujemy punkty jej przecięcia z osiami współrzędnych. Zakładając w (12.14) kolejno y 0 = 0 i z0= 0, odpowiednio, znajdujemy

gdzie a z I i y- odcinki odcięte linią zerową na osiach współrzędnych (ryc. 12.11).

Ustalmy cechy położenia linii zerowej pod ściskaniem mimośrodowym.

• 1. Ze wzorów (12.15) wynika, że i w I a z mają odpowiednio przeciwne znaki y r I z p - W ten sposób linia zerowa przechodzi przez te ćwiartki osi współrzędnych, które nie zawierają punktu przyłożenia siły (ryc. 12.12).
• 2. W miarę zbliżania się punktu przyłożenia siły r w linii prostej do środka ciężkości przekroju współrzędne tego punktu y r I z p zmniejszenie. Z (12.15) wynika, że ​​w tym przypadku bezwzględne wartości długości odcinków i w I a z wzrost, to znaczy linia zerowa odsuwa się od środka ciężkości, pozostając równolegle do siebie (ryc. 12.13). W limicie w Z P = y P = 0 (siła jest przyłożona w środku ciężkości) linia zero jest usuwana do nieskończoności. W takim przypadku naprężenia w przekroju będą stałe i równe o = -P/F.
• 3. Jeżeli punkt przyłożenia siły r znajduje się na jednej z głównych osi, linia zerowa jest równoległa do drugiej osi. Rzeczywiście, wkładając (12.15), na przykład, y r= 0, otrzymujemy to i w= czyli linia zero nie przecina osi OU(Rys. 12.14).
• 4. Jeżeli punkt przyłożenia siły porusza się po linii prostej, która nie przechodzi przez środek ciężkości, to linia zerowa obraca się wokół pewnego punktu. Udowodnijmy tę właściwość. Punkty przyłożenia sił Rx I R 2, znajdujące się na osiach współrzędnych odpowiadają liniom zerowym 1 - 1 i 2-2, równoległym do osi (rys. 12.15), które przecinają się w punkcie D. Ponieważ ten punkt należy do dwóch linii zerowych, naprężenia w tym punkcie od jednocześnie przyłożonych sił Rx I R 2 będzie równy zero. Ponieważ jakakolwiek siła R 3 , punkt przyłożenia znajduje się na linii prostej R ( R 2 , mogą

rozłożyć na dwie równoległe składowe przyłożone w punktach Pj i R 2, z tego wynika, że ​​naprężenia w punkcie D od siły R3 są również równe zero. Tak więc linia zerowa 3-3, odpowiadająca sile R 3 , przechodzi przez punkt D.

Innymi słowy, zestaw punktów R, położony na linii prostej R ( R 2 , odpowiada ołówkowi linii przechodzących przez punkt D. Prawdą jest również stwierdzenie odwrotne: kiedy linia zerowa obraca się wokół pewnego punktu, punkt przyłożenia siły porusza się po linii prostej, która nie przechodzi przez środek ciężkości.

Jeśli linia zerowa przecina przekrój, dzieli go na strefy ściskania i rozciągania. Podobnie jak w przypadku zginania skośnego, z hipotezy płaskiego przekroju wynika, że ​​naprężenia osiągają największe wartości w punktach najbardziej oddalonych od linii zerowej. Charakter wykresu naprężeń w tym przypadku pokazano na ryc. 12.16, ale.

Jeżeli linia zerowa znajduje się poza sekcją, to we wszystkich punktach sekcji naprężenia będą miały ten sam znak (ryc. 12.16, b).

Przykład 12.3. Skonstruujmy wykres naprężeń normalnych w dowolnym przekroju mimośrodowo ściskanego słupa prostokątnego o wymiarach b x h(Rys. 12.17). Kwadraty promieni bezwładności przekroju według (12.22) wynoszą

Odcinki odcięte linią zerową na osiach współrzędnych określają wzory (12.15):

Podstawiając kolejno do (12.12) współrzędne punktów C i najbardziej odległego od linii zerowej W(Rys. 12.18)

znajdować

Wykres o pokazano na ryc. 12.18. Najwyższe naprężenia ściskające w wartości bezwzględnej są czterokrotnie wyższe niż wartości naprężeń, które byłyby w przypadku centralnego przyłożenia siły. Ponadto w przekroju pojawiły się znaczne naprężenia rozciągające. Zauważ, że z (12.12) wynika, że ​​w środku ciężkości (y = z\u003d 0) naprężenia są równe o \u003d -P/F.

Przykład 12.4. Listwa wycinająca obciążona siłą rozciągającą r(ryc. 12.19, ale). Porównaj naprężenia w sekcji lv, wystarczająco daleko od końca i wycięcia, z naprężeniami w przekroju Płyta CD na wycięciu.

w sekcji AB(ryc. 12.19, b) siła r powoduje centralne napięcie i naprężenia są a = P/F = P/mc.

w sekcji Płyta CD(ryc. 12.19, w) linia siły r nie przechodzi przez środek ciężkości sekcji i dlatego występuje napięcie mimośrodowe. Zmieniając znak we wzorze (12.12) na przeciwny i biorąc y r= 0, otrzymujemy dla tego odcinka

Nabierający

Linia zero w sekcji Płyta CD równolegle do osi OU i przecina oś Oz na odległość a =-i 2 r /z P- b/ 12. W punktach odcinka najbardziej oddalonych od linii zerowej C(z - -b/ 4) i D(z-b/ 4) naprężenia według (12.16) są równe

Wykresy naprężeń normalnych dla przekrojów LV I Płyta CD pokazano na ryc. 12.19, pne.

Tak więc pomimo tego, że przekrój Płyta CD ma powierzchnię dwa razy mniejszą od przekroju AB, ze względu na mimośrodowe przyłożenie siły naprężenia rozciągające w osłabionej sekcji zwiększają się nie dwukrotny, ale ośmiokrotny. Ponadto w tej sekcji pojawiają się znaczne naprężenia ściskające.

Należy zauważyć, że powyższe obliczenia nie uwzględniają dodatkowych lokalnych naprężeń, które powstają w pobliżu punktu C ze względu na obecność wgłębienia. Naprężenia te zależą od promienia podcięcia (zwiększają się wraz ze zmniejszającym się promieniem) i mogą znacznie przekroczyć stwierdzoną wartość CZ = 8P/mc. W tym przypadku charakter wykresu naprężeń w pobliżu punktu C będzie znacznie różnił się od liniowego. Definicję naprężeń lokalnych (koncentrację naprężeń) omówiono w rozdziale 18.

Wiele materiałów budowlanych (beton, cegła itp.) nie jest dobrze odpornych na rozciąganie. Ich wytrzymałość na rozciąganie jest wielokrotnie mniejsza niż na ściskanie. Dlatego pojawienie się naprężeń rozciągających w elementach konstrukcyjnych wykonanych z takich materiałów jest niepożądane. Aby ten warunek został spełniony, konieczne jest, aby linia zerowa znajdowała się poza sekcją. W przeciwnym razie linia zerowa przetnie przekrój i pojawią się w niej naprężenia rozciągające. Jeżeli linia zerowa jest styczna do konturu przekroju, to odpowiednie położenie punktu przyłożenia siły jest granicą. Zgodnie z właściwością 2 linii zerowej, jeśli punkt przyłożenia siły zbliży się do środka ciężkości przekroju, linia zerowa oddali się od niego. Miejscem położenia punktów granicznych odpowiadających różnym stycznym do konturu przekroju jest granica jądra sekcji. Rdzeń przekroju to wypukły obszar wokół środka ciężkości, który ma następującą właściwość: jeżeli punkt przyłożenia siły znajduje się wewnątrz lub na granicy tego obszaru, to we wszystkich punktach przekroju naprężenia mają ten sam znak. Rdzeń przekroju jest kształtem wypukłym, ponieważ linie zerowe muszą dotykać obwiedni konturu przekroju i nie przecinać go.

Przez kropkę ALE(ryc. 12.20) możesz narysować nieskończoną liczbę stycznych (linie zerowe); podczas gdy tylko styczna AC jest styczna do obwiedni i musi mu odpowiadać pewien punkt konturu rdzenia przekroju. Jednocześnie nie da się na przykład narysować stycznej do odcinka AB kontur przekroju, ponieważ przecina przekrój.

Zbudujmy jądro sekcji dla prostokąta (ryc. 12.21). Dla stycznej 1 - 1 a 7 - b/ 2; ale= . Z (12.15) znajdujemy dla punktu 1 odpowiadającego tej stycznej, z P \u003d -i 2 y / a 7 \u003d -b / 6; r r - 0. Dla stycznej 2-2 i y - k / 2; 7 \u003d ° °, a współrzędne punktu 2 będą równe wr- -h/6; z p - 0. Zgodnie z właściwością 4 linii zerowej punkty przyłożenia siły odpowiadające różnym stycznym do dolnego prawego punktu narożnego odcinka znajdują się na linii prostej 1-2. Położenie punktów 3 i 4 określa się z warunków symetrii. Zatem jądro przekroju dla prostokąta jest rombem z przekątnymi b/3 i OD.

Aby zbudować jądro przekroju dla koła, wystarczy narysować jedną styczną (ryc. 12.22). W której a = R; ale= °o.

„U ^^

Biorąc to pod uwagę dla koła ja y - J y /F - R / 4, z (12.15) otrzymujemy

Zatem jądro przekroju dla okręgu jest okręgiem o promieniu R/4.

Na ryc. 12.23, a, 6 pokazano rdzenie przekroju dla belki dwuteowej i kanału. Obecność czterech punktów narożnych rdzenia przekroju w każdym z tych przykładów wynika z faktu, że obwiednia konturu zarówno dla belki dwuteowej, jak i kanału jest prostokątem.

Mimośrodowe rozciąganie (ściskanie) jest powodowane siłą równoległą do osi belki, ale nie zbieżną z nią (rys. 9.4).

Rzut punktu przyłożenia siły na przekrój nazywany jest biegunem lub punktem mocy, a linia prosta przechodząca przez biegun i środek przekroju nazywana jest linią siły.

Mimośrodowe rozciąganie (ściskanie) można zredukować do rozciągania osiowego (ściskania) i ukośnego zginania, jeśli siła P zostanie przeniesiona na środek ciężkości przekroju. Tak więc siła P, zaznaczona na ryc. 9.4 z jedną kreską D spowoduje osiowe rozciąganie belki, a para sił zaznaczona dwoma kreskami spowoduje ukośne zgięcie.

W oparciu o zasadę niezależności działania sił naprężeń w punktach przekroju podczas rozciągania mimośrodowego (ściskania) określa się wzorem

W tym wzorze należy zastąpić ich znakami siłę osiową, momenty zginające oraz współrzędne punktu przekroju, w którym wyznaczane jest naprężenie. W przypadku momentów zginających przyjmiemy tę samą zasadę znaku, co w przypadku zginania ukośnego, a siłę osiową będziemy uważać za dodatnią, gdy powoduje rozciąganie.

Jeżeli współrzędne bieguna oznaczone są przez , to moment Formuła (9.5) przyjmuje postać

Z tego równania widać, że końce wektorów naprężeń w punktach przekroju leżą na płaszczyźnie. Linia przecięcia płaszczyzny naprężenia z płaszczyzną przekroju jest linią neutralną, której równanie znajduje się przez zrównanie prawa strona równość (9.6) do zera. Po redukcji przez P otrzymujemy

Zatem linia neutralna podczas rozciągania mimośrodowego (ściskania) nie przechodzi przez środek ciężkości przekroju i nie jest prostopadła do płaszczyzny działania momentu zginającego. Linia neutralna odcina segmenty na osiach współrzędnych

Reprezentujemy momenty bezwładności jako iloczyn pola przekroju i kwadratu odpowiedniego promienia bezwładności

Wtedy wyrażenia (9.8) można zapisać w następujący sposób:

Ze wzorów (9.8) widać, że biegun i linia neutralna znajdują się zawsze po przeciwnych stronach środka ciężkości przekroju, a położenie linii neutralnej określają współrzędne bieguna.

Gdy biegun zbliży się do środka ciężkości odcinka wzdłuż linii siły, linia neutralna odsunie się od środka, pozostając równolegle do swojego pierwotnego kierunku. Na granicy w , linia neutralna cofa się do nieskończoności. W takim przypadku wystąpi centralne naprężenie (ściskanie) belki.

Na linii siły zawsze można znaleźć takie położenie słupa, w którym linia neutralna dotknie konturu przekroju, nigdzie go nie przecinając. Jeśli narysujemy wszystkie możliwe linie neutralne tak, aby dotykały konturu przekroju, nie przecinając go nigdzie i znajdziemy odpowiadające im bieguny, to okaże się, że bieguny będą znajdować się na linii zamkniętej, która jest dość specyficzna dla każdego Sekcja. Obszar ograniczony tą linią nazywany jest rdzeniem odcinka. Na przykład w przekroju kołowym rdzeń jest kołem o średnicy 4 razy mniejszej niż średnica przekroju, a w przekrojach prostokątnych i dwuteowych rdzeń ma kształt równoległoboku (ryc. 9.5).

Z samej konstrukcji rdzenia sekcji wynika, że ​​dopóki słup znajduje się wewnątrz rdzenia, linia neutralna nie będzie przecinać konturu sekcji i naprężenia w całym przekroju będą miały ten sam znak. Jeżeli jednak słup znajduje się poza rdzeniem, to linia neutralna przetnie obrys przekroju, a następnie w przekroju będą działać naprężenia różnych znaków. Ta okoliczność musi być wzięta pod uwagę przy obliczaniu ściśnięcia poza środkiem regałów wykonanych z kruchych materiałów. Ponieważ kruche materiały słabo odbierają obciążenia rozciągające, pożądane jest przyłożenie sił zewnętrznych do zębatki, aby w całej sekcji działały tylko naprężenia ściskające. W tym celu punkt przyłożenia wypadkowej sił zewnętrznych ściskających zębatkę musi znajdować się wewnątrz rdzenia sekcji.

Obliczenia wytrzymałości przy mimośrodowym rozciąganiu i ściskaniu przeprowadza się w taki sam sposób, jak przy zginaniu ukośnym - zgodnie z naprężeniem w niebezpiecznym punkcie przekroju. Niebezpieczny jest punkt odcinka, najbardziej oddalony od jego neutralnej linii. Jednak w przypadkach, gdy w tym miejscu występuje naprężenie ściskające, a materiał rozpórki jest kruchy, punkt, w którym naprężenie rozciągające jest największe, może być niebezpieczny.

Wykres naprężeń jest zbudowany na osi prostopadłej do linii neutralnej przekroju i jest ograniczony linią prostą (patrz rys. 9.4).

Warunek wytrzymałości jest zapisany w następujący sposób.

Ryż. 12.3. Mimośrodowe napięcie belki

Naprężenia w dowolnym punkcie przekroju o współrzędnych (x, y) w oparciu o zasadę niezależności działania sił można obliczyć w następujący sposób (suma algebraiczna)

Z ich równania (12.4) wynika, że ​​wykres naprężeń w rozważanym przekroju tworzy płaszczyznę. Równanie linii neutralnej, w punktach, w których normalne naprężenia są równe zeru, otrzymujemy z (12.4), przyrównując wyrażenie do zera, tj.

(12.5)

Z otrzymanego równania wynika, że ​​linia neutralna nie przechodzi przez środek ciężkości odcinka, który pokrywa się z początkiem. Dodatkowo, jeśli współrzędne punktu przyłożenia siły (x 0, y 0) są dodatnie, to zgodnie z przynajmniej jedna ze współrzędnych x lub y równania (12.4) musi być ujemna, a zatem, jeśli punkt przyłożenia siły znajduje się w pierwszej ćwiartce, to linia neutralna musi przechodzić przez ćwiartki 2, 3 i 4 (rys. 12.4) .

Wiadomo (geometria analityczna), że jeśli prostą da się równaniem postaci

wtedy odległość od początku współrzędnych do prostej będzie równa

W rozważanym przypadku (12.5) otrzymujemy (ryc. 12.4)

(12.5a)

Z otrzymanego wyrażenia wynika, że ​​gdy punkt przyłożenia siły P zbliża się do środka ciężkości przekroju, tj. wraz ze spadkiem wartości współrzędnych x 0 , y 0 zwiększa się odległość ρ od środka ciężkości przekroju do linii neutralnej.

σC

x

tak

ALE

Rys.12.4. Rozkład naprężeń w rozciąganiu mimośrodowym

W limicie przy x 0 = y 0 = 0, tj. gdy siła P jest przyłożona w środku ciężkości przekroju, linia neutralna znajduje się w nieskończoności. W tym przypadku następuje proste (środkowe) rozciąganie lub ściskanie, wszystkie naprężenia w przekroju mają ten sam znak i są sobie równe.

Jeżeli linia neutralna przecina przekrój, to po jednej jej stronie pojawia się strefa rozciągania, a po drugiej strefa ściskania (ryc. 12.4). Rysując linie równoległe do linii neutralnej i styczne do konturu przekroju, można znaleźć najbardziej oddalone od linii neutralnej punkty, w których naprężenia normalne osiągają swoje maksymalne wartości. W rozpatrywanym przypadku są to punkty C i D.

Warunki wytrzymałościowe w tych punktach zapisujemy w formularzu

gdzie x C , y C , x D , y D są współrzędnymi punktów niebezpiecznych. Znaki pojęć we wzorach (12.6) dobierane są na podstawie analizy kierunków działania momentów zginających i siły normalnej. Jeśli linia neutralna nie przecina przekroju, wszystkie normalne naprężenia będą miały ten sam znak.

Obszar w pobliżu środka ciężkości przekroju, który ma tę właściwość, że przy przyłożeniu siły P w tym obszarze naprężenia we wszystkich punktach przekroju będą tego samego znaku, nazywa się jądro sekcji.

Niektóre materiały (beton, cegła, żeliwo szare) wytrzymują rozciąganie znacznie gorzej niż ściskanie. W przypadku odpowiednich konstrukcji ważne jest, aby w materiale nie występowały naprężenia rozciągające, co oznacza, że ​​siły ściskające muszą być przyłożone w rdzeniu przekroju.

Jeżeli siła mimośrodowego rozciągania (ściskania) jest przyłożona na granicy rdzenia przekroju, to linia neutralna dotyka konturu przekroju. Warunek ten służy do określenia wymiarów rdzenia przekroju. Np. dla pręta o przekroju kołowym z warunku symetrii geometrycznej wynika, że ​​rdzeń przekroju powinien mieć kształt koła (rys. 12.5). Niech punkt przyłożenia siły Р będzie leżał na osi Oy w odległości od początku współrzędnych równej r (współrzędne punktu przyłożenia siły to x 0 =0, y 0 =r). Równanie linii neutralnej w tym przypadku ma postać (patrz wzór 12.5)

To jest równanie prostej osi równoległej Ox. Ponieważ rdzeń przekroju jest okręgiem o promieniu r, linia neutralna musi dotykać konturu w punkcie A (ryc. 12.5). Odległość od początku współrzędnych i linii neutralnej jest równa promieniowi obwodu przekroju poprzecznego belki R. Następnie, biorąc pod uwagę wyrażenie (12,5a), znajdujemy

Stąd r=R/4, tj. rdzeń belki o przekroju kołowym o promieniu R jest kołem o promieniu R/4.

Ekscentryczna kompresja. Budynek jądra sekcji. Zginanie ze skrętem. Obliczenia wytrzymałości w złożonym stanie naprężeń.

Kompresja poza środkiem jest rodzaj odkształcenia, w którym siła wzdłużna w przekroju pręta nie jest przykładana w środku ciężkości. Na mimośrodowa kompresja, oprócz siły wzdłużnej (N) występują dwa momenty zginające ( i ).

Uważa się, że pręt ma dużą sztywność zginania, aby pominąć ugięcie pręta przy mimośrodowym ściskaniu.

Przekształćmy wzór momentów na ściskanie mimośrodowe , podstawiając wartości momentów zginających: .

Oznaczmy współrzędne pewnego punktu linii zerowej przy ściskaniu mimośrodowym i podstawmy je do wzoru na naprężenia normalne przy ściskaniu mimośrodowym. Biorąc pod uwagę, że naprężenia w punktach linii zerowej są równe zeru, po redukcji o , otrzymujemy równanie linii zerowej dla ściskania mimośrodowego: .

Linia zerowa dla ściskania mimośrodowego i punkt przyłożenia obciążenia zawsze znajdują się po przeciwnych stronach środka ciężkości przekroju.

Segmenty odcięte linią zerową od osi współrzędnych, oznaczone i , można łatwo znaleźć w równaniu linii zerowej dla kompresji mimośrodowej. Jeśli najpierw zaakceptujemy a potem zaakceptuj , wówczas znajdujemy punkty przecięcia linii zerowej poddanej mimośrodowemu ściskaniu z głównymi osiami centralnymi:

Linia zerowa pod ściskaniem mimośrodowym podzieli przekrój na dwie części. W jednej części naprężenia będą ściskające, w drugiej - rozciągające. Obliczenia wytrzymałościowe, podobnie jak w przypadku zginania skośnego, przeprowadza się według naprężeń normalnych występujących w niebezpiecznym punkcie przekroju (najdalej od linii zerowej).

Rdzeń przekroju - niewielki obszar wokół środka ciężkości przekroju, charakteryzujący się tym, że każda podłużna siła ściskająca przyłożona wewnątrz rdzenia powoduje naprężenia ściskające we wszystkich punktach przekroju.

Przykłady jądra przekroju dla przekrojów prostokątnych i okrągłych prętów.

Zginanie ze skrętem. Takiemu obciążeniu często podlegają wały maszyn i mechanizmów (jednoczesne działanie momentów obrotowych i zginających). Aby obliczyć wiązkę, konieczne jest przede wszystkim ustalenie niebezpiecznych odcinków. W tym celu budowane są krzywe momentów zginających i momentów skręcających.

Wykorzystując zasadę niezależności działania sił, naprężenia powstające w belce wyznaczamy osobno dla skręcania i zginania.

Podczas skręcania w przekrojach belki powstają naprężenia styczne osiągające największą wartość w punktach zarysu przekroju Podczas zginania w przekrojach belki powstają naprężenia normalne, osiągające najwyższą wartość w skrajnych włóknach belki .

Rozważmy pręt prosty obciążony na końcu siłami skierowanymi równolegle do osi Oh. Wypadkowa tych sił F stosowane w punkcie OD. W lokalnym praworęcznym układzie współrzędnych yOz, pokrywające się z głównymi osiami środkowymi przekroju, współrzędne punktu OD równy ale I b(Rys. 5.18).

Zastąpmy przyłożone obciążenie statycznie równoważnym układem sił i momentów. Aby to zrobić, przenosimy wypadkową siłę F do środka ciężkości sekcji O i obciążyć pręt dwoma momentami zginającymi równymi iloczynowi siły T^ na jego ramionach względem osi współrzędnych: Mff = Fa I Mz = Fb.

Należy zauważyć, że zgodnie z zasadą prawoskrętnego układu współrzędnych dla punktu C, który leży w pierwszej ćwiartce, momenty zginające będą formalnie otrzymywać następujące

Ryż. 5.18.Pręt prosty obciążony na końcu siłami skierowanymi równolegle do osiOh

dmuchanie znaków: Mój \u003d Fa i M 7 = -Pełne wyżywienie. W tym przypadku w obszarze elementarnym leżącym w pierwszej ćwiartce oba momenty powodują naprężenie rozciągające.

Wykorzystując zasadę niezależności działania sił wyznaczamy naprężenia w aktualnym punkcie przekroju o współrzędnych w I z z każdego współczynnika mocy osobno. Całkowite napięcie uzyskuje się przez zsumowanie wszystkich trzech składowych napięcia:

Określmy położenie osi neutralnej. W tym celu, zgodnie ze wzorem (5.69), przyrównujemy do zera wartość naprężenia normalnego w aktualnym punkcie:

W wyniku prostych przekształceń otrzymujemy równanie linii neutralnej

gdzie ja ty I i z - główne promienie bezwładności określone wzorami (3.14).

Zatem w przypadku mimośrodowego rozciągania-ściskania linia obojętna nie przechodzi przez środek ciężkości przekroju (rys. 5.19), na co wskazuje obecność w równaniu (5.70) członu swobodnego, który różni się od zera.

Maksymalne naprężenia występują w punktach przekroju ALE I W, najdalej od linii neutralnej. Ustalmy zależność między współrzędnymi punktu przyłożenia siły a położeniem linii neutralnej. Aby to zrobić, określamy punkty przecięcia osi współrzędnych tą linią:

Ryż. 5.19.

Z otrzymanych wzorów wynika, że ​​współrzędna punktu przyłożenia siły ale i współrzędną punktu przecięcia linii neutralnej osi współrzędnych Oz(punkt r 0) mają przeciwne znaki. To samo można powiedzieć o ilościach b I o 0 . Tak więc punkt przyłożenia siły wypadkowej i linia neutralna znajdują się po przeciwnych stronach początku.

Zgodnie z otrzymanymi wzorami, w miarę zbliżania się punktu przyłożenia siły do ​​środka ciężkości przekroju, linia neutralna oddala się od strefa centralna. W przypadku granicznym (a = b = 0) dochodzimy do przypadku centralnego naprężenia-kompresji.

Interesujące jest określenie strefy przyłożenia siły, w której naprężenia w przekroju będą miały ten sam znak. W szczególności w przypadku materiałów słabo odpornych na rozciąganie racjonalne jest przykładanie siły ściskającej właśnie w tej strefie, tak aby w przekroju działały tylko naprężenia ściskające. Taka strefa wokół środka ciężkości odcinka nazywa się rdzeń sekcji.

Jeżeli siła jest przyłożona do rdzenia sekcji, linia neutralna nie przecina sekcji. Jeżeli siła jest przyłożona wzdłuż granicy rdzenia przekroju, linia neutralna dotyka konturu przekroju. Do określenia rdzenia sekcji można użyć wzoru (5.71).

Jeśli przedstawimy linię neutralną jako styczną do konturu przekroju i weźmiemy pod uwagę wszystkie możliwe położenia stycznej oraz punkty przyłożenia siły odpowiadające tym pozycjom, wówczas punkty przyłożenia siły zarysują rdzeń Sekcja.

Ryż. 5.20.

ale - elipsa; 6 - prostokąt