Tutaj zebrane są podstawowe informacje o piramidach i związanych z nimi formułach i koncepcjach. Wszystkie są uczone z korepetytorem z matematyki w ramach przygotowań do egzaminu.
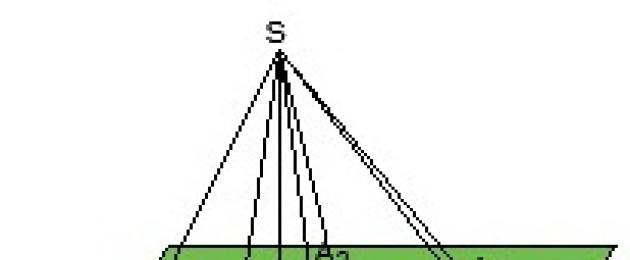
Rozważ płaszczyznę, wielokąt 
leży w nim i punkt S nie leży w nim. Połącz S ze wszystkimi wierzchołkami wielokąta. Powstały wielościan nazywa się piramidą. Segmenty nazywane są krawędziami bocznymi. 
Wielokąt nazywamy podstawą, a punkt S nazywamy wierzchołkiem piramidy. W zależności od liczby n piramida nazywana jest trójkątną (n=3), czworokątną (n=4), pięciokątną (n=5) i tak dalej. Alternatywna nazwa trójkątnej piramidy - czworościan. Wysokość piramidy to prostopadła poprowadzona od jej wierzchołka do płaszczyzny podstawy. 
Piramida nazywana jest poprawną, jeśli wielokąt foremny, a podstawą wysokości piramidy (podstawa pionu) jest jej środek.
Komentarz korepetytora:
Nie myl pojęcia „regularnej piramidy” i „regularnego czworościanu”. W ostrosłupie foremnym krawędzie boczne niekoniecznie są równe krawędziom podstawy, ale w czworościanie foremnym wszystkie 6 krawędzi krawędzi są równe. To jest jego definicja. Łatwo udowodnić, że z równości wynika, że środek wielokąta P z podstawą wysokości, więc czworościan foremny jest regularną piramidą.
Czym jest apotem?
Apotem piramidy jest wysokość jej bocznej ściany. Jeśli piramida jest regularna, wszystkie jej apotemy są równe. Odwrotność nie jest prawdą. 
Nauczyciel matematyki o swojej terminologii: praca z piramidami składa się w 80% z dwóch rodzajów trójkątów:
1) Zawiera apotem SK i wysokość SP
2) Zawiera krawędź boczną SA i jej występ PA 
Aby uprościć odniesienia do tych trójkątów, wygodniej jest, aby nauczyciel matematyki wymienił pierwszy z nich apotemiczny, i drugi żebrowy. Niestety nie znajdziesz tej terminologii w żadnym podręczniku, a nauczyciel musi ją wprowadzić jednostronnie.
Formuła objętości piramidy:
1) 
, gdzie jest pole powierzchni podstawy piramidy, a wysokość piramidy
2) , gdzie jest promieniem wpisanej kuli i jest całkowitą powierzchnią piramidy.
3) 
, gdzie MN jest odległością dowolnych dwóch przecinających się krawędzi i jest obszarem równoległoboku utworzonego przez punkty środkowe czterech pozostałych krawędzi.
Właściwość podstawy wysokości piramidy:
Punkt P (patrz rysunek) pokrywa się ze środkiem okręgu wpisanego u podstawy piramidy, jeśli spełniony jest jeden z następujących warunków:
1) Wszystkie apotemy są równe
2) Wszystkie powierzchnie boczne są jednakowo nachylone w kierunku podstawy
3) Wszystkie apotemy są jednakowo nachylone do wysokości piramidy
4) Wysokość piramidy jest jednakowo nachylona do wszystkich ścian bocznych
Komentarz nauczyciela matematyki: zauważ, że wszystkie punkty łączy jedna wspólna właściwość: tak czy inaczej, ściany boczne uczestniczą wszędzie (apotemy są ich elementami). Dlatego prowadzący może zaproponować mniej precyzyjne, ale wygodniejsze sformułowanie do zapamiętywania: punkt P pokrywa się ze środkiem koła wpisanego, podstawą piramidy, jeśli istnieją jakiekolwiek równe informacje o jej bocznych ścianach. Aby to udowodnić, wystarczy wykazać, że wszystkie apotemiczne trójkąty są równe.
Punkt P pokrywa się ze środkiem opisanego okręgu w pobliżu podstawy piramidy, jeśli spełniony jest jeden z trzech warunków:
1) Wszystkie krawędzie boczne są równe
2) Wszystkie boczne żebra są jednakowo nachylone w kierunku podstawy
3) Wszystkie boczne żebra są równomiernie nachylone do wysokości
Ta lekcja zawiera definicję i właściwości regularnej trójkątnej piramidy i jej szczególnego przypadku - czworościanu (patrz poniżej). Linki do przykładów rozwiązywania problemów znajdują się na końcu lekcji.
Definicja
Regularna trójkątna piramida- To jest piramida, której podstawa jest regularnym trójkątem, a wierzchołek jest rzutowany na środek podstawy.
Rysunek przedstawia:
ABC- Baza piramidy
System operacyjny — wysokość
KS - Apotema
OK - promień okręgu wpisanego w podstawę
AO - promień okręgu opisanego wokół podstawy regularnej trójkątnej piramidy
SKO - kąt dwuścienny między podstawą a lico piramidy (w ostrosłupie regularnej są one równe)
Ważny. W piramidzie trójkątnej foremnej długość krawędzi (na rysunku AS, BS, CS) nie może być równa długości boku podstawy (na rysunku AB, AC, BC). Jeśli długość krawędzi regularnej trójkątnej piramidy jest równa długości boku podstawy, wówczas taka piramida nazywana jest czworościanem (patrz poniżej).
Właściwości regularnej trójkątnej piramidy:
- boczne krawędzie ostrosłupa foremnego są równe
- wszystkie ściany boczne regularnej piramidy są trójkątami równoramiennymi
- w regularnej trójkątnej piramidzie można zarówno wpisać, jak i opisać otaczającą ją sferę
- jeżeli środki sfer wpisanych i opisanych wokół regularnej trójkątnej piramidy pokrywają się, to suma kątów płaskich na szczycie piramidy jest równa π (180 stopni), a każdy z nich odpowiednio jest równy π / 3 (pi podzielone przez 3 lub 60 stopni).
- powierzchnia bocznej powierzchni regularnej piramidy jest równa połowie iloczynu obwodu podstawy i apotemu
- wierzchołek piramidy jest rzutowany na podstawę w środku regularnego trójkąta równobocznego, który jest środkiem okręgu wpisanego i punktem przecięcia środkowych
Wzory na regularną trójkątną piramidę
Wzór na objętość regularnej trójkątnej piramidy to:
V to objętość regularnej piramidy z regularnym (równobocznym) trójkątem u podstawy
h - wysokość piramidy
a - długość boku podstawy piramidy
R - promień okręgu opisanego
r - promień okręgu wpisanego
Ponieważ regularna piramida trójkątna jest szczególnym przypadkiem regularnej piramidy, formuły, które są prawdziwe dla regularnej piramidy, są również prawdziwe dla regularnej piramidy trójkątnej — patrz formuły dla regularnej piramidy.
Przykłady rozwiązywania problemów:
Czworościan
Szczególnym przypadkiem regularnej trójkątnej piramidy jest czworościan.
Czworościan jest foremnym wielościanem (ostrosłupem trójkątnym regularnym), w którym wszystkie ściany są trójkątami foremnymi.
Na czworościanie:
- Wszystkie krawędzie są równe
- 4 ściany, 4 wierzchołki i 6 krawędzi
- Wszystkie kąty dwuścienne na krawędziach i wszystkie kąty trójścienne na wierzchołkach są równe
Mediana czworościanu- jest to odcinek łączący wierzchołek z punktem przecięcia się środkowych przeciwległej ściany (środkowego trójkąta równobocznego naprzeciw wierzchołka)
Czworościan bimedialny- jest to odcinek łączący środki przecinających się krawędzi (łączący środki boków trójkąta, który jest jednym z lic czworościanu)
Wysokość czworościanu- jest to odcinek łączący wierzchołek z punktem przeciwnej ściany i prostopadły do tej ściany (czyli jest to wysokość narysowana z dowolnej ściany, również pokrywa się ze środkiem opisanego koła).
Czworościan ma następujące nieruchomości:
- Wszystkie mediany i bimediany czworościanu przecinają się w jednym punkcie
- Ten punkt dzieli mediany w stosunku 3:1, licząc od góry
- Ten punkt przecina bimediany
Rozdział 1. Teoretyczne badanie rodzajów przekrojów i metod ich budowy w regularnej ostrosłupie czworokątnej
Piramida (starogrecki Πυραμίς, rodzaj P. πυραμίδος) to wielościan, którego podstawą jest wielokąt, a pozostałe ściany to trójkąty o wspólnym wierzchołku. Według liczby rogów podstawy piramidy są trójkątne, czworokątne itp. Piramida jest szczególnym przypadkiem stożka.
Początek geometrii piramidy został położony w starożytnym Egipcie i Babilonie, ale był aktywnie rozwijany w starożytnej Grecji. Pierwszym, który ustalił, jaka jest objętość piramidy, był Demokryt, a Eudoksos z Knidos to udowodnił. Starożytny grecki matematyk Euklides usystematyzował wiedzę o piramidzie w XII tomie swoich „Początków”, a także przedstawił pierwszą definicję piramidy: bryła ograniczona płaszczyznami, które zbiegają się z jednej płaszczyzny w jednym punkcie.
elementy piramidy
apotem - wysokość bocznej ściany regularnej piramidy, narysowana od jej wierzchołka;
ściany boczne - trójkąty zbiegające się na szczycie piramidy;
krawędzie boczne - wspólne strony ścian bocznych;
Wierzchołek piramidy jest punktem łączącym boczne krawędzie i nie leżącym w płaszczyźnie podstawy;
wysokość - odcinek prostopadły poprowadzony przez wierzchołek ostrosłupa do płaszczyzny jego podstawy (końce tego odcinka to wierzchołek ostrosłupa i podstawa prostopadłego);
Przekątna ostrosłupa - przekrój ostrosłupa przechodzący przez szczyt i przekątną podstawy;
podstawa - wielokąt, który nie należy do wierzchołka piramidy.
Właściwości piramidy:
Liczba ścian piramidy jest równa liczbie jej wierzchołków.
Dowolny wielościan o takiej samej liczbie ścian jak liczba wierzchołków jest piramidą. Całkowita liczba wierzchołków w piramidzie wynosi n+1, gdzie n to liczba wierzchołków przy podstawie.
Jeśli wszystkie krawędzie boczne są równe, następnie:
§ w pobliżu podstawy piramidy można opisać okrąg, a wierzchołek piramidy rzutowany jest na jej środek;
§ Żebra boczne tworzą równe kąty z płaszczyzną podstawy.
§ Prawdą jest również odwrotność, to znaczy, jeśli boczne krawędzie tworzą równe kąty z płaszczyzną podstawy lub jeśli w pobliżu podstawy ostrosłupa można opisać okrąg, a wierzchołek ostrosłupa jest rzutowany na jego środek, to wszystko boczne krawędzie piramidy są równe.
Jeśli powierzchnie boczne są nachylone do płaszczyzny bazowej pod jednym kątem, następnie:
§ w podstawę piramidy można wpisać okrąg, a wierzchołek piramidy rzutowany jest na jej środek;
§ wysokości ścian bocznych są równe;
§ pole powierzchni bocznej jest równe połowie iloczynu obwodu podstawy i wysokości lica bocznego.
Rodzaje przekrojów w regularnej piramidzie czworokątnej:
Ukośny przekrój piramidy
- apotem- wysokość ściany bocznej ostrosłupa foremnego, która jest rysowana od jej wierzchołka (dodatkowo apotem to długość pionu, który jest obniżony ze środka wielokąta foremnego na 1 z jego boków);
- twarze boczne (ASB, BSC, CSD, DSA) - trójkąty zbiegające się u góry;
- boczne żeberka ( JAK , BS , CS , D.S. ) - wspólne strony ścian bocznych;
- szczyt piramidy (vs) - punkt, który łączy boczne krawędzie i który nie leży w płaszczyźnie podstawy;
- Wysokość ( WIĘC ) - odcinek prostopadłego, który jest przeciągnięty przez wierzchołek piramidy do płaszczyzny jej podstawy (końce takiego odcinka będą wierzchołkiem piramidy i podstawą prostopadłej);
- przekrój ukośny piramidy- przekrój piramidy przechodzący przez górę i po przekątnej podstawy;
- baza (ABCD) jest wielokątem, do którego nie należy wierzchołek piramidy.
właściwości piramidy.
1. Gdy wszystkie krawędzie boczne mają ten sam rozmiar, wówczas:
- przy podstawie piramidy łatwo opisać okrąg, podczas gdy wierzchołek piramidy będzie rzutowany na środek tego okręgu;
- żebra boczne tworzą równe kąty z płaszczyzną podstawy;
- ponadto prawdziwa jest również odwrotność, tj. gdy krawędzie boczne tworzą równe kąty z płaszczyzną podstawy lub gdy można opisać okrąg w pobliżu podstawy ostrosłupa i wierzchołek ostrosłupa będzie rzutowany na środek tego koła, to wszystkie boczne krawędzie ostrosłupa mają ten sam rozmiar.
2. Gdy ściany boczne mają kąt nachylenia do płaszczyzny podstawy o tej samej wartości, wówczas:
- w pobliżu podstawy piramidy łatwo opisać okrąg, podczas gdy wierzchołek piramidy będzie rzutowany na środek tego okręgu;
- wysokości ścian bocznych są jednakowej długości;
- powierzchnia powierzchni bocznej to ½ iloczynu obwodu podstawy i wysokości powierzchni bocznej.
3. Kulę można opisać w pobliżu piramidy, jeśli podstawą piramidy jest wielokąt, wokół którego można opisać okrąg (warunek konieczny i wystarczający). Środek kuli będzie punktem przecięcia płaszczyzn przechodzących przez środki krawędzi prostopadłych do nich ostrosłupów. Z tego twierdzenia wnioskujemy, że sferę można opisać zarówno wokół dowolnej trójkątnej, jak i wokół dowolnej regularnej piramidy.
4. Kulę można wpisać w piramidę, jeżeli dwusieczne płaszczyzny wewnętrznych kątów dwuściennych piramidy przecinają się w 1. punkcie (warunek konieczny i wystarczający). Ten punkt stanie się centrum kuli.
Najprostsza piramida.
W zależności od liczby rogów podstawy piramidy są one podzielone na trójkątne, czworokątne i tak dalej.
Piramida będzie trójkątny, czworokątny, i tak dalej, gdy podstawą piramidy jest trójkąt, czworokąt i tak dalej. Trójkątna piramida to czworościan - czworościan. Czworokąt - pięciościan i tak dalej.
- W kontakcie z 0
- Google+ 0
- ok 0
- Facebook 0
