"Serien "MSU - School" grundades 1999 av S. M. Sahakyan. Geometry. Lektionsbaserad utveckling. Årskurs 10-11: C12 Lärobok för allmän bildning. organisationer / S. M. Sahakyan, V. F. Butuzov. -...”

-- [ Sida 2 ] --

3. Diskutera muntligt lösningarna på problem 1, 2, 3 som ges i läroboken.

På grund av behovet av att bedriva ett kontinuerligt utvecklingsarbete muntligt tal Eleverna bör av dem åläggas att inte bara konstruera avsnitt i de problem som behandlas, utan också ge en muntlig redogörelse för byggets framsteg med lämpliga motiveringar.

För korta inspelningslösningar kan du använda välkända symboler.

Mer komplexa problem med att konstruera sektioner av en tetraeder och en parallellepiped, när datapunkterna genom vilka sektionen ritas ligger innanför ytorna, kan övervägas i valfria klasser och specialkurser.

För klass och läxor kan du använda uppgift 74, 75, 79-87, ytterligare problem för kapitel I.

Uppgift 105. Rita tetraedern DABC och markera punkterna M och N på kanterna BD och CD och den inre punkten K på ytan ABC. Konstruera en sektion av tetraedern med hjälp av MNK-planet.

Lösning Låt oss beteckna skärplanet med en bokstav.

Då M, N, M CDB, N CDB, CDB = MN.

Två fall är möjliga: 10) MN BC = P; 20) MN BC.

Låt oss överväga dem separat.

10) Rita en rät linje MN. P, K, P ABC, K ABC, ABC = PK. Vi genomför en direkt PK. Låt den skära sidorna AC och AB i punkterna E och F. Rita segmenten NE och MF. Den nödvändiga sektionen är en fyrsidig MNEF (Fig. 1.31).

20) Genom punkt K ritar vi EF BC. Vi ritar segmenten NE och MF. Den obligatoriska sektionen är en fyrsidig MNEF.

Uppgift 85. Rita parallellepipeden ABCDA1B1C1D1 och konstruera dess snitt efter plan BKL, där K är mittpunkten på kanten AA1 och L är mittpunkten på CC1.

Bevisa att den konstruerade sektionen är ett parallellogram.

Lösning Låt oss rita segmentet KL. Enligt axiom A2 ligger den i snittplanet.

Eftersom punkterna K och L är mittpunkterna på de laterala kanterna, passerar segmentet KL genom mittpunkten av diagonalen AC1, och därför, enligt egenskap 20 för parallellepipeden (objekt 13), passerar det genom mittpunkten av diagonalen BD1 (punkt O) i figur 1.32).

B, O, därför BD1. Den nödvändiga sektionen är fyrhörningen BLD1K. Eftersom dess diagonaler KL och BD1 är delade av deras skärningspunkt, är fyrhörningen BLD1K ett parallellogram.

–  –  –

1. Förklara hur man konstruerar en sektion av DABC-tetraedern med ett plan som går genom de givna punkterna M, N, K.

2. I uppgift 1-3, hitta omkretsen av sektionen om M, N, K är mittpunkterna på kanterna och varje kant på tetraedern är lika med a.

–  –  –

1. Förklara hur man konstruerar en sektion av en kub med ett plan som går genom tre givna punkter, som antingen är kubens hörn eller mittpunkterna på dess kanter (de tre givna punkterna är markerade i figurerna).

2. I uppgifterna 1-4 och 6, hitta omkretsen av sektionen om kanten på kuben är lika med a. I uppgift 5, bevisa att AE = 1 a.

–  –  –

1. Förklara hur man konstruerar ett tvärsnitt av en parallelleped med ett plan som går genom punkterna B, D och M, om M är mittpunkten på kanten B1C1.

2. Bevisa att den konstruerade sektionen är lika med lårbenets trapets.

3. Hitta sidorna på trapetsen.

Lösning.

1) Låt vara ett skärplan, ABCD = BD, BCC1B1 = BM, MN BD, och låt sektionen vara en trapetsformad BDNM.

2) BB1M = DD1N, BM = DN, likbent trapetsoid BDNM.

–  –  –

När man löser problem relaterade till sektionen av en tetraeder med ett visst plan, visar sig Menelaos sats ofta vara användbar, och i vissa andra problem Cevas sats. Därför, i klasser med fördjupade studier av matematik, är det lämpligt att kombinera studiet av stycke 14 "Problem med att konstruera sektioner" med studiet av Menelaos och Chevas satser (punkterna 95 och 96). Låt oss ge ett exempel på en sådan uppgift.

Uppgift 1. I tetraedern ABCD är punkterna K, L och M tagna på kanterna AB, AD respektive BC, så att AK: KB = 2: 3, AL = LD, BM: MC = 4: 5.

Konstruera en sektion av tetraedern med hjälp av KLM-planet och hitta förhållandet i vilket detta plan delar kanten CD.

Lösning.

1) Rita segmenten KL och KM, och fortsätt sedan segmenten KL och BD, liggande i ABD-planet, tills de skär varandra i punkt E (Fig. 1.33). Punkterna E och M ligger i skärplanet KLM och även i BCD-planet.

Genom att rita segmentet ME får vi punkt N där skärplanet KLM skär kanten CD.

Fyrdubbel vinkel KLNM är den nödvändiga sektionen.

2) Hitta förhållandet CN:ND. För detta ändamål tillämpar vi Menelaos sats på trianglarna ABD och BCD. På sidorna AB och AD i triangeln ABD finns punkterna K och L, och på förlängningen av sidan BD finns punkt E, och punkterna K, L och E ligger på samma räta linje. Därför, enligt Menelaos teorem, gäller jämlikheten

AK BE DL

= 1.

KB ED LA

–  –  –

MC BE hittar vi det erforderliga förhållandet CN: ND = 15:8.

För att använda Menelaos sats i uppgift 105 i läroboken kan du ge ytterligare en uppgift:

Ta reda på förhållandet i vilket planet MNK delar kanten AB om CN:ND = 2:1, BM = MD och punkt K är mittpunkten av medianen AL i triangeln ABC. (Svar: 3: 2.) En liknande tilläggsuppgift kan ges i uppgift 106:

Hitta förhållandet i vilket planet MNK delar kant BC om det delar kant AB i förhållandet 1:4 (räknat från punkt A), punkt K är mittpunkten på kanten CD och punkt N ligger på medianen DL av triangeln ACD, med m DN: NL = 3: 2. (Svar: 4: 3.) För att tillämpa Cevas teorem kan vi överväga följande problem:

Uppgift 2. På kanterna AB, BC och CA på tetraedern ABCD är punkterna C1, A1, B1 markerade så att AC1: C1B = 1: 2, BA1: A1C = 2: 3, CB1: B1A = 3: 1.

Bevisa att planen ADA1, BDB1 och CAC1 skär varandra i en rät linje.

–  –  –

1. Upprepa huvudfrågorna i ämnet "Parallellism av linjer och plan", efter att ha hört elevernas svar. Dessa frågor är formulerade i korten för prov nr 1.

2. Genomför matematisk diktering nr 1.1. Diktat ges in didaktiskt material.

3. Fundera på lösningar på några problem från styrkorten och från läroboken.

Studiet av ämnet "Parallellism av linjer och plan" avslutas med provarbete nr 1.2 och uppgift nr 1 i detta ämne.

–  –  –

Test nr 1.2 Alternativ 1

10. Linjerna a och b ligger i parallella plan u. Kan dessa linjer vara: a) parallella;

20. Genom punkten O som ligger mellan de parallella planen och dras räta linjer l och m. Linje l skär planen och vid punkterna A1 respektive A2 linje m - vid punkterna B1 och B2. Hitta längden från skärning A2B2 om A1B1 = 12 cm, B1O: OB2 = 3: 4.

3. Rita parallellepipeden ABCDA1B1C1D1 och konstruera dess snitt med ett plan som går genom punkterna M, N och K, som är mittpunkterna på kanterna AB, BC och DD1.

Alternativ 2

10. Linjerna a och b ligger i korsande plan och. Kan dessa linjer vara: a) parallella;

b) korsning? Gör en teckning för alla möjliga tillfällen.

20. Genom punkten O, som inte ligger mellan de parallella planen och, dras räta linjer l och m. Linje l skär planen och vid punkterna A1 respektive A2 linje m - vid punkterna B1 och B2. Hitta längden från skärning A1B1, om A2B2 = 15 cm, OB1: OB2 = 3: 5.

3. Rita tetraedern DABC och konstruera dess snitt genom ett plan som går genom punkterna M och N, som är mittpunkterna på kanterna DC och BC, och punkt K så att K DA, AK: KD = 1:3.

SVAR:

Alternativ 2 Alternativ 1

10. Fig. 1,35, a b, a b.

10. Fig. 1,34, a b, a b.

3. Sektion - trapets.

3. Sektion - femhörning.

Ris. 1.34 Fig. 1,35

Lektion nr 24 Test nr 1. Parallellism av linjer och plan Kort 1

1. Formulera axiomen A1, A2 och A3 för stereometri.

Formulera och bevisa följder från axiomen.

2. Bevisa att genom någon punkt i rymden som inte ligger på en given linje, passerar en linje parallell med den givna, och dessutom bara en.

3. Planet skär sidorna AB och AC i triangeln ABC, respektive, i punkterna B1 och C1. Det är känt att BC, AB: B1B = 5: 3, AC = 15 cm Hitta AC1.

Kort 2

1. Formulera definitionen av parallella linjer och plan. Formulera och bevisa ett teorem som uttrycker tecknet på att en linje och ett plan är parallella.

2. Bevisa att om en av två parallella linjer skär ett givet plan, så skär den andra linjen också detta plan.

3. Varje kant på tetraederns DABC är lika med 2 cm. Konstruera en sektion av tetraedern med ett plan som går genom punkterna B, C och mitten av kanten AD. Beräkna omkretsen av sektionen.

Kort 3

1. Formulera definitionen av sneda linjer. Formulera och bevisa en sats som uttrycker kännetecken för sneda linjer.

2. Bevisa att om två linjer är parallella med en tredje linje, så är de parallella.

3. Konstruera en sektion av parallellepipeden ABCDA1B1C1D1 med ett plan som går genom punkterna A, C och M, där M är mittpunkten på kanten A1D1.

Kort 4

1. Formulera definitionen av parallella plan. Formulera och bevisa ett teorem som uttrycker tecknet på att två plan är parallella.

2. Bevisa att genom var och en av två sneda linjer passerar ett plan parallellt med den andra linjen, och dessutom bara en.

3. ABCDA1B1C1D1 är en kub vars kant är 4 cm. Konstruera en sektion av kuben med ett plan som går genom punkterna A, D1 och M, där M är mittpunkten på kanten BC. Beräkna omkretsen av sektionen.

Kort 5

1. Bevisa att de motsatta ytorna på en parallell lepiped är parallella och lika.

2. Bevisa att om sidorna av två vinklar är i linje med varandra, så är dessa vinklar lika.

3. Parallella plan och skär sidan AB av vinkeln BAC, respektive, i punkterna A1 och A2, respektive sidan AC för denna vinkel, i punkterna B1 och B2. Hitta AA1 om A1A2 = 6 cm, AB2: AB1 = 3:2.

Kort 6

1. Bevisa att diagonalerna på en parallellepiped skär varandra vid en punkt och delas av denna punkt.

2. Bevisa att om två parallella plan skärs av ett tredje, så är linjerna i deras skärningspunkt parallella.

3. Punkt C ligger på segment AB. Ett plan dras genom punkt A, och parallella linjer dras genom punkterna B och C, som skär detta plan vid punkterna B1 respektive C1. Hitta längden på segment BB1 om AC: CB = 4:3, CC1 = 8 cm.

1. Provkort som innehåller grundläggande teorifrågor och några typiska uppgifter ges till eleverna i förväg (cirka två veckor före provet).

2. Som förberedelse för provet gör eleverna några anteckningar. Dessa anteckningar (eventuellt i utkast) indikerar upprepning utbildningsmaterial och förberedelser inför provet visar eleverna läraren på provdagen. De kan användas för kredit. Samtidigt tar läraren, baserat på samtalet och ytterligare frågor, reda på djupet i elevernas förståelse av ämnet.

3. Testet genomförs av läraren med hjälp av de mest förberedda eleverna - konsulter. För att göra detta behöver klassen delas in i flera grupper som var och en har 4-5 elever. En av dem är en lärarassistent i att genomföra prov. Utifrån tidigare lektioner och i början av provet ska läraren se till att konsulterna själva har goda kunskaper i utbildningsmaterialet.

4. Under lektionen gör läraren en undersökning av många elever. I slutet av lektionen godkänner han de betyg som konsulterna sätter. I vissa fall kan läraren efter lektionen kontrollera elevernas anteckningar som gjorts under lektionen och sedan sätta ett slutbetyg på provet.

5. Läraren sätter slutbetyget för halvåret baserat på aktuella betyg för självständigt och provarbete, samt elevernas muntliga svar.

Den avgörande rollen hör här till kreditbedömningen.

P E R P E N D I C U L A R N O S TY RAKA

OCH FLYG

§ 1. LINJENS PERPEDIKULARITET

OCH FLYG

–  –  –

Lektionens huvudmål Introducera begreppet vinkelräta linjer i rymden, bevisa lemmat om vinkelrätheten hos två parallella linjer till en tredje linje, definiera vinkelrätheten för en linje och ett plan, bevisa satser där kopplingen upprättas mellan linjers parallellitet och deras vinkelräthet mot planet.

1. Kom ihåg begreppet en vinkel mellan två skärande linjer, introducera begreppet vinkelräthet mellan två linjer i rymden. Observera att vinkelräta linjer kan skära och kan skära varandra (se bild 43 i läroboken).

2. Bevisa lemmat: om en av två parallella linjer är vinkelrät mot den tredje linjen, så är den andra linjen också vinkelrät mot denna linje.

Beviset bygger på användningen av begreppet en vinkel mellan räta linjer och kan utföras av eleverna själva med utgångspunkt i texten och figur 44 i läroboken.

3. Formulera definitionen av vinkelräthet mellan en linje och ett plan. Ange beteckning a. Jag ville illustrera begreppet vinkelräthet för en rät linje och ett plan med hjälp av figur 45 och exempel från livet.

4. Bevisa satsen: om en av två parallella linjer är vinkelrät mot ett plan, så är den andra linjen vinkelrät mot detta plan.

Beviset för satsen är enkelt. Den är baserad på definitionen av vinkelräthet för en linje och ett plan och det lemma som diskuterats ovan och består av två steg:

1) x, x - en godtycklig rät linje. Av villkor a följer (genom definitionen av en linjes och ett plans vinkelräthet) att a x;

2) eftersom a1 a (efter villkor) och a x, sedan (enligt lemma om vinkelrätheten av två parallella linjer till den tredje linjen) a1 x.

Så linjen a1 är vinkelrät mot en godtycklig linje x som ligger i planet. Och detta betyder att a1.

5. Bevisa den omvända satsen: om två linjer är vinkelräta mot ett plan, så är de parallella.

Beviset utförs enligt läroboken (se fig. 47, a, b). Du kan upprepa detta bevis i följande lektioner.

Vid en första anblick kan det tyckas konstigt varför denna sats kallas motsatsen till föregående sats.

När allt kommer omkring, i föregående sats var villkoret att a a1 och a, och slutsatsen av satsen var: a1. I denna sats är villkoret att a och a1, och slutsatsen är att a är a1.

Alltså, från en formell synvinkel, är denna sats inte motsatsen till den föregående, eftersom tillståndet och slutsatsen för denna sats inte sammanfaller med slutsatsen och villkoret för den föregående satsen. Ändå är det möjligt att formulera dessa satser på ett sådant sätt att var och en av dem är motsatsen till den andra.

Låt oss ge denna formulering.

Låt den räta linjen a vara vinkelrät mot planet. Sedan:

om a a1, sedan a1, och vice versa:

om a1, då a a1.

6. För klass och läxor kan du använda uppgift 116-118, 120.

Uppgift 116 a). Givet parallellepiped ABCDA1B1C1D1.

Bevisa att DC B1C1 och AB A1D1 om BAD = 90°.

Lösning.

1) I en parallellepiped är alla ytor parallellogram. Eftersom BAD = 90° (efter tillstånd), är sidan ABCD en rektangel, därför AB AD och DC BC (Fig. 2.1).

2) B1C1 BC (eftersom ansiktet BB1C1C är ett parallellogram) och BC DC. Därför, genom lemma om vinkelrätheten av två parallella linjer till den tredje B1C1 DC. Ris. 2.1

3) Det är bevisat på liknande sätt att AB A1D1. Faktum är att A1D1 AD (eftersom AA1D1D är ett parallellogram) och AB AD, därför AB A1D1.

Uppgift 120. Genom punkten O för skärningen av kvadratens diagonaler med sidan a, dras en rät linje OK, vinkelrät mot kvadratens plan.

Hitta avståndet från punkt K till kvadratens hörn om Fig. 2.2 OK = b.

Lösning.

2) Trianglarna KAO, KBO, KCO och KDO är lika på två ben, varav KA = KB = KC = KD (Fig. 2.2).

KAO får vi AO = en 2. Eftersom KA =

–  –  –

Lektion nr 26 Lektionsämne: Test för vinkelräthet av en linje och ett plan Huvudmål med lektionen Studera satsen som uttrycker testet för vinkelräthet av en linje och ett plan; överväg problem med att använda detta teorem.

Exempel på lektionsplan

1. Upprepa teoretiskt material föregående lektion genom att kartlägga eleverna.

2. Som ett förarbete för att studera nytt material, lös problem 119.

Uppgift 119. Linjen OA är vinkelrät mot plan OBC, och punkt O är mittpunkten av segmentet AD.

Bevisa att: a) AB = DB; b) AB = AC om OB = OC;

c) OB = OC om AB = AC.

Lösning.

a) OA OBC per villkor, därför OA OB per definition av rät linjes vinkelräthet mot ett plan.

OA = OD enligt villkoren för problemet, därför är den räta linjen OB den vinkelräta bisektrisen till segmentet AD, och därför AB = DB (Fig. 2.3).

b) Eftersom av villkor OA OBC, sedan OA OC. Om OB = OC, då räta trianglar AOC och AOB är lika på två ben, och därför är deras hypotenuser lika, dvs AB = AC.

c) Om AB = AC, då räta trianglar AOC och Fig. 2.3 AOB är lika långa och hypotenusa, vilket betyder att OB = OC.

3. Bevisa ett teorem som uttrycker egenskaperna för vinkelrätheten hos en rät linje och ett plan: om en rät linje är vinkelrät mot två skärande linjer som ligger i ett plan, så är den vinkelrät mot detta plan.

I processen att bevisa satsen särskiljs följande steg:

1) Först betraktar vi fallet när linje a passerar genom skärningspunkten O för linjerna p och q som ligger på planet. Vi bevisar att linje a är vinkelrät mot vilken linje som helst som ligger i planet och går genom punkten O.

2) Med hjälp av lemma om vinkelrätheten av två parallella linjer till en tredje drar vi slutsatsen att linje a är vinkelrät mot vilken linje som helst som ligger i planet. Detta innebär att a.

3) Vi betraktar nu fallet när den räta linjen a inte passerar genom skärningspunkten O för p och q. Dra i detta fall en rät linje a1 genom punkten O, parallell med den räta linjen a. Med stöd av nämnda lemma, a1 p och a1 q, och därför, enligt vad som styrkts i det första fallet, a1. Av den första satsen i punkt 16 följer därför att a. Detta avslutar beviset för satsen.

4. På grund av att beviset på satsen består av flera steg kan du bjuda in eleverna att skriva ner en bevisplan i enlighet med innehållet i bild 2.1.

Bilden kan användas för att sammanfatta den här lektionen och i nästa lektion.

5. För klass och läxor kan du använda uppgift 121, 124, 126, 128.

Uppgift 128. Genom punkten O för skärningspunkten mellan diagonalerna i parallellogrammet ABCD dras en rät linje OM så att MA = MC, MB = MD. Bevisa att linjen OM är vinkelrät mot parallellogrammets plan.

–  –  –

1. Formulera definitionen av vinkelräthet mot en linje och ett plan.

2. Sats. Om en linje är vinkelrät mot två skärande linjer som ligger i ett plan, så är den vinkelrät mot detta plan.

–  –  –

Lösning.

1) Eftersom MA = MC (efter villkor) och AO = OC (diagonalerna i parallellogrammet delas på mitten av skärningspunkten), då är segmentet MO medianen för den ekvifemorala triangeln AMC (Fig. 2.4).

Därför är MO också höjden på denna triangel, d.v.s.

2) Det är bevisat på liknande sätt, fig. 2.4 att MO BD.

3) Sedan MO AC och MO BD, då baserat på den räta linjens vinkelräthet och planet MO ABCD.

Lektion nr 27 Lektionsämne: Sats på en linje vinkelrät mot ett plan Huvudmålen med lektionen Upprepa beviset för satsen som uttrycker tecknet på vinkelrätheten för en linje och ett plan; Betrakta satsen från stycke 18: genom vilken punkt i rymden som helst går en linje vinkelrät mot ett givet plan, och bara en.

Exempel på lektionsplan

1. Upprepa beviset för satsen som uttrycker tecknet på vinkelräthet för en linje och ett plan.

2. Kontrollera selektiva lösningar på problem från läxor.

3. Formulera satsen: genom vilken punkt som helst i rymden går en rät linje vinkelrät mot ett givet plan, och endast en.

Visuellt verkar uttalandet av satsen ganska uppenbart, men dess rigorösa bevis är inte enkelt.

Elever som visar ett ökat intresse för matematik kan uppmanas att själva arbeta fram beviset hemma med hjälp av läroboken. I detta fall bör deras uppmärksamhet uppmärksammas på det faktum att i den första delen av beviset introduceras ett plan, som passerar genom en given punkt M och vinkelrätt mot en given linje a.

Förekomsten av ett sådant plan bevisas i problemet med en lösning som ges i avsnitt 17, och det unika med ett sådant plan bevisas i uppgift 133, som också ges med en lösning. Således är det fullständiga beviset för denna sats mycket besvärligt, och därför kan läraren, efter eget gottfinnande, presentera den med varierande grad av fullständighet, beroende på klassens nivå. Separata fragment av beviset (problem från punkt 17, uppgift 133) kan övervägas i lektionerna nr 28-30, ägnade åt att granska teorin och lösa problem i ämnet.

4. Genomför en frontalundersökning av eleverna med hjälp av bild 2.2.

–  –  –

5. För klass och läxor kan du använda uppgift 122, 123, 125, 127.

Uppgift 122. Linjen CD är vinkelrät mot planet för den regelbundna triangeln ABC. En linje OK dras genom mitten O i denna triangel, parallell med linjen CD. Det är känt att AB = 16 3 cm, OK = 12 cm, CD = 16 cm. Hitta avstånden från punkterna D och K till triangelns hörn A och B.

Lösning.

1) Enligt villkoren för problemet, OK CD, därför OK ABC (Fig. 2.5).

2) Punkt O är centrum för regelbunden triangel ABC, därför OA = OB = OC = AB = 16 cm.

–  –  –

Lektioner nr 28-30 Lektionsämne: Lösa problem om vinkelrätheten hos en linje och ett plan. Upprepning av teorifrågor Huvudmål med lektionerna Utveckla färdigheter i att lösa grundläggande typer av problem på vinkelräthet av en linje och ett plan, upprepa teorifrågor.

1. Upprepa teorifrågorna under elevundersökningen (punkterna 15-18).

2. Lös problem 129-137 selektivt, använd frågorna 1-9 för kapitel II.

3. Betrakta helt eller delvis beviset för satsen från punkt 18.

4. Du kan använda uppgifter från didaktiskt material.

5. Du kan genomföra ett matematiskt diktat (nr 2 i didaktiskt material).

6. Lektionsarbete med bild 2.3 är användbart.

På lektion nr 30 bedrivs självständigt arbete.

Självständigt arbete nr 2.1 Alternativ 1

10. Givet: AB, M och K är godtyckliga punkter i planet. Bevisa att AB MK.

2. Triangel ABC är regelbunden, punkt O är dess mittpunkt. Linjen OM är vinkelrät mot plan ABC.

a)0 Bevisa att MA = MB = MC.

b) Hitta MA om AB = 6 cm, MO = 2 cm.

–  –  –

Alternativ 2

10. Givet: den räta linjen MA är vinkelrät mot triangelns ABC-plan. Bevisa att MA BC.

2. Fyrdubbel ABCD är en kvadrat, punkt O är dess centrum. Den räta linjen OM är vinkelrät mot kvadratens plan.

a)0 Bevisa att MA = MB = MC = MD.

b) Hitta MA om AB = 4 cm, OM = 1 cm.

Svar:

Alternativ 1.

Alternativ 2.

Uppgift 129. Linjen AM är vinkelrät mot planet för en kvadrat ABCD vars diagonaler skär varandra i punkt O. Bevisa att:

a) den räta linjen BD är vinkelrät mot planet AMO;

Lösning.

a) MA ABCD, därför MA BD genom att bestämma vinkelrätheten för en linje och ett plan, BD AC genom egenskapen för en kvadrats diagonaler (Fig. 2.7).

Så, BD AO och BD AM, därför, BD AMO baserat på linjens och planets vinkelräthet.

b) Eftersom BD är MOA, är den räta linjen BD vinkelrät mot varje rät linje som ligger i MOA-planet, i synnerhet BD MO.

Uppgift 134. Bevisa att alla linjer som går genom en given punkt M på en linje a och är vinkelräta mot denna linje ligger i planet som går genom punkten M och vinkelrätt mot linjen a.

Lösning: Låt oss beteckna med en bokstav planet som går genom punkten M på linje a och vinkelrätt mot denna linje, och betrakta en godtycklig linje b, som också går genom punkt M och vinkelrät mot linje a.

Det krävs för att bevisa att b (Fig. 2.8). Låt oss anta att så inte är fallet. Sedan skär planet som går genom linjerna a och b planet längs någon linje b1 som går genom punkten M och skiljer sig från linjen b. Eftersom a och b1, sedan a b1. Vi fann att i planet går två linjer (b och b1) genom punkt M, vinkelräta mot linje a, vilket inte kan vara fallet. Det betyder att antagandet är felaktigt och rät linje b ligger i planet.

Ris. 2.7 Fig. 2.8

Uppgift 136. Bevisa att om punkt X är lika långt från ändarna av ett givet segment AB, så ligger den i planet som går genom mitten av segmentet AB och vinkelrätt mot den räta linjen AB.

Lösning. Låt oss beteckna det bokstavliga planet som passerar genom mittpunkten O i segmentet AB och Fig. 2,9 vinkelrät mot rät linje AB (Fig. 2.9). Låt punkt X vara lika långt från ändarna av segment AB, dvs XA = XB. Vi måste bevisa att X.

Om punkt X ligger på linje AB, så sammanfaller den med punkt O, och därför X.

Om punkt X inte ligger på linjen AB, är segmentet XO medianen för den likbenta triangeln AXB och därför höjden för denna triangel, dvs.

Linjen XO går alltså genom punkt O på linjen AB och är vinkelrät mot linjen AB. Det följer av detta (se uppgift 134) att den räta linjen XO ligger i planet, och därför X.

Uppgift 137. Bevisa att genom var och en av två ömsesidigt vinkelräta snedställda linjer passerar ett plan vinkelrätt mot den andra linjen.

Lösning Låt a och b vara inbördes vinkelräta sneda linjer. Låt oss bevisa att genom linje a passerar ett plan vinkelrätt mot linje b.

1) Genom en godtycklig punkt O på linje a drar vi en linje b1 parallell med linje b. Sedan a b1, eftersom villkoret a b (fig. 2.10).

2) Låt oss med en bokstav beteckna planet som går genom de skärande linjerna a och b1, och dra en rät linje c genom punkt O, vinkelrätt mot planet. Sedan c b1, och sedan b b1, sedan c b.

3) Låt oss med en bokstav beteckna planet som går genom de skärande linjerna a och c. Eftersom b a (efter villkor) och b c, fig. 2.10 sedan b (baserat på linjens och planets vinkelräthet). Så genom linje a passerar ett plan vinkelrätt mot linje b.

Det bevisas på liknande sätt att genom linje b passerar ett plan vinkelrätt mot linje a.

§ 2. PERPENDIKULÄR OCH LUTANDE.

VINKEL MELLAN EN RAKA OCH ETT PLAN

–  –  –

Lektionens huvudmål Introducera begreppet avstånd från en punkt till ett plan, bevisa satsen om tre vinkelräta, visa tillämpningen av denna sats vid problemlösning.

Exempel på lektionsplan

1. Använd bild 51 i läroboken och introducera begreppen vinkelrät mot ett plan, lutande, projektion på ett lutande plan. Med tanke på den räta triangeln AMH (se fig. 51), bevisa att vinkelrät ritat från en given punkt till ett plan är mindre än någon sned dragning från samma punkt till detta plan. Längden av en vinkelrät ritad från en punkt till ett plan kallas avståndet från denna punkt till planet.

2. Var uppmärksam på noterna 1, 2, 3 i punkt 19 i läroboken, där begreppen avstånd mellan parallella plan parallella med en rät linje och ett plan som skär raka linjer introduceras. Det är användbart att göra ritningar och motivera giltigheten av påståendena i kommentarerna.

Anmärkning 1. Om två plan är parallella, är alla punkter i ett plan lika långt från det andra planet.

Låt, A, M. Vi utför AA0 och MM0, sedan Fig. 2.11 AA0 MM0 (Fig. 2.11), därför AA0 = MM0 (som segment av parallella linjer inneslutna mellan parallella plan).

Så avstånden från två godtyckliga punkter A och M i planet till planet är lika med varandra. Detsamma gäller avstånden från punkter på planet till planet.

Avståndet från en godtycklig punkt i ett av de parallella planen till det andra planet kallas avståndet mellan parallella plan.

Anmärkning 2. Om en linje och ett plan är parallella, är alla punkter på linjen på samma avstånd från detta plan.

Beviset för påståendet ges i lösningen till uppgift 144, eleverna kan läsa det självständigt.

Du kan erbjuda en annan version av beviset.

Låt a, A a, B a. Låt oss utföra AA1 och BB1 (Fig. 2.12). Sedan AA1 BB1. Låt oss bevisa att AA1 = BB1.

Planet som går genom de parallella linjerna AA1 och BB1 skär planet längs linjen A1B1 och innehåller linjen AB. Det är tydligt att AB A1B1 (om dessa linjer skärs, så skulle linje AB (det vill säga linje a) skära planet, vilket motsäger villkor a).

Alltså AA1 BB1 och AB A1B1. Därför är fyrhörningen ABB1A1 ett parallellogram, och därför är AA1 = BB1.

Således är avstånden från två godtyckliga punkter A och B på linje a till ett plan parallellt med densamma.

Om en linje och ett plan är parallella, så är avståndet mellan linjen och planet avståndet från en godtycklig punkt på linjen till detta plan.

Anmärkning 3. Om två linjer skär varandra, är avståndet mellan dem avståndet mellan en av dem och planet som går genom den andra linjen parallellt med den första linjen.

Det är tillrådligt att komma ihåg hur man konstruerar ett plan som innehåller en av de skärande linjerna och parallellt med den andra linjen (Fig. 2.13).

Ris. 2.12 Fig. 2.13

Låt ett b. Genom en godtycklig punkt M på linje b drar vi en linje a1 parallell med a. De skärande linjerna a1 och b definierar ett visst plan parallellt med linjen a.

Från en godtycklig punkt A på en rät linje a ritar vi en vinkelrät AA1 mot planet. Längden på denna vinkelrät är avståndet mellan korsningslinjerna a och b.

I framtiden, i processen att lösa problem, kan du visa hur man konstruerar en gemensam vinkelrät mot två givna skärande linjer a och b, det vill säga ett segment vinkelrätt mot linjerna a och b, vars ändar ligger på dessa linjer.

3. Bevisa satsen om tre perpendicularer och dess omvända sats. I det här fallet kan du använda figur 53 i läroboken eller bild 2.4.

–  –  –

4. För klass och läxor kan du använda uppgift 138-145, 153.

Uppgift 143. Avståndet från punkt M till var och en av hörnen i regelbunden triangel ABC är 4 cm. Hitta avståndet från punkt M till plan ABC om AB = 6 cm.

Lösning.

1) Med villkor MA = MB = MC = 4. Låt MO ABC (Fig. 2.14), då OA = OB = OC (som projektioner av lika sneda, se problem 139). Detta betyder att punkten O är mitten av den omslutna cirkeln av triangeln ABC,

–  –  –

och OA är radien för denna cirkel. Det är känt att a3 = R 3, där a3 = AB, R = AO, därför AO = 6 = 2 3.

2) Från MAO får vi MO = MA2 – AO2, MO = 16 – 12 = 4 = 2.

SVAR: 2 cm.

Uppgift 145. Genom spetsen A i en rätvinklig triangel ABC med rät vinkel C dras en linje AD vinkelrätt mot triangelns plan.

a) Bevisa att triangeln CBD är rätvinklig.

b) Hitta BD om BC = a, DC = b.

Lösning.

a) Segment AC - projektion av lutande DC på triangelns ABC-plan (Fig. 2.15). BC AC efter villkor, därför BC DC med satsen om tre x vinkelräta och därför är triangeln CBD rätvinklig.

b) BC = a, DC = b. Från BCD får vi BD = BC2 + CD2, BD = a2 + b2.

SVAR: a2 + b2.

I framtiden, i processen att lösa problem, är det viktigt att uppmärksamma eleverna på den generaliserade satsen om tre vinkelräta, när den räta linjen a1 är vinkelrät mot projektionen av den lutande, men inte passerar genom basen av den lutande.

Lektion nr. Lektionsämne: Vinkel mellan en linje och ett plan Huvudmål med lektionen Introducera begreppet en vinkel mellan en linje och ett plan;

överväga problem där detta begrepp används.

Exempel på lektionsplan

1. Kontrollera selektivt lösningen på problem från läxor. Lösningar på problem som 138-142 och beviset för de tre vinkelräta satserna kan diskuteras muntligt med hjälp av färdiga ritningar och rutschbanor.

2. Introducera begreppet projektion av en punkt på ett plan, projektion av en figur på ett plan. Bevisa att projektionen av en linje på ett plan som inte är vinkelrät mot detta plan är en rät linje. I detta fall används figurerna 54 och 55 i läroboken.

3. Ange definitionen av vinkeln mellan en rät linje och ett plan.

4. Analysera lösningen på problem 162 som ges i läroboken. Bevisa att vinkeln mellan en given linje och ett plan är den minsta av alla vinklar som en given linje bildar med linjer ritade i planet genom skärningspunkten mellan linjen och planet.

Det kan vara till hjälp för eleverna att skriva ner beviset i bild 2.5.

–  –  –

5. För klass och läxor kan du använda uppgift 163-165, 146-148.

Uppgift 165. Från punkt A, på avstånd från planet på ett avstånd d, dras lutande AB och AC till detta plan i en vinkel av 30° mot planet. Deras projektioner på planet bildar en vinkel på 120°. Hitta BC.

–  –  –

Lektioner nr 33-36 Lektionsämne: Upprepning av teori. Lösa problem om tillämpningen av satsen på tre vinkelräta, om vinkeln mellan en linje och ett plan. Huvudmål med lektionerna. Upprepa beviset för satsen på tre vinkelräta, begreppet en vinkel mellan en linje och ett plan, och befästa problemlösningsförmåga.

Exempel på lektionsplan

1. Vid var och en av lektionerna nr 33-35 upprepar du teorifrågorna genom att fråga eleverna.

2. I processen att lösa problem, upprepa sambanden mellan elementen i en rätvinklig triangel, satsen om sinus och cosinus.

3. Var särskilt uppmärksam på lösningen av vissa typiska uppgifter, som kommer att användas senare vid beräkning av ytareor och volymer av polyedrar. Sådana problem inkluderar till exempel problem 147, 151, 158, 161. Det är användbart att i lektionerna använda bild 2.6 nedan, som är avsedd för frontalarbete med elever, där man diskuterar tillvägagångssätt för att lösa problem från läroboken.

4. I lektion nr 36 är det tillrådligt att utföra självständigt arbete av kontrollerande karaktär.

Självständigt arbete nr 2.2

Alternativ 1 Från punkt M dras en vinkelrät MB lika med 4 cm till planet för rektangel ABCD. Sned MA och MC bildar vinklar på 45° respektive 30° med rektangelns plan.

a)0 Bevisa att trianglarna MAD och MCD är räta vinklar.

b)0 Hitta rektangelns sidor.

c) Bevisa att triangeln BDC är projektionen av triangeln MDC på rektangelns plan, och hitta dess area.

Alternativ 2 Från punkt M dras en vinkelrät MD lika med 6 cm till planet för kvadraten ABCD. Den lutande MB bildar en vinkel på 60° med kvadratens plan.

a)0 Bevisa att trianglarna MAB och MCB är räta vinklar.

b)0 Hitta sidan på kvadraten.

c) Bevisa att triangeln ABD är projektionen av triangeln MAB på en kvadrats plan, och hitta dess area.

Svar:

b) AB = 4 cm, BC = 4,3 cm; c) 83 cm2.

Alternativ 1.

b) 6 cm; c) 3 cm2.

Alternativ 2.

–  –  –

Uppgift 147. Från punkt M dras en vinkelrät MB till planet för rektangeln ABCD. Bevisa att trianglarna AMD och MCD är rektangulära.

Lösning.

1) Enligt villkoren för problemet är segmentet MB vinkelrätt mot rektangelns plan, därför är segmentet AB projektionen av den lutande MA på rektangelns plan (fig. 2.17). AD AB (eftersom ABCD är en rektangel), därför AD MA genom satsen om tre vinkelräta. Således är vinkel MAD rät och därför är triangel AMD rätvinklig.

2) På liknande sätt, eftersom DC BC, är DC MC och triangeln MCD rektangulära.

Uppgift 151. Linjen CD är vinkelrät mot triangelns ABC-plan. Bevisa att: a) triangel ABC är projektionen av triangeln ABD på planet ABC;

b) om CH är höjden av triangeln ABC, då är DH höjden av triangeln ABD.

Lösning.

a) Enligt villkoren för problemet är segmentet DC vinkelrät mot ABC-planet, därför är punkt C projektionen av punkt D på ABC-planet, segmentet CB är projektionen på det sneda DB, och segmentet CA är projektionen av den sneda DA på ABC-planet (Fig. 2.18).

Alla punkter i segmentet AB ligger i planet ABC, därför är projektionen av segmentet AB på planet ABC detta segment i sig.

Så, projektionerna av sidorna av triangeln ABD på planet ABC är motsvarande sidor av triangeln ABC.

Det är också uppenbart att projektionen M1 av vilken som helst inre punkt M i triangeln ABD ligger inuti triangeln ABC och vice versa: vilken som helst inre punkt M1 i triangeln ABC är projektionen på planet ABC för någon inre punkt M i triangeln ABD. Detta betyder att triangeln ABC är projektionen av triangeln ABD på planet ABC.

b) AB CH genom villkor, därför AB DH med satsen om tre perpendikulära, dvs DH är höjden av triangeln ABD.

–  –  –

Uppgift 158. Genom vertex B på romben ABCD dras en linje BM vinkelrätt mot dess plan. Hitta avståndet från punkt M till linjerna som innehåller rombens sidor, om AB = 25 cm, BAD = 60°, BM = 12,5 cm.

Lösning.

1) Låt oss utföra BK AD (Fig. 2.19). Segmentet BK är projektionen av den lutande MK på rombens plan, AD BK, därför AD MK med satsen om tre perpendikulära. Längden på segmentet MK är lika med avståndet från punkt M till linje AD.

Liknar ME - avståndet från punkt M till rät linje DC.

ABK får vi BK = AB sin 60°, BK = 25 3.

3) Triangel MBK är rätvinklig eftersom MB är ABC. Vi har

–  –  –

4) BK = BE (som höjden på romben). Rektangulära trianglar MBK och MBE är lika på två sidor, därför är ME = MK = 25 cm.

5) Avstånden från punkt M till linjerna AB och BC är lika med längden på den vinkelräta MB, dvs lika med 12,5 cm.

SVAR: 25 cm, 25 cm, 12,5 cm, 12,5 cm.

Problem 161. Ray BA ligger inte i planet för den outvecklade vinkeln CBD. Bevisa att om ABC = ABD, och ABC är 90°, så är projektionen av strålen BA på planet CBD bisektrisen av vinkeln CBD.

Lösning.

1) Låt AE CBD. I planet ABC ritar vi en vinkelrät AM mot linjen BC, och i planet ABD ritar vi en vinkelrät AK mot linjen BD. Eftersom ABC är 90°, ligger punkt M på strålen BC (och inte på fortsättningen av denna stråle). På samma sätt, eftersom ABD är 90°, ligger punkt K på strålen BD (Fig. 2.20).

Sedan BC AM, sedan BC EM (genom sats, motsatsen till satsen cirka tre vinkelräta). Det kan på liknande sätt bevisas att BD EK.

2) Rätt trianglar ABK och ABM är lika i hypotenusa (AB är den vanliga hypotenusan) och spetsig vinkel (ABC = ABD), därför är BM = BK.

3) Rätt trianglar BME och BKE är lika i hypotenusa (BE - vanlig hypotenusa) och ben (BM = BK), därför är EM = EK.

4) Punkt E är lika långt från sidorna av vinkel CBD, därför ligger den på bisektrisen av denna vinkel, dvs strålen BE är bisektrisen av vinkeln CBD.

§ 3. DIHEDRAL VINKEL.

PLANENS PERPENDICULARITET

Lektion nr 37 Lektionsämne: Dihedrisk vinkel Huvudmålen med lektionen Introducera begreppen för en dihedrisk vinkel och dess linjära vinkel, överväg uppgifter om tillämpningen av dessa begrepp.

Exempel på lektionsplan

1. Introducera konceptet med en dihedrisk vinkel med hjälp av figur 58 i läroboken.

2. Introducera begreppet linjär dihedrisk vinkel.

Bevisa att alla linjära vinklar i en dihedrisk vinkel är lika med varandra (se fig. 59, a, b).

3. Definiera gradmåttet för en dihedrisk vinkel.

Betrakta exempel på spetsiga, räta och trubbiga dihedriska vinklar med hjälp av figur 60 i läroboken. En rät dihedral vinkel kan visas i skärningspunkten mellan två klassrumsväggar, eller en vägg och ett tak eller golv.

4. För klass och läxor kan du selektivt använda uppgifterna 166-170.

Eleverna bör vara uppmärksamma på beteckningen av dihedriska vinklar. En dihedrisk vinkel med en kant AB, på olika ytor av vilka punkterna C och D är markerade, kallas en dihedrisk vinkel CABD.

Uppgift 167. I tetraedern DABC är alla kanter lika, punkt M är mittpunkten på kanten AC. Bevisa att DMB är den linjära vinkeln för den dihedriska vinkeln BACD.

Ris. 2.21 Fig. 2.22

Lösning: Medianerna BM och DM är samtidigt höjderna av regelbundna trianglar ABC och ADC (Fig. 2.21). Därför är BM AC och DM AC, och följaktligen DMB, den linjära vinkeln för den dihedriska vinkeln vid kanten AC av pyramidens bas.

Uppgift 170. Rita en vinkelrät BB1 mot detta plan från vertex B i triangeln ABC, vars sida AC ligger i ett plan. Ta reda på avståndet från punkt B till linjen AC och till planet om AB = 2 cm, BAC = 150° och dihedrisk vinkel BACB1 är 45°.

Lösning.

1) Triangeln BAC är trubbig med trubbig vinkel A, så basen för höjden BK från vertex B ligger på förlängningen av sidan AC. Avstånden från punkt B till rät linje AC och till planet är lika med BK respektive BB1 ​​(Fig. 2.22).

2) Eftersom AC BK, då AC KB1 genom satsen invers till satsen om tre vinkelräta. Därför är BKB1 den linjära vinkeln för den dihedriska vinkeln BACB1. Enligt villkoren för problemet är BKB1 = 45°.

3) Från BAK har vi A = 30°, BK = BA sin 30°, BK = 1.

–  –  –

Lektion nr 38 Lektionsämne: Tecken på vinkelräthet mellan två plan Huvudmål med lektionen Introducera konceptet med en vinkel mellan plan; ge definitionen av vinkelräta plan; bevisa ett teorem som uttrycker tecknet på vinkelräthet för två plan; visa tillämpningen av denna sats för att lösa problem.

Exempel på lektionsplan

1. Kontrollera selektivt lösningen på problem från läxor. Det är lämpligt att använda bilder med färdiga ritningar.

2. Uppmärksamma eleverna på det faktum att när två plan skär varandra bildas fyra dihedriska vinklar. Om är storleken på den av de fyra vinklarna som inte överstiger var och en av de andra, så sägs vinkeln mellan de skärande planen vara lika. Det är tydligt att 0° 90°. Om = 90° kallas planen vinkelräta. I detta fall är var och en av de fyra dihedriska vinklarna som bildas av skärande plan raka.

3. Bevisa ett teorem som uttrycker tecknet att två plan är vinkelräta. Beviset av satsen kan utföras muntligt från texten i läroboken, med hjälp av figur 62. Det traditionella beviset som ges i läroboken bemästras som regel framgångsrikt av eleverna.

4. Det är viktigt att uppmärksamma eleverna på följande två fakta, som ofta används när man löser problem:

a) Ett plan vinkelrätt mot kanten av en dihedrisk vinkel är vinkelrät mot dess ytor. (Detta uttalande i en något annorlunda formulering ges i punkt 23 i läroboken som en följd av satsen.)

b) En vinkelrät ritad från vilken punkt som helst av ett av två ömsesidigt vinkelräta plan till linjen för deras skärningspunkt är en vinkelrät mot det andra planet.

(Detta påstående bevisas i lösningen till uppgift 178 i läroboken.)

5. För klass och läxor kan du använda uppgift 171-180.

Uppgift 171. Hypotenusan för en rät likbent triangel ligger i ett plan och benet lutar mot detta plan i en vinkel av 30°. Hitta vinkeln mellan planet och triangelns plan.

Lösning.

1) Låt ABC vara den givna triangeln, AB, CO. Sedan är segmentet OB projektionen av benet CB på planet. Enligt villkoren för problemet är CBO = 30° (Fig. 2.23).

2) Låt CO = a i triangeln COB, då CB = 2a.

3) Låt oss rita CD AB, sedan AB DO med satsen i riktning mot satsen om tre vinkelräta, och CDO är den linjära vinkeln för den dihedriska vinkeln som bildas när planet skär triangelns plan. Låta

–  –  –

CDO = x. Detta är den önskade vinkeln mellan planet och triangelns plan.

4) Från CDB får vi CBD = 45°, eftersom triangeln ACB genom villkor är likbent och en rektangel

–  –  –

varav = 45°, dvs dihedrisk vinkel DABC är lika med 45°.

5) Eftersom BC DC och AC DC är ACB den linjära vinkeln för den dihedriska vinkeln BDCA.

Eftersom ACB = 60° är den dihedrala vinkeln BDCA lika med 60°.

SVAR: 90°, 45°, 60°.

Uppgift 174. Hitta den dihedriska vinkeln ABCD för tetraedern ABCD om vinklarna DAB, DAC och ACB är räta vinklar, AC = CB = 5, DB = 5 5.

Lösning.

1) Enligt villkoren för problemet är vinklarna DAB och DAC räta vinklar, därför DA AB och DA AC (Fig. 2.25). Av detta följer att segmentet DA är vinkelrät mot planet ABC, och följaktligen är segmentet AC projektionen av den lutande DC på planet ABC. Ris. 2,25

2) Enligt villkoren för problemet är vinkeln ACB rätt, dvs BC AC, och därför BC DC med satsen om tre vinkelräta. Således är ACD den linjära vinkeln för den dihedriska vinkeln ABCD.

3) Från DCB: DC = DB2 – BC2, DC = 25 5 – 25 = 10.

4) Från DAC får vi ACD = x, cos x = AC, cos x = 5,

–  –  –

Huvudmål med lektionen Introducera konceptet rektangulär parallellepiped, överväg egenskaperna hos dess ytor, dihedriska vinklar, diagonaler.

Exempel på lektionsplan

1. Formulera definitionen av en rektangulär parallellepiped. Bevisa att alla sex ytorna på en rektangulär parallellepiped är rektanglar.

2. Bevisa att alla dihedriska vinklar på en rektangulär parallellepiped är rätta.

3. Bevisa satsen: kvadraten på diagonalen för en rektangulär parallellepiped är lika med summan av kvadraterna av dess tre dimensioner.

Var uppmärksam på analogin med egenskapen hos en rektangels diagonal. Det kan också noteras att denna sats är en av varianterna av den rumsliga Pythagoras sats.

Betrakta följden av satsen: diagonalerna för en rektangulär parallellepiped är lika.

4. För klass och läxor kan du selektivt använda uppgifterna 187-192.

Ris. 2.26 Fig. 2.27

Uppgift 191. Givet en kub ABCDA1B1C1D1. Bevisa att planen ABC1 och A1B1D är vinkelräta.

Lösning.

1) BC1 B1C enligt egenskapen hos en kvadrats diagonaler (Fig. 2.26). DC BCC1, alltså DC BC1, sedan BC1 BCC1.

Således är linjen BC1 vinkelrät mot två skärande linjer DC och CB1 som ligger i planet A1B1D. Följaktligen är den räta linjen BC1 vinkelrät mot plan A1B1D baserat på den räta linjens och planets vinkelräthet.

2) Plan ABC1 passerar genom linjen BC1, vinkelrätt mot plan A1B1D, därför ABC1 A1B1D på grund av de två planens vinkelräthet.

Uppgift 192. Hitta tangenten för vinkeln mellan kubens diagonal och planet för en av dess ytor.

Lösning.

1) Låt kanten på kuben ABCDA1B1C1D1 vara lika med a. Då är BD = a 2 (Fig. 2.27). Sedan D1D ABC är linjen BD projektionen av linjen BD1 på ytan ABCDs plan, och därför är vinkeln mellan dessa linjer vinkeln mellan diagonalen BD1 och ytan ABCD. Således krävs det att hitta tangenten för vinkeln D1BD, vars värde betecknas med

2) Från D1DB får vi tg = 1, tg = a, tg = 2.

–  –  –

Lektion nr 40 Lektionsämne: Lösa problem på en rektangulär parallellepiped Huvudmål med lektionen Upprepa egenskaperna hos en rektangulär parallellepiped, lös ett antal problem på en rektangulär parallellepiped.

Exempel på lektionsplan

1. Upprepa teorifrågorna genom att kartlägga eleverna.

2. Kontrollera selektivt lösningen på problem från läxor med hjälp av färdiga ritningar och diabilder.

3. För klass och läxor kan du använda uppgift 193-196.

Uppgift 195. Ta reda på måtten på den rektangulära parallellepipeden ABCDA1B1C1D1 om AC1 = 12 cm och diagonalen BD1 gör en vinkel på 30° med ytans plan AA1D1D, och en vinkel på 45° med kanten DD1.

Lösning.

Liknande verk:

"UTBILDNINGSMINISTERIET OCH VETENSKAP OF THE RUSSIAN FEDERATION Federal State Budgetary Educational Institute of Higher Professional Education "TYUMEN STATE UNIVERSITY" Institutet för geovetenskaper Institutionen för fysisk geografi och ekologi Tyulkova L.A. GEOMORFOLOGI utbildnings- och metodkomplex. Arbetsprogram för studenter i riktningen 03/05/04 "Hydrometeorology", heltid träning Tyumen State University Tyulkova L.A. Geomorfologi. Pedagogisk och metodologisk...”

"UTBILDNINGSMINISTERIET FÖR KALININGRAD REGIONEN STATLIGA BUDGETINSTITUTET FÖR KALININGRAD REGIONEN YRKESUTBILDNINGSORGANISATION "GUSEVSKY AGRICULTURAL COLLEGE" GODKÄNT av direktören för statens budgetinstitut LKO VET GAPK. Grubinov 15 augusti 2014 GRUNDLÄGGANDE PROFESSIONELLA UTBILDNINGSPROGRAM FÖR SYNDAGÄR YRKESUTBILDNING AV STATSUTBILDNINGSINSTITUTET I KALININGRAD REGIONEN PROFESSIONELL UTBILDNINGSORGANISATION "GUSEVSKY AGROINDUSTRIAL"...

"Ämne: UTBILDNING i Ryska federationen. Allmänna bestämmelser. universitet VETERINÄR. SShO.DOU Uppdateringsdatum: 2015-02-24 Analytisk granskning Rekommendationer för uppdatering av federala standarder godkändes högre utbildning för att ta hänsyn till bestämmelserna i de relevanta professionella standarderna, rekommendationer för uppdatering av de nuvarande federala statliga metodologiska utbildningsstandarderna för högre utbildning, med hänsyn till de accepterade professionella standarderna (godkänd av Rysslands utbildnings- och vetenskapsministerium den 22 januari, 2015 N DL-2/05vn)...”

" UTBILDNING) Efternamn Förnamn Patronymkurs_ Fakulteten för kommunikation och juridik Grupp nr. _ Granska resultat (kolumnen fylls i av läraren) _ _ _ _ _ _Lärare _ Minsk 2014 INNEHÅLL KORTFATTAD METODOLOGISKA INSTRUKTIONER AVSNITT 1. ALLMÄNNA UNDERVISNINGAR ÄMNE 1.1 ÄMNE, HISTORIA, SYSTEM, OBJEKT OCH UPPGIFTER. HISTORIA OCH METODOLOGI..."

"Innehållssammanfattning...1. Mål för elevernas självständiga arbete. 2. Mål för elevernas självständiga arbete..5 3. Rekommendationer för självständiga studier av disciplinen..5 4. Typer självständigt arbete studenter..5 5. Krav på minimiinnehållet i disciplinen i enlighet med Federal State Educational Standard... 6. Innehållet i självständigt arbete med ämnets ämnen. 7.Uppgifter för självständigt arbete av studenter 7.1. Ämnen för abstrakt och kreativa verk i disciplin..8...”

”Plan för information och utbildningsseminarier och webbseminarier Första halvan av läsåret 2015-2016 oktober Deltagande är gratis. Alla deltagare (anmälan krävs) kommer att få ett intyg om deltagande i webbseminariet "Metodologiska principer för att utveckla uppgifter för seminarier och webbseminarier" den 16 oktober 2015, 16.00–17.00 (Moskvatid). Internationell tävling"PONY® på besök i Pythagoras" för elever i årskurs 2-4 och deras bedömningskriterier." Webinariet analyserar målen för intellektuella tävlingar,...”

"RYSSSKA FEDERATIONSMINISTERIET FÖR UTBILDNING OCH VETENSKAP Statens utbildningsinstitution för högre yrkesutbildning TYUMEN STATE UNIVERSITY "GODKÄND": vicerektor för pedagogiskt arbete L.M. Volosnikova 08.07. 2011 Organisation av logopedarbetet i förskolans läroverk Utbildnings- och metodkomplex. Arbetsprogram för elever i utbildningsriktning 050700.62 Special (defektologisk) utbildning, utbildningsprofil Logoped, blankett...”

"Statlig budgetmässig professionell utbildningsinstitution i Moskvas stad "First Moscow Educational Complex" Metodologiska rekommendationer för implementering praktiskt arbete Enligt proffsmodulen PM 02. Design av plagg MDK 02.02. Metoder för konstruktiv modellering av plagg, 3:e studieåret 262019 Design, modellering och teknik för plagg, avancerad utbildning (utbildningsprofilens namn) Moscow BBK G1 APPROVED Utvecklad på...”

"UTBILDNINGSMINISTERIET OCH VETENSKAP I RYSSSKA FEDERATIONEN ITMO UNIVERSITY E.P. Suchkova, M.S. Belozerova METODER FÖR FORSKNING AV MJÖLK OCH MEJERIPRODUKTER Utbildnings- och metodhandbok St. Petersburg UDC 637.1/3 Suchkova E.P., Belozerova M.S. Metoder för studier av mjölk och mejeriprodukter: Pedagogisk metod. ersättning. – St. Petersburg: ITMO University; IKhiBT, 2015. – 47 sid. Given laboratoriearbeten i disciplinen "Metoder för studier av mjölk och mejeriprodukter." Verken ägnas åt studiet av moderna metoder...”

”Innehåll 1. Allmänna bestämmelser...2. Träningsriktningens egenskaper...3. Egenskaper för utexaminerades yrkesverksamhet.3.1. Område yrkesverksamhet examen från EP VO.3.2 Objekt för yrkesverksamhet för en examen från EP VO.3.3 Typer av yrkesverksamhet för en examen EP VO.3.4 Generaliserade arbetsfunktioner för akademiker i enlighet med professionella standarder..8 4. Resultat av behärskning utbildningsprogram.. 5. Utbildningsprogrammets struktur...”

"FEDERAL TJÄNST FÖR TILLSYN PÅ FÄLTET FÖR SKYDD AV KONSUMENTRÄTTIGHETER OCH MÄNSKLIGT VÄLBEFINNING Federal Budgetary Institution "Federal Scientific Center for Medical and Preventive Technologies for Public Health Risk Management" Federal State Budgetary Educational Institute of Higher Professional Education "Perm State National forskningsuniversitet» AKTUELLA ANVISNINGAR I UTVECKLING AV SOCIAL OCH HYGIENISK ÖVERVAKNING OCH HÄLSORISKANALYS Material från den allryska vetenskaplig-praktisk konferens med internationellt deltagande (15–17 maj 2013) Redigerad av akademiker vid Ryska akademin för medicinska vetenskaper...”

"ARBETSPROGRAM PÅ ÄMNET "TEKNIK" FÖR 1:A KLASS "F" Sammanställt av: grundskollärare Natalya Sergeevna Tambovtseva Moskva, läsåret 2014-2015 Förklarande anteckning. Teknikarbetsprogrammet är baserat på federala krav statlig standard primär allmän utbildning utbildningsområde"Teknik" och utformad i enlighet med Ungefärligt program primär allmän utbildning, arbetsprogram N.I. Rogovtseva, S.V. Anashchenkova..."

"M. S. Soloveychik N. S. Kuzmenko RUSSISKA SPRÅKMETODOLOGISKA REKOMMENDATIONER för läroboken för 2: a klass av allmänna utbildningsorganisationer Lärarhandbok 7:e upplagan, reviderad Smolensk Association XXI århundradet UDC 372.881.116.11.046. BBK 74.268.1Rus VÄNLIGEN OBS! Var försiktig vid användning metodiska manualer till läroböcker utgivna av andra förlag! Om någon av författarna till den här läroboken inte är listad som redaktör, konsult eller recensent, kanske manualen inte..."

"SPECIALISERAD STRUKTURELL UTBILDNINGSDIVISION FÖR RYSKA FEDERATIONENS AMBASSAD I REPUBLIKEN MADAGASCAR – GRUNDLÄGGANDE GRUNDSKOLA PÅ RYSKA AMBASSADEN I MADAGASCAR ARBETSPROGRAM träningskurs(litteratur) 5.ÅK 2014-2015 akademiskt år lärare: Egorova I.V. Förklarande not Arbetsprogrammet upprättas i enlighet med regleringsdokument Och läromedel: Federal del av staten utbildningsstandard vanligaste..."

”Protokoll nr daterat den 24 augusti 2015 behandlades vid försvarsdepartementets möte. “Verifierad” “Godkänd” _ Biträdande direktör för vattenresursförvaltning, direktör för den kommunala budgetutbildningsinstitutionen “Lyceum “MOK No. 2” Samofalova Yu.V._ Sverdlov V.Ya. Arbetsprogram för fritidsaktiviteter Kurs ”Speech Development School” läsåret 2015-2016 Lärare Asoyan O.I., Bavykina I.E., Ledeneva G.A., Ivashkina N.V., Savvina O.Yu., Sverdlova L.V. Klass 4 “A”, “B”, “C”, “D”, “D”, “E” Ämne “Kurs “TAL”. Till unga smarta människor och smarta tjejer. Skolan för talutveckling" (34 timmar; 1 timme per vecka)..."

"Utbildnings- och vetenskapsministeriet i Ryska federationen Amur State University E.V. Pshenichnikova GRUNDLÄGGANDE OM ATT UTFORMA KLÄDER FÖR ENSKILDA KONSUMENT Lärobok Rekommenderas av Far Eastern Regional Educational and Methodological Center (FE RUMC) som en lärobok för studenter som studerar i kandidatexamen 262000.62 "Teknologi för lätta industriprodukter", 100100.62 "Service"vegouniversities i Blashchensk region Förlag AMSU BBK 37. 24-2 i 73 P 93...”

“SKYDDA BARN FRÅN DISKRIMINERING Tvärvetenskaplig utbildningsmanual CREAN SKYDDAR BARN FRÅN DISKRIMINERING SKYDDAR BARN FRÅN DISKRIMINERING Tvärvetenskaplig utbildningsmanual Redigerad av Dagmar Kutsar och Hannah Warming Ryska översättningsredaktören Zabotkina Vera Ivanovna Dr. Philol. Sciences, Prof., vicerektor för innovativa internationella projekt Russian State University for the Humanities European Consortium of Universities Offering masterprogram om barns rättigheter inom ramen för..."

”Innehåll Avsnitt 1. Lista över planerade lärandemål i disciplinen, korrelerade med de planerade resultaten av att bemästra utbildningsprogrammet. 4 1.1 Lista över planerade lärandemål i disciplinen. 4 1.2 Planerade resultat av att bemästra utbildningsprogrammet. 4 § 2. Disciplinens plats i utbildningsprogrammets struktur. 6 § 3. Disciplinens omfattning.. 6 § 4. Disciplinens uppbyggnad och innehåll. 7 Avsnitt 5. Förteckning över utbildnings- och metodstöd för...”

“INNEHÅLL Krav på resultaten av att bemästra disciplinen 1. 4 Disciplinens plats i BOP:s struktur 2. 5 Disciplinens struktur och innehåll 3. 6 Disciplinens struktur 3.1. 6 Disciplinens innehåll 3.2. 7 Lista över pedagogiskt och metodiskt stöd för självständigt arbete 4. 9 elever per disciplin Utbildande teknologi 5. 9 Former för kontroll över att behärska disciplinen 6. 9 Lista över bedömningsverktyg för strömkontroll behärska disciplinen 6.1. 9 Sammansättning av fonden av bedömningsfonder för att utföra...”
Materialet på denna webbplats publiceras endast i informationssyfte, alla rättigheter tillhör deras upphovsmän.
Om du inte samtycker till att ditt material publiceras på denna sida, skriv till oss, vi tar bort det inom 1-2 arbetsdagar.

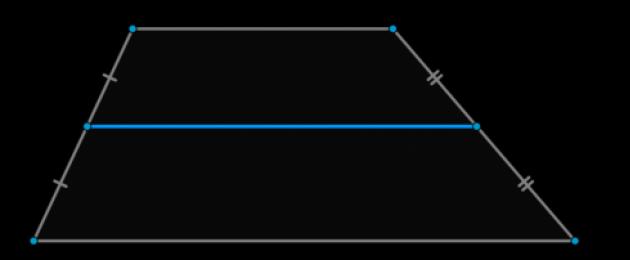
\[(\Large(\text(Fri trapets)))\]

Definitioner

En trapets är en konvex fyrhörning där två sidor är parallella och de andra två sidorna inte är parallella.

De parallella sidorna av en trapets kallas dess baser, och de andra två sidorna kallas dess laterala sidor.

Höjden på en trapets är vinkelrät ritad från valfri punkt på en bas till en annan bas.

Satser: egenskaper hos en trapets

1) Summan av vinklarna vid sidan är \(180^\cirkel\) .

2) Diagonalerna delar trapetsen i fyra trianglar, varav två är lika stora och de andra två är lika stora.

Bevis

1) För att \(AD\parallell BC\), då är vinklarna \(\angle BAD\) och \(\angle ABC\) ensidiga för dessa linjer och den tvärgående \(AB\), därför, \(\angle BAD +\angle ABC=180^\circ\).

2) För att \(AD\parallell BC\) och \(BD\) är en sekant, då ligger \(\vinkel DBC=\vinkel BDA\) korsvis.
Även \(\angle BOC=\angle AOD\) som vertikal.
Därför i två vinklar \(\triangel BOC \sim \triangel AOD\).

Låt oss bevisa det \(S_(\triangel AOB)=S_(\triangel COD)\). Låt \(h\) vara höjden på trapetsen. Sedan \(S_(\triangel ABD)=\frac12\cdot h\cdot AD=S_(\triangel ACD)\). Sedan: \

Definition

Mittlinjen i en trapets är ett segment som förbinder sidornas mittpunkter.

Sats

Trapetsets mittlinje är parallell med baserna och lika med deras halvsumma.

Bevis*

1) Låt oss bevisa parallellitet.

Låt oss rita genom punkten \(M\) den räta linjen \(MN"\parallell AD\) (\(N"\i CD\) ). Sedan, enligt Thales teorem (sedan \(MN"\parallell AD\parallel BC, AM=MB\)) punkten \(N"\) är mitten av segmentet \(CD\). Detta betyder att punkterna \(N\) och \(N"\) kommer att sammanfalla.

2) Låt oss bevisa formeln.

Låt oss göra \(BB"\perp AD, CC"\perp AD\) . Låta \(BB"\cap MN=M", CC"\cap MN=N"\).

Sedan, enligt Thales sats, är \(M"\) och \(N"\) mittpunkterna för segmenten \(BB"\) respektive \(CC"\). Så, \(MM"\) – mittlinje\(\triangle ABB"\) , \(NN"\) är mittlinjen \(\triangle DCC"\). Därför: \

Därför att \(MN\parallell AD\parallel BC\) och \(BB", CC"\perp AD\), då är \(B"M"N"C"\) och \(BM"N"C\) rektanglar. Enligt Thales sats, från \(MN\parallell AD\) och \(AM=MB\) följer att \(B"M"=M"B\) . Därför \(B"M"N"C "\) och \(BM"N"C\) är lika rektanglar, därför \(M"N"=B"C"=BC\) .

Således:

\ \[=\dfrac12 \left(AB"+B"C"+BC+C"D\right)=\dfrac12\left(AD+BC\höger)\]

Sats: egenskap hos en godtycklig trapets

Basernas mittpunkter, skärningspunkten för trapetsens diagonaler och skärningspunkten för sidosidornas förlängningar ligger på samma räta linje.

Bevis*
Det rekommenderas att du bekantar dig med beviset efter att ha studerat ämnet "Trianglars likhet".

1) Låt oss bevisa att punkterna \(P\) , \(N\) och \(M\) ligger på samma linje.

Låt oss rita en rät linje \(PN\) (\(P\) är skärningspunkten för sidosidornas förlängningar, \(N\) är mitten av \(BC\)). Låt den skära sidan \(AD\) vid punkten \(M\) . Låt oss bevisa att \(M\) är mittpunkten av \(AD\) .

Tänk på \(\triangel BPN\) och \(\triangle APM\) . De liknar två vinklar (\(\vinkel APM\) – generell, \(\vinkel PAM=\vinkel PBN\) som motsvarande vid \(AD\parallell BC\) och \(AB\) sekant). Betyder att: \[\dfrac(BN)(AM)=\dfrac(PN)(PM)\]

Tänk på \(\triangel CPN\) och \(\triangle DPM\) . De är lika i två vinklar (\(\angle DPM\) – generell, \(\angle PDM=\angle PCN\) som motsvarande vid \(AD\parallell BC\) och \(CD\) sekant). Betyder att: \[\dfrac(CN)(DM)=\dfrac(PN)(PM)\]

Härifrån \(\dfrac(BN)(AM)=\dfrac(CN)(DM)\). Men \(BN=NC\) därför \(AM=DM\) .

2) Låt oss bevisa att punkterna \(N, O, M\) ligger på samma linje.

Låt \(N\) vara mittpunkten av \(BC\) och \(O\) vara skärningspunkten för diagonalerna. Låt oss rita en rät linje \(NO\) , den kommer att skära sidan \(AD\) vid punkten \(M\) . Låt oss bevisa att \(M\) är mittpunkten av \(AD\) .

\(\triangel BNO\sim \triangel DMO\) längs två vinklar (\(\vinkel OBN=\vinkel ODM\) som ligger korsvis vid \(BC\parallell AD\) och \(BD\) sekant; \(\vinkel BON=\vinkel DOM\) som vertikal). Betyder att: \[\dfrac(BN)(MD)=\dfrac(ON)(OM)\]

likaså \(\triangle CON\sim \triangle AOM\). Betyder att: \[\dfrac(CN)(MA)=\dfrac(ON)(OM)\]

Härifrån \(\dfrac(BN)(MD)=\dfrac(CN)(MA)\). Men \(BN=CN\) därför \(AM=MD\) .

\[(\Large(\text(Isosceles trapetsoid)))\]

Definitioner

En trapets kallas rektangulär om en av dess vinklar är rät.

En trapets kallas likbent om dess sidor är lika.

Satser: egenskaper hos en likbent trapets

1) En likbent trapets har lika stora basvinklar.

2) Diagonalerna för en likbent trapets är lika.

3) Två trianglar bildade av diagonaler och en bas är likbenta.

Bevis

1) Betrakta den likbenta trapetsen \(ABCD\) .

Från hörnen \(B\) och \(C\) släpper vi perpendicularerna \(BM\) och \(CN\) till sidan \(AD\), respektive. Eftersom \(BM\perp AD\) och \(CN\perp AD\) , då \(BM\parallell CN\) ; \(AD\parallel BC\) , då är \(MBCN\) ett parallellogram, därför \(BM = CN\) .

Betrakta de räta trianglarna \(ABM\) och \(CDN\) . Eftersom deras hypotenuser är lika och benet \(BM\) är lika med benet \(CN\) , så är dessa trianglar lika, därför \(\angle DAB = \angle CDA\) .

2)

Därför att \(AB=CD, \vinkel A=\vinkel D, AD\)- allmänt, då enligt första tecknet. Därför \(AC=BD\) .

3) För att \(\triangel ABD=\triangel ACD\), sedan \(\angle BDA=\angle CAD\) . Därför är triangeln \(\triangel AOD\) likbent. På samma sätt är det bevisat att \(\triangel BOC\) är likbent.

Satser: tecken på en likbent trapets

1) Om en trapets har lika stora basvinklar är den likbent.

2) Om en trapets har lika diagonaler så är den likbent.

Bevis

Betrakta trapetsen \(ABCD\) så att \(\vinkel A = \vinkel D\) .

Låt oss komplettera trapetsen till triangeln \(AED\) som visas i figuren. Eftersom \(\angle 1 = \angle 2\) , så är triangeln \(AED\) likbent och \(AE = ED\) . Vinklar \(1\) och \(3\) är lika med motsvarande vinklar för parallella linjer \(AD\) och \(BC\) och sekant \(AB\). På liknande sätt är vinklarna \(2\) och \(4\) lika, men \(\vinkel 1 = \vinkel 2\), då \(\angle 3 = \angle 1 = \angle 2 = \angle 4\), därför är triangeln \(BEC\) också likbent och \(BE = EC\) .

Så småningom \(AB = AE - BE = DE - CE = CD\), det vill säga \(AB = CD\), vilket är det som behövde bevisas.

2) Låt \(AC=BD\) . Därför att \(\triangel AOD\sim \triangle BOC\), då betecknar vi deras likhetskoefficient som \(k\) . Sedan om \(BO=x\) , då \(OD=kx\) . Liknar \(CO=y \Rightarrow AO=ky\) .

Därför att \(AC=BD\) , sedan \(x+kx=y+ky \Högerpil x=y\) . Detta betyder att \(\triangel AOD\) är likbent och \(\angle OAD=\angle ODA\) .

Alltså enligt det första tecknet \(\triangel ABD=\triangel ACD\) (\(AC=BD, \angle OAD=\angle ODA, AD\)– allmänt). Så, \(AB=CD\), varför.