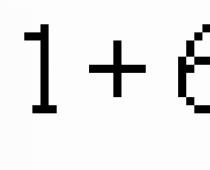Inom matematiken finns det speciella knep med vilka många andragradsekvationer löses mycket snabbt och utan några diskriminanter. Dessutom, med rätt träning börjar många lösa andragradsekvationer verbalt, bokstavligen "i ett ögonkast".
Tyvärr, i den moderna kursen i skolmatematik, studeras sådana tekniker nästan inte. Och du behöver veta! Och idag kommer vi att överväga en av dessa tekniker - Vietas teorem. Låt oss först introducera en ny definition.
En andragradsekvation av formen x 2 + bx + c = 0 kallas reducerad. Observera att koefficienten vid x 2 är lika med 1. Det finns inga andra restriktioner för koefficienterna.
- x 2 + 7x + 12 = 0 är den reducerade andragradsekvationen;
- x 2 − 5x + 6 = 0 reduceras också;
- 2x 2 − 6x + 8 = 0 - men detta ges inte alls, eftersom koefficienten vid x 2 är 2.
Naturligtvis kan vilken andragradsekvation som helst av formen ax 2 + bx + c = 0 reduceras - det räcker att dividera alla koefficienter med talet a . Vi kan alltid göra detta, eftersom det följer av definitionen av en andragradsekvation att a ≠ 0.
Det är sant att dessa transformationer inte alltid är användbara för att hitta rötter. Lite lägre kommer vi att se till att detta endast bör göras när alla koefficienter i den sista kvadratiska ekvationen är heltal. Låt oss nu titta på några enkla exempel:
Uppgift. Konvertera andragradsekvationen till reducerad:
- 3x2 − 12x + 18 = 0;
- −4x2 + 32x + 16 = 0;
- 1,5x2 + 7,5x + 3 = 0;
- 2x2 + 7x − 11 = 0.
Låt oss dividera varje ekvation med koefficienten för variabeln x 2 . Vi får:
- 3x 2 - 12x + 18 \u003d 0 ⇒ x 2 - 4x + 6 \u003d 0 - dividerat allt med 3;
- −4x 2 + 32x + 16 = 0 ⇒ x 2 − 8x − 4 = 0 - dividerat med −4;
- 1,5x 2 + 7,5x + 3 \u003d 0 ⇒ x 2 + 5x + 2 \u003d 0 - dividerat med 1,5, alla koefficienter blev heltal;
- 2x 2 + 7x - 11 \u003d 0 ⇒ x 2 + 3,5x - 5,5 \u003d 0 - dividerat med 2. I detta fall uppstod bråkkoefficienter.
Som du kan se kan de givna andragradsekvationerna ha heltalskoefficienter även om den ursprungliga ekvationen innehöll bråk.
Nu formulerar vi huvudsatsen, för vilken begreppet en reducerad andragradsekvation faktiskt introducerades:
Vietas sats. Betrakta den reducerade andragradsekvationen av formen x 2 + bx + c \u003d 0. Antag att denna ekvation har reella rötter x 1 och x 2. I det här fallet är följande påståenden sanna:
- x1 + x2 = −b. Med andra ord är summan av rötterna i den givna andragradsekvationen lika med koefficienten för variabeln x, taget med motsatt tecken;
- x 1 x 2 = c. Produkten av rötterna i en andragradsekvation är lika med den fria koefficienten.
Exempel. För enkelhetens skull kommer vi endast att överväga de givna andragradsekvationerna som inte kräver ytterligare transformationer:
- x 2 − 9x + 20 = 0 ⇒ x 1 + x 2 = − (−9) = 9; x 1 x 2 = 20; rötter: x 1 = 4; x 2 \u003d 5;
- x 2 + 2x − 15 = 0 ⇒ x 1 + x 2 = −2; x 1 x 2 \u003d -15; rötter: x 1 = 3; x 2 \u003d -5;
- x 2 + 5x + 4 = 0 ⇒ x 1 + x 2 = −5; x 1 x 2 = 4; rötter: x 1 \u003d -1; x 2 \u003d -4.
Vietas teorem ger oss ytterligare information om rötterna till en andragradsekvation. Vid en första anblick kan detta verka komplicerat, men även med minimal träning lär du dig att "se" rötterna och bokstavligen gissa dem på några sekunder.
Uppgift. Lös andragradsekvationen:
- x2 − 9x + 14 = 0;
- x 2 - 12x + 27 = 0;
- 3x2 + 33x + 30 = 0;
- −7x2 + 77x − 210 = 0.
Låt oss försöka skriva ner koefficienterna enligt Vieta-satsen och "gissa" rötterna:
- x 2 − 9x + 14 = 0 är en reducerad andragradsekvation.
Med Vieta-satsen har vi: x 1 + x 2 = −(−9) = 9; x 1 x 2 = 14. Det är lätt att se att rötterna är siffrorna 2 och 7; - x 2 − 12x + 27 = 0 reduceras också.
Enligt Vieta-satsen: x 1 + x 2 = −(−12) = 12; x 1 x 2 = 27. Därav rötterna: 3 och 9; - 3x 2 + 33x + 30 = 0 - Denna ekvation reduceras inte. Men vi kommer att fixa detta nu genom att dividera båda sidor av ekvationen med koefficienten a \u003d 3. Vi får: x 2 + 11x + 10 \u003d 0.
Vi löser enligt Vieta-satsen: x 1 + x 2 = −11; x 1 x 2 = 10 ⇒ rötter: −10 och −1; - −7x 2 + 77x − 210 \u003d 0 - återigen är koefficienten vid x 2 inte lika med 1, d.v.s. ekvation ej given. Vi dividerar allt med talet a = −7. Vi får: x 2 - 11x + 30 = 0.
Enligt Vieta-satsen: x 1 + x 2 = −(−11) = 11; x 1 x 2 = 30; från dessa ekvationer är det lätt att gissa rötterna: 5 och 6.
Av ovanstående resonemang kan man se hur Vietas sats förenklar lösningen av andragradsekvationer. Inga komplicerade beräkningar, inga aritmetiska rötter och bråk. Och även diskriminanten (se lektionen "Lösa andragradsekvationer") Vi behövde inte.
Naturligtvis utgick vi i alla våra reflektioner från två viktiga antaganden, som generellt sett inte alltid uppfylls i verkliga problem:
- Andragradsekvationen reduceras, d.v.s. koefficienten vid x 2 är 1;
- Ekvationen har två olika rötter. Ur algebras synvinkel, i detta fall diskriminanten D > 0 - i själva verket antar vi initialt att denna olikhet är sann.
Men i typiska matematiska problem är dessa villkor uppfyllda. Om resultatet av beräkningarna är en "dålig" andragradsekvation (koefficienten vid x 2 skiljer sig från 1), är detta lätt att fixa - ta en titt på exemplen i början av lektionen. Jag är generellt tyst om rötterna: vad är det för slags uppgift som det inte finns något svar på? Självklart kommer det att finnas rötter.
Således är det allmänna schemat för att lösa andragradsekvationer enligt Vieta-satsen som följer:
- Reducera andragradsekvationen till den givna, om detta inte redan har gjorts i problemets tillstånd;
- Om koefficienterna i ovanstående andragradsekvation visade sig vara bråktal löser vi genom diskriminanten. Du kan till och med gå tillbaka till den ursprungliga ekvationen för att arbeta med mer "bekväma" siffror;
- När det gäller heltalskoefficienter löser vi ekvationen med hjälp av Vieta-satsen;
- Om det inom några sekunder inte gick att gissa rötterna poängsätter vi på Vieta-satsen och löser genom diskriminanten.
Uppgift. Lös ekvationen: 5x 2 − 35x + 50 = 0.
Så vi har en ekvation som inte reduceras, eftersom koefficient a \u003d 5. Dividera allt med 5, vi får: x 2 - 7x + 10 \u003d 0.
Alla koefficienter i andragradsekvationen är heltal - låt oss försöka lösa det med hjälp av Vietas sats. Vi har: x 1 + x 2 = −(−7) = 7; x 1 x 2 \u003d 10. I det här fallet är rötterna lätta att gissa - dessa är 2 och 5. Du behöver inte räkna genom diskriminanten.
Uppgift. Lös ekvationen: -5x 2 + 8x - 2,4 = 0.
Vi ser: −5x 2 + 8x − 2,4 = 0 - denna ekvation reduceras inte, vi dividerar båda sidor med koefficienten a = −5. Vi får: x 2 - 1,6x + 0,48 \u003d 0 - en ekvation med bråkkoefficienter.
Det är bättre att återgå till den ursprungliga ekvationen och räkna genom diskriminanten: −5x 2 + 8x − 2,4 = 0 ⇒ D = 8 2 − 4 (−5) (−2,4) = 16 ⇒ ... ⇒ x 1 = 1,2 ; x 2 \u003d 0,4.
Uppgift. Lös ekvationen: 2x 2 + 10x − 600 = 0.
Till att börja med delar vi allt med koefficienten a \u003d 2. Vi får ekvationen x 2 + 5x - 300 \u003d 0.
Detta är den reducerade ekvationen, enligt Vieta-satsen har vi: x 1 + x 2 = −5; x 1 x 2 \u003d -300. Det är svårt att gissa rötterna till andragradsekvationen i det här fallet - personligen "frös" jag på allvar när jag löste det här problemet.
Vi måste leta efter rötter genom diskriminanten: D = 5 2 − 4 1 (−300) = 1225 = 35 2 . Om du inte kommer ihåg roten till diskriminanten, ska jag bara notera att 1225: 25 = 49. Därför är 1225 = 25 49 = 5 2 7 2 = 35 2 .
Nu när roten till diskriminanten är känd är det inte svårt att lösa ekvationen. Vi får: x 1 \u003d 15; x 2 \u003d -20.
2.5 Vieta-formel för polynom (ekvationer) av högre grader
Formlerna som härleds av Vieta för andragradsekvationer är också sanna för polynom av högre grader.
Låt polynomet
P(x) = a 0 x n + a 1 x n -1 + … +a n
Har n distinkta rötter x 1 , x 2 …, x n .
I det här fallet har den en faktorisering av formen:
a 0 x n + a 1 x n-1 +…+ a n = a 0 (x – x 1)(x – x 2)...(x – x n)
Låt oss dividera båda delarna av denna likhet med en 0 ≠ 0 och utöka parenteserna i den första delen. Vi får jämställdheten:
xn + ()xn -1 + ... + () = xn - (x 1 + x 2 + ... + xn) xn -1 + (x 1 x 2 + x 2 x 3 + ... + xn -1 xn)xn - 2 + … +(-1) nx 1 x 2 … xn
Men två polynom är identiskt lika om och endast om koefficienterna vid samma potenser är lika. Av detta följer att jämställdheten
x 1 + x 2 + … + x n = -
x 1 x 2 + x 2 x 3 + … + x n -1 x n =
x 1 x 2 … x n = (-1) n
Till exempel för polynom av tredje graden
a 0 x³ + a 1 x² + a 2 x + a 3
Vi har identiteter
x 1 + x 2 + x 3 = -
x 1 x 2 + x 1 x 3 + x 2 x 3 =
x 1 x 2 x 3 = -
När det gäller andragradsekvationer kallas denna formel Vieta-formler. De vänstra delarna av dessa formler är symmetriska polynom från rötterna x 1 , x 2 ..., x n i den givna ekvationen, och de högra delarna uttrycks i termer av polynomets koefficient.
2.6 Ekvationer som kan reduceras till kvadrater (biquadratisk)
Ekvationer av fjärde graden reduceras till andragradsekvationer:
ax 4 + bx 2 + c = 0,
kallas biquadratisk, dessutom a ≠ 0.
Det räcker att sätta x 2 \u003d y i denna ekvation, därför,
ay² + by + c = 0
hitta rötterna till den resulterande andragradsekvationen
y 1,2 = ![]()
För att omedelbart hitta rötterna x 1, x 2, x 3, x 4, ersätt y med x och få
x2 = ![]()
x 1,2,3,4 =  .
.
Om ekvationen för fjärde graden har x 1, har den också en rot x 2 \u003d -x 1,
Om har x 3, då x 4 \u003d - x 3. Summan av rötterna till en sådan ekvation är noll.
2x 4 - 9x² + 4 = 0
Vi ersätter ekvationen med formeln för rötterna till biquadratiska ekvationer:
x 1,2,3,4 = ![]() ,
,
att veta att x 1 \u003d -x 2, och x 3 \u003d -x 4, då:
x 3,4 = ![]()
Svar: x 1,2 \u003d ± 2; x 1,2 =
2.7 Studie av biquadratiska ekvationer
Låt oss ta den biquadratiska ekvationen
ax 4 + bx 2 + c = 0,
där a, b, c är reella tal, och a > 0. Genom att introducera en extra okänd y = x² undersöker vi rötterna till denna ekvation, och matar in resultaten i en tabell (se bilaga nr 1)
2.8 Cardano formel
Om vi använder modern symbolik, kan härledningen av Cardano-formeln se ut så här:
x = 
Denna formel bestämmer rötterna till den allmänna ekvationen av tredje graden:
ax 3 + 3bx 2 + 3cx + d = 0.
Denna formel är mycket besvärlig och komplex (den innehåller flera komplexa radikaler). Det gäller inte alltid, eftersom. mycket svår att slutföra.





F ¢(x®) = 0, >0 (<0), то точка xоявляется точкой локального минимума (максимума) функции f(x). Если же =0, то нужно либо пользоваться первым достаточным условием, либо привлекать высшие производные. На отрезке функция y = f(x) может достигать наименьшего или наибольшего значения либо в критических точках, либо на концах отрезка . Пример 3.22. Найти экстремумы функции f(x) ...

Lista eller välj bland 2-3 texter de mest intressanta platserna. Sålunda har vi övervägt de allmänna bestämmelserna för skapande och genomförande av valbara kurser, som kommer att beaktas vid utveckling av en valbar kurs i algebra för årskurs 9 "Kvadrikulära ekvationer och ojämlikheter med en parameter". Kapitel II. Metodik för att genomföra en valbar kurs "Kvadratiska ekvationer och ojämlikheter med en parameter" 1.1. Är vanliga...
Lösningar från numeriska beräkningsmetoder. För att bestämma rötterna till ekvationen krävs inte kunskap om teorierna om Abel, Galois, Lie-grupper etc. och användning av speciell matematisk terminologi: ringar, fält, ideal, isomorfismer, etc. För att lösa en algebraisk ekvation av n:e graden behöver du bara kunna lösa andragradsekvationer och extrahera rötter från ett komplext tal. Rötter kan bestämmas med...





Med måttenheter för fysiska storheter i MathCAD-systemet? 11. Beskriv i detalj text, grafiska och matematiska block. Föreläsning nummer 2. Problem med linjär algebra och lösning av differentialekvationer i MathCAD-miljön I linjära algebraproblem blir det nästan alltid nödvändigt att utföra olika operationer med matriser. Matrixmanöverpanelen finns på Math-panelen. ...
I denna föreläsning kommer vi att bekanta oss med de märkliga sambanden mellan rötterna till en andragradsekvation och dess koefficienter. Dessa samband upptäcktes först av den franske matematikern Francois Viet (1540-1603).
Till exempel, för ekvationen Зx 2 - 8x - 6 \u003d 0, utan att hitta dess rötter, kan du, med hjälp av Vieta-satsen, omedelbart säga att summan av rötterna är , och produkten av rötterna är
dvs - 2. Och för ekvationen x 2 - 6x + 8 \u003d 0 drar vi slutsatsen: summan av rötterna är 6, produkten av rötterna är 8; förresten, det är inte svårt att gissa vad rötterna är lika med: 4 och 2.
Bevis för Vietas sats. Rötterna x 1 och x 2 i andragradsekvationen ax 2 + bx + c \u003d 0 hittas av formlerna
![]()
Där D \u003d b 2 - 4ac är ekvationens diskriminant. Att lägga ner dessa rötter
vi får

Nu beräknar vi produkten av rötterna x 1 och x 2 vi har

Det andra förhållandet är bevisat:
Kommentar.
Vietas sats är också giltig i det fall då andragradsekvationen har en rot (dvs. när D \u003d 0), det är bara det att i det här fallet anses det att ekvationen har två identiska rötter, som ovanstående relationer tillämpas på.
De bevisade relationerna för den reducerade andragradsekvationen x 2 + px + q \u003d 0 har en särskilt enkel form. I det här fallet får vi:
x 1 \u003d x 2 \u003d -p, x 1 x 2 \u003d q
de där. summan av rötterna i den givna andragradsekvationen är lika med den andra koefficienten, taget med motsatt tecken, och produkten av rötterna är lika med den fria termen.
Med hjälp av Vieta-satsen kan man också få andra samband mellan rötter och koefficienter i en andragradsekvation. Låt till exempel x 1 och x 2 vara rötterna till den reducerade andragradsekvationen x 2 + px + q = 0. Sedan

Huvudsyftet med Vietas teorem är dock inte att det uttrycker vissa samband mellan rötter och koefficienter i en andragradsekvation. Mycket viktigare är det faktum att med hjälp av Vieta-satsen härleds en formel för faktorisering av ett kvadrattrinomial, utan vilket vi inte kommer att klara oss i framtiden.

Bevis. Vi har

Exempel 1. Faktorisera det kvadratiska trinomiet 3x 2 - 10x + 3.
Lösning. Efter att ha löst ekvationen Zx 2 - 10x + 3 \u003d 0, hittar vi rötterna till kvadrattrinomialet Zx 2 - 10x + 3: x 1 \u003d 3, x2 \u003d.
Med hjälp av sats 2 får vi
Det är vettigt att istället skriva Zx - 1. Då får vi äntligen Zx 2 - 10x + 3 = (x - 3) (3x - 1).
Observera att det givna kvadrattrinomialet kan faktoriseras utan att använda sats 2, med hjälp av grupperingsmetoden:
Zx 2 - 10x + 3 = Zx 2 - 9x - x + 3 =
\u003d Zx (x - 3) - (x - 3) \u003d (x - 3) (Zx - 1).
Men, som du kan se, med denna metod beror framgång på om vi kan hitta en framgångsrik gruppering eller inte, medan med den första metoden är framgång garanterad.
Exempel 1. Minska fraktion
Lösning. Från ekvationen 2x 2 + 5x + 2 = 0 finner vi x 1 = - 2,

Från ekvationen x2 - 4x - 12 = 0 finner vi x 1 = 6, x 2 = -2. Så
x 2 - 4x - 12 \u003d (x - 6) (x - (- 2)) \u003d (x - 6) (x + 2).
Låt oss nu minska den givna bråkdelen:
![]()
Exempel 3. Faktorisera uttryck:
a) x4 + 5x2 +6; b) 2x+-3
Lösning a) Vi introducerar en ny variabel y = x 2 . Detta kommer att tillåta oss att skriva om det givna uttrycket i form av ett kvadratiskt trinomium med avseende på variabeln y, nämligen i formen y 2 + by + 6.
Efter att ha löst ekvationen y 2 + by + 6 \u003d 0, hittar vi rötterna till kvadrattrinomialet y 2 + 5y + 6: y 1 \u003d - 2, y 2 \u003d -3. Nu använder vi sats 2; vi får
y2 + 5y + 6 = (y + 2) (y + 3).
Det återstår att komma ihåg att y \u003d x 2, d.v.s. återgår till det givna uttrycket. Så,
x 4 + 5x 2 + 6 \u003d (x 2 + 2) (x 2 + 3).
b) Låt oss introducera en ny variabel y = . Detta gör att du kan skriva om det givna uttrycket i form av ett kvadratiskt trinomium med avseende på variabeln y, nämligen i formen 2y 2 + y - 3. Efter att ha löst ekvationen
2y 2 + y - 3 \u003d 0, vi hittar rötterna till kvadrattrinomialet 2y 2 + y - 3:
y 1 = 1, y 2 = . Med hjälp av sats 2 får vi vidare:
Det återstår att komma ihåg att y \u003d, d.v.s. återgår till det givna uttrycket. Så,
Avsnittet avslutas med några överväganden, återigen kopplade till Vieta-satsen, eller snarare, med det omvända påståendet:
om talen x 1, x 2 är sådana att x 1 + x 2 \u003d - p, x 1 x 2 \u003d q, då är dessa tal rötterna till ekvationen
Med hjälp av detta påstående kan du lösa många andragradsekvationer muntligt, utan att använda krångliga rotformler, och även komponera andragradsekvationer med givna rötter. Låt oss ge exempel.
1) x 2 - 11x + 24 = 0. Här x 1 + x 2 = 11, x 1 x 2 = 24. Det är lätt att gissa att x 1 = 8, x 2 = 3.
2) x 2 + 11x + 30 = 0. Här x 1 + x 2 = -11, x 1 x 2 = 30. Det är lätt att gissa att x 1 = -5, x 2 = -6.
Observera: om ekvationens fria term är ett positivt tal, så är båda rötterna antingen positiva eller negativa; detta är viktigt att tänka på när du väljer rötter.
3) x 2 + x - 12 = 0. Här x 1 + x 2 = -1, x 1 x 2 = -12. Det är lätt att gissa att x 1 \u003d 3, x2 \u003d -4.
Observera: om ekvationens fria term är ett negativt tal, är rötterna olika i tecken; detta är viktigt att tänka på när du väljer rötter.
4) 5x 2 + 17x - 22 = 0. Det är lätt att se att x = 1 uppfyller ekvationen, d.v.s. x 1 \u003d 1 - roten till ekvationen. Eftersom x 1 x 2 \u003d -, och x 1 \u003d 1, får vi att x 2 \u003d -.
5) x 2 - 293x + 2830 = 0. Här x 1 + x 2 = 293, x 1 x 2 = 2830. Om du uppmärksammar det faktum att 2830 = 283. 10 och 293 \u003d 283 + 10, då blir det tydligt att x 1 \u003d 283, x 2 \u003d 10 (föreställ dig nu vilka beräkningar som skulle behöva utföras för att lösa denna andragradsekvation med standardformler).
6) Vi komponerar en andragradsekvation så att talen x 1 \u003d 8, x 2 \u003d - 4 fungerar som dess rötter. Vanligtvis i sådana fall utgör de den reducerade andragradsekvationen x 2 + px + q \u003d 0.
Vi har x 1 + x 2 \u003d -p, därför 8 - 4 \u003d -p, det vill säga p \u003d -4. Vidare, x 1 x 2 = q, dvs. 8"(-4) = q, varav vi får q = -32. Så, p \u003d -4, q \u003d -32, vilket betyder att den önskade andragradsekvationen har formen x 2 -4x-32 \u003d 0.
När du studerar sätt att lösa andra ordningens ekvationer i en skolalgebrakurs, överväg egenskaperna hos de erhållna rötterna. De är nu kända som Vietas satser. Exempel på dess användning ges i den här artikeln.
Andragradsekvation
Andra ordningens ekvation är en likhet, som visas på bilden nedan.
Här är symbolerna a, b, c några tal som kallas koefficienterna för ekvationen i fråga. För att lösa en likhet måste du hitta x-värden som gör den sann.
Observera att eftersom det maximala värdet av den potens till vilken x höjs är två, så är antalet rötter i det allmänna fallet också två.
Det finns flera sätt att lösa den här typen av jämställdhet. I den här artikeln kommer vi att överväga en av dem, som involverar användningen av den så kallade Vieta-satsen.
Uttalande av Vietas teorem

I slutet av 1500-talet märkte den berömda matematikern Francois Viet (fransman), när han analyserade egenskaperna hos rötterna till olika andragradsekvationer, att vissa kombinationer av dem uppfyller specifika samband. I synnerhet är dessa kombinationer deras produkt och summa.
Vietas sats fastställer följande: rötterna till en andragradsekvation, när de summeras, ger förhållandet mellan de linjära och andragradskoefficienterna tagna med motsatt tecken, och när de multipliceras leder de till förhållandet mellan den fria termen och den andragradskoefficienten .
Om den allmänna formen av ekvationen skrivs som den visas på bilden i föregående avsnitt av artikeln, kan matematiskt denna sats skrivas som två likheter:
- r 2 + r 1 \u003d -b / a;
- r 1 x r 2 \u003d c/a.
Där r 1 , r 2 är värdet av rötterna till den betraktade ekvationen.
Dessa två likheter kan användas för att lösa ett antal mycket olika matematiska problem. Användningen av Vieta-satsen i exempel med en lösning ges i följande avsnitt av artikeln.
Vietas sats (mer exakt, satsen omvänd till Vietas sats) tillåter oss att minska tiden för att lösa andragradsekvationer. Du behöver bara veta hur du använder den. Hur lär man sig att lösa andragradsekvationer med hjälp av Vietas teorem? Det är lätt om man tänker lite.
Nu ska vi bara prata om lösningen av den reducerade andragradsekvationen med hjälp av Vieta-satsen.Den reducerade andragradsekvationen är en ekvation där a, det vill säga koefficienten framför x², är lika med ett. Ogivna andragradsekvationer kan också lösas med hjälp av Vieta-satsen, men redan där är åtminstone en av rötterna inte ett heltal. De är svårare att gissa.
Satsen motsvarade Vietas sats säger: om talen x1 och x2 är sådana att
då är x1 och x2 rötterna till andragradsekvationen
![]()
När man löser en andragradsekvation med hjälp av Vieta-satsen är endast fyra alternativ möjliga. Om du kommer ihåg resonemangets gång kan du lära dig att hitta hela rötter väldigt snabbt.
I. Om q är ett positivt tal,
detta betyder att rötterna x1 och x2 är tal med samma tecken (eftersom endast när man multiplicerar tal med samma tecken erhålls ett positivt tal).
Bl.a. Om -p är ett positivt tal, (respektive sid<0), то оба корня x1 и x2 — положительные числа (поскольку складывали числа одного знака и получили положительное число).
I.b. Om -p är ett negativt tal, (respektive p>0), då är båda rötterna negativa tal (de lade till tal med samma tecken, fick ett negativt tal).
II. Om q är ett negativt tal,
detta betyder att rötterna x1 och x2 har olika tecken (vid multiplicering av tal erhålls ett negativt tal endast när tecknen för faktorerna är olika). I det här fallet är x1 + x2 inte längre en summa, utan en skillnad (trots allt, när vi lägger till tal med olika tecken, subtraherar vi det mindre från det större modulo). Därför visar x1 + x2 hur mycket rötterna x1 och x2 skiljer sig åt, det vill säga hur mycket en rot är mer än den andra (modulo).
II.a. Om -p är ett positivt tal, (dvs sid<0), то больший (по модулю) корень — положительное число.
II.b. Om -p är ett negativt tal, (p>0), då är den större (modulo) roten ett negativt tal.
Betrakta lösningen av andragradsekvationer enligt Vietas sats med hjälp av exempel.
Lös den givna andragradsekvationen med hjälp av Vietas sats:
Här är q=12>0, så rötterna x1 och x2 är tal med samma tecken. Deras summa är -p=7>0, så båda rötterna är positiva tal. Vi väljer heltal vars produkt är 12. Dessa är 1 och 12, 2 och 6, 3 och 4. Summan är 7 för paret 3 och 4. Därför är 3 och 4 rötterna till ekvationen.
I det här exemplet är q=16>0, vilket betyder att rötterna x1 och x2 är tal med samma tecken. Deras summa -p=-10<0, поэтому оба корня — отрицательные числа. Подбираем числа, произведение которых равно 16. Это 1 и 16, 2 и 8, 4 и 4. Сумма 2 и 8 равна 10, а раз нужны отрицательные числа, то искомые корни — это -2 и -8.
Här är q=-15<0, что означает, что корни x1 и x2 — числа разных знаков. Поэтому 2 — это уже не их сумма, а разность, то есть числа отличаются на 2. Подбираем числа, произведение которых равно 15, отличающиеся на 2. Произведение равно 15 у 1 и 15, 3 и 5. Отличаются на 2 числа в паре 3 и 5. Поскольку -p=2>0, då är det större talet positivt. Så rötterna är 5 och -3.
q=-36<0, значит, корни x1 и x2 имеют разные знаки. Тогда 5 — это то, насколько отличаются x1 и x2 (по модулю, то есть пока что без учета знака). Среди чисел, произведение которых равно 36: 1 и 36, 2 и 18, 3 и 12, 4 и 9 — выбираем пару, в которой числа отличаются на 5. Это 4 и 9. Осталось определить их знаки. Поскольку -p=-5<0, бОльшее число имеет знак минус. Поэтому корни данного уравнения равны -9 и 4.
- I kontakt med 0
- Google Plus 0
- OK 0
- Facebook 0