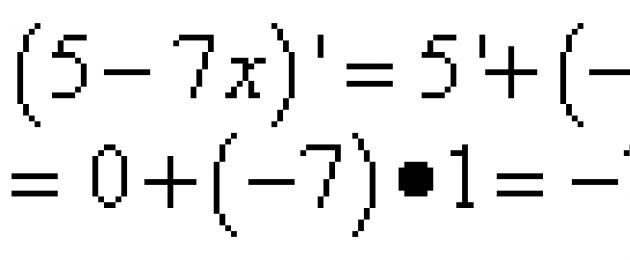Funktsiooni y tuletis on x-i juur. Leia tuletis: algoritm ja lahendusnäited

Tuletise leidmise operatsiooni nimetatakse diferentseerimiseks.

Lihtsamate (ja mitte väga lihtsate) funktsioonide tuletiste leidmise probleemide lahendamise tulemusena, defineerides tuletise juurdekasvu ja argumendi vahekorra piiriks, ilmus tuletisi tabel ja täpselt määratletud diferentseerimisreeglid. . Isaac Newton (1643-1727) ja Gottfried Wilhelm Leibniz (1646-1716) olid esimesed, kes töötasid tuletiste leidmise alal.

Seetõttu ei ole meie ajal vaja mis tahes funktsiooni tuletise leidmiseks arvutada ülalmainitud funktsiooni juurdekasvu ja argumendi juurdekasvu suhte piiri, vaid tuleb kasutada ainult tabelit. tuletistest ja diferentseerimisreeglitest. Tuletise leidmiseks sobib järgmine algoritm.

Tuletise leidmiseks, vajate löögimärgi alla väljendit lagundama lihtsaid funktsioone ja määrake, millised toimingud (produkt, summa, jagatis) need funktsioonid on omavahel seotud. Edasi leiame elementaarfunktsioonide tuletised tuletiste tabelist ning korrutise, summa ja jagatise tuletiste valemid - diferentseerimisreeglitest. Tuletiste ja diferentseerimisreeglite tabel on toodud pärast kahte esimest näidet.

Näide 1 Leia funktsiooni tuletis

Lahendus. Diferentseerimisreeglitest saame teada, et funktsioonide summa tuletis on funktsioonide tuletiste summa, s.o.

Tuletiste tabelist saame teada, et "X" tuletis on võrdne ühega ja siinuse tuletis on võrdne koosinusega. Asendame need väärtused tuletiste summaga ja leiame tuletise, mida nõuab ülesande tingimus:

Näide 2 Leia funktsiooni tuletis

Lahendus. Diferentseerime summa tuletisena, milles teise konstantse teguriga liikme saab tuletise märgist välja võtta:

Kui ikka tekib küsimusi, kust miski pärineb, selguvad need reeglina pärast tuletiste tabeli ja lihtsamate eristamisreeglite lugemist. Me läheme kohe nende juurde.

Lihtfunktsioonide tuletiste tabel

1. Konstandi (arvu) tuletis. Mis tahes arv (1, 2, 5, 200...), mis on funktsiooni avaldises. Alati null. Seda on väga oluline meeles pidada, kuna seda nõutakse väga sageli
2. Sõltumatu muutuja tuletis. Kõige sagedamini "x". Alati võrdne ühega. Seda on samuti oluline meeles pidada
3. Kraadi tuletis. Ülesannete lahendamisel tuleb mitteruutjuured teisendada astmeks.
4. Muutuja tuletis astmega -1
5. Ruutjuure tuletis
6. Siinustuletis
7. Koosinustuletis
8. Puutuja tuletis
9. Kootangensi tuletis
10. Arsiinuse tuletis
11. Kaarkoosinuse tuletis
12. Kaartangensi tuletis
13. Pöördtangensi tuletis
14. Naturaallogaritmi tuletis
15. Logaritmifunktsiooni tuletis
16. Eksponent tuletis
17. Eksponentfunktsiooni tuletis

Eristamise reeglid

1. Summa või vahe tuletis
2. Toote tuletis
2a. Avaldise tuletis, mis on korrutatud konstantse teguriga
3. Jagatise tuletis
4. Kompleksfunktsiooni tuletis

1. reegelKui funktsioonid

on mingil hetkel diferentseeruvad , siis samas punktis funktsioonid

ja

need. funktsioonide algebralise summa tuletis on võrdne nende funktsioonide tuletiste algebralise summaga.

Tagajärg. Kui kaks diferentseeruvat funktsiooni erinevad konstandi poolest, siis on nende tuletised, st.

2. reegelKui funktsioonid

on mingil hetkel eristatavad, siis on ka nende toode samas punktis eristatav

ja

need. kahe funktsiooni korrutise tuletis on võrdne mõlema funktsiooni ja teise funktsiooni korrutiste summaga.

Tagajärg 1. Konstantteguri saab tuletise märgist välja võtta:

Tagajärg 2. Mitme diferentseeruva funktsiooni korrutise tuletis on võrdne iga teguri ja kõigi teiste tuletise korrutiste summaga.

Näiteks kolme kordaja jaoks:

3. reegelKui funktsioonid

mingil hetkel eristuvad Ja , siis siinkohal on ka nende jagatis diferentseeritav.u/v ja

need. kahe funktsiooni jagatise tuletis on võrdne murdosaga, mille lugeja on nimetaja ja lugeja tuletise ning lugeja ja nimetaja tuletise korrutised ning nimetaja on eelmise lugeja ruut .

Kust teistelt lehtedelt vaadata

Korrutise tuletise ja jagatise leidmisel reaalsetes ülesannetes on alati vaja korraga rakendada mitut diferentseerimisreeglit, seega on nende tuletiste kohta rohkem näiteid artiklis."Korrutise ja jagatise tuletis".

kommenteerida. Konstanti (ehk arvu) ei tohiks segi ajada summas oleva liikmena ja konstantse tegurina! Termini puhul on selle tuletis võrdne nulliga ja konstantse teguri korral võetakse see tuletisi märgist välja. See on tüüpiline viga, mis tekib tuletiste uurimise algfaasis, kuid kuna keskmine õpilane lahendab mitu ühe-kahekomponendilist näidet, siis seda viga enam ei tehta.

Ja kui teil on toote või jagatise eristamisel termin u"v, milles u- arv, näiteks 2 või 5, see tähendab konstant, siis on selle arvu tuletis võrdne nulliga ja seetõttu on kogu liige võrdne nulliga (sellist juhtumit analüüsitakse näites 10) .

Teine levinud viga on kompleksfunktsiooni tuletise mehaaniline lahendamine lihtfunktsiooni tuletis. Sellepärast kompleksfunktsiooni tuletis pühendatud eraldi artiklile. Kuid kõigepealt õpime leidma lihtsate funktsioonide tuletisi.

Teel ei saa te ilma väljendite teisendusteta. Selleks peate võib-olla avama uutes Windowsi juhendites Võimude ja juurtega teod Ja Tegevused murdarvudega .

Kui otsite lahendusi võimsuste ja juurtega tuletistele, st millal funktsioon välja näeb , seejärel järgige õppetundi "Tõppude ja juurtega murdude summa tuletis".

Kui teil on ülesanne nagu , siis olete õppetunnis "Lihtsate trigonomeetriliste funktsioonide tuletised".

Samm-sammult näited – kuidas tuletist leida

Näide 3 Leia funktsiooni tuletis

Lahendus. Määrame funktsiooni avaldise osad: kogu avaldis esindab korrutist ja selle tegurid on summad, millest teises üks terminitest sisaldab konstantset tegurit. Rakendame korrutise eristamise reeglit: kahe funktsiooni korrutise tuletis on võrdne mõlema funktsiooni korrutiste summaga ja teise funktsiooni tuletisega:

Järgmisena rakendame summa diferentseerimise reeglit: funktsioonide algebralise summa tuletis võrdub nende funktsioonide tuletiste algebralise summaga. Meie puhul igas summas teine ​​liige miinusmärgiga. Igas summas näeme nii sõltumatut muutujat, mille tuletis on võrdne ühega, kui ka konstanti (arvu), mille tuletis on võrdne nulliga. Niisiis, "x" muutub üheks ja miinus 5 - nulliks. Teises avaldises korrutatakse "x" 2-ga, seega korrutame kaks sama ühikuga kui "x" tuletis. Saame järgmised tuletisinstrumentide väärtused:

Asendame leitud tuletised korrutiste summaga ja saame kogu ülesande tingimuse poolt nõutava funktsiooni tuletise:

Ja ülesande lahendust saate kontrollida tuletisel aadressil .

Näide 4 Leia funktsiooni tuletis

Lahendus. Peame leidma jagatise tuletise. Jagatise eristamiseks rakendame valemit: kahe funktsiooni jagatise tuletis on võrdne murdosaga, mille lugejaks on nimetaja ja lugeja tuletise ning lugeja ja nimetaja tuletise korrutised ning nimetaja on endise lugeja ruut. Saame:

Lugejas olevate tegurite tuletise leidsime juba näites 2. Ärgem unustagem ka seda, et korrutis, mis on lugejas teine ​​tegur, võetakse praeguses näites miinusmärgiga:

Kui otsite lahendusi sellistele probleemidele, mille puhul peate leidma funktsiooni tuletise, kus on pidev hunnik juuri ja astmeid, nagu näiteks, siis tere tulemast klassi "Tõppude ja juurtega murdude summa tuletis" .

Kui teil on vaja rohkem teada saada siinuste, koosinuste, puutujate ja muude trigonomeetriliste funktsioonide tuletisi, st kui funktsioon näeb välja selline , siis on teil õppetund "Lihtsate trigonomeetriliste funktsioonide tuletised" .

Näide 5 Leia funktsiooni tuletis

Lahendus. Selles funktsioonis näeme korrutist, mille üheks teguriks on sõltumatu muutuja ruutjuur, mille tuletisega tutvusime tuletiste tabelis. Korrutise eristamise reegli ja ruutjuure tuletise tabeliväärtuse järgi saame:

Tuletisülesande lahendust saate kontrollida aadressil tuletiskalkulaator võrgus .

Näide 6 Leia funktsiooni tuletis

Lahendus. Selles funktsioonis näeme jagatist, mille dividendiks on sõltumatu muutuja ruutjuur. Vastavalt jagatise diferentseerimise reeglile, mida kordasime ja rakendasime näites 4, ning ruutjuure tuletise tabeliväärtuse järgi saame:

Lugejas olevast murdosast vabanemiseks korrutage lugeja ja nimetaja arvuga.

1. Suvalise astme juure tuletise valemi üldjuhtum- murd, mille lugeja on üks ja nimetaja on arv, mis võrdub juure astmega, mille jaoks tuletis arvutati, korrutatuna sama astme juurega, mille juuravaldis on muutuja juureaste, mille jaoks tuletis arvutati, vähendatakse ühe võrra
2. Ruutjuure tuletis- on eelmise valemi erijuht. x ruutjuure tuletis on murd, mille lugeja on üks ja nimetaja on x kaks korda ruutjuur
3. Kuupjuure tuletis, ka üldvalemi erijuht. Kuupjuure tuletis on ühik, mis on jagatud kolme kuupjuurega x ruudus.

Allpool on toodud teisendused, mis selgitavad, miks ruut- ja kuupjuurte tuletise leidmise valemid on täpselt sellised, nagu joonisel näidatud.

Muidugi ei saa neid valemeid üldse pähe õppida, kui võtta arvesse, et tuletisastme juure eraldamine on sama, mis astmeni murru tõstmine, mille nimetaja on võrdne sama astmega. Seejärel taandatakse juure tuletise leidmine vastava murru astme tuletise leidmise valemi rakendamiseks.

Ruutjuure all oleva muutuja tuletis

(√x)" = 1 / (2√x) või 1/2 x -1/2

Selgitus:
(√x)" = (x 1/2)"

Ruutjuur on täpselt sama toiming kui 1/2 astmeni tõstmine,see tähendab, et juure tuletise leidmiseks saab suvalise astmeni rakendada muutuja tuletise leidmise reegli valemit:

(x 1/2)" \u003d 1/2 x -1/2 \u003d 1 / (2√x)

Kuupjuure tuletis (kolmanda astme juure tuletis)

Kuupjuure tuletis on täpselt sama, mis ruutjuur.

Kujutage ette kuupjuurt astmena 1/3 ja leidke tuletis üldiste diferentseerimisreeglite järgi. Lühike valem on näha ülaloleval pildil ja allpool on selgitus, miks see nii on.

Võimsus -2/3 saadakse 1/3-st ühe lahutamisel

Keerulised funktsioonid ei vasta alati keeruka funktsiooni määratlusele. Kui on olemas funktsioon kujul y \u003d sin x - (2 - 3) a r c t g x x 5 7 x 10 - 17 x 3 + x - 11, siis ei saa seda erinevalt y \u003d sin 2 x pidada keeruliseks.

See artikkel näitab kompleksfunktsiooni mõistet ja selle identifitseerimist. Töötame tuletise leidmise valemitega koos lahendusnäidetega järelduses. Tuletiste tabeli ja diferentseerimisreeglite kasutamine vähendab oluliselt tuletise leidmise aega.

Põhimääratlused

Definitsioon 1

Kompleksfunktsioon on funktsioon, mille argument on ühtlasi funktsioon.

Seda tähistatakse järgmiselt: f (g (x)) . Meil on, et funktsiooni g (x) peetakse argumendiks f (g (x)) .

2. definitsioon

Kui on olemas funktsioon f ja on kotangentne funktsioon, siis g(x) = ln x on naturaallogaritmfunktsioon. Saame, et kompleksfunktsioon f (g (x)) kirjutatakse kui arctg (lnx). Või funktsioon f, mis on 4. astmeni tõstetud funktsioon, kus g (x) \u003d x 2 + 2 x - 3 loetakse terveks ratsionaalseks funktsiooniks, saame, et f (g (x)) \u003d (x 2 + 2 x - 3) 4 .

Ilmselt võib g(x) olla keeruline. Näites y \u003d sin 2 x + 1 x 3 - 5 on näha, et g väärtusel on kuupjuur koos murdosaga. Seda avaldist saab tähistada kui y = f (f 1 (f 2 (x))) . Kui saame, et f on siinusfunktsioon ja f 1 on ruutjuure all asuv funktsioon, siis f 2 (x) \u003d 2 x + 1 x 3 - 5 on murdosaline ratsionaalne funktsioon.

3. määratlus

Pesastumisaste määratakse mis tahes naturaalarvuga ja kirjutatakse y = f (f 1 (f 2 (f 3 (. . . (f n (x)))))) .

4. määratlus

Funktsiooni koostise mõiste viitab pesastatud funktsioonide arvule vastavalt ülesandepüstitusele. Lahenduseks vormi kompleksfunktsiooni tuletise leidmise valem

(f(g(x)))"=f"(g(x)) g"(x)

Näited

Näide 1

Leidke kompleksfunktsiooni tuletis kujul y = (2 x + 1) 2 .

Lahendus

Kokkuleppeliselt on f ruutfunktsioon ja g(x) = 2 x + 1 loetakse lineaarfunktsiooniks.

Rakendame kompleksfunktsiooni tuletisvalemit ja kirjutame:

f "(g (x)) = ((g (x)) 2) " = 2 (g (x)) 2 - 1 = 2 g (x) = 2 (2 x + 1) ; g "(x) = (2x + 1)" = (2x)" + 1" = 2 x" + 0 = 2 1 x 1 - 1 = 2 ⇒ (f(g(x))) "=f" ( g(x)) g"(x) = 2 (2x + 1) 2 = 8x + 4

Tuleb leida funktsiooni lihtsustatud algkujuga tuletis. Saame:

y = (2x + 1) 2 = 4x2 + 4x + 1

Seetõttu on see meil olemas

y"=(4x2+4x+1)"=(4x2)"+(4x)"+1"=4(x2)"+4(x)"+0==4 2 x 2 - 1 + 4 1 x 1–1 = 8 x + 4

Tulemused klappisid.

Seda laadi ülesannete lahendamisel on oluline mõista, kus paiknevad vormi f ja g (x) funktsioon.

Näide 2

Peaksite leidma keeruliste funktsioonide tuletised kujul y \u003d sin 2 x ja y \u003d sin x 2.

Lahendus

Funktsiooni esimene kirje ütleb, et f on ruudu funktsioon ja g(x) on siinusfunktsioon. Siis me saame selle

y "= (sin 2 x)" = 2 sin 2 - 1 x (sin x)" = 2 sin x cos x

Teine kirje näitab, et f on siinusfunktsioon ja g (x) = x 2 tähistab astmefunktsiooni. Sellest järeldub, et kompleksfunktsiooni korrutist saab kirjutada kujul

y " \u003d (sin x 2) " \u003d cos (x 2) (x 2) " \u003d cos (x 2) 2 x 2 - 1 \u003d 2 x cos (x 2)

Tuletise y \u003d f (f 1 (f 2 (f 3 (. . . (fn (x)))))) valem kirjutatakse kujul y "= f" (f 1 (f 2 (f 3) (... ( fn (x)))))) f 1 "(f 2 (f 3 (. . . (fn (x))))) f 2" (f 3 (. . . (fn (x)) )) )) . . . f n "(x)

Näide 3

Leia funktsiooni y = sin (ln 3 a r c t g (2 x)) tuletis.

Lahendus

See näide näitab funktsioonide kirjutamise ja asukoha määramise keerukust. Siis y \u003d f (f 1 (f 2 (f 3 (f 4 (x))))) tähistab, kus f , f 1 , f 2 , f 3 , f 4 (x) on siinusfunktsioon, funktsioon 3 kraadini tõstmise funktsioon, logaritmi ja alusega e, arktangensi funktsioon ja lineaarne funktsioon.

Keerulise funktsiooni definitsiooni valemist saame selle

y "= f" (f 1 (f 2 (f 3 (f 4 (x))))) f 1 "(f 2 (f 3 (f 4 (x)))) f 2 "(f 3 (f) 4 (x))) f 3 "(f 4 (x)) f 4" (x)

Kuidas leida, mida leida

1. f "(f 1 (f 2 (f 3 (f 4 (x))))) kui siinuse tuletis tuletiste tabelis, siis f "(f 1 (f 2 (f 3 (f 4 (x)) ))))))) ) = cos (ln 3 arctg (2 x)) .
2. f 1 "(f 2 (f 3 (f 4 (x)))) kui astmefunktsiooni tuletis, siis f 1 "(f 2 (f 3 (f 4 (x)))) = 3 ln 3 - 1 arctg (2 x) = 3 ln 2 arctg (2 x) .
3. f 2 "(f 3 (f 4 (x))) logaritmilise tuletisena, siis f 2 "(f 3 (f 4 (x))) = 1 a r c t g (2 x) .
4. f 3 "(f 4 (x)) kui arktangensi tuletis, siis f 3 "(f 4 (x)) = 1 1 + (2 x) 2 = 1 1 + 4 x 2.
5. Tuletise f 4 (x) \u003d 2 x leidmisel võtke tuletise märgist välja 2, kasutades astmefunktsiooni tuletise valemit, mille astendaja on 1, seejärel f 4 "(x) \u003d ( 2 x)" \u003d 2 x "\u003d 2 · 1 · x 1 - 1 = 2 .

Me ühendame vahetulemused ja saame selle

y "= f" (f 1 (f 2 (f 3 (f 4 (x))))) f 1 "(f 2 (f 3 (f 4 (x)))) f 2 "(f 3 (f) 4 (x))) f 3 "(f 4 (x)) f 4" (x) = = cos (ln 3 arctaani (2 x)) 3 ln 2 arctaani (2 x) 1 arctaani (2 x) 1 1 + 4 x 2 2 = = 6 cos (ln 3 arctaani (2 x)) ln 2 arctaani (2 x) arctaani (2 x) (1 + 4 x 2)

Selliste funktsioonide analüüs meenutab pesitsevaid nukke. Diferentseerimisreegleid ei saa alati tuletistabelit kasutades selgesõnaliselt rakendada. Sageli peate keerukate funktsioonide tuletiste leidmiseks kasutama valemit.

Kompleksvaate ja keeruka funktsiooni vahel on mõned erinevused. Kui on selge võime seda eristada, on tuletisinstrumentide leidmine eriti lihtne.

Näide 4

Sellise näite toomist on vaja kaaluda. Kui on olemas funktsioon kujul y = tg 2 x + 3 tgx + 1, siis võib seda pidada kompleksfunktsiooniks kujul g (x) = tgx , f (g) = g 2 + 3 g + 1 . Ilmselgelt on vaja rakendada komplekstuletise valemit:

f "(g (x)) \u003d (g 2 (x) + 3 g (x) + 1) " \u003d (g 2 (x)) " + (3 g (x)) " + 1 " == 2 g 2–1 (x) + 3 g "(x) + 0 \u003d 2 g (x) + 3 1 g 1 - 1 (x) \u003d = 2 g (x) + 3 = 2 tgx + 3; g " (x) = (tgx) " = 1 cos 2 x ⇒ y " = (f (g (x))) " = f " (g (x)) g " (x) = (2 tgx + 3 ) 1 cos 2 x = 2 tanx + 3 cos 2 x

Funktsiooni kujul y = t g x 2 + 3 t g x + 1 ei peeta kompleksseks, kuna selle summad on t g x 2 , 3 t g x ja 1 . Kuid t g x 2 peetakse kompleksfunktsiooniks, siis saame astmefunktsiooni kujul g (x) \u003d x 2 ja f, mis on puutuja funktsioon. Selleks tuleb summa järgi eristada. Me saame sellest aru

y " = (tgx 2 + 3 tgx + 1) " = (tgx 2) " + (3 tgx) " + 1 " == (tgx 2) " + 3 (tgx) " + 0 = (tgx 2) " + 3 kuni 2 x

Liigume edasi kompleksfunktsiooni tuletise leidmise juurde (t g x 2) ":

f "(g (x)) \u003d (tg (g (x))) " \u003d 1 cos 2 g (x) \u003d 1 cos 2 (x 2) g " (x) \u003d (x 2) " \u003d 2 x 2 - 1 \u003d 2 x ⇒ (tgx 2) " \u003d f " (g (x)) g " (x) \u003d 2 x cos 2 (x 2)

Saame, et y "= (t g x 2 + 3 t g x + 1)" = (t g x 2) " + 3 cos 2 x = 2 x cos 2 (x 2) + 3 cos 2 x

Kompleksfunktsioonid võivad kuuluda kompleksfunktsioonide hulka ja kompleksfunktsioonid ise võivad olla kompleksse vormi liitfunktsioonid.

Näide 5

Vaatleme näiteks kompleksfunktsiooni kujul y = log 3 x 2 + 3 cos 3 (2 x + 1) + 7 e x 2 + 3 3 + ln 2 x (x 2 + 1)

Seda funktsiooni saab esitada kujul y = f (g (x)) , kus f väärtus on 3 aluse logaritmi funktsioon ja g (x) loetakse kahe funktsiooni summaks kujul h (x) = x 2 + 3 cos 3 (2 x + 1) + 7 ex 2 + 3 3 ja k (x) = ln 2 x (x 2 + 1) . Ilmselgelt y = f (h (x) + k (x)) .

Vaatleme funktsiooni h(x) . See on suhe l (x) = x 2 + 3 cos 3 (2 x + 1) + 7 kuni m (x) = e x 2 + 3 3

Meil on, et l (x) = x 2 + 3 cos 2 (2 x + 1) + 7 = n (x) + p (x) on kahe funktsiooni n (x) = x 2 + 7 ja p ( x) \u003d 3 cos 3 (2 x + 1) , kus p (x) \u003d 3 p 1 (p 2 (p 3 (x))) on kompleksfunktsioon arvulise koefitsiendiga 3 ja p 1 on kuupfunktsioon, p 2 koosinusfunktsioon, p 3 (x) = 2 x + 1 - lineaarfunktsioon.

Leidsime, et m (x) = ex 2 + 3 3 = q (x) + r (x) on kahe funktsiooni q (x) = ex 2 ja r (x) = 3 3 summa, kus q (x) = q 1 (q 2 (x)) on kompleksfunktsioon, q 1 on astendajaga funktsioon, q 2 (x) = x 2 on astmefunktsioon.

See näitab, et h (x) = l (x) m (x) = n (x) + p (x) q (x) + r (x) = n (x) + 3 p 1 (p 2 ( p 3) (x))) q 1 (q 2 (x)) + r (x)

Kui minna avaldisele kujul k (x) \u003d ln 2 x (x 2 + 1) \u003d s (x) t (x), on selge, et funktsioon on esitatud kompleksina s (x) \ u003d ln 2 x \u003d s 1 (s 2 (x)) ratsionaalse täisarvuga t (x) = x 2 + 1, kus s 1 on ruutfunktsioon ja s 2 (x) = ln x on logaritmiline alusega e .

Sellest järeldub, et avaldis on kujul k (x) = s (x) t (x) = s 1 (s 2 (x)) t (x) .

Siis me saame selle

y = log 3 x 2 + 3 cos 3 (2 x + 1) + 7 ex 2 + 3 3 + ln 2 x (x 2 + 1) = = fn (x) + 3 p 1 (p 2 (p 3 () x))) q 1 (q 2 (x)) = r (x) + s 1 (s 2 (x)) t (x)

Funktsiooni struktuuride järgi sai selgeks, kuidas ja milliseid valemeid tuleb avaldise diferentseerimisel avaldise lihtsustamiseks rakendada. Selliste probleemidega tutvumiseks ja nende lahenduse mõistmiseks on vaja viidata funktsiooni eristamise ehk selle tuletise leidmise punktile.

Kui märkate tekstis viga, tõstke see esile ja vajutage Ctrl+Enter

Astumusfunktsiooni tuletise valemi tuletamine (x astmeni a). Arvesse võetakse juurte tuletisi x-st. Kõrgemat järku võimsusfunktsiooni tuletise valem. Näiteid tuletisinstrumentide arvutamisest.

Sisu

Vaata ka: Positiivne funktsioon ja juured, valemid ja graafik
Võimsusfunktsiooni graafikud

Põhivalemid

x tuletis a astmega on x korda miinus ühe astmega:
(1) .

x-i n-nda juure tuletis m-ndast astmest on:
(2) .

Astumusfunktsiooni tuletise valemi tuletamine

Juhtum x > 0

Vaatleme muutuja x astmefunktsiooni eksponendiga a:
(3) .
Siin a on suvaline reaalarv. Vaatleme esmalt juhtumit.

Funktsiooni (3) tuletise leidmiseks kasutame astmefunktsiooni omadusi ja teisendame selle järgmisele kujule:
.

Nüüd leiame tuletise, rakendades:
;
.
siin .

Valem (1) on tõestatud.

Valemi tuletamine x astme n juure astmeni m

Nüüd kaaluge funktsiooni, mis on järgmise vormi juur:
(4) .

Tuletise leidmiseks teisendame juure võimsusfunktsiooniks:
.
Võrreldes valemiga (3), näeme seda
.
Siis
.

Valemi (1) abil leiame tuletise:
(1) ;
;
(2) .

Praktikas ei ole vaja valemit (2) pähe õppida. Palju mugavam on esmalt teisendada juured astmefunktsioonideks ja seejärel leida nende tuletised valemi (1) abil (vt näiteid lehe lõpus).

Juhtum x = 0

Kui , siis on eksponentsiaalfunktsioon defineeritud ka muutuja x = väärtusele 0 . Leiame funktsiooni (3) tuletise x = korral 0 . Selleks kasutame tuletise määratlust:
.

Asendage x = 0 :
.
Sel juhul peame tuletise all silmas parempoolset limiiti, mille puhul .

Niisiis leidsime:
.
Sellest on näha, et kell , .
Kell , .
Kell , .
See tulemus saadakse ka valemiga (1):
(1) .
Seetõttu kehtib valem (1) ka x = korral 0 .

juhtum x< 0

Mõelge uuesti funktsioonile (3):
(3) .
Mõne konstandi a väärtuse puhul on see defineeritud ka muutuja x negatiivsete väärtuste jaoks. Nimelt olgu a ratsionaalne arv. Siis saab seda esitada taandamatu murdena:
,
kus m ja n on täisarvud, millel puudub ühine jagaja.

Kui n on paaritu, siis on eksponentsiaalfunktsioon defineeritud ka muutuja x negatiivsete väärtuste jaoks. Näiteks kui n = 3 ja m = 1 meil on x-i kuupjuur:
.
See on määratletud ka x negatiivsete väärtuste jaoks.

Leiame võimsusfunktsiooni (3) tuletise konstandi a ratsionaalsetele väärtustele, mille jaoks see on defineeritud. Selleks esindame x-i järgmisel kujul:
.
Siis ,
.
Leiame tuletise, võttes konstandi tuletise märgist välja ja rakendades kompleksfunktsiooni diferentseerimise reeglit:

.
siin . Aga
.
Sellest ajast
.
Siis
.
See tähendab, et valem (1) kehtib ka:
(1) .

Kõrgemate tellimuste tuletisväärtpaberid

Nüüd leiame astmefunktsiooni kõrgemat järku tuletised
(3) .
Oleme juba leidnud esimest järku tuletise:
.

Võttes tuletise märgist välja konstandi a, leiame teist järku tuletise:
.
Samamoodi leiame kolmanda ja neljanda järgu tuletised:
;

.

Siit on selge, et suvalise n-nda järku tuletis sellel on järgmine vorm:
.

Märka seda kui a on naturaalarv, , siis n-s tuletis on konstantne:
.
Siis on kõik järgnevad tuletised võrdsed nulliga:
,
aadressil .

Tuletisnäited

Näide

Leia funktsiooni tuletis:
.

Teisendame juured astmeteks:
;
.
Seejärel võtab algfunktsioon järgmise kuju:
.

Leiame kraadide tuletised:
;
.
Konstandi tuletis on null:
.

Juhend

Enne juure tuletise leidmist pöörake tähelepanu muudele lahendatavas näites esinevatele funktsioonidele. Kui probleemil on palju radikaalavaldisi, kasutage ruutjuure tuletise leidmiseks järgmist reeglit:

(√x)" = 1/2√x.

Ja kuupjuure tuletise leidmiseks kasutage valemit:

(³√x)" \u003d 1/3 (³√x)²,

kus ³√x tähistab x-i kuupjuurt.

Kui eristamiseks on murdosaline muutuja, siis teisendage juur vastava eksponendiga astmefunktsiooniks. Ruutjuure korral on see võimsus ½ ja kuupjuure puhul ⅓:

√x \u003d x ^ ½,
³√x = x ^ ⅓,

kus ^ tähistab astmelisust.

Positiivse funktsiooni tuletise leidmiseks üldiselt ja konkreetselt x^1, x^⅓ kasutage järgmist reeglit:

(x ^ n)" = n * x^(n-1).

Juure tuletise puhul tähendab see seos järgmist:

(x^½)" = ½ x ^ (-½) ja
(x^⅓)" = ⅓ x ^ (-⅔).

Olles kõik eristanud, vaadake ülejäänud näidet tähelepanelikult. Kui said vastuses väga tülika väljendi, siis kindlasti saab seda lihtsustada. Enamik koolinäiteid on kujundatud nii, et tulemuseks on väike arv või kompaktne avaldis.

Paljudes tuletisülesannetes esinevad juured (ruut ja kuup) koos teiste funktsioonidega. Sel juhul juure tuletise leidmiseks järgige järgmisi reegleid:
konstandi tuletis (konstantne arv, C) võrdub nulliga: C" = 0;
konstanttegur võetakse tuletise märgist välja: (k*f)" = k * (f)" (f on suvaline funktsioon) ;
mitme funktsiooni summa tuletis võrdub tuletiste summaga: (f + g)" = (f)" + (g)";
kahe funktsiooni korrutise tuletis on ... ei, mitte tuletiste korrutis, vaid järgmine avaldis: (fg)" = (f)"g + f (g)";
jagatise tuletis ei ole samuti võrdne tuletiste jagatisega, vaid leitakse järgmise reegli järgi: (f / g)" = ((f)"g - f(g)") / g².

Märge

Sellel lehel saate võrgus arvutada funktsiooni tuletise koos probleemi üksikasjaliku lahendusega. Funktsiooni tuletiste lahendus tehakse diferentseerimisreeglite abil, mida üliõpilased õpivad instituudis matemaatilise analüüsi käigus. Funktsiooni tuletise leidmiseks tuleb väljale "Funktsioon" sisestada eristamiseks funktsioon vastavalt andmesisestuse reeglitele.

Kasulikud nõuanded

Funktsiooni tuletis on funktsiooni juurdekasvu ja argumendi juurdekasvu suhte piir, kui argumendi juurdekasv kipub olema null: Selle definitsiooni matemaatilist tähendust pole väga lihtne mõista, kuna koolis algebra kursus funktsiooni piiri mõistet kas ei uurita üldse või uuritakse väga pealiskaudselt. Kuid selleks, et õppida leidma erinevate funktsioonide tuletisi, pole see vajalik.

Allikad:

• x juurtuletis