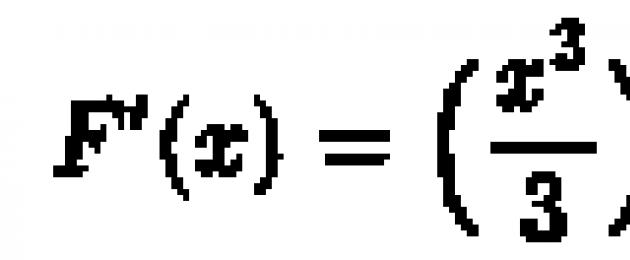Le proprietà più semplici degli integrali. Le proprietà più semplici degli integrali 2 definizione di integrale indefinito e sue proprietà

Queste proprietà vengono utilizzate per eseguire trasformazioni dell'integrale in modo da portarlo a uno degli integrali elementari e ulteriori calcoli.

1. La derivata dell'integrale indefinito è uguale all'integrando:

2. Il differenziale dell'integrale indefinito è uguale all'integrando:

3. L'integrale indefinito del differenziale di qualche funzione è uguale alla somma di questa funzione e di una costante arbitraria:

4. Dal segno di integrale si può estrarre un fattore costante:

Inoltre, a ≠ 0

5. L'integrale della somma (differenza) è uguale alla somma (differenza) degli integrali:

6. La proprietà è una combinazione delle proprietà 4 e 5:

Inoltre, a ≠ 0 ˄ b ≠ 0

7. La proprietà di invarianza dell'integrale indefinito:

Se poi

8. Proprietà:

Se poi

In effetti, questa proprietà è un caso speciale di integrazione utilizzando il metodo di modifica delle variabili, che verrà discusso più dettagliatamente nella sezione successiva.

Considera un esempio:

Per prima cosa abbiamo applicato la proprietà 5, quindi la proprietà 4, quindi abbiamo utilizzato la tabella delle antiderivate e ottenuto il risultato.

L'algoritmo del nostro calcolatore integrale online supporta tutte le proprietà sopra elencate e troverà facilmente una soluzione dettagliata per il tuo integrale.

Nel calcolo differenziale, il problema è risolto: sotto la data funzione ƒ(x) trova la sua derivata(o differenziale). Il calcolo integrale risolve il problema inverso: trovare la funzione F (x), conoscendo la sua derivata F "(x) \u003d ƒ (x) (o differenziale). La funzione desiderata F (x) è chiamata antiderivata della funzione ƒ (x).

Viene chiamata la funzione F(x). primitivo funzione ƒ(x) sull'intervallo (a; b), se per ogni x є (a; b) l'uguaglianza

F " (x)=ƒ(x) (o dF(x)=ƒ(x)dx).

Per esempio, la funzione antiderivativa y \u003d x 2, x є R, è una funzione, poiché

Ovviamente, anche gli antiderivati ​​saranno funzioni

dove C è una costante, perché

Teorema 29. 1. Se la funzione F(x) è l'antiderivata della funzione ƒ(x) su (a;b), allora l'insieme di tutte le antiderivate per ƒ(x) è dato dalla formula F(x)+ C, dove C è un numero costante.

▲ La funzione F(x)+C è l'antiderivata di ƒ(x).

Infatti, (F(x)+C) "=F" (x)=ƒ(x).

Sia F(x) un'altra, diversa da F(x), funzione antiderivativa ƒ(x), cioè Ф "(x)=ƒ(x). Allora per ogni x є (a; b) abbiamo

E questo significa (vedi Corollario 25.1) che

dove C è un numero costante. Pertanto, Ф(х)=F(x)+С.▼

Viene chiamato l'insieme di tutte le funzioni primitive F(x)+C per ƒ(x). integrale indefinito della funzione ƒ(x) ed è indicato dal simbolo ∫ ƒ(x) dx.

Quindi per definizione

∫ ƒ(x)dx= F(x)+C.

Qui viene chiamato ƒ(x). integrando, ƒ(x)dx — integrando, X - variabile di integrazione, ∫ -segno integrale indefinito.

L'operazione per trovare un integrale indefinito di una funzione è chiamata integrazione di questa funzione.

L'integrale geometricamente indefinito è una famiglia di curve "parallele" y \u003d F (x) + C (ogni valore numerico di C corrisponde a una determinata curva della famiglia) (vedi Fig. 166). Viene chiamato il grafico di ciascuna antiderivata (curva). curva integrale.

Ogni funzione ha un integrale indefinito?

Esiste un teorema che afferma che “ogni funzione continua su (a;b) ha un'antiderivata su questo intervallo”, e, di conseguenza, un integrale indefinito.

Notiamo un certo numero di proprietà dell'integrale indefinito che seguono dalla sua definizione.

1. Il differenziale dell'integrale indefinito è uguale all'integrando e la derivata dell'integrale indefinito è uguale all'integrando:

d(∫ ƒ(x)dx)=ƒ(x)dх, (∫ ƒ(x)dx) "=ƒ(x).

Infatti, d (∫ ƒ (x) dx) \u003d d (F (x) + C) \u003d dF (x) + d (C) \u003d F "(x) dx \u003d ƒ (x) dx

(∫ ƒ (x) dx) "=(F(x)+C)"=F"(x)+0 =ƒ(x).

Grazie a questa proprietà, la correttezza dell'integrazione è verificata per differenziazione. Ad esempio, l'uguaglianza

∫(3x 2 + 4) dx=x h + 4x+C

vero, poiché (x 3 + 4x + C) "= 3x 2 +4.

2. L'integrale indefinito del differenziale di qualche funzione è uguale alla somma di questa funzione e di una costante arbitraria:

∫dF(x)=F(x)+C.

Veramente,

3. Il fattore costante può essere estratto dal segno di integrale:

α ≠ 0 è una costante.

Veramente,

(metti C 1 / a \u003d C.)

4. L'integrale indefinito della somma algebrica di un numero finito di funzioni continue è uguale alla somma algebrica degli integrali dei termini delle funzioni:

Sia F"(x)=ƒ(x) e G"(x)=g(x). Quindi

dove C 1 ± C 2 \u003d C.

5. (Invarianza della formula di integrazione).

Se una , dove u=φ(x) è una funzione arbitraria che ha una derivata continua.

▲ Sia x una variabile indipendente, ƒ(x) una funzione continua e F(x) la sua antiderivata. Quindi

Poniamo ora u=φ(x), dove φ(x) è una funzione continuamente differenziabile. Si consideri una funzione complessa F(u)=F(φ(x)). A causa dell'invarianza della forma del primo differenziale della funzione (vedi p. 160), abbiamo

Da qui▼

Pertanto, la formula per l'integrale indefinito rimane valida indipendentemente dal fatto che la variabile di integrazione sia una variabile indipendente o qualsiasi sua funzione che abbia una derivata continua.

Quindi, dalla formula sostituendo x con u (u=φ(x)) otteniamo

In particolare,

Esempio 29.1. Trova l'integrale

dove C \u003d C1 + C 2 + C 3 + C 4.

Esempio 29.2. Trova la soluzione integrale:

• 29.3. Tabella degli integrali indefiniti di base

Sfruttando il fatto che l'integrazione è l'inverso della differenziazione, si può ottenere una tabella di integrali di base invertendo le corrispondenti formule del calcolo differenziale (tabella dei differenziali) e utilizzando le proprietà dell'integrale indefinito.

Per esempio, perché

d(peccato u)=cos u . du,

La derivazione di alcune formule tabellari sarà data quando si considerano i principali metodi di integrazione.

Gli integrali nella tabella seguente sono chiamati integrali tabulari. Dovrebbero essere conosciuti a memoria. Nel calcolo integrale non ci sono regole semplici e universali per trovare antiderivate da funzioni elementari, come nel calcolo differenziale. I metodi per trovare antiderivate (cioè, integrare una funzione) si riducono a indicare metodi che portano un dato integrale (desiderato) a uno tabulare. Pertanto, è necessario conoscere gli integrali tabulari ed essere in grado di riconoscerli.

Si noti che nella tabella degli integrali di base, la variabile di integrazione e può denotare sia una variabile indipendente che una funzione di una variabile indipendente (secondo la proprietà di invarianza della formula di integrazione).

La validità delle formule seguenti può essere verificata prendendo il differenziale sul lato destro, che sarà uguale all'integrando sul lato sinistro della formula.

Dimostriamo, ad esempio, la validità della formula 2. La funzione 1/u è definita e continua per tutti i valori diversi da zero di u.

Se u > 0, allora ln|u|=lnu, allora Ecco perchè

Se tu<0, то ln|u|=ln(-u). НоSignifica

Quindi la formula 2 è corretta. Allo stesso modo, controlliamo la formula 15:

Tabella degli integrali di base

Gli amici! Ti invitiamo a discutere. Se hai un'opinione, scrivici nei commenti.

In questo articolo, elenchiamo le principali proprietà di un integrale definito. La maggior parte di queste proprietà sono dimostrate sulla base dei concetti di Riemann e Darboux di integrale definito.

Il calcolo dell'integrale definito molto spesso viene effettuato utilizzando le prime cinque proprietà, per cui faremo riferimento ad esse quando necessario. Le restanti proprietà dell'integrale definito vengono utilizzate principalmente per valutare varie espressioni.

Prima di passare a proprietà di base di un integrale definito, concordiamo che a non supera b .

Per la funzione y = f(x) , definita per x = a , l'uguaglianza è vera.

Cioè, il valore dell'integrale definito con gli stessi limiti di integrazione è zero. Questa proprietà è conseguenza della definizione dell'integrale di Riemann, poiché in questo caso ogni somma integrale per qualsiasi partizione dell'intervallo ed ogni scelta di punti è uguale a zero, poiché, quindi, il limite delle somme integrali è zero.

Per una funzione integrabile su un segmento, abbiamo .

In altre parole, quando i limiti superiore e inferiore di integrazione sono invertiti, il valore dell'integrale definito viene invertito. Questa proprietà di integrale definito deriva anche dal concetto di integrale di Riemann, solo la numerazione della partizione di un segmento dovrebbe iniziare dal punto x = b.

per funzioni y = f(x) e y = g(x) integrabili su un intervallo.

Prova.

Scriviamo la somma integrale della funzione per una data partizione del segmento e una data scelta di punti:

dove e sono le somme integrali delle funzioni y = f(x) e y = g(x) per una data partizione del segmento, rispettivamente.

Passando al limite a otteniamo che, per la definizione dell'integrale di Riemann, è equivalente all'asserzione della proprietà dimostrata.

Il fattore costante può essere estratto dal segno di un integrale definito. Cioè, per una funzione integrabile su un segmento y = f(x) e un numero arbitrario k, l'uguaglianza .

La dimostrazione di questa proprietà di integrale definito è assolutamente simile alla precedente:


Sia la funzione y = f(x) integrabile sull'intervallo X , e poi .

Questa proprietà è valida per entrambi e per o .

La dimostrazione può essere eseguita in base alle proprietà precedenti dell'integrale definito.

Se una funzione è integrabile su un segmento, allora è integrabile anche su qualsiasi segmento interno.

La dimostrazione si basa sulla proprietà delle somme di Darboux: se vengono aggiunti nuovi punti alla partizione esistente del segmento, la somma di Darboux inferiore non diminuirà e quella superiore non aumenterà.

Se la funzione y = f(x) è integrabile sull'intervallo e per qualsiasi valore dell'argomento , allora .

Questa proprietà è dimostrata attraverso la definizione dell'integrale di Riemann: qualsiasi somma integrale per qualsiasi scelta di punti di divisione del segmento e punti a sarà non negativa (non positiva).

Conseguenza.

Per funzioni y = f(x) e y = g(x) integrabili su un intervallo, valgono le seguenti disuguaglianze:


Questa affermazione significa che l'integrazione delle disuguaglianze è ammissibile. Useremo questo corollario per dimostrare le seguenti proprietà.

Sia la funzione y = f(x) integrabile sul segmento , quindi la disuguaglianza .

Prova.

È ovvio che . Nella proprietà precedente, abbiamo scoperto che la disuguaglianza può essere integrata termine per termine, quindi è vero . Questa doppia disuguaglianza può essere scritta come .

Sia le funzioni y = f(x) e y = g(x) integrabili sull'intervallo e per qualsiasi valore dell'argomento , allora , dove e .

La dimostrazione viene eseguita in modo simile. Poiché m e M sono i valori più piccoli e più grandi della funzione y = f(x) sul segmento, allora . Moltiplicando la doppia disuguaglianza per la funzione non negativa y = g(x) si ottiene la seguente doppia disuguaglianza. Integrandolo sul segmento si arriva all'asserzione da dimostrare.

Funzione antiderivativa e integrale indefinito

Fatto 1. L'integrazione è l'opposto della differenziazione, vale a dire, il ripristino di una funzione dalla derivata nota di questa funzione. La funzione ripristinata in questo modo F(X) è chiamato primitivo per funzione f(X).

Definizione 1. Funzione F(X f(X) su un certo intervallo X, se per tutti i valori X da questo intervallo l'uguaglianza F "(X)=f(X), ovvero questa funzione f(X) è la derivata della funzione antiderivativa F(X). .

Ad esempio, la funzione F(X) = peccato X è l'antiderivata della funzione f(X) = cos X sull'intera riga dei numeri, poiché per qualsiasi valore di x (peccato X)" = (cos X) .

Definizione 2. Integrale indefinito di una funzione f(X) è la raccolta di tutti i suoi antiderivati. Questo usa la notazione

∫

f(X)dx

,

dov'è il segno ∫ è chiamato segno di integrale, la funzione f(X) è un integrando, e f(X)dx è l'integrando.

Quindi, se F(X) è un antiderivato per f(X) , poi

∫

f(X)dx = F(X) +C

dove C - costante arbitraria (costante).

Per comprendere il significato dell'insieme delle antiderivate di una funzione come integrale indefinito, è appropriata la seguente analogia. Lascia che ci sia una porta (una tradizionale porta di legno). La sua funzione è "essere una porta". Di cosa è fatta la porta? Da un albero. Ciò significa che l'insieme delle antiderivate dell'integrando "essere una porta", cioè il suo integrale indefinito, è la funzione "essere un albero + C", dove C è una costante, che in questo contesto può denotare, per esempio, una specie di albero. Così come una porta è fatta di legno con alcuni utensili, il derivato di una funzione è "fatto" della funzione antiderivativa con formula che abbiamo appreso studiando la derivata .

Quindi la tabella delle funzioni degli oggetti comuni e delle loro primitive corrispondenti ("essere una porta" - "essere un albero", "essere un cucchiaio" - "essere un metallo", ecc.) è simile alla tabella di integrali indefiniti di base, che verranno riportati di seguito. La tabella degli integrali indefiniti elenca le funzioni comuni, indicando le antiderivate da cui queste funzioni sono "fatte". Come parte dei compiti per trovare l'integrale indefinito, sono dati tali integrandi che possono essere integrati direttamente senza particolari sforzi, cioè secondo la tabella degli integrali indefiniti. In problemi più complessi, l'integrando deve prima essere trasformato in modo da poter utilizzare gli integrali tabulari.

Fatto 2. Ripristinando una funzione come antiderivata, dobbiamo prendere in considerazione una costante arbitraria (costante) C e per non scrivere un elenco di antiderivate con varie costanti da 1 a infinito, è necessario annotare un insieme di antiderivate con una costante arbitraria C, in questo modo: 5 X³+C. Quindi, una costante arbitraria (costante) è inclusa nell'espressione dell'antiderivativa, poiché l'antiderivativa può essere una funzione, ad esempio 5 X³+4 o 5 X³+3 e quando si differenzia 4 o 3 o qualsiasi altra costante svanisce.

Poniamo il problema di integrazione: per una data funzione f(X) trovare una tale funzione F(X), il cui derivatoè uguale a f(X).

Esempio 1 Trova l'insieme delle antiderivate di una funzione

Soluzione. Per questa funzione, l'antiderivata è la funzione

Funzione F(X) è chiamata antiderivata per la funzione f(X) se la derivata F(X) è uguale a f(X), o, che è la stessa cosa, il differenziale F(X) è uguale a f(X) dx, cioè.

(2)

Pertanto, la funzione è antiderivata per la funzione . Tuttavia, non è l'unico antiderivato per . Sono anche funzioni

dove DAè una costante arbitraria. Questo può essere verificato per differenziazione.

Quindi, se esiste un'antiderivativa per una funzione, allora per essa esiste un insieme infinito di antiderivate che differiscono per una somma costante. Tutte le antiderivate per una funzione sono scritte nella forma precedente. Ciò segue dal seguente teorema.

Teorema (affermazione formale del fatto 2). Se una F(X) è l'antiderivata della funzione f(X) su un certo intervallo X, quindi qualsiasi altro antiderivato per f(X) sullo stesso intervallo può essere rappresentato come F(X) + C, dove DAè una costante arbitraria.

Nell'esempio seguente, passiamo già alla tabella degli integrali, che sarà data nel paragrafo 3, dopo le proprietà dell'integrale indefinito. Lo facciamo prima di familiarizzare con l'intera tabella, in modo che l'essenza di quanto sopra sia chiara. E dopo la tabella e le proprietà, le useremo nella loro interezza durante l'integrazione.

Esempio 2 Trova insiemi di antiderivate:

Soluzione. Troviamo insiemi di funzioni antiderivate da cui queste funzioni sono "fatte". Quando menzioniamo formule dalla tabella degli integrali, per ora, accetta solo che ci siano tali formule e studieremo la tabella degli integrali indefiniti per intero un po' più avanti.

1) Applicazione della formula (7) dalla tabella degli integrali per n= 3, otteniamo

2) Utilizzando la formula (10) dalla tabella degli integrali per n= 1/3, abbiamo

3) Dal momento che

quindi secondo la formula (7) a n= -1/4 trova

Sotto il segno di integrale non scrivono la funzione stessa f, e il suo prodotto per il differenziale dx. Questo viene fatto principalmente per indicare quale variabile viene ricercata l'antiderivata. Per esempio,

, ;

qui in entrambi i casi l'integrando è uguale a , ma i suoi integrali indefiniti nei casi considerati risultano diversi. Nel primo caso, questa funzione è considerata come una funzione di una variabile X, e nel secondo - in funzione di z .

Il processo per trovare l'integrale indefinito di una funzione è chiamato integrazione di quella funzione.

Il significato geometrico dell'integrale indefinito

Sia richiesto di trovare una curva y=F(x) e sappiamo già che la tangente della pendenza della tangente in ciascuno dei suoi punti è una funzione data f(x) ascissa di questo punto.

Secondo il significato geometrico della derivata, la tangente della pendenza della tangente in un dato punto della curva y=F(x) uguale al valore della derivata F"(x). Quindi, dobbiamo trovare una tale funzione F(x), per cui F"(x)=f(x). Funzione richiesta nell'attività F(x)è derivato da f(x). La condizione del problema è soddisfatta non da una curva, ma da una famiglia di curve. y=F(x)- una di queste curve, e qualsiasi altra curva può essere ricavata da essa per traslazione parallela lungo l'asse Ehi.

Chiamiamo il grafico della funzione antiderivativa di f(x) curva integrale. Se una F"(x)=f(x), quindi il grafico della funzione y=F(x)è una curva integrale.

Fatto 3. L'integrale indefinito è geometricamente rappresentato dalla famiglia di tutte le curve integrali come nella foto qui sotto. La distanza di ciascuna curva dall'origine è determinata da una costante arbitraria (costante) di integrazione C.

Proprietà dell'integrale indefinito

Fatto 4. Teorema 1. La derivata di un integrale indefinito è uguale all'integrando e il suo differenziale è uguale all'integrando.

Fatto 5. Teorema 2. L'integrale indefinito del differenziale di una funzione f(X) è uguale alla funzione f(X) fino a un termine costante , cioè.

(3)

I teoremi 1 e 2 mostrano che differenziazione e integrazione sono operazioni reciprocamente inverse.

Fatto 6. Teorema 3. Il fattore costante nell'integrando può essere dedotto dal segno dell'integrale indefinito , cioè.

Lascia che la funzione y = f(X) è definito sull'intervallo [ un, b ], un < b. Eseguiamo le seguenti operazioni:

1) dividere [ un, b] punti un = X 0 < X 1 < ... < X io- 1 < X io < ... < X n = b sul n segmenti parziali [ X 0 , X 1 ], [X 1 , X 2 ], ..., [X io- 1 , X io ], ..., [X n- 1 , X n ];

2) in ciascuno dei segmenti parziali [ X io- 1 , X io ], io = 1, 2, ... n, scegli un punto arbitrario e calcola il valore della funzione a questo punto: f(z io ) ;

3) trovare opere f(z io ) · Δ X io , dove è la lunghezza del segmento parziale [ X io- 1 , X io ], io = 1, 2, ... n;

4) comporre somma integrale funzioni y = f(X) sul segmento [ un, b ]:

Da un punto di vista geometrico, tale somma σ è la somma delle aree dei rettangoli le cui basi sono segmenti parziali [ X 0 , X 1 ], [X 1 , X 2 ], ..., [X io- 1 , X io ], ..., [X n- 1 , X n ], e le altezze sono f(z 1 ) , f(z 2 ), ..., f(zn) rispettivamente (Fig. 1). Indica con λ lunghezza del segmento parziale più grande:

5) trova il limite della somma integrale quando λ → 0.

Definizione. Se esiste un limite finito della somma integrale (1) e non dipende dal metodo di divisione del segmento [ un, b] in segmenti parziali, né dalla scelta dei punti z io in essi si chiama allora questo limite integrale definito dalla funzione y = f(X) sul segmento [ un, b] e indicato

In questo modo,

In questo caso, la funzione f(X) è chiamato integrabile sul [ un, b]. Numeri un e b sono chiamati rispettivamente il limite inferiore e superiore di integrazione, f(X) è l'integrando, f(X ) dx- integrando, X– variabile di integrazione; segmento [ un, b] è chiamato intervallo di integrazione.

Teorema 1. Se la funzione y = f(X) è continua sul segmento [ un, b], allora è integrabile su questo intervallo.

L'integrale definito con gli stessi limiti di integrazione è uguale a zero:

Se una un > b, quindi, per definizione, impostiamo

2. Il significato geometrico di un integrale definito

Lascia il segmento [ un, b] funzione continua non negativa y = f(X ) . Trapezio curvilineoè chiamata figura delimitata dall'alto dal grafico di una funzione y = f(X), dal basso - dall'asse Ox, a sinistra ea destra - con linee rette x = a e x = b(Fig. 2).

Integrale definito di una funzione non negativa y = f(X) da un punto di vista geometrico è uguale all'area di un trapezio curvilineo delimitato superiormente dal grafico della funzione y = f(X) , a sinistra ea destra per segmenti di linea x = a e x = b, dal basso - da un segmento dell'asse Ox.

3. Proprietà fondamentali di un integrale definito

1. Il valore dell'integrale definito non dipende dalla notazione della variabile di integrazione:

2. Dal segno di un integrale definito si può estrarre un fattore costante:

3. L'integrale definito della somma algebrica di due funzioni è uguale alla somma algebrica degli integrali definiti di queste funzioni:

4.se funzione y = f(X) è integrabile su [ un, b] e un < b < c, poi

5. (teorema del valore medio). Se la funzione y = f(X) è continua sul segmento [ un, b], allora su questo segmento esiste un punto tale che

4. Formula di Newton-Leibniz

Teorema 2. Se la funzione y = f(X) è continua sul segmento [ un, b] e F(X) è uno dei suoi antiderivati ​​su questo segmento, allora è vera la seguente formula:

che è chiamato Formula di Newton-Leibniz. Differenza F(b) - F(un) è scritto come segue:

dove il carattere è chiamato carattere jolly doppio.

Pertanto, la formula (2) può essere scritta come:

Esempio 1 Calcola integrale

Soluzione. Per l'integrando f(X ) = X 2 un antiderivato arbitrario ha la forma

Poiché qualsiasi antiderivata può essere utilizzata nella formula di Newton-Leibniz, per calcolare l'integrale prendiamo l'antiderivativa, che ha la forma più semplice:

5. Cambiamento di variabile in un integrale definito

Teorema 3. Lascia che la funzione y = f(X) è continua sul segmento [ un, b]. Se una:

1) funzione X = φ ( t) e la sua derivata φ "( t) sono continui per ;

2) un insieme di valori di funzione X = φ ( t) for è il segmento [ un, b ];

3) φ ( un) = un, φ ( b) = b, quindi la formula

che è chiamato cambio di formula variabile in un integrale definito .

Diversamente dall'integrale indefinito, in questo caso non necessario per tornare alla variabile di integrazione originaria - basta trovare nuovi limiti di integrazione α e β (per questo è necessario risolvere per la variabile t equazioni φ ( t) = un e φ ( t) = b).

Invece di sostituzione X = φ ( t) puoi usare la sostituzione t = g(X). In questo caso, trovare nuovi limiti di integrazione rispetto alla variabile t semplifica: α = g(un) , β = g(b) .

Esempio 2. Calcola integrale

Soluzione. Introduciamo una nuova variabile secondo la formula . Al quadrato di entrambi i membri dell'equazione otteniamo 1 + x= t 2 , dove x= t 2 - 1, dx = (t 2 - 1)"dt= 2tdt. Troviamo nuovi limiti di integrazione. Per fare ciò, sostituiamo i vecchi limiti nella formula x= 3 e x= 8. Otteniamo: , da dove t= 2 e α = 2; , dove t= 3 e β = 3. Quindi,

Esempio 3 Calcolare

Soluzione. Permettere tu=ln X, poi , v = X. Per formula (4)