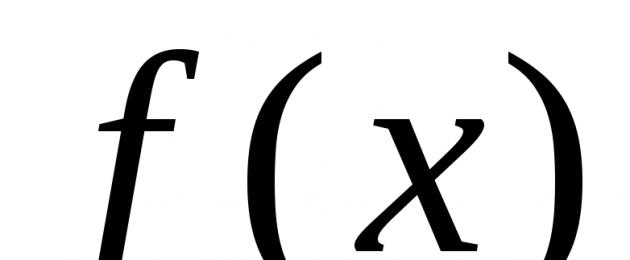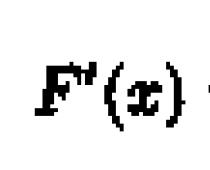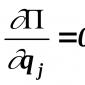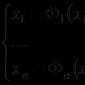Formula di interpolazione lagrangiana. Polinomio di interpolazione di Lagrange Come trovare i coefficienti del polinomio di Lagrange

Nella pratica computazionale, si ha spesso a che fare con funzioni definite da tabelle dei loro valori per un insieme finito di valori X : .

Nel processo di risoluzione del problema, è necessario utilizzare i valori
per valori intermedi dell'argomento. In questo caso, viene costruita una funzione Ф(x), abbastanza semplice per i calcoli, che in determinati punti X 0 , X 1 ,...,X n , chiamati nodi di interpolazione, assume valori, e in altri punti del segmento (x 0 ,x n) appartenenti al dominio di definizione
, rappresenta approssimativamente la funzione
con un certo grado di precisione.

Quando si risolve il problema in questo caso, invece della funzione
operare con la funzione Ф(x). Il compito di costruire tale funzione Ф(x) è chiamato problema di interpolazione. Molto spesso, la funzione di interpolazione Ф(x) si trova nella forma di un polinomio algebrico.

1. Polinomio di interpolazione

Per ogni funzione
definito il [ a, b] e qualsiasi insieme di nodi X 0 , X 1 ,...,X n (X io
[a, b], X io X j per i j) tra i polinomi algebrici di grado al massimo n, esiste un unico polinomio di interpolazione Ф(x), che può essere scritto nella forma:

, (3.1)

dove
è un polinomio di ennesimo grado, che ha la seguente proprietà:

Per un polinomio di interpolazione, il polinomio
sembra:

Questo polinomio (3.1) risolve il problema dell'interpolazione ed è chiamato polinomio di interpolazione di Lagrange.

Si consideri ad esempio una funzione del form
sull'intervallo
data in forma tabellare.

È necessario determinare il valore della funzione nel punto x-2.5. Usiamo il polinomio di Lagrange per questo. Sulla base delle formule (3.1 e 3.3), scriviamo esplicitamente questo polinomio:

(3.4).

Sostituendo quindi nella formula (3.4) i valori iniziali della nostra tabella, otteniamo

Il risultato ottenuto corrisponde alla teoria cioè .

1. Formula di interpolazione di Lagrange

Il polinomio di interpolazione di Lagrange può essere scritto in un'altra forma:

(3.5)

Scrivere un polinomio nella forma (3.5) è più conveniente per la programmazione.

Quando si risolve il problema di interpolazione, il valore nè chiamato ordine del polinomio interpolante. In questo caso, come si evince dalle formule (3.1) e (3.5), il numero dei nodi di interpolazione sarà sempre uguale a n+1 e significato X, per cui si determina il valore
, deve trovarsi all'interno del dominio dei nodi di interpolazione quelli.

. (3.6)

In alcuni casi pratici, il numero totale noto di nodi di interpolazione m può essere maggiore dell'ordine del polinomio interpolante n.

In questo caso, prima di implementare la procedura di interpolazione secondo la formula (3.5), è necessario determinare quei nodi di interpolazione per i quali vale la condizione (3.6). Va ricordato che l'errore più piccolo si ottiene quando si trova il valore X al centro della regione di interpolazione. Per garantire ciò, si suggerisce la seguente procedura:

Lo scopo principale dell'interpolazione è calcolare i valori di una funzione tabulata per valori di argomenti non nodali (intermedi), motivo per cui l'interpolazione viene spesso definita "l'arte di leggere le tabelle tra le righe".

Il campione di dati sperimentali è una matrice di dati che caratterizza il processo di modifica del segnale misurato durante un dato tempo (o relativo a un'altra variabile). Per eseguire un'analisi teorica del segnale misurato, è necessario trovare una funzione di approssimazione che collegherà un insieme discreto di dati sperimentali con una funzione continua: un polinomio di interpolazione n -gradi. Un modo per rappresentare un dato polinomio di interpolazione di n gradi consiste nell'utilizzare un polinomio nella forma di Lagrange.

Polinomio di interpolazione a forma diLagrangeè una funzione matematica che permette di scrivere un polinomio n -degree, che collegherà tutti i punti dati da un insieme di valori ottenuti empiricamente o mediante campionamento casuale in momenti diversi con un passo temporale di misurazione non costante.

1. Formula di interpolazione di Lagrange

In generale, il polinomio di interpolazionenella forma di Lagrange è scritto come segue:

dove ˗ grado polinomiale;

˗ il valore del valore della funzione di interpolazione al punto ;

˗ polinomi di base (moltiplicatore di Lagrange), che sono determinati dalla formula:

Ad esempio, il polinomio di interpolazionenella forma di Lagrange passante per tre punti dati, sarà scritto nella seguente forma:

Il polinomio di Lagrange contiene esplicitamente i valori della funzione ai nodi di interpolazione, quindi è utile quando i valori della funzione cambiano ma i nodi di interpolazione rimangono invariati. Il numero di operazioni aritmetiche richieste per costruire il polinomio di Lagrange è proporzionale aed è il più piccolo per tutte le forme di notazione. Gli svantaggi di questa forma di scrittura includono il fatto che quando si costruisce un polinomio di grado n + 1, le informazioni sul precedente polinomio di grado n vengono completamente perse, ad es. con una modifica del numero di nodi, l'intero calcolo deve essere eseguito nuovamente.

2. Errore del polinomio di interpolazione nella forma di Lagrange

Considera la funzione f(x ), che è continua e differenziabile sul segmento considerato. Polinomio di interpolazione l (x) nella forma Lagrange prende i puntisetpoint di funzione. In altri punti, il polinomio di interpolazione L(x) diverso dal valore della funzione f(x) per l'importo membro residuo , che determina l'errore assoluto della formula di interpolazione di Lagrange:

MA L'errore assoluto della formula di interpolazione di Lagrange è determinato come segue:

dove n ˗ grado polinomiale

Variabile rappresenta il limite superiore del valore del modulo (n+1)esima derivata della funzione f(x) su un dato intervallo

L'errore di interpolazione del metodo di Lagrange dipende dalle proprietà della funzione f(x) e anche dalla posizione dei nodi di interpolazione e dal punto X. Se l'errore non raggiunge la precisione richiesta, è necessario dividere il segmento in parti e interpolare ciascuna parte separatamente, interpolazione a tratti.

Selezione dei nodi di interpolazione

Con l'aiuto di una corretta scelta dei nodi, si può minimizzare il valorenella stima dell'errore, migliorando così l'accuratezza dell'interpolazione. Questo problema può essere risolto usando il polinomio di Chebyshev:

Come nodi, dovresti prendere le radici di questo polinomio, cioè i punti:

3. Tecnica per il calcolo di un polinomio nella forma di Lagrange

L'algoritmo per il calcolo di un polinomio nella forma di Lagrange consente di separare i compiti di determinazione dei coefficienti e calcolare i valori del polinomio per diversi valori dell'argomento:

1. Un campione da n -punti, che include i valori della funzione e i valori dell'argomento della funzione.

2. Un polinomio di n gradi viene calcolato nella forma di Lagrange utilizzando la seguente formula:

Algoritmo per il calcolo di un polinomio nella forma Lagrange mostrato in Figura 1.

Tecnica per calcolare un polinomio nella forma Lagrange

Polinomio di Lagrange

Polinomio di interpolazione di Lagrangeè il polinomio di grado minimo che assume i valori dati nel dato insieme di punti. Per n+ 1 coppia di numeri, dove tutto X io sono diversi, esiste un unico polinomio l(X) non più laurea n, per cui l(X io) = y io .

Nel caso più semplice ( n= 1 ) è un polinomio lineare il cui grafico è una retta passante per due punti dati.

Definizione

Questo esempio mostra il polinomio di interpolazione Lagrange a quattro punti (-9.5) , (-4.2) , (-1,-2) e (7.9) e i polinomi y j l j (x), ognuno dei quali passa per uno dei punti selezionati e assume valore zero nel resto x io

Lascia per la funzione f(X) i valori sono noti y j = f(X j) in alcuni punti. Quindi possiamo interpolare questa funzione come

In particolare,

Valori di integrali da l j non dipendono f(X) , e possono essere calcolati in anticipo, conoscendo la sequenza X io .

Per il caso di distribuzione uniforme sul segmento dei nodi di interpolazione

In questo caso si può esprimere X io attraverso la distanza tra i nodi di interpolazione h e il punto di partenza X 0 :

,

e quindi

.

Sostituendo queste espressioni nella formula del polinomio di base e sottraendo h dai segni di moltiplicazione al numeratore e al denominatore, otteniamo

Ora possiamo introdurre un cambio di variabile

e ottieni un polinomio da y, che viene costruito utilizzando solo l'aritmetica intera. Lo svantaggio di questo approccio è la complessità fattoriale del numeratore e denominatore, che richiede l'uso di algoritmi con rappresentazione multibyte dei numeri.

link esterno

Fondazione Wikimedia. 2010.

Guarda cos'è il "polinomio di Lagrange" in altri dizionari:

La forma di scrittura di un polinomio di grado n (polinomio di interpolazione di Lagrange) interpolando una data funzione f (x) ai nodi x 0, x1, ..., x n: (х x0)/h=t formula (1)… … Enciclopedia matematica

In matematica, i polinomi oi polinomi in una variabile sono funzioni della forma in cui ci sono coefficienti fissi e x è una variabile. I polinomi costituiscono una delle classi più importanti di funzioni elementari. Lo studio delle equazioni polinomiali e delle loro soluzioni ... ... Wikipedia

Nella matematica computazionale, i polinomi di Bernstein sono polinomi algebrici che sono una combinazione lineare dei polinomi di base di Bernstein. Un algoritmo stabile per il calcolo dei polinomi in forma di Bernstein è l'algoritmo ... ... Wikipedia

Il polinomio di grado minimo che assume i valori dati nel dato insieme di punti. Per coppie di numeri in cui tutti sono diversi, esiste al massimo un unico polinomio di grado per cui. Nel caso più semplice (... Wikipedia

Il polinomio di interpolazione di Lagrange è il polinomio di grado minimo che assume i valori dati nel dato insieme di punti. Per n + 1 coppie di numeri, dove tutti xi sono diversi, esiste un unico polinomio L(x) di grado al massimo n per cui L(xi) = yi. ... ... Wikipedia

Il polinomio di interpolazione di Lagrange è il polinomio di grado minimo che assume i valori dati nel dato insieme di punti. Per n + 1 coppie di numeri, dove tutti xi sono diversi, esiste un unico polinomio L(x) di grado al massimo n per cui L(xi) = yi. ... ... Wikipedia

Per la funzione, vedere: Interpolante. L'interpolazione nella matematica computazionale è un modo per trovare valori intermedi di una quantità da un insieme discreto esistente di valori noti. Molti di coloro che si trovano spesso ad affrontare calcoli scientifici e ingegneristici... Wikipedia

Per la funzione, vedere: Interpolante. L'interpolazione, l'interpolazione nella matematica computazionale è un modo per trovare valori intermedi di una quantità da un insieme discreto esistente di valori noti. Molti di quelli che si confrontano con la scienza e... ... Wikipedia

Cercheremo un polinomio di interpolazione nella forma

VANDERMOND ALEXANDER THEOPHILE (Vandermonde Alexandre Theophill; 1735-1796) - Matematico francese, il cui lavoro principale riguarda l'algebra. V. ha posto le basi e ha dato una presentazione logica della teoria dei determinanti (il determinante di Vandermonde), e l'ha anche distinta dalla teoria delle equazioni lineari. Ha introdotto la regola dell'espansione dei determinanti con l'aiuto dei minori di secondo ordine.

Qui 1.(x) sono polinomi di grado n, i cosiddetti LAGRANGE INFLUENCE POLYNOMIALS, che soddisfano la condizione

L'ultima condizione significa che qualsiasi polinomio l t (x)è uguale a zero per ogni x-y Oltretutto X. a cioè. x 0 y x v ...» x ( _ v x io + v ...» x n sono le radici di questo polinomio. Pertanto, i polinomi lagrangiani Ifjx) assomigliare

Dal momento che secondo la condizione 1.(x.) = 1, quindi

Pertanto, i polinomi di influenza lagrangiana possono essere scritti nella forma

e il polinomio di interpolazione (2.5) può essere scritto nella forma

LAGRANGE JOSEPH LOUIS (Lagrange Joseph Louis; 1736-1813) - un eccezionale matematico e meccanico francese, le cui opere più importanti riguardano il calcolo delle variazioni, la meccanica analitica e teorica. L. pone alla base della statica il principio dei possibili spostamenti (virtuali). Introdusse le coordinate generalizzate e diede alle equazioni del moto di un sistema meccanico la forma a lui intitolata. L. ha ricevuto alcuni importanti risultati nel campo dell'analisi (la formula per il termine residuo della serie di Taylor, la formula per gli incrementi finiti, la teoria degli estremi condizionali); in teoria numeri(teorema di Lagrange); in algebra (teoria delle frazioni continue, riduzione di una forma quadratica a una somma di quadrati); nella teoria delle equazioni differenziali (trovare un particolare soluzioni studio di un'equazione differenziale ordinaria del primo ordine, lineare rispetto alla funzione desiderata e variabile indipendente, a coefficienti variabili dipendenti dalla derivata della funzione desiderata); nella teoria dell'interpolazione (formula dell'interpolazione di Lagrange).

Il polinomio di interpolazione nella forma (2.6) è chiamato POLINOMIALE DI INTERPOLAZIONE DI LAGRANGE. Elenchiamo i principali vantaggi di questa forma di scrittura del polinomio di interpolazione.

• Il numero di operazioni aritmetiche richieste per costruire il polinomio di Lagrange è proporzionale a p 2 ed è il più piccolo per tutte le forme di notazione.
• La formula (2.6) contiene esplicitamente i valori delle funzioni ai nodi di interpolazione, il che è conveniente per alcuni calcoli, in particolare, quando si costruiscono formule per l'integrazione numerica.
• La formula (2.6) è applicabile sia per i nodi equidistanti che disuguali.
• Il polinomio di interpolazione di Lagrange è particolarmente conveniente quando i valori delle funzioni cambiano e i nodi di interpolazione rimangono invariati, come accade in molti studi sperimentali.

Gli svantaggi di questa forma di notazione includono il fatto che con una modifica del numero di nodi, tutti i calcoli devono essere eseguiti nuovamente. Ciò rende difficile effettuare stime di accuratezza a posteriori (stime ottenute in corso di calcolo).

Introduciamo la funzione y l f , = (x - x 0)(x - Xj)...(x - xn)= fl (* " *;)

Notare che w n + : (x) è polinomio di grado n + 1. Allora la formula (2.6) può essere scritta come

Ecco le formule per l'interpolazione Lagrange lineare e quadratica:

Il polinomio di Lagrange è un polinomio di 1° grado nella formula (2.8) e un polinomio di 2° grado nella formula (2.9).

Queste formule sono più spesso utilizzate nella pratica. Lasciati dare (n+ 1) nodo di interpolazione. Su questi nodi si può costruire un polinomio di interpolazione P esimo grado, (P - 1) un polinomio di primo grado e un grande insieme di polinomi di grado minore di P, sulla base di alcuni di questi nodi. Teoricamente, la massima precisione è fornita da un polinomio di grado superiore. Tuttavia, in pratica, i polinomi di gradi bassi sono più spesso utilizzati per evitare errori nel calcolo dei coefficienti per gradi grandi di un polinomio.

Lascia il segmento funzione y=f(x) dato in una tabella, cioè (x io , y io), (i=0,1,..,n), dove y io =f(x i). Questa funzione si chiama " griglia».

Formulazione del problema: trova polinomio algebrico (polinomio):

nessun grado superiore n tale che

L n (x i)=y io , a io= 0,1,..,n,(5.6)

quelli. avendo a determinati nodi x io, (io=0,1,..,n) gli stessi valori della funzione griglia a=f(x).

Il polinomio stesso L n (x) chiamato polinomio di interpolazione, e il compito è interpolazione polinomiale .

Trova il polinomio L n (x)- questo significa trova i suoi coefficienti a 0 , un 1 ,…,un n. Per questo c'è n+ 1 condizione (5.6), che si scrivono come un sistema di equazioni algebriche lineari in incognite un io,(io=0, 1,…,n):

dove X Io e y io ( io=0,1,…,n) – valori tabulari dell'argomento e della funzione.

È noto dal corso di algebra che il determinante di questo sistema, chiamato determinante di Vandermonde:

diverso da zero e, di conseguenza, il sistema (5.7) ha unica decisione.

Dopo aver determinato i coefficienti un 0 , un 1 ,…,un, risolvendo il sistema (5.7), otteniamo il cosiddetto Polinomio di interpolazione di Lagrange per funzione f(x):

(5.8)

che può essere scritto come:

È dimostrato che per il dato n+1 valori di funzione possono essere tracciati l'unico polinomio di interpolazione di Lagrange(5.8).

In pratica, i polinomi di interpolazione di Lagrange del primo ( n= 1) e secondo ( n= 2) gradi.

In n= 1 informazione sulla funzione interpolata y=f(x) fissata in due punti: (X 0 ,y 0 ) e (x 1 ,y 1 ), e il polinomio di Lagrange ha la forma

Per n= 2 Il polinomio di Lagrange è costruito secondo la tabella a tre punti

Soluzione: Sostituiamo i dati iniziali nella formula (5.8). Il grado del polinomio di Lagrange risultante non è maggiore del terzo, poiché la funzione è data da quattro valori:

Utilizzando il polinomio di interpolazione di Lagrange, si può trovare il valore della funzione in qualsiasi punto intermedio, ad esempio in X=4:

= 43

Polinomi di interpolazione di Lagrange usato in metodo degli elementi finiti, ampiamente utilizzato nella risoluzione di problemi di costruzione.

Sono note anche altre formule di interpolazione, ad esempio Formula di interpolazione di Newton, utilizzato in interpolazione nel caso di nodi equidistanti o polinomio di interpolazione Eremita.

interpolazione spline. Quando si utilizza un numero elevato di nodi di interpolazione, viene utilizzata una tecnica speciale: interpolazione polinomiale a tratti quando la funzione è interpolata da un polinomio di grado t tra tutti i nodi della griglia vicini.

Approssimazione di funzioni RMS

Formulazione del problema

Approssimazione RMS functions è un approccio diverso per ottenere espressioni analitiche per approssimare funzioni. Una caratteristica di tali problemi è il fatto che è noto che i dati iniziali per la costruzione di determinati modelli hanno carattere approssimativo.

Questi dati sono ottenuti come risultato di qualche esperimento o come risultato di qualche processo computazionale. Di conseguenza, questi dati contengono errori sperimentali (errori delle apparecchiature e delle condizioni di misurazione, errori casuali, ecc.) o errori di arrotondamento.

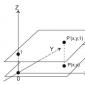
Diciamo che si sta indagando su qualche fenomeno o processo. In termini generali, l'oggetto di studio può essere rappresentato da un sistema cibernetico (“scatola nera”) mostrato in figura.

Variabile Xè una variabile indipendente e controllata (parametro di input).

Variabile Y- questa è la reazione (risposta) dell'oggetto di studio all'impatto del parametro di input. Questa è la variabile dipendente.

Assumiamo che durante l'elaborazione dei risultati di questo esperimento si trovi una certa dipendenza funzionale y=f(x) tra variabile indipendente X e variabile dipendente y. Questa dipendenza è presentata sotto forma di tabella. 5.1 valori x io , y io (i=1,2,…,n) ottenuto durante l'esperimento.

Tabella 5.1

x io	x 1	x2	…	x n
si io	y 1	y 2	…	si n

Se l'espressione analitica della funzione y=f(x) sconosciuto o molto difficile, allora sorge il problema di trovare la funzione y= j (X), i cui valori a x=x io, forse un po' diverso da dati sperimentali si io, (io=1,..,n). Pertanto, la dipendenza studiata è approssimata dalla funzione y= j (X) sul segmento [ X 1 ,xn]:

f(x) @ j (X). (5.9)

Funzione di approssimazione y= j (X) chiamato formula empirica (EF) o equazione di regressione (UR).

Le formule empiriche non pretendono di essere leggi di natura, ma sono solo ipotesi che descrivono più o meno adeguatamente i dati sperimentali. Tuttavia, il loro significato è molto grande. Ci sono casi nella storia della scienza in cui una formula empirica di successo ha portato a grandi scoperte scientifiche.

La formula empirica è adeguato, se può essere utilizzato per descrivere l'oggetto in studio con sufficiente accuratezza per la pratica.

A cosa serve questa dipendenza?

Se si trova l'approssimazione (5.9), allora è possibile:

Fare una previsione sul comportamento dell'oggetto in studio al di fuori del segmento ( estrapolazione );

Scegliere ottimale direzione di sviluppo del processo in esame.

L'equazione di regressione può avere una forma diversa e un diverso livello di complessità, a seconda delle caratteristiche dell'oggetto in studio e dell'accuratezza di rappresentazione richiesta.

Geometricamente il compito di costruire un'equazione di regressione è disegnare una curva l: y= j (X) « possibilmente più vicino» adiacente al sistema dei punti sperimentali M io (x io , y io), io= 1,2,..,n, tabella data. 5.1 (fig.5.2).

La costruzione dell'equazione di regressione (funzione empirica) consiste in 2 fasi:

1. scelta di visione generale equazioni di regressione,

2. determinandone i parametri.

Riuscito scelta l'equazione di regressione dipende in gran parte dall'esperienza dello sperimentatore che indaga su qualsiasi processo o fenomeno.

Spesso, un polinomio (polinomio) viene scelto come equazione di regressione:

Il secondo compito trovare parametri le equazioni di regressione vengono risolte con metodi regolari, ad esempio minimi quadrati(LSM), che trova largo impiego nello studio di qualsiasi regolarità basata su osservazioni o esperimenti.

Lo sviluppo di questo metodo è associato ai nomi di famosi matematici del passato: K. Gauss e A. Legendre.

Metodo dei minimi quadrati

Assumiamo che i risultati dell'esperimento siano presentati sotto forma di tabella. 5.1. E l'equazione di regressione è scritta nella forma (5.11), cioè dipende da ( m+1) parametro

Questi parametri determinano la posizione del grafico dell'equazione di regressione rispetto ai punti sperimentali M io (x io , y io), io= 1,2,..,n(fig.5.2).

Tuttavia, questi parametri non sono definiti in modo univoco. È necessario scegliere i parametri in modo che si trovi il grafico dell'equazione di regressione " il più vicino possibile» al sistema di questi punti sperimentali.

Introduciamo il concetto deviazioni i valori dell'equazione di regressione (5.11) dal valore tabulare si io per x io : , io= 1,2,..,n.

Ritenere la somma delle deviazioni al quadrato, che dipende da( m+1) parametro

Secondo i migliori coefficienti dei minimi quadrati un io(io=0,1,..,m) sono quelli che minimizzano la somma delle deviazioni al quadrato, cioè funzione .

Usando condizioni necessarie per l'estremo della funzione diverse variabili, otteniamo le cosiddette sistema normale per determinare coefficienti sconosciuti :

Per la funzione di approssimazione (5.11), il sistema (5.14) è un sistema di equazioni algebriche lineari in incognite .

Possibili casi:

1. Se , allora ci sono infiniti polinomi (5.11) che minimizzano la funzione (5.13).

2. Se m=n–1, allora esiste un solo polinomio (5.11) che minimizza la funzione (5.13).

Il meno m, più semplice è la formula empirica, ma non è sempre migliore. Va ricordato che la formula empirica risultante deve essere adeguato l'oggetto in esame.