Lavoro di laboratorio
Previsione dei processi economici
utilizzando un foglio di calcolo Excel.
Requisiti per il contenuto, la progettazione e l'ordine di esecuzione
Per eseguire il lavoro di laboratorio, è necessario creare una nuova cartella di lavoro Excel con il nome "Il tuo cognome, Lavoro di laboratorio n. 1, Opzione n. _" (ad esempio: "Ivanov I.P. Lavoro di laboratorio n. 1" Opzione n. 4).
Prima di svolgere il lavoro di laboratorio, studia la parte teorica e la metodologia per completare i compiti.
Gli incarichi devono essere completati e secondo la tua scelta . I fogli di lavoro nella cartella di lavoro devono essere denominati Task1, Task2. Immettere i risultati delle attività nel file di rapporto.
Le varianti del lavoro di laboratorio sono distribuite in base al numero N. nell'elenco del gruppo, vedere la tabella
| № | Var. | № | Var. | № | Var. | № | Var. | № | Var. | № | Var. | № | Var. |
Dopo aver completato il laboratorio, rispondi alle domande di follow-up. Inserisci le risposte alle domande di controllo nel file del rapporto. La tua cartella di lavoro, insieme al file del rapporto, deve essere fornita all'insegnante su un dischetto, firmandola “Rapporto sul lavoro di laboratorio n. 2 dello studente Ivanov I.P., gr. 170404".
Parte teorica
Previsione- questo è un metodo di ricerca scientifica, che mira a fornire possibili opzioni per quei processi e fenomeni che sono scelti come oggetto di analisi.
compiti previsione economica sono: anticipazione della possibile distribuzione delle risorse nei vari ambiti; determinazione dei limiti inferiore e superiore dei risultati ottenuti; valutazione della quantità massima possibile di risorse necessarie per risolvere problemi economici, scientifici e tecnici, ecc.
A seconda del periodo di tempo per il quale viene effettuata la previsione (leading period), le previsioni possono essere:
· breve termine;
a medio termine;
· lungo termine;
lungo termine.
La gradazione temporale delle previsioni è relativa e dipende dalla natura e dallo scopo della previsione data.
Per l'esecuzione previsione a breve termine Il metodo più utilizzato è l'estrapolazione.
metodo di estrapolazioneè trovare i valori che si trovano al di fuori della serie statistica data: i valori noti della serie statistica vengono utilizzati per trovare altri valori che si trovano al di fuori di questa serie.
Quando si estrapola, le conclusioni tratte quando si studiano le tendenze nello sviluppo di un fenomeno nel passato e nel presente vengono trasferite al futuro, ad es. L'estrapolazione si basa sul presupposto di una certa stabilità delle caratteristiche dei fattori che influenzano lo sviluppo di questo fenomeno.

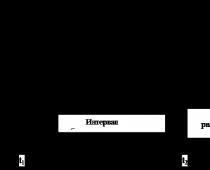
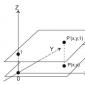
Fig. 1. Designazioni di base del metodo di estrapolazione.
Durante l'estrapolazione (vedi Fig. 1.), viene utilizzata la seguente terminologia:
t 1 - profondità di retrospezione;
t 2 è il momento della previsione;
t 3 - orizzonte di previsione;
t 2 - t 1 - intervallo di osservazione (intervallo di tempo sulla base del quale viene studiata la storia dello sviluppo dell'oggetto di previsione);
t 3 - t 2 - lead interval (intervallo di tempo per il quale viene sviluppata la previsione).
Quanto più stabili sono i processi e le tendenze previsti, tanto più l'orizzonte di previsione può essere spostato indietro. Come mostra la pratica, l'intervallo di osservazione dovrebbe essere tre o più volte più lungo dell'intervallo di piombo. Di norma, questo periodo è piuttosto breve. Il metodo di estrapolazione non funziona con i processi di salto.
Il metodo di estrapolazione è facilmente implementabile su un personal computer. L'uso di moderni processori di fogli di calcolo come MS Excel consente di prevedere rapidamente i processi economici utilizzando il metodo di estrapolazione.
Per migliorare l'accuratezza della previsione, è necessario tenere conto della dipendenza del valore previsto Y da fattori esterni X. La totalità dei valori studiati è, di regola, soggetta all'influenza di fattori casuali. A questo proposito, la dipendenza del valore previsto Y da fattori esterni X è il più delle volte statistica o correlazionale.
Statistico si chiama la dipendenza delle variabili casuali, in cui ogni valore di una di esse corrisponde alla legge di distribuzione dell'altra, ovvero una variazione di una delle variabili comporta una variazione della distribuzione dell'altra.
correlazione detta dipendenza statistica di variabili casuali, in cui una variazione di una delle quantità comporta una variazione del valore medio dell'altra.
La misura della dipendenza dalla correlazione di due variabili casuali X e Y è il coefficiente di correlazione r, che è una quantità adimensionale, e quindi non dipende dalla scelta delle unità di misura delle grandezze in esame.
Proprietà del coefficiente di correlazione:
1) Se due variabili casuali X e Y sono indipendenti, il loro coefficiente di correlazione è zero, cioè r=0.
2) Il modulo del coefficiente di correlazione non supera l'unità, cioè |r|£1, che equivale alla doppia disuguaglianza: -1£r£1.
3) L'uguaglianza del coefficiente -1 o +1 mostra la presenza di una connessione funzionale (diretta). Il segno “+” indica una relazione diretta (un aumento o una diminuzione di una caratteristica è accompagnato da un cambiamento simile in un'altra caratteristica), un segno “-” indica una relazione inversa (un aumento o una diminuzione di una caratteristica è accompagnato da un opposto modificare un'altra funzione).
Dopo aver determinato le caratteristiche fattoriali più significative che incidono sul valore previsto, è altrettanto importante stabilirne la descrizione matematica (equazione), che consente di valutare numericamente l'indicatore efficace attraverso le caratteristiche dei fattori.
Viene chiamata l'equazione che esprime la variazione del valore medio dell'indicatore effettivo in base ai valori delle caratteristiche dei fattori equazione di regressione.
Vengono chiamate le linee sul piano delle coordinate corrispondenti alle equazioni di regressione linee di regressione .
Le dipendenze di correlazione possono essere espresse da equazioni di regressione di vario tipo: lineari, paraboliche, iperboliche, esponenziali, ecc.
Regressione lineare
Equazione di regressione lineare(selettivo) Y sul Xè chiamata dipendenza dai valori osservati della quantità X, espressa come una funzione lineare:
dove il valore r chiamato coefficiente di regressione lineare Y sul X, b- costante.
Un'approssimazione lineare descrive bene la variazione di quantità che si verifica a velocità costante.
Se il coefficiente di correlazione di due quantità X e Yè uguale a r=±1, allora queste quantità sono collegate da una dipendenza lineare. Il coefficiente di correlazione serve come misura della forza (tenuta) della dipendenza lineare dei valori misurati. In pratica, se il coefficiente di correlazione di due quantità X e Y|r|>0.5, allora si ritiene che vi sia ragione di presumere la presenza di una relazione lineare tra queste grandezze. Tuttavia, quando si sceglie il tipo di retta di regressione (lineare o non lineare), è meglio navigare attraverso la forma della dipendenza empirica dei valori X e Y.
Regressione parabolica e polinomiale.
Parabolico dipendenza del valore Y dal valore X la dipendenza espressa da una funzione quadratica (parabola del 2° ordine) si chiama:
![]() . (2)
. (2)
Questa equazione è chiamata regressione parabolica Y sul X. Opzioni un, b, Insieme a chiamato coefficienti di regressione parabolica. Il calcolo dei coefficienti di regressione parabolica è sempre macchinoso, quindi si consiglia di utilizzare un computer per i calcoli.
L'equazione (2) della regressione parabolica è un caso speciale di una regressione più generale chiamata polinomiale. polinomio dipendenza del valore Y dal valore Xè chiamata dipendenza espressa dal polinomio n-esimo ordine:
dove sono i numeri un io (io=0,1,…, n) sono chiamati coefficienti di regressione polinomiale.
L'approssimazione polinomiale viene utilizzata per descrivere quantità che aumentano e diminuiscono alternativamente. È utile, ad esempio, analizzare un ampio insieme di dati su una quantità instabile.
Regressione del potere.
Potenza dipendenza del valore Y dal valore Xè chiamata dipendenza della forma:
Questa equazione è chiamata equazione di regressione della potenza Y sul X. Opzioni un e b chiamato coefficienti di regressione della potenza.
L'approssimazione della potenza è utile per descrivere una quantità monotonicamente crescente o monotonicamente decrescente, come la distanza percorsa da un'auto in accelerazione. Non è possibile utilizzare un adattamento della legge di potenza se i dati contengono valori zero o negativi.
regressione esponenziale.
esemplare(o esponenziale) dipendenza della quantità Y dal valore Xè chiamata dipendenza della forma:
Questa equazione è chiamata equazione esponenziale(o esponenziale) regressione Y sul X. Opzioni un(o K) e b chiamato esponenziale(o esponenziale) regressione.
L'approssimazione esponenziale è utile quando la velocità di modifica dei dati è in continuo aumento. Tuttavia, per i dati che contengono zero o valori negativi, questo tipo di approssimazione non è applicabile.
regressione logaritmica.
logaritmico dipendenza del valore Y dal valore Xè chiamata dipendenza della forma:
![]() (6)
(6)
Questa equazione è chiamata regressione logaritmica Y sul X. Opzioni un e b chiamato coefficienti di regressione logaritmica.
L'approssimazione logaritmica è utile per descrivere una quantità che dapprima sale o scende rapidamente e poi si stabilizza gradualmente. L'approssimazione logaritmica utilizza valori sia negativi che positivi.
regressione iperbolica.
Iperbolico dipendenza del valore Y dal valore Xè chiamata dipendenza della forma:
Questa equazione è chiamata equazione di regressione iperbolica Y sul X. Opzioni un e b chiamato coefficienti di regressione iperbolica.
La qualità della costruzione delle equazioni di regressione è caratterizzata dall'errore medio di approssimazione o dall'errore di previsione relativo:
 (8)
(8)
dove Y e è il valore empirico dell'indicatore previsto; Y è il valore calcolato dell'indicatore previsto.
L'analisi di regressione può essere suddivisa in tre fasi: la scelta della forma di dipendenza (il tipo di equazione) in base a dati statistici, il calcolo dei coefficienti dell'equazione selezionata e la valutazione dell'affidabilità dell'equazione selezionata.
L'uso di un foglio di calcolo semplifica l'esecuzione di tutti i passaggi dell'analisi di regressione.
1. Quale delle seguenti misure appartiene alla classe dei nomi delle scale di misura:
a) numeri che codificano il temperamento;
d) recapiti telefonici.
2. Quale delle seguenti misure appartiene alla classe d'ordine delle scale di misura:
b) il grado accademico come misura di promozione;
c) sistema di misurazione della distanza metrica;
d) recapiti telefonici.
3. Quale delle seguenti misure appartiene alla classe dei rapporti delle scale di misura:
a) numeri che codificano il temperamento;
b) il grado accademico come misura di promozione;
c) sistema di misurazione della distanza metrica;
d) recapiti telefonici.
4. Quale delle seguenti caratteristiche si riferisce a specie quantitative:
b) legami familiari dei familiari;
c) sesso ed età della persona;
d) lo stato sociale del depositante;
e) il numero dei figli in famiglia;
f) fatturato al dettaglio delle imprese commerciali.
5. Quali delle seguenti caratteristiche sono legate a specie qualitative:
a) il numero dei dipendenti nell'impresa;
b) legami familiari dei familiari;
c) sesso ed età della persona;
d) lo stato sociale del depositante;
e) il numero dei figli in famiglia;
f) fatturato al dettaglio delle imprese commerciali.
6. Quale scala viene utilizzata per misurare il livello di intelligenza umana:
a) nomi;
b) ordinale;
c) intervallo;
d) relazioni.
7. La deviazione standard è:
a) il quadrato dell'intervallo della serie di variazioni;
b) la radice quadrata della dispersione;
c) il quadrato del coefficiente di variazione;
d) la radice quadrata dell'intervallo di variazione.
8. Il coefficiente di variazione della serie è determinato dal rapporto:
a) la deviazione standard dalla media aritmetica della serie;
b) dispersione alla mediana della serie;
c) dispersione al valore massimo della serie;
d) l'indicatore assoluto di variazione della media aritmetica della serie.
9. Modo di una data serie di variazioni
x 10 15 35
n 1 2 3
questo è:
a) 20;
b) 16;
alle 3;
d) 35.
10. La media aritmetica della popolazione è:
a) il valore dell'elemento al centro della serie di variazioni;
b) semidifferenza dei valori massimo e minimo della serie di variazioni;
c) metà della somma dei valori massimo e minimo della serie di variazioni;
d) il rapporto tra la somma di tutti i valori della popolazione e il loro numero totale.
11. Dati noti sull'anzianità di servizio di sette commesse: 2; 3; 2; 5; dieci; 7; 1 anno Trova il valore medio della loro esperienza lavorativa.
a) 4,3 anni;
b) 5 anni;
c) 3 anni;
d) 3,8 anni.
12. Il numero di distribuzione è:
a) sequenza di dati campione;
b) disposizione ordinata dei dati secondo un attributo quantitativo;
c) sequenza numerica dei dati;
d) una sequenza di valori, ordinata per caratteristiche qualitative.
13. La frequenza delle varianti della serie di variazioni si chiama:
a) dimensione del campione;
b) il valore delle varianti della serie variazionale;
c) il numero delle singole varianti o dei gruppi di varianti;
d) il numero dei gruppi della serie di variazioni.
14. La moda è:
a) il valore massimo della caratteristica della popolazione;
b) il valore della caratteristica più comune;
c) la media aritmetica della popolazione.
15. Dati noti sull'esperienza lavorativa delle commesse di negozio: 2; 3; 2; 5; dieci; 7; 1. Trova la mediana della loro esperienza lavorativa:
a) 4,5 anni;
b) 4,3 anni;
c) 3 anni;
d) 5 anni.
16. Intervallo di variazione di questa serie di variazioni:
x 10 15 20 30
n 1 2 3 2
questo è:
a) 15;
b) 10;
c) 30;
d) 20.
17. Il numero di serie ordinate si divide a metà:
una moda;
b) media aritmetica;
c) media armonica;
d) mediana.
18. Il raggruppamento statistico è:
a) combinare o separare i dati secondo le caratteristiche essenziali;
b) organizzazione scientifica dell'osservazione statistica;
c) tipologie di segnalazione;
d) raccolta diretta di dati di massa.
19. Il coefficiente di oscillazione è:
a) un indicatore assoluto;
b) media;
c) il relativo indicatore di variazione.
20. La dispersione della serie di variazioni caratterizza:
a) il valore medio delle caratteristiche individuali;
b) dispersione dei singoli valori dei segni dal valore medio;
c) deviazione standard.
21. L'equazione della funzione di regressione rettilinea mostra la dinamica dello sviluppo:
a) con accelerazione variabile;
c) uniforme;
d) uniformemente accelerato.
22. Se il valore del coefficiente di correlazione è 0,6, sulla scala Chadd.ka:
a) non c'è praticamente alcun collegamento;
b) la connessione è debole;
c) la comunicazione è moderata;
d) la connessione è forte.
23. I dati rappresentano i punteggi degli adulti nel test del QI Stanford-Binet 104, 87, 101, 130, 148, 92, 97, 105, 134, 121. Trova l'intervallo di variazione:
a) 61;
b) 60;
c) 75.
24. Trova la media aritmetica ponderata per le seguenti serie di intervalli:
li ni
10-14 1
15-19 1
20-24 4
25-29 2
30-34 4
a) 24;
b) 24.92;
c) 25.38.
25. Calcolare la mediana della riga successiva 2.1; 1.5; 1.6; 2.1; 2.4:
a) 2;
b) 1.5;
c) 2.1.
26. Calcolare la modalità della successiva serie di intervalli
frequenza 5-7 8-10 11-13 14-16
intervallo 4 7 26 41
a) 14;
b) 14.54;
c) 15.23;
27. Quale delle seguenti misure appartiene alla classe dei nomi delle scale di misura:
a) la diagnosi del paziente;
b) numeri di auto;
c) la durezza del minerale;
d) orario di calendario;
d) il peso della persona.
28. Quale delle seguenti misure appartiene alla classe delle scale di misura ordinali:
a) la diagnosi del paziente;
b) numeri di auto;
c) la durezza del minerale;
d) orario di calendario;
d) il peso della persona.
29. Quale delle seguenti misurazioni appartiene alla classe delle scale di misurazione degli intervalli:
a) la diagnosi del paziente;
b) numeri di auto;
c) la durezza del minerale;
d) orario di calendario;
d) il peso della persona.
30. Quale delle seguenti misure appartiene alla classe dei rapporti delle scale di misura:
a) la diagnosi del paziente;
b) numeri di auto;
c) la durezza del minerale;
d) orario di calendario;
d) il peso della persona.
31. Quale scala viene utilizzata per misurare il tempo:
a) intervallo;
b) relazioni;
c) Chaddok.
32. Le specie quantitative includono le seguenti caratteristiche:
a) altezza umana;
b) premi al merito;
c) colore degli occhi;
d) targhe.
33. Le specie qualitative includono le seguenti caratteristiche:
a) altezza umana;
b) premi al merito;
c) colore degli occhi;
d) numeri di auto
34. Calcola la moda
xi 5 8 10 13 14
ni 7 4 5 9 1
a) 10;
b) 11;
c) 13
35. Nelle classi più grandi, l'acquisizione di conoscenze per trimestre è minore rispetto alle classi più piccole. Che cos'è un indicatore di performance?
a) il numero degli studenti della classe;
b) successo nell'acquisizione di conoscenze,
c) il numero di studenti che hanno avuto successo nell'acquisizione delle conoscenze.
36. La lunghezza dell'intervallo nella serie di intervalli è:
a) l'intervallo di variazione diviso per la media aritmetica;
b) range di variazione diviso per il numero dei gruppi;
c) varianza divisa per la dimensione del campione.
37. Un esempio di correlazione di coppia: gli studenti che hanno imparato a leggere prima di altri tendono a ottenere risultati migliori. Quale di questi tratti: capacità di lettura precoce o rendimento elevato degli studenti è un tratto fattoriale?
a) la capacità di leggere presto;
b) alto rendimento scolastico;
c) nessuno di essi.
38. Quale dei seguenti metodi può essere utilizzato per confrontare le medie di tre o più campioni:
a) Prova dello studente;
b) Prova del pescatore;
c) analisi della varianza.
39. Dimensioni del campione della serie di variazioni
xi 10 15 20 30
ni 1 2 3 2
a) 5;
b) 8;
alle 12;
d) 30.
40. Moda della serie variazione
xi 10 15 20 25
ni 1 5 4 3
a) 15;
b) 5;
c) 23;
d) 3.
41. L'equazione della funzione di regressione parabolica riflette la dinamica dello sviluppo:
a) con accelerazione variabile;
b) con un rallentamento della crescita a fine periodo;
c) uniforme;
d) uniformemente accelerato.
42. Il coefficiente di regressione B mostra:
a) il valore atteso della variabile dipendente quando il valore del predittore è zero
b) il valore atteso della variabile dipendente quando il predittore cambia di uno
c) probabilità di errore di regressione
d) la questione non è stata ancora del tutto risolta
43. Un campione è:
a) l'insieme degli oggetti sui quali si costruisce il ragionamento del ricercatore;
b) un insieme di oggetti disponibili per la ricerca empirica;
c) tutti i possibili valori di dispersione;
d) lo stesso della randomizzazione.
44. Quale dei seguenti coefficienti di correlazione mostra la maggiore connessione di variabili:
a) -0,90;
b) 0;
c) 0,07;
d) 0,01.
45. La popolazione generale è:
a) l'insieme degli oggetti sui quali si costruisce il ragionamento del ricercatore;
b) un insieme di oggetti disponibili per la ricerca empirica;
c) tutti i possibili valori dell'aspettativa matematica;
d) distribuzione normale.
46. Come si confrontano le dimensioni del campione e la popolazione generale:
a) il campione è generalmente molto più piccolo della popolazione generale;
b) la popolazione generale è sempre più piccola del campione;
c) il campione e la popolazione generale coincidono quasi sempre;
d) non esiste una risposta corretta.
47. Il coefficiente di correlazione biseriale tratteggiato è un caso speciale del coefficiente di correlazione:
a) Lanciere
b) Pearson;
c) Kendala;
d) tutte le risposte sono corrette.
48. A quale livello minimo di significatività è consuetudine rifiutare l'ipotesi nulla?
a) Livello 5%.
b) Livello 7%.
c) Livello 9%.
d) Livello 10%.
49. Quale dei seguenti metodi viene solitamente utilizzato quando si confrontano le medie di due campioni normali:
a) Prova dello studente;
b) Prova del pescatore;
c) analisi unidirezionale della varianza;
d) analisi di correlazione.
50. Con l'aiuto del quale vengono verificate ipotesi statistiche:
a) uno statistico
b) parametri;
c) esperimenti;
d) osservazioni.
51. Quale dei seguenti valori del coefficiente di correlazione è impossibile:
a) -0,54;
b) 2.18;
c) 0; d) 1.
52. Quale trasformazione deve essere eseguita quando si confrontano due coefficienti di correlazione:
uno studente
b) Pescatore;
c) Pearson;
d) Lanciatore.
53. Qual è la mediana della distribuzione:
a) uguale alla bisettrice;
b) come la moda;
c) media aritmetica;
d) quantile di distribuzione del 50%;
e) non esiste una risposta corretta.
54. Il coefficiente di correlazione biseriale punteggiato è un caso speciale del coefficiente di correlazione:
a) Lanciere
b) Pearson;
c) Kendall;
d) tutte le risposte sono corrette.
55. Quale delle seguenti variabili è discreta:
a) tipo di temperamento;
b) il livello di intelligenza;
c) tempo di reazione;
d) tutte le risposte sono corrette.
56. In quale intervallo può cambiare il coefficiente di correlazione:
a) da -1 a 1;
b) da 0 a 1;
c) da 0 a 100;
d) in qualsiasi.
57. Su quali ipotesi statistiche vengono avanzate:
a) concetti;
b) statistico;
c) campioni;
d) parametri.
58. Qual è il nome dell'analogo non parametrico dell'analisi della varianza:
a) Prova dello studente;
b) metodo Kruskal-Wallis;
c) test di Wilcoxon;
d) Prova di Mann-Whitney.
59. Il concetto di coefficiente di correlazione è stato sviluppato per la prima volta nei lavori:
a) Pescatore;
b) Studente;
c) Pearson;
d) Lanciatore.
60. Quale delle seguenti statistiche è una stima imparziale del valore atteso:
a) media aritmetica;
b) moda;
c) mediana;
d) tutte le risposte sono corrette.
61. Come si confrontano i coefficienti di correlazione di Pearson e Spearman:
a) il coefficiente di Pearson è un caso speciale di Spearman;
b) il coefficiente di Spearman è un caso speciale di Pearson;
c) tali coefficienti hanno logiche di costruzione diverse;
d) sono uguali.
62. Secondo le ipotesi teoriche dell'analisi della varianza, l'F-ratio non può essere:
a) è uguale a 1;
b) più di 1;
c) inferiore a 1;
d) non esiste una risposta corretta.
Analisi di regressione e correlazione - metodi di ricerca statistica. Questi sono i modi più comuni per mostrare la dipendenza di un parametro da una o più variabili indipendenti.
Di seguito, usando esempi pratici concreti, considereremo queste due analisi molto popolari tra gli economisti. Daremo anche un esempio di come ottenere risultati quando vengono combinati.
Analisi di regressione in Excel
Mostra l'influenza di alcuni valori (indipendenti, indipendenti) sulla variabile dipendente. Ad esempio, come il numero di popolazione economicamente attiva dipende dal numero di imprese, salari e altri parametri. Oppure: in che modo gli investimenti esteri, i prezzi dell'energia, ecc. influiscono sul livello del PIL.
Il risultato dell'analisi consente di stabilire le priorità. E sulla base dei fattori principali, prevedere, pianificare lo sviluppo delle aree prioritarie, prendere decisioni di gestione.
La regressione avviene:
- lineare (y = a + bx);
- parabolico (y = a + bx + cx 2);
- esponenziale (y = a * exp(bx));
- potenza (y = a*x^b);
- iperbolico (y = b/x + a);
- logaritmico (y = b * 1n(x) + a);
- esponenziale (y = a * b^x).
Considera l'esempio della creazione di un modello di regressione in Excel e dell'interpretazione dei risultati. Prendiamo un tipo di regressione lineare.
Un compito. In 6 imprese sono stati analizzati lo stipendio medio mensile e il numero di dipendenti usciti. È necessario determinare la dipendenza del numero dei pensionati dalla retribuzione media.
Il modello di regressione lineare ha la seguente forma:
Y \u003d a 0 + a 1 x 1 + ... + a k x k.
Dove a sono i coefficienti di regressione, x sono le variabili che influenzano e k è il numero di fattori.
Nel nostro esempio, Y è l'indicatore delle dimissioni dei lavoratori. Il fattore che influenza è il salario (x).
Excel dispone di funzioni integrate che possono essere utilizzate per calcolare i parametri di un modello di regressione lineare. Ma il componente aggiuntivo Analysis ToolPak lo farà più velocemente.
Attiva un potente strumento analitico:


Una volta attivato, il componente aggiuntivo sarà disponibile nella scheda Dati.

Ora ci occuperemo direttamente dell'analisi di regressione.


Prima di tutto, prestiamo attenzione al quadrato R e ai coefficienti.
R-quadrato è il coefficiente di determinazione. Nel nostro esempio, è 0,755, o 75,5%. Ciò significa che i parametri calcolati del modello spiegano la relazione tra i parametri studiati del 75,5%. Maggiore è il coefficiente di determinazione, migliore è il modello. Buono - superiore a 0,8. Scarso - inferiore a 0,5 (un'analisi del genere difficilmente può essere considerata ragionevole). Nel nostro esempio - "non male".
Il coefficiente 64.1428 mostra quale sarà Y se tutte le variabili nel modello in esame sono uguali a 0. Cioè, anche altri fattori non descritti nel modello influiscono sul valore del parametro analizzato.
Il coefficiente -0,16285 mostra il peso della variabile X su Y. Cioè, lo stipendio medio mensile all'interno di questo modello influisce sul numero di abbandoni con un peso di -0,16285 (questo è un piccolo grado di influenza). Il segno “-” indica un impatto negativo: più alto è lo stipendio, meno abbandoni. Il che è giusto.
Analisi di correlazione in Excel
L'analisi di correlazione aiuta a stabilire se esiste una relazione tra gli indicatori in uno o due campioni. Ad esempio, tra il tempo di funzionamento della macchina e il costo delle riparazioni, il prezzo dell'attrezzatura e la durata del funzionamento, l'altezza e il peso dei bambini, ecc.
Se c'è una relazione, allora se un aumento di un parametro porta ad un aumento (correlazione positiva) o una diminuzione (negativa) nell'altro. L'analisi di correlazione aiuta l'analista a determinare se il valore di un indicatore può prevedere il possibile valore di un altro.
Il coefficiente di correlazione è indicato con r. Varia da +1 a -1. La classificazione delle correlazioni per le diverse aree sarà diversa. Quando il valore del coefficiente è 0, non esiste una relazione lineare tra i campioni.
Considera come utilizzare Excel per trovare il coefficiente di correlazione.
La funzione CORREL viene utilizzata per trovare i coefficienti accoppiati.
Compito: determinare se esiste una relazione tra il tempo di funzionamento di un tornio e il costo della sua manutenzione.

Posiziona il cursore in una cella qualsiasi e premi il pulsante fx.
- Nella categoria "Statistiche", selezionare la funzione CORRELAZIONE.
- Argomento "Array 1" - il primo intervallo di valori - il tempo della macchina: A2: A14.
- Argomento "Array 2" - il secondo intervallo di valori - il costo delle riparazioni: B2:B14. Fare clic su OK.

Per determinare il tipo di connessione, è necessario guardare il numero assoluto del coefficiente (ogni campo di attività ha una propria scala).
Per l'analisi di correlazione di più parametri (più di 2), è più conveniente utilizzare "Analisi dei dati" (componente aggiuntivo "Pacchetto di analisi"). Nell'elenco, è necessario selezionare una correlazione e designare una matrice. Tutto.
I coefficienti risultanti verranno visualizzati nella matrice di correlazione. Come questo:

Analisi di correlazione-regressione
In pratica, queste due tecniche sono spesso usate insieme.
Esempio:



Ora i dati dell'analisi di regressione sono visibili.
La dipendenza parabolica ha la forma:
I risultati dei calcoli ausiliari per costruire un modello di regressione parabolica e le caratteristiche della qualità del modello sono presentati nella Tabella 5.
Tabella 5
Dati stimati
|
Significare |
||||||||||
|
Somma dei quadrati |
||||||||||
1. Determinare i parametri a, b, c del modello parabolico
Pertanto, la dipendenza del costo di 1 tonnellata di colata y (rubli) dal rifiuto dei getti x (t) per 10 fonderie di fabbriche può essere rappresentata come una dipendenza parabolica:
2. Verificare la significatività dei coefficienti di regressione secondo il criterio di Student
Come nel caso della regressione a coppie, la significatività dei coefficienti della regressione lineare multipla con m variabili esplicative viene verificata sulla base della statistica t.
deviazione standard,
errore standard di regressione, m - numero di variabili esplicative del modello
Costruiamo una matrice
Definiamo il prodotto delle due matrici costruite sopra (in Excel utilizzando la funzione "MULTIPLE"):
Determiniamo l'errore standard della regressione con la formula:
Determiniamo le deviazioni standard con la formula:
Determiniamo i valori calcolati per i coefficienti di regressione multipla:
In base alla tabella di distribuzione di Student, determiniamo la teoria:
|tcalc|< tтеор, следовательно, коэффициенты а, с и b незначимы при уровне значимости 0,05.
3. Troviamo la relazione di correlazione, con l'aiuto della quale, nel caso di una dipendenza non lineare, si determina la tenuta della connessione tra due variabili casuali xey.
Il valore del rapporto di correlazione è abbastanza vicino a 1, il che indica una forte relazione tra x e y, cioè tra il costo di 1 tonnellata di colata (y) in rubli. e casting matrimoniale (x) incl.
4. Determinare l'autocorrelazione dei residui utilizzando il test di Durbin-Watson
Determiniamo il valore del criterio d con la formula:
Sostituiamo i risultati dei calcoli preliminari (vedi tabella 5) nella formula:

Utilizzando la tabella di Durbin-Watson, determiniamo i limiti critici d1 e d2 per N = 10 e m = 2:
d1=0,697; d2 = 1.641
d2 5. Determinare l'errore di approssimazione relativo medio in percentuale Sostituiamo i risultati dei calcoli preliminari (vedi tabella 5) nella formula: , > 8-10%, quindi, il modello è inaccettabile per la previsione, il che può essere spiegato da un piccolo numero di osservazioni (N=10). Affinché il modello possa essere utilizzato per la previsione, è sufficiente aumentare il numero di osservazioni da 10 a 15, quindi<10 %. Conclusioni sul modello: Non c'è autocorrelazione dei residui, la relazione è forte, ma i coefficienti sono insignificanti e il modello è inaccettabile per la previsione. Pertanto, il modello non riflette adeguatamente la relazione tra il costo di 1 tonnellata di getto Y (rubli) e il rifiuto di getto X (t). Potrebbe essere necessario ampliare l'elenco delle osservazioni o considerare un campione diverso dalla popolazione generale. Specifica del modello Per scegliere la dipendenza che meglio corrisponderebbe all'effettiva relazione tra il costo di 1 tonnellata di colata Y (rubli) e il rifiuto di colata X (t) per 10 fonderie di stabilimenti, è necessario analizzare i dati presentati nella tabella riassuntiva 6. Tabella riepilogativa 6. Lineare iperbolico logaritmico Potenza Parabolico Parametri sconosciuti dell'equazione di regressione Tenuta della connessione tra y e x Significato dei parametri dell'equazione di regressione (+ per significato lineare del coefficiente di correlazione) tcalc(rxy)=3.367 significativo tcalc(a)=4.618 significativo tcalc(b)=3,367 significativo tcalc(a)=11.968 significativo tcalc(b)=-2.685 significativo tcalc(a)=3,75 tcalc(b)=3,429 significativo tcalc(a)=25.999 significativo tcalc(b)=3.071 significativo tcalc(a)=1.661 insignificante tcalc(b)=1.505 insignificante tcalc(c)= -0,833 insignificante Errore di approssimazione relativo medio, in % inaccettabile inaccettabile inaccettabile inaccettabile inaccettabile Il valore del criterio di autocorrelazione dei residui nessuna autocorrelazione nessuna autocorrelazione nessuna autocorrelazione nessuna autocorrelazione autocorrelazione mancante Nella specificazione del modello si escludono innanzitutto i modelli in cui avviene l'autocorrelazione dei residui ei parametri di regressione sono insignificanti. L'autocorrelazione dei residui è assente in tutti i modelli. I parametri di tutte le regressioni costruite, ad eccezione di quella parabolica, sono significativi. Pertanto, il modello parabolico non può essere il modello che meglio riflette la relazione tra x e y - lo escludiamo da ulteriori considerazioni. Quindi è necessario selezionare tra le restanti dipendenze la dipendenza che ha il valore più alto del rapporto di correlazione o coefficiente di correlazione. Tra i nostri modelli, esiste approssimativamente la stessa rigidità della relazione tra xey nei modelli lineare (rxy=0,776) e power(). In una situazione del genere, viene data preferenza al modello il cui errore di approssimazione è minore. Ma il modello lineare è una specie di eccezione, perché è preferito indipendentemente dall'entità dell'errore di approssimazione. Inoltre, va notato che nei modelli costruiti lineare e di potenza, i valori dell'errore di approssimazione sono abbastanza vicini (lineare: ; potenza:). Pertanto, nonostante il modello di potenza rifletta abbastanza bene la relazione tra xey, preferiamo il modello lineare. Quindi, di tutti i modelli, riflette al meglio l'effettiva relazione tra il costo di 1 tonnellata di colata Y (rubli) e il rifiuto di colata X (t) per 10 fonderie di fabbriche: un modello lineare. Non c'è autocorrelazione dei residui in questo modello, i coefficienti sono significativi, la relazione tra xey è forte, ma il modello è inaccettabile per la previsione. Allo stesso tempo, l'errore di approssimazione di questo modello è abbastanza vicino al valore critico - 10%, quindi, per eliminare questo inconveniente e rendere il modello accettabile per la previsione, è sufficiente aggiungere diverse osservazioni. Istruzione. Specificare la quantità di dati di origine. La soluzione risultante viene salvata in un file Word. Un modello di soluzione viene generato automaticamente anche in Excel. Nota: se è necessario determinare i parametri di dipendenza parabolica (y = ax 2 + bx + c), è possibile utilizzare il servizio di allineamento analitico. Equazione di regressione del primo ordineè un'equazione di regressione lineare a coppie. Equazione di regressione del secondo ordine questa è un'equazione di regressione polinomiale del secondo ordine: y = a + bx + cx 2 . Equazione di regressione del terzo ordine rispettivamente, l'equazione di regressione polinomiale del terzo ordine: y = a + bx + cx 2 + dx 3 . Per portare le dipendenze non lineari a una lineare, vengono utilizzati metodi di linearizzazione (vedi il metodo di allineamento): Soluzione. Nella calcolatrice, seleziona tipi di regressione non lineare. Otteniamo la tabella seguente. L'equazione di regressione della potenza ha la forma y = a x b L'equazione di regressione iperbolica è y = b/x + a + ε L'equazione di regressione logaritmica ha la forma y = b ln(x) + a + ε L'equazione di regressione esponenziale ha la forma y = a b x + ε 
![]()
È possibile limitare un insieme omogeneo di unità eliminando oggetti di osservazione anomali attraverso il metodo di Irwin o con la regola del tre sigma (eliminare quelle unità per le quali il valore del fattore esplicativo si discosta dalla media di oltre tre volte lo standard deviazione).Tipi di regressione non lineare
Qui ε è un errore casuale (deviazione, perturbazione), che riflette l'influenza di tutti i fattori non contabilizzati. 

Esempio. In base ai dati ricavati dalla tabella corrispondente, procedere come segue: y = f(x) trasformazione Metodo di linearizzazione
y = b x a Y = log(y); X = log(x) Logaritmo
y = be ax Y = log(y); X=x Combinato
y = 1/(ax+b) Y = 1/a; X=x Cambio di variabili
y = x/(ax+b) Y=x/y; X=x Cambio di variabili. Esempio
y = aln(x)+b Y=y; X = log(x) Combinato
y = a + bx + cx2 x 1 = x; x2 = x2 Cambio di variabili
y = a + bx + cx2 + dx3 x 1 = x; x 2 \u003d x 2; x 3 = x 3 Cambio di variabili
y = a + b/x x 1 = 1/x Cambio di variabili
y = a + sqrt(x)b x 1 = sqrt(x) Cambio di variabili
Anno Consumo finale effettivo delle famiglie (a prezzi correnti), miliardi di rubli (1995 - trilioni di rubli), y Reddito medio pro capite in contanti della popolazione (al mese), rub. (1995 - mille rubli), x
1995
872
515,9
2000
3813
2281,1
2001
5014
3062
2002
6400
3947,2
2003
7708
5170,4
2004
9848
6410,3
2005
12455
8111,9
2006
15284
10196
2007
18928
12602,7
2008
23695
14940,6
2009
25151
16856,9
L'equazione di regressione esponenziale è y = a e bx
Dopo la linearizzazione, otteniamo: ln(y) = ln(a) + bx
Otteniamo coefficienti di regressione empirica: b = 0,000162, a = 7,8132
Equazione di regressione: y = e 7.81321500 e 0.000162x = 2473.06858e 0.000162x
Dopo la linearizzazione, otteniamo: ln(y) = ln(a) + b ln(x)
Coefficienti di regressione empirica: b = 0,9626, a = 0,7714
Equazione di regressione: y = e 0,77143204 x 0,9626 = 2,16286x 0,9626
Dopo la linearizzazione, otteniamo: y=bx + a
Coefficienti di regressione empirica: b = 21089190.1984, a = 4585.5706
Equazione di regressione empirica: y = 21089190.1984 / x + 4585.5706
Coefficienti di regressione empirica: b = 7142,4505, a = -49694,9535
Equazione di regressione: y = 7142,4505 ln(x) - 49694,9535
Dopo la linearizzazione, otteniamo: ln(y) = ln(a) + x ln(b)
Coefficienti di regressione empirica: b = 0,000162, a = 7,8132
y = e 7,8132 *e 0,000162x = 2473,06858*1,00016xX y 1/x registro(x) log(y)
515.9
872
0.00194
6.25
6.77
2281.1
3813
0.000438
7.73
8.25
3062
5014
0.000327
8.03
8.52
3947.2
6400
0.000253
8.28
8.76
5170.4
7708
0.000193
8.55
8.95
6410.3
9848
0.000156
8.77
9.2
8111.9
12455
0.000123
9
9.43
10196
15284
9.8E-5 9.23
9.63
12602.7
18928
7.9E-5 9.44
9.85
14940.6
23695
6.7E-5 9.61
10.07
16856.9
25151
5.9E-5 9.73
10.13