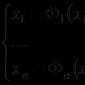Il rango della matrice di identità è uguale. Calcolo del rango di una matrice mediante trasformazioni elementari

Il numero r è detto rango della matrice A se:
1) la matrice A contiene un minore di ordine r diverso da zero;
2) tutti i minori di ordine (r+1) e superiori, se presenti, sono uguali a zero.
In caso contrario, il rango di una matrice è l'ordine più alto di un minore diverso da zero.
Denominazioni: rangA , r A o r .
Dalla definizione consegue che r è un intero positivo. Per una matrice nulla, il rango è considerato zero.

Incarico di servizio. Il calcolatore online è progettato per trovare rango di matrice. La soluzione viene salvata in formato Word ed Excel. vedi esempio di soluzione.

Istruzione. Selezionare la dimensione della matrice, fare clic su Avanti.

Definizione. Sia data una matrice di rango r. Qualsiasi matrice minore diversa da zero e avente ordine r è chiamata di base e le righe e le colonne dei suoi componenti sono chiamate righe e colonne di base.
Secondo questa definizione, la matrice A può avere più basi minori.

Il rango della matrice identità E è n (numero di righe).

Esempio 1 . Date due matrici, e i loro minori , . Quale di essi può essere preso come base?
Soluzione. Il minore M 1 = 0, quindi non può essere una base per nessuna delle matrici. Minore M 2 =-9≠0 ed ha ordine 2, quindi può essere assunta come matrici di base di A o / e B, purché abbiano ranghi pari a 2 . Poiché detB=0 (come determinante con due colonne proporzionali), allora rangB=2 e M 2 possono essere presi come base minore della matrice B. Il rango della matrice A è 3, per il fatto che detA=-27≠ 0 e, quindi, l'ordine della base minore di questa matrice deve essere 3, cioè M 2 non è una base per la matrice A . Si noti che la matrice A ha un'unica base minore uguale al determinante della matrice A .

Teorema (sulla minore di base). Qualsiasi riga (colonna) di una matrice è una combinazione lineare delle sue righe di base (colonne).
Conseguenze dal teorema.

1. Qualsiasi (r+1) colonna (righe) di una matrice di rango r è linearmente dipendente.
2. Se il rango di una matrice è inferiore al numero delle sue righe (colonne), le sue righe (colonne) sono linearmente dipendenti. Se rangA è uguale al numero delle sue righe (colonne), le righe (colonne) sono linearmente indipendenti.
3. Il determinante di una matrice A è uguale a zero se e solo se le sue righe (colonne) sono linearmente dipendenti.
4. Se un'altra riga (colonna) moltiplicata per un numero diverso da zero viene aggiunta alla riga (colonna) della matrice, il rango della matrice non cambierà.
5. Se si cancella una riga (colonna) nella matrice, che è una combinazione lineare di altre righe (colonne), il rango della matrice non cambierà.
6. Il rango di una matrice è uguale al numero massimo delle sue righe (colonne) linearmente indipendenti.
7. Il numero massimo di righe linearmente indipendenti è uguale al numero massimo di colonne linearmente indipendenti.

Esempio 2. Trova il rango di una matrice .
Soluzione. Sulla base della definizione del rango di una matrice, cercheremo un minore di ordine massimo diverso da zero. Innanzitutto, trasformiamo la matrice in una forma più semplice. Per fare ciò, moltiplica la prima riga della matrice per (-2) e aggiungi alla seconda, quindi moltiplicala per (-1) e aggiungi alla terza.

Grado di matriceè l'ordine più grande dei suoi minori diversi da zero. Il rango di una matrice è indicato da o .

Se tutti i minori di ordine di una data matrice sono zero, allora anche tutti i minori di ordine superiore di questa matrice sono zero. Ciò deriva dalla definizione del determinante. Ciò implica un algoritmo per trovare il rango di una matrice.

Se tutti i minori di primo ordine (elementi della matrice) sono uguali a zero, allora . Se almeno uno dei minori di primo ordine è diverso da zero e tutti i minori di secondo ordine sono uguali a zero, allora . Inoltre, basta guardare solo a quei minori di secondo ordine, che confinano con il minore diverso da zero di primo ordine. Se esiste un minore di secondo ordine diverso da zero, si indaga sui minori di terzo ordine che circondano il minore di secondo ordine diverso da zero. Ciò si protrae fino al raggiungimento di uno dei due casi: o tutti gli ordini minori che confinano con il minore diverso da zero dell'ordine -esimo sono uguali a zero, oppure non vi sono tali minori. Quindi .

Esempio 10 Calcola il rango della matrice.

Il minore di primo ordine (elemento ) è diverso da zero. Anche il minore che lo circonda è diverso da zero.

Tutti questi minori sono uguali a zero, quindi .

L'algoritmo di cui sopra per trovare il rango di una matrice non è sempre conveniente, poiché comporta il calcolo di un gran numero di determinanti. Quando si calcola il rango di una matrice, è più conveniente utilizzare trasformazioni elementari, con l'aiuto delle quali la matrice viene ridotta a una forma così semplice che è ovvio quale sia il suo rango.

Trasformazioni di matrici elementari chiamato le seguenti trasformazioni:

Ø moltiplicazione di una qualsiasi riga (colonna) della matrice per un numero diverso da zero;

Ø somma ad una riga (colonna) di un'altra riga (colonna), moltiplicata per un numero arbitrario.

Mezza Giordania trasformazione della riga della matrice:

con un elemento risolutivo viene chiamato il seguente insieme di trasformazioni con righe di matrice:

Ø aggiungere u moltiplicato per un numero alla prima riga, ecc.;

Ø aggiungi u moltiplicato per il numero all'ultima riga.

Trasformazione semigiordana di colonne di matrice con un elemento risolutivo è chiamato il seguente insieme di trasformazioni con colonne di matrice:

Ø alla prima colonna aggiungi th, moltiplicato per un numero, ecc.;

Ø all'ultima colonna aggiungi th, moltiplicato per il numero.

Dopo aver eseguito queste trasformazioni, la matrice risultante è:

La trasformazione semigiordana di righe o colonne di una matrice quadrata non cambia il suo determinante.

Le trasformazioni elementari di una matrice non ne cambiano il rango. Mostriamo un esempio come calcolare il rango di una matrice usando trasformazioni elementari. le righe (colonne) sono linearmente dipendenti.

Sia data qualche matrice:

.

Seleziona in questa matrice linee arbitrarie e colonne arbitrarie
. Poi il determinante esimo ordine, composto da elementi di matrice
situato all'intersezione di righe e colonne selezionate è chiamato minore -matrice del esimo ordine
.

Definizione 1.13. Grado di matrice
è l'ordine più grande del minore diverso da zero di questa matrice.

Per calcolare il rango di una matrice, si dovrebbero considerare tutti i suoi minori di ordine minimo e, se almeno uno di essi è diverso da zero, procedere alla considerazione dei minori di ordine più alto. Questo approccio alla determinazione del rango di una matrice è chiamato metodo bordering (o metodo bordering minors).

Compito 1.4. Con il metodo dei minori confinanti, determina il grado di una matrice
.

.

Considera il confine di primo ordine, ad esempio,
. Passiamo quindi alla considerazione di alcuni confinanti di secondo ordine.

Per esempio,
.

Infine, analizziamo il confine del terzo ordine.

.

Quindi l'ordine più alto di un minore diverso da zero è 2, quindi
.

Quando si risolve il Problema 1.4, si può notare che le serie di minori confinanti di secondo ordine sono diverse da zero. Al riguardo, si pone la seguente nozione.

Definizione 1.14. La base minore di una matrice è qualsiasi minore diverso da zero il cui ordine è uguale al rango della matrice.

Teorema 1.2.(Teorema minore di base). Le righe di base (colonne di base) sono linearmente indipendenti.

Si noti che le righe (colonne) di una matrice sono linearmente dipendenti se e solo se almeno una di esse può essere rappresentata come una combinazione lineare delle altre.

Teorema 1.3. Il numero di righe di matrice linearmente indipendenti è uguale al numero di colonne di matrice linearmente indipendenti ed è uguale al rango della matrice.

Teorema 1.4.(Condizione necessaria e sufficiente affinché il determinante sia uguale a zero). In ordine per il determinante -esimo ordine è uguale a zero, è necessario e sufficiente che le sue righe (colonne) siano linearmente dipendenti.

Calcolare il rango di una matrice in base alla sua definizione è troppo macchinoso. Questo diventa particolarmente importante per le matrici di ordine superiore. A questo proposito, in pratica, il rango di una matrice viene calcolato in base all'applicazione dei Teoremi 10.2 - 10.4, nonché all'uso dei concetti di equivalenza matriciale e trasformazioni elementari.

Definizione 1.15. Due matrici
e sono detti equivalenti se i loro ranghi sono uguali, cioè
.

Se matrici
e sono equivalenti, quindi nota
 .

Teorema 1.5. Il rango di una matrice non cambia rispetto alle trasformazioni elementari.

Chiameremo trasformazioni elementari della matrice
una delle seguenti azioni sulla matrice:

Sostituzione di righe con colonne e colonne con righe corrispondenti;

Permutazione di righe di matrice;

Cancellare una linea i cui elementi sono tutti uguali a zero;

Moltiplicando qualsiasi stringa per un numero diverso da zero;

Sommando agli elementi di una riga gli elementi corrispondenti di un'altra riga moltiplicati per lo stesso numero
.

Corollario del Teorema 1.5. Se la matrice
ottenuto dalla matrice utilizzando un numero finito di trasformazioni elementari, quindi le matrici
e sono equivalenti.

Quando si calcola il rango di una matrice, dovrebbe essere ridotta a una forma trapezoidale utilizzando un numero finito di trasformazioni elementari.

Definizione 1.16. Chiameremo trapezio una tale forma di rappresentazione di una matrice, quando nel minore confinante del più grande ordine diverso da zero, tutti gli elementi al di sotto di quelli diagonali svaniscono. Per esempio:

.

Qui
, elementi di matrice
girare a zero. Quindi la forma di rappresentazione di tale matrice sarà trapezoidale.

Di norma, le matrici vengono ridotte a una forma trapezoidale utilizzando l'algoritmo gaussiano. L'idea dell'algoritmo gaussiano è che, moltiplicando gli elementi della prima riga della matrice per i fattori corrispondenti, ottengono che tutti gli elementi della prima colonna situati sotto l'elemento
, verrebbe a zero. Quindi, moltiplicando gli elementi della seconda colonna per i moltiplicatori corrispondenti, otteniamo che tutti gli elementi della seconda colonna situati sotto l'elemento
, verrebbe a zero. Procedi ulteriormente allo stesso modo.

Compito 1.5. Determina il rango di una matrice riducendola a una forma trapezoidale.

.

Per comodità di applicare l'algoritmo gaussiano, puoi scambiare la prima e la terza riga.








.

Ovviamente qui
. Tuttavia, per portare il risultato a una forma più elegante, è possibile continuare con ulteriori trasformazioni sulle colonne.










.

Per lavorare con il concetto di rango di una matrice, abbiamo bisogno di informazioni dal tema "Complementi algebrici e minori. Tipi di minori e complementi algebrici" . Si tratta in primo luogo del termine "matrice minore", poiché determineremo il rango di una matrice proprio attraverso i minori.

Grado di matrice nominare l'ordine massimo dei suoi minori, tra i quali ve ne sia almeno uno diverso da zero.

Matrici equivalenti sono matrici i cui ranghi sono uguali tra loro.

Spieghiamo più in dettaglio. Supponiamo che ce ne sia almeno uno tra i minori di secondo ordine diverso da zero. E tutti i minori, il cui ordine è maggiore di due, sono uguali a zero. Conclusione: il rango della matrice è 2. Oppure, ad esempio, tra i minori del decimo ordine ce n'è almeno uno diverso da zero. E tutti i minori, il cui ordine è maggiore di 10, sono uguali a zero. Conclusione: il rango della matrice è 10.

Il rango della matrice $A$ è indicato come segue: $\rang A$ o $r(A)$. Il rango della matrice zero $O$ è posto uguale a zero, $\rang O=0$. Lascia che ti ricordi che per formare una matrice minore, è necessario barrare righe e colonne, ma è impossibile barrare più righe e colonne di quante la matrice stessa contenga. Ad esempio, se la matrice $F$ ha dimensione $5\volte 4$ (cioè contiene 5 righe e 4 colonne), l'ordine massimo dei suoi minori è quattro. Non sarà più possibile formare minori di quinto ordine, poiché richiederanno 5 colonne (e ne abbiamo solo 4). Ciò significa che il rango della matrice $F$ non può essere maggiore di quattro, cioè $\suona F≤4$.

In una forma più generale, quanto sopra significa che se la matrice contiene $m$ righe e $n$ colonne, il suo rango non può superare il più piccolo dei numeri $m$ e $n$, cioè $\suona A≤\min(m,n)$.

In linea di principio, il metodo per trovarlo deriva dalla definizione stessa del grado. Il processo per trovare il rango di una matrice per definizione può essere schematicamente rappresentato come segue:

Lascia che ti spieghi questo diagramma in modo più dettagliato. Iniziamo a ragionare fin dall'inizio, cioè con minori del primo ordine di qualche matrice $A$.

1. Se tutti i minori di primo ordine (cioè gli elementi della matrice $A$) sono uguali a zero, allora $\rang A=0$. Se tra i minori di primo ordine ce n'è almeno uno diverso da zero, allora $\rang A≥ 1$. Si passa alla verifica dei minori di secondo ordine.
2. Se tutti i minori di secondo ordine sono uguali a zero, allora $\rang A=1$. Se tra i minori di secondo ordine ce n'è almeno uno diverso da zero, allora $\rang A≥ 2$. Si passa alla verifica dei minori di terzo ordine.
3. Se tutti i minori di terzo ordine sono uguali a zero, allora $\rang A=2$. Se tra i minori del terzo ordine ce n'è almeno uno diverso da zero, allora $\rang A≥ 3$. Passiamo alla verifica dei minori di quarto ordine.
4. Se tutti i minori di quarto ordine sono uguali a zero, allora $\rang A=3$. Se c'è almeno un minore diverso da zero del quarto ordine, allora $\rang A≥ 4$. Si passa alla verifica dei minori di quinto ordine, e così via.

Cosa ci aspetta al termine di questa procedura? È possibile che tra i minori del k-esimo ordine ce ne sia almeno uno diverso da zero, e tutti i minori del (k + 1)-esimo ordine siano uguali a zero. Ciò significa che k è l'ordine massimo di minori tra i quali ve ne sia almeno uno diverso da zero, cioè il rango sarà pari a k. La situazione può essere diversa: tra i minori del k-esimo ordine ce ne sarà almeno uno diverso da zero, e i minori del (k + 1)° ordine non possono essere formati. Anche in questo caso il rango della matrice è pari a k. In parole povere, l'ordine dell'ultimo minore composto diverso da zero e sarà uguale al rango della matrice.

Passiamo agli esempi in cui verrà illustrato chiaramente il processo per trovare il rango di una matrice per definizione. Ancora una volta, sottolineo che negli esempi di questo argomento, troveremo il rango delle matrici utilizzando solo la definizione del rango. Altri metodi (calcolo del rango di una matrice con il metodo dei minori confinanti, calcolo del rango di una matrice con il metodo delle trasformazioni elementari) sono considerati nei seguenti argomenti.

A proposito, non è affatto necessario avviare la procedura per trovare il grado dai minori dell'ordine più piccolo, come è stato fatto negli esempi n. 1 e n. 2. Puoi andare immediatamente a minori di ordine superiore (vedi esempio n. 3).

Esempio 1

Trova il rango di una matrice $A=\left(\begin(array)(ccccc) 5 & 0 & -3 & 0 & 2 \\ 7 & 0 & -4 & 0 & 3 \\ 2 & 0 & -1 & 0 & 1 \end(array)\right)$.

Questa matrice ha dimensione $ 3 \ x 5 $, cioè contiene tre righe e cinque colonne. Dei numeri 3 e 5, 3 è il minimo, quindi il rango della matrice $A$ è al massimo 3, cioè $\grado A≤ 3$. E questa disuguaglianza è ovvia, poiché non possiamo più formare minori del quarto ordine: hanno bisogno di 4 righe e ne abbiamo solo 3. Procediamo direttamente al processo di ricerca del rango di una data matrice.

Tra i minori del primo ordine (cioè tra gli elementi della matrice $A$) ve ne sono di diversi da zero. Ad esempio, 5, -3, 2, 7. In generale, non siamo interessati al numero totale di elementi diversi da zero. C'è almeno un elemento diverso da zero - e questo è sufficiente. Poiché c'è almeno un diverso da zero tra i minori di primo ordine, concludiamo che $\rang A≥ 1$ e procediamo alla verifica dei minori di secondo ordine.

Iniziamo ad esplorare i minori di secondo ordine. Ad esempio, all'intersezione delle righe #1, #2 e delle colonne #1, #4 ci sono elementi dei seguenti minori: $\left|\begin(array)(cc) 5 & 0 \\ 7 & 0 \end (array) \right| $. Per questo determinante, tutti gli elementi della seconda colonna sono uguali a zero, quindi il determinante stesso è uguale a zero, cioè $\left|\begin(array)(cc) 5 & 0 \\ 7 & 0 \end(array) \right|=0$ (vedi proprietà #3 nella proprietà dei determinanti). Oppure puoi semplicemente calcolare questo determinante usando la formula n. 1 dalla sezione sul calcolo dei determinanti del secondo e del terzo ordine:

$$ \left|\begin(array)(cc) 5 & 0 \\ 7 & 0 \end(array) \right|=5\cdot 0-0\cdot 7=0. $$

Il primo minore del secondo ordine che abbiamo verificato è risultato uguale a zero. Cosa dice? Sulla necessità di un ulteriore controllo sui minori di secondo ordine. O risultano tutti nulli (e quindi il rango sarà pari a 1), oppure tra di essi c'è almeno un minore diverso da zero. Proviamo a fare una scelta migliore scrivendo un minore di secondo ordine i cui elementi si trovano all'intersezione delle righe #1, #2 e delle colonne #1 e #5: $\left|\begin(array)(cc) 5 & 2 \\ 7 e 3 \end(array)\right|$. Troviamo il valore di questo minore del secondo ordine:

$$ \left|\begin(array)(cc) 5 e 2 \\ 7 e 3 \end(array) \right|=5\cdot 3-2\cdot 7=1. $$

Questo minore non è uguale a zero. Conclusione: tra i minori di secondo ordine ce n'è almeno uno diverso da zero. Quindi $\rank A≥ 2$. Occorre procedere allo studio dei minori di terzo ordine.

Se per la formazione dei minori del terzo ordine sceglieremo la colonna n. 2 o la colonna n. 4, tali minori saranno uguali a zero (perché conterranno una colonna zero). Resta da controllare solo un minore del terzo ordine, i cui elementi si trovano all'intersezione delle colonne n. 1, n. 3, n. 5 e delle righe n. 1, n. 2, n. 3. Scriviamo questo minore e troviamo il suo valore:

$$ \left|\begin(array)(ccc) 5 & -3 & 2 \\ 7 & -4 & 3 \\ 2 & -1 & 1 \end(array) \right|=-20-18-14 +16+21+15=0. $$

Quindi, tutti i minori di terzo ordine sono uguali a zero. L'ultimo minore diverso da zero che abbiamo compilato era del secondo ordine. Conclusione: l'ordine massimo dei minori, tra i quali ve ne sia almeno uno diverso da zero, è pari a 2. Pertanto, $\rang A=2$.

Risposta: $\grado A=2$.

Esempio #2

Trova il rango di una matrice $A=\left(\begin(array) (cccc) -1 & 3 & 2 & -3\\ 4 & -2 & 5 & 1\\ -5 & 0 & -4 & 0 \\ 9 e 7 e 8 e -7 \end(array) \right)$.

Abbiamo una matrice quadrata del quarto ordine. Notiamo subito che il rango di questa matrice non supera 4, cioè $\grado A≤ 4$. Iniziamo a trovare il rango di una matrice.

Tra i minori del primo ordine (cioè tra gli elementi della matrice $A$) ce n'è almeno uno diverso da zero, quindi $\rang A≥ 1$. Si passa alla verifica dei minori di secondo ordine. Ad esempio, all'intersezione delle righe n. 2, n. 3 e delle colonne n. 1 e n. 2, otteniamo il seguente minore del secondo ordine: $\left| \begin(array) (cc) 4 & -2 \\ -5 & 0 \end(array) \right|$. Calcoliamolo:

$$ \sinistra| \begin(array) (cc) 4 & -2 \\ -5 & 0 \end(array) \right|=0-10=-10. $$

Tra i minori di secondo ordine ce n'è almeno uno che non è uguale a zero, quindi $\rang A≥ 2$.

Passiamo ai minori di terzo ordine. Troviamo, ad esempio, un minore i cui elementi si trovano all'intersezione delle righe n. 1, n. 3, n. 4 e colonne n. 1, n. 2, n. 4:

$$ \sinistra | \begin(array) (cccc) -1 & 3 & -3\\ -5 & 0 & 0\\ 9 & 7 & -7 \end(array) \right|=105-105=0. $$

Poiché questo minore di terzo ordine è risultato uguale a zero, è necessario indagare su un altro minore di terzo ordine. O tutti saranno uguali a zero (quindi il grado sarà uguale a 2), o tra questi ce ne sarà almeno uno diverso da zero (quindi inizieremo a studiare i minori di quarto ordine). Si consideri un minore di terzo ordine i cui elementi si trovano all'intersezione delle righe n. 2, n. 3, n. 4 e delle colonne n. 2, n. 3, n. 4:

$$ \sinistra| \begin(array) (ccc) -2 & 5 & 1\\ 0 & -4 & 0\\ 7 & 8 & -7 \end(array) \right|=-28. $$

C'è almeno un minore diverso da zero tra i minori di terzo ordine, quindi $\rang A≥ 3$. Passiamo alla verifica dei minori di quarto ordine.

Qualsiasi minore del quarto ordine si trova all'intersezione di quattro righe e quattro colonne della matrice $A$. In altre parole, il minore di quarto ordine è il determinante della matrice $A$, poiché questa matrice contiene solo 4 righe e 4 colonne. Il determinante di questa matrice è stato calcolato nell'esempio n. 2 dell'argomento "Ridurre l'ordine del determinante. Decomposizione del determinante in una riga (colonna)", quindi prendiamo solo il risultato finale:

$$ \sinistra| \begin(array) (cccc) -1 e 3 e 2 e -3\\ 4 e -2 e 5 e 1\\ -5 e 0 e -4 e 0\\ 9 e 7 e 8 e -7 \end (matrice)\destra|=86. $$

Quindi, il minore di quarto ordine non è uguale a zero. Non possiamo più formare minori di quinto ordine. Conclusione: l'ordine più alto di minori, tra i quali ce n'è almeno uno diverso da zero, è 4. Risultato: $\rang A=4$.

Risposta: $\grado A=4$.

Esempio #3

Trova il rango di una matrice $A=\left(\begin(array) (cccc) -1 & 0 & 2 & -3\\ 4 & -2 & 5 & 1\\ 7 & -4 & 0 & -5 \end( array)\right)$.

Nota subito che questa matrice contiene 3 righe e 4 colonne, quindi $\rang A≤ 3$. Negli esempi precedenti, abbiamo iniziato il processo di ricerca del grado considerando i minori del più piccolo (primo) ordine. Qui cercheremo di controllare immediatamente i minori dell'ordine più alto possibile. Per la matrice $A$, questi sono minori di terzo ordine. Si consideri un minore di terzo ordine i cui elementi si trovano all'intersezione delle righe n. 1, n. 2, n. 3 e delle colonne n. 2, n. 3, n. 4:

$$ \sinistra| \begin(array) (ccc) 0 & 2 & -3\\ -2 & 5 & 1\\ -4 & 0 & -5 \end(array) \right|=-8-60-20=-88. $$

Quindi, l'ordine più alto dei minori, tra i quali ce n'è almeno uno diverso da zero, è 3. Pertanto, il rango della matrice è 3, cioè $\grado A=3$.

Risposta: $\grado A=3$.

In generale, trovare il rango di una matrice per definizione è, nel caso generale, un compito piuttosto dispendioso in termini di tempo. Ad esempio, una matrice relativamente piccola $ 5 \ x 4 $ ha 60 minori di secondo ordine. E anche se 59 di loro sono uguali a zero, il 60° minore potrebbe risultare diverso da zero. Quindi devi esplorare i minori di terzo ordine, di cui questa matrice ha 40 pezzi. Solitamente si cerca di utilizzare metodi meno macchinosi, come il metodo del limite dei minori o il metodo delle trasformazioni equivalenti.

Consideriamo una matrice rettangolare. Se in questa matrice selezioniamo arbitrariamente K linee e K colonne, quindi gli elementi all'intersezione delle righe e delle colonne selezionate formano una matrice quadrata del k-esimo ordine. Viene chiamato il determinante di questa matrice k-esimo ordine minore matrice A. Ovviamente, la matrice A ha minori di qualsiasi ordine da 1 al più piccolo dei numeri m e n. Tra tutti i minori diversi da zero della matrice A, c'è almeno un minore il cui ordine è il più grande. Viene chiamato il più grande degli ordini diversi da zero dei minori di una data matrice rango matrici. Se il rango della matrice A è r, allora questo significa che la matrice A ha un ordine minore diverso da zero r, ma ogni minore di ordine maggiore di r, è uguale a zero. Il rango di una matrice A è indicato con r(A). È ovvio che la relazione

Calcolo del rango di una matrice usando i minori

Il rango di una matrice si trova o dal confine di minori o dal metodo delle trasformazioni elementari. Quando si calcola il rango di una matrice nel primo modo, si dovrebbe passare da minori di ordine inferiore a minori di ordine superiore. Se è già stato trovato un D minore diverso da zero del k-esimo ordine della matrice A, allora devono essere calcolati solo i (k + 1)° ordine minori confinanti con il D minore, cioè contenendolo come minore. Se sono tutti zero, allora il rango della matrice è K.

Esempio 1Trova il rango di una matrice con il metodo dei minori confinanti

.

Soluzione.Si comincia con i minori di 1° ordine, cioè dagli elementi della matrice A. Scegliamo, ad esempio, il minore (elemento) М 1 = 1 situato nella prima riga e nella prima colonna. Confinando con l'ausilio della seconda riga e della terza colonna si ottiene la minore M 2 = , che è diversa da zero. Passiamo ora ai minori di 3° ordine, confinanti con M 2 . Ce ne sono solo due (puoi aggiungere una seconda colonna o una quarta). Li calcoliamo: = 0. Pertanto, tutti i minori confinanti di terzo ordine sono risultati pari a zero. Il rango della matrice A è due.

Calcolo del rango di una matrice mediante trasformazioni elementari

ElementareSi chiamano le seguenti trasformazioni matriciali:

1) permutazione di due righe (o colonne) qualsiasi,

2) moltiplicando una riga (o una colonna) per un numero diverso da zero,

3) sommando a una riga (o colonna) un'altra riga (o colonna) moltiplicata per un certo numero.

Si chiamano le due matrici equivalente, se uno di essi è ottenuto dall'altro con l'ausilio di un insieme finito di trasformazioni elementari.

Le matrici equivalenti non sono, in generale, uguali, ma i loro ranghi sono uguali. Se le matrici A e B sono equivalenti, allora si scrive come segue: A~b.

Canonicouna matrice è una matrice che ha diversi 1 di fila all'inizio della diagonale principale (il cui numero può essere zero) e tutti gli altri elementi sono uguali a zero, ad esempio,

.

Con l'aiuto di trasformazioni elementari di righe e colonne, qualsiasi matrice può essere ridotta a una canonica. Il rango di una matrice canonica è uguale al numero di quelli sulla sua diagonale principale.

Esempio 2Trova il rango di una matrice

e portarlo alla forma canonica.

Soluzione. Sottrarre la prima riga dalla seconda riga e riordinare queste righe:

.

Ora, dalla seconda e dalla terza riga, sottrai la prima, moltiplicata rispettivamente per 2 e 5:

;

sottrarre il primo dalla terza riga; otteniamo la matrice

che è equivalente alla matrice A, poiché da essa si ottiene utilizzando un insieme finito di trasformazioni elementari. Ovviamente il rango della matrice B è 2, e quindi r(A)=2. La matrice B può essere facilmente ridotta a quella canonica. Sottraendo la prima colonna, moltiplicata per opportuni numeri, da tutte quelle successive, azzeriamo tutti gli elementi della prima riga, tranne la prima, e gli elementi delle righe rimanenti non cambiano. Quindi, sottraendo la seconda colonna, moltiplicata per i numeri appropriati, da tutti quelli successivi, azzeriamo tutti gli elementi della seconda riga, tranne la seconda, e otteniamo la matrice canonica:

.