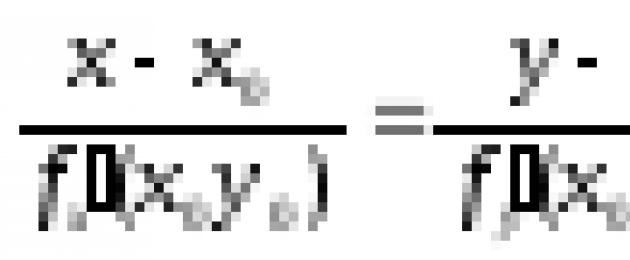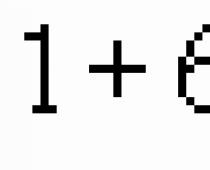täielik diferentsiaal. Kogudiferentsiaali geomeetriline tähendus

Puutetasand ja pind normaalne.

puutuja tasapind

Olgu N ja N 0 antud pinna punktid. Tõmbame sirge NN 0 . Tasapinda, mis läbib punkti N 0, nimetatakse puutuja tasapind pinnale, kui nurk sekandi NN 0 ja selle tasandi vahel kipub olema null, kui kaugus NN 0 kipub olema null.

Definitsioon. normaalne Pinnale punktis N 0 nimetatakse sirget, mis läbib punkti N 0 risti selle pinna puutujatasandiga.

Mingil hetkel on pinnal kas ainult üks puutujatasand või puudub see üldse.

Kui pind on antud võrrandiga z \u003d f (x, y), kus f (x, y) on punktis M 0 (x 0, y 0) diferentseeruv funktsioon, siis puutuja tasand punktis N 0 (x 0, y 0, ( x 0, y 0)) on olemas ja sellel on võrrand:

Pinnanormaali võrrand selles punktis on järgmine:

geomeetriline tunne kogu diferentsiaal Kahe muutuja funktsioonid f (x, y) punktis (x 0, y 0) on pinna puutujatasandi rakenduse (z-koordinaadi) juurdekasv punktist (x 0, y 0) liikumisel punktini (x 0 +x, y 0 +у).

Nagu näete, on kahe muutuja funktsiooni kogudiferentsiaali geomeetriline tähendus ühe muutuja funktsiooni diferentsiaali geomeetrilise tähenduse ruumiline analoog.

Näide. Leidke pinna puutujatasandi ja normaalvõrrandid

punktis M(1, 1, 1).

Puutujatasandi võrrand:

Tavaline võrrand:

20.4. Ligikaudsed arvutused kogudiferentsiaali abil.

Olgu funktsioon f(x, y) punktis (x, y) diferentseeruv. Leiame selle funktsiooni kogukasvu:

Kui asendame selle valemiga avaldise

siis saame ligikaudse valemi:

Näide. Arvutage ligikaudne väärtus, võttes aluseks funktsiooni väärtuse x = 1, y = 2, z = 1.

Antud avaldisest määrame x = 1,04 - 1 = 0,04, y = 1,99 - 2 = -0,01,

z \u003d 1,02 - 1 \u003d 0,02.

Leia funktsiooni u(x, y, z) = väärtus

Leiame osatuletised:

Funktsiooni u kogudiferentsiaal on:

Selle avaldise täpne väärtus on 1,049275225687319176.

20.5. Kõrgema järjekorra osatuletised.

Kui funktsioon f(x, y) on defineeritud mõnes domeenis D, siis defineeritakse ka selle osatuletised samas domeenis või selle osas.

Me nimetame neid tuletisteks esimest järku osatuletised.

Nende funktsioonide tuletised on teist järku osatuletised.

Jätkates saadud võrrandite diferentseerimist, saame kõrgema järgu osatuletised.

Definitsioon. Vormi osatuletised jne. helistas segatud derivaadid.

Teoreem. Kui funktsioon f(x, y) ja selle osatuletised on defineeritud ja pidevad punktis M(x, y) ja selle naabruses, siis on seos tõene:

Need. kõrgema järgu osatuletised ei sõltu diferentseerumisjärjekorrast.

Kõrgemat järku diferentsiaalid defineeritakse sarnaselt.

…………………

Siin on n tuletise sümboolne võimsus, mis pärast sulgudes oleva avaldise sellele tõstmist asendatakse tegeliku võimsusega.

Kahe muutuja funktsiooni f (x, y) summaarse diferentsiaali geomeetriline tähendus punktis (x 0, y 0) on pinda puudutava tasandi aplikatsiooni (z-koordinaadi) juurdekasv ülemineku ajal. punktist (x 0, y 0) punkti (x 0 + Dx, y 0 + Dy).

Kõrgema järjekorra osatuletised. : Kui funktsioon f(x, y) on defineeritud mõnes domeenis D, siis selle osatuletised ja defineeritakse ka samas domeenis või selle osas. Nimetame neid tuletisi esimest järku osatuletisteks.

Nende funktsioonide tuletised on teist järku osatuletised.

Jätkates saadud võrrandite diferentseerimist, saame kõrgema järgu osatuletised. Definitsioon. Vormi osatuletised jne. nimetatakse segatuletisteks. Schwartzi teoreem:

Kui kõrgema järgu osatuletised f.m.s. on pidevad, siis sama järku segatuletised, mis erinevad ainult eristumise järjekorra poolest = omavahel.

Siin on n tuletise sümboolne võimsus, mis pärast sulgudes oleva avaldise sellele tõstmist asendatakse tegeliku võimsusega.

14. Pinna puutujatasandi ja normaal võrrand!

Olgu N ja N 0 antud pinna punktid. Tõmbame sirge NN 0 . Tasapinda, mis läbib punkti N 0, nimetatakse puutuja tasapind pinnale, kui nurk sekandi NN 0 ja selle tasandi vahel kipub olema null, kui kaugus NN 0 kipub olema null.

Definitsioon. normaalne Pinnale punktis N 0 nimetatakse sirget, mis läbib punkti N 0 risti selle pinna puutujatasandiga.

Mingil hetkel on pinnal kas ainult üks puutujatasand või puudub see üldse.

Kui pind on antud võrrandiga z \u003d f (x, y), kus f (x, y) on punktis M 0 (x 0, y 0) diferentseeruv funktsioon, puutuja tasapind punktis N 0 (x 0, y 0, (x 0, y 0)) eksisteerib ja sellel on võrrand:

Pinnanormaali võrrand selles punktis:

geomeetriline tunne kahe muutuja funktsiooni summaarsest diferentsiaalist f (x, y) punktis (x 0, y 0) on pinda puudutava tasandi aplikatsiooni (z-koordinaadi) juurdekasv üleminekul punktist. (x 0, y 0) punktini (x 0 + Dx, y 0 + Dy).

Nagu näete, on kahe muutuja funktsiooni kogudiferentsiaali geomeetriline tähendus ühe muutuja funktsiooni diferentsiaali geomeetrilise tähenduse ruumiline analoog.

16. Skalaarväli ja selle omadused Tasandijooned, tuletissuunad, skalaarvälja gradient.

Kui igale ruumipunktile on määratud skalaarsuurus , siis tekib skalaarväli (näiteks temperatuuriväli, elektripotentsiaaliväli). Kui on sisestatud Descartes'i koordinaadid, siis tähistage ka või Keskmiselt võib põld olla tasane (sfääriline) kui silindriline, kui

Tasapinnad ja jooned: Skalaarväljade omadusi saab visualiseerida tasapindade abil. Need on ruumipinnad, millel see omandab konstantse väärtuse. Nende võrrand on: . Tasapinnalises skalaarväljas on tasapinnalised jooned kõverad, millel väli omandab konstantse väärtuse: Mõnel juhul võivad tasapinnalised jooned degenereeruda punktideks ja tasapinnad punktideks ja kõverateks.

Skalaarvälja suunatuletis ja gradient:

Olgu koordinaatidega ühikvektor skalaarväli. Suunatuletis iseloomustab välja muutust antud suunas ja arvutatakse valemiga Suunatuletis on vektori ja koordinaatidega vektori skalaarkorrutis , mida nimetatakse funktsiooni gradiendiks ja mida tähistatakse , kus nurk ja vahel, siis vektor näitab välja kiireima kasvu suunda ja selle moodul on võrdne selle suuna tuletisega. Kuna gradiendi komponendid on osatuletised, on lihtne saada järgmised gradiendi omadused:

17. FMP äärmus Fmp lokaalne ekstreemum, vajalikud ja piisavad tingimused selle olemasoluks. Suurim ja väikseim f.m.s. piiratud suletud ala.

Olgu funktsioon z = ƒ(x;y) defineeritud mingis domeenis D, punkt N(x0;y0)

Punkti (x0; y0) nimetatakse funktsiooni z=ƒ(x; y) maksimumpunktiks, kui punktil (x0; y0) on selline d-naabruskond, et iga punkti (x; y) puhul, välja arvatud (xo; yo), see naabruskond rahuldab ebavõrdsuse ƒ(х;у)<ƒ(хо;уо). Аналогично определяется точка минимума функции: для всех точек (х; у), отличных от (х0;у0), из d-окрестности точки (хо;уо) выполняется неравенство: ƒ(х;у)>ƒ(х0;y0). Funktsiooni väärtust maksimumi (miinimum) punktis nimetatakse funktsiooni maksimumiks (miinimum). Funktsiooni maksimumi ja miinimumi nimetatakse selle ekstreemumiteks. Pange tähele, et definitsiooni kohaselt asub funktsiooni äärmuspunkt funktsiooni domeeni sees; maksimumil ja miinimumil on kohalik (kohalik) märk: funktsiooni väärtust punktis (x0; y0) võrreldakse selle väärtustega punktidele (x0; y0) piisavalt lähedal. Piirkonnas D võib funktsioonil olla mitu äärmust või mitte ükski.

Vajalikud (1) ja piisavad (2) tingimused eksisteerimiseks:

(1) Kui punktis N (x0; y0) on diferentseeruval funktsioonil z \u003d ƒ (x; y) ekstreemum, siis on selle osatuletised selles punktis võrdsed nulliga: ƒ "x (x0; y0) \u003d 0, ƒ" y (x0; y0 )=0. kommenteerida. Funktsioonil võib olla ekstreemum punktides, kus vähemalt üht osatuletist ei eksisteeri. Punkti, kus funktsiooni z ≈ ƒ(x; y) esimest järku osatuletised on võrdsed nulliga, st f "x=0, f" y=0, nimetatakse funktsiooni z statsionaarseks punktiks.

Statsionaarseid punkte ja punkte, kus vähemalt ühte osatuletist ei eksisteeri, nimetatakse kriitilisteks punktideks.

(2) Olgu funktsioonil ƒ(x; y) pidevad osatuletised kuni teist järku (kaasa arvatud) statsionaarses punktis (xo; yo) ja mõnes selle naabruses. Arvutame punktis (x0;y0) väärtused A=f""xx(x0;y0), B=ƒ""xy(x0;y0), C=ƒ""yy(x0;y0) . Tähistage Seejärel:

1. kui Δ > 0, siis funktsioonil ƒ(x; y) punktis (x0; y0) on ekstreemum: maksimaalne, kui A< 0; минимум, если А > 0;

2. kui Δ< 0, то функция ƒ(х;у) в точке (х0;у0) экстремума не имеет.

3. Kui Δ = 0, võib punktis (x0; y0) ekstreemum olla, kuid ei pruugi olla. Vaja on rohkem uuringuid.

$E \subset \mathbb(R)^(n)$. Öeldakse, et $f$ on kohalik maksimum punktis $x_(0) \in E$, kui punkti $x_(0)$ naabrus $U$ on selline, et kõigi $x \in U$ korral on ebavõrdsus $f\left(x\right) \leqslant f \left(x_(0)\right)$.

Kohalikku maksimumi nimetatakse range , kui naabruskonna $U$ saab valida nii, et kõigi $x \in U$ jaoks, mis erinevad $x_(0)$, on $f\left(x\right)< f\left(x_{0}\right)$.

Definitsioon
Olgu $f$ reaalfunktsioon avatud hulgal $E \subset \mathbb(R)^(n)$. Öeldakse, et $f$ on kohalik miinimum punktis $x_(0) \in E$, kui punkti $x_(0)$ naabrus $U$ on selline, et kõigi $x \in U$ korral on ebavõrdsus $f\left(x\right) \geqslant f \left(x_(0)\right)$.

Kohalikku miinimumi peetakse rangeks, kui naabruskonna $U$ saab valida nii, et kõik $x \in U$ erinevad väärtusest $x_(0)$ $f\left(x\right) > f\left(x_ ( 0)\paremal)$.

Lokaalne ekstreemum ühendab kohaliku miinimumi ja kohaliku maksimumi mõisted.

Teoreem ( vajalik tingimus diferentseeruva funktsiooni äärmus)
Olgu $f$ reaalfunktsioon avatud hulgal $E \subset \mathbb(R)^(n)$. Kui punktis $x_(0) \in E$ on funktsioonil $f$ ka selles punktis lokaalne ekstreemum, siis $$\text(d)f\left(x_(0)\right)=0. $$ Võrdsus nulliga võrdub sellega, et kõik on võrdsed nulliga, st. $$\displaystyle\frac(\partial f)(\partial x_(i))\left(x_(0)\right)=0.$$

Ühemõõtmelisel juhul on see . Tähistage $\phi \left(t\right) = f \left(x_(0)+th\right)$, kus $h$ on suvaline vektor. Funktsioon $\phi$ on defineeritud piisavalt väikeste $t$ moodulväärtuste jaoks. Veelgi enam, suhtes , on see diferentseeritav ja $(\phi)' \left(t\right) = \text(d)f \left(x_(0)+th\right)h$.
Olgu $f$ kohalik maksimum x $0$. Seega on funktsioonil $\phi$ väärtusel $t = 0$ lokaalne maksimum ja Fermat' teoreemi järgi $(\phi)' \left(0\right)=0$.
Niisiis, saime $df \left(x_(0)\right) = 0$, st. funktsioon $f$ punktis $x_(0)$ on võrdne nulliga mis tahes vektoril $h$.

Definitsioon
Punktid, kus diferentsiaal on võrdne nulliga, st. statsionaarseteks nimetatakse neid, mille kõik osatuletised on võrdsed nulliga. kriitilised punktid funktsioonid $f$ on need punktid, kus $f$ ei ole diferentseeritav või võrdub nulliga. Kui punkt on statsionaarne, siis ei järeldu sellest veel, et funktsioonil on selles punktis ekstreemum.

Näide 1
Olgu $f \left(x,y\right)=x^(3)+y^(3)$. Siis $\displaystyle\frac(\partial f)(\partial x) = 3 \cdot x^(2)$,$\displaystyle\frac(\partial f)(\partial y) = 3 \cdot y^(2 )$, seega $\left(0,0\right)$ on statsionaarne punkt, kuid funktsioonil pole selles punktis ekstreemumit. Tõepoolest, $f \left(0,0\right) = 0$, kuid on lihtne näha, et punkti $\left(0,0\right)$ mis tahes läheduses on funktsioon nii positiivseid kui ka negatiivseid väärtusi.

Näide 2
Funktsiooni $f \left(x,y\right) = x^(2) − y^(2)$ koordinaatide alguspunkt on statsionaarne, kuid on selge, et selles punktis ekstreemumit pole.

Teoreem (ekstreemumi piisav tingimus).
Olgu funktsioon $f$ kaks korda pidevalt diferentseeritav avatud hulgal $E \subset \mathbb(R)^(n)$. Olgu $x_(0) \in E$ statsionaarne punkt ja $$\displaystyle Q_(x_(0)) \left(h\right) \equiv \sum_(i=1)^n \sum_(j=1 ) ^n \frac(\partial^(2) f)(\partial x_(i) \partial x_(j)) \left(x_(0)\right)h^(i)h^(j).$ $ Siis

1. kui $Q_(x_(0))$ – , siis funktsioonil $f$ punktis $x_(0)$ on lokaalne ekstreemum, nimelt miinimum, kui vorm on positiivne-määratav ja maksimum, kui vorm on negatiivne-kindel;
2. kui ruutvorm $Q_(x_(0))$ on määramatu, siis funktsioonil $f$ punktis $x_(0)$ ei ole ekstreemumit.

Kasutame laiendust Taylori valemi järgi (12,7 lk 292) . Arvestades, et esimest järku osatuletised punktis $x_(0)$ on võrdsed nulliga, saame $$\displaystyle f \left(x_(0)+h\right)−f \left(x_(0 )\right) = \ frac(1) (2) \sum_(i=1)^n \sum_(j=1)^n \frac(\partial^(2) f)(\partial x_(i) \ osaline x_(j)) \left(x_(0)+\theta h\right)h^(i)h^(j),$$ kus $0<\theta<1$. Обозначим $\displaystyle a_{ij}=\frac{\partial^{2} f}{\partial x_{i} \partial x_{j}} \left(x_{0}\right)$. В силу теоремы Шварца (12.6 стр. 289-290) , $a_{ij}=a_{ji}$. Обозначим $$\displaystyle \alpha_{ij} \left(h\right)=\frac{\partial^{2} f}{\partial x_{i} \partial x_{j}} \left(x_{0}+\theta h\right)−\frac{\partial^{2} f}{\partial x_{i} \partial x_{j}} \left(x_{0}\right).$$ По предположению, все непрерывны и поэтому $$\lim_{h \rightarrow 0} \alpha_{ij} \left(h\right)=0. \left(1\right)$$ Получаем $$\displaystyle f \left(x_{0}+h\right)−f \left(x_{0}\right)=\frac{1}{2}\left.$$ Обозначим $$\displaystyle \epsilon \left(h\right)=\frac{1}{|h|^{2}}\sum_{i=1}^n \sum_{j=1}^n \alpha_{ij} \left(h\right)h_{i}h_{j}.$$ Тогда $$|\epsilon \left(h\right)| \leq \sum_{i=1}^n \sum_{j=1}^n |\alpha_{ij} \left(h\right)|$$ и, в силу соотношения $\left(1\right)$, имеем $\epsilon \left(h\right) \rightarrow 0$ при $h \rightarrow 0$. Окончательно получаем $$\displaystyle f \left(x_{0}+h\right)−f \left(x_{0}\right)=\frac{1}{2}\left. \left(2\right)$$ Предположим, что $Q_{x_{0}}$ – положительноопределенная форма. Согласно лемме о положительноопределённой квадратичной форме (12.8.1 стр. 295, Лемма 1) , существует такое положительное число $\lambda$, что $Q_{x_{0}} \left(h\right) \geqslant \lambda|h|^{2}$ при любом $h$. Поэтому $$\displaystyle f \left(x_{0}+h\right)−f \left(x_{0}\right) \geq \frac{1}{2}|h|^{2} \left(λ+\epsilon \left(h\right)\right).$$ Так как $\lambda>0$ ja $\epsilon \left(h\right) \rightarrow 0$ $h jaoks \rightarrow 0$, seejärel parem osa on positiivne iga piisavalt väikese pikkusega vektori $h$ korral.
Seega oleme jõudnud järeldusele, et punkti $x_(0)$ mõnes läheduses on ebavõrdsus $f \left(x\right) >f \left(x_(0)\right)$ täidetud, kui ainult $ x \neq x_ (0)$ (paneme $x=x_(0)+h$\paremale). See tähendab, et punktis $x_(0)$ on funktsioonil range lokaalne miinimum ja seega on meie teoreemi esimene osa tõestatud.
Oletame nüüd, et $Q_(x_(0))$ on määramatu vorm. Siis on vektorid $h_(1)$, $h_(2)$ nii, et $Q_(x_(0)) \left(h_(1)\right)=\lambda_(1)>0$, $Q_ ( x_(0)) \left(h_(2)\right)= \lambda_(2)<0$. В соотношении $\left(2\right)$ $h=th_{1}$ $t>0 $. Siis saame $$f \left(x_(0)+th_(1)\right)−f \left(x_(0)\right) = \frac(1)(2) \left[ t^(2) \ lambda_(1) + t^(2) |h_(1)|^(2) \epsilon \left(th_(1)\right) \right] = \frac(1)(2) t^(2) \ vasak[ \lambda_(1) + |h_(1)|^(2) \epsilon \left(th_(1)\right) \right].$$ Piisavalt väikese $t>0$ puhul on parem pool positiivne. See tähendab, et mis tahes punkti $x_(0)$ läheduses võtab funktsioon $f$ väärtused $f \left(x\right)$, mis on suuremad kui $f \left(x_(0)\right)$.
Samamoodi saame, et punkti $x_(0)$ mis tahes läheduses võtab funktsioon $f$ väärtused, mis on väiksemad kui $f \left(x_(0)\right)$. See koos eelmisega tähendab, et funktsioonil $f$ ei ole punktis $x_(0)$ ekstreemumit.

Kaaluge erijuhtum selle teoreemi funktsiooni $f \left(x,y\right)$ kahe muutuja jaoks, mis on määratletud punkti $\left(x_(0),y_(0)\right)$ mõnes naabruses ja millel on pidevad osatuletised esimesest ja teisest tellimusest. Olgu $\left(x_(0),y_(0)\right)$ statsionaarne punkt ja $$\displaystyle a_(11)= \frac(\partial^(2) f)(\partial x ^( 2)) \left(x_(0) ,y_(0)\right), a_(12)=\frac(\partial^(2) f)(\partial x \partial y) \left(x_( 0) , y_(0)\right), a_(22)=\frac(\partial^(2) f)(\partial y^(2)) \left(x_(0), y_(0)\right ). $$ Siis saab eelmine teoreem järgmise kuju.

Teoreem
Olgu $\Delta=a_(11) \cdot a_(22) − a_(12)^2$. Seejärel:

1. kui $\Delta>0$, siis on funktsioonil $f$ lokaalne ekstreemum punktis $\left(x_(0),y_(0)\right)$, nimelt miinimum, kui $a_(11)> 0$ ja maksimum, kui $a_(11)<0$;
2. kui $\Delta<0$, то экстремума в точке $\left(x_{0},y_{0}\right)$ нет. Как и в одномерном случае, при $\Delta=0$ экстремум может быть, а может и не быть.

Näited probleemide lahendamisest

Algoritm paljude muutujate funktsiooni ekstreemumi leidmiseks:

1. Leiame statsionaarsed punktid;
2. Leiame 2. järku diferentsiaali kõikidest statsionaarsetest punktidest
3. Kasutades mitme muutuja funktsiooni ekstreemumi piisavat tingimust, arvestame teist järku diferentsiaali igas statsionaarses punktis

1. Uurige funktsiooni ekstreemumini $f \left(x,y\right) = x^(3) + 8 \cdot y^(3) + 18 \cdot x — 30 \cdot y$.
   Lahendus

   Leidke esimese järgu osatuletised: $$\displaystyle \frac(\partial f)(\partial x)=3 \cdot x^(2) — 6 \cdot y;$$ $$\displaystyle \frac(\partial f)(\partial y)=24 \cdot y^(2) — 6 \cdot x.$$ Koostage ja lahendage süsteem: $$\displaystyle \begin(cases)\frac(\partial f)(\partial x ) = 0\\\frac(\partial f)(\partial y)= 0\end(cases) \Paremnool \begin(cases)3 \cdot x^(2) - 6 \cdot y= 0\\24 \ cdot y^(2) - 6 \cdot x = 0\end(cases) \Rightnarrow \begin(cases)x^(2) - 2 \cdot y= 0\\4 \cdot y^(2) - x = 0 \end(cases)$$ 2. võrrandist väljendame $x=4 \cdot y^(2)$ — asendame 1. võrrandiga: $$\displaystyle \left(4 \cdot y^(2)\ parem )^(2)-2 \cdot y=0$$ $$16 \cdot y^(4) — 2 \cdot y = 0$$ $$8 \cdot y^(4) — y = 0$$ $$ y \left(8 \cdot y^(3) -1\right)=0$$ Selle tulemusena saadakse 2 statsionaarset punkti:
   1) $y=0 \paremnool x = 0, M_(1) = \left(0, 0\right)$;
   2) $\displaystyle 8 \cdot y^(3) -1=0 \Rightarrow y^(3)=\frac(1)(8) \Paremnool y = \frac(1)(2) \Rightarrow x=1 , M_(2) = \left(\frac(1)(2), 1\right)$
   Kontrollime piisava äärmuse tingimuse täitmist:
   $$\displaystyle \frac(\partial^(2) f)(\partial x^(2))=6 \cdot x; \frac(\partial^(2) f)(\partial x \partial y)=-6; \frac(\partial^(2) f)(\partial y^(2))=48 \cdot y$$
   1) Punkti $M_(1)= \left(0,0\right)$ jaoks:
   $$\displaystyle A_(1)=\frac(\partial^(2) f)(\partial x^(2)) \left(0,0\right)=0; B_(1)=\frac(\partial^(2) f)(\partial x \partial y) \left(0,0\right)=-6; C_(1)=\frac(\partial^(2) f)(\partial y^(2)) \left(0,0\right)=0;$$
   $A_(1) \cpunkt B_(1) - C_(1)^(2) = -36<0$ , значит, в точке $M_{1}$ нет экстремума.
   2) Punkti $M_(2)$ puhul:
   $$\displaystyle A_(2)=\frac(\partial^(2) f)(\partial x^(2)) \left(1,\frac(1)(2)\right)=6; B_(2)=\frac(\partial^(2) f)(\partial x \partial y) \left(1,\frac(1)(2)\right)=-6; C_(2)=\frac(\partial^(2) f)(\partial y^(2)) \left(1,\frac(1)(2)\right)=24;$$
   $A_(2) \cdot B_(2) — C_(2)^(2) = 108>0$, seega on punktis $M_(2)$ ekstreemum ja kuna $A_(2)>0 $, siis see on miinimum.
   Vastus: Punkt $\displaystyle M_(2) \left(1,\frac(1)(2)\right)$ on funktsiooni $f$ miinimumpunkt.
   

2. Uurige ekstreemumi $f=y^(2) + 2 \cdot x \cdot y - 4 \cdot x - 2 \cdot y - 3$ funktsiooni.
   Lahendus

   Otsige statsionaarseid punkte: $$\displaystyle \frac(\partial f)(\partial x)=2 \cdot y - 4;$$ $$\displaystyle \frac(\partial f)(\partial y)=2 \cdot y + 2 \cdot x — 2.$$
   Koostage ja lahendage süsteem: $$\displaystyle \begin(cases)\frac(\partial f)(\partial x)= 0\\\frac(\partial f)(\partial y)= 0\end(cases) \ Paremnool \begin(cases)2 \cdot y - 4= 0\\2 \cdot y + 2 \cdot x - 2 = 0\end(juhtumid) \Paremnool \begin(cases) y = 2\\y + x = 1\lõpp(juhtumid) \Paremnool x = -1$$
   $M_(0) \left(-1, 2\right)$ on statsionaarne punkt.
   Kontrollime piisava ekstreemumi tingimuse täitmist: $$\displaystyle A=\frac(\partial^(2) f)(\partial x^(2)) \left(-1,2\right)=0; B=\frac(\partial^(2) f)(\partial x \partial y) \left(-1,2\right)=2; C=\frac(\partial^(2) f)(\partial y^(2)) \left(-1,2\right)=2;$$
   $A \cdot B - C^(2) = -4<0$ , значит, в точке $M_{0}$ нет экстремума.
   Vastus: äärmusi pole.
   

Ajapiirang: 0

Navigeerimine (ainult töönumbrid)

0 4-st ülesandest täidetud

Teave

Selle viktoriiniga saate testida oma teadmisi äsja loetud teema kohta: Paljude muutujate funktsioonide kohalik äärmuslikkus.

Olete testi juba varem teinud. Te ei saa seda uuesti käivitada.

Testi laaditakse...

Testi alustamiseks peate sisse logima või registreeruma.

Selle testi alustamiseks peate täitma järgmised testid.

tulemused

Õiged vastused: 0/4

Sinu aeg:

Aeg on läbi

Sa said 0 punkti 0-st (0)

Sinu tulemus on edetabelisse kantud

1. Koos vastusega
2. Välja vaadatud

Ülesanne 1/4

1 .

Punktide arv: 1

Uurige funktsiooni $f$ ekstreemide jaoks: $f=e^(x+y)(x^(2)-2 \cdot y^(2))$

Õige


Mitte korralikult


1. Ülesanne 2/4

   2 .

   Punktide arv: 1

   Kas funktsioon $f = 4 + \sqrt((x^(2)+y^(2))^(2))$

   Õige

Ühe muutuja funktsiooni jaoks y = f(x) punktis x 0 diferentsiaali geomeetriline tähendus tähendab funktsiooni graafikule tõmmatud puutuja ordinaadi juurdekasvu abstsisspunktis x 0 punkti liikudes x 0 +  x. Ja kahe muutuja funktsiooni erinevus on selles osas juurdekasv aplikatsioonid puutuja lennuk tõmmatud võrrandiga antud pinnale z = f(x, y) , punktis M 0 (x 0 , y 0 ) punkti liikudes M(x 0 +  x, y 0 +  y). Anname mingi pinna puutujatasandi definitsiooni:

Df . Tasand, mis läbib punkti R 0 pinnad S, kutsutakse puutuja tasapind antud punktis, kui nurk selle tasandi ja kahte punkti läbiva sekandi vahel R 0 ja R(ükskõik milline punkt pinnal S) , kipub nulli, kui punkt R kaldub piki seda pinda punktini R 0 .

Lase pinnale S võrrandiga antud z = f(x, y). Siis saab näidata, et sellel pinnal on punkt P 0 (x 0 , y 0 , z 0 ) puutuja tasapind siis ja ainult siis, kui funktsioon z = f(x, y) on sel hetkel eristatav. Sel juhul saadakse puutuja tasapind võrrandiga:

z – z 0 = +
(6).

§5. Suunatuletis, funktsiooni gradient.

Osatuletisfunktsioonid y= f(x 1 , x 2 .. x n ) muutujate järgi x 1 , x 2 . . . x n väljendada funktsiooni muutumise kiirust koordinaatide telgede suunas. Näiteks, on funktsiooni muutumise kiirus X 1 - ehk eeldatakse, et funktsiooni definitsiooni valdkonda kuuluv punkt liigub ainult paralleelselt teljega Oh 1 , ja kõik muud koordinaadid jäävad muutumatuks. Samas võib eeldada, et funktsioon võib muutuda ka mõnes muus suunas, mis ei ühti ühegi telje suunaga.

Vaatleme kolme muutuja funktsiooni: u= f(x, y, z).

Parandage punkt M 0 (x 0 , y 0 , z 0 ) ja mõni suunatud sirgjoon (telg) l selle punkti läbimine. Lase M(x, y, z) - selle sirge suvaline punkt ja  M 0 M - kaugus M 0 enne M.

u = f (x, y, z) – f(x 0 , y 0 , z 0 ) – funktsiooni juurdekasv punktis M 0 .

Leia funktsiooni juurdekasvu ja vektori pikkuse suhe
:

Df . Tuletisfunktsioon u = f (x, y, z) poole l punktis M 0 nimetatakse funktsiooni juurdekasvu ja vektori pikkuse suhte piiriks  M 0 Mkui viimane kipub olema 0 (või mis on sama asi, piiramatu lähendusega M To M 0 ):

(1)

See tuletis iseloomustab funktsiooni muutumise kiirust punktis M 0 suunas l.

Laske telg l (vektor M 0 M) vormid telgedega HÄRG, OY, oz nurgad
vastavalt.

Tähistage x-x 0 =
;

y - y 0 =
;

z - z 0 =
.

Siis vektor M 0 M = (x - x 0 , y - y 0 , z - z 0 )=
ja selle suunakoosinused:

;

;

.

(4).

(4) on suunatuletise arvutamise valem.

Vaatleme vektorit, mille koordinaadid on funktsiooni osatuletised u= f(x, y, z) punktis M 0 :

grad u - funktsiooni gradient u= f(x, y, z) punktis M(x, y, z)

Gradiendi omadused:

Järeldus: funktsiooni gradiendi pikkus u= f(x, y, z) - on suurim võimalik väärtus sel hetkel M(x, y, z) , ja vektori suund grad u langeb kokku punktist väljuva vektori suunaga M, mida mööda funktsioon muutub kõige kiiremini. See tähendab funktsiooni gradiendi suund grad u on funktsiooni kiireima suurenemise suund.

MITME MUUTUJA FUNKTSIOONIDE DIFERENTSIAALARVUTUS.

Põhimõisted ja määratlused.

Arvestades mitme muutuja funktsioone, piirdume kahe muutuja funktsioonide üksikasjaliku kirjeldusega, kuna kõik saadud tulemused kehtivad suvalise arvu muutujate funktsioonide jaoks.

Kui igale teatud hulga vastastikku sõltumatute arvude paarile (x, y) omistatakse mingi reegli kohaselt muutuja z üks või mitu väärtust, siis nimetatakse muutujat z. kahe muutuja funktsioon.

Kui arvupaar (x, y) vastab ühele z väärtusele, kutsutakse funktsioon välja üheselt mõistetav ja kui rohkem kui üks, siis - mitmetähenduslik.

Määratluse ulatus funktsioon z on paaride hulk (x, y), mille jaoks funktsioon z on olemas.

Naabruskonna punkt M 0 (x 0, y 0) raadiusega r on kõikide punktide (x, y) hulk, mis vastavad tingimusele.

Kutsutakse numbrit A piir funktsioon f(x, y) punktina M(x, y) kaldub punkti M 0 (x 0, y 0), kui iga arvu e > 0 korral on selline arv r > 0, et mis tahes punktis M (x, y), mille tingimus

tingimus on ka tõsi .

Kirjuta üles:

Punkt M 0 (x 0, y 0) kuulugu funktsiooni f(x, y) valdkonda. Siis kutsutakse funktsioon z = f(x, y). pidev punktis M 0 (x 0, y 0), kui

(1)

pealegi kaldub punkt M(x, y) suvaliselt punkti M 0 (x 0, y 0).

Kui tingimus (1) ei ole üheski punktis täidetud, nimetatakse seda punkti murdepunkt funktsioonid f(x, y). See võib juhtuda järgmistel juhtudel:

1) Funktsioon z \u003d f (x, y) ei ole punktis M 0 (x 0, y 0) määratletud.

2) Piiranguid pole.

3) See piir on olemas, kuid see ei ole võrdne f(x 0 , y 0).

Mitme muutuja funktsioonide omadused, mis on seotud nende pidevusega.

Kinnisvara. Kui funktsioon f(x, y, …) on defineeritud ja pidev suletud ja piiratud domeenis D, siis selles domeenis on vähemaltüks punkt

N(x 0 , y 0 , …) nii, et ebavõrdsus

f(x 0, y 0, …) ³ f(x, y, …)

samuti punkt N 1 (x 01 , y 01 , ...), nii et kõigi teiste punktide ebavõrdsus on tõene

f(x 01, y 01, …) £ f(x, y, …)

siis f(x 0 , y 0 , …) = M – kõrgeim väärtus funktsioonid ja f(x 01 , y 01 , ...) = m - väikseim väärtus funktsioonid f(x, y, …) domeenis D.

Pidev funktsioon suletud ja piiratud domeenis D saavutab vähemalt üks kord suurima väärtuse ja üks kord väikseima.

Kinnisvara. Kui funktsioon f(x, y, …) on defineeritud ja pidev suletud piiritletud domeenis D ning M ja m on vastavalt funktsiooni suurimad ja väikseimad väärtused selles valdkonnas, siis mis tahes punkti m О korral on seal on punkt

N 0 (x 0, y 0, …), nii et f(x 0, y 0, …) = m.

Lihtsamalt öeldes võtab pidev funktsioon domeeni D all vahepealsed väärtused M ja m vahel. Selle omaduse tagajärjeks võib olla järeldus, et kui arvudel M ja m on erinevad märgid, siis domeenis D funktsioon kaob vähemalt korra.

Kinnisvara. Funktsioon f(x, y, …), pidev suletud piiratud domeenis D, piiratud selles piirkonnas, kui on selline arv K, et piirkonna kõigi punktide puhul on ebavõrdsus tõene .

Kinnisvara. Kui funktsioon f(x, y, …) on defineeritud ja pidev suletud piiriga domeenis D, siis see ühtlaselt pidev sellel alal, st. iga positiivse arvu e korral on selline arv D > 0, et piirkonna mis tahes kahe punkti (x 1, y 1) ja (x 2, y 2) korral, mis asuvad D-st väiksemal kaugusel, on ebavõrdsus

2. Osatuletised. Kõrgema järjekorra osatuletised.

Olgu mingis valdkonnas antud funktsioon z = f(x, y). Võtke suvaline punkt M(x, y) ja määrake muutuja x juurdekasv Dx. Siis nimetatakse suurust D x z = f(x + Dx, y) – f(x, y) funktsiooni osaline juurdekasv x-is.

Võib kirjutada

.

Siis helistati osaline tuletis funktsioonid z = f(x, y) x-is.

Määramine:

Funktsiooni osatuletis y suhtes on defineeritud sarnaselt.

geomeetriline tunne osatuletis (oletame) on punktis N 0 (x 0, y 0, z 0) joonestatud puutuja kalde puutuja pinnalõikele tasapinnaga y \u003d y 0.

Kui funktsioon f(x, y) on defineeritud mõnes domeenis D, siis selle osatuletised ja defineeritakse ka samas domeenis või selle osas.

Me nimetame neid tuletisteks esimest järku osatuletised.

Nende funktsioonide tuletised on teist järku osatuletised.

Jätkates saadud võrrandite diferentseerimist, saame kõrgema järgu osatuletised.

Vormi osatuletised jne. helistas segatud derivaadid.

Teoreem. Kui funktsioon f(x, y) ja selle osatuletised on defineeritud ja pidevad punktis M(x, y) ja selle naabruses, siis on seos tõene:

Need. kõrgema järgu osatuletised ei sõltu diferentseerumisjärjekorrast.

Kõrgemat järku diferentsiaalid defineeritakse sarnaselt.

…………………

Siin on n tuletise sümboolne võimsus, mis pärast sulgudes oleva avaldise sellele tõstmist asendatakse tegeliku võimsusega.

täielik diferentsiaal. geomeetriline tunne täielik diferentsiaal. Puutetasand ja pind normaalne.

Väljendit nimetatakse täielik juurdekasv funktsioonid f(x, y) mingis punktis (x, y), kus a 1 ja a 2 on lõpmata väikesed funktsioonid vastavalt Dх ® 0 ja Dу ® 0.

täielik diferentsiaal funktsioon z = f(x, y) on funktsiooni Dz inkremendi põhiline lineaarne osa Dx ja Dy suhtes punktis (x, y).

Suvalise arvu muutujate funktsiooni jaoks:

Näide 3.1. Leidke funktsiooni täielik erinevus.