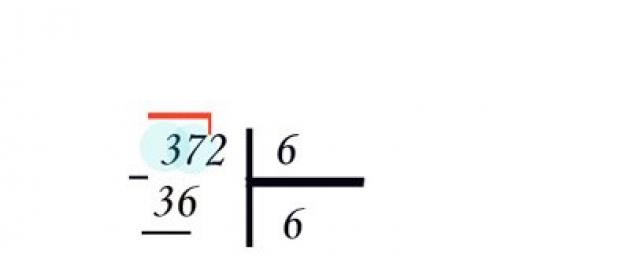Instrukcja
Najpierw przetestuj umiejętności mnożenia dziecka. Jeśli dziecko nie zna dobrze tabliczki mnożenia, może mieć również problemy z dzieleniem. Następnie, wyjaśniając podział, możesz zajrzeć do ściągawki, ale nadal musisz nauczyć się tabeli.
Wpisz dywidendę i dzielnik przez pionową kreskę oddzielającą. Pod dzielnikiem wpiszesz odpowiedź - iloraz, oddzielając go linią poziomą. Weź pierwszą cyfrę 372 i zapytaj dziecko, ile razy liczba sześć „pasuje” w trójkę. Zgadza się, wcale nie.
Następnie weź już dwie liczby - 37. Dla jasności możesz podświetlić je rogiem. Powtórz pytanie jeszcze raz - ile razy liczba sześć jest zawarta w 37. Aby szybko policzyć, przyda się. Wybierz odpowiedź razem: 6 * 4 = 24 - wcale nie jest podobna; 6*5 = 30 – blisko 37. Ale 37-30 = 7 – sześć znów „pasuje”. Wreszcie 6*6 = 36, 37-36 = 1 jest w porządku. Pierwszy znaleziony iloraz to 6. Zapisz go pod dzielnikiem.

Napisz 36 pod liczbą 37, narysuj linię. Dla jasności znak może być użyty w zapisie. Resztę umieść pod kreską - 1. Teraz "obniż" następną cyfrę liczby, dwie, do jednej - okazało się, że 12. Wyjaśnij dziecku, że liczby zawsze "spadają" pojedynczo. Ponownie zapytaj ile "szóstek" jest w 12. Odpowiedź to 2, tym razem bez śladu. Wpisz drugi numer prywatny obok pierwszego. Ostateczny wynik to 62.

Rozważ również szczegółowo przypadek podziału. Na przykład 167/6 \u003d 27, reszta to 5. Najprawdopodobniej twoje potomstwo nie słyszało jeszcze nic o prostych ułamkach. Ale jeśli zadaje pytania, co zrobić z resztą, można to wyjaśnić na przykładzie jabłek. 167 jabłek podzielono pomiędzy sześć osób. Każdy dostał 27 sztuk, a pięć jabłek pozostało niepodzielonych. Możesz je również podzielić, krojąc każdy na sześć plasterków i równomiernie rozprowadzając. Każda osoba dostała po jednym kawałku z każdego jabłka - 1/6. A ponieważ było pięć jabłek, każde miało pięć plasterków - 5/6. Oznacza to, że wynik można zapisać w następujący sposób: 27 5/6.

W tym artykule przeanalizujemy dzielenie liczb całkowitych z resztą. Zacznijmy ogólna zasada dzieleniu liczb całkowitych przez resztę formułujemy i dowodzimy twierdzenie o podzielności liczb całkowitych przez resztę, śledzimy związki między dzielną, dzielnikiem, ilorazem niepełnym i resztą. Następnie ogłosimy zasady, według których przeprowadza się dzielenie liczb całkowitych przez resztę i rozważymy zastosowanie tych zasad podczas rozwiązywania przykładów. Następnie dowiemy się, jak sprawdzić wynik dzielenia liczb całkowitych z resztą.
Nawigacja po stronach.
Ogólna idea dzielenia liczb całkowitych przez resztę
Dzielenie liczb całkowitych z resztą rozważymy jako uogólnienie dzielenia z resztą liczb naturalnych. Dzieje się tak, ponieważ liczby naturalne są część integralna wszystkie liczby.
Zacznijmy od terminów i notacji użytych w opisie.
Przez analogię do dzielenia liczb naturalnych przez resztę zakładamy, że wynik dzielenia przez resztę dwóch liczb całkowitych a i b (b nie jest równe zeru) to dwie liczby całkowite c i d . Liczby a i b nazywają się podzielny I rozdzielacz odpowiednio liczba d to reszta z dzielenia a przez b, a liczba całkowita c nazywa się niekompletny prywatny(lub po prostu prywatny jeśli reszta wynosi zero).
Umówmy się, że reszta jest nieujemną liczbą całkowitą, a jej wartość nie przekracza b, to znaczy (spotkaliśmy się z podobnymi łańcuchami nierówności, gdy mówiliśmy o porównywaniu trzech lub więcej liczb całkowitych).
Jeżeli liczba c jest ilorazem częściowym, a liczba d jest pozostałością z dzielenia liczby a przez liczbę b, to krótko napiszemy ten fakt jako równość postaci a:b=c (pozostaje d) .
Zauważ, że gdy liczba całkowita a jest podzielona przez liczbę całkowitą b, reszta może wynosić zero. W tym przypadku mówimy, że a jest podzielne przez b bez śladu(lub całkowicie). Zatem dzielenie liczb całkowitych bez reszty jest szczególnym przypadkiem dzielenia liczb całkowitych przez resztę.
Warto również powiedzieć, że dzieląc zero przez jakąś liczbę całkowitą, zawsze mamy do czynienia z dzieleniem bez reszty, ponieważ w tym przypadku iloraz będzie równy zero (patrz rozdział dotyczący teorii dzielenia zera przez liczbę całkowitą), a reszta również będzie równa zeru.
Zdecydowaliśmy się na terminologię i notację, teraz zastanówmy się nad znaczeniem dzielenia liczb całkowitych przez resztę.
Sensowne może być również dzielenie ujemnej liczby całkowitej a przez dodatnią liczbę całkowitą b. Aby to zrobić, rozważ ujemną liczbę całkowitą jako dług. Wyobraźmy sobie taką sytuację. Dług składający się na pozycje musi spłacić b osób, wnosząc ten sam wkład. Wartość bezwzględna niepełnego ilorazu c w tym przypadku określi wysokość zadłużenia każdej z tych osób, a reszta d wskaże, ile pozycji pozostanie po spłaceniu długu. Weźmy przykład. Powiedzmy, że 2 osoby są winne 7 jabłek. Jeśli przyjmiemy, że każdy z nich jest winien 4 jabłka, to po spłaceniu długu pozostanie mu 1 jabłko. Ta sytuacja odpowiada równości (−7):2=−4 (pozostałe 1).
Dzieląc resztę dowolnej liczby całkowitej a przez liczbę całkowitą ujemną, nie będziemy przywiązywać żadnego znaczenia, ale pozostawimy jej prawo do istnienia.
Twierdzenie o podzielności dla liczb całkowitych z resztą
Kiedy mówiliśmy o dzieleniu liczb naturalnych przez resztę, okazało się, że dzielna a, dzielnik b, iloraz cząstkowy ci reszta d są powiązane równością a=b c+d. Liczby całkowite a , b , c i d mają tę samą relację. To połączenie jest potwierdzone przez: twierdzenie o podzielności z resztą.
Twierdzenie.
Każda liczba całkowita a może być reprezentowana w unikalny sposób przez liczbę całkowitą i niezerową b w postaci a=b q+r , gdzie q i r są liczbami całkowitymi, oraz .
Dowód.
Wykażmy najpierw możliwość reprezentowania a=b·q+r .
Jeśli liczby całkowite a i b są takie, że a jest równo podzielne przez b, to z definicji istnieje liczba całkowita q taka, że a=b q . W tym przypadku równość a=b q+r obowiązuje dla r=0 .
Teraz założymy, że b jest dodatnią liczbą całkowitą. Liczbę całkowitą q wybieramy w taki sposób, aby iloczyn b·q nie przekraczał liczby a , a iloczyn b·(q+1) jest już większy niż a . Oznacza to, że bierzemy q takie, że nierówności b q Pozostaje udowodnić możliwość przedstawienia a=b q+r dla ujemnego b . Ponieważ moduł liczby b w tym przypadku jest liczbą dodatnią, istnieje reprezentacja dla , gdzie q 1 jest liczbą całkowitą, a r jest liczbą całkowitą spełniającą warunki . Następnie, zakładając q=−q 1 , otrzymujemy wymaganą reprezentację a=b q+r dla ujemnego b . Zwracamy się do dowodu wyjątkowości. Załóżmy, że oprócz reprezentacji a=b q+r, qir są liczbami całkowitymi i , istnieje jeszcze inna reprezentacja a=b q 1 +r 1 , gdzie q 1 ir 1 są liczbami całkowitymi, a q 1 ≠ q i . Po odjęciu od lewej i prawej części pierwszej równości odpowiednio lewej i prawej części drugiej równości, otrzymujemy 0=b (q−q 1)+r−r 1 , co jest równoważne równości r− r 1 = b (q 1 − q) . Wtedy równość formy Z warunków możemy wywnioskować, że . Ponieważ q i q 1 są liczbami całkowitymi i q≠q 1 , to , skąd wnioskujemy, że Równość a=b c+d pozwala znaleźć nieznaną dzielną a, jeśli dzielnik b, iloraz cząstkowy c i reszta d są znane. Rozważ przykład. Przykład. Ile wynosi dywidenda, jeśli jej dzielenie przez liczbę całkowitą −21 daje niepełny iloraz równy 5 i resztę 12? Rozwiązanie. Musimy obliczyć dzielną a, gdy znamy dzielnik b=−21 , iloraz cząstkowy c=5 i resztę d=12 . Przechodząc do równości a=b c+d , otrzymujemy a=(−21) 5+12 . Obserwując , najpierw mnożymy liczby całkowite −21 i 5 zgodnie z zasadą mnożenia liczb całkowitych o różnych znakach , po czym dokonujemy dodawania liczb całkowitych o różnych znakach : (−21) 5+12=−105+12 =−93 . Odpowiedź: −93
.
Zależności między dzielną, dzielnikiem, ilorazem częściowym i resztą są również wyrażone równościami postaci b=(a−d):c , c=(a−d):bi d=a−b·c . Te równości pozwalają nam obliczyć odpowiednio dzielnik, iloraz cząstkowy i resztę. Często musimy znaleźć resztę z dzielenia liczby całkowitej a przez liczbę całkowitą b, gdy znana jest dzielna, dzielnik i iloraz częściowy, korzystając ze wzoru d=a−b•c . Aby uniknąć dalszych pytań, przeanalizujemy przykład obliczenia reszty. Przykład. Znajdź resztę z dzielenia liczby całkowitej -19 przez liczbę całkowitą 3, jeśli wiadomo, że iloraz częściowy wynosi -7. Rozwiązanie. Aby obliczyć resztę z dzielenia, używamy wzoru w postaci d=a−b·c . Z warunku mamy wszystkie potrzebne dane a=−19 , b=3 , c=−7 . Otrzymujemy d=a−bc=−19−3 (−7)= −19−(−21)=−19+21=2 (różnica −19−(−21) obliczyliśmy według zasady odejmowania liczba całkowita ). Odpowiedź: Jak już wielokrotnie zauważyliśmy, liczby całkowite dodatnie są liczbami naturalnymi. Dlatego dzielenie z resztą liczb całkowitych dodatnich odbywa się zgodnie ze wszystkimi zasadami dzielenia z resztą liczb naturalnych. Bardzo ważne jest, aby móc łatwo przeprowadzić dzielenie z resztą liczb naturalnych, ponieważ to on jest podstawą dzielenia nie tylko dodatnich liczb całkowitych, ale także podstawą wszystkich reguł dzielenia z resztą dowolnych liczb całkowitych. Z naszego punktu widzenia najwygodniej jest przeprowadzić dzielenie według kolumny, ta metoda pozwala uzyskać zarówno niepełny iloraz (lub tylko iloraz) jak i resztę. Rozważ przykład dzielenia z resztą dodatnich liczb całkowitych. Przykład. Wykonaj dzielenie z resztą 14671 przez 54 . Rozwiązanie. Przeprowadźmy dzielenie tych dodatnich liczb całkowitych przez kolumnę: Niepełny iloraz okazał się równy 271, a reszta to 37. Odpowiedź: 14 671:54=271 (odpoczynek 37). Sformułujmy regułę, która pozwala wykonać dzielenie z resztą dodatniej liczby całkowitej przez ujemną liczbę całkowitą. Iloraz cząstkowy z dzielenia dodatniej liczby całkowitej a przez ujemną liczbę całkowitą b jest przeciwieństwem ilorazu cząstkowego z dzielenia a przez moduł b, a pozostała część z dzielenia a przez b jest pozostałością z dzielenia przez . Z tej reguły wynika, że niepełny iloraz dzielenia dodatniej liczby całkowitej przez ujemną liczbę całkowitą jest liczbą całkowitą niedodatnią. Przekształćmy dźwięczną regułę w algorytm dzielenia z resztą dodatniej liczby całkowitej przez ujemną liczbę całkowitą: Podajmy przykład użycia algorytmu dzielenia dodatniej liczby całkowitej przez ujemną liczbę całkowitą. Przykład. Podziel z resztą dodatniej liczby całkowitej 17 przez ujemną liczbę całkowitą -5 . Rozwiązanie. Użyjmy algorytmu dzielenia z resztą dodatniej liczby całkowitej przez ujemną liczbę całkowitą. Działowy Odwrotna liczba 3 to -3. Zatem wymagany iloraz cząstkowy dzielenia 17 przez -5 wynosi -3, a reszta to 2. Odpowiedź: 17 :(-5)=-3 (reszta 2). Przykład. Dzielić 45 na -15 . Rozwiązanie. Moduły dywidendy i dzielnika wynoszą odpowiednio 45 i 15. Liczba 45 jest podzielna przez 15 bez reszty, a iloraz wynosi 3. Zatem dodatnia liczba całkowita 45 jest podzielna przez ujemną liczbę całkowitą -15 bez reszty, podczas gdy iloraz jest równy liczbie przeciwnej do 3, czyli -3. Rzeczywiście, zgodnie z zasadą dzielenia liczb całkowitych o różnych znakach, mamy . Odpowiedź: 45:(−15)=−3
.
Sformułujmy zasadę dzielenia z resztą ujemnej liczby całkowitej przez dodatnią liczbę całkowitą. Aby otrzymać niepełny iloraz c z dzielenia ujemnej liczby całkowitej a przez dodatnią liczbę całkowitą b, należy wziąć liczbę przeciwną do niepełnego ilorazu z dzielenia modułów liczb pierwotnych i odjąć od niej jeden, po czym obliczana jest reszta d używając wzoru d=a−bc . Z tej zasady dzielenia z resztą wynika, że niepełny iloraz dzielenia ujemnej liczby całkowitej przez dodatnią jest liczbą całkowitą ujemną. Z dźwięcznej reguły wynika algorytm dzielenia z resztą ujemnej liczby całkowitej a przez dodatnią liczbę całkowitą b: Przeanalizujmy rozwiązanie przykładu, w którym korzystamy z zapisanego algorytmu dzielenia z resztą. Przykład. Znajdź iloraz cząstkowy i resztę ujemnej liczby całkowitej −17 podzielonej przez dodatnią liczbę całkowitą 5 . Rozwiązanie. Moduł dzielnej -17 wynosi 17, a moduł dzielnika 5 wynosi 5. Działowy 17 na 5 , otrzymujemy niepełny iloraz 3 i resztę 2 . Przeciwieństwem 3 jest -3 . Odejmij jeden od -3: -3−1=−4 . Zatem pożądanym ilorazem niepełnym jest -4. Pozostaje obliczyć resztę. W naszym przykładzie a=−17 , b=5 , c=−4 , następnie d=a−b c=−17−5 (−4)= −17−(−20)=−17+20=3 . Zatem częściowy iloraz ujemnej liczby całkowitej -17 podzielony przez dodatnią liczbę całkowitą 5 wynosi -4, a reszta wynosi 3. Odpowiedź: (-17):5=-4 (odpoczynek 3) . Przykład. Podziel ujemną liczbę -1 404 przez dodatnią liczbę 26 . Rozwiązanie. Moduł dywidendy to 1404, moduł dzielnika to 26. Podziel 1404 przez 26 w kolumnie: Ponieważ moduł dywidendy został podzielony przez moduł dzielnika bez reszty, pierwotne liczby całkowite są dzielone bez reszty, a pożądany iloraz jest równy liczbie przeciwnej do 54, czyli -54. Odpowiedź: (−1 404):26=−54
.
Sformułujmy regułę dzielenia z resztą ujemnych liczb całkowitych. Aby otrzymać niepełny iloraz c z dzielenia ujemnej liczby całkowitej a przez ujemną liczbę całkowitą b, należy obliczyć niepełny iloraz z dzielenia modułów liczb pierwotnych i dodać do niego jeden, a następnie obliczyć resztę d ze wzoru d =a-bc . Z tej reguły wynika, że niepełny iloraz dzielenia liczb całkowitych ujemnych jest liczbą całkowitą dodatnią. Przepiszmy regułę dźwięczną w postaci algorytmu dzielenia liczb całkowitych ujemnych: Rozważ zastosowanie algorytmu dzielenia ujemnych liczb całkowitych podczas rozwiązywania przykładu. Przykład. Znajdź iloraz cząstkowy i resztę ujemnej liczby całkowitej -17 podzielonej przez ujemną liczbę całkowitą -5. Rozwiązanie. Używamy odpowiedniego algorytmu dzielenia z resztą. Moduł dywidendy wynosi 17 , moduł dzielnika wynosi 5 . Podział 17 razy 5 daje niepełny iloraz 3, a reszta 2. Do niepełnego ilorazu 3 dodajemy jeden: 3+1=4. Dlatego pożądany niepełny iloraz dzielenia -17 przez -5 wynosi 4. Pozostaje obliczyć resztę. W tym przykładzie a=−17 , b=−5 , c=4 , następnie d=a−b c=−17−(−5) 4= −17−(−20)=−17+20=3 . Tak więc iloraz częściowy ujemnej liczby całkowitej −17 podzielony przez ujemną liczbę całkowitą −5 wynosi 4 , a reszta to 3 . Odpowiedź: (-17):(-5)=4 (reszta 3). Po wykonaniu dzielenia liczb całkowitych przez resztę warto sprawdzić wynik. Weryfikacja odbywa się w dwóch etapach. W pierwszym etapie sprawdzane jest, czy reszta d jest liczbą nieujemną, a także sprawdzany jest warunek. Jeśli wszystkie warunki pierwszego etapu weryfikacji są spełnione, można przejść do drugiego etapu weryfikacji, w przeciwnym razie można argumentować, że gdzieś popełniono błąd podczas dzielenia z resztą. W drugim etapie sprawdzana jest poprawność równości a=b·c+d. Jeśli ta równość jest prawdziwa, to dzielenie z resztą zostało wykonane poprawnie, w przeciwnym razie gdzieś popełniono błąd. Rozważmy rozwiązania przykładów, w których sprawdzany jest wynik dzielenia liczb całkowitych z resztą. Przykład. Dzieląc liczbę -521 przez -12, iloraz cząstkowy wynosił 44, a reszta 7 , sprawdź wynik. Rozwiązanie. -2 dla b=-3 , c=7 , d=1 . Mamy b c+d=−3 7+1=−21+1=−20. Zatem równość a=b c+d jest niepoprawna (w naszym przykładzie a=−19 ). Dlatego podział z resztą został przeprowadzony niepoprawnie. Wielu liczb nie można całkowicie podzielić, podczas dzielenia często pozostaje reszta różna od zera. W tym artykule przeanalizujemy sposoby dzielenia liczb naturalnych przez resztę i szczegółowo rozważymy ich zastosowanie na przykładach. Zacznijmy od dzielenia liczb naturalnych z resztą w kolumnie, potem rozważymy dzielenie przy użyciu kolejnego odejmowania. Na koniec kończymy analizą metody doboru niepełnego ilorazu. Przedstawiamy algorytm dzielenia z resztą dla najbardziej ogólnego przypadku i pokazujemy jak sprawdzić wynik dzielenia liczb naturalnych z resztą. To jeden z najwygodniejszych sposobów dzielenia. Zostało to szczegółowo opisane w osobnym artykule poświęconym dzieleniu liczb naturalnych przez kolumnę. Tutaj nie będziemy od nowa podawać całej teorii, ale skoncentrujemy się na przypadku dzielenia z resztą. Podamy przykładowe rozwiązanie, gdyż istotę metody najłatwiej zrozumieć w praktyce. Przykład 1. Jak podzielić liczby naturalne przez resztę? Podziel liczbę naturalną 273844 przez liczbę naturalną 97 . Dzielimy przez kolumnę i piszemy: Wynik: iloraz częściowy to 2823 , a reszta to 13 . Aby znaleźć niepełny iloraz i resztę, możesz uciec się do kolejnego odejmowania dzielnika od dywidendy. Ta metoda nie zawsze jest odpowiednia, ale w niektórych przypadkach jest bardzo wygodna w użyciu. Spójrzmy ponownie na przykład. Przykład 2. Dzielenie z resztą przez kolejne odejmowanie. Powiedzmy, że mamy 7 jabłek. Musimy włożyć te 7 jabłek do torebek po 3 jabłka. Innymi słowy, 7 podzielone przez 3 . Z początkowej ilości jabłek bierzemy 3 sztuki i wkładamy je do jednego opakowania. Pozostało nam 7 - 3 = 4 jabłka. Teraz z pozostałych jabłek ponownie zabieramy 3 kawałki i wkładamy je do innej torby. Pozostało 4 - 3 = 1 jabłko. 1 jabłko to pozostała część podziału, ponieważ na tym etapie nie możemy już uformować kolejnego opakowania z trzema jabłkami i podział jest właściwie zakończony. Wynik dywizji: 7 ÷ 3 = 2 (pozostałe 1) Oznacza to, że liczba 3 niejako pasuje do liczby 7 dwukrotnie, a jednostka to reszta mniejsza niż 3. Rozważmy jeszcze jeden przykład. Tym razem podamy tylko obliczenia matematyczne, bez uciekania się do analogii. Przykład 3. Dzielenie z resztą przez kolejne odejmowanie. Obliczmy: 145 ÷ 46 . Liczba 99 jest większa niż 46 , więc kontynuujemy odejmowanie sekwencyjne dzielnika: Powtarzamy tę operację jeszcze raz: W rezultacie musieliśmy 3 razy sukcesywnie odjąć dzielnik od dywidendy, zanim otrzymaliśmy resztę - wynik odejmowania, który jest mniejszy niż dzielnik. W naszym przypadku reszta to liczba 7. 145 ÷ 46 = 3 (pozostałe 7) . Metoda odejmowania sukcesywnego nie jest odpowiednia, gdy dywidenda jest mniejsza niż dzielnik. W takim przypadku możesz od razu zapisać odpowiedź: niepełny iloraz wynosi zero, a reszta jest równa największej podzielności. Jeśli< b , то a ÷ b = 0 (остаток a) . Na przykład: 12 ÷ 36 = 0 (pozostała 12) 47 ÷ 88 = 0 (pozostała 47) Również w odniesieniu do metody sukcesywnego odejmowania należy zauważyć, że jest ona wygodna tylko w przypadkach, gdy cała operacja dzielenia sprowadza się do niewielkiej liczby odejmowań. Jeżeli dzielna jest wielokrotnie większa niż dzielnik, to zastosowanie tej metody będzie niepraktyczne i będzie wymagało wielu kłopotliwych obliczeń. Dzieląc liczby naturalne przez resztę, możesz obliczyć wynik, wybierając iloraz niepełny. Pokażemy, jak można przeprowadzić proces selekcji i na czym się opiera. Najpierw określamy, wśród których liczb musimy szukać niepełnego ilorazu. Z samej definicji procesu dzielenia wynika, że niepełny iloraz jest równy zero lub jest jedną z liczb naturalnych 1, 2, 3 itd. Po drugie ustalimy relację między dzielnikiem, dywidendą, ilorazem częściowym i resztą. Rozważ równanie d = a - b c . Tutaj d to reszta z dzielenia, a to dzielna, b to dzielnik, c to iloraz cząstkowy. Po trzecie, nie zapominajmy, że reszta jest zawsze mniejsza niż dzielnik. Przyjrzyjmy się teraz procesowi selekcji. Dywidenda a i dzielnik b są nam znane od samego początku. Jako iloraz niepełny będziemy brać kolejno liczby z szeregu 0, 1, 2, 3 itd. Stosując wzór d = a - b c i obliczając wynikową wartość za pomocą dzielnika, kończymy proces, gdy reszta d jest mniejsza niż dzielnik b . Liczba przyjęta za c na tym etapie będzie niepełnym ilorazem. Przyjrzyjmy się zastosowaniu tej metody na przykładzie. Przykład 4. Dzielenie z resztą przez wybór Podziel 267 przez 21. a = 267 b = 21 . Wybierzmy iloraz niepełny. Użyjmy formuły d = a - b · c i wykonaj iterację przez c , nadając jej wartości 0 , 1 , 2 , 3 i tak dalej. Jeśli c \u003d 0, mamy: d \u003d a - b c \u003d 267 - 21 0 \u003d 267. Liczba 267 jest większa niż 21 , więc kontynuujemy zastępowanie. Z c \u003d 1 mamy: d \u003d a - b c \u003d 267 - 21 1 \u003d 246. Dlatego 246 > 21, powtórz proces jeszcze raz. Z c \u003d 2 mamy: d \u003d a - b c \u003d 267 - 21 2 \u003d 267 - 42 \u003d 225; 225 > 21 . Z c \u003d 3 mamy: d \u003d a - b c \u003d 267 - 21 3 \u003d 267 - 63 \u003d 204; 204 > 21 . Z c \u003d 12 mamy: d \u003d a - b c \u003d 267 - 21 12 \u003d 267 - 252 \u003d 15; 15< 21 . Gdy omówione powyżej metody ilorazu częściowego i kolejnych odejmowań wymagają zbyt uciążliwych obliczeń, do dzielenia z resztą stosuje się następującą metodę. Rozważ algorytm dzielenia liczby naturalnej a przez liczbę b z resztą. Przypomnij sobie, że jeśli< b, неполное частное равно нулю, а остаток равен делимомому a . Мы будем рассматривать случай, когда a >b. Formułujemy trzy pytania i odpowiadamy na nie: Początkowo znana jest dywidenda i dzielnik: a i b. Musisz znaleźć niepełny iloraz c i resztę d. Oto wzór, który definiuje relację między dzielną, dzielnikiem, ilorazem niepełnym i resztą. a = b c + d. To właśnie ten stosunek przyjmiemy za podstawę algorytmu dzielenia liczb naturalnych przez resztę. Dywidenda a musi być reprezentowana jako suma a = b c + d, wtedy znajdziemy wymagane wartości. Algorytm dzielenia, dzięki któremu reprezentujemy a jako sumę a = b c + d, jest bardzo podobny do algorytmu dzielenia liczb naturalnych bez reszty. Poniżej znajdują się kroki algorytmu na przykładzie dzielenia liczby 899 przez 47. 1. Przede wszystkim patrzymy na dywidendę i dzielnik. Dowiadujemy się i zapamiętujemy, o ile cyfr liczba we wpisie dywidendy jest większa niż liczba w dzielniku. W naszym konkretny przykład Dywidenda ma trzy cyfry, a dzielnik dwie. Zapamiętajmy ten numer. 2. Po prawej stronie we wpisie dzielnika dodaj liczbę zer określoną przez różnicę między liczbą znaków w dzielniku a dzielnikiem. W naszym przypadku musisz dodać jedno zero. Jeśli zapisana liczba jest większa niż podzielna, należy odjąć jeden od liczby zapamiętanej w pierwszym akapicie. W naszym przykładzie dodajemy zero na prawo od 47. Od 470< 899 , запомненное в предыдущем пункте число не нужно уменьшать на единицу. Таким образом, число 1 так и остается у нас в памяти. 3. Po prawej stronie do liczby 1 przypisujemy liczbę zer równą liczbie określonej w poprzednim akapicie. W naszym przykładzie przypisując jedno zero do jedynki, otrzymujemy liczbę 10. W wyniku tej akcji otrzymaliśmy działającą jednostkę absolutorium, z którą będziemy dalej pracować. 4. Kolejno pomnożymy dzielnik przez 1, 2, 3. . itp. jednostki cyfry roboczej, aż otrzymamy liczbę większą lub równą podzielności. Cyfra robocza w naszym przykładzie to dziesiątki. Po pomnożeniu dzielnika przez jedną jednostkę bitu roboczego otrzymujemy 470. 470 < 899 , поэтому умножаем на еще одну единицу рабочего разряда. Получаем: 47 · 20 = 940 ; 940 > 899 . Liczba, którą otrzymaliśmy w przedostatnim kroku (470 = 47 10) jest pierwszym z wymaganych wyrazów. 5. Znajdź różnicę między dywidendą a pierwszym znalezionym terminem. Jeśli wynikowa liczba jest większa niż dzielnik, przystępujemy do znalezienia drugiego wyrazu. Powtarzamy kroki 1 - 5, jednak otrzymaną tutaj liczbę bierzemy jako dywidendę. Jeśli znowu otrzymamy liczbę większą niż dzielnik, ponownie powtórz kroki 1 - 5 w kółku, ale z nową liczbą jako dzielną. Kontynuujemy, aż uzyskana tutaj liczba będzie mniejsza niż dzielnik. Przejdźmy do ostatniego etapu. Patrząc w przyszłość, powiedzmy, że ostatnia otrzymana liczba będzie równa reszcie. Spójrzmy na przykład. 899 - 470 = 429, 429 > 47. Powtarzamy kroki 1 - 5 algorytmu z liczbą 429 jako dywidendą. 1. We wpisie z numerem 429 jest o jeden znak więcej niż we wpisie z numerem 47. Pamiętamy różnicę - numer 1. 2. W zapisie dywidendy po prawej stronie dodajemy jedno zero. Otrzymujemy numer 470. Ponieważ 470 > 429, odejmij 1 od liczby 1 zapamiętanej w poprzednim akapicie i uzyskaj 1 - 1 = 0. Pamiętamy 0 . 3. Ponieważ w poprzednim akapicie otrzymaliśmy liczbę 0 i zapamiętaliśmy ją, nie musimy dodawać żadnego zera do jednej po prawej stronie. Tak więc cyfra robocza to jednostki 4. Kolejno pomnóż dzielnik 47 przez 1 , 2 , 3 . . itp. Nie będziemy podawać szczegółowych obliczeń, ale zwrócimy uwagę na wynik końcowy: 47 9 = 423< 429 , 47 · 10 = 470 >429 . Zatem drugi wymagany termin to 47 9 = 423. 5. Różnica między 429 a 423 jest równa liczbie 6 . Od 6< 47 , это третье, и последнее искомое слагаемое. Перейдем к завершающему этапу алгоритма деления столбиком. 6. Celem poprzednich kroków było przedstawienie dywidendy jako sumy kilku terminów. W naszym przykładzie otrzymaliśmy 899 = 470 + 423 + 6 . Przypomnijmy, że 470 = 47 10 , 423 = 47 9 . Przepiszmy równanie: 899 = 47 10 + 47 9 + 6 Zastosuj rozdzielność mnożenia. 899 = 47 10 + 47 9 + 6 = 47 (10 + 9) + 6 899 = 47 19 + 6 . W ten sposób przedstawiliśmy dywidendę w postaci wcześniej podanej formuły a \u003d b c + d. Wymagane niewiadome: niepełny iloraz c \u003d 19, reszta d \u003d 6. Oczywiście przy rozwiązywaniu praktycznych przykładów nie ma potrzeby tak szczegółowego opisywania wszystkich działań. Pokażmy to: Przykład 5. Dzielenie liczb naturalnych przez resztę Podziel liczby 42252 i 68. Użyjmy algorytmu. Pierwsze pięć kroków daje pierwszy wyraz - liczba 40800 = 68 600 . Powtarzamy pierwsze pięć kroków algorytmu ponownie z liczbą 1452 = 42252 - 40800 i otrzymujemy drugi wyraz 1360 = 68 20 Za trzecim razem przechodzimy przez stopnie aglorytmu, ale z nową liczbą 92 = 1452 - 1360. Trzeci wyraz jest równy 68 = 68 1 . Reszta to 24 = 92 - 68. W rezultacie otrzymujemy: 42252 = 40800 + 1360 + 68 + 24 = 68 600 + 68 20 + 68 1 + 24 = = 68 (600 + 20 + 1) + 24 = 68 621 + 24 Niepełny iloraz to 621, reszta to 24. Dzielenie liczb naturalnych przez resztę, zwłaszcza gdy duże liczby, dość pracochłonny i kłopotliwy proces. Każdy może popełnić błąd w obliczeniach. Dlatego sprawdzenie wyniku dzielenia pomoże ci zrozumieć, czy zrobiłeś wszystko dobrze. Sprawdzanie wyniku dzielenia liczb naturalnych przez resztę odbywa się w dwóch etapach. W pierwszym etapie sprawdzamy, czy reszta jest większa od dzielnika. Jeśli nie, to wszystko jest w porządku. W przeciwnym razie możemy stwierdzić, że coś poszło nie tak. Ważny! Reszta jest zawsze mniejsza niż dzielnik! W drugim etapie sprawdzana jest poprawność równości a = b · c + d. Jeżeli równość po podstawieniu wartości okaże się prawdziwa, to podział został wykonany bez błędów. Przykład 6. Sprawdzanie wyniku dzielenia liczb naturalnych przez resztę. Sprawdźmy, czy to prawda, że 506 ÷ 28 = 17 (reszta 30) . Porównaj resztę i dzielnik: 30 > 28 . Więc podział jest zły. Przykład 7. Sprawdzanie wyniku dzielenia liczb naturalnych przez resztę. Uczeń podzielił 121 przez 13 iw rezultacie otrzymał niepełny iloraz 9 z resztą 5. Czy postąpił właściwie? Aby się tego dowiedzieć, najpierw porównujemy resztę i dzielnik: 5< 13 . Minął pierwszy punkt kontrolny, przejdźmy do drugiego. Zapiszmy wzór a = b c + d. a = 121 ; b = 13; c = 9 d = 5 . Zastąp wartości i porównaj wyniki 13 9 + 5 = 117 + 5 = 122; 121 ≠ 122 Oznacza to, że gdzieś w obliczeniach ucznia wkradł się błąd. Przykład 8. Sprawdzanie wyniku dzielenia liczb naturalnych przez resztę. Uczeń wystąpił Praca laboratoryjna w fizyce. Podczas egzekucji musiał podzielić 5998 na 111 . W rezultacie otrzymał numer 54 z resztą 4. Czy wszystko jest poprawnie obliczone? Sprawdźmy! Reszta 4 jest mniejsza niż dzielnik 111 , więc przechodzimy do drugiego etapu sprawdzania. Używamy wzoru a \u003d b c + d, gdzie a \u003d 5998; b = 111; c = 54 ; d = 4 . Po podstawieniu mamy: 5998 = 111 54 + 4 = 5994 + 4 = 5998 . Równość jest poprawna, co oznacza, że podział jest poprawny. Jeśli zauważysz błąd w tekście, zaznacz go i naciśnij Ctrl+Enter Łatwo jest nauczyć dziecko dzielić kolumną. Konieczne jest wyjaśnienie algorytmu tego działania i utrwalenie omawianego materiału. Ważne: Aby dziecko rozumiało dzielenie liczb, musi dokładnie znać tabliczkę mnożenia. Jeśli dzieciak nie zna dobrze mnożenia, nie zrozumie dzielenia. Na domowych zajęciach dodatkowych można korzystać ze ściągawek, ale przed przystąpieniem do tematu „Podział” dziecko musi nauczyć się tabliczki mnożenia. Więc jak wytłumaczysz dziecku? podział kolumn: Dzielenie zawsze jest nieco trudniejsze niż mnożenie. Ale pracowity dodatkowe zajęcia w domu pomogą dziecku zrozumieć algorytm tego działania i nadążyć za rówieśnikami w szkole. Zacznij prosto - dzielenie przez jedną cyfrę: Ważne: Oblicz w swoim umyśle, aby podział przebiegł bez reszty, w przeciwnym razie dziecko może się pomylić. Na przykład 256 podzielone przez 4: Kiedy dziecko opanuje dzielenie przez jedną liczbę, możesz przejść dalej. Pisemny podział według liczby dwucyfrowej jest nieco bardziej skomplikowany, ale jeśli dziecko zrozumie, jak wykonuje się tę czynność, nie będzie mu trudno rozwiązać takie przykłady. Ważne: Ponownie zacznij wyjaśniać od prostych kroków. Dziecko nauczy się poprawnie dobierać liczby i łatwo będzie mu dzielić liczby zespolone. Wykonajcie razem tę prostą czynność: 184:23 - jak to wytłumaczyć: Ważne: Aby dziecko zrozumiało, spróbuj wziąć 9 zamiast ośmiu, niech pomnoży 9 przez 23, okazuje się, że 207 - to więcej niż mamy w dzielniku. Liczba 9 nam nie odpowiada. Tak więc stopniowo dziecko zrozumie podział i będzie mu łatwo dzielić bardziej złożone liczby: Jeśli dziecko nauczyło się dzielić przez liczbę dwucyfrową, musisz przejść do następnego tematu. Algorytm dzielenia przez liczbę trzycyfrową jest taki sam, jak algorytm dzielenia przez liczbę dwucyfrową. Na przykład: Ważne: Aby sprawdzić poprawność podziału, pomnóż razem z dzieckiem w kolumnie - 204x716 = 146064. Podział jest prawidłowy. Czas, aby dziecko wyjaśniło, że podział może być nie tylko całością, ale także resztą. Reszta jest zawsze mniejsza lub równa dzielnikowi. Dzielenie z resztą należy wyjaśnić na prostym przykładzie: 35:8=4 (reszta 3): Następnie dziecko powinno się nauczyć, że możesz kontynuować dzielenie, dodając 0 do liczby 3: Wskazówka: Jeśli dziecko czegoś nie rozumie, nie gniewaj się. Poczekaj kilka dni i spróbuj ponownie wyjaśnić materiał. Lekcje matematyki w szkole również wzmocnią wiedzę. Czas minie a dzieciak szybko i łatwo rozwiąże wszelkie przykłady dzielenia. Algorytm dzielenia liczb jest następujący: Zgodnie z tym algorytmem dzielenie odbywa się zarówno według liczb jednocyfrowych, jak i dowolnych liczb wielocyfrowych (dwucyfrowych, trzycyfrowych, czterocyfrowych itd.). Ucząc się z dzieckiem, często pytaj go o przykłady do oszacowania. Musi szybko obliczyć odpowiedź w swoim umyśle. Na przykład: Aby skonsolidować wynik, możesz skorzystać z następujących gier dywizji: Warunek dla dziecka: Spośród kilku przykładów tylko jeden jest rozwiązany poprawnie. Znajdź go za minutę.
Gdy dziecko uczy się dodatkowo w domu, utrwala materiał objęty w szkole. Dzięki temu łatwiej mu się uczyć i nie zostanie w tyle za rówieśnikami. Dlatego pomóżcie swoim dzieciom, uczcie się z nimi w domu. a dziecko odniesie sukces!
Przeczytaj temat lekcji: „Podział z resztą”. Co już wiesz na ten temat? Czy można równo podzielić 8 śliwek na dwa talerze (rys. 1)? Ryż. 1. Ilustracja na przykład Na każdy talerz można umieścić 4 śliwki (rys. 2). Ryż. 2. Ilustracja na przykład Czynność, którą wykonaliśmy, można zapisać w następujący sposób. 8: 2 = 4
Jak myślisz, czy można równo podzielić 8 śliwek na 3 talerze (ryc. 3)? Ryż. 3. Ilustracja na przykład Zachowujmy się tak. Najpierw na każdy talerz włóż jedną śliwkę, a następnie drugą śliwkę. Pozostaną nam 2 śliwki, ale 3 talerze. Więc nie możemy tego podzielić równo. Do każdego talerza wkładamy 2 śliwki i zostają nam 2 śliwki (rys. 4). Ryż. 4. Ilustracja na przykład Kontynuujmy monitorowanie. Przeczytaj liczby. Wśród podanych liczb znajdź te, które są podzielne przez 3. 11, 12, 13, 14, 15, 16, 17, 18, 19
Sprawdź się. Pozostałe liczby (11, 13, 14, 16, 17, 19) nie są podzielne przez 3 lub mówią „Podziel z resztą”. Znajdźmy wartość prywatnego. Dowiedzmy się, ile razy 3 zawiera się w liczbie 17 (ryc. 5). Ryż. 5. Ilustracja na przykład Widzimy, że 3 owale pasują 5 razy i pozostały 2 owale. Podjęte działanie można zapisać w następujący sposób. 17: 3 = 5 (odpoczynek 2) Można go również zapisać w kolumnie (ryc. 6) Ryż. 6. Ilustracja na przykład Przejrzyj rysunki. Wyjaśnij podpisy pod tymi rysunkami (rys. 7). Ryż. 7. Ilustracja na przykład Rozważ pierwszy rysunek (ryc. 8). Ryż. 8. Ilustracja na przykład Widzimy, że 15 owali podzielono przez 2,2. 2 powtórzono 7 razy, w pozostałych - 1 owal. Rozważ drugą figurę (ryc. 9). Ryż. 9. Ilustracja na przykład Na tej figurze 15 kwadratów podzielono przez 4, 4 powtórzono 3 razy, w pozostałych - 3 kwadraty. Rozważ trzeci rysunek (ryc. 10). Ryż. 10. Ilustracja na przykład Można powiedzieć, że 15 owali podzielono na 3,3 powtórzone 5 razy po równo. W takich przypadkach mówi się, że reszta wynosi 0. Zróbmy podział. Dzielimy siedem kwadratów na trzy. Dostajemy dwie grupy i pozostaje jeden kwadrat. Zapiszmy rozwiązanie (ryc. 11). Ryż. 11. Ilustracja na przykład Zróbmy podział. Dowiadujemy się, ile razy cztery zawiera się w liczbie 10. Widzimy, że w liczbie 10 cztery zawiera się 2 razy i pozostają 2 kwadraty. Zapiszmy rozwiązanie (ryc. 12). Ryż. 12. Ilustracja na przykład Zróbmy podział. Dowiadujemy się, ile razy dwa są zawarte w liczbie 11. Widzimy, że w liczbie 11 dwa są zawarte 5 razy i pozostaje 1 kwadrat. Zapiszmy rozwiązanie (ryc. 13). Ryż. 13. Ilustracja na przykład Zróbmy wniosek. Dzielenie przez resztę oznacza sprawdzenie, ile razy dzielnik jest zawarty w dzielnej i ile jednostek pozostało. Dzielenie z resztą można również wykonać na osi liczbowej. Na osi liczbowej zaznaczamy odcinki 3 dywizji i zobaczymy, że trzy dywizje okazały się trzykrotne i pozostała jedna dywizja (ryc. 14). Ryż. 14. Ilustracja na przykład Zapiszmy rozwiązanie. 10: 3 = 3 (odpoczynek.1) Zróbmy podział. Na belce numerycznej zaznaczamy odcinki 3 podziałów i zobaczymy, że trzy podziały okazały się trzykrotne i pozostały dwa podziały (rys. 15). Ryż. 15. Ilustracja na przykład Zapiszmy rozwiązanie. 11: 3 = 3 (odpoczynek.2) Zróbmy podział. Na promieniu liczbowym zaznaczamy odcinki 3 podziałów i zobaczymy, że otrzymaliśmy dokładnie 4 razy, nie ma reszty (ryc. 16). Ryż. 16. Ilustracja na przykład Zapiszmy rozwiązanie. 12: 3 = 4
Dzisiaj na lekcji zapoznaliśmy się z dzieleniem z resztą, nauczyliśmy się wykonywać nazwaną akcję za pomocą obrazka i belki liczbowej, przećwiczyliśmy rozwiązywanie przykładów na temat lekcji. Bibliografia Praca domowa 1. Zapisz liczby podzielne przez 2 bez reszty. 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12, 13, 14, 15, 16, 17, 18, 19 2. Wykonaj dzielenie z resztą za pomocą rysunku. 3. Dokonaj dzielenia z resztą za pomocą osi liczbowej. 4. Zrób zadanie swoim towarzyszom na temat lekcji.![]() , a ze względu na właściwości modułu liczby - i równości
, a ze względu na właściwości modułu liczby - i równości ![]() .
.
![]() . Z uzyskanych nierówności i
. Z uzyskanych nierówności i ![]() wynika z tego, że równość formy
wynika z tego, że równość formy ![]() niemożliwe w naszym założeniu. Dlatego nie ma innej reprezentacji liczby a , z wyjątkiem a=b·q+r .
niemożliwe w naszym założeniu. Dlatego nie ma innej reprezentacji liczby a , z wyjątkiem a=b·q+r .Relacje między dywidendą, dzielnikiem, ilorazem częściowym i resztą
Dzielenie z resztą liczb całkowitych dodatnich, przykłady

Zasada dzielenia z resztą dodatniej liczby całkowitej przez ujemną liczbę całkowitą, przykłady
Dzielenie z resztą ujemnej liczby całkowitej przez dodatnią liczbę całkowitą, przykłady

Reguła dzielenia z resztą ujemnych liczb całkowitych, przykłady
Sprawdzanie wyniku dzielenia liczb całkowitych przez resztę
Dzielenie liczb z resztą przez kolejne odejmowanie
Metoda wyboru niepełnego ilorazu
Algorytm dzielenia liczb naturalnych przez resztę
Podział liczb naturalnych przez resztę. Sprawdzanie wyniku




Pisemny dzielenie przez dwie cyfry










Wideo: Gra arytmetyczna dla dzieci dodawanie odejmowanie dzielenie mnożenie
Wideo: kreskówka edukacyjna Matematyka Nauka na pamięć tabliczki mnożenia i dzielenia przez 2
Wideo: Wprowadzenie do podziału | Zabawna MATEMATYKA dla dzieci
Wideo: Dzielenie liczby dwucyfrowej przez jedną
Wideo: Długi podział, część 1
Wideo: Długi podział, część 2
Wideo: Długi podział, część 3
Wideo: Długi podział, część 4
Wideo: Długi podział, część 5