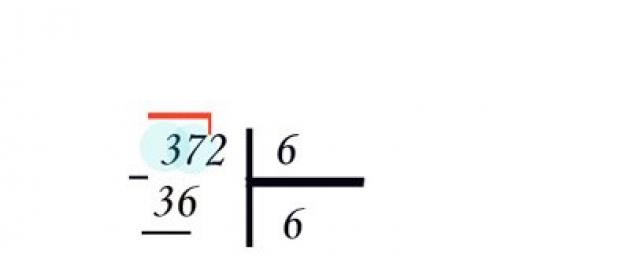Instrucción

Primero, pruebe las habilidades de multiplicación de su hijo. Si un niño no conoce bien la tabla de multiplicar, entonces también puede tener problemas con la división. Luego, al explicar la división, se le puede permitir echar un vistazo a la hoja de trucos, pero aún tiene que aprenderse la tabla.

Escribe el dividendo y el divisor a través de la barra vertical de separación. Debajo del divisor, escribirá la respuesta: el cociente, separándolo con una línea horizontal. Tome el primer dígito de 372 y pregúntele a su hijo cuántas veces el número seis "encaja" en un tres. Así es, en absoluto.

Luego, tome dos números: 37. Para mayor claridad, puede resaltarlos con una esquina. Repita la pregunta nuevamente: cuántas veces el número seis está contenido en 37. Para contar rápidamente, será útil. Elija la respuesta juntos: 6 * 4 = 24 - nada similar; 6*5 = 30 - cerca de 37. Pero 37-30 = 7 - seis "encajarán" de nuevo. Finalmente, 6*6 = 36, 37-36 = 1 está bien. El primer cociente encontrado es 6. Escríbelo debajo del divisor.

Escribe 36 debajo del número 37, dibuja una línea. Para mayor claridad, el signo se puede utilizar en el registro. Coloque el resto debajo de la línea: 1. Ahora "baje" el siguiente dígito del número, dos, a uno: resultó 12. Explíquele al niño que los números siempre "bajan" uno a la vez. Vuelva a preguntar cuántos "seises" hay en 12. La respuesta es 2, esta vez sin dejar rastro. Escribe el segundo número privado al lado del primero. La puntuación final es 62.

Considere también el caso de la división en detalle. Por ejemplo, 167/6 \u003d 27, el resto es 5. Lo más probable es que su descendencia aún no haya escuchado nada sobre fracciones simples. Pero si pregunta qué hacer con el resto, se puede explicar con el ejemplo de las manzanas. Se repartieron 167 manzanas entre seis personas. Cada uno recibió 27 piezas y quedaron cinco manzanas sin dividir. También puede dividirlos cortando cada uno en seis rebanadas y distribuyéndolos por igual. Cada persona recibió una rebanada de cada manzana: 1/6. Y como había cinco manzanas, cada una tenía cinco rebanadas: 5/6. Es decir, el resultado se puede escribir de la siguiente manera: 27 5/6.

En este artículo analizaremos división de enteros con resto. Empecemos con principio general división de enteros con resto, formulamos y demostramos un teorema sobre la divisibilidad de enteros con resto, trazamos las conexiones entre el dividendo, el divisor, el cociente incompleto y el resto. A continuación, anunciaremos las reglas por las cuales se realiza la división de números enteros con resto, y consideraremos la aplicación de estas reglas al resolver ejemplos. Después de eso, aprenderemos cómo verificar el resultado de dividir números enteros con un resto.

Navegación de página.

Idea general de división de enteros con resto

La división de números enteros con resto la consideraremos como una generalización de la división con resto de números naturales. Esto se debe a que los números naturales son parte integral números enteros

Comencemos con los términos y la notación que se utilizan en la descripción.

Por analogía con la división de números naturales con resto, suponemos que el resultado de la división con resto de dos enteros a y b (b no es igual a cero) es dos enteros c y d. Los números a y b se llaman divisible Y divisor respectivamente, el número d es recordatorio de dividir a por b, y el entero c se llama privado incompleto(o simplemente privado si el resto es cero).

Acordemos que el resto es un entero no negativo, y su valor no excede b, es decir, (nos encontramos con cadenas de desigualdades similares cuando hablamos de comparar tres o más enteros).

Si el número c es un cociente parcial, y el número d es el resto de dividir un entero a por un entero b, entonces escribiremos brevemente este hecho como una igualdad de la forma a:b=c (resto d) .

Tenga en cuenta que cuando un entero a se divide por un entero b, el resto puede ser cero. En este caso, decimos que a es divisible por b sin dejar rastro(o completamente). Así, la división de enteros sin resto es un caso especial de división de enteros con resto.

También vale la pena decir que al dividir cero por algún número entero, siempre se trata de una división sin resto, ya que en este caso el cociente será igual a cero (ver la sección sobre la teoría de la división de cero por un número entero), y el resto también será igual a cero.

Hemos decidido la terminología y la notación, ahora averigüemos el significado de dividir números enteros con un resto.

Dividir un entero negativo a por un entero positivo b también puede tener sentido. Para hacer esto, considere un número entero negativo como una deuda. Imaginemos una situación así. La deuda que conforma las partidas debe ser reembolsada por b personas, realizando la misma aportación. El valor absoluto del cociente incompleto c en este caso determinará el monto de la deuda de cada una de estas personas, y el resto d mostrará cuántos artículos quedarán después de pagar la deuda. Tomemos un ejemplo. Digamos que 2 personas deben 7 manzanas. Si asumimos que cada uno debe 4 manzanas, luego de pagar la deuda les quedará 1 manzana. Esta situación corresponde a la igualdad (−7):2=−4 (1 restante) .

División con resto de un entero arbitrario a por un entero negativo, no le daremos ningún significado, pero le dejaremos el derecho a existir.

Teorema de divisibilidad de enteros con resto

Cuando hablamos de dividir números naturales con resto, descubrimos que el dividendo a, el divisor b, el cociente parcial c y el resto d están relacionados por la igualdad a=b c+d. Los enteros a , b , c y d comparten la misma relación. Esta conexión es confirmada por la siguiente teorema de divisibilidad con resto.

Teorema.

Cualquier número entero a se puede representar de forma única a través de un número entero y un número b distinto de cero en la forma a=b q+r , donde q y r son algunos números enteros, y .

Prueba.

Probemos primero la posibilidad de representar a=b·q+r .

Si los enteros ayb son tales que a es divisible por b, entonces por definición existe un entero q tal que a=b q . En este caso, la igualdad a=b q+r se cumple para r=0.

Ahora supondremos que b es un entero positivo. Elegimos un número entero q de tal forma que el producto b·q no supere el número a , y el producto b·(q+1) ya sea mayor que a . Es decir, tomamos q tal que las desigualdades b q

Queda por probar la posibilidad de representar a=b q+r para b negativa.

Dado que el módulo del número b en este caso es un número positivo, entonces hay una representación para , donde q 1 es un número entero y r es un número entero que satisface las condiciones . Luego, suponiendo q=−q 1 , obtenemos la representación requerida a=b q+r para b negativa.

Pasamos a la prueba de unicidad.

Supongamos que además de la representación a=b q+r, q y r son números enteros y , existe otra representación a=b q 1 +r 1 , donde q 1 y r 1 son algunos números enteros, y q 1 ≠ q y .

Luego de restar de la parte izquierda y derecha de la primera igualdad, respectivamente, la parte izquierda y derecha de la segunda igualdad, obtenemos 0=b (q−q 1)+r−r 1 , que es equivalente a la igualdad r− r 1 = segundo (q 1 - q) . Entonces la igualdad de la forma , y debido a las propiedades del módulo del número - y la igualdad .

De las condiciones y podemos concluir que . Dado que q y q 1 son números enteros y q≠q 1 , entonces , de donde concluimos que . A partir de las desigualdades obtenidas y se sigue que una igualdad de la forma imposible bajo nuestra suposición. Por lo tanto, no hay otra representación del número a, excepto a=b·q+r.

Relaciones entre dividendo, divisor, cociente parcial y resto

La igualdad a=b c+d permite encontrar un dividendo desconocido a si se conocen el divisor b, el cociente parcial c y el resto d. Considere un ejemplo.

Ejemplo.

¿A qué es igual el dividendo si su división por el entero −21 da como resultado un cociente incompleto de 5 y un resto de 12?

Solución.

Necesitamos calcular el dividendo a cuando conocemos el divisor b=−21, el cociente parcial c=5 y el resto d=12. Volviendo a la igualdad a=b c+d , obtenemos a=(−21) 5+12 . Observando , primero realizamos la multiplicación de enteros −21 y 5 según la regla de la multiplicación de enteros con diferente signo , luego realizamos la suma de enteros con diferente signo : (−21) 5+12=−105+12 =−93 .

Responder:

−93 .

Las relaciones entre dividendo, divisor, cociente parcial y resto también se expresan mediante igualdades de la forma b=(a−d):c , c=(a−d):b y d=a−b·c . Estas igualdades nos permiten calcular el divisor, el cociente parcial y el resto, respectivamente. A menudo necesitamos encontrar el resto de dividir un entero a por un entero b cuando se conocen el dividendo, el divisor y el cociente parcial, usando la fórmula d=a−b·c . Para evitar más preguntas, analizaremos un ejemplo de cálculo del resto.

Ejemplo.

Encuentra el resto de dividir el entero −19 por el entero 3 si se sabe que el cociente parcial es −7.

Solución.

Para calcular el resto de la división, usamos una fórmula de la forma d=a−b·c . De la condición tenemos todos los datos necesarios a=−19 , b=3 , c=−7 . Obtenemos d=a−bc=−19−3 (−7)= −19−(−21)=−19+21=2 (la diferencia −19−(−21) que calculamos con la regla de restar un negativo entero).

Responder:

División con resto de enteros positivos, ejemplos

Como ya hemos señalado más de una vez, los enteros positivos son números naturales. Por lo tanto, la división con resto de números enteros positivos se realiza de acuerdo con todas las reglas para la división con resto de números naturales. Es muy importante poder realizar fácilmente la división con un resto de números naturales, ya que es la base de la división no solo de números enteros positivos, sino también la base de todas las reglas de división con un resto de números enteros arbitrarios.

Desde nuestro punto de vista, lo más conveniente es realizar la división por una columna, este método le permite obtener tanto un cociente incompleto (o solo un cociente) como un resto. Considere un ejemplo de división con un resto de números enteros positivos.

Ejemplo.

Realiza una división con un resto de 14671 por 54 .

Solución.

Realicemos la división de estos enteros positivos por una columna:

El cociente incompleto resultó ser 271 y el resto es 37.

Responder:

14 671:54=271 (resto 37) .

La regla de la división con resto de un entero positivo por un entero negativo, ejemplos

Formulemos una regla que le permita realizar una división con un resto de un entero positivo por un entero negativo.

El cociente parcial de dividir un entero positivo a por un entero negativo b es lo opuesto al cociente parcial de dividir a por el módulo de b, y el resto de dividir a entre b es el resto de dividir entre .

De esta regla se deduce que el cociente incompleto de dividir un entero positivo por un entero negativo es un entero no positivo.

Rehagamos la regla expresada en un algoritmo para dividir con un resto de un entero positivo por un entero negativo:

Dividimos el módulo del dividendo por el módulo del divisor, obtenemos el cociente incompleto y el resto. (Si en este caso el resto resultó ser igual a cero, entonces los números originales se dividen sin resto, y de acuerdo con la regla para dividir números enteros con signos opuestos, el cociente deseado es igual al número opuesto al cociente de dividiendo los módulos.)
Anotamos el número opuesto al cociente incompleto recibido y el resto. Estos números son, respectivamente, el cociente deseado y el resto de dividir el entero positivo original por un entero negativo.

Demos un ejemplo del uso del algoritmo para dividir un entero positivo por un entero negativo.

Ejemplo.

Divida con un resto de un entero positivo 17 por un entero negativo −5.

Solución.

Usemos el algoritmo de división con el resto de un entero positivo por un entero negativo.

Divisor

El número opuesto de 3 es −3. Por lo tanto, el cociente parcial requerido para dividir 17 entre −5 es −3 y el resto es 2.

Responder:

17 :(−5)=−3 (resto 2).

Ejemplo.

Dividir 45 por -15 .

Solución.

Los módulos del dividendo y del divisor son 45 y 15, respectivamente. El número 45 es divisible por 15 sin resto, mientras que el cociente es 3. Por tanto, el entero positivo 45 es divisible por el entero negativo −15 sin resto, mientras que el cociente es igual al número opuesto a 3, es decir, −3. En efecto, según la regla de la división de enteros con diferente signo, tenemos .

Responder:

45:(−15)=−3 .

División con resto de un entero negativo por un entero positivo, ejemplos

Formulemos la regla de la división con resto de un entero negativo por un entero positivo.

Para obtener un cociente incompleto c de dividir un entero negativo a por un entero positivo b, debe tomar el número opuesto al cociente incompleto de dividir los módulos de los números originales y restarle uno, después de lo cual se calcula el resto d usando la fórmula d=a−bc .

De esta regla de división con resto se sigue que el cociente incompleto de dividir un entero negativo por un entero positivo es un entero negativo.

De la regla expresada se sigue el algoritmo de división con el resto de un entero negativo a por un entero positivo b:

Encontramos los módulos del dividendo y el divisor.
Dividimos el módulo del dividendo por el módulo del divisor, obtenemos el cociente incompleto y el resto. (Si el resto es cero, entonces los enteros originales son divisibles sin resto, y el cociente deseado es igual al número opuesto al cociente de dividir los módulos).
Anotamos el número opuesto al cociente incompleto recibido y le restamos el número 1. El número calculado es el cociente parcial deseado c de dividir el entero negativo original por un entero positivo.

Analicemos la solución del ejemplo, en el que usamos el algoritmo de división escrita con resto.

Ejemplo.

Encuentra el cociente parcial y el resto del entero negativo −17 dividido por el entero positivo 5 .

Solución.

El módulo del dividendo −17 es 17 y el módulo del divisor 5 es 5.

Divisor 17 por 5 , obtenemos un cociente incompleto de 3 y un resto de 2 .

El opuesto de 3 es −3 . Resta uno de −3: −3−1=−4 . Entonces, el cociente incompleto deseado es −4.

Queda por calcular el resto. En nuestro ejemplo a=−17 , b=5 , c=−4 , luego d=a−b c=−17−5 (−4)= −17−(−20)=−17+20=3 .

Por lo tanto, el cociente parcial del entero negativo −17 dividido por el entero positivo 5 es −4 y el resto es 3.

Responder:

(−17):5=−4 (resto 3) .

Ejemplo.

Divide el entero negativo −1 404 por el entero positivo 26 .

Solución.

El módulo del dividendo es 1404, el módulo del divisor es 26.

Divide 1404 por 26 en una columna:

Como el módulo del dividendo se dividió por el módulo del divisor sin resto, los enteros originales se dividen sin resto y el cociente buscado es igual al número opuesto a 54, es decir, −54.

Responder:

(−1 404):26=−54 .

Regla de división con resto de enteros negativos, ejemplos

Formulemos la regla de la división con el resto de los enteros negativos.

Para obtener un cociente incompleto c de dividir un entero negativo a por un entero negativo b, debe calcular el cociente incompleto de dividir los módulos de los números originales y agregarle uno, después de eso, calcule el resto d usando la fórmula d =a−bc.

De esta regla se sigue que el cociente incompleto de la división de enteros negativos es un entero positivo.

Reescribamos la regla expresada en forma de algoritmo para dividir enteros negativos:

Encontramos los módulos del dividendo y el divisor.
Dividimos el módulo del dividendo por el módulo del divisor, obtenemos el cociente incompleto y el resto. (Si el resto es cero, entonces los enteros originales son divisibles sin resto, y el cociente deseado es igual al cociente de dividir el módulo del divisible por el módulo del divisor).
Agregamos uno al cociente incompleto resultante, este número es el cociente incompleto deseado al dividir los enteros negativos originales.
Calcula el resto usando la fórmula d=a−b·c .

Considere la aplicación del algoritmo para dividir enteros negativos al resolver un ejemplo.

Ejemplo.

Encuentra el cociente parcial y el resto del entero negativo −17 dividido por el entero negativo −5.

Solución.

Usamos el algoritmo de división apropiado con un resto.

El módulo del dividendo es 17 , el módulo del divisor es 5 .

División 17 veces 5 da el cociente incompleto 3 y el resto 2.

Sumamos uno al cociente incompleto 3: 3+1=4. Por lo tanto, el cociente incompleto deseado de dividir −17 por −5 es 4.

Queda por calcular el resto. En este ejemplo a=−17 , b=−5 , c=4 , luego d=a−b c=−17−(−5) 4= −17−(−20)=−17+20=3 .

Entonces, el cociente parcial del entero negativo −17 dividido por el entero negativo −5 es 4 , y el resto es 3 .

Responder:

(−17):(−5)=4 (resto 3) .

Comprobación del resultado de dividir números enteros con resto

Después de realizar la división de enteros con resto, es útil verificar el resultado. La verificación se lleva a cabo en dos etapas. En la primera etapa, se verifica si el resto d es un número no negativo y también se verifica la condición. Si se cumplen todas las condiciones de la primera etapa de verificación, puede continuar con la segunda etapa de verificación; de lo contrario, se puede argumentar que se cometió un error en algún lugar al dividir con un resto. En la segunda etapa, se comprueba la validez de la igualdad a=b·c+d. Si esta igualdad es verdadera, entonces la división con resto se realizó correctamente, de lo contrario, se cometió un error en alguna parte.

Consideremos las soluciones de ejemplos en los que se verifica el resultado de la división de números enteros con un resto.

Ejemplo.

Al dividir el número -521 entre -12, el cociente parcial fue 44 y el resto fue 7, comprueba el resultado.

Solución. −2 para b=−3 , c=7 , d=1 . Tenemos b c+d=−3 7+1=−21+1=−20. Por lo tanto, la igualdad a=b c+d es incorrecta (en nuestro ejemplo a=−19 ).

Por lo tanto, la división con resto se realizó incorrectamente.

Muchos números no se pueden dividir por completo; al dividir, a menudo queda un resto distinto de cero. En este artículo, analizaremos las formas de dividir números naturales con un resto y consideraremos su aplicación en detalle con ejemplos.

Comencemos con la división de números naturales con resto en una columna, luego consideraremos la división usando restas sucesivas. Finalmente, terminamos con un análisis del método de selección de un cociente incompleto. Presentamos un algoritmo para la división con resto para el caso más general y mostramos cómo comprobar el resultado de la división de números naturales con resto.

Esta es una de las formas más convenientes de dividir. Se describe en detalle en un artículo separado dedicado a la división de números naturales por una columna. Aquí no daremos toda la teoría de nuevo, sino que nos concentraremos en el caso de la división con resto.

Daremos una solución de ejemplo, ya que es más fácil comprender la esencia del método en la práctica.

Ejemplo 1. ¿Cómo dividir números naturales con resto?

Divide el número natural 273844 por el número natural 97 .

Dividimos por una columna y escribimos:

Resultado: el cociente parcial es 2823 y el resto es 13.

División de números con resto mediante restas sucesivas

Para encontrar el cociente incompleto y el resto, puedes recurrir a la resta sucesiva del divisor del dividendo. Este método no siempre es apropiado, pero en algunos casos es muy conveniente de usar. Veamos el ejemplo de nuevo.

Ejemplo 2. División con resto mediante restas sucesivas.

Digamos que tenemos 7 manzanas. Necesitamos poner estas 7 manzanas en bolsas de 3 manzanas. En otras palabras, 7 dividido por 3.

Tomamos 3 piezas del número inicial de manzanas y las ponemos en un paquete. Nos quedarán 7 - 3 = 4 manzanas. Ahora, de las manzanas restantes, nuevamente quitamos 3 piezas y las ponemos en otra bolsa. Quedan 4 - 3 = 1 manzana.

1 manzana es el resto de la división, ya que en esta etapa ya no podemos formar otro paquete con tres manzanas y la división, de hecho, está completa. resultado de la división:

7 ÷ 3 = 2 (resto 1)

Esto significa que el número 3, por así decirlo, cabe dos veces en el número 7, y la unidad es un resto menor que 3.

Consideremos un ejemplo más. Esta vez, daremos solo cálculos matemáticos, sin recurrir a analogías.

Ejemplo 3. División con resto mediante restas sucesivas.

Calculemos: 145 ÷ 46 .

El número 99 es mayor que 46, así que continuamos con la resta secuencial del divisor:

Repetimos esta operación una vez más:

Como resultado, necesitábamos restar sucesivamente el divisor del dividendo 3 veces antes de obtener el resto, el resultado de la resta, que es menor que el divisor. En nuestro caso, el resto es el número 7.

145 ÷ 46 = 3 (resto 7) .

El método de restas sucesivas no es adecuado cuando el dividendo es menor que el divisor. En este caso, puede escribir inmediatamente la respuesta: el cociente incompleto es cero y el resto es igual al más divisible.

si un< b , то a ÷ b = 0 (остаток a) .

Por ejemplo:

12 ÷ 36 = 0 (resto 12) 47 ÷ 88 = 0 (resto 47)

También con respecto al método de resta sucesiva, cabe señalar que es conveniente solo en los casos en que toda la operación de división se reduce a un pequeño número de restas. Si el dividendo es muchas veces mayor que el divisor, usar este método no será práctico e implicará muchos cálculos engorrosos.

Método de selección de cociente incompleto

Al dividir números naturales con resto, puede calcular el resultado eligiendo un cociente incompleto. Mostraremos cómo se puede llevar a cabo el proceso de selección y en qué se basa.

Primero, determinamos entre qué números necesitamos buscar un cociente incompleto. De la definición misma del proceso de división, es claro que el cociente incompleto es igual a cero, o es uno de los números naturales 1, 2, 3, etc.

En segundo lugar, estableceremos una relación entre el divisor, el dividendo, el cociente parcial y el resto. Considere la ecuación d = a - b c . Aquí d es el resto de la división, a es el dividendo, b es el divisor, c es el cociente parcial.

En tercer lugar, no olvidemos que el resto siempre es menor que el divisor.

Ahora echemos un vistazo al proceso de selección. El dividendo a y el divisor b nos son conocidos desde el principio. Como cociente incompleto, tomaremos sucesivamente números de la serie 0, 1, 2, 3, etc. Aplicando la fórmula d = a - b c y calculando el valor resultante con un divisor, terminamos el proceso cuando el resto d es menor que el divisor b. El número tomado para c en este paso será un cociente incompleto.

Veamos la aplicación de este método con un ejemplo.

Ejemplo 4. División con resto por selección

Divide 267 entre 21.

un = 267 b = 21 . Elijamos un cociente incompleto.

Usemos la fórmula d = a - b · c e iteremos sobre c, dándole los valores 0, 1, 2, 3, y así sucesivamente.

Si c \u003d 0, tenemos: d \u003d a - b c \u003d 267 - 21 0 \u003d 267. El número 267 es mayor que 21, así que continuamos con la sustitución.

Con c \u003d 1 tenemos: d \u003d a - b c \u003d 267 - 21 1 \u003d 246. Porque 246 > 21, repite el proceso nuevamente.

Con c \u003d 2 tenemos: d \u003d a - b c \u003d 267 - 21 2 \u003d 267 - 42 \u003d 225; 225 > 21 .

Con c \u003d 3 tenemos: d \u003d a - b c \u003d 267 - 21 3 \u003d 267 - 63 \u003d 204; 204 > 21 .

Con c \u003d 12 tenemos: d \u003d a - b c \u003d 267 - 21 12 \u003d 267 - 252 \u003d 15; 15< 21 .

Algoritmo para dividir números naturales con resto

Cuando los métodos de cociente parcial y resta sucesiva discutidos anteriormente requieren cálculos demasiado engorrosos, se usa el siguiente método para la división con un resto. Considere un algoritmo para dividir un número natural a por un número b con un resto.

Recuerda que si un< b, неполное частное равно нулю, а остаток равен делимомому a . Мы будем рассматривать случай, когда a >B.

Formulamos tres preguntas y las respondemos:

¿Qué se sabe allí?
¿Qué necesitamos encontrar?
¿Como vamos a hacerlo?

Inicialmente se conocen el dividendo y el divisor: a y b.

Necesitas encontrar el cociente incompleto c y el resto d.

Aquí hay una fórmula que define la relación entre el dividendo, el divisor, el cociente incompleto y el resto. a = b c + d. Es esta razón la que tomaremos como base del algoritmo para dividir números naturales con resto. El dividendo a debe representarse como una suma a = b c + d, luego encontraremos los valores requeridos.

El algoritmo de división, gracias al cual representamos a como una suma a = b c + d, es muy similar al algoritmo para dividir números naturales sin resto. A continuación se muestran los pasos del algoritmo usando el ejemplo de dividir el número 899 por 47.

1. En primer lugar, nos fijamos en el dividendo y el divisor. Averiguamos y recordamos cuántos dígitos es mayor el número en la entrada de dividendos que el número en el divisor. En nuestro ejemplo específico El dividendo tiene tres dígitos y el divisor tiene dos.

Recordemos este número.

2. A la derecha en la entrada del divisor, agregue el número de ceros determinado por la diferencia entre el número de caracteres en el dividendo y el divisor. En nuestro caso, debe agregar un cero. Si el número escrito es mayor que el divisible, debe restar uno del número memorizado en el primer párrafo.

En nuestro ejemplo, sumamos cero a la derecha de 47. Desde 470< 899 , запомненное в предыдущем пункте число не нужно уменьшать на единицу. Таким образом, число 1 так и остается у нас в памяти.

3. A la derecha, al número 1, le atribuimos el número de ceros igual al número definido en el párrafo anterior. En nuestro ejemplo, asignando un cero a uno, obtenemos el número 10. Como resultado de esta acción, recibimos una unidad de trabajo de la descarga, con la que seguiremos trabajando.

4. Multiplicaremos secuencialmente el divisor por 1, 2, 3. . etc unidades del dígito de trabajo hasta obtener un número mayor o igual que el divisible.

El dígito de trabajo en nuestro ejemplo es decenas. Después de multiplicar el divisor por una unidad del bit de trabajo, obtenemos 470.

470 < 899 , поэтому умножаем на еще одну единицу рабочего разряда. Получаем: 47 · 20 = 940 ; 940 > 899 .

El número que obtuvimos en el penúltimo paso (470 = 47 10) es el primero de los términos requeridos.

5. Encuentra la diferencia entre el dividendo y el primer término encontrado. Si el número resultante es mayor que el divisor, entonces procedemos a encontrar el segundo término.

Repetimos los pasos 1 - 5, sin embargo, tomamos el número obtenido aquí como dividendo. Si nuevamente obtenemos un número mayor que el divisor, nuevamente repita los pasos 1 - 5 en un círculo, pero con un nuevo número como dividendo. Continuamos hasta que el número obtenido aquí sea menor que el divisor. Pasemos a la etapa final. De cara al futuro, digamos que el último número recibido será igual al resto.

Veamos un ejemplo. 899 - 470 = 429, 429 > 47. Repetimos los pasos 1 - 5 del algoritmo con el número 429 tomado como dividendo.

1. En la entrada del número 429 hay un signo más que en la entrada del número 47. Recordamos la diferencia: el número 1.

2. En el registro del dividendo de la derecha, sumamos un cero. Obtenemos el número 470. Como 470 > 429, resta 1 al número 1 memorizado en el párrafo anterior y obtienes 1 - 1 = 0. Recordamos 0 .

3. Como en el párrafo anterior obtuvimos el número 0 y lo recordamos, no necesitamos agregar ningún cero al de la derecha. Por lo tanto, el dígito de trabajo son las unidades.

4. Multiplica secuencialmente el divisor 47 por 1 , 2 , 3 . . etc No daremos cálculos detallados, pero preste atención al resultado final: 47 9 = 423< 429 , 47 · 10 = 470 >429 . Por lo tanto, el segundo término requerido es 47 9 = 423.

5. La diferencia entre 429 y 423 es igual al número 6. Desde el 6< 47 , это третье, и последнее искомое слагаемое. Перейдем к завершающему этапу алгоритма деления столбиком.

6. El propósito de los pasos anteriores fue representar el dividendo como la suma de varios términos. Para nuestro ejemplo, obtuvimos 899 = 470 + 423 + 6. Recuerda que 470 = 47 10 , 423 = 47 9 . Reescribamos la ecuación:

899 = 47 10 + 47 9 + 6

Aplicar la propiedad distributiva de la multiplicación.

899 = 47 10 + 47 9 + 6 = 47 (10 + 9) + 6

899 = 47 19 + 6 .

Por lo tanto, presentamos el dividendo en la forma de la fórmula dada anteriormente a \u003d b c + d.

Incógnitas requeridas: cociente incompleto c \u003d 19, resto d \u003d 6.

Por supuesto, al resolver ejemplos prácticos, no es necesario describir todas las acciones con tanto detalle. Vamos a mostrarlo:

Ejemplo 5. División de números naturales con resto

Divide los números 42252 y 68.

Usemos un algoritmo. Los primeros cinco pasos dan el primer término: el número 40800 = 68 600.

Repetimos los primeros cinco pasos del algoritmo nuevamente con el número 1452 = 42252 - 40800 y obtenemos el segundo término 1360 = 68 20

La tercera vez pasamos por los pasos del aglorritmo, pero con el nuevo número 92 = 1452 - 1360. El tercer término es igual a 68 = 68 1 . El resto es 24 = 92 - 68.

Como resultado, obtenemos:

42252 = 40800 + 1360 + 68 + 24 = 68 600 + 68 20 + 68 1 + 24 = = 68 (600 + 20 + 1) + 24 = 68 621 + 24

El cociente incompleto es 621, el resto es 24.

División de números naturales con resto. Comprobando el resultado

División de números naturales con resto, especialmente cuando números grandes, un proceso bastante laborioso y engorroso. Cualquiera puede cometer un error en los cálculos. Por eso, comprobar el resultado de la división te ayudará a saber si hiciste todo bien. La comprobación del resultado de la división de números naturales con resto se realiza en dos etapas.

En la primera etapa, verificamos si el resto es mayor que el divisor. Si no, entonces todo está bien. De lo contrario, podemos concluir que algo salió mal.

¡Importante!

¡El resto siempre es menor que el divisor!

En la segunda etapa, se comprueba la validez de la igualdad a = b · c + d. Si la igualdad después de sustituir los valores resulta ser cierta, entonces la división se realizó sin errores.

Ejemplo 6. Comprobación del resultado de dividir números naturales con resto.

Comprobemos si es cierto que 506 ÷ 28 = 17 (resto 30) .

Compara el resto y el divisor: 30 > 28 .

Entonces la división está mal.

Ejemplo 7. Comprobación del resultado de la división de números naturales con resto.

El estudiante dividió 121 entre 13 y como resultado recibió un cociente incompleto de 9 con un resto de 5. hizo el lo correcto?

Para averiguarlo, primero comparamos el resto y el divisor: 5< 13 .

Se ha superado el primer punto de control, pasemos al segundo.

Escribamos la fórmula a = b c + d. a = 121 ; b = 13; c = 9 re = 5 .

Sustituye los valores y compara los resultados.

13 9 + 5 = 117 + 5 = 122; 121 ≠ 122

Significa que se ha deslizado un error en los cálculos del estudiante en alguna parte.

Ejemplo 8. Comprobación del resultado de la división de números naturales con resto.

El estudiante realizó trabajo de laboratorio en física. Durante la ejecución, necesitaba dividir 5998 entre 111. Como resultado, obtuvo el número 54 con un resto de 4. ¿Está todo calculado correctamente?

¡Vamos a revisar! El resto 4 es menor que el divisor 111, por lo que procedemos a la segunda etapa de la comprobación.

Usamos la fórmula a \u003d b c + d, donde a \u003d 5998; b = 111; c = 54 ; re = 4 .

Después de la sustitución, tenemos:

5998 = 111 54 + 4 = 5994 + 4 = 5998 .

La igualdad es correcta, lo que significa que la división es correcta.

Si nota un error en el texto, resáltelo y presione Ctrl+Enter

Es fácil enseñar a un niño a dividir por una columna. Es necesario explicar el algoritmo de esta acción y consolidar el material cubierto.

De acuerdo a currículum escolar, la división por una columna comienza a explicar a los niños que ya están en el tercer grado. Los estudiantes que captan todo "sobre la marcha" entienden rápidamente este tema
Pero, si el niño se enferma y se pierde las lecciones de matemáticas, o no entiende el tema, entonces los padres deben explicarle el material al niño por su cuenta. Es necesario transmitirle la información lo más claramente posible.
mamás y papás durante proceso educativo los niños deben ser pacientes, mostrando tacto hacia su hijo. En ningún caso debes gritarle a un niño si algo no le sale bien, porque así puedes desanimarlo de todas las ganas de estudiar.

Importante: Para que un niño entienda la división de números, debe conocer a fondo la tabla de multiplicar. Si el niño no sabe bien la multiplicación, no entenderá la división.

Durante las clases adicionales en casa, se pueden usar hojas de trucos, pero el niño debe aprender la tabla de multiplicar antes de continuar con el tema "División".

Entonces, ¿cómo le explicas a un niño división de columnas:

Trate de explicar primero en números pequeños. Tome palos de conteo, por ejemplo, 8 piezas
Pregúntele al niño cuántos pares hay en esta fila de palos. Correcto - 4. Entonces, si divides 8 entre 2, obtienes 4, y si divides 8 entre 4, obtienes 2
Deje que el niño divida por sí mismo otro número, por ejemplo, uno más complejo: 24:4
Cuando el bebé haya dominado la división de números primos, puede proceder a la división de números de tres dígitos en números de un solo dígito.

La división siempre se les da a los niños un poco más difícil que la multiplicación. pero diligente clases extra en casa ayudarán al niño a comprender el algoritmo de esta acción y mantenerse al día con sus compañeros en la escuela.

Comience simple - división por un solo dígito:

Importante: Calcula en tu mente para que la división quede sin resto, de lo contrario el niño puede confundirse.

Por ejemplo, 256 dividido por 4:

Dibuja una línea vertical en una hoja de papel y divídela por la mitad en el lado derecho. Escribe el primer número a la izquierda y el segundo a la derecha encima de la línea.
Pregúntele al bebé cuántos cuatro caben en un dos, nada
Luego tomamos 25. Para mayor claridad, separe este número de arriba con una esquina. Nuevamente pregúntele al niño cuántos cuatro caben en veinticinco. Así es, seis. Escribimos el número "6" en la esquina inferior derecha debajo de la línea. El niño debe usar la tabla de multiplicar para la respuesta correcta.
Escriba el número 24 debajo de 25 y subraye para escribir la respuesta: 1
Pregunte de nuevo: ¿cuántos cuatros caben en una unidad? No, en absoluto. Luego derribamos el número "6" a uno
Resultó 16, ¿cuántos cuatro caben en este número? Correcto - 4. Escribimos "4" al lado de "6" en la respuesta
Debajo de 16 escribimos 16, subrayamos y resulta “0”, lo que significa que dividimos correctamente y la respuesta resultó ser “64”

División escrita por dos dígitos

Cuando el niño haya dominado la división por un solo número, puede continuar. La división escrita por un número de dos dígitos es un poco más complicada, pero si el bebé comprende cómo se realiza esta acción, no le resultará difícil resolver tales ejemplos.

Importante: nuevamente, comience a explicar con pasos simples. El niño aprenderá a seleccionar números correctamente y le será fácil dividir números complejos.

Realicen juntos esta simple acción: 184:23 - cómo explicar:

Primero dividimos 184 por 20, resulta aproximadamente 8. Pero no escribimos el número 8 en la respuesta, ya que este es un número de prueba.
Compruebe si 8 encaja o no. Multiplicamos 8 por 23, resulta 184, este es exactamente el número que tenemos en el divisor. la respuesta sera 8

Importante: para que el niño entienda, intente tomar 9 en lugar de ocho, déjelo multiplicar 9 por 23, resulta 207: esto es más de lo que tenemos en el divisor. El número 9 no nos conviene.

Entonces, gradualmente, el bebé comprenderá la división y le será fácil dividir números más complejos:

Divida 768 por 24. Determine el primer dígito del privado: dividimos 76 no por 24, sino por 20, resulta 3. Escribimos 3 en respuesta debajo de la línea a la derecha
Debajo de 76 escribimos 72 y dibujamos una línea, escribimos la diferencia: resultó 4. ¿Esta cifra es divisible por 24? No, demolimos 8, resulta 48
¿48 es divisible por 24? Así es, sí. Resulta 2, escribimos esta cifra en respuesta.
Resultó 32. Ahora puede verificar si realizamos la acción de división correctamente. Multiplique en una columna: 24x32, resulta 768, entonces todo está correcto

Si el niño ha aprendido a dividir por un número de dos dígitos, entonces debe pasar al siguiente tema. El algoritmo para dividir por un número de tres dígitos es el mismo que el algoritmo para dividir por un número de dos dígitos.

Por ejemplo:

Divida 146064 por 716. Primero tomamos 146; pregúntele al niño si este número es divisible por 716 o no. Así es, no, entonces tomamos 1460
¿Cuántas veces cabe el número 716 en el número 1460? Correcto - 2, entonces escribimos esta cifra en la respuesta
Multiplicamos 2 por 716, resulta 1432. Escribimos esta cifra debajo de 1460. Resulta que la diferencia es 28, la escribimos debajo de la línea
Demolición 6. Pregúntale al niño: ¿286 es divisible por 716? Así es, no, entonces escribimos 0 en la respuesta al lado de 2. Destruimos otro número 4
Dividimos 2864 por 716. Tomamos 3 cada uno - un poco, 5 cada uno - mucho, lo que significa que obtenemos 4. Multiplicamos 4 por 716, obtenemos 2864
Escribe 2864 debajo de 2864 para una diferencia de 0. Respuesta 204

Importante: para verificar la corrección de la división, multiplique junto con el niño en una columna: 204x716 = 146064. La división es correcta.

Es hora de que el niño explique que la división no solo puede ser total, sino también con un resto. El resto siempre es menor o igual que el divisor.

La división con resto debe explicarse con un ejemplo simple: 35:8=4 (resto 3):

¿Cuántos ochos caben en 35? Correcto - 4. Resta 3
¿Es este número divisible por 8? Así es, no. Entonces el resto es 3.

Después de eso, el niño debe aprender que puede continuar la división sumando 0 al número 3:

La respuesta es el número 4. Después de él, escribimos una coma, ya que sumar cero indica que el número será con una fracción
Resultó 30. Divida 30 por 8, resulta 3. Escribimos en respuesta, y debajo de 30 escribimos 24, subrayamos y escribimos 6
Llevamos el número 0 al número 6. Divida 60 entre 8. Saque 7 cada uno, resulta 56. Escriba debajo de 60 y anote la diferencia 4
Agregamos 0 al número 4 y dividimos por 8, resulta 5, lo escribimos en respuesta
Restamos 40 de 40, obtenemos 0. Entonces, la respuesta es: 35:8=4.375

Consejo: si el niño no entiende algo, no se enoje. Deje pasar un par de días e intente explicar el material nuevamente.

Las lecciones de matemáticas en la escuela también reforzarán el conocimiento. el tiempo pasara y el niño resolverá rápida y fácilmente cualquier ejemplo de división.

El algoritmo para dividir números es el siguiente:

Haz una estimación del número que estará en la respuesta
Encuentre el primer dividendo incompleto
Determinar el número de dígitos en un cociente
Encuentra los dígitos en cada dígito del cociente
Encuentre el resto (si lo hay)

Según este algoritmo, la división se realiza tanto por números de un solo dígito como por cualquier número de varios dígitos (dos dígitos, tres dígitos, cuatro dígitos, etc.).

Cuando estudie con un niño, a menudo pídale ejemplos para hacer una estimación. Debe calcular rápidamente la respuesta en su mente. Por ejemplo:

1428:42
2924:68
30296:56
136576:64
16514:718

Para consolidar el resultado, puede utilizar los siguientes juegos de división:

"Rompecabezas". Escribe cinco ejemplos en una hoja de papel. Sólo uno de ellos debe ser con la respuesta correcta.

Condición para el niño: Entre varios ejemplos, solo uno se resuelve correctamente. Encuéntralo en un minuto.

Video: Juego de aritmética para niños suma resta división multiplicación

Vídeo: Dibujo educativo Matemáticas Aprendiendo de memoria las tablas de multiplicar y dividir por 2

Vídeo: Introducción a la división | MATEMÁTICAS divertidas para niños

Video: Dividir un número de dos dígitos por uno solo

Cuando el niño estudia adicionalmente en casa, consolida el material cursado en la escuela. Gracias a esto, es más fácil para él aprender y no se quedará atrás de sus compañeros. Por lo tanto, ayuda a tus hijos, estudia en casa con ellos. ¡y el bebé tendrá éxito!

Video: División larga parte 1

Video: División larga parte 2

Video: División larga parte 3

Video: División larga parte 4

Video: División larga parte 5

Lea el tema de la lección: "División con resto". ¿Qué sabes ya sobre este tema?

¿Puedes dividir 8 ciruelas en partes iguales en dos platos (fig. 1)?

Arroz. 1. Ilustración por ejemplo

Puedes poner 4 ciruelas en cada plato (Fig. 2).

Arroz. 2. Ilustración por ejemplo

La acción que realizamos se puede escribir de la siguiente manera.

8: 2 = 4

¿Qué piensas, es posible dividir 8 ciruelas en partes iguales en 3 platos (Fig. 3)?

Arroz. 3. Ilustración por ejemplo

Actuemos así. Primero, ponga una ciruela en cada plato, luego la segunda ciruela. Nos quedarán 2 ciruelas, pero 3 platos. Así que no podemos dividirlo en partes iguales. Ponemos 2 ciruelas en cada plato, y nos quedan 2 ciruelas (Fig. 4).

Arroz. 4. Ilustración por ejemplo

Sigamos monitoreando.

Lee los números. Entre los números dados, encuentra aquellos que son divisibles por 3.

11, 12, 13, 14, 15, 16, 17, 18, 19

Pruébate.

Los números restantes (11, 13, 14, 16, 17, 19) no son divisibles por 3, o dicen "dividir con el resto".

Encontremos el valor de lo privado.

Averigüemos cuántas veces 3 está contenido en el número 17 (Fig. 5).

Arroz. 5. Ilustración por ejemplo

Vemos que 3 óvalos caben 5 veces y quedan 2 óvalos.

La acción tomada se puede escribir de la siguiente manera.

17: 3 = 5 (resto 2)

También se puede escribir en una columna (Fig. 6)

Arroz. 6. Ilustración por ejemplo

Revisa los dibujos. Explique los títulos de estas figuras (Fig. 7).

Arroz. 7. Ilustración por ejemplo

Considere la primera figura (Fig. 8).

Arroz. 8. Ilustración por ejemplo

Vemos que 15 óvalos se dividieron por 2. 2 se repitió 7 veces, en el resto, 1 óvalo.

Considere la segunda figura (Fig. 9).

Arroz. 9. Ilustración por ejemplo

En esta figura, 15 cuadrados se dividieron por 4. 4 se repitió 3 veces, en el resto, 3 cuadrados.

Considere la tercera figura (Fig. 10).

Arroz. 10. Ilustración por ejemplo

Podemos decir que 15 óvalos se dividieron en 3. 3 se repitió 5 veces por igual. En tales casos, se dice que el resto es 0.

Hagamos la división.

Dividimos los siete cuadrados en tres. Obtenemos dos grupos, y queda un cuadrado. Escribamos la solución (Fig. 11).

Arroz. 11. Ilustración por ejemplo

Hagamos la división.

Averiguamos cuántas veces cuatro está contenido en el número 10. Vemos que en el número 10 cuatro está contenido 2 veces y quedan 2 cuadrados. Escribamos la solución (Fig. 12).

Arroz. 12. Ilustración por ejemplo

Hagamos la división.

Averiguamos cuántas veces dos están contenidos en el número 11. Vemos que en el número 11 dos están contenidos 5 veces y queda 1 cuadrado. Escribamos la solución (Fig. 13).

Arroz. 13. Ilustración por ejemplo

Hagamos una conclusión. Dividir con resto significa averiguar cuántas veces el divisor está contenido en el dividendo y cuántas unidades quedan.

La división con resto también se puede realizar en una recta numérica.

En la recta numérica marcamos segmentos de 3 divisiones y veremos que tres divisiones resultaron ser tres veces y quedó una división (Fig. 14).

Arroz. 14. Ilustración por ejemplo

Escribamos la solución.

10: 3 = 3 (resto.1)

Hagamos la división.

En la recta numérica marcamos segmentos de 3 divisiones y veremos que tres divisiones resultaron ser tres veces y quedaron dos divisiones (Fig. 15).

Arroz. 15. Ilustración por ejemplo

Escribamos la solución.

11: 3 = 3 (resto.2)

Hagamos la división.

En la semirrecta numérica marcamos segmentos de 3 divisiones y veremos que obtuvimos exactamente 4 veces, no queda resto (Fig. 16).

Arroz. 16. Ilustración por ejemplo

Escribamos la solución.

12: 3 = 4

Hoy, en la lección, nos familiarizamos con la división con un resto, aprendimos cómo realizar la acción nombrada usando una imagen y un haz numérico, practicamos la resolución de ejemplos sobre el tema de la lección.

Bibliografía

MI. Moro, M. A. Bantova y otros Matemáticas: Libro de texto. Grado 3: en 2 partes, parte 1. - M .: "Ilustración", 2012.
MI. Moro, M. A. Bantova y otros Matemáticas: Libro de texto. Grado 3: en 2 partes, parte 2. - M .: "Ilustración", 2012.
MI. Moreau. Lecciones de Matemáticas: Pautas para el maestro Grado 3 - M.: Educación, 2012.
Documento reglamentario. Seguimiento y evaluación de los resultados del aprendizaje. - M.: "Ilustración", 2011.
"Escuela de Rusia": Programas para escuela primaria. - M.: "Ilustración", 2011.
SI. Volkov. Matemáticas: Trabajo de verificación. Grado 3 - M.: Educación, 2012.
VN Rudnitskaya. Pruebas. - M.: "Examen", 2012.