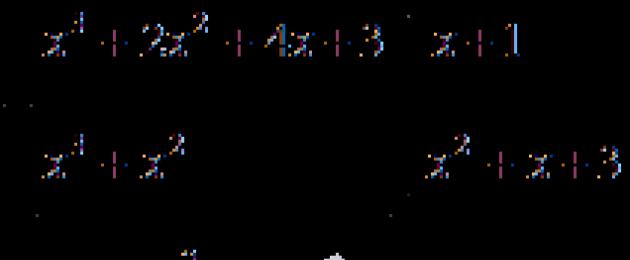5. astme võrrandi lahendus radikaalides. Kõrgema astme võrrandite lahendus

Meie saidi YouTube'i kanalile, et olla kursis kõigi uute videotundidega.

Kõigepealt tuletame meelde kraadide põhivalemeid ja nende omadusi.

Arvu korrutis a juhtub iseendaga n korda, saame selle avaldise kirjutada kujul a a … a=a n

1. a 0 = 1 (a ≠ 0)

3. a n a m = a n + m

4. (a n) m = a nm

5. a n b n = (ab) n

7. a n / a m \u003d a n - m

Võimsus või eksponentsiaalvõrrandid - need on võrrandid, milles muutujad on astmetes (või astendajates) ja alus on arv.

Näited eksponentsiaalvõrranditest:

Selles näites on number 6 alus, see on alati allosas ja muutuja x aste või mõõt.

Toome rohkem näiteid eksponentsiaalvõrrandite kohta.
2 x *5=10
16x-4x-6 = 0

Vaatame nüüd, kuidas eksponentsiaalvõrrandid lahendatakse?

Võtame lihtsa võrrandi:

2 x = 2 3

Sellist näidet saab lahendada isegi mõttes. On näha, et x=3. Ju siis nii, et vasak ja parem osa olid võrdsed, tuleb x asemel panna arv 3.
Nüüd vaatame, kuidas see otsus tuleks teha:

2 x = 2 3
x = 3

Selle võrrandi lahendamiseks eemaldasime samadel alustel(ehk deuces) ja kirjutas üles, mis järele jäi, need on kraadid. Saime vastuse, mida otsisime.

Nüüd teeme oma lahenduse kokkuvõtte.

Algoritm eksponentsiaalvõrrandi lahendamiseks:
1. Vaja kontrollida sama kas võrrandi alused paremal ja vasakul. Kui põhjused pole samad, otsime selle näite lahendamise võimalusi.
2. Kui alused on samad, võrdsustama kraadi ja lahendage saadud uus võrrand.

Nüüd lahendame mõned näited:

Alustame lihtsast.

Vasakul ja paremal küljel olevad alused on võrdsed arvuga 2, mis tähendab, et saame aluse kõrvale jätta ja nende kraadid võrdsustada.

x+2=4 Selgunud on kõige lihtsam võrrand.
x = 4–2
x=2
Vastus: x=2

Järgmises näites näete, et alused on erinevad, need on 3 ja 9.

3 3x - 9 x + 8 = 0

Alustuseks viime üheksa paremale küljele, saame:

Nüüd peate tegema samad alused. Teame, et 9=3 2 . Kasutame astme valemit (a n) m = a nm .

3 3x \u003d (3 2) x + 8

Saame 9 x + 8 \u003d (3 2) x + 8 \u003d 3 2 x + 16

3 3x \u003d 3 2x + 16 nüüd on selge, et vasakul ja paremal küljel olevad alused on samad ja võrdsed kolmega, mis tähendab, et saame need ära visata ja kraadid võrdsustada.

3x=2x+16 sai kõige lihtsama võrrandi
3x-2x=16
x=16
Vastus: x=16.

Vaatame järgmist näidet:

2 2x + 4 - 10 4 x \u003d 2 4

Kõigepealt vaatame aluseid, alused on erinevad kaks ja neli. Ja me peame olema samad. Teisendame neliku vastavalt valemile (a n) m = a nm .

4 x = (2 2) x = 2 2x

Ja me kasutame ka ühte valemit a n a m = a n + m:

2 2x+4 = 2 2x 2 4

Lisa võrrandile:

2 2x 2 4 - 10 2 2x = 24

Samadel põhjustel tõime näite. Aga meid segavad teised numbrid 10 ja 24. Mida nendega peale hakata? Kui vaatate tähelepanelikult, näete, et vasakul pool kordame 2 2x, siin on vastus - saame sulgudest välja panna 2 2x:

2 2x (2 4 - 10) = 24

Arvutame sulgudes oleva avaldise:

2 4 — 10 = 16 — 10 = 6

Jagame kogu võrrandi 6-ga:

Kujutage ette 4 = 2 2:

2 2x \u003d 2 2 alust on samad, visake need ära ja võrdsustage kraadid.
2x \u003d 2 osutus lihtsaimaks võrrandiks. Jagame selle 2-ga, saame
x = 1
Vastus: x = 1.

Lahendame võrrandi:

9 x - 12 x 3 x +27 = 0

Muutame:
9 x = (3 2) x = 3 2x

Saame võrrandi:
3 2x - 12 3 x +27 = 0

Alused on meil samad, võrdne kolmega.Selles näites on näha, et esimesel kolmikul on kraad kaks korda (2x) kui teisel (just x). Sel juhul saate ise otsustada asendusmeetod. Väikseima astmega number asendatakse järgmisega:

Siis 3 2x \u003d (3 x) 2 \u003d t 2

Asendame kõik kraadid x-idega võrrandis t-ga:

t 2 - 12t + 27 \u003d 0
Saame ruutvõrrandi. Lahendame diskriminandi kaudu, saame:
D = 144-108 = 36
t1 = 9
t2 = 3

Tagasi muutuja juurde x.

Võtame t 1:
t 1 \u003d 9 \u003d 3 x

See on,

3 x = 9
3 x = 3 2
x 1 = 2

Leiti üks juur. Otsime teist, alates t 2:
t 2 \u003d 3 = 3 x
3 x = 3 1
x 2 = 1
Vastus: x 1 \u003d 2; x 2 = 1.

Saidil saate jaotises AITA OTSUSTADA esitada huvipakkuvaid küsimusi, me vastame teile kindlasti.

Liituge grupiga

Üldiselt ei saa võrrandit, mille aste on suurem kui 4, radikaalides lahendada. Kuid mõnikord võime siiski leida vasakpoolse polünoomi juured kõrgeima astme võrrandist, kui esitame selle polünoomide korrutisena astmes, mis ei ületa 4. Selliste võrrandite lahendus põhineb polünoomi jaotamisel teguriteks, seega soovitame teil see teema enne selle artikliga tutvumist läbi vaadata.

Kõige sagedamini tuleb tegeleda täisarvu koefitsientidega kõrgema astme võrranditega. Sellistel juhtudel võime proovida leida ratsionaalsed juured ja seejärel polünoomi faktoriseerimine, et teisendada see madalama astme võrrandiks, mida on lihtne lahendada. Selle materjali raames vaatleme just selliseid näiteid.

Kõrgema astme võrrandid täisarvu koefitsientidega

Kõik võrrandid kujul a n x n + a n - 1 x n - 1 + . . . + a 1 x + a 0 = 0, saame taandada sama astme võrrandiks, korrutades mõlemad pooled a n n - 1-ga ja muutes muutujat nagu y = a n x:

a n x n + a n - 1 x n - 1 + . . . + a 1 x + a 0 = 0 ann xn + an - 1 ann - 1 xn - 1 + … + a 1 (an) n - 1 x + a 0 (an) n - 1 = 0 y = anx ⇒ yn + bn - 1 yn - 1 + … + b 1 y + b 0 = 0

Saadud koefitsiendid on samuti täisarvud. Seega peame lahendama täisarvu koefitsientidega n-nda astme taandatud võrrandi, mille vorm on x n + a n x n - 1 + ... + a 1 x + a 0 = 0.

Arvutame võrrandi täisarvude juured. Kui võrrandil on täisarvu juured, tuleb need otsida vaba liikme a 0 jagajate hulgast. Paneme need kirja ja asendame tulemust kontrollides ükshaaval algsesse võrdusse. Kui oleme saanud identiteedi ja leidnud ühe võrrandi juurtest, võime selle kirjutada kujul x - x 1 · P n - 1 (x) = 0 . Siin on x 1 võrrandi juur ja P n - 1 (x) on x n + a n x n - 1 + ... + a 1 x + a 0 jagatis x - x 1 -ga.

Asendage ülejäänud jagajad väärtusega P n - 1 (x) = 0, alustades x 1-st, kuna juuri saab korrata. Pärast identiteedi saamist loetakse juur x 2 leituks ja võrrandi saab kirjutada kujul (x - x 1) (x - x 2) P n - 2 (x) \u003d 0. Siin P n - 2 (x) ) on jagatis P n - 1 (x) jagamisel x - x 2 .

Jätkame jagajate sorteerimist. Leia kõik täisarvu juured ja märgi nende arv m-ga. Pärast seda saab esialgset võrrandit esitada kujul x - x 1 x - x 2 · … · x - x m · P n - m (x) = 0 . Siin on P n - m (x) n - m -nda astme polünoom. Arvutamiseks on mugav kasutada Horneri skeemi.

Kui meie algsel võrrandil on täisarvu koefitsiendid, ei saa me lõpuks murdosa juurtega.

Selle tulemusena saime võrrandi P n - m (x) = 0, mille juured võib leida mis tahes sobival viisil. Need võivad olla irratsionaalsed või keerulised.

Näitame edasi konkreetne näide kuidas sellist lahendusskeemi rakendatakse.

Näide 1

Seisukord: leiame võrrandi x 4 + x 3 + 2 x 2 - x - 3 = 0 lahendi.

Lahendus

Alustame täisarvu juurte leidmisega.

Meil on lõikepunkt, mis võrdub miinus kolmega. Sellel on jagajad 1, -1, 3 ja -3. Asendame need algsesse võrrandisse ja vaatame, milline neist annab tulemuseks identiteedid.

Kui x on võrdne ühega, saame 1 4 + 1 3 + 2 1 2 - 1 - 3 \u003d 0, mis tähendab, et üks on selle võrrandi juur.

Nüüd jagame polünoomi x 4 + x 3 + 2 x 2 - x - 3 (x - 1) veergu:

Seega x 4 + x 3 + 2 x 2 - x - 3 = x - 1 x 3 + 2 x 2 + 4 x + 3.

1 3 + 2 1 2 + 4 1 + 3 = 10 ≠ 0 (- 1) 3 + 2 (- 1) 2 + 4 - 1 + 3 = 0

Saime identiteedi, mis tähendab, et leidsime võrrandi teise juure, mis on võrdne - 1-ga.

Jagame polünoomi x 3 + 2 x 2 + 4 x + 3 (x + 1) veerus:

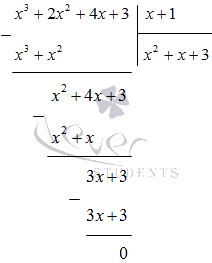
Me saame sellest aru

x 4 + x 3 + 2 x 2 - x - 3 = (x - 1) (x 3 + 2 x 2 + 4 x + 3) = = (x - 1) (x + 1) (x 2 + x + 3)

Asendame järgmise jagaja võrrandis x 2 + x + 3 = 0, alustades -1:

1 2 + (- 1) + 3 = 3 ≠ 0 3 2 + 3 + 3 = 15 ≠ 0 (- 3) 2 + (- 3) + 3 = 9 ≠ 0

Saadud võrrandid on valed, mis tähendab, et võrrandil pole enam täisarvu juuri.

Ülejäänud juured on avaldise x 2 + x + 3 juured.

D \u003d 1 2 - 4 1 3 \u003d - 11< 0

Sellest järeldub, et sellel ruudukujulisel trinoomil pole reaalseid juuri, vaid sellel on komplekssed konjugeeritud juured: x = - 1 2 ± i 11 2 .

Selgitame, et veeruks jagamise asemel võib kasutada Horneri skeemi. Seda tehakse nii: pärast võrrandi esimese juure määramist täidame tabeli.

Koefitsientide tabelis näeme kohe polünoomide jagamise jagatise koefitsiente, mis tähendab x 4 + x 3 + 2 x 2 - x - 3 = x - 1 x 3 + 2 x 2 + 4 x + 3.

Pärast järgmise juure leidmist, mis on võrdne -1, saame järgmise:

Vastus: x \u003d - 1, x \u003d 1, x \u003d - 1 2 ± i 11 2.

Näide 2

Seisukord: lahendage võrrand x 4 - x 3 - 5 x 2 + 12 = 0.

Lahendus

Vabaliikmel on jagajad 1 , - 1 , 2 , - 2 , 3 , - 3 , 4 , - 4 , 6 , - 6 , 12 , - 12 .

Kontrollime neid järjekorras:

1 4 - 1 3 - 5 1 2 + 12 = 7 ≠ 0 (- 1) 4 - (- 1) 3 - 5 (- 1) 2 + 12 = 9 ≠ 0 2 4 2 3 - 5 2 2 + 12 = 0

Seega on x = 2 võrrandi juur. Jagage x 4 - x 3 - 5 x 2 + 12 x - 2-ga, kasutades Horneri skeemi:

Selle tulemusena saame x - 2 (x 3 + x 2 - 3 x - 6) = 0 .

2 3 + 2 2 - 3 2 - 6 = 0

Nii et 2 on jälle juur. Jagage x 3 + x 2 - 3 x - 6 = 0 x - 2-ga:

Selle tulemusena saame (x - 2) 2 (x 2 + 3 x + 3) = 0 .

Ülejäänud jagajate kontrollimine ei ole mõttekas, kuna võrdsust x 2 + 3 x + 3 = 0 on diskriminandi abil kiirem ja mugavam lahendada.

Lahendame ruutvõrrandi:

x 2 + 3 x + 3 = 0 D = 3 2 - 4 1 3 = - 3< 0

Saame kompleksse konjugeeritud juurepaari: x = - 3 2 ± i 3 2 .

Vastus: x = - 3 2 ± i 3 2 .

Näide 3

Seisukord: leidke võrrandi x 4 + 1 2 x 3 - 5 2 x - 3 = 0 tegelikud juured.

Lahendus

x 4 + 1 2 x 3 - 5 2 x - 3 = 0 2 x 4 + x 3 - 5 x - 6 = 0

Korrutame võrrandi mõlema osa 2 3:

2 x 4 + x 3 - 5 x - 6 = 0 2 4 x 4 + 2 3 x 3 - 20 2 x - 48 = 0

Asendame muutujad y = 2 x:

2 4 x 4 + 2 3 x 3 - 20 2 x - 48 = 0 a 4 + y 3 - 20 a - 48 = 0

Selle tulemusena saime 4. astme standardvõrrandi, mida saab lahendada standardskeemi järgi. Kontrollime jagajaid, jagame ja lõpuks saame, et sellel on 2 reaaljuurt y \u003d - 2, y \u003d 3 ja kaks kompleksset juurt. Me ei esita siin kogu lahendust. Asenduse tõttu on selle võrrandi tegelikud juured x = y 2 = - 2 2 = - 1 ja x = y 2 = 3 2 .

Vastus: x 1 \u003d - 1, x 2 = 3 2

Kui märkate tekstis viga, tõstke see esile ja vajutage Ctrl+Enter

16. sajandil komistasid matemaatikud kompleksarvude otsa peaaegu juhuslikult (vt 11. peatükk). TO XVIII sajand kompleksarve peeti reaalarvude domeeni laienduseks, kuid nendega töötamine tõi siiski kaasa paarsusvea, kuna Leonard E vältis oma suures arvuteooria alases töös Aritmeetilised uuringud (1801) nn kujuteldavate arvude kasutamist. numbrid". Mulle tundub, et selle töö kõige olulisem osa on algebra fundamentaalse teoreemi esimene tõestus. Gauss mõistis, kui oluline see teoreem oli, luues järgnevate aastate jooksul mitmeid täiendavaid tõestusi. Aastal 1849 muutis ta esimest versiooni, kasutades seekord kompleksarve. Kasutades tänapäevaseid termineid, võime öelda, et mis tahes lõpliku polünoomvõrrandi puhul, millel on reaal- või komplekskordajad, on kõik selle juured reaal- või kompleksarvud. Nii saame eitava vastuse igivanale küsimusele, kas polünoomvõrrandite lahendamine nõuab kõrge järjekord luua keerukatest suuremat järku arve.

Tolle aja algebra üks keerulisemaid ülesandeid oli küsimus, kas algebraliste meetoditega ehk lõpliku arvu algebralisi samme kasutades on võimalik lahendada viiendat järku polünoomi – kvintikut. Nüüd õpetatakse koolis ruutvõrrandite lahendamise valemit ning alates 16. sajandist on sarnased meetodid tuntud ka kolmanda ja neljanda astme võrrandite lahendamisel (11. ptk). Kuid kvintikate jaoks pole meetodit leitud. Võib tunduda, et algebra fundamentaalteoreem sisaldab positiivse vastuse lubadust, kuid tegelikult garanteerib see lihtsalt lahenduste olemasolu, ei ütle midagi täpseid lahendusi andvate valemite olemasolu kohta (ligikaudsed numbrilised ja graafilised meetodid olid juba olemas Sel ajal). Ja siis oli kaks traagilise saatusega matemaatikageeniust.

Niels Henrik Abel (1802–1829) sündis suures vaeses peres, mis elas väikeses külas Norras, riigis, mida laastanud pikad sõjad Inglismaa ja Rootsiga. Poisi vastu sõbralik õpetaja andis talle eratunde, kuid pärast isa surma kaheksateistkümneaastaselt, hoolimata noor vanus ja hapra tervise tõttu oli Abel sunnitud oma perekonda ülal pidama. Aastal 1824 avaldas ta teadusliku artikli, milles ta väitis, et kvintiik ei ole algebraliselt lahendatav, nagu ka iga kõrgemat järku polünoom. Abel uskus, et see artikkel on tema pääsmeks teadusmaailma, ja saatis selle Gaussile Göttingeni ülikooli. Kahjuks ei jõudnud Gauss kunagi noaga lehti lõigata (seda pidi tol ajal iga lugeja tegema) ega lugenud artiklit läbi. 1826. aastal eraldas Norra valitsus lõpuks raha, et Abel saaks Euroopas ringi reisida. Kartes, et isiklik kokkupuude Gaussiga talle suurt rõõmu ei valmista, otsustas matemaatik Göttingeni mitte külastada ja sõitis hoopis Berliini. Seal sõbrunes ta matemaatiku, arhitekti ja inseneri August Leopold Crellega (1780–1855), kes nõustas Preisi haridusministeeriumi matemaatika küsimustes. Krell asus asutama ajakirja Journal of Clean ja rakendusmatemaatika". Nii sai Abel võimaluse oma tööd levitada ja avaldas palju, eriti ajakirja esimestes numbrites, mida hakati kohe pidama väga mainekaks ja autoriteetseks teadusväljaandeks. Norralane avaldas seal laiendatud versiooni oma tõendist, et kvintika on algebraliste meetoditega lahendamatu. Ja siis läks ta Pariisi. See reis häiris Abelit väga, sest ta praktiliselt ei saanud prantsuse matemaatikute toetust, mida ta nii väga vajas. Ta sai lähedaseks Augustin Louis Cauchyga (1789-1857), kes oli sel ajal peamine valgustaja. matemaatiline analüüs aga see oli väga keeruline. Nagu Abel ise ütles: "Cauchy on hull ja sellega ei saa midagi ette võtta, kuigi praegu on ta matemaatikas ainuke, kes millekski võimeline." Kui püüda õigustada Gaussist ja Cauchyst lähtuvat lugupidamatust ja põlgust, võib öelda, et Quintic saavutas teatud kuulsuse ja äratas nii lugupeetud matemaatikute kui originaalide tähelepanu. Abel naasis Norrasse, kus ta põdes üha enam tuberkuloosi. Ta jätkas oma tööde saatmist Crelle'ile, kuid suri 1829. aastal, teadmata, mil määral oli tema maine teadusmaailm. Kaks päeva pärast surma sai Abel pakkumise asuda Berliinis teaduslikule ametikohale.

Abel näitas, et ühtegi neljandat järku kõrgemat polünoomi ei saa lahendada radikaalide, näiteks ruutjuurte, kuupjuurte või kõrgema järgu abil. Siiski sõnastas Galois selgesõnalised tingimused, mille alusel neid polünoomid erijuhtudel lahendada sai, ja nende lahendamise meetodi. Évariste Galois (1811–1832) elas lühikest ja sündmusterohket elu. Ta oli uskumatult andekas matemaatik. Galois oli halastamatu nende suhtes, keda ta pidas endast vähem andekateks, ja samas ei talunud ta sotsiaalset ebaõiglust. Ta ei näidanud üles matemaatikaks sobivust enne, kui luges Legendre'i geomeetria elemente (ilmus 1794, see raamat oli järgmise saja aasta peamine õpik). Siis neelas ta sõna otseses mõttes alla ülejäänud Legendre ja hiljem Abeli ​​teosed. Tema entusiasm, enesekindlus ja sallimatus viisid tema suhetes õpetajate ja eksamineerijatega tõeliselt kohutavate tagajärgedeni. Galois osales Prantsuse matemaatika hälli - polütehnilise kooli sisseastumiskonkursil, kuid ettevalmimatuse tõttu kukkus ta eksamil läbi. Mõni aeg pärast kohtumist uue õpetajaga, kes tundis ära tema ande, suutis ta oma tuju kontrolli all hoida. 1829. aasta märtsis avaldas Galois oma esimese töö jätkumurrude kohta, mida ta pidas oma kõige olulisemaks tööks. Ta saatis oma avastuste kohta teate Teaduste Akadeemiale ja Cauchy lubas need esitada, kuid unustas. Pealegi kaotas ta käsikirja lihtsalt ära.

Galoisi teine ​​läbikukkumine polütehnilisse kooli sisenes matemaatilisse folkloori. Ta oli nii harjunud, et tema peas keerlevad pidevalt keerulised matemaatilised ideed, et ta vihastas eksamineerijate väiklast nipet-näpet. Kuna eksamineerijatel oli raskusi tema selgitustest aru saada, viskas ta ühele neist kustutuslapi näkku. Varsti pärast seda suri tema isa, kes sooritas kiriklike intriigide tagajärjel enesetapu. Peaaegu puhkes tema matustel mäss. 1830. aasta veebruaris kirjutas Galois järgmised kolm artiklit, saates need Teaduste Akadeemiale matemaatika Grand Prix'le. Joseph Fourier, tollane akadeemia sekretär, suri neid lugemata ja pärast tema surma neid artikleid tema paberite hulgast ei leitud. Selline pettumuste voog kukutaks kedagi. Galois mässas võimulolijate vastu, kuna tundis, et nad ei tunnustanud tema teeneid ja tappis ta isa. Ta sukeldus ülepeakaela poliitikasse, saades tulihingeliseks vabariiklaseks – mitte just kõige targem otsus Prantsusmaal 1830. aastal. Viimasel meeleheitlikul katsel saatis ta teadusliku artikli kuulsale prantsuse füüsikule ja matemaatikule Siméon Denis Poissonile (1781–1840), kes nõudis vastuseks täiendavaid tõendeid.

See oli viimane piisk karikasse. 1831. aastal arreteeriti Galois kaks korda – esmalt väidetavalt kuningas Louis Philippe’i mõrvamise eest ja seejärel tema kaitsmiseks – võimud kartsid vabariiklaste mässu! Seekord mõisteti talle kuus kuud vangistust väljamõeldud süüdistusega laiali saadetud suurtükiväepataljoni vormiriietuse ebaseaduslikus kandmises, millega ta liitus. Tingimisi vabastatuna asus ta tegelema äriga, mis tekitas temas sama vastikust kui kõik muu elus. Kirjades oma pühendunud sõbrale Chevalierile on tunda tema pettumust. 29. mail 1832 võttis ta vastu väljakutse duellile, mille põhjuseid ei mõisteta täielikult. «Sattusin autu koketi ohvriks. Minu elu hääbub armetu tüli tõttu,” kirjutab ta kirjas kõigile vabariiklastele. Kõige tähelepanuväärne töö Galois visandati saatuslikule duellile eelneval õhtul. Kaebused on veeris laiali: "Mul pole enam aega, mul pole enam aega." Vahesammude üksikasjad, mis põhiidee mõistmiseks polnud hädavajalikud, pidi ta teistele jätma. Tal oli vaja paberile visata oma avastuste alused – praeguse Galois’ teoreemi päritolu. Ta lõpetas oma testamendi, paludes Chevalier'l "paluda Jacobilt ja Gaussil avaldada oma arvamus avalikult, mitte nende teoreemide õigsuse, vaid tähtsuse kohta". Varahommikul läks Galois oma rivaaliga kohtuma. Tulistada tuli 25 sammu kauguselt. Galois sai haavata ja suri järgmisel hommikul haiglas. Ta oli vaid kahekümneaastane.

Galois tugines Lagrange'i ja Cauchy töödele, kuid töötas välja üldisema meetodi. See oli ülimalt oluline saavutus kvintikate lahendamise alal. Teadlane pööras vähem tähelepanu algvõrranditele või graafilisele tõlgendusele ning mõtles rohkem juurte endi olemusele. Lihtsustamiseks võttis Galois arvesse ainult niinimetatud taandamatuid kvintikuid, st neid, mida ei saanud faktoriseerida madalama järgu polünoomide kujul (nagu me ütlesime, on iga kuni neljanda järgu polünoomvõrrandi jaoks olemas valemid nende juurte leidmiseks ). Üldjuhul on ratsionaalsete kordajatega taandamatu polünoom polünoom, mida ei saa lagundada lihtsamateks ratsionaalsete koefitsientidega polünoomideks. Näiteks (x 5 - 1) saab faktoriseerida (x-1) (x 4 + x 3 + x 2 + x + 1), kusjuures (x 5–2) taandamatu. Galois’ eesmärk oli määrata kindlaks tingimused, mille korral on võimalik leida radikaalide mõistes üldise taandamatu polünoomvõrrandi kõik lahendid.

Lahenduse võti seisneb selles, et ühegi taandamatu algebralise võrrandi juured ei ole sõltumatud, neid saab väljendada üksteisega. Need seosed vormistati kõigi võimalike permutatsioonide rühmaks, nn juursümmeetria rühmaks - kvintika jaoks sisaldab see rühm 5! = 5 x 4 x 3 x 2 x 1 = 120 elementi. Galois' teooria matemaatilised algoritmid on väga keerulised ja tõenäoliselt osalt seetõttu saadi neist esialgu aru suurte raskustega. Kuid pärast seda, kui abstraktsioonitase võimaldas liikuda võrrandite algebralistelt lahendustelt nendega seotud rühmade algebralisele struktuurile, suutis Galois ennustada võrrandi lahendatavust selliste rühmade omaduste põhjal. Veelgi enam, tema teooria pakkus ka meetodi, mille abil need juured ise üles leiti. Kvintika osas avaldas matemaatik Joseph Liouville (1809–1882), kes 1846. a. enamus Galois oma ajakirjas Journal of Pure and Applied Mathematics märkis, et noor teadlane tõestas "ilusat teoreemi" ja selleks, et "algastme taandamatu võrrand oleks radikaalide osas lahendatav, on vajalik ja piisav, et kõik selle juured on nende kahe ratsionaalsed funktsioonid." Kuna see on kvintiku jaoks võimatu, ei saa seda radikaalidega lahendada.

Kolme aastaga on matemaatikamaailm kaotanud kaks oma säravaimat uut tähte. Järgnesid vastastikused süüdistamised ja hinge otsimine ning Abel ja Galois saavutasid väljateenitud tunnustuse, kuid alles postuumselt. 1829. aastal sai Carl Jacobi Legendre vahendusel teada Abeli ​​"kadunud" käsikirjast ja 1830. aastal lahvatas diplomaatiline skandaal, kui Norra konsul Pariisis nõudis oma kaasmaalase artikli leidmist. Lõpuks leidis Cauchy artikli üles, kuid akadeemia toimetusse läks see taas kaduma! Samal aastal pälvis Abel matemaatika Grand Prix (koos Jacobiga) – kuid ta oli juba surnud. 1841. aastal avaldati tema elulugu. 1846. aastal toimetas Liouville avaldamiseks mõned Galois' käsikirjad ja väljendas oma sissejuhatuses kahetsust, et akadeemia oli Galois' teose selle keerukuse tõttu algselt tagasi lükanud – "tõepoolest, esituse selgus on vajalik, kui autor juhib lugeja läbimöödatud rajalt kõrvale. kaardistamata metsikud alad." Ta jätkab: “Galois’d pole enam! Ärgem langegem asjatu kriitika alla. Heitkem kõrvale vead ja vaadakem voorusi! Puuviljad lühike elu Galois mahtus vaid kuuekümnele leheküljele. École Normale ja Ecole Polytechnique'i kandidaatidele mõeldud matemaatikaajakirja toimetaja kommenteeris Galois' juhtumit järgmiselt: „Madalama mõtlemistasemega eksamineerija rookis välja kõrge intelligentsusega kandidaadi. Barbarus hic ego summa, quia non intelligor illis."

Esiteks ei ole selle teose teine ​​lehekülg koormatud nimede, perekonnanimede, positsiooni kirjeldustega ühiskonnas, tiitlite ja eleegiatega mõne ihne printsi auks, kelle rahakott nende viirukiga avatakse – ähvardusel sulgeda. kui kiitused lõppevad. Siin ei näe te lugupidavat kiitust, mis on kirjutatud tekstist kolm korda suuremate tähtedega, mis on suunatud neile, kellel on kõrge positsioon teaduses, mõnele targale patroonile - midagi kohustuslikku (ma ütleksin, et paratamatu) kellegi jaoks vanuses. kahekümnest, kes tahab midagi kirjutada. Ma ei ütle siin kellelegi, et olen nende nõu ja toetuse võlgu kõigi heade asjade eest oma töös. Ma ei ütle seda, sest see oleks vale. Kui ma peaksin mainima üht ühiskonna või teaduse suurkuju (praegu on erinevus nende kahe inimklassi vahel peaaegu märkamatu), siis ma vannun, et see poleks tänutäheks. Olen neile tänu võlgu, et avaldasin esimese neist kahest artiklist nii hilja ja et ma kirjutasin seda kõike vanglas - kohas, mida ei saa pidada teaduslikuks mõtisklemiseks sobivaks, ja ma olen sageli hämmastunud oma vaoshoitusest ja võimest hoia mu suu lahti seoses lollide ja tigedate Zoilidega. Mulle tundub, et võin kasutada sõna "Zoils", kartmata, et mind süüdistatakse sündsuses, sest nii viitan ma oma vastastele. Ma ei hakka siin kirjutama, kuidas ja miks mind vanglasse saadeti, kuid pean ütlema, et mu käsikirjad läksid enamasti lihtsalt akadeemia härrasmeeste kaustadesse, kuigi tõtt-öelda ei kujuta ma sellist ebakreetsust ette. inimeste poolt, kelle südametunnistusel Aabeli surm. Minu arvates tahaks igaüks, et teda võrreldaks selle särava matemaatikuga. Piisab, kui öelda, et minu artikkel võrrandite teooriast saadeti Teaduste Akadeemiale 1830. aasta veebruaris, väljavõtted sellest saadeti veebruaris 1829, kuid ometi ei trükitud sellest midagi ja isegi käsikiri osutus võimatu tagasi saada.

Galois, avaldamata eessõna, 1832

Klass: 9

Põhieesmärgid:

1. Kinnitada th astme täisarvulise ratsionaalvõrrandi mõiste.
2. Sõnastage peamised meetodid kõrgema astme võrrandite lahendamiseks (n > 3).
3. Õpetada põhilisi kõrgema astme võrrandite lahendamise meetodeid.
4. Õpetada võrrandi vormi järgi määrama kõige rohkem tõhus meetod tema otsused.

Vormid, meetodid ja pedagoogilised tehnikad mida õpetaja tunnis kasutab:

• Loeng-seminari koolitussüsteem (loengud - uue materjali selgitamine, seminarid - probleemide lahendamine).
• Info- ja kommunikatsioonitehnoloogiad (frontaalküsitlus, suuline töö klassiga).
• Diferentseeritud koolitus, rühma- ja individuaalsed vormid.
• Uurimismeetodi kasutamine arengule suunatud koolituses matemaatiline aparaat ja iga õpilase vaimsed võimed.
• Trükimaterjal - tunni individuaalne kokkuvõte (põhimõisted, valemid, väited, loengumaterjal on tihendatud diagrammide või tabelite kujul).

Tunniplaan:

1. Aja organiseerimine.
   Etapi eesmärk: kaasata õpilasi õppetegevused määratleda tunni sisu.
2. Õpilaste teadmiste täiendamine.
   Etapi eesmärk: värskendada õpilaste teadmisi varem õpitud seotud teemadel
3. Uue teema õppimine (loeng). Etapi eesmärk: sõnastada peamised meetodid kõrgema astme võrrandite lahendamiseks (n > 3)
4. Kokkuvõtteid tehes.
   Etapi eesmärk: tõsta veel kord esile tunnis õpitud materjali põhipunktid.
5. Kodutöö.
   Etapi eesmärk: sõnastada kodutööõpilastele.

Tunni kokkuvõte

1. Organisatsioonimoment.

Tunni teema sõnastus: „Kõrgemate astmete võrrandid. Nende lahendamise meetodid”.

2. Õpilaste teadmiste aktualiseerimine.

Teoreetiline küsitlus - vestlus. Mõne varem uuritud teabe kordamine teooriast. Õpilased formuleerivad põhimõisteid ja esitavad vajalikke teoreeme. On toodud näiteid, mis demonstreerivad varem omandatud teadmiste taset.

• Ühe muutujaga võrrandi mõiste.
• Võrrandi juure mõiste, võrrandi lahend.
• kontseptsioon lineaarvõrrandühe muutujaga ruutvõrrandi mõiste ühe muutujaga.
• Võrrandite samaväärsuse mõiste, võrrand-tagajärjed (kõrvajuurte mõiste), üleminek mitte tagajärje järgi (juurte kadumise juhtum).
• Terviku kontseptsioon ratsionaalne väljendusühe muutujaga.
• Kogu ratsionaalvõrrandi mõiste n aste. Terve ratsionaalvõrrandi standardvorm. vähendatud täisarv ratsionaalne võrrand.
• Üleminek madalama astme võrrandite kogumile, arvutades algse võrrandi.
• Polünoomi mõiste n kraad alates x. Bezouti teoreem. Bezouti teoreemi tagajärjed. Juureteoreemid ( Z-juured ja K-juured) terve ratsionaalvõrrandi täisarvu koefitsientidega (vastavalt taandatud ja taandamata).
• Horneri skeem.

3. Uue teema õppimine.

Vaatleme kogu ratsionaalset võrrandit n standardvormi aste ühe tundmatu muutujaga x:Pn(x)= 0, kus P n (x) = a n x n + a n-1 x n-1 + a 1 x + a 0- polünoom n kraad alates x, a n ≠ 0. Kui a n = 1, siis nimetatakse sellist võrrandit taandatud täisratsionaalvõrrandiks n aste. Vaatleme selliseid võrrandeid erinevate väärtuste jaoks n ja loetlege nende lahendamise peamised meetodid.

n= 1 on lineaarvõrrand.

n= 2 on ruutvõrrand. Diskrimineeriv valem. Juurte arvutamise valem. Vieta teoreem. Täisruudu valik.

n= 3 on kuupvõrrand.

rühmitamise meetod.

Näide: x 3 – 4x 2 – x+ 4 = 0 (x - 4) (x 2– 1) = 0 x 1 = 4 , x2 = 1,x 3 = -1.

Vormi vastastikune kuupvõrrand kirves 3 + bx 2 + bx + a= 0. Lahendame samade koefitsientidega termineid kombineerides.

Näide: x 3 – 5x 2 – 5x + 1 = 0 (x + 1)(x 2 – 6x + 1) = 0 x 1 = -1, x 2 = 3 + 2, x 3 = 3 – 2.

Z-juurte valik teoreemi alusel. Horneri skeem. Selle meetodi rakendamisel on vaja rõhutada, et loendus on sel juhul lõplik ja juured valime teatud algoritmi järgi vastavalt teoreemile Z-ratsionaalvõrrandi taandatud täisarvude juured.

Näide: x 3 – 9x 2 + 23x– 15 = 0. Võrrand on taandatud. Kirjutame välja vaba liikme jagajad ( + 1; + 3; + 5; + 15). Rakendame Horneri skeemi:

	x 3	x 2	x 1	x 0	väljund
	1	-9	23	-15
1	1	1 x 1 - 9 = -8	1 x (-8) + 23 = 15	1 x 15–15 = 0	1 - juur
	x 2	x 1	x 0

Saame ( x – 1)(x 2 – 8x + 15) = 0 x 1 = 1, x 2 = 3, x 3 = 5.

Täisarvu koefitsientidega võrrand. Q-juurte valik teoreemi alusel. Horneri skeem. Selle meetodi rakendamisel on vaja rõhutada, et loendus on sel juhul lõplik ja juured valime teatud algoritmi järgi vastavalt teoreemile K-täisarvuliste kordajatega taandamata terve ratsionaalvõrrandi juured.

Näide: 9 x 3 + 27x 2 – x– 3 = 0. Võrrandit ei taandata. Kirjutame välja vaba liikme jagajad ( + 1; + 3). Kirjutame välja koefitsiendi jagajad tundmatu suurimal astmel. ( + 1; + 3; + 9) Seetõttu otsime väärtuste hulgast juuri ( + 1; + ; + ; + 3). Rakendame Horneri skeemi:

	x 3	x 2	x 1	x 0	väljund
	9	27	-1	-3
1	9	1 x 9 + 27 = 36	1 x 36 – 1 = 35	1 x 35 - 3 = 32 ≠ 0	1 ei ole juur
-1	9	-1 x 9 + 27 = 18	-1 x 18 - 1 = -19	-1 x (-19) - 3 = 16 ≠ 0	-1 ei ole juur
	9	x9 + 27 = 30	x 30 - 1 = 9	x 9 - 3 = 0	juur
	x 2	x 1	x 0

Saame ( x – )(9x 2 + 30x + 9) = 0 x 1 = , x 2 = - , x 3 = -3.

Arvutamise hõlbustamiseks Q valimisel -juured võib olla mugav muuta muutujat, minna ülaltoodud võrrandisse ja kohandada Z -juured.

• Kui lõikepunkt on 1

.

• Kui on võimalik kasutada vormi asendust y=kx

.

Vormel Cardano. Kuupvõrrandite lahendamiseks on universaalne meetod - see on Cardano valem. Seda valemit seostatakse itaalia matemaatikute Gerolamo Cardano (1501–1576), Nicolo Tartaglia (1500–1557), Scipio del Ferro (1465–1526) nimedega. See valem jääb meie kursuse ulatusest välja.

n= 4 on neljanda astme võrrand.

rühmitamise meetod.

Näide: x 4 + 2x 3 + 5x 2 + 4x – 12 = 0 (x 4 + 2x 3) + (5x 2 + 10x) – (6x + 12) = 0 (x + 2)(x 3 + 5x- 6) = 0 (x + 2)(x– 1)(x 2 + x + 6) = 0 x 1 = -2, x 2 = 1.

Muutuv asendusmeetod.

• Vormi bikvadraatvõrrand kirves 4 + bx 2+s = 0 .

Näide: x 4 + 5x 2 - 36 = 0. Asendamine y = x 2. Siit y 1 = 4, y 2 = -9. Sellepärast x 1,2 = + 2 .

• Vormi neljanda astme pöördvõrrand kirves 4 + bx 3+c x 2 + bx + a = 0.

Lahendame samade koefitsientidega termineid kombineerides vormi asendamisega

• kirves 4 + bx 3 + cx 2 – bx + a = 0.

• Vormi neljanda astme üldistatud tagurpidi võrrand kirves 4 + bx 3 + cx 2 + kbx + k2 a = 0.

• Üldine asendus. Mõned standardsed asendused.

Näide 3 . Üldvaate vahetus(tuleneb konkreetse võrrandi vormist).

n = 3.

Täisarvu koefitsientidega võrrand. Q-juurte valik n = 3.

Üldvalem. Neljanda astme võrrandite lahendamiseks on universaalne meetod. See valem on seotud Ludovico Ferrari (1522-1565) nimega. See valem jääb meie kursuse ulatusest välja.

n > 5 - viienda ja kõrgema astme võrrandid.

Täisarvu koefitsientidega võrrand. Z-juurte valik teoreemi alusel. Horneri skeem. Algoritm on sarnane ülalkirjeldatud algoritmiga n = 3.

Täisarvu koefitsientidega võrrand. Q-juurte valik teoreemi põhjal. Horneri skeem. Algoritm on sarnane ülalkirjeldatud algoritmiga n = 3.

Sümmeetrilised võrrandid. Igal paaritu astme pöördvõrrandil on juur x= -1 ja pärast selle lagundamist teguriteks saame, et ühel teguril on vorm ( x+ 1) ja teine ​​tegur on paarisastmega pöördvõrrand (selle aste on ühe võrra väiksem kui algse võrrandi aste). Mis tahes paarisastmeline pöördvõrrand koos vormi juurega x = φ sisaldab ka vormi juurt . Neid väiteid kasutades lahendame ülesande uuritava võrrandi astet alandades.

Muutuv asendusmeetod. Homogeensuse kasutamine.

Puudub üldvalem tervete viienda astme võrrandite lahendamiseks (seda näitasid itaalia matemaatik Paolo Ruffini (1765–1822) ja norra matemaatik Nils Henrik Abel (1802–1829)) ja kõrgemaid jõude (seda näitasid prantslased matemaatik Evariste Galois (1811–1832) )).

• Tuletage uuesti meelde, et praktikas on seda võimalik kasutada kombinatsioonidülaltoodud meetodid. Mugav on minna üle madalama astme võrrandite kogumile algvõrrandi faktoriseerimine.
• Väljaspool meie tänase arutelu ulatust kasutatakse neid praktikas laialdaselt graafilised meetodid võrrandite lahendamine ja ligikaudsed lahendusmeetodid kõrgema astme võrrandid.
• On olukordi, kus võrrandil pole R-juuri.
Seejärel taandub lahendus näitamisele, et võrrandil pole juuri. Selle tõestamiseks analüüsime vaadeldavate funktsioonide käitumist monotoonsuse intervallidel. Näide: võrrand x 8 – x 3 + 1 = 0 ei oma juuri.
• Funktsioonide monotoonsuse omaduse kasutamine
. On olukordi, kus funktsioonide erinevate omaduste kasutamine võimaldab ülesannet lihtsustada.
Näide 1: võrrand x 5 + 3x– 4 = 0 on ühe juurega x= 1. Analüüsitavate funktsioonide monotoonsuse omaduse järgi pole muid juuri.
Näide 2: võrrand x 4 + (x– 1) 4 = 97 on juurtega x 1 = -2 ja x 2 = 3. Olles analüüsinud vastavate funktsioonide käitumist monotoonsuse intervallidel, järeldame, et muid juuri pole.

4. Kokkuvõtete tegemine.

Kokkuvõte: Nüüd oleme omandanud põhimeetodid erinevate kõrgema astme võrrandite lahendamiseks (n jaoks > 3). Meie ülesanne on õppida ülaltoodud algoritme tõhusalt kasutama. Sõltuvalt võrrandi tüübist peame õppima, kuidas määrata, milline lahendusmeetod on antud juhul kõige tõhusam, ning samuti valitud meetodit õigesti rakendama.

5. Kodutöö.

: punkt 7, lk 164–174, nr 33–36, 39–44, 46,47.

: №№ 9.1–9.4, 9.6–9.8, 9.12, 9.14–9.16, 9.24–9.27.

Selle teema aruannete või kokkuvõtete võimalikud teemad:

• Vormel Cardano
• Graafiline meetod võrrandite lahendamiseks. Lahendusnäited.
• Võrrandite ligikaudse lahendamise meetodid.

Materjali omastamise ja õpilaste huvi teema vastu analüüs:

Kogemus näitab, et õpilaste huvi on eelkõige valikuvõimalus Z-juured ja K-võrrandite juured, kasutades Horneri skeemi kasutades üsna lihtsat algoritmi. Õpilasi huvitavad ka erinevad muutujate asendamise standardtüübid, mis võivad probleemi tüüpi oluliselt lihtsustada. Graafilised lahendusmeetodid pakuvad tavaliselt erilist huvi. Sel juhul saate ülesanded täiendavalt sõeluda võrrandite lahendamise graafiliseks meetodiks; arutage graafiku üldvaadet 3, 4, 5 kraadi polünoomi jaoks; analüüsida, kuidas on 3, 4, 5 kraadi võrrandite juurte arv seotud vastava graafiku tüübiga. Allpool on nimekiri raamatutest, kust leiate selle teema kohta lisateavet.

Bibliograafia:

1. Vilenkin N.Ya. jne “Algebra. Õpik 9. klassi õpilastele matemaatika süvaõppega ”- M., Haridus, 2007 - 367 lk.
2. Vilenkin N.Ya., Shibasov L.P., Shibasova Z.F.“Matemaatikaõpiku lehekülgede taga. Aritmeetika. Algebra. 10-11 klass” – M., Valgustus, 2008 – 192 lk.
3. Vygodsky M.Ya."Matemaatika käsiraamat" - M., AST, 2010 - 1055 lk.
4. Galitsky M.L.“Algebra ülesannete kogumine. Õpetus 8.-9. klassile matemaatika süvaõppega ”- M., Haridus, 2008 - 301 lk.
5. Zvavich L.I. jt “Algebra ja analüüsi algus. 8-11 rakku Matemaatika süvaõppega koolide ja klasside käsiraamat ”- M., Drofa, 1999 - 352 lk.
6. Zvavich L.I., Averyanov D.I., Pigarev B.P., Trushanina T.N.“Matemaatika ülesanded 9. klassi kirjalikuks eksamiks valmistumiseks” - M., Haridus, 2007 - 112 lk.
7. Ivanov A.A., Ivanov A.P."Teemaatilised testid matemaatika teadmiste süstematiseerimiseks" 1. osa - M., Fizmatkniga, 2006 - 176 lk.
8. Ivanov A.A., Ivanov A.P."Teemaatilised testid matemaatika teadmiste süstematiseerimiseks" 2. osa - M., Fizmatkniga, 2006 - 176 lk.
9. Ivanov A.P.“Testid ja proovipaberid matemaatika. Õpetus". - M., Fizmatkniga, 2008 - 304 lk.
10. Leibson K.L.“Matemaatika praktiliste ülesannete kogu. Osa 2–9 klass” – M., MTsNMO, 2009 – 184 lk.
11. Makarychev Yu.N., Mindyuk N.G."Algebra. Täiendavad peatükid jaoks kooliõpik 9. klass Õpik matemaatika süvaõppega koolide ja klasside õpilastele. - M., Haridus, 2006 - 224 lk.
12. Mordkovich A.G."Algebra. Põhjalik õpe. 8. klass. Õpik” – M., Mnemosyne, 2006 – 296 lk.
13. Savin A.P. “entsüklopeediline sõnaraamat noor matemaatik” – M., Pedagoogika, 1985 – 352 lk.
14. Survillo G.S., Simonov A.S. “Didaktilised materjalid algebras 9. klassile matemaatika süvaõppega” – M., Valgustus, 2006 – 95 lk.
15. Chulkov P.V.“Võrrandid ja ebavõrdsused matemaatika koolikursuses. Loengud 1–4” – M., 1. september 2006 – 88 lk.
16. Chulkov P.V.“Võrrandid ja ebavõrdsused matemaatika koolikursuses. Loengud 5–8” – M., 1. september 2009 – 84 lk.

Kaaluge võrrandite lahendamine, mille muutuja on astme võrra kõrgem kui teine.

Võrrandi aste P(x) = 0 on polünoomi P(x) aste, s.o. selle liikmete astmetest suurim nullist erineva koefitsiendiga.

Näiteks võrrandil (x 3 - 1) 2 + x 5 \u003d x 6 - 2 on viies aste, sest pärast sulgude avamise ja sarnaste toomise toiminguid saame viienda astme samaväärse võrrandi x 5 - 2x 3 + 3 \u003d 0.

Tuletage meelde reegleid, mida on vaja teisest kõrgema astme võrrandite lahendamiseks.

Väited polünoomi juurte ja selle jagajate kohta:

1. Polünoom n aste on juurte arv, mis ei ületa arvu n, ja kordsuse m juured esinevad täpselt m korda.

2. Paaritu astmega polünoomil on vähemalt üks reaaljuur.

3. Kui α on Р(х) juur, siis Р n (х) = (х – α) · Q n – 1 (x), kus Q n – 1 (x) on astme polünoom (n – 1) .

4.

5. Täisarvukoefitsientidega redutseeritud polünoomil ei saa olla murdarvulisi ratsionaalseid juuri.

6. Kolmanda astme polünoomi jaoks

P 3 (x) \u003d ax 3 + bx 2 + cx + d üks kahest asjast on võimalik: kas see laguneb kolme binoomarvu korrutiseks

P 3 (x) \u003d a (x - α) (x - β) (x - γ) või laguneb binoom- ja ruuttrinoomi korrutiseks P 3 (x) \u003d a (x - α) ( x 2 + βx + γ).

7. Iga neljanda astme polünoom laieneb kahe ruuttrinoomi korrutiseks.

8. Polünoom f(x) jagub ilma jäägita polünoomiga g(x), kui on olemas selline polünoom q(x), et f(x) = g(x) q(x). Polünoomide jagamiseks rakendatakse "nurgaga jagamise" reeglit.

9. Selleks, et polünoom P(x) oleks jagatav binoomiga (x – c), on vajalik ja piisav, et arv c oleks P(x) juur (Bezouti teoreemi järeldus).

10. Vieta teoreem: Kui x 1, x 2, ..., x n on polünoomi tegelikud juured

P (x) = a 0 x n + a 1 x n - 1 + ... + a n, siis kehtivad järgmised võrdsused:

x 1 + x 2 + ... + x n \u003d -a 1 / a 0,

x 1 x 2 + x 1 x 3 + ... + x n - 1 x n \u003d a 2 / a 0,

x 1 x 2 x 3 + ... + x n - 2 x n - 1 x n \u003d -a 3 / a 0,

x 1 x 2 x 3 x n \u003d (-1) n a n / a 0.

Näidete lahendus

Näide 1

Leidke jääk pärast P (x) \u003d x 3 + 2/3 x 2 - 1/9 jagamist (x - 1/3).

Lahendus.

Bezouti teoreemi järelduse kohaselt: "Polünoomi binoomiga jagamise jääk (x - c) võrdub polünoomi väärtusega c-s." Leiame P(1/3) = 0. Seetõttu on jääk 0 ja arv 1/3 on polünoomi juur.

Vastus: R = 0.

Näide 2

Jagage "nurk" 2x 3 + 3x 2 - 2x + 3 (x + 2). Leia jääk ja mittetäielik jagatis.

Lahendus:

2x 3 + 3x 2 – 2x + 3| x + 2

2x 3 + 4x 2 2x 2 - x

X 2-2 x

Vastus: R = 3; jagatis: 2x 2 - x.

Põhilised meetodid kõrgema astme võrrandite lahendamiseks

1. Uue muutuja sisseviimine

Uue muutuja sisseviimise meetod on näitest juba tuttav bikvadraatvõrrandid. See seisneb selles, et võrrandi f (x) \u003d 0 lahendamiseks sisestatakse uus muutuja (asendus) t \u003d xn või t \u003d g (x) ja f (x) väljendatakse t kaudu, saades a uus võrrand r (t). Seejärel lahendades võrrandi r(t), leidke juured:

(t 1, t 2, …, t n). Pärast seda saadakse n võrrandite hulk q(x) = t 1, q(x) = t 2, ... , q(x) = t n, millest leitakse algvõrrandi juured.

Näide 1

(x 2 + x + 1) 2 - 3x 2 - 3x - 1 = 0.

Lahendus:

(x 2 + x + 1) 2 - 3 (x 2 + x) - 1 = 0.

(x 2 + x + 1) 2 - 3 (x 2 + x + 1) + 3 - 1 = 0.

Asendamine (x 2 + x + 1) = t.

t 2 - 3t + 2 = 0.

t 1 \u003d 2, t 2 \u003d 1. Vastupidine asendamine:

x 2 + x + 1 = 2 või x 2 + x + 1 = 1;

x 2 + x - 1 = 0 või x 2 + x = 0;

Vastus: Esimesest võrrandist: x 1, 2 = (-1 ± √5) / 2, teisest: 0 ja -1.

2. Faktoriseerimine rühmitamise ja lühendatud korrutusvalemite meetodil

Selle meetodi alus ei ole samuti uus ja seisneb terminite rühmitamises nii, et iga rühm sisaldab ühtset tegurit. Selleks tuleb vahel kasutada mõningaid kunstlikke nippe.

Näide 1

x 4 - 3x 2 + 4x - 3 = 0.

Lahendus.

Kujutage ette - 3x 2 = -2x 2 - x 2 ja rühmitage:

(x 4 - 2x 2) - (x 2 - 4x + 3) = 0.

(x 4 - 2x 2 +1 - 1) - (x 2 - 4x + 3 + 1 - 1) = 0.

(x 2 - 1) 2 - 1 - (x - 2) 2 + 1 = 0.

(x 2 - 1) 2 - (x - 2) 2 \u003d 0.

(x 2 - 1 - x + 2) (x 2 - 1 + x - 2) = 0.

(x 2 - x + 1) (x 2 + x - 3) = 0.

x 2 - x + 1 \u003d 0 või x 2 + x - 3 = 0.

Vastus: Esimeses võrrandis pole juuri, alates teisest: x 1, 2 \u003d (-1 ± √13) / 2.

3. Faktoriseerimine määramata koefitsientide meetodil

Meetodi olemus seisneb selles, et algne polünoom lagundatakse tundmatute koefitsientidega teguriteks. Kasutades omadust, et polünoomid on võrdsed, kui nende koefitsiendid on samadel astmetel võrdsed, leitakse tundmatud laienduskoefitsiendid.

Näide 1

x 3 + 4x 2 + 5x + 2 = 0.

Lahendus.

3. astme polünoomi saab lagundada lineaar- ja ruuttegurite korrutiseks.

x 3 + 4x 2 + 5x + 2 \u003d (x - a) (x 2 + bx + c),

x 3 + 4x 2 + 5x + 2 = x 3 + bx 2 + cx - ax 2 - abx - ac,

x 3 + 4x 2 + 5x + 2 \u003d x 3 + (b - a) x 2 + (cx - ab) x - ac.

Süsteemi lahendamine:

(b – a = 4,
(c – ab = 5,
(-ac=2,

(a = -1,
(b=3,
(c = 2, st.

x 3 + 4x 2 + 5x + 2 \u003d (x + 1) (x 2 + 3x + 2).

Võrrandi (x + 1) (x 2 + 3x + 2) = 0 juured on kergesti leitavad.

Vastus: -1; -2.

4. Suurima ja vaba koefitsiendi järgi juure valimise meetod

Meetod põhineb teoreemide rakendamisel:

1) Täisarvu koefitsientidega polünoomi mis tahes täisarv juur on vaba liikme jagaja.

2) Selleks, et taandamatu murd p / q (p on täisarv, q on loomulik) oleks täisarvuliste kordajatega võrrandi juur, on vajalik, et arv p oleks vaba liikme a 0 täisarvu jagaja ja q on kõrgeima koefitsiendi loomulik jagaja.

Näide 1

6x 3 + 7x 2 - 9x + 2 = 0.

Lahendus:

6: q = 1, 2, 3, 6.

Seega p/q = ±1, ±2, ±1/2, ±1/3, ±2/3, ±1/6.

Olles leidnud ühe juure, näiteks - 2, leiame teised juured, kasutades nurgaga jagamist, määramata koefitsientide meetodit või Horneri skeemi.

Vastus: -2; 1/2; 1/3.

Kas teil on küsimusi? Kas te ei tea, kuidas võrrandeid lahendada?
Juhendaja abi saamiseks - registreeru.
Esimene tund on tasuta!

saidil, materjali täieliku või osalise kopeerimise korral on nõutav link allikale.